¹ This information together with the assessment of the date and the photograph comes from the excavator Professor K. T. Erim, to whom I am most grateful, Thanks are especially due to Miss J. M. Reynolds for making a squeeze and for drawing my attention to the dial.

² Hyperbola: the curve formed when a plane cuts a cone at an angle greater than the slope of the cone. In the case of a horizontal sundial the point of the cone is the tip of the gnomon and the cone itself is generated by the sun's apparent movement during the day around this point. The circular base of the cone is thus in a plane parallel with the plane in which the sun seems to be moving. The plane of the horizon cuts through this at an angle equal to the complement of the latitude of the place of observation.

³ Gibbs, S. L., Greek and Roman Sundials (New Haven/London 1976)Google Scholar (hereafter Gibbs) 78, 323–38, cat. nos. 4401G–4015 (reviewed by the present writer, CR xxviii [1978] 336–9)Google Scholar.

⁴ Cf. Gibbs 79.

⁵ Ibid.Cf. also Cetius Faventinus De Diversis Fabr. Arch. 29 (ed. V. Rose, p. 310, l. 9)—paululum inclinis ponitur. See below.

⁶ Cf. Gibbs 89.

⁷ Vitruv. De Arch. ix 8. 1: Patrocles pelecinum dicitur invenisse—see Gibbs 61; Cetius Faventinus (n. 5) ch. 29 on which see Pattenden, P., ‘Sundials in Cetius Favenrtinus’, CQ xxix (1979) 203–12CrossRefGoogle Scholar.

⁸ Gibbs 41 f., 323.

⁹ These measurements were taken from a squeeze soon after it was made, and have been checked on site by Mossman Roueché. There may still be errors, since I have not seen the actual stone.

¹⁰ Vitruv. De Arch, ix 7.2.4 (‘one fifteenth of a circle’): see Heath, T. L., Aristarchus of Samos (Oxford 1913) 131Google Scholar n. 4 for ancient opinions on the question. The true value was 23° 41′ 7″ in the time of Ptolemy (second century A.D.) RE s.v. Ekliptik, v (1905) 2208–13,Google Scholar esp. 2212 (A. Rehm). Today it is 23° 26′ 51″. On the subject see Neugebauer, O., A History of Ancient Mathematical Astronomy (Berlin 1899;Google Scholar New York 1975) ii 733–4, esp. 734 n. 11. The Inclination of the Ecliptic or great circle of the heavens in which the sun appears to move (and hence in which eclipses always occur when the moon crosses this plane) is actually the angle at which the earth's axis of rotation is inclined to the plane of the orbit in which the whole planet moves around the sun. Looked at geocentrically this makes the sun appear to move from day to day along a plane at an angle with the plane of rotation of the earth, so that from day to day it appears a little higher or lower in the sky according to the part of the year. The difference in the figure for this inclination between antiquity and today is caused by the earth's nutation, or wobbling very slowly on its axis, The sun's declination (δ) is the angular measure of the position of the sun along this apparent path with the plane of the earth's rotation, the celestial equator. The figure for the declination thus passes from a negative maximum number of degrees south of the equator at the winter solstice to a positive maximum of the same magnitude north of it at the summer solstice. The points on the earth's surface at which the sun is then overhead at noon are called the Tropics.

¹¹ The three immediate factors which determine the position of the tip of the shadow of a gnomon at any time are as follows: (i) the azimuth of the sun, that is its angular distance round the horizon from where the observer is standing. This is usually reckoned to the east or west of due south on sundials, but in astronomy and navigation a full clockwise circle of 360 degrees beginning at north is used; (ii) the altitude of the sun, or angle between the centre of the sun and the true horizon as seen by the observer. Astronomers and navigators often use the complement of this angle, measured from the zenith, the point directly overhead, downwards to the sun (zenith distance); (iii) the effective height of the gnomon (here AB).

The altitude and azimuth of the sun may be deduced from its declination and the latitude required from, for instance, the formulae

where a is the sun's altitude, A its azimuth, δ its declination, ϕ the required latitude, and H the hour angle (above, p. 103). To find the hour angle on any day, when the temporary or seasonal hour system is to be used, first find the hour angle of sunrise/sunset using the formula

In all these formulae, when δ is to the south of the equator (from the autumn equinox to the winter solstice and back to the spring equinox) its sine and tangent will be negative, with resulting negative effects on other parts of the formulae. Thus the hour angle (h) of sunrise/sunset has a positive cosine in the winter, and so falls between 0° and 90°, but a negative one in summer, putting it between 90° and 180°. When the hour angle of sunrise/sunset has been found, this should be divided into six (the six hours from noon to the point in question). Each sixth part, or seasonal hour for the day in question, thus has an hour angle for use in the formulae above. Since hour angles are reckoned from the meridian (noon, hour 6) the sixth part itself will correspond with seasonal hours 5 and 7, two-sixths with 4 and 6, three sixths with 3 and 9, etc. The azimuth quantity gives the direction of the shadow from the foot of the gnomon (here B); the vertical height of the gnomon (AB) multiplied by the cotangent of the altitude of the sun gives its distance from the foot of the gnomon. For the reader who is not a professiona astronomer but is equipped with another aid not available to his ancient counterpart, the electronic calculator, a lucid account of how to calculate the position of the sun (though using the current value for the Inclination of the Ecliptic and the modern equatorial hour system) will be found in Duffet-Smith, P., Practical Astronomy with your Calculator (Cambridge 1979) 16–21,Google Scholar and esp. 24. A more sophisticated explanation will be found in the Explanatory Supplement to the Astronomical Ephemeris, etc. (London 1961,Google Scholar repr. 1974) 24–6. On the change in the Inclination of the Ecliptic since antiquity (above, n. 10) see ibid. 28.

¹² The hour points on the three seasonal curves can be fixed from co-ordinates taken from the squeeze and checked on the stone by Mossman Roueché. The equinoctial line on the dial (FDO in FIG. I) may be taken as the x axis and the meridian or 6 line (BDE) as the γ axis. The hour points on the stone may then be expressed as distances from perpendicular to BDE (x co-ordinates) and perpendicular to FDO (γ co-ordinates) as follows

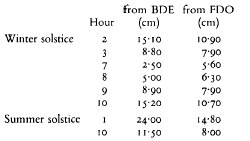
The equatorial co-ordinates at the equinoxes are given above in TABLE I. The broken lines in the grid from the dial in FIG. 3 are reproduced from measurements from the squeeze.

¹³ Still taking ε = 24° (δ = −24°).

¹⁴ In equatorial hours, etc., these times are: lat. 31° 49·7 mins (winter), 1 h 10·3 mins (summer); lat. 38° 46·4 mins (winter), I h 13·6 mins (summer). Gibbs (17) believes that the marking of the date was less important in the Roman period than the record of the hours.

¹⁵ Pliny, NH vii 60 (214)Google Scholar ff., cf. Censorinus De Die Natali 23.

¹⁶ See Gibbs 12–39, 122–322.

¹⁷ Cf. Gibbs 71, 90–1.

¹⁸ Vitruvius ix 7; Ptolemy, περὶ ἀναλήμματος (ed. Heiberg 1907).

¹⁹ Cf. Gibbs 79–80 and cat. nos. 4004G, 4005G.

²⁰ Gibbs, 66, 73, 78.

²¹ There are exceptions, e.g. Gibbs, cat. no. 3008G, p. 227 and pl. 28, p. 228; and a medieval hemicycle still stands for use as a public dial on a shop roof on the Ponte Vecchio in Florence. See e.g. Cousins, F., Sundials (London 1969) 35Google Scholar.

²² Gibbs, 87. On the wind-vane of the ancients, see A. Rehm, ‘Antike Windrosen’, Sitz. kön. Bay. Akad. Wiss. philos.-phil. u. hist. Kl. (1916) esp. 51, 67.

²³ See Stuart, J. and Revett, N., The Antiquities of Athens (London 1762)Google Scholar i ch. 3, pls I, III, = Travlos, J., Pictorial Dictionary of Ancient Athens (London 1971) 283;Google Scholar Gibbs 342–5.

²⁴ De Arch, ix 7 7.

²⁵ Ptolemaei, Claudii, Opera, ed. Heiberg, J. L. (Leipzig 1907) iiGoogle Scholar. The palimpsest fragments of the Greek are from manuscript Ambrosianus Gr. L 99 (saec. VII); the thirteenth-century Latin translation by William of Moerbeke (from the autograph archetype, Vat. Ottob. Lat. 1850). The Greek text may have disappeared at the time of the Fourth Crusade.

²⁶ Ptolemaei, Claudii, Liber de Analemmate a Federico Commandino Urbinate inslauratus et commentariis illustratus (Rome 1562)Google Scholar.

²⁷ De Analemmate 11 (p. 216 Heiberg); see also Gibbs 116.

²⁸ Gibbs, Appendix, 105–17.

²⁹ De Diversis Fabr. Arch. 29.

³⁰ Apocolocyntosis 2.

I should like to express my gratitude to Adrian Gratwick for his very searching comments on this article.