Detailed measurements of the positions of stakes along the center-line of the lower Nisqually Glacier were made over a period of two years. Variations in the basal sliding speed were calculated from the measured changes in surface speed, surface slope, and thickness, using the glacier flow model of Nye (1952) and allowing for the effect of the valley walls, longitudinal stress gradients, and uncertainties in the flow law of ice. The flow is predominantly by basal sliding and has a pronounced seasonal variation of approximately ±25%. Internal deformation contributes progressively less to the total motion with distance up-glacier. Neither the phase nor the magnitude of the seasonal velocity fluctuations can be accounted for by seasonal variations in the state of stress within the ice or at the bed, and the variations do not correlate directly with the melt-water discharge from the terminus. A seasonal wave in the ice flow travels down the glacier at a speed too high for propagation by internal deformation or the pressure melting/enhanced creep mechanism of basal sliding.

The rate of sliding appears to be determined primarily by the amount of water in temporary storage in the glacier. The peak in sliding speed occurs, on the average, at the same time as the maximum liquid water storage of the South Cascade Glacier. The data support the idea that glaciers store water in the fall, winter and spring and then release it in the summer. This temporary storage may be greatest near the equilibrium line. The amount of stored water may increase over a period of years and be released catastrophically as a jökulhlaup. Any dependence of sliding on the basal shear stress is probably masked by the effect of variations in the hydrostatic pressure of water having access to the bed.

A statistical analysis has been made of the annual balances collected during 16 consecutive years at 32 sites on the ablation area of the Glacier de Saint-Sorlin (French Alps). Only 38% of the 32 × 16 balances are known; moreover in 8 cases only the total balance for 2 consecutive years is known, and in one case the balance for 4 consecutive years. A comprehensive study of the errors leads us to assume the following linear model for the annual balance xjt at site j for year t:

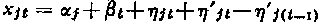
where αj and βt are parameters depending upon the site and the year respectively, ηjt and η’jt are random errors with a Gaussian distribution and standard errors σ and σ’ respectively. Assuming some known value for σ’2/σ2 = ρ, the parameters αj and βt, their variance–covariance matrix, and the variance covariance matrix of the residuals are estimated in the most general case. The estimators being stable against variations in ρ, the value ρ = o may be assumed; this value docs not conflict with the behaviour of the estimates of the residuals. A test of the linear model derived from Tukey’s non-additivity test is positive. Although a much more general, non-linear model

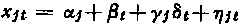gives a better representation of 13 × 6 balances forming a complete table of data, the linear model with σ ≈ 0.20 m is good enough to be used in theoretical studies or in routine work.

Some flutes which occur on the surface of a series of glacio-fluvial sediments at the margin of Blomstrandbreen, north-west Spitsbergen, are described. A section in one has revealed a complex internal structure, in which originally horizontal beds have been folded into an anticline whose axis is normal to the ice margin, and whose structure is related to the morphology of the flute.

Comparison of the observed deformation with the theoretical distribution of stresses around the base of a subglacial tunnel shows that this deformation could have resulted from How under such a stress system. It is considered that these observations support the hypothesis that flutes are formed when unfrozen, water-soaked materials deform subglacially due to the pressure differences which exist in the vicinity of an ice tunnel formed in the lee of some rigid obstruction to ice flow.

As part of the feasibility study for the development of an open-pit mine at the edge of the Greenland ice sheet, a study is made of the ice flow toward the proposed pit. The flow is analyzed by considering the two-dimensional flow along seven cross-sections. The most favorable profile is determined for each cross-section and its flow calculated. The excavation necessary to expose the ore is 106 × 106 m3 of ice. 66 × 106 m3 of ice will have to be removed in order to establish favorable profiles and an additional 7.9 × 106 m3 of ice will have to be removed each year in order to prevent the glacier from thickening and advancing into the mine. Many other glaciological problems must be considered, and field work continues in order to provide more information about the area.

The results of airborne radio-echo (R/E) depth sounding over Wilson Piedmont Glacier, Mackay, Ferrar and Taylor outlet glaciers, and over the ice sheet bordering the mountains, provide ice thicknesses and subglacial topography accurate to 20 m and to 1 km areally. The R/E records show that flours of the Debenham, Wright and Victoria Valleys occur beneath the Wilson Piedmont at elevations of –260 m, and up to 260 and 670 m, respectively. The 670 m “threshold” may have blocked easterly marine and glacial invasions experienced by lower valleys. Profiles along the outlet glaciers display large depressions, some below sea-level. These are associated with erosion by tributaries and with glacial erosion through thick dolerite sills. Elevated ridges thought to be sills submerged beneath the heads of these glaciers also limit nourishment from the adjacent part of the ice sheet. The subglacial west flank of the mountains is formed by a series of high steep-sided plateaux with gentle west-sloping surfaces. Block faulting, west-dipping dolerite and sandstone units, and glacial erosion must explain this topography.

Measurements of the concentrations of Na+ K+, Mg2+, and Ca2+ were made on 28 samples from the 255 m deep ice core from Little America V. All concentrations decrease sharply with depth from the firn–ice transition at 52 m to somewhere between 125 m and 150 m. From 150 m to 250 m the cationic concentrations are relatively constant. This is interpreted to indicate that the ice above 125 m fell as snow on the Ross Ice Shelf and that ice below 150 m originated inland on Marie Byrd Land.

Measurements of mesoscale sea-ice deformation over a region approximately 20 km in diameter were carried out over a five-week period in the spring of 1972 at the main AIDJEX camp in the Beaufort Sea. They have been analyzed to determine non-linearities in the ice velocity field (due to the discrete small-scale nature of the ice pack), as well as a continuum mode of deformation represented by a least-squares strain-rate tensor and vorticity. The deformation-rate time series between Julian day 88 and 112 exhibited net areal changes as large as 3% and deformation rates up to 0.16% per hour. In the principal axis co-ordinate system, the strain-rate typically exhibited a much larger compression (or extension) along one axis than along the other. Persistent cycles at ≈ 12 h wavelengths were observed in the divergence rate.

A comparison of the average residual error with the average strain-rate magnitude indicated that strains measured on a scale of 10 km or greater can serve as a valid measure of the continuum motion of the sea ice. This conclusion is also substantiated by a comparison between the mesoscale deformation, and macroscale deformation measured over a ≈ 100 km diameter region.

Regarding pack-ice rotation, vorticity calculations indicate that at low temporal frequencies (0.02 h−1), the whole mesoscale array rotates essentially as an entity and consequently the low-frequency vorticity can be estimated accurately from the rotation of a single floe.

A comparison of mesoscale strain measurements with the atmospheric pressure field and the wind velocity field indicate that the ice divergence rate and vorticity follow the local pressure and wind divergence with significant correlation. For low atmospheric pressures and converging winds the divergence rate was found to be negative with the vorticity being counter-clockwise. The inverse behavior was observed for high pressures and diverging winds. This behavior was shown to agree with predictions based upon the infinite boundary solution of a linearized drift theory in the absence of gradient current effects and using the constitutive law proposed by Glen (1970) for pack ice. The best least-squares values of the constitutive law parameters η and ζ were found to be ≈ 1012 kg/s. Using typical divergence rates these values yield compressive stresses of the magnitude of 105 N/m which are similar to values suggested by the Parmerter and Coon (1972) ridge model. In general, the infinite boundary solution of the linear drift equation indicates that in a low-pressure region that is reasonably localized in space, the ice would be expected to converge for high compactness (winter) and diverge for low compactness (summer).

Calculations were also carried out using a more general linear visco-elastic constitutive law that includes memory effects and which includes a generalized Hooke’s law as well as the Glen law as special cases. A best fit of this more general calculation with strain measurements indicates overall a better agreement with viscous behavior than with elastic behavior, with the frequency behavior of the estimated “viscosities” similar to the Glen law behavior at temporal frequencies less than ≈ 0.01 h−1.

This paper describes laboratory research performed to determine the effects of crude and diesel oils on the porous sub-structure of Arctic sea ice. It includes a qualitative description of what occurs when oil is placed under the ice and an evaluation of some quantitative measurements made to determine the maximum extent to which crude oil can spread in an Arctic environment.

Nucleation and growth of bubbles during freezing of solutions of air and helium in water has been investigated experimentally using different techniques to give freezing rates between 1 μ m s−1 and 10 mm s−1. Bubbles grow as cylinders below 5 μ m s−1, becoming egg shaped, the narrow ends towards the freezing interlace, at higher ice growth velocities. Bubble concentration increases and size decreases with increase of growth rate. The detail of bubble size and concentration is influenced appreciably by the particulate content of the water sample. Very high freezing rates give initially clear ice. Subsequently, bubbles nucleate and grow at grain boundaries within the ice. Bubbles do not move with recrystallization, their spatial distribution showing the grain boundary positions at the time of nucleation.

Observations are interpreted in terms of nucleation on particles in suspension in the water and a significant incorporation of air molecules into the ice lattice. The relevance of the results to bubble-containing ice formed under natural conditions is discussed.

Soil temperatures were recorded over periods of several weeks in the years 1909 and 1970 in two sites to a depth of 100 cm. It was found that snow depth was of major importance in the rate of freezing of the soil in winter; where snow cover was less than 5 cm in depth freezing rates were almost double those where snow depth was over 1 m. Snow cover also insulated the soil surface from above-zero air temperatures during spring, and soil thawing commenced from the surface only following the clearance of snow. Similarly, insulation of the soil surface by snow prevented short-term freezing and thawing cycles penetrating the soil, although even where snow cover was absent such short-term cycles were not observed to penetrate the soil to depths in excess of 5 cm. This surficial freezing and thawing of the soil took place more readily in spring than in the autumn. It was concluded that the annual cycle of soil freezing and thawing was the dominant factor in the thermal regime of these soils, short-term freezing cycles affecting only the immediate surface soil layers.

In Les météores (1637), in the midst of a father far-fetched theory of their origin, Descartes incorporated a detailed description, from actual observation, of a variety or kinds of snow crystals and hail particles. These even include the tsuzumi crystals, described as “wheels joined two by two by an axle” or as “little crystal columns decorated at each end with a six-petalled rose”, and such exceptional forms as twelve-rayed and eight-rayed stars. The accompanying diagrams, which have been reproduced a number of times, are distinctly inferior to his verbal description.