Research Article
A study of ablation variations on the tongue of Hintereisferner, Austrian Alps
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 319-324
-
- Article
-
- You have access
- HTML
- Export citation
Ice-core dating and chemistry by direct-current electrical conductivity
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 325-332
-
- Article
-
- You have access
- HTML
- Export citation
Observations of the water-vein system in polycrystalline ice
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 333-347
-
- Article
-
- You have access
- HTML
- Export citation
Intra-seasonal changes in deformation profiles revealed by borehole studies, Storglaciären, Sweden
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 348-358
-
- Article
-
- You have access
- HTML
- Export citation
The thermal behaviour of the water-vein system in polycrystalline ice
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 359-374
-
- Article
-
- You have access
- HTML
- Export citation
Melting of ice shelves and the mass balance of Antarctica
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 375-387
-
- Article
-
- You have access
- HTML
- Export citation
Tools for examining subglacial bed deformation
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 388-396
-
- Article
-
- You have access
- HTML
- Export citation
Climate at the Equilibrium Line of Glaciers
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 397-411
-
- Article
-
- You have access
- HTML
- Export citation
Determination of a flow center on an ice cap
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 412-416
-
- Article
-
- You have access
- HTML
- Export citation

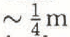 at a depth of ~25 m near the center of the glacier in July 1985. The shear took place in the zone in which cold ice near the surface gives way to temperate ice deeper in the glacier.
at a depth of ~25 m near the center of the glacier in July 1985. The shear took place in the zone in which cold ice near the surface gives way to temperate ice deeper in the glacier.