Introduction
If air temperatures increase as predicted in the next century, mountain glaciers will continue to lose mass (Radić and Reference Radić and HockHock, 2011). Although mountain glaciers hold only a small fraction of the total terrestrial ice, ice loss from mountain glaciers currently accounts for roughly half the eustatic sea-level rise that occurs because of ice loss to the oceans (Reference MeierMeier and others, 2007; Reference Rignot, Velicogna, Van den Broeke, Monaghan and LenaertsRignot and others, 2011). Mountain glaciers also regulate freshwater availability by storing water during cold periods and releasing water during warm periods. As mountain glaciers retreat, glacier melt contributes less fresh water to glacier-fed river basins (Reference Comeau, Pietroniro and DemuthComeau and others, 2009). Reduced freshwater availability may negatively affect hydropower generation, agriculture, recreation and the health of aquatic ecosystems (Reference Stahl and MooreStahl and Moore, 2006; Reference Jacobsen, Milner, Brown and DanglesJacobsen and others, 2012).
The glaciers of Banff National Park in the Canadian Rocky Mountains attract more than three million tourists per year (Reference Scott, Jones and KonopekScott and others, 2008; Reference ParksParks Canada, 2012) and provide water to both the North and South Saskatchewan Rivers, which flow into the agricultural lands of the Canadian prairie provinces. As the Canadian prairie provinces are sensitive to drought (Töyrä and others, 2005), glacier and snow melt are important water sources to the region. Several recent studies have assessed glacier mass balance in Banff National Park (e.g. Reference LuckmanLuckman, 1998; Reference Østrem, Demuth, Munro and YoungDemuth and Keller, 2006). Marshall and others (2011) showed that glaciers along the eastern slopes of the Canadian Rocky Mountains will likely lose 80–90% of their volume by 2100. Reduced glacier volume will cause a long-term decrease in annual streamflow in the North and South Saskatchewan Rivers, particularly in the late summer (Reference Comeau, Pietroniro and DemuthComeau and others, 2009).
In this study, we quantify the volume of lower Peyto Glacier in Banff National Park (Fig. 1; 51°40’41” N, 116°32’50” W) from ground-penetrating radar (GPR) surveys conducted during the period 2008–10. The lower glacier is defined by Holdsworth and others (2006) as the region extending from the glacier terminus to stake 85 (Table 1), or an altitude of ~2300 m a.s.l. Demuth and Keller (2006) found an average equilibrium-line altitude of 2700 m a.s.l. for 1966–95, so the lower glacier is dominated by ablation. In 1984, the lower glacier encompassed ~10% of the glacier area and ~20% of the glacier volume (Reference Holdsworth, Demuth, Beck, Demuth, Munro and YoungHoldsworth and others, 2006). We compare our volume estimate from 2008–10 with previous estimates from 1966 and 1984 (Reference Holdsworth, Demuth, Beck, Demuth, Munro and YoungHoldsworth and others, 2006) to assess volume change over time and to predict the future mass balance of the glacier.
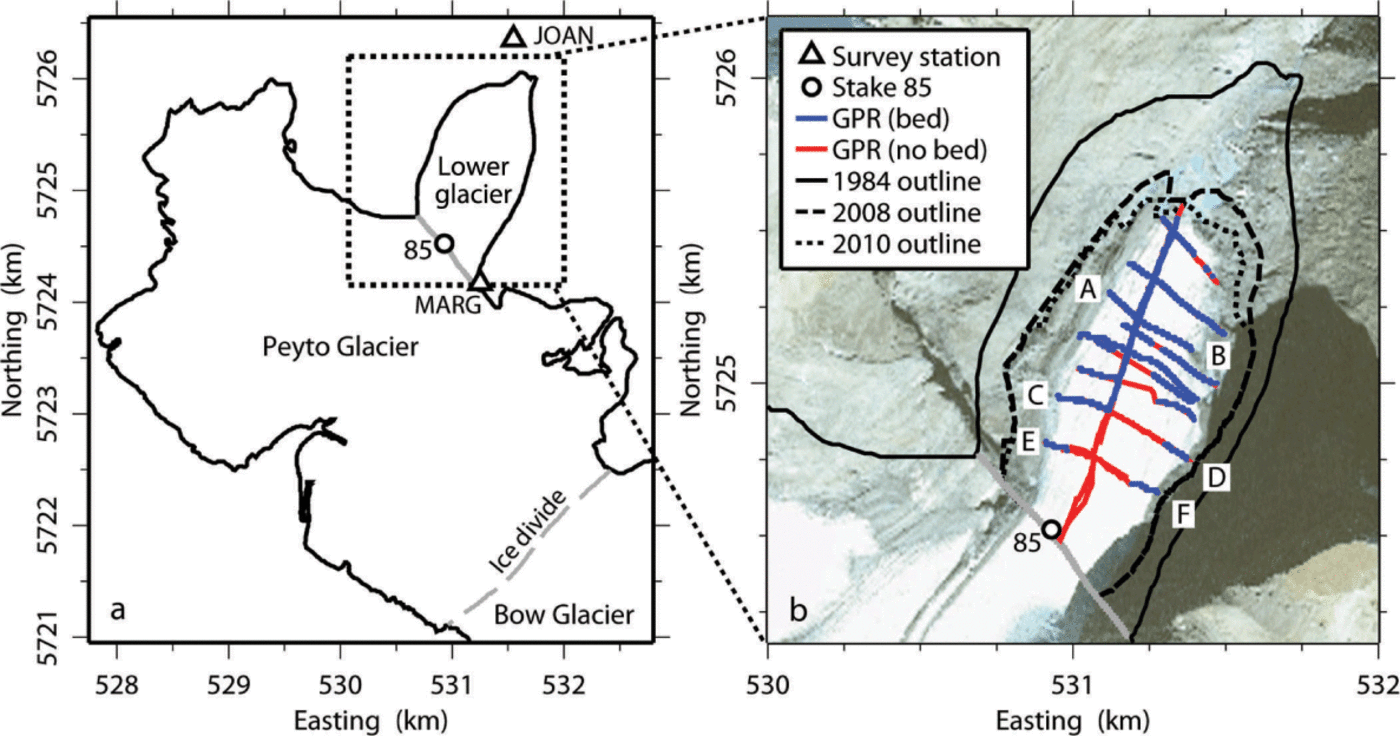
Fig. 1. Map of Peyto Glacier, Banff National Park, Alberta, Canada. (a) Peyto Glacier in 1984 (black outline; Reference Holdsworth, Demuth, Beck, Demuth, Munro and YoungHoldsworth and others, 2006). This study focuses on the lower glacier, which is defined by Holdsworth and others (2006) as the region extending from the glacier terminus to stake 85 (black circle). The dotted box is expanded in (b). (b) Lower Peyto Glacier in 1984 (full curve), 2008 (dashed curve) and 2010 (dotted curve). Ice-cored moraines are included in the glacier extent. We recorded GPR transects across the lower glacier (red and blue lines) from 2008 to 2010. Blue lines indicate locations where we could trace the bed reflection and thereby determine an ice thickness; red lines indicate locations where we could not. GPR transects AB and CD are shown in Figure 2. The satellite image is a SPOTMaps image recorded on 5 May 2010. Coordinates are given in UTM zone 11 WGS84.
Table 1. Ice thicknesses in 1984 and 2008–10 at stakes listed by Holdsworth and others (2006). Ice thicknesses for 2008–10 are interpolated from nearby measured ice thicknesses. Note that the coordinates listed here are in UTM zone 11 WGS84 and differ from those given by Holdsworth and others (2006), who used the UTM zone 11 NAD27 coordinate system (personal communication from G. Holdsworth, 2012)

Methods
Ice thickness
We measured ice thickness across lower Peyto Glacier using GPR during three fieldwork campaigns from August 2008 to May 2010 (Fig. 1). In August 2008, we recorded five GPR transects across the lower glacier using a Geophysical Survey Systems Inc. (GSSI) SIR-3000 GPR with a 100 MHz antenna. We determined position along the transects using differential GPS, with a base station installed on a high point near the glacier terminus. As we identified bed reflections in only two of the five transects, we returned in September 2009 with a lower-frequency antenna (50 MHz) to further survey the glacier bed. At 50 MHz, we traced bed reflections to ice depths of 70–90 m. Consequently, ice depths still remained poorly constrained over about half of the study area. We hypothesized that this occurred because of dielectric attenuation and englacial scattering due to water within the ice (Reference Kotlyakov and MacheretKotlyakov and Macheret, 1987) and returned in late winter when water should be absent. We found bed reflections in all five transects recorded in March 2010, but lost bed reflections at ice depths >80–110 m (Figs 1 and 2). We recorded position along the transects in September 2009 and March 2010 with a handheld GPS. Altogether, we recorded 15 GPR transects during the period 2008–10 and recorded bed reflections in 11 of these transects (Fig. 1).

Fig. 2. GPR data along two of the 15 transects: (a) AB and (c) CD in Figure 1. (b) and (d) show picked surfaces and beds (solid, thick black curves) for AB and CD, respectively. In transect CD, we lose the bed reflection at ice thicknesses >80 m and therefore assume a parabolic bed profile that best fits the measured ice thicknesses (solid, thin black curve). We assess the uncertainty of this assumption by determining the maximum and minimum plausible bed depths in this region (dashed, thin black curves) by interpolating between known bed depths with a triangle or line, respectively.
To better detect bed reflections in the GPR data, we stacked every ten traces along the GPR transects and removed ‘ringing’ by subtracting the mean trace for each transect (Reference Kim, Cho and YiKim and others, 2007). By subtracting the mean trace, we were better able to identify bed reflections in areas where the bed slope was high; in areas where the bed slope was low, we picked the same bed as we would have picked had we only stacked the GPR data. We manually picked bed reflections as the two-way travel time with the minimum power return (Fig. 2). To convert two-way travel time to ice thickness, we set the direct-coupling wave to zero time and used a velocity in ice of 167 m μs−1 as determined by Goodman (1975) for the accumulation area of Peyto Glacier. Holdsworth and others (2006) also used this value in their volume calculations for 1966 and 1984. As the radar wave velocity changes with water content (e.g. Reference Bradford and HarperBradford and Harper, 2005; Reference Navarro, Macheret and BenjumeaNavarro and others, 2005), which is both seasonally and spatially variable across Peyto Glacier, we assume that this velocity is accurate to within ±5 m μs−1 and take this uncertainty into account in our volume calculations.
We assessed the precision of our ice-thickness measurements by comparing measured ice thicknesses at locations where the GPR transects cross one another. Measured ice thicknesses can differ at crossover locations due to errors in the position estimates from the handheld GPS or due to our technique for picking the bed. In total, we found 29 crossovers with an average difference of 3: 1 ± 2: 3 m. As the mean crossover difference across the 2008, 2009 and 2010 campaigns (3: 3 ± 2: 8 m) was similar to that within the same campaign (3: 1 ± 2: 0 m), we do not have sufficient resolution to calculate separate ice volume estimates for 2008, 2009 and 2010.
Glacier extent
We determined glacier extent by walking along the glacier margin with a differential GPS in August 2008 (Fig. 1). Glacier extent includes ice-cored moraines. To assess the uncertainty of our mapped glacier extent, we compared our mapped glacier extent with glacier extent in a SPOTMaps (Satellite Pour l’Observation de la Terre) satellite image. Although the SPOTMaps product achieves global coverage by combining orthorectified SPOT 5 images (2.5 m resolution) recorded on different dates, all pixels in the chosen image were recorded on 5 May 2010. We found that the glacier area in August 2008 (7: 3 × 105 m2) was 0: 6 × 105 m2 greater than the glacier area in May 2010 (6: 7 × 105 m2).
Volume calculations
We combine our mapped glacier extent from 2008 and ice-thickness measurements from all three years to calculate a single glacier volume estimate for 2008–10. This leads to a well-constrained ice thickness near the glacier terminus. At greater elevations, the ice thickness is not as well constrained, because we could not trace bed reflections along transects CD and EF (Figs 1 and 2). Bed reflections disappear for ~200 m in the middle of these transects. To determine a likely bed depth in this region, we first constrain the bed geometry to a parabola that best fits the measured depths (black curve in Fig. 2d). Glacier beds often approximate the shape of a parabola due to glacier erosion (Reference SvenssonSvensson, 1959; Reference GrafGraf, 1970; Reference HarborHarbor, 1992). We also consider minimum and maximum constraints on the bed depth in this region (dashed black curves in Fig. 2d). In the minimum case, we interpolate linearly between known depths. In the maximum case, we extrapolate the slopes of known depths to form a triangle. We use the minimum and maximum constraints to assess uncertainty, and the parabolic bed geometry to calculate glacier volume.
Although several different techniques now exist for volume estimation from GPR measurements (Reference Binder, Brückl, Roch, Behm, Schöner and HynekBinder and others, 2009; Reference FischerFischer, 2009), in this study we use a simple Laplacian interpolation between ice-thickness measurements, which performs well in our case. We first resample our measured bed depths and assumed bed depths in transects CD and EF into 10 m gridcells in the east and north directions. At the glacier margin, we constrain the ice thickness to 0 m. We then solve the Laplace equation at each gridcell assuming minimum curvature. Finally, we integrate the interpolated ice thicknesses to calculate a volume estimate for the lower glacier.
Uncertainties in glacier area and thickness contribute to uncertainty in our volume estimate. To assess the uncertainty of our ice-thickness measurements, we consider three possible sources. First, we examine the uncertainty related to our assumed radar wave velocity. Assuming that Goodman (1975) calculated a velocity within ±5 m µs-1 of the true value (e.g. Reference Bradford and HarperBradford and Harper, 2005; Reference Navarro, Macheret and BenjumeaNavarro and others, 2005), we estimate a volume uncertainty of 0: 10 × 107 m3 associated with the radar wave velocity, which is equal to 3% of the estimated volume. Second, we estimate the volume uncertainty associated with our ice-thickness measurements by extrapolating the mean crossover difference across the glacier area. This leads to a volume uncertainty of 0: 23 × 107 m3, which is 7% of the estimated volume. Third, we calculate the uncertainty that results from the poorly constrained ice thicknesses in transects CD and EF (Fig. 2). To assess this uncertainty, we interpolate ice thicknesses across the glacier area using the maximum and minimum constraints on bed depths that we developed for this region (dashed black curves in Fig. 2d). This leads to a volume uncertainty of up to 0: 14 × 107 m3, or 4% of the estimated volume. Finally, we assess the volume uncertainty that occurs because of uncertainty in the glacier area by comparing volume estimates using our glacier margin from 2008 and using a digitized glacier margin from a SPOTMaps image in 2010 (Fig. 1). This leads to an uncertainty of 0.08 × 107 m3, or 2% of the estimated volume. To combine all four uncertainty estimates, we calculate the root-sum-of-squares, which is equal to 0.30 × 107 m3, or 9% of the estimated volume.
Results
Figure 3 shows the measured and interpolated ice thicknesses across lower Peyto Glacier, which reach a maximum of 122 m near the middle of transect EF. When we integrate the interpolated ice thicknesses across the glacier area (7.3 × 105 m2), we calculate a volume of (3.39 ± 0.30) × 107 m3, which is 30 ± 3% of the volume calculated for the lower glacier in 1984 (Reference Holdsworth, Demuth, Beck, Demuth, Munro and YoungHoldsworth and others, 2006). Figure 4 shows volume estimates for lower Peyto Glacier from 1966–2010. We find a linear decrease in glacier volume at a rate of (3.3 ± 0.2) × 106 m3 a–1. If we extrapolate this trend into the future, the lower glacier will disappear by ~2019.

Fig. 3. Measured and interpolated ice thicknesses across the lower glacier for the period 2008–10. Black outlines indicate the GPR transects, and the colors inside the outlines represent the measured ice thicknesses.
Table 1 compares individual ice-thickness measurements from 1984 (Reference Holdsworth, Demuth, Beck, Demuth, Munro and YoungHoldsworth and others, 2006) with the interpolated ice thicknesses for 2008–10. We find that the glacier has retreated from five of the stakes installed by Holdsworth and others (2006) and, consequently, no glacier ice exists at these locations. Ice thicknesses decreased by 40–98 m between 1984 and 2008–10, with an average thinning rate of 3: 0 ± 0: 6 m a−1.
Discussion
Similar to other mountain glaciers around the world (Reference Kaser, Cogley, Dyurgerov, Meier and OhmuraKaser and others, 2006; Reference MeierMeier and others, 2007), Peyto Glacier has retreated significantly since its Little Ice Age maximum in the mid-19th century. Over this period, it has retreated ~3 km and lost ~70% of its volume (Reference Watson and LuckmanWatson and Luckman, 2004; Reference Østrem, Demuth, Munro and YoungØstrem, 2006). Matulla and others (2009) predict that mass loss will be more sustained and substantial in the future as temperatures increase in the Canadian Rocky Mountains. Comeau and others (2009) found a mass loss of 7.1– 8: 0 × 106 m3 w.e. a−1 for the entire glacier for the period 1966–98, increasing to ~10 × 106 m3 w.e. a−1 for the period 2000–02 (Reference Hopkinson and DemuthHopkinson and Demuth, 2006). We find that mass loss from the lower glacier ((3.0 × 0.2) × 106 m3 w.e. a−1) accounts for ~30–40% of the total loss from 1966 to 2010.
Although we cannot directly compare our volume estimate for the lower glacier with previous estimates for the total glacier (Reference Watson and LuckmanWatson and Luckman, 2004; Reference Hopkinson and DemuthHopkinson and Demuth, 2006; Reference Comeau, Pietroniro and DemuthComeau and others, 2009), our results agree well with other estimates of glacier thinning (Reference Hopkinson and DemuthHopkinson and Demuth, 2006; Reference Comeau, Pietroniro and DemuthComeau and others, 2009; Reference MarshallMarshall and others, 2011). We measure thinning rates of 1–5 m a−1 across the lower glacier, which are similar to but slightly smaller than those reported by Hopkinson and Demuth (2006) for 2000–02 (2–5 m a−1). We suggest that the slightly higher thinning rates for 2000–02 than for 1966–2010 may be explained by our finding of a linearly decreasing glacier volume over this period (Fig. 4). As the glacier area decreased from 1966 to 2010, thinning rates had to increase over the remaining glacier area to maintain the linear decrease in glacier volume. In fact, Demuth and Keller (2006) found that mass-balance rates became more negative across the lower glacier from 1966 to 1995. By 2100, Marshall and others (2011) predict that the average glacier thinning rate in the Canadian Rocky Mountains will increase from ~1 m w.e. a−1 to between 2 and 4 m w.e. a−1, based on the Intergovernmental Panel on Climate Change (IPCC) A1B and B1 emissions scenarios.
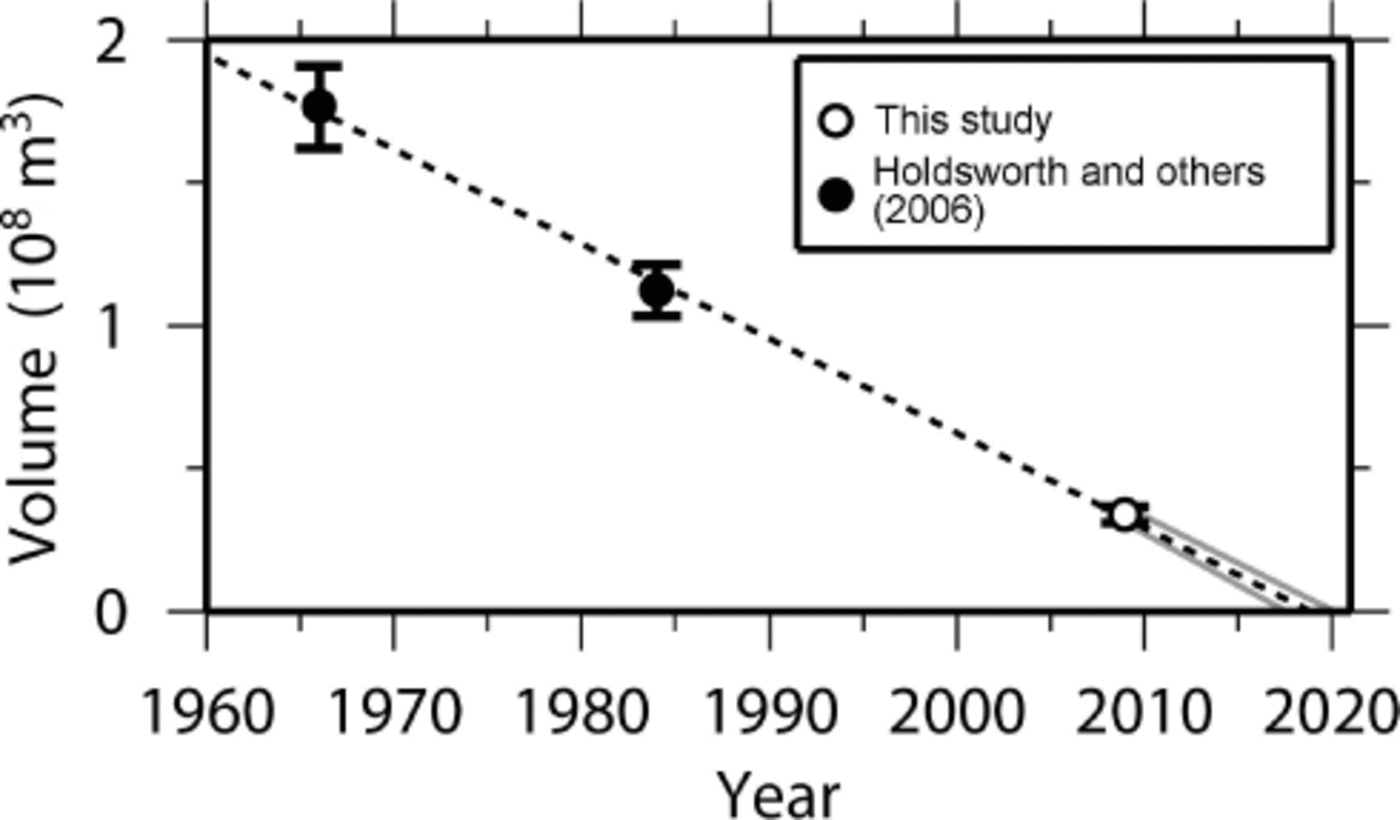
Fig. 4. Measured and predicted volume of the lower glacier for the period 1960–2020. As Holdsworth and others (2006) do not report uncertainties for the 1966 and 1984 volume estimates (black circles), we use our relative uncertainty estimate for 2008–10 (white circle) for all volumes. We find a linear decrease in volume (dashed line). If this trend persists, the lower glacier will disappear by ~2019. The gray lines from 2009 to 2020 indicate the uncertainty of this prediction, which takes into account the volume uncertainties for all three years.
The results of this and other studies (Reference Watson and LuckmanWatson and Luckman, 2004; Reference Holdsworth, Demuth, Beck, Demuth, Munro and YoungHoldsworth and others, 2006; Reference Matulla, Watson, Wagner and SchönerMatulla and others, 2009) indicate that lower Peyto Glacier is disappearing rapidly. If we extrapolate our finding of a linear decrease in glacier volume from 1966 to 2010 into the future (Fig. 4), the lower glacier will disappear by ~2019 and Peyto Glacier will retreat by ~1 km. As this prediction is based on a linear trend from only three volume estimates, its value is limited. Furthermore, the prediction does not take into account any future changes in ice dynamics. For example, as glacier thinning lowers the surface elevation, glacier melt rates will likely increase and the lower glacier may disappear sooner than predicted. As a result, our prediction provides only a ballpark estimate for the disappearance of the lower glacier, indicating that it will likely disappear within the next few decades.
Like Peyto Glacier, many glaciers in western Canada are retreating. From 1985 to 2005, glacier area in western Canada decreased by ~ 11 ± 4% (Reference Bolch, Menounos and WheateBolch and others, 2010). In particular, Peyto Glacier and other glaciers along the eastern slopes of the Canadian Rocky Mountains lost 25 ± 4% of their area over this period (Reference Bolch, Menounos and WheateBolch and others, 2010). Our results agree well with this regional trend: from 1984 to 2008, lower Peyto Glacier lost ~40% of its area. By 2100, Marshall and others (2011) predict that Peyto Glacier and other nearby glaciers will lose an additional 80–90% of their present-day volume. As glaciers in the region continue to retreat, decreased freshwater availability may contribute to water shortages in the Canadian prairie provinces (Töyrä and others, 2005; Reference Comeau, Pietroniro and DemuthComeau and others, 2009), with negative effects on ecosystems, hydropower generation and agriculture. As a result, we suggest that future studies should continue to monitor glacier mass balance in the region and its effects on freshwater availability.
Conclusions
We calculate a mean volume of (3.39 ± 0.30) × 107 m3 for lower Peyto Glacier from 2008 to 2010. When we compare our volume estimate with previous volume estimates (Reference Holdsworth, Demuth, Beck, Demuth, Munro and YoungHoldsworth and others, 2006), we find that the volume of the lower glacier decreased linearly from 1966 to 2010, with an annual loss of (3.3 ± 0.2) × 106 m3 a−1. If this trend persists into the future, the lower glacier will disappear by ~2019 and Peyto Glacier will have retreated by ~1 km. As the glaciers of the Canadian Rocky Mountains are important for tourism and freshwater availability, future studies should continue to monitor glacier mass balance in the region.
Acknowledgements
We thank Seth Campbell, Tina Praprotnik and Matt Siegfried for help in the field. We also thank Jonathan Chipman and Steve Arcone for technical assistance, Parks Canada for permission to work on Peyto Glacier and Mike Demuth for advice about conducting fieldwork on Peyto Glacier. Comments from David Rippin (Scientific Editor), Joe MacGregor and an anonymous reviewer helped improve the manuscript. Fieldwork was supported by the Stefansson Fellowship at the Dickey Institute for Arctic Studies, the Andrew W. Mellon Grant for Environmental Research and the Earth Sciences Department at Dartmouth College.







