Introduction
The style of flow of ice streams is an important but poorly understood aspect of ice sheets. Ice streams account for the bulk of ice drainage from the West Antarctic ice sheet. Moreover, they are changing with time, indicating unsteadiness, if not instability, in the ice-sheet system (Reference Alley and WhillansAlley and Whillans, 1991). It is clear, that if the flow of the ice sheet as a whole is to be understood, then the flow of ice streams must be understood.
Ice streams contain unusual features. Most notably, crevasses are arranged in trains in which each crevasse is transverse to flow. Also, there are longitudinal surface topographic ridges. The geneses of these features are not understood. Their origin needs to be addressed, because that may bear on the essential reason for fast ice-stream flow. For example, the presence of transverse crevasses has been used to argue that longitudinal tension is the most important stress in the ice stream (Reference Vornberger and WhillansVornberger and Whillans, 1986).
The present work focuses on a part of Ice Stream Β near its onset (Fig. 1). The studied section crosses the full width of tributary B2 of Ice Stream Β and includes the UpB field camp. Of special interest are the contrasts in flow style, from slow flow in the ridges that lie between the ice streams, to strong shearing in the margins of the ice stream, to the strain rates in intensely crevassed regions within the ice-stream body and to the behavior of the part around the UpB camp that is free of surface crevasses. For obvious reasons, most earlier detailed studies of Ice Stream Β have been conducted in regions without surface crevasses (e.g. Reference Blankenship, Bentley, Rooney and AlleyBlankenship and others, 1986; Reference Bindschadler, Stephenson, MacAyeal and ShabtaieBindschadler and others, 1987; Reference Alley and BentleyAlley and Bentley, 1988; Reference Engelhardt, Humphrey, Kamb and FahnestockEngelhardt and others, 1990; Reference KambKamb, 1991; Reference Whillans and van der VeenWhillans and Van der Veen, 1993b).

Fig. 1. The studied region is outlined by a heavy box. The stations with velocity vectors in the photoblock also serve as ground control for the photography. Base map is from Reference Whillans and van der VeenWhillans and Van der Veen (1993a). Selected polar grid coordinate intersections are shown.
Repeat aerial photogrammetry is effective in measuring velocities and surface slopes of glaciers in regions which are intensely crevassed. Such zones may be mechanically critical to glacier flow but are not safe for ground-based work. Very closely spaced velocity and elevation data can be obtained at small unit cost. The difficulty is in obtaining quality photography. Also, the photo-measurement and analysis program is labor intensive.
Methods
The photogrammetric method applied here involves several steps. First, ground control is established and marked. Aerial photographs are then obtained and linked together to form blocks of stereo-models. Next, the positions of trackable features, such as crevasses, in at least two epochs of photography are measured. Ice velocities are calculated from the change in position of these features and the time elapsed. Elevations are obtained at the same time. The irregularly distributed data are then gridded to obtain values at regularly spaced grid points. Differentiation of the gridded velocities provides strain rates.
Since there is no exposed bedrock or other fixed points, the ground control must be located on the moving ice. Black plastic sheets, 3 m by 3 m, were suspended from bamboo poles several decimeters above the surface to delay the accumulation of drift snow on top of the target. The distribution of the six ground-control stations is shown in Figure 1. Due to an error in aircraft navigation, the photography does not cover one of the ground-control stations (station 21) in January 1985. The ground control was renewed and resurveyed for each photograph epoch.
The surveying for ground control uses receivers that track Doppler (Transit) satellites and record the data on tape. About 24 h of tracking data are used for each position. The tapes are later processed together with orbital information to compute the positions of the receivers’ antennas. The positions are calculated in a network adjustment involving all simultaneously operating receivers and tied to two fiducial sites. This is the most precise method for calculating positions using Transit data (Reference McDonald and WhillansMcDonald and Whillans, 1988).
The two fiducial sites are on the slowly moving inter-stream ridges on either side of the photographed region (marked “south camp” and “north camp” in Figure 1). The velocities of these fiducial sites were first determined by point-positioning with precise satellite orbits obtained from the U.S. Defence Mapping Agency. Their speeds are 2.2 m a−1 for “north camp” on ridge B/C and 10.9 m a−1 for “south camp” on ridge A/B. The accuracy of the positions is about 1 m r.m.s. for each year.
The positions of the remaining stations are computed in a network calculation that ties them to the positions of these fiducial stations (Reference Whillans and van der VeenWhillans and Van der Veen, 1993a). Relative positions are accurate to about 0.3 m. Absolute positions are accurate to about 1 m. Errors in the absolute positions of the fiducial sites propagate through the calculations mainly as systematic displacements. The errors can affect velocities but have little effect on strain rates. The relative errors lead to relative velocity errors of ![]() m/(time interval), or 0.4 m a−1.
m/(time interval), or 0.4 m a−1.
The surveying for ground control was conducted several weeks earlier than the photography. A linear interpolation or extrapolation over time is performed to calculate the ground-control positions at the times of photography. The inherent assumption, that the ice is moving at a constant velocity, is supported by the work of Reference Harrison and EchelmeyerHarrison and Echclmeyer (1989) and Reference McDonald and WhillansMcDonald and Whillans (1992), who found no detectable velocity change at the UpB camp over intervals of up to 2 years.
The photographs are at a scale of 1: 50 000. There are three (January 1985) or four (January 1986) flight lines across the photograph block, each with about 23 photographs taken from a height of approximately 8000 m. The photographs are taken at similar sun-illumination angles and scales. The photograph coverage is about 60% end-lap (overlap between consecutive photographs in the same strip) and about 20% side-lap (overlap of adjacent photographs in neighboring flight lines). The overlap varies a little along the flight lines. An area of 38 km (across the ice stream) by 26 km (along the ice stream) is common to both epochs of photography. Using a Wild model BC-1 analytic plotter, the photographs are formed into stereo models using crevasses and sastrugi as linkages.
An aerotriangulation calculation forms a mathematical photo-mosaic for each epoch and ties it to the ground control. The program is a bundle, block adjustment written by one of us (Y.H.T.). The limit to precision within each aerotriangulation comes from the ground control and from the accuracy of ties between the photographs. Other inaccuracies, such as those associated with camera calibration and emulsion deformation, are much smaller.
Features on individual crevasses are tracked from one year to the next. About 10 h of operator time are required to measure 50 displacements. Most of the tracked features are distinctive parts of crevasses but some drift mounds are used.
In the crevasse-free center of the ice stream, velocity measurements derive from a strain grid that was surveyed in the 1984–85 and 1985–86 field seasons, and which is tied to satellite tracking at the UpB camp (station 01) and another station (Reference Whillans and van der VeenWhillans and Van der Veen, 1993a). The strain grid can be recognized in Figure 2b, c and d because the marks form a nearly regular grid up-glacier from the UpB camp.

Fig. 2. The lefl-to-right axis is the x-direction, along flow (units are km), and y-axis is toward top. North is toward the bottom of the figure, (a) Snow-surface elevation relative to the WGS84 ellipsoid. Each spot represents an elevation determination, either from trackable features or ephemeral sastrugi (pass-and-tie points). Very thick contours highlight two ridges in the ice stream. Contour interval is 10 m. These data come from the 1986 photography. The 1985 results are virtually identical. The UpB camp is labeled. The drilling programs of Reference Alley and BentleyAlley and Bentley (1988) and Reference Kamb, Heard, Borg, Carter and RaleighKamb ( 1991) have been in the valley marked by the 330 m contour at (x,y) = (27,24) km. The seismic work of Reference Blankenship, Bentley, Rooney and AlleyBlankenship and others (1986) was done near (x,y) = (23,27) km. (b) Ice-motion vectors. Flow is left to right. Arrowheads are omitted, (c) Component of velocity, ux, parallel to the x-axis (positive to the right). Isotach interval is 40 ma−l. Spots mark locations of tracked features, (d) Component of velocity, uy, parallel to the y-axis (positive toward top). Isotach interval is 10 ma−1.
The total number of velocity data from photogrammetry and ground surveying is 1621, but 80 have been eliminated as unreliable, as discussed below. The displacement measurements are concentrated at the sides of the ice stream, especially in the shear margins. This concentration is dictated by the availability of suitable trackable features, such as crevasses.
The distribution of data is irregular. A regular grid of values is most convenient for subsequent operations such as central differencing to obtain velocity gradients and producing isoline maps. Several methods of gridding were tried. The ideal method is one in which the gridded values are faithful to data close to the grid points and reasonably interpolated across large data gaps. The seemingly least objectionable method discovered is the minimum curvature routine by Golden Software, Inc. (no date). It performs well in regions of dense data and interpolates reasonably across gaps. Grids at 500 m interval are made of the longitudinal component, ux, transverse component, uy and 1986 ellipsoidal height, h.
Both the quality of gridding and presence of oudying measurements are determined by comparing the input data with the gridded results. Differences are computed between the measurements and planes fitted through the three nearest grid values. Velocity vectors that differ by more than 10 m a−1 in the x-component and 7 m a−1 in the y-component are rejected as being tracking mistakes. Larger latitude is allowed for the x-component because a plane is not the best surface to fit to that data set. Fiftyeight such vectors are eliminated. This technique works best where data density is large. Elsewhere, in small-density regions, velocity gradients were studied for paired highs and lows, with a measurement point between. There are 22 such patterns and they are attributed to errors. There is no special geographic pattern to the locations of the rejected vectors. After rejection of the 80 suspect points, the root-mean-squared differences between the input data and the gridded results are 3.0 m a−1 for ux and 2.0 m a−1 for uy. There are no significant arithmetic biases. These deviations are somewhat less than the estimated error of 3.2 m a−1, discussed below, as may be expected because the grid also is affected by data errors.
Many of the largest remaining discrepancies lie in regions where photograph models overlap. The difference between velocity determinations of the same region using different pairs of stereo-models is often about 5 m a−1. This points to a problem with at least one of the aerotriangulations, probably due to imprecision in the tie points. Thus, there are additional errors that are systematic within model pairs. These do not affect calculated velocity gradients except at model boundaries.
Some discrepancies could be due to non-homogenous flow, such as associated with discrete slip as reported for Chungpar or Tarshing Glacier in the northwest Himalaya by Reference KickKick (1989), or as suggested by Reference MacAyeal, Shabtaie, Bentley and KingMacAyeal and others (1986), in which balls or pillars of ice roll past one another. These could be identifiable as discrepancies that form a coherent linear or curved pattern. No such patterns are identified.
The gridding scheme does poorly at representing the sharp changes in the along-flow component of velocity, ux, at the north and south shear margins. First attempts to alleviate this problem added synthetic data to the outer parts of the data set before gridding. However, this affects the gridded results even within the shear margin. The grid is more faithful to the data within the ice stream if no attempt is made to follow the sharp gradient at the margin and if the gridded values are allowed to go to unrealistic values outside of the data region. Moreover, velocity data from the ground-control stations outside of the ice stream (stations 71, 21, 15 and 19) are removed before gridding because they perturb the gridded surfaces in their vicinity, even within the shear margins. These stations are shown in Figures 1 and 4 but not on the figures of velocity. The problem is not one of measurement but that the gridding routines cannot properly follow an abrupt change in slope.
In many of the data gaps, the grids are warped. The regions with most extreme warps are omitted or are shown with dashed lines in the maps.
Apart from mistakes, errors in the displacements originate mainly with the ground control or from photograph measurement. As noted above, relative errors in ground control amount to 0.4 m a−1 and cause systematic errors within parts of the photography between the ground control. Errors in setting the mark in the photograph-measuring equipment on features are 0.5 m for each epoch, or 0.7 m a−1 in velocity, and should be random. Distortions in the photograph block due to weak ties are 1.5 m, or 2.1 m a−1, and should be systematic over 11.5 km, the photograph dimension. The root sum of squares of these known errors is 2.2 m a−1. Errors due to incorrect tracking of features between epochs are difficult to assess, but an additional 1.0 m a−1 random error seems reasonable. Certain errors, such as in the absolute positions of the control stations are systematic over the entire region and so do not affect strain rates. The estimate of the net error in each component of velocity is thus 3.2 ma−1, which as noted is consistent with the check on self-consistency once the supposed blunders have been removed.
Errors in elevation are difficult to estimate. Systematic slope errors can result if stereo-models are tilted, which would result in a checkerboard pattern in Figure 2a or the corresponding map for 1985 with squares about 11.5 km on a side. No such patterns are evident, so the problem is discounted. Typically, elevations are about twice as poorly determined as horizontal positions in this type of photogrammetry, meaning that elevations are precise to about 3 m.
Elevations, Velocities and Strain Rates
Elevations of the snow surface are shown in Figure 2a. The grid and contouring use elevations from within the region depicted, as well as from pass-points outside the map. As already noted by Reference Schulson and HiblerShabtaie and others (1987), the ice-stream surface is lower than the inter-stream ridges to either side, and there is important relief in the ice stream.
Speeds are fastest in the center of the ice stream (Fig. 2b and c). They decrease toward each shear margin and drop off rapidly within the shear margins. Within the ice stream, flow directions are approximately parallel to the margins. At the margins, there is flow into the ice stream from the inter-stream ridges.
Variations in the transverse component of velocity (Fig. 2d) are larger than variations in the longitudinal component (Fig. 2c). This contrasts with Dye 3 on the inland ice of Greenland (Reference Whillans, Jezek and GundestrupWhillans and others, 1984). The cause of the lateral motions in Ice Stream Β is not known but it is suggested below that it is due to adjustments as the ice slides over basal irregularities.
Two coordinate systems are used. The first, (x,y) system as used in Figure 2, is externally defined (Appendix 1) and is parallel to the edges of the figures. The second, (l,t) system follows the flow, in which the longitudinal axis, l, is parallel to the local velocity vector and the tranverse axis, t, is perpendicular and anticlockwise from the l-axis. The major disadvantage of the (x,y) system is that it cannot be parallel to both shear margins; strong simple shear parallel to the shear margin results in large normal strain rates that dominate maps.
Velocity gradients (Fig. 3) are taken over two grid intervals in the (x,y) system (that is over 1000 m). Because the velocity values are accurate to about 3.2 m a−1, there is a standard error of 4.5 × 10−3 a−1 in velocity gradient and in normal strain rate and 3.2 × 10 a−1 in shear strain rate. Shear strain rates are more precise because they are the average of two velocity gradients. Velocity gradients in the flow-following coordinate system are calculated from those in the (x,y) system.

Fig. 3. Strain rates in the flow-following coordinate system. The flow direction is the angle from x-axis, positive anticlockwise. Isoline interval is 5° for the angles and 5 × 10−3 a−1 for strain rates.
There is longitudinal stretching and lateral convergence. Longitudinal extension, ![]() is small and positive within most of the ice stream (Fig. 3b). Lateral extension, (
is small and positive within most of the ice stream (Fig. 3b). Lateral extension, (![]() in Figure 3d) is generally negative but varies in a complex fashion, largely in association with surface relief as discussed below. A pattern of longitudinal stretching and lateral compression is consistent with maintenance of discharge in the progressively narrower width of the ice stream.
in Figure 3d) is generally negative but varies in a complex fashion, largely in association with surface relief as discussed below. A pattern of longitudinal stretching and lateral compression is consistent with maintenance of discharge in the progressively narrower width of the ice stream.
The shear margins are marked by zones of very closely spaced and intersecting crevasses, called chaotic zones. The outer margin of the chaotic zone has a well-defined boundary but the inner margin is diffuse. The shear strain, ![]() (Fig. 3c) also shows this sharp outer boundary.
(Fig. 3c) also shows this sharp outer boundary.
Lateral shearing, ![]() is the dominant velocity gradient on the ice stream. For 71% of the studied area, its value exceeds that of other velocity gradients, meaning that longitudinal tension and lateral compression are secondary in importance. The value of shearing reaches values of ±0.15 a−1 near each side, a value in close agreement with that obtained by Reference Vornberger and WhillansVornberger and Whillans (1990) through modeling the hook-shaped marginal crevasses outboard of the chaotic zone.
is the dominant velocity gradient on the ice stream. For 71% of the studied area, its value exceeds that of other velocity gradients, meaning that longitudinal tension and lateral compression are secondary in importance. The value of shearing reaches values of ±0.15 a−1 near each side, a value in close agreement with that obtained by Reference Vornberger and WhillansVornberger and Whillans (1990) through modeling the hook-shaped marginal crevasses outboard of the chaotic zone.
Another measure of the importance of lateral shearing to the flow of the ice stream is the fraction of ice speed that is faster than or equal to the mean. The larger the fraction, the more plug-like the profile is. A V-shaped transverse profile of speed would have a fraction of 50% and extreme plug flow would have a fraction that is 100%. For Ice Stream B, this “plugness” fraction increases from 58% at x = 0 km to 65% at x = 12 km and 70% at x = 32 km. In the transect of Reference Whillans and BindschadlerWhillans and Bindschadler (1988), 130 km down-glacier, the fraction is 68%. Lateral shearing dominates the ice stream.
The flow direction (Figs 2b and 3a) varies in a very simple manner, showing ice from the inter-stream ridges joining the ice stream.
Crevasse Orientation
Crevasses are easily mapped on glaciers and may be used to infer features of the flow (as done by Reference Vornberger and WhillansVornberger and Whillans (1986, Reference Vornberger and Whillans1990)). Both mapped crevasses and measured velocities are available in the present case. This provides an opportunity to discuss the origin and dynamic significance of crevasses. It turns out that some of the deductions of Reference Vornberger and WhillansVornberger and Whillans (1986) are incorrect and there are challenging problems concerning the origin of crevasses.
Crevasses are taken to form in a direction perpendicular to that of the principal extending strain rate if that strain rate exceeds some threshold value (Reference Meier, Kamb and SharpMeier and others, 1974; Reference Raymond and ColbeckRaymond, 1980). This prediction for crevasse orientation seems to be valid for Blue Glacier, Washington State, U.S.A. (Reference Meier, Kamb and SharpMeier and others, 1974), Columbia Glacier, Alaska, U.S.A., near the terminus (our study of a photograph provided by R. Krimmel and principal strain rates in Reference Meier, Rasmussen, Krimmel, Olsen and FrankMeier and others (1985)), and Byrd Glacier, Antarctica (photographs provided by Η. H. Brecher and strain rates in Reference Whillans, Chen, van der Veen and HughesWhillans and others (1989)). The Ross Ice Shelf near the Bay of Whales shows general agreement between crevasses and principal-strain axes except near large folds in the ice (Reference Zumberge, Giovinetto, Kehle and ReidZumberge and others, 1960). (However, there seems to be a problem with the orientations of principal extending-strain rates in their table 1, p. 138. These show no angles outside the range of ±45°. There may be an error in calculating ½ arctangent.) Frequently, crevasse orientations are perpendicular to principal extending-strain rates.
There are examples of other crevasse orientations. Near the Bay of Whales, some crevasses were observed showing strike-slip motion. For a site in northwest Greenland, strain rate and crevasse orientation disagree (Reference MeierMeier, 1958). These exceptions could be old and rotated crevasses, and so be misaligned with their present strain-rate field.
On Ice Stream B, theoretical orientations of crevasses are mainly diagonal to flow (Fig. 4b) but observed crevasses are mainly transverse (Fig. 4a). The short diagonal crevasses at the outer edges of the chaotic zones and crevasses in certain small regions within the body of the ice stream are perpendicular to extension. However, disagreements are more widespread.

Fig. 4. (a) Observed crevasses from a mosaic of aerial photographs. Stippling indicates the chaotic zone, and lines within it different degrees of crevasse intensity. Ground-control stations are indicated by squares. The crevasse train marked Τ and roß marked R are discussed in the text, (b) Modeled crevasses. Each hair is perpendicular to the direction of the principal extending strain rate. The length of each hair is proportional to (principal extension strain rate −0.005 a−1). No hair is drawn if that strain rate is less than 0.005 a−1.
The directions of calculated crevasses are the same whether deviatoric stresses or full stresses are used, although, of course, the position of the boundary of crevassed zones depends on the threshold used for crevasse onset.
On Ice Stream B, it may be supposed that the discrepancy between observed and predicted crevasse orientations is due to crystallographic anisotropy, the c axes in the ice stream being directed across the flow. Such a crystal orientation makes the ice soft to lateral drag and would allow rapid lateral shearing without large shear stresses. Longitudinal tension would be larger and lateral drag smaller than the corresponding strain rates would suggest. The quantitative effect of anisotropy has been inferred from the Dye 3 corehole (Reference Dahl-Jensen and GundestrupDahl-Jensen and Gundestrup, 1987). Enhancement factors reach values of about 3 at Dye 3, when expressed in terms of a flow law written to provide strain rates in terms of stress. When converted to the inverse form of the flow law for calculating stress from strain rate, the factor of 3 becomes 0.7 or 1.4, depending on whether the fabric favors or disfavors deformation, respectively. The effect is small. Observed shear strain rates are about 4 times the longitudinal stretching for most of the ice stream (Fig. 3c and b). Even with strong crystal anisotropy, lateral drag stress is about twice as large as longitudinal tension and crevasses should form diagonally. The presence of anisotropic ice is not sufficient to account for the discrepancy.
Nor can the crevasses be due to compressive stress. Such cracks have been reported by Reference Schulson and HiblerSchulson and Hibler (1991) for sea-ice and laboratory samples. However, on Ice Stream Β the principal compressive strain axis is diagonal not transverse like the crevasses. Moreover, no wing-like steps have been noticed in the ice stream, as expected if they were compressively formed.
Thus, the misalignment of crevasses with strain rate is not explained by special stress orientations.
Crevasses are not formed where they are first observed. To be detected on the imagery, they must open sufficiently for the snow bridge over them to sag or collapse. During this time, the crevasse can rotate from its orientation of formation. The hook-shaped crevasses at the extreme outboard margins of the ice stream are formed in this way; they form diagonally to the ice stream, then their older ends are rotated by simple shear to form curved crevasses that are concave down-glacier (Reference Vornberger and WhillansVornberger and Whillans, 1990). This process of progressive crevasse rotation must be common on the ice stream.
However, progressive rotation is not evident on the map of crevasse trains, despite the presence of strong, simple shear. For example, the prominent train near the southern edge of the ice stream (labelled “T” in Figure 4a) is in a region where the velocity gradient, ![]() is −0.02 a−1. Ice velocity is about 350 m a−1. The length of the train is 20 km. Combining these numbers and assuming steady conditions, one finds that each transverse crevasse should rotate about 1.1 rad in traveling the length of the train. However, the crevasses in this train are all transverse (Fig. 4a). They do not undergo the expected progressive change in orientation as they move along the train.
is −0.02 a−1. Ice velocity is about 350 m a−1. The length of the train is 20 km. Combining these numbers and assuming steady conditions, one finds that each transverse crevasse should rotate about 1.1 rad in traveling the length of the train. However, the crevasses in this train are all transverse (Fig. 4a). They do not undergo the expected progressive change in orientation as they move along the train.
The explanation is that crevasses require time to open to a visible size or form a snow bridge that sags to a noticeable degree. In a region of simple shear, they reach a maximum opening once they are transverse to flow. After crevasses swing beyond that orientation, velocity gradients tend to close them. Thus, the most obvious crevasses should be transverse, as observed. If the snow-burial rate can nearly keep up with crevasse opening, only transverse crevasses appear, despite the regime of simple shear. Transverse crevasses dominate Ice Stream B, although there are some exceptions. On Ice Stream B, it must be that crevasse burial by drifting snow is very effective.
The analysis of the map of crevasses, together with the measured velocity gradients, leads to the conclusion that crevasses in an accumulation zone cannot be used reliably to infer direction of stress. Snow accumulation hides both new and old crevasses.
A further consequence of the discovery that most crevasses are transverse in a regime of simple shear is that visible crevasses are as old as the time needed to rotate 45° which, in this case, means that they are formed only about 15 km up-glacier. They are not advected in from great distances.
Crevasse Trains
It is not clear why crevasses occur in trains. We speculate that this grouping is due to zones of strong crystal-orientation fabric or higher temperature. Crevasse trains are supposed to overlie zones of weak ice. Strong foliation is commonly observed in valley glaciers (e.g. Reference Allen, Kamb, Meier and SharpAllen and others, 1960). The degree of foliation varies from site to site and tends to be aligned longitudinally. There could be associated variations in ice strength. Warm ice can be formed by lateral shearing and would be distributed in bands corresponding to relict shear margins, as noted in Appendix 2. We postulate that zones of foliation or warmth that are weak to lateral drag have been advected into the ice stream, and that crevasse trains mark these zones.
Ice-crystal-orientation fabric has been determined near the UpB camp where there is no visible crevasse train. There, the c axes form a large-circle girdle whose axis of symmetry is directed down-glacier (Reference BlankenshipBlankenship, 1989). In agreement with the postulate, this fabric is not especially soft to lateral shearing.
The interpretation of the results of the strain grid near the UpB camp also point to structural or temperature variation in the ice stream. Unusual spatial variations in strain rate near the UpB camp are interpreted to be due to horizontal changes in the strength of the ice (Reference Whillans and van der VeenWhillans and Van der Veen, 1993b).
The hypotheses advanced for the formation of crevasse trains may also apply to longitudinal ridges (Reference Vornberger and WhillansVornberger and Whillans, 1986) as well as flow traces (Reference Merry and WhillansMerry and Whillans, 1993). Under lateral compression, soft ice must be squeezed upward more than neighboring stiff ice. These longitudinal features may mark zones of ice that are soft because of strain heating or special crystal-orientation fabric.
Crevasse Intersection
The crevasses in crevasse trains often intersect at shallow angles. It had been expected that a crevasse, once formed, would alter the stress field near it, such that any later-formed crevasses would intersect it at right-angles (e.g. Reference HughesHughes, 1977). However, orthogonally intersecting crevasses are unusual on the ice stream (for example, in the crevasse trains in Figure 4a).
The conclusion must be that stresses are not greatly relieved by crevasse formation. This is difficult to understand in terms of the conventional model. A stress is necessary to break the ice but, once broken, the void within a crevasse cannot support stress. The observation of acute crevasse intersections indicates that the conditions that form crevasses act in a place where crevasses do not affect stress transmission, i.e. at depth in the glacier, below the depth of penetration of crevasse openings. Evidently, new crevasses form independently of old crevasses and crevasses are a surface manifestation of a deeper-seated process.
This is a severe problem in understanding the significance of crevasses. By way of stimulating discussion, we speculate that this deeper process is recrystalliz-ation to form veins of soft ice. It is known that ice crystals that are undergoing creep are periodically consumed and new crystals are formed. The new crystals form at orientations that favor deformation (Reference KambKamb, 1972). These new crystals are weak and cause increased stress on adjacent crystals. This favors the recrystallization of adjacent crystals. Such a feed-back may cause a front of recrystallization to move through the glacier, leaving a plane-shaped scar. Certain veins in rocks may form in this way and so we term the scars “veins”. The veins propagate in many directions, including upward. We speculate that, when a vein due to tension approaches the free surface, the ice and firn part by fracture and form a crevasse. The veins harden quickly. A strain of about 7% is sufficient for the new crystals to become as stiff as older, country ice (Reference Jacka and MaccagnanJacka and Maccagnan, 1984). This takes about 7 years, or a travel distance of 2.5 km for the crevasse train marked “T”. Thus, new veins can cross old veins without great deflection. According to this interpretation, crevasses indicate the existence of cyclic recrystallization in the glacier and form perpendicularly to tensile stresses large enough to break the firn.
Possible Rafts
A raft is a section of inland ice that has been incorporated wholesale into the ice stream and that is stiffer than the surrounding ice stream (Reference Whillans, Bolzan and ShabtaieWhillans and others, 1987; Reference Bindschadler, Vornberger, Stephenson, Roberts and MacAyealBindschadler and others, 1988). At (x,y) = (4,7.5) km in Figure 4 and marked with the letter “R” is a possible raft. This anomalous region contains fewer exposed crevasses and is deforming by lateral shearing more slowly than the ice north and south (Fig. 3c). Both observations indicate that the region is different from the surrounding ice. There is another possible raft at (x,y) = (4,14) km, just to the south ofthat marked with the letter “R”.
The region marked “R” may be the down-glacier tip of tributary B2b, as mapped by Reference Merry and WhillansMerry and Whillans (1993) using SPOT HRV imagery. A definite correlation between the feature marked “R” and tributary B2b is not possible because the photograph block and SPOT imagery do not overlap. However, extrapolation of the shear margins defining tributary B2b into the photograph block strongly indicates such an identity. The zone of extra shear-strain rate (about 0.010 a−1 ) in Figure 3c, at y = 10 km, may be the shear zone between tributaries B2a and B2b. Tributary B2b is wedge-shaped, having shear zones on either side, and becomes narrower down-glacier. Because of the extreme along-flow decrease in width of the tributary, some kind of non-steady flow is probable.
The possibility that a basal sticky spot could account for this feature is discounted. Reference Retzlaff, Lord and BentleyRetzlaff and others (1993) have mapped ice thickness in this region. There are no related features in the bed (Fig. 5) that can account for these features. A sticky spot at about y = 12 km may be supposed to underlie the southern edge of the feature, which is at y = 10km. Sticky spots retard basal ice flow and, if large enough, generate special strain rates at the surface. For example, larger lateral shear rate at y = 10 km, on the southern side of the feature (attributed above to the shear zone between tributaries B2a and B2b) may be due to ice shearing past a basal resistance. However, there is no appropriate variation in longitudinal stretching (Fig. 3b), which is nearly constant. Over a sticky spot, there should be an along-flow switch from more to less stretching, as modeled and observed elsewhere by Reference Whillans and JohnsenWhillans and Johnsen (1983). Also, if a sticky spot can cause extra shearing to the south, it should have a similar retarding effect on ice flowing past its northern side. The shearing rate to the north is of the wrong sense for this. Both the lack of appropriate variation in longitudinal stretching and shearing of the wrong sense on the north side rule against a sticky-spot interpretation.

Fig. 5. Ice thickness. Data were collected along flight lines indicated. Data are provided by N. Lord (personal communication) and described by Reference Retzlaff, Lord and BentleyRetzlaff and others (1993). Isopach interval is 20 m, which is somewhat finer than the standard error of the measurements (30 m).
Spreading Ridges
Shallow ridges and troughs are common in the ice-stream surface (Reference Vornberger and WhillansVornberger and Whillans, 1986; Reference Shabtaie, Whillans and BentleyShabtaie and others, 1987). Two such ridges are highlighted by very thick contours in Figure 2a. Their long axes are about 15° and 40° from the flow direction. A major diagonal surface trough runs close to the UpB camp. In contrast with most of the rest of the ice stream, transverse spreading, ![]() is positive (Fig. 3d) at the topographic ridges.
is positive (Fig. 3d) at the topographic ridges.
On other glaciers, there is a correlation between spreading and surface slope. That is, the along-glacial surface slope is steep where longitudinal extension changes from a maximum to a minimum. This pattern exists along the Byrd Station Strain Network in West Antarctica (Reference Van der Veen and WhillansVan der Veen and Whillans, 1989), on Storglaciären, Sweden (Reference Hooke, Calla, Holmlund, Nilsson and StroevenHooke and others, 1989), on Variegated Glacier, Alaska, U.S.A. (Reference Raymond and ColbeckRaymond, 1980, Fig. 10b and c), near Dye 3 in Greenland (Reference Whillans, Jezek and GundestrupWhillans and others, 1984) and on Byrd Glacier, in the Transantarctic Mountains (Reference Whillans, Bolzan and ShabtaieWhillans and others, 1989). Such a pattern is readily explained as being due to some local resistance to flow such as a basal obstruction or sticky spot (Reference Whillans, Van der Veen and OerlemansWhillans, 1987). No such patterns are found on Ice Stream B.
On Ice Stream B, not only are spreading and slope linked differently in phase but the major spreading anomalies are perpendicular to the ridges and not longitudinal. As noted by Reference Bindschadler, Stephenson, MacAyeal and ShabtaieBindschadler and others (1987, p. 8888) for a ridge near the DNB camp, the pattern of spreading strain tends to diminish the ridges. These patterns of slope and strain rate are reminiscent of upwellings in water, although of course inertial forces are not important in ice flow.
We suggest that the ridges are formed by riding of the glacier up reverse basal slopes. Surface topographic highs overlie sites where the bed has a reverse along-flow slope (Figure 5; and note that gradients in the map of ice thickness are almost entirely due to bed elevation). The forward motion of the ice up this slope lifts the glacier to form the ridges. Such positive topographic features tend to collapse toward isostasy. There may be some contribution from bending of ice as it moves over the top of a basal feature but the effect is relatively minor. The relaxation tendency accounts for the observed strain rates according to an altered version of the model in Reference Whillans and JohnsenWhillans and Johnsen (1983), in which the ice is taken to have Newtonian viscosity. Ice viscosity in the range of 50100 MPa a is used, as found applicable at Dye 3 (Reference Whillans, Van der Veen and OerlemansWhillans and Jezek, 1987) and at Byrd Station (Reference Whillans and JohnsenWhillans and Johnsen, 1983). According to this model, the ridges are tied to basal features, in line with the assumption of Reference Bindschadler and ScambosBindschadler and Scambos (1991) that long-wavelength features on Ice Stream Ε are fixed with respect to the bed. However, at least on Ice Stream B, there is no paired up-glacial extension and down-glacial compression, so the ridges are not associated with a large variation in basal drag, nor does the topographic effect of the reverse slope seem to have much effect on the forward motion of the glacier.
Discussion
On the broad scale, the measurements confirm earlier deductions that Ice Stream Β is well-defined by intense shear zones (Reference RoseRose, 1979; Reference Vornberger and WhillansVornberger and Whillans, 1986; Reference Shabtaie, Whillans and BentleyShabtaie and others, 1987). Important shearing extends across the width of the ice stream. Comparable results, also using repeat photogrammetry, are found down-glacier near the narrowest part of the ice stream (Reference Whillans and BindschadlerWhillans and Bindschadler, 1988).
Some earlier analyses of the relative roles of different strain-rate components are largely incorrect. Reference Vornberger and WhillansVornberger and Whillans (1986) made the seemingly reasonable assumption that the observed orientations of crevasses indicate stress directions, the principal tensile stress and strain rate being perpendicular to crevasses. However, the present work shows that, by the time that crevasses are wide enough to cause observable sagging or collapsed snow bridges, they have been rotated considerably by simple shear from their orientation at formation. Thus, the conclusion that longitudinal tension is the largest map-view stress is invalid. In another study, Reference Whillans, Van der Veen and OerlemansWhillans (1987) used measured bending of a line of poles near the center of the ice stream to argue that lateral shearing is unimportant. That line is at the dynamic center of the ice stream and is not representative. Both works incorrectly concluded that side drag is unimportant. The present work shows that the dominant strain rate is shearing from the sides.
The problem of the origin of crevasses is common to many, if not most, glaciers: crevasses often intersect at acute angles. This means that crevasse formation is not a simple matter of stress relief. If it were, crevasses would have perpendicular intersections. Crevasses must be caused by a process acting deeper than the depth of crevasse penetration. We speculate that crevasses are surface manifestations of veins of recrystallized ice. In any case, crevasses must first form at depth, say 50 m below the snow surface, and then grow upward. Thus, the depth of burial of crevasse voids is not simply linked to the time since crevasse activity: buried crevasses can still be active. This must be considered in estimating the time since ice streams became inactive, as Reference RoseRose (1979) has done on the basis of crevasse burial.
It is curious that crevasses form in trains. This issue is not resolved here. Extreme interpretations are that entire crevasse trains are formed almost at once, perhaps associated with an acceleration in ice motion, or that there are filaments of strong and weak ice in the ice stream due to lateral changes in ice temperature or ice-crystal orientation.
The complex variations in ice-flow direction within Whillans and others: Velocity pattern across Ice Stream B, Antarctica the ice stream also are difficult to understand. The largest side-to-side fluctuations in ice flow are associated with narrow surface topographic ridges. These show spreading perpendicular to their axes. The features are interpreted to have been caused by ice riding up reverse basal slopes. There is at least one raft of stiff ice within the study area that may be being advected within the ice stream. An analysis of SPOT imagery indicates that this raft is very large, and may be part of a tributary extending about 75 km up-glacier (Reference Merry and WhillansMerry and Whillans, 1993). Presumably, the rafts are due to spatial and temporal irregularities in the transition from inland-ice to ice-stream flow. Certain parts of the ice have been subjected to more strain heating or have acquired a stronger crystal-orientation fabric, and so are soft. Such lateral heterogeneity of the ice may account for many of the unusual features observed on ice streams.
Significantly, there is no evidence for sticky spots or obstructions as usually envisioned. Such basal features are expected to retard deep flow by exerting extra basal drag, by partially blocking flow, or both. At the feature, basal resistance should be large and basal speed small. In order to maintain continuity, the ice must have thickened up-glacier to overcome the partial blockage and must have especially large surface speed over the blockage. Basal sticky spots or obstructions can be identified by steeper surface slopes and an associated along-glacier change from large to smaller stretching rate. Such patterns are common on most glaciers but none are found within the studied transect of Ice Stream B. We conclude that the properties of the bed, as they affect basal sliding, are nearly uniform despite the presence of reverse basal slopes.
The spreading ridges are due to flow over basal topographic features but they do not exhibit the effects of extra-basal resistance. There is no along-flow switch from extra to less stretching. Rather, the surface topography and strain rates seem to be due to simple lifting on to a higher bed, and the tendency for the surface feature to flatten with time. The spreading ridges can be accounted for with no special drag concentration. They are formed by approximately constant slip and constant drag on a reverse basal slope.
Acknowledgements
The photography was obtained by J. Mullins of the United States Geological Survey; this was a very difficult undertaking. We thank a referee, R. B. Alley, OR. Bentley and C.J. van der Veen for very valuable comments. This research was supported by U.S. National Science Foundation grant No. DPP-9020760. This is contribution No. 882 of the Byrd Polar Research Center.
The acuracy of references in the text and in this lût is the responñbility of the authors, to whom queues should be addressed.
Appendix 1 Coordinate Systems
The aerotriangulation uses a secant-plane coordinate system (x,1,y1,Z1). This system is Cartesian and involves no map projection or distortions. Its origin is at 83°28′ S, 138° 10′ W, 340 m ellipsoidal height (near the UpB camp), and the x1 and y1 axes are parallel to the tangent plane to the WGS84 ellipsoid at the origin, y1 directed southward. A problem in display is that the z1 coordinates of the surface generally become increasingly negative with distance from the origin due to the curvature of the Earth’s surface. To avoid this, the elevations shown in Figure 2a are ellipsoidal heights.
For plotting convenience, translated and rotated x and y coordinates are used. The x-axis is selected to be approximately down-glacier and perpendicular to the photograph flight lines. The origin is such that all x- and y-coordinate values are positive for the studied region. The transformation is given by:

the value of θ is 7°. Secant-plane coordinates are represented by x1 and y1 .
A further, flow-following coordinate system is used. In this, the l-axis is longitudinal (along flow) and the t-axis is anticlockwise and transverse.
The present maps may be linked to geographic (WGS84) coordinates by utilizing the following equivalents. The coordinates of (0,0) are 83°12′56″S, 136°19′ 27″ W, of (27 km, 0) are 83°14′54″ S, 138°21′23″ W, of (0, 38 km) are 83°33′05″S, 135°51′33″W, and of (27 km, 38 km) are 83°35′10″S, 137°59′42″W.
Appendix 2 Strain Heating
Some of the features within the ice stream may be due to horizontal strength variations. These features include crevasse trains, the rafts and shear margins. Here, a simple calculation is conducted to determine whether strain heating can significantly affect the strength of the ice and potentially account for some of these features.
Temperature increases due to strain heating. For a simple shear rate of, ![]() and the conventional flow law, the causative shear stress is
and the conventional flow law, the causative shear stress is
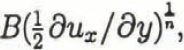
Β being the rate factor and η the exponent. The net heat generated due to this stress and shear rate, while crossing from y = y0 to y = y0 + Δy, is calculated by integrating the product of shear rate and stress over the time needed to transit the width of the shear margin. The heat generation is

in which Cv represents heat capacity per unit volume. To obtain a numerical estimate of this quantity, the shearing rate at the outside part of the shear margin is approximated with a linear relationship to the y-coordinate:
Measurements for the northern shear margin (snake) indicate a value for ![]() of 0.15 a−1 and y = 2 km. Other parameters are: Β = 700 kPaa1/3, Cv = 2 × 106J m−3°C−1 and uy = 5ma−1. The calculation yields a temperature increase of 3.8°C. This is enough to soften the ice by 19% (Reference HookeHooke, 1981). The net heating is directly proportional to Δy/uy
(the transit time through the shear zone) and to
of 0.15 a−1 and y = 2 km. Other parameters are: Β = 700 kPaa1/3, Cv = 2 × 106J m−3°C−1 and uy = 5ma−1. The calculation yields a temperature increase of 3.8°C. This is enough to soften the ice by 19% (Reference HookeHooke, 1981). The net heating is directly proportional to Δy/uy
(the transit time through the shear zone) and to ![]() . We consider the calculation is accurate to a factor of about 2, largely because of uncertainties in the parameters, especially in the value selected for Δy. More strain heating is indicated by a calculation for the southern shear margin (dragon), where uy
is half the value used here.
. We consider the calculation is accurate to a factor of about 2, largely because of uncertainties in the parameters, especially in the value selected for Δy. More strain heating is indicated by a calculation for the southern shear margin (dragon), where uy
is half the value used here.
The model assumes steady transport of ice across the shear margin. For the results to be fully valid, the process must have been operative for Δy/uy = 400 years. This seems improbable, given that the ice streams are changing now. However, strain heating can be important even after shorter time periods.
There are many shear margins up-glacier of the studied part. Tributaries coalesce to form wider ice streams. Warm signatures of former shear margins exist within the ice stream and may account for some of its unusual features.







