1. Introduction
Mountain glaciers are good indicators of climate variability (Reference HoughtonHoughton and others, 2001), since variations in their climatic environment lead to changes in their geometry and dynamics. This relationship remains complex, however, and there is no simple theory connecting glacier changes (extent, thickness, surface velocities) to the driving climatic variations. Apart from some attempts to infer mass balance from terminus positions with the help of a linearized approach (Reference NyeNye, 1963), full numerical ice-flow models seem to be the only way to capture the complexity of such a lagged non-linear response, which involves many processes like ice rheology or basal sliding. Although difficult to model, this lagged response of a glacier to varying climatic conditions offers interesting possibilities of inferring past climatic conditions during periods for which no mass-balance measurements are available. An ice-flow model is also the only way of predicting mid- to long-term glacier response to climatic scenarios. Large ice masses such as polar ice sheets have been extensively modelled over the past few decades mainly for past climate studies and ice-core dating purposes. Most of these approaches rely for their success on the geometrical properties of these ice caps, more specifically their small “aspect ratio” which allows the shallow-ice approximation (SIA) to be used, thereby considerably simplifying the problem (Reference HutterHutter, 1983; Reference MorlandMorland, 1984). The SIA is based on a scaling analysis which expands the equations under the form of series of powers of a scaling parameter, the aspect ratio ϵ (generally the thickness-to-extent ratio (see Reference HutterHutter 1983; Reference Baral, Hutter and GreveBaral and others, 2001)). The order of the problem equals the maximum power of the aspect ratio ϵ after truncation of the series. The SIA traditionally refers to the zeroth-order problem (only terms of the zeroth power ϵ of in the equations, as in the present paper), whereas systems including higher powers are referred to as first-order SIA, second-order SIA and so forth. If a small enough aspect ratio is a prerequisite for the power series to be meaningful, it should be stressed that for a given ϵ, the accuracy of the SIA approach increases with the order of the problem. In other words, the smallness criterion for the aspect ratio becomes even more stringent with the zeroth-order approach.
Unfortunately, the geometrical properties of alpine-type valley glaciers, unlike those of large ice sheets, usually make their vertical- to longitudinal-extent aspect ratio too large for correct applicability of the SIA (Reference FowlerFowler,1992). Moreover, when bedrock slopes become more pronounced or exhibit significant changes at a scale of similar order to that of the mesh spacing, a topography-related aspect ratio significantly larger than the preceding one takes over (Reference Baral, Hutter and GreveBaral and others, 2001), therefore requiring higher-order terms in the series to be incorporated or, at worst, solution of the full Stokes equations.
However, as a “cirque”-type glacier (Fig. 1), Glacier de Saint-Sorlin, France, is somewhat atypical, with its fairly large extent-to-thickness ratio leading to an overall aspect ratio smaller than that of a typical valley glacier with for instance a relatively thick ice tongue channelled into a narrow valley. With a typical thickness of 100 m (and a maximum of 140 m above the central trough), compared to a typical longitudinal extent of 2 km (see Figs 1 and 2), the ce geometry aspect ratio for Glacier de Saint-Sorlin is an acceptably small one of about 5 × 10−2. On the other hand, prescribing the bedrock topography at each of the mesh points of a 50 m spacing grid can potentially increase the topography-induced aspect ratio unless bedrock changes are very smooth. A 50 m spacing yields a 100 m Nyquist wavelength (λN; see Reference Baral, Hutter and GreveBaral and others, 2001), which would require typical vertical variations of <5 m in order for the corresponding bedrock aspect ratio to stay as low as 5 × 10−2. Although the bedrock topography used in the model is fairly smooth at the short scale (see section 3.3) and does not show pronounced slopes at a larger scale nor any major accident such as icefalls, typical variations in bedrock heights can locally be as large as 50 m which certainly reduces the accuracy of the SIA zeroth-order equations. Indeed, as demonstrated by Reference Kamb and EchelmeyerKamb and Echelmeyer (1986), over short-scale undulating beds, the longitudinal coupling exerted by longitudinal stress gradients significantly modifies the flow over a coupling length of the order of several times the ice thickness. Since one of the consequences of restricting to zeroth-order equations is to neglect these longitudinal stress gradients, the SIA we consider in our approach will not allow for accurate modelling of short-scale glacier dynamics.

Fig. 1. Outline of Glacier de Saint-Sorlin based on “mechanical” grounds from interpretation of a 1998 summer picture. Using visible and estimated bergschrund positions, some peripheral permanent snowfields or areas of slow ice motion have been disregarded. See Reference Vincent, Vallon, Reynaud and MeurVincent and others (2000, fig. 1) for a more general location of the glacier.

Fig. 2. 1957–99 averaged net mass-balance data obtained by interpolation and extrapolation of stake measurements (in m w.e. a−1). Outlined are the present-day extent (solid line) and theglacier terminus of 1905 (dashed line).
If SIA-based models are unable to correctly predict diffusion and propagation time-scales, they can still compute the right volume time-scales (Reference Gudmundsson, Raymond and BindschadlerGudmundsson and others, 1998), which are in fact primarily driven by mass-balance changes. Since our main concern is to model glacier past thickness and extent changes and not small-scale dynamical properties (as expressed by surface velocities), the zeroth- order approach should still yield useful results. It was therefore thought that before getting into more complex models by either including higher-order terms (Reference BlatterBlatter, 1995; Reference Hubbard, Blatter, Nienow, Mair and HubbardHubbard and others, 1998; Reference Baral, Hutter and GreveBaral and others, 2001) or explicitly including deviatoric-stress gradients (Reference Colinge and BlatterColinge and Blatter, 1998; Reference GudmundssonGudmundsson 1999), a simple two-dimensional SIA approach was worth performing given the wealth of available data for Glacier de Saint-Sorlin.
A previous modelling attempt based on the SIA but restricted to the one-dimensional case along a flowline (Reference Vincent, Vallon, Reynaud and MeurVincent and others, 2000) provided interesting results which compared well to some of the data. The idea here is to extend to the two-dimensional case, allowing for a better account of the real geometry of the flow and for correct computation of the glacier averaged front positions (see section 5.2.1).
After a short description of the model (section 2), the glacier’s main characteristics and the input data are presented (section 3). Section 4 describes the experimental setup including initial conditions and model parameters. The results section (5) starts with steady-state runs for the present-day and 1905 ice distributions, which yield interesting information about mass balance and show the model’s ability to reproduce past glacier extents. This ability is promising for future inference of past climatic conditions, such as those during the Little Ice Age. Time-dependent simulations follow in order to simulate as realistically as possible the glacier’s behaviour over recent decades. From the comparison with available data, an extensive sensitivity study on ice rheology and sliding factors is carried out and allows us to find a combination of these two parameters that gives the best match for both thickness changes and snout positions through time. Finally, results and their interpretation are discussed in section 6.
2. The Two-Dimensional Ice-Flow Model
2.1. Continuity equation
Spatial variables for the model refer to a right-handed x, y, z Cartesian coordinate system ![]() with x directed towards the east, y the principal direction of flow (north) and z pointing vertically upwards, denoting altitude (z = 0 at the geoid height). The time-dependent changes for the ice thickness H are given by the continuity equation:
with x directed towards the east, y the principal direction of flow (north) and z pointing vertically upwards, denoting altitude (z = 0 at the geoid height). The time-dependent changes for the ice thickness H are given by the continuity equation:
where ![]() stands for the horizontal ice flux and a is the surface accumulation rate expressed as a water equivalent column (m w.e. a−1).
stands for the horizontal ice flux and a is the surface accumulation rate expressed as a water equivalent column (m w.e. a−1).
The flux ![]() is obtained from vertical integration of the ice velocity
is obtained from vertical integration of the ice velocity ![]() from the ice bottom B (bedrock altitude) up to the free surface S according to:
from the ice bottom B (bedrock altitude) up to the free surface S according to:
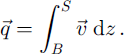
This ice motion results from internal deformation and possibly from basal sliding when basal conditions allow for it. For simplicity, only internal ice deformation is considered at this point. See further below for discussion of how basal sliding is incorporated into the calculations.
2.2. Governing equations under the SIA
The main effect of the SIA is to considerably simplify the conservation-of-momentum equations, which reduce to the expression of the vertical gradient of the two basal shear stresses τ xz and τ yz in the x and y directions as a function of the glacier topography only (for more details see, e.g., Reference MahaffyMahaffy,1976):

where ρ is the ice density (917 kg m−3) and g the gravitational acceleration. With vertical integration (from altitude z to surface S) the two shear stresses are expressed as functions solely of the local geometry (and altitude z), according to:
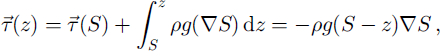
assuming that the surface undergoes no shear stress (τ xz (z) = τ yz (z) = 0). The most commonly used stress–strain relation for the creep of polycrystalline ice in ice sheets and glaciers is a non-linear viscous power flow law of Glen type with exponent n = 3 and a temperature-dependent rate factor A(T) (e.g. Reference GlenGlen,1955):
where ![]() is the deviatoric-stress tensor,
is the deviatoric-stress tensor, ![]() is the strain-rate tensor, T is the temperature measured relative to the pressure-melting point and τ* is the second invariant of the stress tensor. It should be noticed that, as for most alpine glaciers, the ice is considered to be isothermal throughout, with a temperature of 0°C corresponding to the ice melting point at the ambient pressure. Therefore no temperature dependence is taken into account for the rate factor A(T) which then becomes a constant (hereafter referred to as A).
is the strain-rate tensor, T is the temperature measured relative to the pressure-melting point and τ* is the second invariant of the stress tensor. It should be noticed that, as for most alpine glaciers, the ice is considered to be isothermal throughout, with a temperature of 0°C corresponding to the ice melting point at the ambient pressure. Therefore no temperature dependence is taken into account for the rate factor A(T) which then becomes a constant (hereafter referred to as A).
In the SIA, τ* depends only upon the two shear stresses τ xz and τ yz according to:
Given the deviatoric strain-rates expression and noting that under the SIA the horizontal gradients of the vertical component of the velocity vector, ∂w/∂x and ∂w/∂y, can be neglected, the two main deviatoric strain rates ![]() and
and ![]() reduce to (∂u/∂z)/2 and (∂v/∂z)/2, respectively, and some reordering of Equations (3–6) allows us to write:
reduce to (∂u/∂z)/2 and (∂v/∂z)/2, respectively, and some reordering of Equations (3–6) allows us to write:
where ![]() is now the horizontal two-dimensional velocity vector and |∇S|2 stands for (∂S/∂x)2 + (∂S/∂y)2. Integration from z = B (bedrock height) to z finally allows us to express the horizontal velocity
is now the horizontal two-dimensional velocity vector and |∇S|2 stands for (∂S/∂x)2 + (∂S/∂y)2. Integration from z = B (bedrock height) to z finally allows us to express the horizontal velocity ![]() as a function of altitude z within the glacier, ice thickness H and surface gradient terms ∂S/∂x and ∂S/∂y. Now making use of Equation (2), the flux finally becomes:
as a function of altitude z within the glacier, ice thickness H and surface gradient terms ∂S/∂x and ∂S/∂y. Now making use of Equation (2), the flux finally becomes:

Here ![]() represents the contribution
represents the contribution ![]() of any basal horizontal velocity
of any basal horizontal velocity ![]() to the flux. In the present model, basal velocity (if any) is prescribed as a Weertman-type sliding law (Reference WeertmanWeertman, 1964,Reference Weertman1972):
to the flux. In the present model, basal velocity (if any) is prescribed as a Weertman-type sliding law (Reference WeertmanWeertman, 1964,Reference Weertman1972):
in which A
s is a sliding rate factor, p and q are two exponents whose values have been set to 3 and 1 respectively following a study of Reference BindschadlerBindschadler (1983) on basal sliding for West Antarctic outlet glaciers, and ![]() is the basal shear stress. The flux
is the basal shear stress. The flux ![]() due to sliding can then be expressed in a form very similar to that due to ice deformation, according to:
due to sliding can then be expressed in a form very similar to that due to ice deformation, according to:
From Equations (8) and (10), the basic time-dependent equation of the model (Equation (1)) can finally adopt the general form:
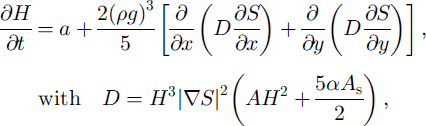
in which the value for the diffusion coefficient D depends on whether sliding is allowed (α = 1) or not (α = 0).
2.3. Numerical approach
Although analytical solutions for the mass-continuity equation do exist for the one-dimensional case, a numerical approach is necessary for a two-dimensional approach. We therefore chose to treat the problem with a time-dependent finite-difference method by digitizing the mass-continuity equation (Equation (11)) onto a regular 50 m × 50 m grid covering a 3.15 km × 3.15 km area over and around the glacier as can be seen in Figure 2. The discretization method follows from the use of a staggered grid in space in which the diffusion coefficient D is computed at gridpoints that are offset from those where the ice surface S is defined by half a grid spacing. This spatial discretization scheme has been fully described by Reference Hindmarsh and PayneHindmarsh and Payne (1996) (method 1). The fully implicit scheme is more stable and allows larger time-steps, but the method is tedious to solve in the two-dimensional case. Instead, we use the alternating-direction-implicit (ADI) scheme, a two-step semi-implicit scheme which solves the x and y directions alternately and results in a matrix formulation (see Reference HuybrechtsHuybrechts,1992, for details).
Boundary conditions for the system are implicitly expressed in the way the diffusivity D is computed. The latter is set to 0 over deglaciated areas at the periphery of the domain, and for points lying exactly on the ice border the computation of the ice-thickness gradient makes use of a backward difference instead of centred finite difference.
3. Glacier Characteristics and Input Datasets
3.1 Glacier main features
Glacier de Saint-Sorlin is a small glacier (3 km2) located in the Grandes Rousses range in the French Alps, with a small altitude range from about 2500 m at the snout to about 3300 m at the upper bergschrund downstream of Pic de l’Etendard as shown in Figure 1.
Because the present-day glacier serves as initial conditions for some simulations, proper outlining of the glacier boundaries was necessary in order to obtain a “mechanically” consistent and continuous body of mobile ice. The limits were essentially set from bergschrund positions when localizable from a 1998 summer aerial picture of the glacier and from proper knowledge of the site. This led us to discard some peripheral misleading snowfields and areas of supposedly immobile ice referred to as “dead ice”as can be seen in Figure 1.
3.2. Mass-balance data
Mass-balance data used to feed the ice-flow model come from direct glaciological measurements for the 1957–99 period and from a relationship between mass balance and meteorological data for the 1907–57 period (Reference VincentVincent, 2002). A linear mass-balance model (Reference LliboutryLliboutry,1974) was used to calculate (i) the 1957–99 averaged net mass balance at each point of the grid from direct stake measurements scattered all over the glacier (seeReference Vincent, Vallon, Reynaud and MeurVincent and others, 2000; Fig. 2), and (ii) interannual variations of this mass balance over the whole period 1907–99 (Fig. 3). The resulting yearly mass-balance forcing was then obtained by adding to the time-in-dependent 1957–99 average distribution (i) the time-dependent variation (ii) which, according to the linear mass-balance model, is the same everywhere. The small altitudinal range for the glacier certainly contributes to the validity of such an assumption (Reference Vallon, Vincent and ReynaudVallon and others, 1998). Obtaining this time-dependent interannual variation is straightforward and reliable for the 1957–99 period (direct stake measurements), whereas its extension back to 1907 (earliest date for which an estimate of the glacier extent is available from a 1905 map) relies on the previously mentioned meteorological relationship. Despite missing data for 1905 and 1906, these reconstructed mass-balance data have been checked against volume changes estimated from the 1905 map and from geodetic measurements of the glacier surface (topography and photogrammetry) carried out in 1952 (similar measurements are also available for 1971, 1989 and 1998). In other words, the 1907–99 time variation in the annual net mass balance as depicted in Figure 3 can be considered a reliable forcing for the ice-flow model. As for mass-balance data downstream of the current snout (necessary for the steady-state simulation of the 1905 extent in section 5.1.2), since no measurements are available, the values were deduced from the closest ones available on the glacier by applying a mass-balance altitudinal gradient of 0.008 m w.e. m−1 (see the resulting distribution extension off the snout in Figure 2). All these mass-balance data are the same (except that 1998 and 1999 measurements are now included) as in Reference Vincent, Vallon, Reynaud and MeurVincent and others (2000) where more information on how they were obtained as well as their accuracy can be found.

Fig. 3. Time variation of the yearly net mass balance with reference to the spatial distribution of Figure 2.The righthandside values from1957 (black dots) come from stake measurements, whereas those before 1957 (gray dots) result from a mass-balance reconstruction (see text).
3.3. Bedrock and ice-surface topographies
The last set of required data for the model consists of the respective bedrock and current ice topographies (some of our simulations start from the present-day ice distribution). As for the bedrock, the digital elevation model (DEM) results from a compilation of various measurement techniques including borehole coring, seismic soundings and gravimetric measurements. The first seismic campaign was carried out on the lower part of the glacier in 1961 (Reference BelinBelin, 1962), but is believed to contain mistakes (Reference LliboutryLliboutry, 2002) probably because of the method used (Reference SüsstrunkSusstrunk, 1951). New seismic soundings were undertaken by Vallon in 1975 and 1976 over the ablation zone and along the central line of the glacier almost up to Col des Quirlies, with an improved method for determining mirror-point locations (Reference VallonVallon, 1978). About 20 regularly scattered boreholes were also drilled between 1967 and 1977, offering an accurate (albeit sparse) coverage of the glacier. These boreholes provided a good check on the seismic data and were also used as constraining thicknesses for gravimetric measurements that were also made by Vallon in 1975. These measurements (M.Vallon, unpublished information) were performed with an accuracy of 10−2 mgal (Warden gravimeter) and were corrected for topography over a distance of 65 km.
All these measurements, in combination with a present-day surface DEM obtained by photogrammetry (1998 aerial photograph), served as a basis for compiling and kriging maps of bedrock elevation and present-day ice thickness. Because of the scarcity of the measurements (limited number of survey lines and measurement spots) and also the variety in the methods, data have been interpolated and extrapolated over large distances and a global accuracy is difficult to assess. Reference LliboutryLliboutry (2002) estimates a standard error of ±5 m but it is expected that over the most poorly covered places (e.g. in the area of Pic de l’Etendard) the uncertainty of the bedrock height can locally be as much as 20–30 m. This interpolation/extrapolation process over large distance onto our 50 m grid led to a significant smoothing of the bedrock data, a prerequisite for the SIA to apply (see section 1). Corresponding bedrock topography is shown in Figure 4, and also in more detail but only for the lower part of the glacier in Reference LliboutryLliboutry (2002, fig. 3). As for the current surface DEM obtained by photogrammetry, the accuracy is of the order of 1 m. The present (1998) ice thickness obtained by difference between the two maps is shown in Figure 5.

Fig. 4. Bedrock topography from the DEM (see text). Also outlined is the 1998 extent of the glacier.

Fig. 5. Present-day (1998) ice distribution.The maximum ice thickness of slightly less than 140 m lies above a southwest–northeast-oriented trough between points “600 m” and “1400 m’. Points labelled 600, 1400, 1800 and 2200 m refer to the distance from Col des Quirlies and are the same reference points as inReference Vincent, Vallon, Reynaud and MeurVincent and others (2000). Also shown is the cross-section location (near point 2200 m) used for computing the snout average position (see section 5.2.1).
4. Experimental Set-Up
4.1. Initial conditions
The model is run forward in time from initial conditions usually consisting of the 1998 ice distribution or that of 1905 derived from a 1:10 000 scale map whose accuracy is uncertain but assumed to be <5 m. Since the ice is considered to be isothermal, the only forcing comes from the changes in mass balance at each gridpoint, obtained by adding the appropriate time correction as depicted in Figure 3 to the 1957–99 average mass-balance distribution shown in Figure 2.
4.2. Basal hydrology and general seasonal effects
Basal conditions play an important role in glacier dynamics by essentially controlling whether the ice is sliding on the bed and, if so, the intensity of the sliding. These conditions are of two main types: those relating to the bedrock itself, which can be assumed constant through time, and those due to the basal hydrology, which are highly dependent upon seasonal changes (e.g. Reference Hubbard, Blatter, Nienow, Mair and HubbardHubbard and others, 1998). Although time-steps in the model are in the order of several days, seasonal effects are not accounted for, essentially because time-dependent mass-balance data are yearly averages and therefore do not carry any seasonal forcing. As a consequence, time dependence of the basal hydrologic forcing cannot be properly accounted for. We are therefore led to prescribe a general sliding law that is supposed to account for both bedrock properties and a time-independent hydrology.The spatial variability of sliding is also a problem since its correct modelling would require detailed knowledge of both bedrock characteristics (roughness, hardness) and the hydrologic system. A Weertman-type sliding law like the one proposed in this studycan reproduce any spatial variability only very crudely, and in a way that in some places must be quite far from reality.
The seasonality in sliding is necessarily reflected in the glacier observed surface velocities. For the reasons explained above, the model is not capable of reproducing seasonality, so it only outputs yearly-averaged fields. It might therefore be tempting to overcome the problem by comparing modelled velocities to yearly velocities measured in the field from differences in stake positions from one year to the next, as inReference Vincent, Vallon, Reynaud and MeurVincent and others (2000). As discussed in section 1, however, the geometry of the problem (that of the ice body itself but also that of the bedrock) makes the restricted SIA equations unsuitable for reproducing small-scale dynamics such as surface velocities. Moreover, even if one assumes favourable geometry with a sufficiently small aspect ratio, water input at the base of the glacier reduces basal friction. Theoretical considerations by Reference Hindmarsh and PeltierHindmarsh (1993, Reference Hindmarsh1996) show the necessity of quite a high basal traction for the SIA to apply. This statement has recently been confirmed by Reference GudmundssonGudmundsson (2003), according to whom longitudinal stresses become important when friction at the bed is small. This means that even yearly mean velocities cannot be reproduced by a SIA model (Reference Vincent, Vallon, Reynaud and MeurVincent and others, 2000), so it is irrelevant to model velocities with such an approach. Consequently, velocities are not considered in this paper. It also means that during phases of high melting, the appropriateness of the SIA in predicting thickness or length changes of the glacier is temporarily reduced. Resulting inaccuracies must, however, be more or less smoothed out when outputting yearly averages for these fields as our model does.
4.3. Model parameters
Table 1 summarizes the main parameters used in the model. Some of them are kept fixed throughout the study, whereas the ice rate factor, the sliding factor and the mass-balance change will vary within the depicted ranges as required by the forthcoming experiments. The time-step was set to 0.05 years (18 days) from a small experiment (not shown) in which a continuous range of values was tested until a convergence criterion was safely met. For the ice rate factor A, a value of 1.3 × 10−24 Pa−3 s−1 (Reference Vincent, Vallon, Reynaud and MeurVincent and others,2000) was used until later in the sensitivity study when the value was allowed to vary. The sliding factor was initially set so as to produce as much ice flow as that from ice deformation for a typical ice thickness of 100 m (A s = 15 × 10−14 m8 N−3 a−1). This parameter will also vary in a similar fashion to the ice rate factor during the forthcoming sensitivity study.
Table 1. Main parameters used in the model and their possible range of variation

5. Results
Results are of two types.We first present various steady-state experiments for which the optimal choice of dynamic parameters (ice rate and sliding factors) is not so crucial, but which give some insight into mass-balance characteristics for the glacier. Conversely, the following time-dependent experiments will appear more sensitive to these two parameters, as will be seen in the parameter study.
5.1. Steady-state experiments
5.1.1. Present-day ice distribution
The simplest experiment started from the present-day (1998) ice distribution and involved running the model forward in time with the 1957–99 average mass-balance field (Fig. 2) until steady state was reached. Unless otherwise specified, parameters are those appearing in the “Reference value” column of Table 1. The initial ice distribution is depicted in Figure 5, whereas the final state of the glacier after steady state has been reached is shown in Figure 6. Inspection of these figures shows that the current ice distribution is far from equilibrium and has not entirely adjusted to the last four decades of mass balance. In other words, the glacier still reflects the effects of pre-1957 mass-balance values which were significantly higher than for the last 45 years (see Reference VincentVincent, 2002, fig. 9a). This is in line with a generally decreasing mass balance since at least the beginning of the 20th century, to which the glacier has been responding with some lag. Indeed, as can be seen from the 1905 extent in Figure 6, the current glacier retreat is already pronounced today and could easily continue, should the mass balance stay the same, as demonstrated by the steady-state run. From this simulation, we found an average loss of 9.6 mw.e. over the present (1998) surface. Cumulative specific net balance over a similar period, 1957–97 (Reference Vincent, Vallon, Reynaud and MeurVincent and others, 2000), gave an average loss of 12.4 m w.e. over a significantly larger glacier area (that of 1971). The reason for such a discrepancy is that the 1957 glacier configuration is more out of balance than that of 1998 with regard to the 1957–99 (or 1957–97) average mass-balance distribution.

Fig. 6. Steady-state ice distribution corresponding to the 1957–99 average mass-balance distribution and obtained after 250 years of simulation.The longitudinal profile used in Figure 8 for assessing the necessary mass-balance increase in section is also depicted.
Another interesting issue is the time required for the glacier to reach steady state. For this purpose, the model outputs a “stationarity index” which represents the average of yearly thickness changes over all glacier-covered gridpoints. This index is represented in Figure 7 and shows that it takes about 250 years of constant forcing for the glacier to asymptotically reach equilibrium with the 1957–99 average mass-balance distribution.

Fig. 7. Stationarity index for the model in terms of averaged yearly thickness changes (in m w.e. a−1). Also shown is the corresponding cumulative curve, which reveals that the average loss for the glacier is 25 m w.e. Experimental design is that of the steady-state run of section 5.1.1. After 40 years, the glacier has lost an equivalent layer of 9.6 m, whereas 71 years of simulation are necessary for the initial imbalance to reduce by 63% after15.7 m have been lost (see conclusion).
An alternative way of quantifying the present glacier degree of imbalance with regard to the 1957–99 average mass-balance distribution consists of assessing by how much this mass balance should be raised for the corresponding steadystate glacier to remain the same as today. Given the previous initial “thickness imbalance”as depicted in Figure 7, the expected increase should be close to + 0.30 m w.e. a−1. The same experiment was therefore repeated, but now with various uniform increases of the 1957–99 mass-balance distribution. Results are depicted on a longitudinal profile in Figure 8 where it can be seen that the required increase lies between the + 0.25 and + 0.30 m w.e. a−1 curves, but closer to + 0.25 m w.e. a−1 (probably a consequence of the evolving surface of the glacier over which this mass-balance increase is applied).The two “extreme”runs show the quite high sensitivity to the balance shift, since the + 0.10 m w.e. a−1 run gives a significant recession, whereas the + 0.50 m w.e. a−1 run leads to a major advance. In order to ensure that the simulations have been carried out for a long enough time for a steady state to be reached, the “stationarity index” was used again and showed about the same required time of about 250 years of simulation as was found earlier.

Fig. 8. Glacier steady-state longitudinal profiles as a function of the mass-balance increase (cm w.e. a−1) applied to the 1957–99 average distribution. A good match with the 1998 profile requires an increase of 25–30 cm w.e. a−1. Profile location is depicted on Figure 6.
Finally, careful inspection of Figure 8 reveals an overthickening at several places along the profile (except for the + 0.10 m w.e. a−1 run). A different parameter set, especially for the ice deformation rate or the sliding factors, may give a better match, although such steady-state experiments appeared to be quite insensitive to these dynamic parameters. Uncertainties in the bedrock heights can also explain this mismatch. The inferred mass-balance shifts nevertheless remain reliable owing to the extreme sensitivity of the snout position to the shift values (Fig. 8).
5.1.2. The 1905 ice extent
Given the rather precisely known extent of the glacier in 1905, it was also interesting to find out whether, starting from different initial conditions like the present ones, any steady-state simulation could reproduce this shape. Moreover, assuming that the glacier was close enough to steady state at the beginning of the 20th century, the increase required on top of the 1957–99 mass-balance field for such a steady-state simulation to match the 1905 extent should give an indication of what the mass balance may have been at that time. Precise information as to how close to steady state the glacier was at the time is currently lacking. Some concomitant indications (temperature estimations, dated frontal moraines, pictures), however, suggest a long period of stagnation for alpine glaciers after the major recession at the end of the Little Ice Age around the mid-19th century. This would make the 1905 ice distribution suitable for initial conditions when modelling the time-dependent behaviour of the glacier during the 20th century, as is done in section 5.2.
A whole range of mass-balance increases was thus tested and the 1905 glacier extent was best reproduced for a value of + 0.58 m w.e. a−1 on top of the 1957–99 field (Fig. 9). Because of the high sensitivity of the snout position to mass balance, and because elevations on the 1905 map seem more questionable than the outer contour, it was the 1905 glacier extent rather than its thickness distribution that was used as a matching criterion. Reference VincentVincent (2002) found a similar value of + 0.55 m w.e. a−1, but owing to his approach he was only able to constrain it by matching the 1905 thicknesses along their flowline (a possible explanation for the small discrepancy given uncertainties on these thicknesses). As can be seen in the figure, our match is fairly good, except for the western snout which is not entirely reproduced, probably as a result of inaccurate mass-balance values from an extrapolation over far too large distances in this area.

Fig. 9. Steady-state ice distribution following a 0.58 m w.e. a−1 increase applied to the 1957–99 average mass-balance distribution.
5.2. Ice rheology and sliding conditions
Our aim now is to use the constraining power of thickness and length changes measured on Glacier de Saint-Sorlin over most of the century as shown in figure 7 (left) and figure 9 in Reference Vincent, Vallon, Reynaud and MeurVincent and others (2000). Owing to the inability of the model to reproduce surface velocities (see discussion in section 1), no attempt has been made to match the velocity field as did Reference Vincent, Vallon, Reynaud and MeurVincent and others (2000). The experiment involved taking the 1905 glacier as initial conditions and running the model forward in time by forcing it with the time-dependent mass balance as shown in Figure 3.
5.2.1. Snout positions and ice-thickness changes
A first run over the last 90 years with the “reference”parameters (first column in Table 1) was performed and corresponding ice-thickness and terminus position changes checked against data as shown in Figure 10. Figure 10a displays snout positions both computed (solid line) and measured (with error bars). These snout measurements correspond to an averaged terminus position obtained by dividing the glaciated area downstream of a theoretical cross-section (depicted in Fig. 5) by the width of this section. Corresponding errors are due to the uncertainties when mapping the various points constituting the bottom contour of the glacier and interpolating them into a continuous curve. Early data (measurements performed before 1960) are thus believed to give the snout position to within ±15 m, whereas the more recent ones have an estimated accuracy of 10 m (see error bars in Fig.10). It should be stressed that because of this “surficial” method used to record the snout positions over the last century, only a two-dimensional approach as proposed here can provide meaningful similar results to compare to the data. As can be seen in Figure 10a, the match is quite satisfactory except for the 1935–85 period during which the retreat is first too pronounced before reducing and lagging behind from the 1960s.

Fig. 10. Measured (with error bars) and modelled (solid line) snout positions (a) and thickness changes (b1–4), 1907–97.The distance indicated in parentheses in each of the bottom frames refers to the distance from Col des Quirlies and corresponds to the points labelled in Figures 5, 6 and 9. The rate factors for ice deformation and basal sliding are the “Reference value”ones shown inTable 1.
Figure 10b1–4 is the exact equivalent of figure 7 (left) in Reference Vincent, Vallon, Reynaud and MeurVincent and others (2000), where modelled thickness changes are compared to the data for the four reference points labelled according to their distance from Col des Quirlies along the flowline of Reference Vincent, Vallon, Reynaud and MeurVincent and others (2000) and which are also represented in Figures 5, 6 and 9. The 1905 data are from the corresponding map, the uncertainty of whose thicknesses is difficult to assess (they are, however, represented with a ±5 m error bar). Except for 1997, when measurements were performed by topographic means (with an estimated accuracy of <0.50 m), all thickness measurements were obtained by photogrammetric methods. Their accuracy, depending upon the quality of the aerial photographs, is generally around 2 m except over the accumulation zone (600 m; Fig. 10a) where the lack of contrast due to the permanent snow reduces the accuracy to about 3–4 m. Last, for the 1952 photographs, the characteristics of the camera lens led to large distortions in the picture, there-by increasing the uncertainty to 4 m. As can be seen in Figure 10, the overall match is fairly poor and definitely not as well reproduced as byReference Vincent, Vallon, Reynaud and MeurVincent and others (2000). This misfit probably results from a wrong choice of ice rheology and/or sliding parameters, which justifies the following sensitivity study. The fact that, despite a similar ice rate factor, our results differ from those of Reference Vincent, Vallon, Reynaud and MeurVincent and others (2000) can be explained by their neglect of basal sliding (even if they tune it afterwards) as well as their crude treatment of two-dimensional effects by prescribing a convergence parameter along the flow.
5.2.2. Parameter study
The fact that the deformation rate factor A and the sliding coefficient A S both contribute to the ice flow makes it difficult to optimize each of these two parameters individually. A systematic double scanning of these two parameters was therefore carried out with exactly the same experimental protocol as in section 5.2.1, and the corresponding results compared to snout positions and thickness changes as above. The two parameters were varied according to the range specified inTable 1, and the corresponding parameter space can be seen in Figure 11. Then for each of the two datasets, a matching criterion β was defined as the standard deviation between the N measured points Xi and their modelled counterparts Yi according to:


Fig. 11. Matching index, in metres, between measured and modelled dataset as shown in Figure 10. (a) Standard deviations for snout positions at 14 equally spaced dates between 1907 and 1997 (selected among those represented in Figure 10a). (b) The same, but for thicknesses at all of the 24 measurement points at the reference locations depicted in Figure 10b1–4. The grey and black crosses represent the exact locations of the pairs of parameters used in Figures 10 (initial set) and 12 (optimal set) respectively.
Figure 11a displays β for snout positions throughout the parameter space, whereas Figure 11b is for thickness changes. The interesting result is that these two sets of independent data give a similar area of minimal mismatch in the two-parameter space. The uncertainties in these data (see error bars in Fig. 10) provide some slack and widen the areas of acceptable match such that a rate factor of about 2 × 10−24 Pa−3 s−1 associated with a sliding coefficient around 5 × 10−14 m8 N−3 a−1 (located by the black crosses in the parameter space in Figure 11) represent approximately the optimal combination with respect to both datasets.
The corresponding results in terms of snout position and thickness changes for this “optimal” combination of parameters are depicted in Figure 12. Regarding glacier termini positions, no improvement is noticeable compared to Figure 10. This is to be expected from inspection of Figure 11 where it can be seen that the two pairs of parameters (1.3 × 10−24 Pa−3 s−1, 15 × 10−14 m8 N−3 a−1) and (2 × 10−24 Pa−3 s−1, 5 × 10−14 m8 N−3 a−1) lie at about the same level of match (about 40 m; see crosses). Conversely, thickness changes are better reproduced, especially for Figure 12b3 and 4, whereas the mismatch for Figure 12b1 remains about the same.

Fig. 12. Same as Figure 10, but with the inferred “optimal”parameter set (A = 2 × 10−24 Pa−3 s−1 and ![]() ).
).
6. Discussion
One of the main assumptions underlying the previous sensitivity study is that the 1905 glacier was in steady state, which is questionable. Therefore, the question remains how much the delayed response of the glacier to pre-1905 mass-balance history can “contaminate” the results and for how long. Resulting deviations from the theoretical model prediction will depend upon two factors, the degree of initial imbalance and the time required for it to be damped out.
With regard to the first, there are good reasons to believe that the initial imbalance at the turn of the century, if any, must have been moderate (see section 5.1.2). Concerning the second, it is the response time of the glacier which controls for how long a given imbalance will persist, and in the present case it is the volume time-scale that is of concern, as was discussed in section 1.
6.1. Volume time-scale of the glacier
According to Reference Jóhannesson, Raymond and WaddingtonJóhannesson and others (1989), the volume time-scale for a glacier is given by the thickness scale divided by the mass balance at the terminus, which for Glacier de Saint-Sorlin gives about 40 years. (Reference Vincent, Vallon, Reynaud and MeurVincent and others (2000) found 60 years by applying the formula of Reference PatersonPaterson (1994) who considers the maximum thickness instead.) This time-scale is the time required for a step mass-balance change to supply the volume difference between initial and final steady states (Reference Jóhannesson, Raymond and WaddingtonJóhannesson and others, 1989). It is analogous to the characteristic time-scale of a glacier asymptotically relaxing to a new steady state following a step change in mass balance. This is illustrated by the steady-state experiment in section 5.1.1, and more particularly by Figure 7 where the exponential decay is observable and from which the corresponding time-scale of about 70 years can be estimated after 63% of the total change has been achieved. This relative consistency gives some credibility to these inferred short time-scales and means that errors resulting from a possible initial imbalance would rapidly decay after the first decades of simulation. Therefore, provided the deviation from steady state in 1905 is not too pronounced as we believe, only minor impacts on the inferred parameter values of the sensitivity test are to be expected.
6.2. Inferred parameters
The inferred value for the ice rate factor A is substantially larger than that of 1.3 × 10−24 Pa−3 s−1 used byReference Vincent, Vallon, Reynaud and MeurVincent and others (2000). Although they directly obtained good results for thickness changes, they did not perform a sensitivity test, and it is not known whether a different value for this parameter could have given even better results. Their different approach (one-dimensional approach, different treatment of basal sliding) could also explain this difference for the ice rate factor. It should be noted that the values for the ice rate factor at the pressure-melting point found in the literature span an order of magnitude, ranging roughly from 1.3 × 10−24 Pa−3 s−1 (Reference LliboutryLliboutry, 1964; Reference Vincent, Vallon, Reynaud and MeurVincent and others, 2000) to 1.4 × 10−23 Pa−3 s−1 (Reference LliboutryLliboutry, 2002), with various intermediate values such as the widely used one of 6.8 × 10−24 Pa−3 s−1 (Reference PatersonPaterson, 1994) or that of 5.1 × 10−24 Pa−3 s−1 (Reference Iken and TrufferIken and Truffer,1997) for the extreme bottom part of a temperate alpine glacier. The reason for this large scatter is to be found in the numerous factors influencing the rheology of the ice (e.g. impurity and water contents) and also sometimes in the common use of enhancement factors to account for the effects of fabrics in ice sheets. Our inferred optimal value of 2.0 × 10−24 Pa−3 s−1 seems to be more in agreement with more recent modelling studies on alpine glaciers. For instance, Reference Hubbard, Blatter, Nienow, Mair and HubbardHubbard and others (1998) obtained an optimal fit with data by using 2 × 10−24 Pa−3 s−1, while Reference GudmundssonGudmundsson (1999) inferred a value of 2.37×10−24 Pa−3 s−1 by comparing modelled and measured velocities. These authors acknowledged the fact that their inferred values are substantially smaller than that recommended by Reference PatersonPaterson (1994).
As regards the sliding factor, one should be very cautious in interpreting the inferred value since the validity of the sliding law can be criticized on the same grounds as those explained in section 4.2. Accounting for the short-term variations in sliding due to the water supply in the basal hydrological system would require the model to be able to output seasonal (ideally daily) results, therefore implying a similar variability in the input mass balance. Moreover, spatial variations in both basal hydrology and bedrock characteristics definitely influence basal sliding. The resulting variability in basal velocities can only be correctly reproduced if basal conditions can be assessed at a relatively short scale, which for most glaciers represents an unrealistic amount of fieldwork. Should these conditions be met, the appropriate sliding law would still have to be able to reproduce a variety of sliding behaviours in response to the variety of basal conditions usually encountered under a glacier. In other words, the approach proposed here only contributes to a global estimation of the effects of basal sliding, allowing for a better constraint on other processes such as ice deformation. A better understanding of the physics involved in basal processes would require a different method strongly relying on field measurements. This could explain our relatively low sliding coefficient of 5 × 10−14 m8 N−3 a−1, which, associated with the optimal rate factor as deduced earlier, would give a ratio of basal velocity to surface velocity of about 0.16 for an ice thickness of 100 m. This relatively low ratio, however, still fits in the range obtained over glaciers in various parts of the world compiled by Reference PatersonPaterson (1994). Last, considering a thickness of 50 m which is probably more representative of Glacier de Saint-Sorlin, our sliding law gives a ratio of about 0:65; which is closer to to the confidence interval of 0.9–1.5 inferred by Reference Gudmundsson, Bauder, Lüthi, Fischer and FunkGudmundsson and others (1999) from tilt measurements on Unteraargletscher, Switzerland.
6.3. The two-dimensional approach
The interest of such a two-dimensional approach is two-fold in the sense that, first, it allows for a better account of the flow geometrical properties and, second, it offers a richer output to compare to data maps than its one-dimensional counterpart. Indeed, over most of the glacier, flowlines are usually not parallel (compressive or extensive flow), making it necessary to compute a two-dimensional flow divergence in order to account for lateral contributions. A one-dimensional approach can only crudely deal with this aspect by prescribing the glacier width along the flowline. Such a parameterization is constant and can hardly be properly up-dated in the case of a changing glacier.
Secondly, by modelling the entire geometry of the glacier, the two-dimensional approach allows for more constraining geometrical comparisons with data in terms of glacier extent and/or ice-thickness distribution. This is all the more important in our case as those geometry changes constitute the only reliable output of the model.
6.4. Applicability of the SIA; neglect of longitudinal stress gradients
This study confirms that a SIA zeroth-order model remains appropriate for modelling the response of a mountain glacier to climate changes provided that two conditions are fulfilled. First, a minimum “shallowness” must hold with regard to both the ice-body geometry and the bedrock topography, a prerequisite which restricts the applicability of the model to a limited category of glaciers, which includes Glacier de Saint-Sorlin. Secondly, the method is only valid if large-scale dynamics represented by volume or glacier length changes are concerned. Indeed, the main consequence of the SIA approach is that longitudinal stress gradients are neglected. Longitudinal effects mainly result from short-scale disturbances usually issued from sharp transitions in basal conditions (bed roughness) such that they cancel out over horizontal distances of several times the ice thickness. This explains (partly) why local horizontal velocities, for instance, cannot be correctly modelled with the SIA, whereas larger-scale outputs like volume changes or glacier extents usually give better results. Indeed, as stated earlier, the SIA is not incompatible with a correct volume time-scale whose prediction does not require inclusion of longitudinal stress gradients. This follows from the fact that the shallowness of the problem reduces the importance of the horizontal gradient of the flux in the continuity equation (Equation (1)), making the thickness rate of change mainly depend upon the mass-balance term.
7. Conclusion
This study represents the continuation of a preliminary one-dimensional modelling approach aiming at exploiting the wealth of available data on Glacier de Saint-Sorlin. By extending to a two-dimensional model, the spectrum of usable data has been broadened and made more constraining. In particular, snout positions provided an extra independent dataset against which model results were tested, yielding “optimal” factors for ice deformation and basal sliding similar to those inferred from thickness-change data (respectively 2 × 10−24 Pa−3 s−1 and 5 ×10−14 m8 N−3 a−1). However, the SIA upon which the model is based has limitations and excludes the possibility of using surface velocity data, for instance. The next upgrade therefore includes longitudinal stress gradients, and will possibly account for the strong variability in basal conditions in order to be able to better reproduce the detailed dynamics of the glacier. Nevertheless, our SIA model has several applications, as can be seen from its ability to reproduce past glacier extents, for instance. This offers interesting possibilities of inferring past climatic conditions during the Little Ice Age. In similar fashion to what we did for the beginning of the 20th century, the appropriate mass balance for this epoch can certainly be constrained by matching a modelled glacier extent with evidence from dated moraines.
Acknowledgements
The authors wish to thank all those who contributed to the data collection effort on Glacier de Saint-Sorlin. Financial support from the European programme EVG1-2000-00512, “Glaciorisk, survey and prevention of extreme glaciological hazards in European mountainous regions” is gratefully acknowledged. This work also benefited from financial support from the French glaciers survey observatory part of Observatoire des Sciences de l’Univers de Grenoble and from the French national programme on climate, ECLIPSE. We are deeply indebted to R. Hindmarsh and an anonymous referee for their constructive criticisms and suggestions which significantly improved the paper. Last but not least, our special thanks to C. S. Hvidberg for her thorough editing and reviewing of this paper.















