Introduction
A knowledge of the thermal expansion coefficient of sea ice is needed to solve a variety of ice-engineering problems. These include: estimating thermal ice pressures on offshore Arctic structures; studying thermal cracking and weakening of sea-ice sheets; and examining the effects of differential thermal expansion between frozen-in ice stress sensors and the surrounding ice.
The only information on the coefficient of thermal expansion of sea ice is summarized by Reference AndersonAnderson (1960). Anderson reviews the experimental results of Pettersson (given originally in Reference MalmgrenMalmgren, 1927) and also calculates the thermal expansion coefficient of sea ice from theoretical sea-ice density values. His calculations indicate that the thermal expansion coefficient of sea ice can vary over several orders of magnitude and be either positive or negative depending on the ice salinity and temperature. For example, for an ice salinity of about 5‰, the ice first expands as it is cooled and then at about −10 °C it begins to contract. His results also suggest marked discontinuities in the expansion coefficient at the NaCl·2H2O eutectic temperature, −22.9 °C. In general, Anderson’s calculated coefficients are in good agreement with those obtained by Pettersson who examined the coefficient of thermal expansion of sea ice in a closed system. Most solids, including pure ice, have a positive expansion coefficient and show relatively very little variation at ambient temperatures.
Anderson calculated the volume expansion coefficient of air-free sea ice from theoretical values of ice density based on Reference AssurAssur’s (1958) phase equilibrium tables for sea ice. While the calculated densities for air-free sea ice are believed to be correct (Reference Cox and WeeksCox and Weeks, 1983), the calculated expansion coefficients are in error. For a fixed ice salinity, the density of air-free sea ice first decreases with decreasing temperature. Anderson and others have, therefore, assumed that sea ice first expands with cooling since its density decreases, that is

where β is the volume expansion coefficient for sea ice, ρ is the sea-ice density and T is the ice temperature. However, as the temperature of sea ice changes, both the volume and the mass of the ice change (Reference Cox and WeeksCox and Weeks, 1975) and Equation (1) does not apply. Sea ice is not a closed system. As air-free sea ice is cooled, brine is expelled, and as air-free sea ice is warmed, its air or gas volume increases.
In the present paper, equations are first derived for the volume coefficient of thermal expansion of NaCl ice. The density of NaCl ice varies in the same manner as that of sea ice (Reference WeeksWeeks, 1962); however, in considering NaCl ice at temperatures above −21.1 °C we do not have to deal with the presence of precipitated solid salts. Equations are then derived for the volume coefficient of thermal expansion of natural sea ice. Since the linear coefficient of thermal expansion of pure ice does not appear to be direction dependent (Reference HobbsHobbs, 1974; Reference YenYen, 1981), the volume expansion coefficient is used in this paper for convenience.
Derivation of Equations for NaCl Ice
A sample of NaCl ice above the NaCl·2H2O eutectic temperature (−21.1 °C) is composed of pure ice, brine, and air. In the following equations, ml , ρl , Vl , and βl are the mass, density, volume, and volume coefficient of thermal expansion of component l and the subscripts a, b, s, and i denote the component air, brine, salt, and pure ice, respectively. M is the bulk mass, V is the bulk volume, ρ is the bulk density, and β is the bulk volume coefficient of thermal expansion of the ice. The term
The salinity of the ice S i is defined as

The salinity of the brine S b is defined as

The total volume of the ice V is
and the bulk volume coefficient of thermal expansion β is

The problem at hand is to determine how the volume of each component varies with temperature.
Warming of NaCl Ice
To simplify the problem, warming of the ice is first considered. During warming, the brine in the ice is diluted by the melting of ice around the brine cavities to maintain phase equilibrium. No brine is expelled; however, due to the phase change and the difference in density between pure ice and brine, the air or gas volume in the ice increases.
Since no brine is expelled during warming, the mass of salt in the brine remains constant and

Solving for the change of mass of the brine we obtain

and

for the change in brine volume where

The bulk mass of the ice also remains essentially constant during warming since the mass of air is negligible. Thus,

and so

Expanding Equation (11) and solving for the change in pure-ice volume we obtain

where
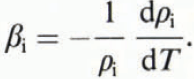
Obtaining a relationship for the change in air or gas volume with temperature is less straightforward. Cox and Weeks (1983) give an equation for the air volume of sea ice as a function of the ice salinity, bulk density, and temperature. For NaCl ice, their equation simplifies to

This equation cannot be used, as the bulk volume appears explicitly on the right-hand side.
By considering various hypothetical porous materials, the following equation was finally obtained for the change in air volume with temperature:

The first term on the right-hand side of Equation (15)

accounts for the increase in air volume due to the phase change of ice to brine. The second term
reflects the decrease in air volume due to expansion of the brine with increasing temperature. The third and fourth terms
describe the increase in air volume as the ice matrix expands.
If the ice did not contain any brine, we would have
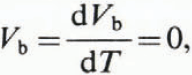

and

Substituting these values into Equation (5), we obtain the relation
for bubbly pure ice.
If the ice contained an inert, constant-density brine and air, we would have no phase change,


and

Again, as expected, we obtain by substitution
for the bulk thermal expansion coefficient.
If the density of the inert brine were allowed to vary with temperature


and

resulting in
Finally, for NaCl ice during warming where there is a phase change of pure ice to brine we find that by substituting Equations (8), (12), and (15) into Equation (5)

The coefficient of thermal expansion of NaCl ice during warming is the same as that of pure ice.
Cooling of air-free NaCl ice
The brine in saline ice is in phase equilibrium with the surrounding ice. As the temperature of the ice decreases, the salinity of the brine increases to maintain phase equilibrium. This is accomplished by freezing water in the brine on the cavity walls. Associated with this phase change is a volume increase of approximately 10% which produces pressure in the cavity and results in the expulsion of brine out of the ice (Reference BenningtonBennington, 1963).
In cold sea ice, where the brine cavities may not be connected, freezing pressures are sufficient to create cracks and perforations in the ice and permit brine expulsion (Reference KnightKnight, 1962; Reference BenningtonBennington, 1963). Initially, this cracking may cause the ice to dilate; however, once the cracks are formed, brine expulsion is unimpeded (Reference Cox and WeeksCox and Weeks, 1975).
For air-free NaCl ice the change in mass of salt with cooling is equal to

where

The change in the bulk mass of the ice is also equal to the mass of the expelled brine and

Substituting Equation (30) into Equation (31) we obtain

for the change in mass of pure ice. It is interesting to note that the same equation is obtained during warming when no brine is expelled. Solving for the change in pure ice volume we obtain

The change in brine volume of the ice is found from Equation (31)

where

The amount of expelled brine and increase in air volume are determined by the same processes. We thus have

The first term on the right-hand side of Equation (36) accounts for the amount of brine expelled as a result of the phase change of brine to ice. The second term covers contraction of the brine during cooling and the third term gives the amount of brine expelled as a result of contraction of the pure ice matrix. Substituting Equation (36) into Equation (34) gives

for the change in brine volume in the ice during cooling.
The bulk coefficient of thermal expansion is found by substituting Equations (33) and (37) into Equation (5) and noting that

The volume coefficient of thermal expansion of air-free NaCl ice during cooling is found to be equal to that of pure ice:

Derivation of equations for natural sea ice
Natural sea ice behaves in the same manner as NaCl ice; however, the situation is complicated by the presence of solid salts. In the following equations m ss, V ss, ρ ss, and β ss denote the mass, volume, density, and volume coefficient of thermal expansion of the solid salts in the ice. Using the same line of reasoning for the derivation of the equations for NaCl ice, we obtain for warming of natural sea ice



and

Thermal strains between the solid salts and pure ice are neglected. Substituting these equations into Equation (5) we obtain
For the cooling of air-free natural sea ice we have


and

where

Substituting these equations into Equation (5) again gives
Discussion
The thermal expansion coefficients of NaCl ice during warming and air-free NaCl ice during cooling are shown to be equal to that of pure ice. When thermal strains between the solid salts and pure ice are neglected, the same results are obtained for natural sea ice. This is a reasonable assumption, in that recent work by Reference Cox and WeeksCox and Weeks (1983) has demonstrated that neglecting the presence of solid salts in sea ice has little effect on mass and volume calculations.
In saline ice, the matrix of pure ice expands and contracts without regard to the localized phase changes in the brine cavities. For saline ice containing air, the same result would be found during cooling, only less brine would be expelled from the ice. To derive the appropriate equations, assumptions would have to be made about the distribution of air in the ice.
The observed behaviour is analogous to a pure ice cup filled with liquid brine. Changes in temperature cause the cup to expand and contract as pure ice, while the associated phase changes inside the cup govern the amounts of brine and air present at each temperature.
It is also interesting to point out that Equation (48) can be used to estimate brine loss from sea-ice samples obtained in the field during shipping and storage. It is common practice to pack ice samples in dry ice for shipping and then store the ice at a temperature below the NaCl·2H2O eutectic (−22.9 °C). Cooling the samples results in brine expulsion and a lowering of the salinity of the sample.
Conclusion
The coefficient of thermal expansion of NaCl ice and natural sea ice is the same as that of pure ice.
Acknowledgements
This work was sponsored by the Minerals Management Service of the U.S. Department of the Interior. The author appreciates the comments provided by Drs W. F. Weeks and S. F. Ackley during the preparation of this paper.


