Symbols

Introduction
The subject of water percolation in snow is of fundamental importance in snow hydrology. Water percolation at various depths has been measured in isothermal glacier firn (Reference Hughes and SeligmanHughes and Seligman, 1939; Reference SharpSharp, [1952]) and the water discharge has been measured at the base of a seasonal snowpack (Reference BoyerBoyer, 1954; Reference HauptHaupt, 1969). The permeability of snow to a single fluid (either air or kerosene) has been investigated by a variety of workers, e.g. Reference BenderBender (1957), Reference KuroiwaKuroiwa (1968), Reference Waterhouse and BuntenWaterhouse and Bunten (1969). Dye-tracing experiments have shown that large spatial inhomogeneities exist within the snow (e.g. Reference Hughes and SeligmanHughes and Seligman, 1939; Reference GerdelGerdel, 1954) in the form of horizontal ice bands and vertical drainage tubes.
In view of the substantial interest in water percolation and the importance of this process in general glaciology, it is surprising that no method exists by which quantitative predictions of water percolation in isothermal snow can be made. In this paper the general theory of Darcian flow of two-fluid phases flowing through porous media is applied to the problem of gravity drainage of water in snow. In this problem the presence of interstitial air is necessarily considered because this second fluid phase substantially changes the character of the flow. Only the isothermal case is considered because the problem is sufficiently difficult without the blocking effect of refreezing. Also, the isothermal case is of considerable glaciological interest since isothermal flow occurs in temperate glacier firn and seasonal snowpacks during the ablation season.
This theory is limited to vertical water flow in snow although the actual process is never so simple. Natural inhomogeneities such as ice layers and drainage tubes (Reference SharpSharp, [1952]) probably exist within all temperate snow. Ice layers block the downward flow of water forcing the water to follow a horizontal path for some distance before continuing the vertical descent. Drainage tubes provide easier passage through the surrounding snow allowing more rapid vertical descent of the water within the tube. The one-dimensional theory can only be applied to an area of sufficient size where these spacial inhomogeneities can be eliminated by averaging the properties of the snow over the area. The evidence from dye tracing studies indicates that the characteristic area over which this averaging must take place is very small compared to the aerial extent of a glacier or snowfield. The problem of flow-field distortions by local inhomogeneities affects essentially all studies of multi-phase flow in porous media. This phenomenon, which is known as “fingering” on the small scale, is discussed later in reference to the interpretation of lysimeter data.
A vertical gradient of porosity exists within all natural snow covers and is included in this theory. This is an important feature because the permeability of natural materials is highly dependent upon the porosity and a large porosity change occurs in the snow-to-ice transition region of a temperate glacier. In the seasonal snowpack, this effect could probably be ignored. The porosity gradient is taken as linear because the depth–density relationship has been shown to be approximately linear throughout most of the Blue Glacier (a temperate glacier studied by E. R. LaChapelle), and it is a good approximation over small depth intervals for any snow deposit. Other gradients could be included without significant difficulty. Although phase changes could also be included in the theory, their effect, from energy considerations, is believed to be insignificant.
In a later section the theory is compared to Reference SharpSharp’s ([1952]) measurements of water reaching various depths in the isothermal firn of the Seward Glacier. Although it is difficult to isolate the effects which the ice layers have on the travel time, wave shape and amplitude, the predictions of the theory are in good agreement with the character of the waves of water flux reaching each level and so the theory is thought to be essentially correct.
Darcian theory
Darcy’s law is a phenomenological relationship which describes the flow of fluids through porous media. Another way of thinking about Darcy’s law, when only one fluid is present, is that it defines the “permeability” k of the medium. Thus permeability, as popularized by Reference Wyckoff, Wyckoff, Botset, Muskat and ReedWyckoff and others (1933), characterizes the porous medium only and is independent of the properties of the fluid used in the experiment. Permeability has the dimensions of area (cm2 is used here) and therefore is different from the “coefficient of permeability” which has been used to date to characterize snow (e.g. Reference BenderBender, 1957 ; Reference KuroiwaKuroiwa, 1968; Reference Waterhouse and BuntenWaterhouse and Bunten, 1969). The “coefficient of permeability” includes properties of both the fluid used in the experiment and the pore geometry of the snow.
When two fluids are present (air and water in this case) Darcy’s law is applied to each phase (Reference ScheideggerScheidegger, 1960, p. 216), thus

and

where the z axis originates at the surface and is positive downwards. Now the concept of permeability has been significantly modified to account for the permeability of the porous medium to each fluid phase under given conditions, i.e. for some given liquid water content and pressure gradient. Thus the permeability to the water phase (k w) determines, for a given pressure gradient in the water phase (∂P w/∂z), what water flux u w will occur. While the total permeability is dependent only upon the pore geometry, the permeability to the water phase will in general depend upon both the pore geometry and the volume of water present. Specifically, for a given pore geometry and pressure gradient, the water flux will increase as increases and k w will increase as the area available for water flow (the liquid water content) increases. As the upper limit, when water completely fills the pore spaces (when the medium is water-saturated), the permeability to the water phase is equal to the total permeability. When the water saturation has decreased to the state at which the only water present is held in place by capillary forces, k w is zero and the water is immobile. Then, according to Equation (2), no water flow can occur regardless of the pressure gradient imposed on the medium. This value of saturation is called the “irreducible water saturation” S wi. Flow can no longer occur because the water film is not continuous (see Fig. 1) from grain to grain (in snow the water film becomes thin enough that water flow is negligible). The water present concentrates at the intersections of grain boundaries and other small-angle corners.

Fig. 1. An idealized thin section of snow showing snow grains, residual water, and continuous pores filled with air.
The permeability to the water phase, k w, is of fundamental importance in the theory of two-phase Darcian flow. There exist many experimental and theoretical relationships between k w and water saturation S w (defined as water volume/pore volume) and therefore is necessarily used in this theory rather than the “liquid water content”. This is done because of the inherent meaning of S w in Darcian theory (see the original work by Reference Wyckoff and BotsetWycoff and Botset, 1936; also Figure 2) and in spite of the fact that “liquid water content” is in general use in the glaciological literature. The functional dependence of k w on porosity ϕ and liquid water saturation is developed later.

Fig. 2. Typical relative permeability curves showing permeability to air and water as functions of water saturation.
Capillary pressure P c is another variable of fundamental importance in Darcian theory and, like k w, capillary pressure has been related to water saturation and porosity by numerous experiments (see Reference ScheideggerScheidegger, 1960, p. 54). By definition, capillary pressure is the difference between the pressures in the air and the water phases,
where the pressure in the air phase will always be greater than the pressure in the water phase since snow is a hygroscopic material. The capillary pressure can now be seen to be the pressure drop across the air–water meniscus. Intuitively it is possible to understand that this pressure drop is related to porosity since the pore size generally increases with porosity and P c is inversely proportional to radius in a capillary. The functional dependence on water saturation is somewhat more complicated but in general, at lower values of water saturation, only the smaller pores will be occupied by the water phase and hence a larger pressure drop across the meniscus should be expected.
Upon differentiating Equation (3) and combining with Equations (1) and (2), this result is obtained for the water flux:

where u t ≡ u a + u w.
Equation (4) can be simplified by recognizing that ρ w ⪢ ρ a and μ w k a ⪢ μ a k w except where k a is very small, i.e. S w is very large (see Fig. 2). Water saturation, however, is generally small in snow undergoing simple gravity flow. The only case where k a is small is the two-dimensional flow problem where simple gravity flow is interrupted by an impermeable layer. Here the water saturation increases above the layer and horizontal flow occurs under a combination of gravity and capillary control. An analysis of this problem is beyond the scope of his theory and ice bands will be treated in the manner discussed above, that is by reducing the permeability of the snow as a large mass. By including these simplifications,

In temperate glacier firn and seasonal snowpacks counter-current flow probably occurs where the downward migration of the water causes an upward migration of the air. This certainly occurs where the lower boundary is impermeable ice and large water saturations exist but it probably also occurs within a seasonal snowpack just because end effects cause large water saturations at the lower boundary (Colbeck, in preparation). Now, when the air flux must balance the water flux,
thenFootnote *
Now where

The first two terms of this equation are the capillarity terms and the third term is the gravity term. In the two-dimensional flow problem the second term controls the flow in regions of high saturation gradient (around an ice layer) but the third term controls the flow when gravity is the main consideration. To show that capillarity can be ignored in the one-dimensional gravity flow problem, the general relationship for all porous media proposed by Reference LeverettLeverett (1941) is used. Accordingly ∂P c/∂ϕ is estimated as −103 dyn cm−2 (−102 N m−2) whereas ∂ϕ/∂z (from Reference SharpSharp, 1951) is estimated as −0.287 × 10−3 cm−1. Hence the first term is between three and four orders of magnitude smaller than the third term (ρ w g = 980 dyn cm−3 = 9 800 N m−3).
Also from the Leverett relationship, ∂P c/∂S w ≈ 210 dyn cm−2 = 21 N m−2 for snow whereas ∂S w/∂z should take on values of less than 10−2 cm−1 (it seems very unlikely that homogeneous snow can be completely saturated 100 cm away from where it is completely dry). Now the second term is also almost three orders of magnitude less than the gravity term.
Thus, under normal conditions of gravity drainage in snow, the flow occurs under the influence of gravity with little capillary influence and capillarity can be ignored. Accordingly, the simplified form of Darcy’s law can be used,
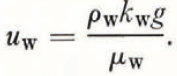
Aside from the case already mentioned (large S w), there are two other circumstances under which Equation (5) should be invalid. As S w approaches S wi, ∂P c/∂S w becomes very large (Reference LeverettLeverett, 1941), and capillary forces dominate over gravity. This is not a serious limitation of this theory, however, because as S w decreases, k w approaches zero (see Fig. 2) and water drainage proceeds very slowly. Thus S wi is approached very slowly, a fact which is shown by the onset of continuous (rather than intermittent) flow in snow at depth (Reference SharpSharp, [1952]; see Fig. 3). Before S w becomes so small that capillary forces dominate over the force of gravity, another wave of melt water (which is generated at the surface of the snow) passes through and S w increases again.

Fig. 3. Sharp’s data recorded at hourly intervals.
The other condition under which Equation (5) is invalid occurs at the front of an advancing wave. Wave propagation in porous media often proceeds as a shock front (see Reference Buckley and LeverettBuckley and Leverett, 1942) in which case ∂S w/∂z is infinite. The region of a shock front can be adequately treated in the current theory just by preserving mass so this condition does not constitute a serious objection to the use of Equation (5).
After simplifying Darcy’s law, the only remaining problem is to relate the permeability of the water phase to other variables. Fortunately, much laboratory work of this type has been done (see Reference ScheideggerScheidegger, 1960, p. 218) and, as discussed earlier, k w can be related to the porosity and the water saturation. Here it is necessary to use the concepts from flow studies done on other porous materials because of the thermal equilibrium problems which would be involved in flowing water through snow in the laboratory. In Figure 2 typical curves of relative permeability (k w/k and k a/k) for each phase are shown as functions of water saturation. The curve for the water phase is typical of curves for a wetting fluid. Theoretical explanations of this behaviour have been offered (Reference Reznik, Reznik, Fulton and ColbeckReznik and others, 1967) which show that this behaviour can be expected in any porous medium containing two fluids, Thus while similar laboratory experiments have not been done for snow, the same general relationships should apply.
For values of water saturation less than S wi, the permeability to the water phase is zero. This suggests a more useful variable to relate k w and S w, namely
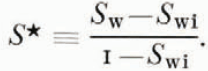
Here S wi is assumed to be independent of porosity although we expect that, in general, S wi will increase with decreasing porosity (S wi is taken to be zero because of the lack of appropriate methods of measurement).
Now, for a given porosity, k w is related only to S*. Reference Morel-Seytoux and De WiestMorel-Seytoux (1969, p. 486) reported that
where n is about equal to 3 for unconsolidated sands. This value, however, varies somewhat for different materials and for snow the value of 2 is postulated. This choice is somewhat arbitrary. The final test of this assumption will be the comparison between the wave distortion predicted by the theory and that observed experimentally. Unfortunately, the existing experimental data (Reference SharpSharp, [1952]) do not provide a rigorous test of the theory because tile effect of ice layers within the snow cannot be isolated. Further field experiments without the effect of ice layers are now being done. The existing experimental data show that wave distortion will occur with or without ice layers (Reference HauptHaupt, 1969). There cannot be any doubt that n > 1, because if n = 1, no wave distortion occurs. A value of n greater than 2 would predict more distortion than the experimental data show. Thus it is assumed that
The dependence of permeability k on porosity generally takes the form
where m is about 6 (Reference ScheideggerScheidegger, 1960). Reference KuroiwaKuroiwa (1968) found a similar relationship for snow,
where b = 15.9. Combining Equations (6) and (7) with a constant of proportionality a,
Now, substituting into Darcy’s law,
where α = ρ w g/μ w = 54 700 cm−1 s−1 at 0° C. In this theory the porosity is assumed to be ϕ = ϕ 0+cz, where ϕ 0 is the porosity at the surface.
When u w and S* are functions of depth and time, the continuity equation takes the form

Substituting Equation (8) into Equation (9),

and likewise in terms of u w,

The general solution of Equation (10) is (see Reference SneddonSneddon, 1957, p. 50)
where

and
F(C 1, C 2) is an arbitrary functional relationship which, when taken with any boundary condition at the surface, describes S* in terms of z and t. Thus any surface condition can be analyzed as a Fourier series and can then be combined with Equation (12) to predict the propagation of water through snow. A particular solution is given later, but for the details of the method of solution the reader is referred to Reference SneddonSneddon (1957).
Characteristics
No satisfactory method exists by which the permeability k of water-bearing snow can be measured. This problem arises because of the difficulty of maintaining thermal equilibrium while handling water-bearing snow samples and because the porosity would be decreased if the samples were frozen in order to work with them at a more convenient temperature. The permeability of a snow sample can be estimated from the porosity by using the results of Reference KuroiwaKuroiwa (1968), but porosity estimates must in turn be made from density measurements and uncertain measurements of the water saturation.
An alternative method is suggested here for calculating the permeability of the snow using the present theory together with lysimeter data. When the snow is homogeneous this method is probably no better than the one described above but it has definite advantages when the snow includes inhomogeneities and the average permeability of the entire mass is desired.
When u w depends upon z and t,

When a constant value of volume flux is being considered du w = 0 and

Substituting from Equation (11),
This equation describes the speed of propagation of a value of constant volume flux moving through z—t space. Because the speed of propagation depends upon the magnitude of the volume flux, the waves distort as they move. This distortion was noted by Reference SharpSharp ([1952]), and it represents the tendency of the wave crest to override the slower moving parts of the wave causing a rapid build-up of flux as the wave crest approaches and a gradual decline after the wave crest has passed. Theoretically this type of displacement proceeds as a shock front which grows with depth. Reference Buckley and LeverettBuckley and Leverett (1942) predicted this behavior in the analagous situation of petroleum displacement by water in a porous reservoir and many field and laboratory experiments have confirmed their prediction. The development of a shock front, however, requires that ∂S w/∂z be infinite at the position of the shock front and, as discussed above, one assumption made during the development of the Darcian theory was that ∂S w/∂z is always small. Thus the theory fails at the shock front and in fact the shock-front solution only occurs because capillarity was ignored.
To calculate the total permeability k of snow with a known porosity, it suffices to find the value of a because
where b is 15.9. By choosing a value of water flux u
w and measuring the rate at which that value propagates ![]() , the value of a can be calculated from Equation (13). This procedure is illustrated in the next section where the value of a is calculated from Sharp’s data and then the predicted wave speed is compared with the measured speed. The value of u
w chosen should be an average value between the largest and smallest measured fluxes since the largest values disappear with depth and capillary forces become increasingly important at the lower values of flux. Also the time at which the chosen value of u
w passes any depth should be taken from the trailing edge of the wave rather than the leading edge (see Fig. 4 for examples of these wave forms) since simple drainage occurs after the wave crest has passed but, during the build-up stage of the wave movement, the wave form is complicated by “fingering” and by the distortion associated with the development of the shock front.
, the value of a can be calculated from Equation (13). This procedure is illustrated in the next section where the value of a is calculated from Sharp’s data and then the predicted wave speed is compared with the measured speed. The value of u
w chosen should be an average value between the largest and smallest measured fluxes since the largest values disappear with depth and capillary forces become increasingly important at the lower values of flux. Also the time at which the chosen value of u
w passes any depth should be taken from the trailing edge of the wave rather than the leading edge (see Fig. 4 for examples of these wave forms) since simple drainage occurs after the wave crest has passed but, during the build-up stage of the wave movement, the wave form is complicated by “fingering” and by the distortion associated with the development of the shock front.

Fig. 4. Sharp’s data smoothed.
The use of Equation (13) is complicated by the dependence of propagation rate dz/dt on porosity ϕ since porosity decreases with depth. Thus Equation (13) is integrated along a characteristic (the path of a constant u w in z—t space). Rewriting Equation (13),
Integrating by parts from the surface to any point in z—t space, where u w is constant and

This equation describes, for any particular snow (ϕ 0, c and a), the depth of a value of water flux (u w) at any time.
Seward Glacier firn
Reference SharpSharp ([1952]) measured the water flux at various levels in the firn of the upper Seward Glacier, a temperature glacier in the St Elias Mountains. The data were collected on 11 and (2 August as well as on 17 and 18 August, sufficiently late in the ablation season for isothermal conditions to exist. The water was introduced at the surface entirely by melting during the day and it was collected in 30 cm diameter funnels and measured at six different locations as the resulting melt-water waves passed depths of 60, 120, 180, 240, 300 and 340 cm. Practically no melt-water was measured at depths of 120 and 300 cm, so these levels are not considered. This was probably the result of horizontal diversion of melt water by impermeable ice layers above those receptors.
Sharp’s data are shown in Figure 3 as recorded every hour and in Figure 4 as smoothed curves. Some of the most important features of these moving waves of water are the development of a skewed wave form with asymmetry increasing with depth and increasing value of the minimum volume flux with depth. The wave amplitude appears to be constant with depth until 240 cm and then to decrease. The 11–12 August data, however, show a steadily decreasing value of amplitude at all depths. Although no definite conclusion can be reached because of the unknown effects arising from the ice layers, the “diffusion-like” result of decreasing wave amplitude seems most plausible. The constant wave amplitude down to a depth of 240 cm may be due to the greater volumes of water collected at 180 and 240 cm than at 60 or 340 cm. Thus it is assumed that if the same volumes had been collected at each level, the amplitude of the wave would have decreased steadily with depth.
The density profile was not reported for this site but it can be estimated from numerous density measurements made in this area of the Seward Glacier (Reference SharpSharp, 1951). Accordingly, the porosity is estimated as
where ϕ 0 = 0.5 and c = −0.287 × 10−3 cm−1.
Before particular solutions can be generated from Equation (12), the total permeability of the firn at Sharp’s site will be estimated. Having estimated the porosity–depth relationship from the density–depth measurements, it is now necessary to calculate the value of the constant a. From Sharp’s data on Figure 4 the speed of propagation ![]() of the value of water flux, 0.42 × 10−4 cm3 s−1 per cm2, is 0.006 25 cm s−1. Accordingly, from Equation (13) the value of a is 0.625 × 10−9 cm2. This value is about correct for the snow as a large unit, including ice bands, since the permeability at the surface of the snow would be
of the value of water flux, 0.42 × 10−4 cm3 s−1 per cm2, is 0.006 25 cm s−1. Accordingly, from Equation (13) the value of a is 0.625 × 10−9 cm2. This value is about correct for the snow as a large unit, including ice bands, since the permeability at the surface of the snow would be
and the upper limit for the permeability of loose sand grains is about 1.8 × 10−6 cm2. The measured value of a for snow with this same porosity is 3.3 × 10−6 cm2 (Reference KuroiwaKuroiwa, 1968). Thus the effect of including the ice layers is to reduce the total permeability of the snow by a factor of just over 2.
Taking the values already given for the constants, Equation (14) becomes
To verify the validity of Equation (15), the characteristic paths of 0.19 × 10−4 cm s−1 and 0.38 × 10−4 cm s−1 are computed and shown on Figure 5, together with the actual values as measured by Sharp.Footnote * The calculated paths for these values of water flux are very close to the measured paths. Although the shapes of characteristics were determined from Equation (15) for these values of water flux, the time at which those values left the surface cannot be calculated. Normally, a problem of this type is solved by using a known boundary condition and then applying Equation (15) to predict the propagation of the boundary values into the interior. However, obtaining a sufficiently accurate boundary condition in the form of very precise ablation measurements does not seem very likely (personal communication from Dr M. F. Meier). The boundary condition can be deduced by extrapolating backward from beneath the surface, i.e. the shape of the characteristics is found from Equation (15) and is then fitted to the data. The resulting intercept at the surface gives the time at which that value of water flux was generated at the surface.

Fig. 5. The characteristics of two values of volume flux.
The boundary condition is not reconstructed here because of the many limitations of both the theory and the experimental data (horizontal diversion of melt water and elimination of capillary forces) would reduce the accuracy of the result. In principle it is possible to use any boundary condition because any input of water at the surface in the form of either rain or melt could be represented as a Fourier series. The one-half sine wave, periodic (24 h per cycle) function,

is assumed to represent the surface condition and from Figure 5 it is estimated that U max occurred at 11.30 h. This boundary condition is shown on Figure 6. The maximum surface flux was assumed to occur at 11.30 h in spite of the fact that the temperature record suggests that the maximum value should have occurred later. The following calculations verify the assumption.

Fig. 6. The assumed flux at z = 0 and the computed fluxes at 60, 180, 240 and 340 cm.
The particular solution to Equation (12) (see Reference SneddonSneddon, 1957, p. 56) is (S* and u w are related by Equation (8)),

where

Using the values of a, b, S wi, c and ϕ 0 already chosen and estimating U max = 0.42 × 10−4 cm s−1,

where
Equation (16) is an implicit functional relationship giving u w as a function of ϕ, t and θ where ϕ = ϕ 0+cz and θ is a function of ϕ and u w. To find particular values of u w at some depth z, it is necessary to assume a value for ω(t+θ) where 0⩽ω(t+θ) ⩽ π, calculate u w from Equation (16) and then calculate t using Equation (17). Thus using an iterative technique corresponding values of u w and t can be calculated at each depth.
The wave form at each depth can be constructed from the calculated values of u w and t if it is assumed that the same volume of water passes each depth during one period, i.e. if continuity is preserved. The calculated function at each depth is double-valued, that is at each time there are two values of u w. The only possible interpretation of this result is that the trailing side of the wave form is given by the larger values of u w and the leading edge of the wave form propagates as a shock front. This interpretation follows that of Reference Buckley and LeverettBuckley and Leverett (1942) who found a triple valued function (see Reference ScheideggerScheidegger (1960, p. 224)) for a discussion of immiscible displacement). The position of the shock front is determined from continuity considerations.
Figure 6 shows the assumed boundary condition and the calculated wave forms at 60, 180, 240 and 340 cm. In each case the shock front was located by trial and error—the area under each curve must be equal since the same volume of water passes each level. Apparently the shock front grows with depth until the entire leading edge of the wave propagates as a shock front. Thereafter the maximum value of volume flux decreases with depth as the minimum value increases. Also note the increasing distortion of the wave form from its initially symmetrical shape to one which is increasingly skewed toward larger time. The ultimate result would be steady-state flow at sufficient depth.
The computed and the measured water fluxes for depths of 60, 180, 240 and 340 cm are shown on Figures 7, 8, 9 and 10. In general the agreement between the theoretical and experimental values is quite good and shows that the physical concepts are correct and the assumptions are justified. Better agreement could be obtained simply by increasing the value of a, shifting the assumed position of the maximum surface flux, or by assuming another porosity profile. However, the uncertainty of heterogeneous flow around ice layers would still be present, so that changing these constants to achieve improved agreements would serve no useful purpose. Certain differences between the theory and experiment can be explained.

Fig. 7. The measured and computed fluxes at 60 cm.

Fig. 8. The measured and computed fluxes at 180 cm.

Fig. 9. The measured and computed fluxes at 240 cm.

Fig. 10. The measured and computed fluxes at 340 cm.
At 60 cm (see Fig. 7) the measured values form a curve which is more peaked than the theoretical curve. Thus the actual wave at the surface is probably more peaked than the assumed surface condition but since no surface measurements were made, a more realistic boundary condition will not be assumed. While this difference is noticeable at 60 cm it is not so noticeable at lower depths. It has been shown (Reference ColbeckColbeck, 1971) that the exact shape of the surface wave is not important, since the mechanics of the percolation process will determine the wave form at depths below 1 to 2 m and large differences in wave shape at the surface will be quickly removed with depth.
The area under each of the theoretical curves is equal (an equal volume of water passes each depth) but the area under the experimental curves varies three-fold. The theory predicts that larger volumes of water should have passed 60 and 340 cm than were measured and vice versa at 180 and 240 cm. If the excess volumes were removed from the leading edges of the experimental curves at 180 and 240 cm, the agreement between the theoretical and experimental curves would be substantially improved. In particular the magnitude of the experimental wave would decrease in the same manner as the theoretical wave.
The theory predicts that the minimum flux increases with depth in much the same manner as is shown by Sharp’s data. Also the increasing distortion of the wave form can be seen in the experimental data, but the data do not verify the existence of a shock front. Although lysimeters may not be sufficiently sophisticated to detect such an event, it seems very likely that a wave undergoing gravity drainage would not propagate as a smooth surface but would proceed with much “fingering” (Reference ScheideggerScheidegger, 1960, p. 202). Thus while the concept of the shock front is very useful mathematically, the failure to observe such an event in practice should not be interpreted as a serious failure of the theory. In general, the distortion of the wave form is closely approximated by the shock-front theory.
Conclusion
The general theory of two-phase fluid flow through porous media has been used to construct a theory of water percolation in isothermal snow. The existing information about snow as a porous material was used whenever possible. When no information was available, the general theory was used in making the necessary assumptions. The fundamental assumption was that capillarity could be ignored during gravity drainage in snow. This was shown to be true only if water saturations occur which are somewhat greater than the irreducible value and somewhat less than the complete saturation, i.e. S w always exists within the “midrange” of saturations. In this case ∂P c/∂S w is small and capillary forces are negligible. While high values of S w do not occur within highly porous snow (Reference DavarDavar, 1967), high values should occur where porosity decreases at greater depths. However at these depths the wave forms are sufficiently diffuse that steady-state flow should prevail.
The method of characteristics was used to calculate the permeability of the firn in the situation studied by Sharp. The total permeability of the snow as a large unit was found to be less than one-half of the permeability of similar snow samples studied in the laboratory. While this is a reasonable value, much further effort will be required to establish if it generally holds.
The assumption that the relative permeability to the water phase is proportional to S*2 was made for lack of an appropriate experimental relationship. In fact the laboratory experiments will probably never be performed on the snow–water–air system because of the inherent difficulty of relative permeability experiments, even under circumstances where thermal equilibrium is not a problem. Therefore only the application of the theory can test this assumption, and the application of the theory to Seward firn data verifies the theory. The distortion of waves of flux by inhomogeneities within the snow is largely unknown and when current experiments on percolation in homogeneous snow are completed, the theory will be re-examined to test this assumption.
As a summary, when volumes of water are periodically introduced by surface melt, the resulting waves of water flux propagate in a predictable manner with a decreasing maximum flux, increasing minimum flux and increasing distortion with depth. The waves propagate approximately as a shock front which grows with depth until the entire wave proceeds as a shock front after which the shock front decays with depth. Steady-state flow occurs at sufficient depth.
Acknowledgements
I wish to thank Dr W. D. Hibler III and Dr M. Mellor for critically reviewing this manuscript. Helpful comments and suggestions have been offered by Mr A. J. Gow, Dr G. M. Keeler and Dr Y. C. Yen.












