Introduction
The development of a realistic description of polycrystalline ice rheology is one of the keys to improving the accuracy of models used to study polar ice-sheet dynamics and to constrain the depth-age models for ice-core palaeoclimate records (Reference SolomonSolomon and others, 2007). The pioneering work of Reference GlenGlen (1955) provided the basis for early numerical descriptions of polycrystalline ice flow. Based on a series of compression experiments on isotropic polycrystalline ice at stresses from 0.1 to 1.0MPa and temperatures between approximately −13 and −0.02°C, Reference GlenGlen (1955) proposed an empirical power-law flow relation, based on secondary (minimum) creep rates, where

![]() is the strain rate (s-1), σ is the stress (MPa) and the exponent n = 3. The flow parameter, k0, is a function of the activation energy for creep, Q (kJmol-1), the universal gas constant, R = 8.314J mol-1 K-1, and the absolute temperature, T (K). The term (3o is assumed to be dependent upon material-specific factors, including ice density, crystal size and the concentration of soluble and insoluble impurities (e.g. Reference Budd and JackaBudd and Jacka, 1989; Reference Cuffey and PatersonCuffey and Paterson, 2010). Following the work of Reference GlenGlen (1955), Reference NyeNye (1957) proposed a generalized flow relation to relate the minimum (secondary) creep data of Reference GlenGlen (1955) from compression experiments to other stress configurations relevant to the flow of ice. Assuming ice to be an incompressible, isotropic material Reference NyeNye (1957) proposed a relation between the second- order strain-rate (
is the strain rate (s-1), σ is the stress (MPa) and the exponent n = 3. The flow parameter, k0, is a function of the activation energy for creep, Q (kJmol-1), the universal gas constant, R = 8.314J mol-1 K-1, and the absolute temperature, T (K). The term (3o is assumed to be dependent upon material-specific factors, including ice density, crystal size and the concentration of soluble and insoluble impurities (e.g. Reference Budd and JackaBudd and Jacka, 1989; Reference Cuffey and PatersonCuffey and Paterson, 2010). Following the work of Reference GlenGlen (1955), Reference NyeNye (1957) proposed a generalized flow relation to relate the minimum (secondary) creep data of Reference GlenGlen (1955) from compression experiments to other stress configurations relevant to the flow of ice. Assuming ice to be an incompressible, isotropic material Reference NyeNye (1957) proposed a relation between the second- order strain-rate (![]() ) and deviatoric-stress (Sj) tensors. To a first approximation, polycrystalline ice can be considered incompressible, provided the ice temperature is expressed in terms of its difference from the in situ pressure-melting point (Reference RigsbyRigsby, 1958). Under this assumption, strain rates are not influenced by the hydrostatic pressure, and Reference GlenGlen (1958) further generalized the flow relation for secondary creep of isotropic polycrystalline ice to
) and deviatoric-stress (Sj) tensors. To a first approximation, polycrystalline ice can be considered incompressible, provided the ice temperature is expressed in terms of its difference from the in situ pressure-melting point (Reference RigsbyRigsby, 1958). Under this assumption, strain rates are not influenced by the hydrostatic pressure, and Reference GlenGlen (1958) further generalized the flow relation for secondary creep of isotropic polycrystalline ice to
where the constant B is a function of the flow parameter, ko, and the scalar second invariant of the deviatoric stress tensor,
As Eqn (2) broadly accounts for the effects of deviatoric stresses and temperature on ice deformation it has been applied widely in modelling ice dynamics (e.g. Reference PattynPattyn and others, 2008) and is often referred to as the Reference GlenGlen (1958) flow relation. A small J2-independent residual stress is often incorporated into the definition of B(ko, J2) to avoid a singularity and numerical errors associated with prescription of infinite viscosities as strain rates approach zero (Reference Hutter, Legerer and SpringHutter and others, 1981; Reference Greve and BlatterGreve and others, 2009; Reference CalovCalov and others, 2010). Equation (2) defines an isotropic flow relation since B(ko, J2) is a scalar, and under conditions of constant temperature and stress the proportionality between ![]() and Sjj is constant for all orientations and stress configurations.
and Sjj is constant for all orientations and stress configurations.
Extensive experiments of Reference SteinemannSteinemann (1954, Reference Steinemann1958a) to strains of ∊ > 10% were among the first to indicate the importance of tertiary creep and the development of preferred patterns of crystallographic c-axis orientations (crystal orientation fabrics) to ice dynamics. Subsequent field observations (Reference BuddBudd, 1972) and experimental work (Reference KambKamb, 1972) provided further early descriptions of how the development of crystal orientation fabrics and textures (grain size and shape) in natural ice masses induces large- scale visco-plastic anisotropy, which cannot be described by the Reference GlenGlen (1958) flow relation for secondary creep. In this work we concentrate our discussion on the dynamics of polycrystalline ice within large polar ice sheets. The importance of microstructural changes, including the development of crystal orientation fabrics, to the dynamics of polycrystalline ice has been highlighted by numerous field, laboratory and model studies (e.g. Reference Gow and WilliamsonGow and Williamson, 1976; Reference LileLile, 1978; Reference Russell-HeadRussell-Head and Budd, 1979; Reference Duval, Ashby and AndermanDuval and others, 1983; Reference Azuma and HigashiAzuma and Higashi, 1984; Reference Pimienta and DuvalPimienta and Duval, 1987; Reference Budd and JackaBudd and Jacka, 1989; Reference AlleyAlley, 1992; Reference Tison, Thorsteinsson, Lorrain and KipfstuhlTison and others, 1994; Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998; Reference Wang, Warner and BuddWang and others, 2002; Reference DiPrinzio, Wilen, Alley, Fitzpatrick, Spencer and GowDiPrinzio and others, 2005; Reference DurandDurand and others, 2007).
Laboratory ice-deformation experiments provide a convenient means of investigating microstructural and strain- rate evolution as a function of strain (or time). The lower curve in Figure 1 provides a schematic representation of the strain-rate vs strain behaviour for a constant stress and temperature creep deformation experiment on initially isotropic polycrystalline ice. During primary creep the strain rate decreases rapidly and the strain is recoverable with both elastic and anelastic components (Reference Budd and JackaBudd and Jacka, 1989). The minimum in strain rate, ![]() , atan octahedral shear strain of ε0
= 0.5-2.0% is characteristic of the creep deformation of initially isotropic polycrystalline ice, and can be considered the point where microstructural processes controlling recoverable creep and strain hardening are balanced by the onset of dynamic recovery and recrystallization processes (Reference JackaJacka, 1984; Reference Budd and JackaBudd and Jacka, 1989; Reference Montagnat, Durand and DuvalMontagnat and others, 2009; Reference Schulson and DuvalSchulson and Duval, 2009). During primary creep, deformation predominantly occurs by the movement of dislocations on the basal planes of grains (Reference Montagnat, Durand and DuvalMontagnat and others, 2009), so thatthe crystal orientation fabric and texture of initially isotropic polycrystalline ice remain unchanged at the strain corresponding to
, atan octahedral shear strain of ε0
= 0.5-2.0% is characteristic of the creep deformation of initially isotropic polycrystalline ice, and can be considered the point where microstructural processes controlling recoverable creep and strain hardening are balanced by the onset of dynamic recovery and recrystallization processes (Reference JackaJacka, 1984; Reference Budd and JackaBudd and Jacka, 1989; Reference Montagnat, Durand and DuvalMontagnat and others, 2009; Reference Schulson and DuvalSchulson and Duval, 2009). During primary creep, deformation predominantly occurs by the movement of dislocations on the basal planes of grains (Reference Montagnat, Durand and DuvalMontagnat and others, 2009), so thatthe crystal orientation fabric and texture of initially isotropic polycrystalline ice remain unchanged at the strain corresponding to ![]() (which is often referred to as the isotropic minimum strain rate).
(which is often referred to as the isotropic minimum strain rate).

Fig. 1. Typical creep curves illustrating the difference in strain required to develop stable tertiary strain rates for samples with initially isotropic and compatible initially anisotropic crystal orientation fabrics. For initially isotropic polycrystalline samples the strain rate decreases to a minimum value, ![]() , prior to increasing to the stable tertiary creep rate,
, prior to increasing to the stable tertiary creep rate, ![]() . In the case of unconfined vertical compression, the compatible crystal orientation fabric that develops during tertiary creep, as depicted here, is a small-circle girdle. Illustration based on the laboratory deformation experiments of Reference Gao and JackaGao and Jacka (1987).
. In the case of unconfined vertical compression, the compatible crystal orientation fabric that develops during tertiary creep, as depicted here, is a small-circle girdle. Illustration based on the laboratory deformation experiments of Reference Gao and JackaGao and Jacka (1987).
During the transition from secondary (minimum) to tertiary creep, dynamic recovery processes are activated, resulting in accelerating strain rates (Reference PoirierPoirier, 1985; Reference Budd and JackaBudd and Jacka, 1989; Reference Montagnat, Durand and DuvalMontagnat and others, 2009; Reference Cuffey and PatersonCuffey and Paterson, 2010). At strains of ˜10% a dynamic balance between strain hardening and microstructural recovery processes (e.g. grainboundary migration, rotation and recrystallization) develops and is associated with the development of crystal orientation fabrics and a steady-state tertiary creep strain rate (Reference PoirierPoirier, 1985; Reference Budd and JackaBudd and Jacka, 1989; Reference Montagnat, Durand and DuvalMontagnat and others, 2009; Reference Schulson and DuvalSchulson and Duval, 2009). With the exception of the uppermost regions of polar ice masses, large strains are generally prevalent, so steady-state tertiary creep, indicated by ![]() in Figure 1, is the deformation mode relevant to their flow. Factors controlling the difference between
in Figure 1, is the deformation mode relevant to their flow. Factors controlling the difference between ![]() and
and ![]() in Figure 1 include the initial crystal orientation fabric and the stress configuration. For experiments conducted at a constant stress and temperature on initially isotropic polycrystalline ice, the ratio of the strain rates,
in Figure 1 include the initial crystal orientation fabric and the stress configuration. For experiments conducted at a constant stress and temperature on initially isotropic polycrystalline ice, the ratio of the strain rates, ![]() and
and ![]() , gives the strain-rate enhancement, E (Reference LileLile, 1978), where
, gives the strain-rate enhancement, E (Reference LileLile, 1978), where
As isotropic polycrystalline ice for experimental creep studies can be readily produced in the laboratory (Reference JackaJacka and Lile, 1984), ![]() values determined at ˜1% strain provide a reference for normalizing tertiary creep strain rates and making comparisons over a range of temperature and stress regimes.
values determined at ˜1% strain provide a reference for normalizing tertiary creep strain rates and making comparisons over a range of temperature and stress regimes.
The deformation of polycrystalline ice in shear and compression
In addition to the effects of temperature and stress, the development of crystal orientation fabrics during tertiary creep also strongly influences ice dynamic properties: strain rates for anisotropic polycrystalline ice may be up to an order of magnitude higher than corresponding values for isotropic ice under similar conditions. Enhancement values ranging from ˜3 to 12 have been reported for simple shear deformation experiments (Reference DuvalDuval, 1981; Reference LileLile, 1984; Reference Li, Jacka and BuddLi and others, 1996). Enhancement values within this range have also been estimated for the high-shear zones that exist at depth in ice sheets, by logging the deformation of boreholes or conducting deformation experiments on ice-core samples retrieved from depths where high shear strain rates occur (Reference Russell-HeadRussell-Head and Budd, 1979; Reference Azuma and HigashiAzuma and Higashi, 1984; Reference Dahl-Jensen and GundestrupDahl-Jensen and Gundestrup, 1987; Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998; Reference Thorsteinsson, Waddington, Taylor, Alley and BlankenshipThorsteinsson and others, 1999).
The crystal orientation fabric that evolves in simple shear is a cluster of near-vertical c-axes, referred to as a single maximum (Reference Gow and WilliamsonGow and Williamson, 1976; Reference Russell-HeadRussell-Head and Budd, 1979; Reference Azuma and HigashiAzuma and Higashi, 1984; Reference Tison, Thorsteinsson, Lorrain and KipfstuhlTison and others, 1994; Reference GowGow and others, 1997; Reference Morgan, Wookey, Li, Van Ommen, Skinner and FitzpatrickMorgan and others, 1997; Reference ThorsteinssonThorsteinsson and others, 1997; Reference AzumaAzuma and others, 1999; Reference DiPrinzio, Wilen, Alley, Fitzpatrick, Spencer and GowDiPrinzio and others, 2005; Reference DurandDurand and others, 2007). In this orientation the basal planes of individual grains are favourably aligned with the macroscopic shear plane, leading to high resolved basal shear stresses and enhanced rates of macroscopic deformation.
Some laboratory deformation experiments and ice-core records indicate a transient two-maxima fabric occurs in simple shear, where the maxima are aligned along the direction of flow. Horizontal simple-shear experiments conducted in a torsion apparatus indicate the second maximum, initially oriented perpendicular to the dominant vertical maximum, becomes weaker and rotates towards the vertical with accumulating shear strain, resulting in a single maximum normal to the plane of maximum resolved shear stress; also referred to as the permanent or non-rotating shear plane (Reference BuddBudd, 1972; Reference KambKamb, 1972; Reference DuvalDuval, 1979, 1981; Reference Bouchez and DuvalBouchez and Duval, 1982).
The crystal orientation fabric that develops at high strains in unconfined vertical compression is characterized by a clustering of c-axes about a conical surface. There are few grains in near-vertical or near-horizontal orientations, so the c-axes form a small-circle girdle pattern about the compression axis. During compression, many c-axes rotate towards the compression axis (Reference BuddBudd, 1972; Reference AlleyAlley, 1992). Nucleation, grain rotation, boundary migration and other recrystallization processes contribute to the formation of a small-circle girdle pattern with a mean c-axis colatitude of 25-30° (Reference JackaJacka and Maccagnan, 1984). Small-circle girdle fabrics have been recorded in the upper third of Law and Siple Domes, where the stress configuration is dominated by compression (Reference Russell-HeadRussell-Head and Budd, 1979; Reference Thwaites, Wilson and McCrayThwaites and others, 1984; Reference Gow and EngelhardtGow and Engelhardt, 2000). Similar patterns have also been observed in regions of the Ross (Reference Gow and WilliamsonGow and Williamson, 1976) and Amery (Reference WakahamaWakahama, 1974) ice shelves, where nearly equivalent longitudinal and transverse strain rates lead to an unconfined vertical compression stress configuration. Laboratory compression experiments of Reference Jacka and LiJacka and Li (2000) suggest that fabric evolution rates as a function of strain might be reduced at lower temperatures and stresses. In comparison with simple shear, enhancements are lower for uniaxial compression, with typical values E =1-4 (Reference JackaJacka and Maccagnan, 1984; Reference Gao and JackaGao and Jacka, 1987; Reference Jacka and LiJacka and Li, 2000). Similar values have been predicted by the grain- scale polycrystalline flow relations of Reference LileLile (1978), Reference Azuma and Goto-AzumaAzuma and Goto-Azuma (1996) and Reference ThorsteinssonThorsteinsson (2001).
Anisotropic flow relations for polycrystalline ice
While steady-state tertiary flow is the deformation mode of most relevance to natural ice masses, the empirically based and well-established Reference GlenGlen (1958) flow relation, derived from isotropic minimum strain rates, continues to be widely applied in model studies. To help alleviate this inconsistency, values of E selected from the literature can be used as a multiplication factor (Eqn (5)) to incorporate a simple parameterization of polycrystalline anisotropy and other microstructural factors, including impurities and grain size, into strain-rate predictions (e.g. Reference HookeHooke, 2005; Reference Greve and BlatterGreve and Blatter, 2009),
A diverse range of fl w relations incorporating a more physically based treatment of polycrystalline anisotropy have also been proposed. In homogenization models, the macroscopic deformation is derived from the volume- averaged response of individual grains or aggregates of neighbouring grains. Flow relations defined at the scale of individual grains include descriptions of intragranular deformation processes and intergranular interactions (Reference LileLile, 1978; Reference Van der Veen and WhillansVan der Veen and Whillans, 1994; Reference Azuma and Goto-AzumaAzuma and Goto-Azuma, 1996; Reference Castelnau, Duval, Lebensohn and CanovaCastelnau and others, 1996; Reference ThorsteinssonThorsteinsson, 2001, Reference Thorsteinsson2002; Reference Gillet-Chaulet, Gagliardini, Meyssonnier, Montagnat and CastelnauGillet-Chaulet and others, 2005; Reference Martin, Gudmundsson, Pritchard and GagliardiniMartin and others, 2009). Some other polycrystal-scale flow relations are less physically based, and the effects of anisotropy are parameterized based on the crystal orientation fabric and stress configuration or deformation (Reference Placidi and HutterPlacidi and Hutter, 2006; Reference Seddik, Greve, Placidi, Hamann and GagliardiniSeddik and others, 2008; Reference Placidi, Greve, Seddik and FariaPlacidi and others, 2010). For flow relations where crystal orientation fabrics are an input variable, a scheme describing fabric evolution as a function of stress configuration and strain is required when modelling ice-sheet evolution, which adds greatly to the computational complexity. A further subclass of flow relations includes phenomenological descriptions in which the anisotropic rheology is derived from a parameterization of the stress configuration alone, or the crystal orientation fabric and stress configuration (Reference Warner, Jacka, Li, Budd, Hutter, Wang and BeerWarner and others, 1999; Reference Wang, Warner and BuddWang and others, 2002; Reference Morland and StaroszczykMorland and Staroszczyk, 2003; Reference Pettit and WaddingtonPettit and Waddington, 2003; Reference PettitPettit and others, 2011). A full discussion on the current state of anisotropic flow relation development is beyond the scope of the present work: recent reviews by Reference MarshallMarshall (2005), Reference Placidi and HutterPlacidi and others (2006), Reference Gagliardini, Gillet-Chaulet and MontagnatGagliardini and others (2009), Reference Greve and BlatterGreve and Blatter (2009) and Reference Schulson and DuvalSchulson and Duval (2009) provide further details. Key constraints in flow relation development include achieving an acceptable balance between physical accuracy, computational efficiency and the ability to be coupled with or incorporated into regional- to continental-scale ice dynamic models.
In this work we present data from uniaxial-compression and simple-shear ice deformation experiments, conducted with the aim of providing further insight into the rheology of polycrystalline ice that may be applied to flow relation development and validation.
Experimental Method
Deformation experiments were conducted using the apparatus described by Li and others (1996, 2000), which can accommodate a range of sample geometries and stress configurations (Fig. 2). Isotropic polycrystalline ice was produced using a method similar to that of Reference JackaJacka and Lile (1984) (Table 1; Fig. 3). By producing polycrystalline ice using ultraclean deionized and filtered water, with a minimum resistivity of 18.2 MΩ cm, the interrelated lower- order effects of grain size and impurities (Reference Li and JackaLi and others, 1998; Reference Thorsteinsson, Waddington, Taylor, Alley and BlankenshipThorsteinsson and others, 1999) on experimental flow rates were minimized, since concentrations of trace ion species are below those considered necessary to significantly influence deformation processes.

Fig. 2. Schematic diagram of the combined shear and compression deformation apparatus (figure adapted from Reference Li, Jacka and BuddLi and others, 2000).
Table 1. Trace ion species contained in laboratory-made initially isotropic polycrystalline ice measured using a DIONEX DX500 ion chromatograph. Methanesulphonic acid (MSA) levels were below the instrument detection limits
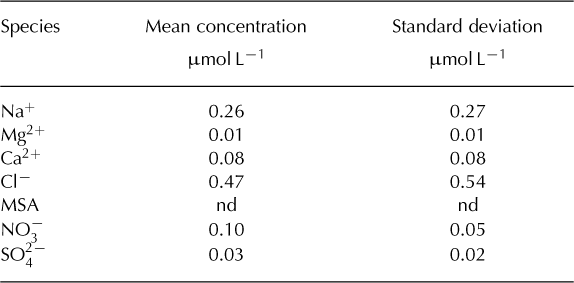

Fig. 3. Crystal orientation fabric data for experimental samples prior to deformation. simple-shear experiment samples from the Dome Summit South (DSS) ice core: (a) DSS 107 (146m), (b) small-circle girdle fabric from DSS 521 (550m) and (c) single-maximum fabric DSS 1012 (963 m). Laboratory-made, initially isotropic material (d) was also used in uniaxial compression and horizontal shear experiments. Data include: eigenvalues, ai, of the second-order orientation tensor; the mean grain area, ga (mm2); the cone angle containing the first quartile of c-axis colatitudes, φ 1/4 ; the median c-axis colatitude, φ 1/2; and the number of grains within the thin section, N.
To maintain stable experimental temperatures the deformation apparatus is placed in a recirculating silicone oil bath with thermistor-controlled heating elements. The maximum error in bath temperatures due to circulation effects and measurement uncertainty is ±0.075°C. Sample displacements used to determine strain rates were recorded using digital dial indicators with a maximum error of ±6 gm. The maximum total error in strain rates due to measurement uncertainties and experimental control is 3% (Reference TreverrowTreverrow, 2009). The difference in strain rates recorded for otherwise identical deformation experiments may be significantly higher; in the order of 10-30% (Reference GaoGao and others, 1989; Reference TreverrowTreverrow, 2009). Due to an inverse relationship between stress and the steady-state tertiary creep grain size, the ratio between sample dimensions and grain size decreases at low stress, leading to individual grains having a disproportionate influence on strain rate at low stress which introduces variability (Reference Jones and ChewJones and Chew, 1983; Reference PoirierPoirier, 1985; Reference Jacka and LiJacka and Li, 1994).
Uniaxial compression experiments
A series of 12 unconfined uniaxial compression experiments was conducted on cylindrical samples of the laboratory- made initially isotropic polycrystalline ice. The samples were machined to a nominal diameter, D = 25.4mm, using a lathe, had initial heights z0 = 70−80 mm and a mean grain area of ˜4mm2. The experiments were conducted at three constant octahedral shear stresses, to
= 0.20, 0.40 and 0.80MPa at −2.0°C. Stresses and strain rates are expressed in terms of the octahedral shear stress, to, and strain rate, ![]() , which are defined in the Appendix.
, which are defined in the Appendix.
Transverse extension of cylindrical samples during vertical compression leads to barrelling at large strains (Poisson effect), which increases the sample cross-sectional area and reduces to. To minimize variations in to the load was periodically increased during experiments at to = 0.20 and 0.40MPa, based on the accumulated vertical strain. The additional load necessary to maintain to was estimated by assuming incompressibility and that transverse strains are uniform along the sample length, leading to a uniform increase in sample cross-sectional area. Despite the use of this technique, the potential for errors in to increases as strains exceed 10%. To further reduce uncertainty in to the samples were removed from the apparatus and machined back to a nominal diameter of D = 25.4 mm, which allowed the load to be accurately reset prior to recommencing the experiment. A similar two-stage experimental procedure was used by Reference Gao and JackaGao and Jacka (1987) to provide more accurate control of to when total strains exceed ˜20%. This procedure takes less than an hour, was conducted at −18°C to minimize microstructural modification due to stress relaxation and provides the opportunity to cut a horizontal thin section from the middle of the sample for mid-experiment crystallographic examination. Following removal of a thin section, precision machining of the end-faces with a lathe enabled the two sections of the original sample to be easily rejoined.
Tertiary creep strain rates at strains εo > 10% were determined for the 12 experiments commenced on initially isotropic samples. Following the sectioning and machining procedure (only for experiments at to = 0.20 and 0.40 MPa) a further eight tertiary creep rates were determined at strains exceeding 10%. These particular experiments were commenced on samples with initially anisotropic small- circle girdle crystal orientation fabrics, which are compatible with the uniaxial compression stress configuration.
Simple-shear experiments
Horizontal shear experiments were conducted on samples with initially anisotropic crystal orientation fabrics obtained from the 1196m Dome Summit South (DSS) ice core, drilled 4.7 km from the summit of Law Dome, East Antarctica (Reference Morgan, Wookey, Li, Van Ommen, Skinner and FitzpatrickMorgan and others, 1997). Additional initially isotropic samples were prepared from laboratory-made material. All shear experiment samples were prepared using a bandsaw, and dimensions varied according to the amount of material available from the selected ice-core sections. Typically, samples were 85-100mm long and 15−20mm wide and high.
Reference Russell-HeadRussell-Head and Budd (1979) and Reference Gao and JackaGao and Jacka (1987) have shown experimentally that where deformation samples have an initial crystal orientation fabric compatible with the applied stress configuration, the strain rate decreases directly to the steady-state value, cter, i.e. the minimum strain rate for samples with the compatible fabric is the steady-state tertiary rate. This creep behaviour is illustrated schematically by the upper curve in Figure 1. We used a similar experimental technique to obtain pseudo-tertiary-creep rates at strains of 1-3% for DSS ice-core samples with pre-existing anisotropic crystal orientation fabrics.
Individual samples from three distinct depth zones within the DSS core (DSS 107 (146 m), DSS 521 (550 m) and DSS 1012 (963 m) - depths are from the surface to the top of the core sections) were used to investigate the influence of crystal orientation fabric strength on the magnitude of strain-rate enhancement at to = 0.1 MPa. Crystal orientation fabrics measured prior to deformation are presented in Figure 3. Repeat measurements of the DSS borehole inclination (Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998) and flow modelling of the drill site (Reference Wang, Warner and BuddWang and others, 2002) confirm the DSS 1012 sample is from a high-shear region, ˜230m above bedrock. This sample was selected to provide an estimate of the maximum strain-rate enhancement resulting from simple shear on the compatible strong single-maximum crystal orientation fabric. Based on surface deformation measurements, compression at the DSS borehole site is nearly uniaxial: the longitudinal (in the line of flow) strain rate of 3.2 × 10˜4a˜1 is slightly lower than the transverse strain rate of 4.5 × 10˜4 a˜1 (Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998). Modelling by Reference Wang, Warner and BuddWang and others (2002) suggests a vertical compression-dominated stress configuration at 146 m for DSS 107 and a combined shear and compression configuration at 550 m for DSS 521. Thus, unlike the DSS 1012 sample, the experimental simple-shear stress configuration does not match the in situ stress configuration for the DSS 107 and DSS 521 samples. Strain rates for these samples will indicate the relative magnitude of crystal orientation fabric strength on strain-rate enhancement.
Experiments by Reference Gao and JackaGao and Jacka (1987) and Reference Li and JackaLi and Jacka (1998) on samples with initially anisotropic crystal orientation fabrics not compatible with the applied stress configuration show that the minimum strain rate at ˜1% strain differs from the value for initially isotropic samples. For the majority of high-strain deformation in polar ice masses a dynamic balance exists between deviatoric stress, strain rate and fabric evolution. Therefore, while incompatible combinations of anisotropy and stress configuration do not replicate in situ conditions within natural ice masses, deformation experiments involving such combinations allow the influence of fabric on strain-rate enhancement to be assessed.
Uniaxial-compression (Reference JackaJacka and Maccagnan, 1984) and simple-shear (Reference GaoGao and others, 1989) experiments on initially isotropic polycrystalline ice samples have shown that at strains below εo ≈2−3% microstructural and strain-rate changes relative to the minimum isotropic state are minimal. Based on these results, the total accumulated strain for experiments where the samples had a pre-existing anisotropy was restricted to 1−3%, in order to limit microstructural evolution and ensure the measured strain rates correspond to the initial fabric.
A series of seven simple-shear experiments at to = 0.075, 0.10 and 0.20MPa on isotropic laboratory-made ice were used to determine control values for the isotropic minimum strain rate. For these experiments and those on DSS ice-core samples, a temperature-cycling procedure was used to obtain strain-rate estimates at various temperatures. Experiments were commenced at −5°C. Once the minimum strain rate had been reached, at εo ≈ 1%, the temperature was cycled down through −10 and −15°C before cycling in reverse through the same temperatures and −2 ° C. Once the samples had equilibrated to each new temperature set point, it was found that a minimum accumulated strain of 0.1% was adequate to achieve a stable strain rate prior to the next temperature step. Reference Russell-HeadRussell-Head (1979) has shown that for a given temperature, minimum strain rates determined while stepping down through a range of temperatures are equivalent to those when stepping up through a temperature range, and are also equivalent to those determined in experiments conducted at a single constant temperature. A further two simple-shear experiments were conducted on initially isotropic laboratory-made ice at t 0 = 0.4MPa and −2.0°C where the total accumulated strain exceeded 10%, allowing development of stable tertiary creep strain rates.
At the conclusion of all experiments, horizontal thin sections were cut from the samples for mean grain area and crystal orientation fabric analysis. Crystal orientation fabrics were measured using a Russell-Head Instruments G- 50 automated ice crystal fabric analyser. Fabric data are presented for a horizontal reference frame using lower- hemisphere projection Schmidt equal-area plots. The mean grain area was determined from the total number of grains within a thin section and the thin-section area. The total number of grains was determined during crystal orientation fabric measurement, and the pixel count for the corresponding thin-section bitmap image (produced by the automated fabric analyser) was determined via digital image analysis. The bitmap pixel dimensions are 43 µm×43µm.
Results
Uniaxial compression experiments
Representative creep curves for uniaxial compression experiments at t 0 = 0.20, 0.40 and 0.80 MPa are presented in Figure 4. Distinct minima in for experiments commenced on initially isotropic ice are visible at ˜1% strain. In the two-stage experiments at t 0 = 0.20 and 0.40MPa, co decreases directly to the tertiary creep rate during the second stage, as samples have pre-existing small-circle girdle crystal orientation fabrics. Crystal orientation fabrics measured at the conclusion of uniaxial compression experiments at t 0 = 0.20 and 0.40MPa, where the total accumulated strain was εo > 20%, are presented in Figure 5.

Fig. 4. Octahedral shear strain rate as a function of octahedral shearstrain for uniaxial compression experiments at τ o = 0.20, 0.40and 0.80MPa and −2°C. Representative data from experiments on initially isotropic samples and those with an initial small-circle girdle crystal orientation fabric are presented. A distinct minimum in strain rates occurs for initially isotropic samples. For experiments commenced at τ o = 0.20 and 0.40MPa, on samples with an initially anisotropic small-circle girdle crystal orientation fabric, strain rates decrease directly towards the steady-state tertiary value.
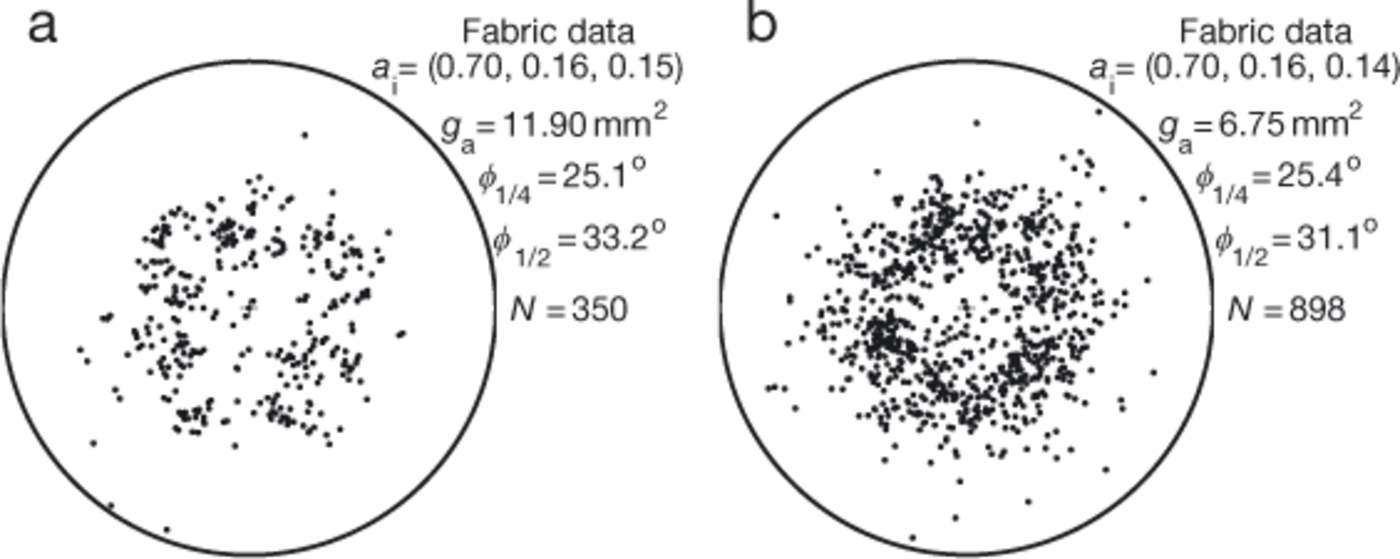
Fig. 5. Crystal orientation fabric data measured after the completion of uniaxial compression experiments at −2ºC. (a) τ o = 0.20MPa, (b) τ o = 0.40MPa. (Crystal orientation fabric data as Fig. 3.)
The effect on strain rates of increasing the compression load to account for sample barrelling is most apparent in experiments at t 0 = 0.40MPa (Fig. 4). Distinct step increases in strain rates at strains ≳3% indicate where the load adjustments were made. A gradual decline in strain rates, due to a continued decrease in t 0 with accumulating strain, is evident between load adjustments. Step changes in strain rates are smaller for experiments at t 0 = 0.20MPa, as the required load increments are smaller than those for t 0 = 0.40 MPa and the lower strain rates allow more frequent load adjustments as a function of strain.
Isotropic minimum and steady-state tertiary creep strain rates for all compression experiments are shown in Figure 6. From linear regression of the ![]() data, 95% confidence intervals were determined for the creep power- law stress exponent (n in Eqn (2)); n = 3.8 ± 0.3 for steady- state tertiary strain rates and n = 3.3 ± 0.3 for isotropic minimum strain rates. The higher value of n for tertiary creep compared with that for (secondary) minimum creep can be interpreted as a stress-dependent level of strain-rate enhancement, where
data, 95% confidence intervals were determined for the creep power- law stress exponent (n in Eqn (2)); n = 3.8 ± 0.3 for steady- state tertiary strain rates and n = 3.3 ± 0.3 for isotropic minimum strain rates. The higher value of n for tertiary creep compared with that for (secondary) minimum creep can be interpreted as a stress-dependent level of strain-rate enhancement, where ![]() , such that enhancement increases from E ≈ 2.8 at τo = 0.20 MPa to E ≈ 6.3 at τ0 = 0.80 MPa.
, such that enhancement increases from E ≈ 2.8 at τo = 0.20 MPa to E ≈ 6.3 at τ0 = 0.80 MPa.

Fig. 6. Isotropic minimum and steady-state tertiary creep octahedral shear strain rates for uniaxial compression experiments at τ
o = 0.20, 0.40 and 0.80MPa and −2°C. Strain-rate enhancement, ![]() increases as a function of τo. Limits of the creep powerlaw stress exponent, n, are 95% confidence intervals. The dottedlines illustrate the small difference in the isotropic minimum and tertiary creep rates when adjusted to stress exponents of n = 3.0 and n = 3.5, respectively. The widely accepted stress exponent of n = 3 for the minimum creep rate of isotropic polycrystalline ice isdiscussed in the text, while n = 3.5 for steady-state tertiary creep is based on simple-shear experiments (Fig. 9) conducted over a wider range of stresses.
increases as a function of τo. Limits of the creep powerlaw stress exponent, n, are 95% confidence intervals. The dottedlines illustrate the small difference in the isotropic minimum and tertiary creep rates when adjusted to stress exponents of n = 3.0 and n = 3.5, respectively. The widely accepted stress exponent of n = 3 for the minimum creep rate of isotropic polycrystalline ice isdiscussed in the text, while n = 3.5 for steady-state tertiary creep is based on simple-shear experiments (Fig. 9) conducted over a wider range of stresses.
Simple-shear experiments
Minimum strain rates for the simple-shear experiments on initially isotropic ice at temperatures from —2 to −20°C (Fig. 7) illustrate the significant effects of stress and temperature on isotropic polycrystalline ice flow. Minimum isotropic strain rates from the similar simple-shear experiments of Reference Russell-HeadRussell-Head and Budd (1979) have been included to provide additional data at each temperature, and to extend coverage down to shear stresses to = 0.022 MPa. Creep power-law stress exponents of n≈ 3.0 determined from the minimum isotropic strain-rate data are consistent with other compilations of minimum isotropic strain rates (e.g. Reference Budd and JackaBudd and Jacka, 1989).
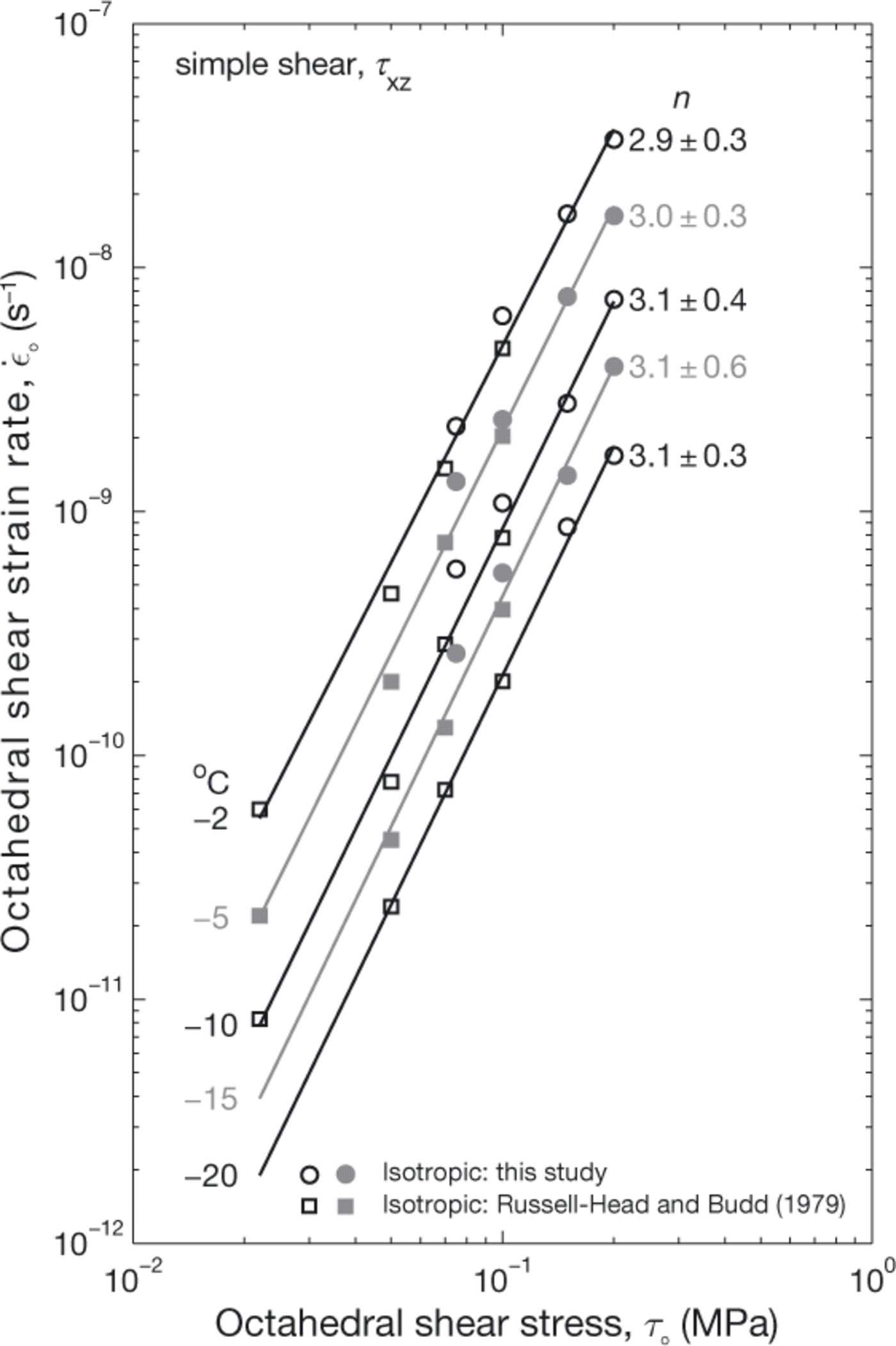
Fig. 7. Minimum octahedral shear strain rates for simple-shear experiments on initially isotropic laboratory-made polycrystalline ice. Additional data are from Reference Russell-HeadRussell-Head and Budd (1979). Solid lines indicate a least-squares fit to ![]() data for each temperature. Limits of n, the creep power-law stress exponent, for each dataset are 95% confidence intervals. Alternating black and grey symbols and lines distinguish adjacent datasets at different temperatures.
data for each temperature. Limits of n, the creep power-law stress exponent, for each dataset are 95% confidence intervals. Alternating black and grey symbols and lines distinguish adjacent datasets at different temperatures.
The minimum strain rates determined for DSS samples with initially anisotropic crystal orientation fabrics at strains of ε o = 1-3% vary according to the nature of the pre-existing fabric (Fig. 8). These strain rates can be compared via enhancement factors calculated using isotropic minimum strain rates from the control experiments (Fig. 7) as a reference. In general, enhancement decreased for increasing φ 1/4 values, where φ 1/4 is the cone angle containing the first quartile of c-axis colatitudes. The highest mean enhancement, E = 5.2, occurs for the DSS 1012 (963 m) ice-core sample obtained from the high-shear layer identified in the DSS borehole (Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998). As simple shear is the in situ stress configuration for this sample, E = 5.2 provides an estimate of the maximum strain-rate enhancement for shear on a strong single-maximum crystal orientation fabric at τ o = 0.10MPa and temperatures from −2 to −15ºC. The crystal orientation fabrics for the DSS 521 and DSS 107 samples are only partially compatible with the experimental simple-shear stress configuration. The lower mean E values for these samples are related to their reduced proportion of near-vertical c-axes in comparison with the DSS 1012 sample (Fig. 3), which is indicated by generally higher φ 1/2 and φ 1/4 values. Unlike the effect of stress on enhancement, Figure 8 indicates temperature does not influence the level of strain-rate enhancement.

Fig. 8. Octahedral shear strain rates for horizontal simple-shear experiments on initially isotropic laboratory-made polycrystalline ice and initially anisotropic samples from the DSS ice coreconducted at τ o = 0.10MPa. Additional isotropic minimum strainrate data are from Reference Russell-HeadRussell-Head and Budd (1979). Lower values of φ 1/4 indicate fabrics that are more strongly vertically clustered.
As the simple-shear tertiary creep data from the current study are limited, results from previous experiments conducted using the same or similar apparatus have been included to further illustrate differences in isotropic minimum and steady-state tertiary creep rates as a function of stress at −2
°
C. The sources of additional data are indicated in Figure 9. Due to the scarcity of low-stress tertiary creep data, additional data from experiments by Reference LileLile (1984) at −6°C have been included after rescaling to −2°C based on strain-rate, stress and temperature relationships determined from the isotropic minimum creep data of Figure 7. For stresses between τ0
= 0.04 and 0.40 MPa the tertiary creep power-law stress exponent in simple shear (n = 3.5 ± 0.5) is higher than that for isotropic minimum strain rates (n = 3.0 ± 0.2). These data suggest the enhancement−stress proportionality of ![]() determined from uniaxial compression experiments, also applies to simple shear; however, the magnitude of E is greater for simple shear. Analysis of the
determined from uniaxial compression experiments, also applies to simple shear; however, the magnitude of E is greater for simple shear. Analysis of the ![]() data in Figure 9 indicates enhancement increases from E = 2.9 at to
= 0.04MPa to E = 9.1 at To = 0.40 MPa. 10
data in Figure 9 indicates enhancement increases from E = 2.9 at to
= 0.04MPa to E = 9.1 at To = 0.40 MPa. 10
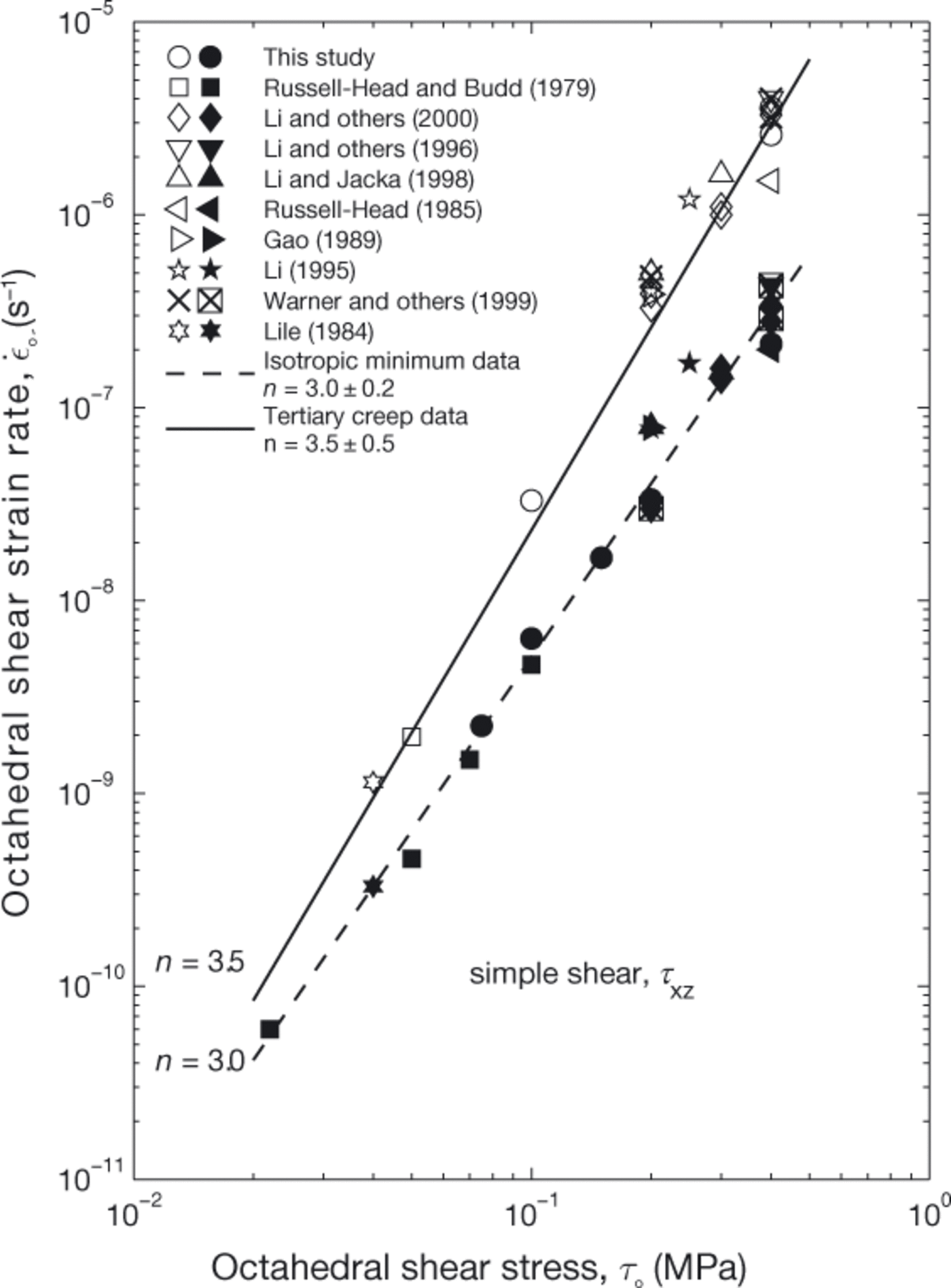
Fig. 9. Tertiary creep octahedral shear strain rate, ![]() (open symbols), vs octahedral shear stress, τ
o, for simple-shear experiments. The corresponding isotropic minimum strain rates (filled symbols) are presented for comparison. All experiments were conducted at −2°C using the same or similar apparatus. Sources of additional experimental data are listed in the legend. Limits for the creep power-law stress exponents, n, for isotropic minimum and steady- state tertiary creep are 95% confidence intervals.
(open symbols), vs octahedral shear stress, τ
o, for simple-shear experiments. The corresponding isotropic minimum strain rates (filled symbols) are presented for comparison. All experiments were conducted at −2°C using the same or similar apparatus. Sources of additional experimental data are listed in the legend. Limits for the creep power-law stress exponents, n, for isotropic minimum and steady- state tertiary creep are 95% confidence intervals.
Discussion
Our experimental results clearly indicate consistent differences in the creep rate power-law stress exponents for isotropic minimum and steady-state tertiary creep. From the simple-shear deformation experiments a power-law stress exponent of n = 3 was determined for isotropic minimum strain rates. This value agrees with previous compilations of laboratory and field studies (e.g. reviews by Reference Budd and JackaBudd and Jacka, 1989; Reference Cuffey and PatersonCuffey and Paterson, 2010). At strains exceeding 10%, when crystal orientation fabrics compatible with the applied stress have developed during tertiary steady-state creep, the data indicate a higher stress exponent of n = 3.5. In comparison with isotropic minimum strain rates, tertiary creep rate data from experiments conducted over a sufficiently broad range of stresses to enable calculation of n are sparse, despite the importance of steady-state tertiary creep to the flow of polar ice masses. In previous laboratory studies where tertiary creep rates have been observed, Reference SteinemannSteinemann (1958b) found n increased with stress up to n ≈ 4 at 8 MPa and Reference Kirby, Durham, Beeman, Heard and DaleyKirby and others (1987) found n = 4.0±0.6for experiments at stresses up to 10MPa. While these n values exceed those reported here, they are associated with higher- stress experiments. As such, they are compatible with the tertiary creep stress exponent of n = 3.5 for experiments at stresses between to = 0.04 and 0.40 MPa, which are more relevant to polar ice dynamics.
The simple-shear and uniaxial compression strain-rate data indicate that a similar proportionality of ![]() exists between strain-rate enhancement and the octahedral shear stress in both stress configurations. For simple shear this proportionality was determined over stresses from τ
o
= 0.04 to 0.40MPa; for uniaxial compression strain rate, data are from a narrower range of higher-magnitude stresses from τ
o
= 0.20 to 0.80 MPa. To enable direct comparison of the simple-shear and uniaxial compression steady-state tertiary creep rates (Fig. 10), the uniaxial compression strain-rate data have been extrapolated down to τ
o
= 0.04MPa, the minimum stress within the simple-shear tertiary creep data compilation. As a steady-state tertiary creep stress exponent of n = 3.5 applies down to τ
o
= 0.04MPa at −2°C for simple shear, we assume this is also the case for unconfined compression and rescale the data appropriately. Similarly, we assume a stress exponent of n = 3 for isotropic minimum creep rates in compression.
exists between strain-rate enhancement and the octahedral shear stress in both stress configurations. For simple shear this proportionality was determined over stresses from τ
o
= 0.04 to 0.40MPa; for uniaxial compression strain rate, data are from a narrower range of higher-magnitude stresses from τ
o
= 0.20 to 0.80 MPa. To enable direct comparison of the simple-shear and uniaxial compression steady-state tertiary creep rates (Fig. 10), the uniaxial compression strain-rate data have been extrapolated down to τ
o
= 0.04MPa, the minimum stress within the simple-shear tertiary creep data compilation. As a steady-state tertiary creep stress exponent of n = 3.5 applies down to τ
o
= 0.04MPa at −2°C for simple shear, we assume this is also the case for unconfined compression and rescale the data appropriately. Similarly, we assume a stress exponent of n = 3 for isotropic minimum creep rates in compression.
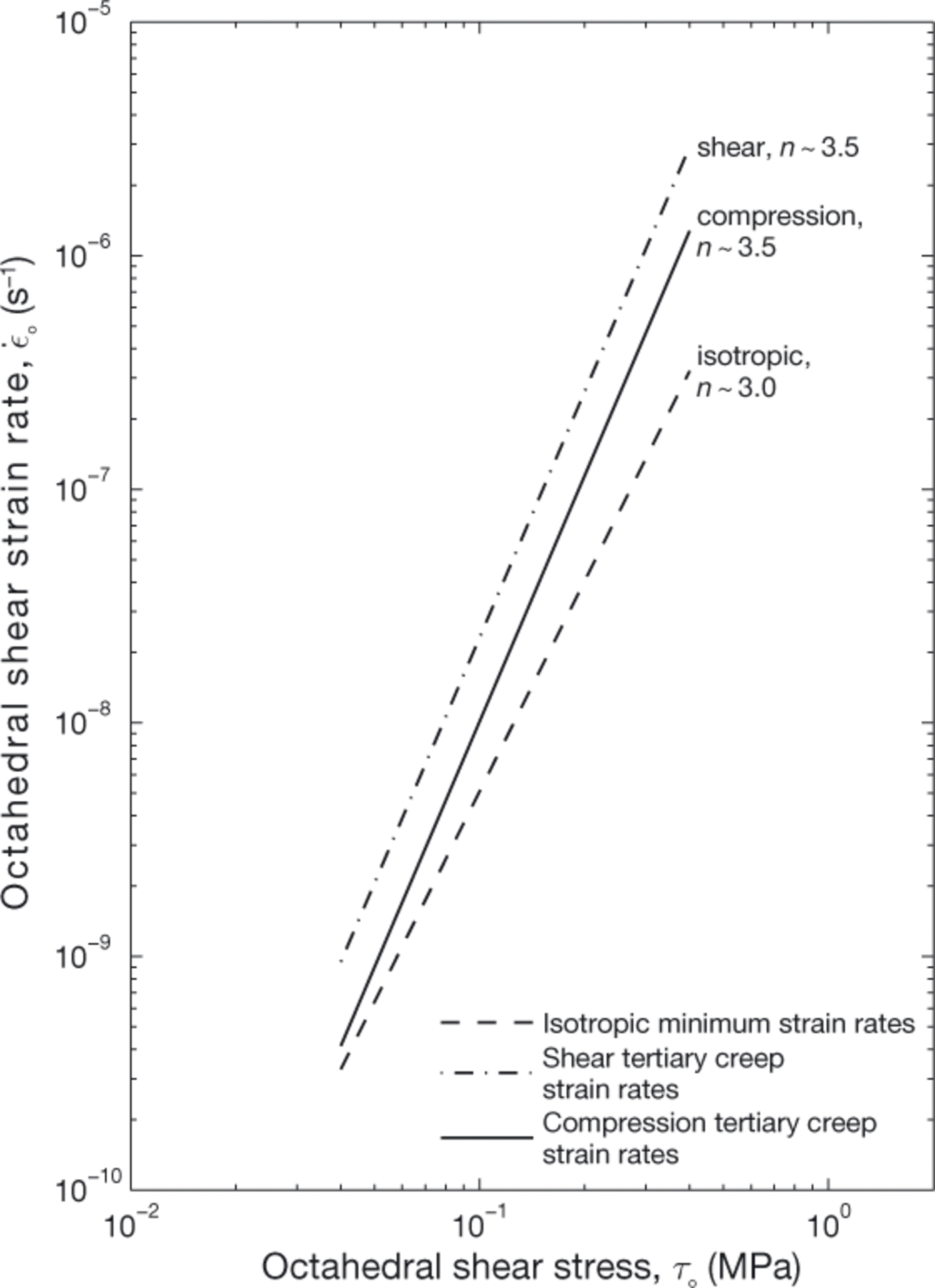
Fig. 10. Octahedral shear strain rate, ![]() in tertiary creep vs octahedral shear stress, τo, for unconfined compression and simpleshear ice deformation experiments. Minimum strain rates for isotropic polycrystalline ice are based on the data presented in Figure 9. All experiments were conducted at −2°C. The compression data from Figure 6 have been referred to a tertiary creep stress exponent of n = 3.5 and an isotropic minimum creep stress exponent of n = 3.0. For stresses between τo = 0.04 and 0.40MPa the simple-shear enhancement increases from E = 2.9 to 9.1 and for uniaxial compression from E = 1.3 to 4.0.
in tertiary creep vs octahedral shear stress, τo, for unconfined compression and simpleshear ice deformation experiments. Minimum strain rates for isotropic polycrystalline ice are based on the data presented in Figure 9. All experiments were conducted at −2°C. The compression data from Figure 6 have been referred to a tertiary creep stress exponent of n = 3.5 and an isotropic minimum creep stress exponent of n = 3.0. For stresses between τo = 0.04 and 0.40MPa the simple-shear enhancement increases from E = 2.9 to 9.1 and for uniaxial compression from E = 1.3 to 4.0.
The isotropic minimum and tertiary strain rates from both uniaxial-compression and simple-shear experiments at −2°C are summarized in Figure 10, which clearly illustrates the difference in shear and compression tertiary creep strain rates and their relation to isotropic minimum strain rates.
Flow relations for shear and compression
The relationship between stress and tertiary creep rate for simple-shear and unconfined compression alone (Fig. 10) provides the basis for flow relations in these single component stress configurations. The tertiary creep stress exponent of n = 3.5 may be interpreted in the context of a flow relation with a cubic dependence on to
and a stress-dependent level of enhancement, where ![]() Based on Eqn (5) and Figure 6, a suitable expression for
Based on Eqn (5) and Figure 6, a suitable expression for ![]() in compression alone is
in compression alone is
where Ec is the stress-dependent uniaxial compression strain- rate enhancement. The constant, ec, is an enhancement scale factor for compression, and ec − 6.3(MPa)-1/2 when t 0 has units of MPa. Similarly for shear alone,
The shear strain-rate enhancement, Es (Fig. 9), is determined by the shear enhancement scale factor, es −14.4(MPa)-1/2. The ratio es: ec −2.3 describes the relative magnitude of simple-shear and uniaxial-compression strain rates and is similar to values determined in other experimental studies (e.g. Reference Budd and JackaBudd and Jacka, 1989). Modelling using grain-scale anisotropic flow relations (Azuma and Goto-Reference Azuma and Goto-AzumaAzuma, 1996; Reference ThorsteinssonThorsteinsson, 2001) has shown that where crystal orientation fabrics compatible with simple shear (single maximum) and unconfined compression (small- circle girdle) exist, the higher levels of shear strain-rate enhancement in shear have a geometric origin. For an aggregate of grains, the mean resolved shear stress on the basal planes of the individual grains is higherfor simple shear on a single-maximum fabric where the mean orientation of c-axes is approximately normal to the plane of shear.
Flow relations for combined stress configurations
The stress configurations in natural ice masses are invariably a complex combination of compression, extension and shear components, which should all be considered when describing the flow. The laboratory deformation experiments in combined vertical compression and horizontal simple shear of Reference Li, Jacka and BuddLi and others (1996) and Reference Warner, Jacka, Li, Budd, Hutter, Wang and BeerWarner and others (1999) led to the development of flow relations for combined simple shear and confined compression. These experiments showed that a transition in enhancement occurs when stress configurations vary from compression alone to shear alone. Our results add to this previous knowledge by refining values of Ec and Es and describing their dependence on t 0. Since Ec and Es display a similar proportionality to t 0 we propose a development of the flow relation of Reference Warner, Jacka, Li, Budd, Hutter, Wang and BeerWarner and others (1999), on the basis that a similar dependence of E on t 0 exists in combined stress configurations. From the current experimental stress configurations, we define an orthogonal coordinate system, where the shear stress, t , is applied in the x-direction, compression, a, in the vertical z-coordinate and the y-coordinate is normal to the xz-plane. In this reference frame, the deviatoric stress tensor, Sj, for simple shear and unconfined compression is
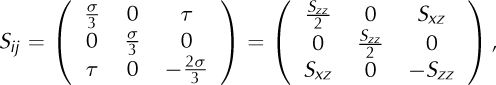
where Sxz = τ and Szz = 2σ/3 are the shear and compression deviators and the magnitude of the corresponding octahedral shear stress is

In combined unconfined compression and simple shear (Eqn (8)), the proportions of the deviatoric components can be described by the shear fraction, λs (Reference Li, Jacka and BuddLi and others, 1996),

where for unconfined compression alone λs = 0 and in shear alone λs = 1.
Under similar conditions the shear-alone enhancement, Es, is greater than that in compression alone, i.e. Es
/Ec
= 2.3, which suggests that in combined stress configurations there may not be a direct relation between ![]() and t
0 and the components of Sij
should be weighted by the appropriate component enhancements. Accordingly, we introduce the weighted anisotropic mean shear stress, T
o, of Reference Warner, Jacka, Li, Budd, Hutter, Wang and BeerWarner and others (1999),
and t
0 and the components of Sij
should be weighted by the appropriate component enhancements. Accordingly, we introduce the weighted anisotropic mean shear stress, T
o, of Reference Warner, Jacka, Li, Budd, Hutter, Wang and BeerWarner and others (1999),

where a = Es
1/3 and β = Ec
1/3
. Following Reference Warner, Jacka, Li, Budd, Hutter, Wang and BeerWarner and others (1999), the corresponding shear (![]() ) and compression (
) and compression (![]() ) component strain rates in combined shear and compression are
) component strain rates in combined shear and compression are
The octahedral shear strain rate for tertiary creep, defined in terms of T o, is (Reference Warner, Jacka, Li, Budd, Hutter, Wang and BeerWarner and others, 1999)
By substitution of Eqns (9-11) into Eqn (14) the stress dependence of component strain-rate enhancement during tertiary creep is explicitly incorporated into the octahedral shear strain rate:

When λs = 0 or 1, Eqn (15) reduces to the corresponding relations for ![]() in compression or shear alone (Eqns (6) and (7)). In combined stress configurations where 0 < λs < 1 the octahedral shear strain-rate enhancement, Eo, is given by
in compression or shear alone (Eqns (6) and (7)). In combined stress configurations where 0 < λs < 1 the octahedral shear strain-rate enhancement, Eo, is given by

By making the substitutions a = Es 1/3 and β = Ec 1/3, and recalling that Es =esT0 1/2 and Ec = ecT0 1/2, Eqn (16) provides a description of enhancement factor Eo as a function of both stress configuration and magnitude. The family of curves in Figure 11 is based on this relation, and presents a hypothetical interpolation of enhancement in combined uniaxial compression and simple shear (Eqn (8)), for stresses from τ0 = 0.025 to 0.40MPa. In developing their flow relation for combined shear and compression, Reference Warner, Jacka, Li, Budd, Hutter, Wang and BeerWarner and others (1999) assumed a ratio of shear to compression enhancement factors of Es /Ec ≈ 4. Our compilation of unconfined compression and simple-shear experimental data over a broader range of stresses provides a refinement of this ratio to Es /Ec ≈ 2.3. Additionally, Eqn (16) builds on this previous work by providing a simple parameterization of the effect of stress magnitude, to, on enhancement that can be easily incorporated into other anisotropic flow relations that relate the strain-rate and deviatoric stress tensors. Examples include the phenomenological flow relation of Reference Warner, Jacka, Li, Budd, Hutter, Wang and BeerWarner and others (1999) and the grain-scale crystal orientation fabric based flow relations of Reference Azuma and Goto-AzumaAzuma and Goto-Azuma (1996), Reference Castelnau, Duval, Lebensohn and CanovaCastelnau and others (1996), Reference ThorsteinssonThorsteinsson (2001), Reference Gillet-Chaulet, Gagliardini, Meyssonnier, Montagnat and CastelnauGillet-Chaulet and others (2005) and Reference Placidi, Greve, Seddik and FariaPlacidi and others (2010).

Fig. 11. Tertiary creep octahedral shear strain-rate enhancement, Eo, as a function the shear fraction, λ s, in combined unconfined compression and simple-shear stress configurations. As λ s →0 the shear deviatoric stress Sxz →0, while as λ s →1 the compression deviatoric stress Szz → 0. The E o–λ s relationship (Eqn (16)) is plotted for a range of octahedral shear stresses, τ o (MPa). The strain-rate enhancement for shear alone (λ s =1) is ∼2.3 times the corresponding value in compression alone (λ s = 0) for all valuesof τ o.
Our results provide a clear illustration of the influence of stress configuration and magnitude on tertiary strain rates. Additional experiments over a broader range of temperatures and stresses are required to further describe flow in combined stress configurations relevant to the dynamics of large polar ice masses. Equation (15) has been developed from strain-rate data for stress configurations incorporating unconfined compression and/or simple shear: the limited availability of tertiary creep data from deformation experiments in other stress configurations currently precludes a broader description of Eo. We have recently completed a series of experiments that will assist with flow relation development by providing further data on individual component strain rates and their stress-dependent enhancement in combined shear and confined compression.
Low-stress tertiary creep behavior
Unlike isotropic minimum strain rates, which are associated with a transient stage of secondary creep at ˜1% total strain, steady-state tertiary creep rates are controlled by a dynamic balance between deformation processes, which increase the dislocation density, and recovery processes involving grain-boundary migration and the formation of strain-free nuclei. Other processes, including non-basal slip, grain-boundary sliding and diffusion, are considered to provide a minor contribution to recovery (Reference Montagnat, Durand and DuvalMontagnat and others, 2009; Reference Schulson and DuvalSchulson and Duval, 2009). Differences in the stress dependence of tertiary and isotropic minimum strain rates (Fig. 10) may be due to differences in ratecontrolling processes for the two creep regimes (Reference Schulson and DuvalSchulson and Duval, 2009). The convergence of tertiary and isotropic minimum strain rates at low stresses due to differences in their stress dependence (Fig. 10) raises the question of what, if any, changes to the stress dependence of steady-state tertiary creep occur at very low stresses. The availability of laboratory data to validate the low-stress creep behaviour is limited by the difficulties associated with conducting the long-running experiments necessary to determine very low tertiary creep rates.
The uniaxial compression experiments of Reference Jacka and LiJacka and Li (2000) at stresses from τ0 =0.10 to 0.80MPa and temperatures of −5 to −45°C support the observed stress- dependent levels of strain-rate enhancement during steady- state tertiary creep and the resulting convergence of tertiary and minimum isotropic strain rates with decreasing stress. Reference Jacka and LiJacka and Li (2000) conclude this behaviour reflects a temperature-dependent shift in rate-controlling processes: at higher stresses and temperatures, migration recrystallization is dominant. As temperature and stress decrease, migration recrystallization becomes less influential, with other deformation modes, including rotation recrystallization and poly- gonization, controlling strain rates (Reference Montagnat, Durand and DuvalMontagnat and others, 2009; Reference Schulson and DuvalSchulson and Duval, 2009). In general, Reference Jacka and LiJacka and Li (2000) report lower enhancements than those determined from the current experiments, including E ≈ 1 at τ0 = 0.10−20 MPa for experiments at −15 and −19°C. Two factors may have contributed to these low enhancement values. Firstly, the applied load was not periodically increased to offset the reduction in τ0 resulting from sample barrelling. If no load adjustments are made during unconfined vertical compression, by 10% strain the strain rate will be reduced to ˜70% of the anticipated value. Secondly, in the experiments at τ0 = 0.10 MPa the total accumulated strains may have been insufficient to develop a steady-state tertiary creep rate (e.g. total strains were <5% for experiments at −15 and −19°C). In comparison, an enhancement of E = 2.8 was determined from the current experiments at τ0 = 0.20 MPa and −2°C when εo > 15% (Fig. 6). A single experiment at −45°C with τo = 0.20 MPa by Reference Jacka and LiJacka and Li (2000), in which two-stage experimental procedures were used to maintain a stable load, provides better agreement with the current results. The resulting enhancement of E =1.7 determined at ε0 = 6% is an estimate of the minimum enhancement at τ0 = 0.20MPa and −45°C, as the experiment was incomplete and the strain rate still accelerating when the results were published (Reference Jacka and LiJacka and Li, 2000). These observations suggest that while a low-stress reduction in enhancement to E ≈ 1 is possible, such a transition is likely to occur at a stress below the τ0 ≈ 0.1 MPa suggested by the data of Reference Jacka and LiJacka and Li (2000) and therefore at a stress below which there are currently sufficient field and laboratory data to enable accurate quantification.
A range of experimental studies indicate a shift in the stress dependence of the creep power law to n < 3 at stresses of 0.1-0.3MPa (e.g. Reference SteinemannSteinemann, 1958b; Reference JackaJacka, 1984; Reference Pimienta and DuvalPimienta and Duval, 1987; Reference De La Chapelle, Milsch, Castelnau and DuvalDe La Chapelle and others, 1999; Reference Song, Cole and BakerSong and others, 2005). These data must be applied cautiously to steady-state tertiary creep as, with the exception of Reference SteinemannSteinemann (1958b), they relate to either isotropic minimum (secondary) strain rates or estimates of isotropic minimum strain rates determined by extrapolation of experimental data where total strains were significantly less than 1% (e.g. Reference Pimienta and DuvalPimienta and Duval, 1987). In uniaxial compression experiments where minimum creep rates were clearly determined, indications of a stress-dependent shift in creep behaviour are variable: Reference De La Chapelle, Milsch, Castelnau and DuvalDe La Chapelle and others (1999) report a transition to n = 1.8 ± 0.2 at axial stresses below ˜0.1 MPa (τ0 < 0.05 MPa); the data of Reference JackaJacka (1984) indicate n ≈ 2 for τ0 < 0.1 MPa, and Reference Song, Cole and BakerSong and others (2005) found n = 1 below 0.3 MPa (τ0 = 0.14 MPa). Reference Song, Cole and BakerSong and others (2005) attribute their relatively high-stress transition in n to sample preparation techniques.
The derivation of robust estimates of n from field observations has proven difficult. As the stresses driving borehole closure are related to the overburden pressure, the Reference PatersonPaterson (1977) estimates of n = 3 from the closure of five polar boreholes generally correspond to stresses greater than 0.1 MPa, and the measured deformation is not steady- state, since primary, secondary and tertiary creep of the ice adjacent to the boreholes contributes to their closure. Reference Dahl-Jensen and GundestrupDahl-Jensen and Gundestrup (1987) obtained n = 2-3 from several different analyses of Dye-3 borehole tilt data; however, the derivation of robust estimates of n from inclinometer measurements is confounded by the requirement that all factors that influence the viscosity (temperature, polycrystalline anisotropy, impurities) be quantified in order to accurately determine the stress.
Despite a lack of conclusive laboratory and field data indicating a transition in the power-law stress dependence of tertiary creep, if one assumes that tertiary creep rates are always greater than or equal to the corresponding isotropic minimum values, then indications of a transition to n < 3 for isotropic minimum creep necessitate a transition to a similar or lower value of n during tertiary creep. Based on experimental indications of a transition to n < 3 for isotropic minimum creep rates at stresses below to = 0.1MPa, a transition from n = 3.5 to n < 3 during tertiary creep may occur at a similar or lower stress. Figure 9 indicates that for simple shear any transition in n must occur at t 0 < 0.04 MPa.
In modelling flow in low deviatoric stress environments, such as ice divides, Reference Pettit and WaddingtonPettit and Waddington (2003) proposed a multicomponent flow relation with n = 1,3 and 5 terms. The linear term was found to be dominant at low stresses, and Reference Pettit and WaddingtonPettit and Waddington (2003) define the crossover stress as the deviatoric stress where the n = 1 and n = 3 components of the flow relation contribute equally to the total deformation. Using a combination of modelling and observations at Siple Dome, West Antarctica, Reference PettitPettit and others (2011) reported a crossover stress equivalent to τ0= (1.5 × 10-2) ± (2.0 ×10-3) MPa.
Extrapolation of the experimental ![]() data for tertiary and isotropic minimum creep strain rates (Fig. 10) to low stresses allows calculation of a critical stress
t0
c
at which the tertiary (n = 3.5) and isotropic minimum (n = 3) strain rates will be equivalent, resulting in E = 1. No physical significance is attached to τ0
c
;
it merely provides a reference for assessing differences in tertiary and isotropic minimum creep rates. For uniaxial compression
t0
c = (2.5 × 10-2) ± (5.0 × 10-3) MPa and τ0
c= (4.8 × 10-3) ± (2.0 × 10-3) MPa for simple shear. It is noteworthy that the crossover stress of Reference PettitPettit and others (2011) is similar to t
0
c = (2.5 × 10-2) ± (5.0 × 10-3)MPa for uniaxial compression, as
t0
c provides a lower bound for any transition from a tertiary creep regime with n = 3.5 to one with n < 3. While the occurrence of a transition in the tertiary creep regime is not excluded by the observed differences in n for tertiary and isotropic minimum creep, the mechanisms responsible plus the combined influence of factors including stress configuration, stress magnitude and temperature remain unclear. These uncertainties highlight the need for additional laboratory and field observations of low-stress steady-state tertiary creep behaviour. Conducting well-controlled laboratory experiments under the low-stress and -temperature conditions necessary to address these uncertainties is not trivial: depending upon experimental variables and techniques, 5 years or more may be required to obtain steady-state tertiary creep rates.
data for tertiary and isotropic minimum creep strain rates (Fig. 10) to low stresses allows calculation of a critical stress
t0
c
at which the tertiary (n = 3.5) and isotropic minimum (n = 3) strain rates will be equivalent, resulting in E = 1. No physical significance is attached to τ0
c
;
it merely provides a reference for assessing differences in tertiary and isotropic minimum creep rates. For uniaxial compression
t0
c = (2.5 × 10-2) ± (5.0 × 10-3) MPa and τ0
c= (4.8 × 10-3) ± (2.0 × 10-3) MPa for simple shear. It is noteworthy that the crossover stress of Reference PettitPettit and others (2011) is similar to t
0
c = (2.5 × 10-2) ± (5.0 × 10-3)MPa for uniaxial compression, as
t0
c provides a lower bound for any transition from a tertiary creep regime with n = 3.5 to one with n < 3. While the occurrence of a transition in the tertiary creep regime is not excluded by the observed differences in n for tertiary and isotropic minimum creep, the mechanisms responsible plus the combined influence of factors including stress configuration, stress magnitude and temperature remain unclear. These uncertainties highlight the need for additional laboratory and field observations of low-stress steady-state tertiary creep behaviour. Conducting well-controlled laboratory experiments under the low-stress and -temperature conditions necessary to address these uncertainties is not trivial: depending upon experimental variables and techniques, 5 years or more may be required to obtain steady-state tertiary creep rates.
Summary
The high strain creep that predominates in polar ice masses can be considered similar to the steady-state tertiary creep strain rates determined in laboratory deformation experiments. Isotropic minimum strain rates, which are easily measured in the laboratory, provide a useful, reproducible reference for investigating tertiary strain rates in shear and compression stress configurations. Strain-rate enhancement, defined as the ratio of corresponding tertiary and isotropic minimum strain rates, ![]() , has been used to compare steady-state tertiary creep rates in shear and compression. The results presented here help to clarify the wide range of enhancement factors for tertiary creep by showing there is a systematic increase in enhancement with stress in both simple shear and unconfined compression.
, has been used to compare steady-state tertiary creep rates in shear and compression. The results presented here help to clarify the wide range of enhancement factors for tertiary creep by showing there is a systematic increase in enhancement with stress in both simple shear and unconfined compression.
Based on unconfined compression and simple-shear creep deformation experiments at stresses ranging from τ0 = 0.02 to 0.80 MPa the creep power-law stress exponentfor isotropic minimum strain rates is n =3. This value agrees with those found in many previous experimental studies of isotropic minimum strain rates. Uniaxial-compression and simple- shear tertiary creep data at stresses from τ0 = 0.04 to 0.80MPa are best described by a power law where n = 3.5. Various studies (e.g. Reference PettitPettit and others, 2011) have suggested the existence of a low-stress linear (n =1) creep regime. Based on experiments at —2°C in this study, any transition to a n =1 creep regime would occur at τ0 < 0.04 MPa.
The difference in n for isotropic minimum and steady-state tertiary creep rates can be interpreted as a stress-dependent level of strain-rate enhancement where ![]() Under similar conditions of temperature and stress, the shear and compression enhancement factors are related as Es/Ec
≈ 2.3. Experimental results show that for stresses from τ0= 0.04 to 0.50MPa the shear strain-rate enhancement increases from Es = 2.8 to 10.2, while in compression at τ0 = 0.20- 0.80MPa the enhancement increases from Ec = 2.8 to 5.6. Extrapolation of the compression data down to τ0 = 0.04MPa gives an enhancement of E =1.3.
Under similar conditions of temperature and stress, the shear and compression enhancement factors are related as Es/Ec
≈ 2.3. Experimental results show that for stresses from τ0= 0.04 to 0.50MPa the shear strain-rate enhancement increases from Es = 2.8 to 10.2, while in compression at τ0 = 0.20- 0.80MPa the enhancement increases from Ec = 2.8 to 5.6. Extrapolation of the compression data down to τ0 = 0.04MPa gives an enhancement of E =1.3.
Based on a compilation of experimental data and the flow relation of Reference Warner, Jacka, Li, Budd, Hutter, Wang and BeerWarner and others (1999) we have provided a simple example of how the stress dependence of enhancement identified for shear and compression alone might be propagated into more complex deformations. At present, there are limited experimental data from combined shear and compression deformation, and a systematic series of experiments in complex stress configurations relevant to the flow of polar ice masses, combined with field observations of strain rates and crystallography, is required to further develop and validate the necessary flow relations. Similarly, description of the low-stress and -temperature rheology of polycrystalline ice is incomplete and requires further investigation. In particular, details of a low-stress transition to a creep regime with a power law stress exponent of n < 3 remain unclear.
Acknowledgements
This work is supported by the Australian Government Cooperative Research Centres Programme, through the Antarctic Climate and Ecosystems Cooperative Research Centre (ACE CRC). The Australian Antarctic Division provided the laboratory facilities used in this study. A.T. was supported by an Australian Postgraduate Award at the University of Tasmania. We thank Jason Roberts, Jun Li and Denis Samyn for thoughtful reviews which improved the manuscript, and also Ralf Greve who acted as Scientific and Chief Editor.
Appendix
Reference JaegerJaeger (1962) describes a plane whose normal has direction cosines ![]() relative to the principal axes and is thus equally inclined to the principal axes. This plane is referred to as the octahedral plane, as there are a total of eight planes which can be defined with direction cosines of
relative to the principal axes and is thus equally inclined to the principal axes. This plane is referred to as the octahedral plane, as there are a total of eight planes which can be defined with direction cosines of ![]() relative to the principal axes. The shear stress acting on this plane is known as the octahedral shear stress, τo, and is a function of only the second invariant of the deviatoric stress tensor,
relative to the principal axes. The shear stress acting on this plane is known as the octahedral shear stress, τo, and is a function of only the second invariant of the deviatoric stress tensor, ![]() . The octahedral shear stress, τ0, is the root mean square of the principal stress deviators, making it a useful quantity for comparing the magnitude of stresses in different configurations,
. The octahedral shear stress, τ0, is the root mean square of the principal stress deviators, making it a useful quantity for comparing the magnitude of stresses in different configurations,

Similarly, the octahedral shear strain rate, ![]() (Eqn (A2)), is the shear strain rate on the octahedral plane and provides a useful measure of generalized strain-rate magnitude,
(Eqn (A2)), is the shear strain rate on the octahedral plane and provides a useful measure of generalized strain-rate magnitude,
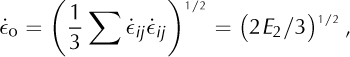
where E
2 is the second invariant of the second-order strain- rate tensor, ![]() The effective shear stress,
The effective shear stress,

and effective strain rate,

defined by Reference NyeNye (1957) are also functions of J2 and E2 and provide alternative, less physically relevant measures of stress and strain rate, particularly when comparisons between stress configurations are being made.


 , were determined at strains exceeding 10% in either uniaxial-compression or simple-shear experiments. Isotropic minimum strain rates,
, were determined at strains exceeding 10% in either uniaxial-compression or simple-shear experiments. Isotropic minimum strain rates,  , determined at ˜1 % strain, provide a reference for comparing the relative magnitude of tertiary creep rates in shear and compression through the use of strain-rate enhancement factors, E, defined as the ratio of corresponding tertiary and isotropic minimum creep rates, i.e.
, determined at ˜1 % strain, provide a reference for comparing the relative magnitude of tertiary creep rates in shear and compression through the use of strain-rate enhancement factors, E, defined as the ratio of corresponding tertiary and isotropic minimum creep rates, i.e. 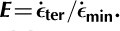 . The magnitude of strain-rate enhancement in simple shear was found to exceed that in uniaxial compression by a constant factor of 2.3. Results of experiments conducted at octahedral shear stresses of
. The magnitude of strain-rate enhancement in simple shear was found to exceed that in uniaxial compression by a constant factor of 2.3. Results of experiments conducted at octahedral shear stresses of 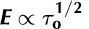 .The implications of these results for deformation in complex multicomponent stress configurations and at stresses below those used in the current experiments are discussed.
.The implications of these results for deformation in complex multicomponent stress configurations and at stresses below those used in the current experiments are discussed.











