1. Introduction
Taku Glacier (700 km2; 60 km long) is the major outlet glacier of the Juneau Ice Field (4000 km2), Alaska, USA. It has an interesting history, with an advance/retreat pattern that is largely out of phase with regional glacier change (Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002; Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007). The glacier reached a maximum extent around AD 1750, at which time it blocked the Taku River and created a glacier-dammed lake extending into modern-day Canada (Reference Post and MotykaPost and Motyka, 1995; Reference Motyka and BegétMotyka and Begét, 1996). Thereafter, a rapid tidewater glacier retreat (e.g. Reference Meier and PostMeier and Post, 1987) was initiated and the glacier retreated for about a century. After 1850 it began a steady advance that continues today. A large sediment supply from the Taku River and from glacial excavation created proglacial moraines that protect the glacier from marine water (Reference Kuriger, Truffer, Motyka and BuckiKuriger and others, 2006; Reference Motyka, Truffer, Kuriger and BuckiMotyka and others, 2006). Currently, the glacier is land-terminating along most of its perimeter, with a short section exposed to calving into a river. The protection from tidewater enables Taku Glacier’s continued advance, which is driven by a positive surface mass balance. Ice gain in the terminus region occurs by advance and increases in ice thickness. This thickness increase manifests itself not only in surface elevation increase, but also by entrenching into soft basal sediments at rates that can exceed 3 m a−1 (Reference Nolan, Motyka, Echelmeyer and TrabantNolan and others, 1995; Reference Motyka, Truffer, Kuriger and BuckiMotyka and others, 2006). Taku Glacier is a maritime temperate glacier characterized by high accumulation rates and very high melt rates (>10 m a−1) at low elevations, resulting in a large mass turnover. It is one of the thickest temperate glaciers that have ever been measured, with maximum thickness reaching almost 1500 m (Reference Nolan, Motyka, Echelmeyer and TrabantNolan and others, 1995). Its unusual history provides the rare opportunity to study the dynamics of an advancing glacier. In previous papers we have discussed the interaction of the advancing ice with its proglacial moraine (Reference Motyka and EchelmeyerMotyka and Echelmeyer, 2003; Reference Kuriger, Truffer, Motyka and BuckiKuriger and others, 2006) and the rapid excavation of overridden subglacial sediments (Reference Motyka, Truffer, Kuriger and BuckiMotyka and others, 2006). Here we discuss ice-flow measurements from the near-terminus area (<1 km from the ice front), with special emphasis on temporal changes in ice flow. We interpret these changes with the help of a flowline model.
2. Methods
2.1. Data
2.1.1. GPS measurements
Ice velocities were measured during the 2003, 2004 and 2005 melt seasons. We used dual-frequency geodetic GPS receivers (Trimble 5700) at two, and in 2004 at three, points on the glacier (Fig. 1). Antenna installation in the high-ablation near-terminus region followed a method of using three poles steam-drilled into the ice that was established by Reference AndersonAnderson and others (2004). We used 1 in (∼2.54 cm) EMT conduit in 10 ft (∼3 m) sections that were connected by steel couplers and plugged at the bottom with a wooden plug. All GPS data were post-processed to a base station on the proglacial outwash plane with baseline lengths <2 km. The position of the base station was obtained through Auto-GIPSY (milhouse.jpl.nasa.gov/ag/), and rechecked in successive years to assure that no significant changes occurred at that location. We processed the data of the moving stations kinematically, using the tool track (version 1.15), which is part of the Massachusetts Institute of Technology (MIT)’s GPS processing software GAMIT/GLOBK (Reference ChenChen, 1999, and http://www-gpsg.mit.edu/simon/gtgk/index.htm). Carrier-phase data from both L1 and L2 were used without forming the ionosphere-free linear combination (Reference LeickLeick, 2004). A kinematic data analysis strategy is essential if processing-related spurious signals are to be avoided (Reference KingKing, 2004). The processing resulted in geographic positions for every 15 s. The results were then converted to Universal Transverse Mercator (UTM) coordinates using the MatlabTM (v.7.5.0) Map Toolbox. Stakes sometimes had to be reset in mid-summer due to excessive melt. We assumed a constant velocity across that data gap by linearly extrapolating several hours of data from before the resetting. This was done in order to shift the position record of the second half of the summer to obtain a continuous record across the time of resetting stakes. Errors were estimated by calculating the standard deviation of a short section of data (3 days) from a linear change at a time when there was no evidence of diurnal or other short-term variation in flow. The resulting standard deviation was 7 mm in the horizontal. A point on the glacier moved about two orders of magnitude less than that during the 15 s between consecutive data points. Calculating velocities thus requires smoothing: we used a robust loess algorithm with a smoothing window of 1.5 days, implemented in MatlabTM (v.7.5.0), and applied it to the time–position data series. This smoothing window proved sufficiently large to reduce noise in the data, and sufficiently small to show diurnal variations in flow.

Fig. 1. (a) Schematic map of the lower Taku Glacier with terminus positions in 1890, 1948 and 2004 (adapted from Reference Kuriger, Truffer, Motyka and BuckiKuriger and others, 2006). The rectangle outlines the approximate area shown in (b). (b) Tracks of GPS stations deployed in 2003 (red), 2004 (green) and 2005 (blue). The image is a composite aerial orthophoto from 2005.
The procedure of calculating a velocity record from locally weighted polynomial fits to time–position data does not allow us to give a good formal error estimate, but we can provide error bounds as a function of time intervals. For daily average velocities the errors are 0.01 m d−1, while for hourly averages they increase to 0.24 m d−1.
In addition to the continuously recording GPS stations, we repeatedly surveyed ‘ablation wires’ that were steam-drilled into the ice. These observations were also made with dual-frequency GPS receivers and typically lasted 15–30 min (fast static mode). They were processed with Trimble Geomatics Office against the same base station as the continuously recording GPS. Estimated errors in horizontal position are very small (order few cm), and velocity errors over seasonal and annual timescales are thus negligible (< 1%).
2.1.2. Mass balance
Remeasuring the exposed lengths of ablation wires provided us with specific (point) mass-balance measurements. We preferred this method over survey poles because of the highablation-rate environment. The wires were weighted and lowered into a steam-drilled borehole. We have not attempted to assess the accuracy of this measurement by comparing it to other methods, but we estimate the uncertainty to be about 5 cm. The point balances reported here are between August 2002, 2003, 2004 and 2005. This does not correspond to the hydrologic year, nor is August at the end of the summer ablation season. We only use these data for comparison with surface elevation changes as determined from repeat digital elevation models (DEMs; section 2.1.3). A long-term series of surface mass-balance measurements for Taku Glacier is reported by Reference PeltoPelto and others (2008).
2.1.3. Vertical photogrammetry
We acquired vertical aerial photographs of the lower glacier on 2 September 2002, 4 September 2003, 7 June 2004, 24 August 2004 and 9 September 2005. These photos were digitized and then orthorectified with the help of stable control points on the proglacial moraines and on the ice. We produced DEMs with 10 m grid spacing. For each air-photo epoch we used the DEMs to produce orthophoto mosaics (e.g. Fig. 1b) with a pixel resolution of 2 m and a geolocation root-mean-square error of 1.5 m. The DEMs were used to calculate surface elevation changes. This work was done with the digital photogrammetry software BAE Socet Set.
The orthophoto mosaics were then used to determine velocity fields using an improved version of the IMCORR algorithm (Reference Scambos, Dutkiewicz, Wilson and BindschadlerScambos and others, 1992; Reference Howat, Joughin, Tulaczyk and GogineniHowat and others, 2005). This algorithm optimizes the sizes of the pixel and search/reference pixel subsets used in the fast Fourier transform (FFT) cross-correlation procedure to provide the sharpest peak in the correlation magnitudes. This increases the number of matches above the acceptance threshold for confidence. Displacement vectors are culled using both automated and manual filtering to remove spurious matches. Errors in feature-tracking derived velocities increase with the sizes of the pixels, search chip and width of the peak in the cross-correlation field (i.e. cross-correlation ambiguity), and decrease with the length of time between image pairs. Pixel sizes of up to 8 m were used in the correlation algorithm, and the cross-correlation ambiguity typically results in uncertainty of 1–2 pixels, giving a maximum error of 16 m a−1 for the annual velocities and 34 m a−1 for the summer 2004 velocities. Velocity fields were determined for the periods 2 September 2002 to 4 September 2003, 4 September 2003 to 24 August 2004, 7 June to 24 August 2004, and 24 August 2004 to 9 September 2005.
2.1.4. Bed topography
Bed topography was obtained by ground-based radio-echo sounding (RES). The principal aim was to find subglacial erosion rates, but we will use parts of the data as input for the numerical model described below. The method and results are presented in Reference Motyka, Truffer, Kuriger and BuckiMotyka and others (2006).
2.2. Model
We developed a two-dimensional flow model to interpret the measured surface velocities in terms of changing basal boundary conditions. The model calculates pressures and velocities in a vertical plane, which is oriented along flow. It solves the full Stokes equations under the assumption that out-of-plane gradients are zero. In a coordinate system with x horizontal and z vertical, the momentum balance equations (e.g. Reference PatersonPaterson, 1994) reduce to

where ρ is the density of ice (here assumed to be 900 kg m−3), g the gravitational acceleration, and the comma signifies differentiation. The deviatoric stress tensor d is defined by
where σ is the stress tensor, p = (1/3)tr(σ) is one-third of the trace of σ, and δ ij is the Kronecker symbol. The deviatoric stresses can be written in terms of velocity gradients using Glen’s flow law (Reference PatersonPaterson, 1994):
where the strain rates ![]() ; ui
are the velocity components. The strain-rate dependent η viscosity 77 in Equation (3) is defined by
; ui
are the velocity components. The strain-rate dependent η viscosity 77 in Equation (3) is defined by
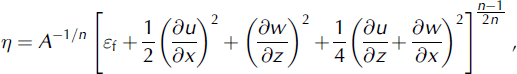
where A is a flow rate parameter, here assumed to be 0.1 bar− n a−1 (Reference Truffer, Echelmeyer and HarrisonTruffer and others, 2001, and references therein) and n is the flow-law exponent, which is taken as 3 (Reference PatersonPaterson, 1994). The finite viscosity parameter ε f prevents the problem of infinite viscosity at zero strain rate (Reference HutterHutter, 1983) and leads to a linear flow law at low stresses (Reference Pettit and WaddingtonPettit and Waddington, 2003). We use a value of 10−10a−2, which is sufficiently small not to influence the solution, and sufficiently large to guarantee convergence of the Newton iteration.
The model is solved using the finite-element method and the commercial software package Comsol Multiphysics. This code has been tested against analytical solutions for non-linear viscous flow, and we have previously used it for modeling two-dimensional ice flow (Reference Truffer and EchelmeyerTruffer and Echelmeyer, 2003; Reference Amundson, Truffer and LüthiAmundson and others, 2006). We use a triangular mesh with 13 996 elements and linear shape functions for p, and quadratic shape functions for u and w. The model domain is separated into three parts (Fig. 2): the frontal part is an approximately 2 km long longitudinal profile derived from RES and GPS data. The middle part is a linear extension to a point approximately 4 km from the terminus, where the surface and bottom topography have also been measured. The third part is a steep wedge that is used to supply the correct amount of ice to the lower domain. The details of this upper part are not important. It simply serves as a numerically convenient way to supply sufficient amounts of ice to the glacier section that is of interest here. The middle part serves as a long transition zone from the unrealistic (in terms of geometry and boundary condition) upper zone to the lower zone, which is of interest here. We only interpret results in the lowest of the three zones. The surface is modeled as a stress-free boundary. The bottom boundary on the up-glacier wedge has a prescribed constant velocity, which is tuned to match the measured velocity magnitude lower on the glacier. The bottom of the middle and lower parts is assumed to be a plastically deforming sediment with a yield strength depending on water pressure.

Fig. 2. Model domain: the frontal 2 km are derived from radio-echo sounding (Reference Motyka, Truffer, Kuriger and BuckiMotyka and others, 2006), the middle part (2–4 km) is a linear extension to another measured surface and bed point, and the back part is a sliding wedge that is added to provide the correct ice flux into the model domain. Only results in the front part are interpreted here. Note that there is no vertical exaggeration. Also shown is the mesh used for the calculations.
This is motivated by the fact that Taku Glacier overrides a combination of fluvial and proglacial sediments (Reference Kuriger, Truffer, Motyka and BuckiKuriger and others, 2006; Reference Motyka, Truffer, Kuriger and BuckiMotyka and others, 2006), and that the deformation of sediments is best approximated by perfect plasticity with very low coherence (e.g. Reference Iverson, Hooyer and BakerIverson and others, 1998). We use a simplistic model for the subglacial water pressure p w:
where x is the distance from the terminus, p w the density of water, and z b the vertical coordinate of the glacier bed, relative to sea level. β = 0 describes a situation with a flat phreatic surface and therefore no gradients to drive drainage.
This water pressure leads to an effective pressure p eff = p 0 − p w, where the ice overburden pressure p 0 = ρgh, and h is the ice thickness. This leads to a sediment yield strength
We chose a friction angle of φ = 26° because we obtained good velocity fits with that value and it is reasonable for subglacial till (e.g. Reference Fischer, Porter, Schuler, Evans and GudmundssonFischer and others, 2001). The coherence c 0 was neglected, which is also in agreement with laboratory data (Reference Iverson, Hooyer and BakerIverson and others, 1998). In general, a plastic sediment boundary defines a free boundary problem, where part of the till is yielding (and Equation (6) applies) and another part of the till does not yield (because the basal stress is below the till shear strength) and a no-sliding condition applies (Reference Truffer, Echelmeyer and HarrisonTruffer and others, 2001; Reference SchoofSchoof, 2006). Here we only encountered scenarios where the entire till was yielding and the free boundary problem did not have to be solved. The motivation for using a perfect plasticity boundary condition (Equation (6)) stems from ample evidence that Taku Glacier flows over a soft sediment that is actively being excavated (Reference Motyka, Truffer, Kuriger and BuckiMotyka and others, 2006). The proglacial till is also actively being deformed (Reference Kuriger, Truffer, Motyka and BuckiKuriger and others, 2006) and it is reasonable to assume that this also occurs subglacially. Much evidence from laboratory work on till shows that it can be well described by a plastic rheology (e.g. Reference KambKamb, 1991; Reference Iverson, Hooyer and BakerIverson and others, 1998), and this has also been successfully used as a basal boundary condition for glacier models (e.g. Reference Truffer, Echelmeyer and HarrisonTruffer and others, 2001; Reference Amundson, Truffer and LüthiAmundson and others, 2006). We have not tested alternative boundary conditions, but we suspect that any sliding law with an asymptotic dependence of basal motion on effective pressure will show similar results to those presented here.
3. Results
The longest velocity record was collected in 2003 (March–August). That record captured a gradual increase from slow and steady winter flow to fast and variable summer flow (Fig. 3). The two markers were separated by ∼400 m and were almost located on the same flowline (Fig. 1). The record reveals an interesting transition in flow behavior that occurred gradually near day 125. Before that time, the flow was clearly compressive, with a strain rate of approximately −1 × 10−4d−1 (Fig. 4). This condition then gradually switched to block flow or even slight extension. This same flow transition was apparent in the 2005 record (not shown here), when stakes were set up at nearly identical positions to 2003 (Fig. 1). However, the 2005 record only began on day 140, by which time the transition was nearly complete.

Fig. 3. Velocity record from 2003. The lower marker (blue) moves slower than the upper marker (red) during the first part of the record, but the flow transitions gradually from compressive flow to block flow starting near day 125.

Fig. 4. Strain rates computed from 2003 GPS velocities averaged over 4 days.
The locations of the GPS markers were generally not repeated between years, except for one location (see Fig. 1). At this location we can directly compare the velocity progression in the melt seasons of the years 2003–05. Interestingly, and perhaps unexpectedly, there are large interannual variations in flow speed (Fig. 5). While the flow velocities measured during the 2003 and 2004 melt seasons were almost identical, there was a significant deceleration in summer 2005.

Fig. 5. Comparison of velocity records from the summers of 2003, 2004 and 2005. The markers traversed near-identical map coordinates in the three years (within 20 m).
An independent measure of velocity on seasonal and annual timescales is available from feature tracking (Fig. 6). These velocity fields were interpolated from irregularly spaced data. The extent of the vertical imagery and the success of the feature tracking varied between years, which explains the differences in areal extent in Figure 6. Several points on the glacier were measured by repeat GPS (data in Reference KurigerKuriger (2005) and unpublished). Generally, they compare well with the values derived from feature tracking (Fig. 7). The two exceptions are one point very close to the terminus during summer 2004, where feature tracking is problematic due to the steep local slope; and another point for 2003/04, which was farther up-glacier, where co-registration problems become larger, as the distance from control points increases.

Fig. 6. Velocity fields derived from feature tracking on vertical aerial photographs. The area shown is approximately that in Figure 1b. (a) 2 September 2002 to 4 September 2003; (b) 4 September 2003 to 24 August 2004; (c) 7 June 2004 to 24 August 2004; and (d) 24 August 2004 to 9 September 2005. The color bar (m d−1) and the map plane are identical in each panel to facilitate direct comparison. Red arrows show velocities determined by GPS. The black circle in (c) outlines the moraine complex shown in Figure 13.

Fig. 7. Comparison of velocities derived from feature tracking and GPS-derived velocities over nearly identical times. Error bars show the formal error estimate for feature tracking.
Figure 6a, b and d show annual velocities (fall to fall), whereas Figure 6c shows a seasonal velocity for summer 2004. Additionally, Figure 8 shows velocities along the three profiles shown in Figure 6a for all available time intervals. These figures help put the GPS measurements into spatial context. The GPS stations whose records are shown in Figure 3 are situated along the lower 1000 m of the center profile. The errors for the feature tracking are too large to deduce strain rate on the scale of a few hundred meters, and the flow transition discussed above cannot be resolved with these measurements.

Fig. 8. Velocities along the three profiles shown in Figure 6a.
The seasonal velocity changes showed an interesting pattern (Fig. 6b and c). It is clearly recognizable that the summer velocities were significantly higher than the annual averages in the southeastern part of the observed area. This confirms the point GPS measurements. However, the velocity maps also show a large area in the northwestern part, where seasonal velocity changes are not observed. The annual velocity maps also confirm the GPS measurements (Fig. 5) and showed similar velocities for 2003 and 2004 and slower ice flow for 2005.
We have generated DEMs for 2002, 2003, 2004 and 2005 and used these to derive maps of surface elevation change (Fig. 9). These maps show near-terminus elevation increase exceeding 10 m from 2002 to 2003, slight surface lowering (0–5 m) from 2003 to 2004 and increased surface lowering of 5–10 m from 2004 to 2005. If we also consider the current excavation rates of about 3 m a−1(Reference Motyka, Truffer, Kuriger and BuckiMotyka and others, 2006), then the ice thickness increased between 2002 and 2003, remained nearly constant between 2003 and 2004, but decreased between 2004 and 2005.
Annual specific ablation appears to follow a linear relationship with elevation (Fig. 10). Contrary to velocity and ice surface elevation, there is no obvious difference between the three years of measurements.

Fig. 10. Annual melt between late-August measurements as a function of height above World Geodetic System 1984 (WGS84) ellipsoid.
4. Discussion
4.1. Short-term variations in ice flow
The GPS record of all stakes contained short-timescale variations in ice flow. This includes strong diurnal signals, as well as speed-up events that lasted several days (Figs 3 and 5). The stations are located too close to each other to discuss propagation of such speed-up events. In 2003 the record started in March, before the onset of melting and a gradual increase in speed occurred as the melt season started. None of these variations are unusual or surprising, and many examples can be found in the literature (e.g. review by Reference WillisWillis, 1995). We therefore do not discuss these variations further here. Rather, we concentrate on the observed near-terminus switch in flow behavior.
4.2. An early melt-season switch in flow behavior
Figures 3 and 4 show a gradual decrease from compressive strain rate in the near-terminus area to block flow, or even slight extension (see section 3). We attempted to find boundary conditions that would reproduce the average velocities during winter conditions and after the switch in flow behavior. We did not do this by a rigorous inverse methods procedure, but rather just tuned the parameter β in Equation (5), which describes the gradient of the ‘water table’, until we obtained the measured strain rate. The prescribed basal velocity at the up-glacier part of the model domain was adjusted to fit the measured velocity magnitude, and the sediment friction angle φ = 26° reproduced the correct strain rates for the winter regime with β = 0. This corresponds to a situation with a flat ‘water table’, and therefore no water drainage. In summer, significant amounts of water are evacuated from under the glacier, which requires a positive gradient β. We obtained a very good correspondence with the measured velocities and strain rates for β = 249 Pa m−1 (Figs 11 and 12). This can be compared to the maximal gradient of 880 Pa m−1, that could be created without the basal water pressure locally exceeding the ice overburden pressure.

Fig. 11. Plots of the modeled velocity distribution during winter (top) and summer (bottom). A change from shear deformation to block flow is obvious. Note also the positive vertical velocities (arrows). The position of the continuously recording GPS stations was at approximately the second and third set of arrows from the left. Color scale is identical for both plots, but arrow lengths are rescaled for better visibility.

Fig. 12. Comparison of modeled and measured velocities. Winter velocities with compressional flow (lower curve) and summer velocities with block flow (upper curve). Solid curves are model results, and dots are measured average velocities.
We also checked the model performance by comparing measured and modeled vertical velocities. Unfortunately, the vertical velocities of the continuous GPS markers are unreliable during summer. Despite the distribution of the antenna weight to three poles (see section 2) and the plugging of all poles, there was significant melting of the antenna poles into the glacier ice. At the upper GPS station we measured ablation and vertical surface position of a wire drilled into the ice. The vertical velocity of the GPS antenna was negative during the summer of 2003, while the summer 2004 vertical velocity derived from the ablation wire was +6.9 m a−1, which compares well with the modeled 7.1 m a−1. The measured winter 2003/04 vertical velocity was +4.5 m a−1, compared to the modeled 5.8 m a−1. It should be noted that we inferred positive subglacial excavation rates up to 3 m a−1 in that area (Reference Motyka, Truffer, Kuriger and BuckiMotyka and others, 2006), which are not accounted for in the model. This would tend to make modeled vertical velocities larger than the measured vertical velocities, which is indeed the case. The subglacial excavation is expected to be spatially non-uniform, so direct quantitative comparisons should not be attempted at single points.
Our model is an attempt to compare winter conditions with little or no water drainage to summer conditions with water drainage by exploring a stress boundary condition. It is not capable of resolving short-term (hours to days) variation in basal conditions, although strain-rate reversals are expected to be quite common in that case (e.g. Reference GudmundssonGudmundsson, 2002; Reference Howat, Tulaczyk, Waddington and BjörnssonHowat and others, 2008).
The basal water pressure gradient β is a function not only of water discharge, but also efficiency of the basal drainage system. There is much evidence that subglacial drainage systems become more efficient as water discharge increases during the summer, and larger channels are formed (Reference RöthlisbergerRöthlisberger, 1972). This would result in a decrease in β and lower surface velocity. Indeed, Figure 5 shows a steady decline in surface velocities during the summers of all three years.
4.3. Seasonal variation in ice flow
The flow switch observed by GPS and modeled in section 4.2 only describes the flow behavior very close to the terminus. The larger regional pattern is more variable. The velocity maps in Figure 6 clearly show seasonal acceleration in the southeastern part of the observed area, but not in the northwest. We lack the necessary subglacial topographical information to capture these differences in a numerical model. However, the area where seasonality is lacking coincides spatially with an area of laterally diverging flow. This flow divergence seems to be related to the presence of a large moraine complex there (circle in Fig. 6c and Fig. 13). It is possible that this moraine and the topographic high behind it also lead to water flow divergence and keep values of basal water pressure relatively low, even during summer.

Fig. 13. Photograph of a large moraine complex. The location is marked with a circle in Figure 6c. Buttressing of ice is evident. The glacier surface slope is much shallower in the picture foreground, where no terminal moraine exists.
4.4. Interannual changes
Comparisons at one location on the glacier show that ice velocities were quite similar in summer 2003 and 2004 and significantly lower (up to almost 50%) in 2005 (Fig. 5). A slowdown is also apparent in the velocity maps (Figs 6 and 8), although it is almost within formal error estimates. We lack the measurements to conclusively explain the causes for this slowdown, but it is at least plausible to attribute it to a change in basal conditions. Our flowline model shows that small changes in basal conditions can lead to relatively large changes in surface velocities. Changes at the glacier base can be due to changes in subglacial topography (as discussed by Reference Motyka, Truffer, Kuriger and BuckiMotyka and others, 2006) that can lead to diversion of subglacial water flow and hence changes in basal water pressure and till yield stress. A change in surface velocity has an immediate effect on the surface elevation. The vertical velocities at several markers on the terminal lobe were almost zero or even slightly positive. This is manifested in clearly positive emergence velocities v e, which were calculated from
where v h and vz are horizontal and vertical velocities and α is the surface slope (Reference PatersonPaterson, 1994, p. 258), which was derived from the DEMs. The emergence velocity is plotted against the horizontal velocity for each marker (Fig. 14), and the direction shows little variability for different measurement epochs. This is also reflected in the flow model (Fig. 11). Lower horizontal velocities therefore lead to lower emergence velocities and less thickening under the same surface mass-balance conditions. The mass balance did not show changes between the different years (Fig. 10), so the slower velocities must be responsible for the observed decrease in surface elevation in 2005 (Fig. 9). Mass conservation dictates that in a constant climate the reduced surface velocities would have to be compensated by thickening upstream or by increased amounts of subglacial excavation.

Fig. 14. Emergence velocity versus horizontal velocity. Each group of arrows (shown by a different color and offset horizontally for better visibility) represents a different marker (ablation wire). The different arrows within the group refer to different time periods.
5. Conclusion
We measured topography and velocities in the near-terminus area of the advancing Taku Glacier. The seasonal evolution of the velocity field evolved from slow and steady winter flow to fast and variable summer flow. Flow variation occurs on hourly, daily and seasonal timescales, and the flow characteristics are similar to those observed on other temperate glaciers.
The strain field in the near-terminus area undergoes a clear transition from compressive flow to block flow. This transition can be captured in a model where the basal yield stress is varied as a function of water pressure, and water pressure is calculated from a hypothetical water table that increases linearly with distance from the terminus. Such a positive gradient is necessary for drainage along the glacier base to occur. A zero gradient can successfully reproduce the winter compressive conditions, and an increase in the water-table gradient leads to block flow. Glacier beds that dip up-glacier are subjected to relatively large basal water pressures, if water is to be drained subglacially. The effect is most impressive when a retreating glacier thins to near flotation (Reference PfefferPfeffer, 2007), but we can also demonstrate this effect at Taku Glacier, which is advancing.
Consistently modeling the flow of a glacier under several flow regimes with one basal boundary condition can be a useful exercise when trying to find basal boundary conditions that can be used to model the longer-term behavior of a glacier. It is still a major problem to predict the coupling of ice to its base in glacier change scenarios. This study shows that a simple stress boundary condition can be sufficient to reproduce the major seasonal flow feature of at least this glacier.
Changes in basal conditions can have a noticeable effect on surface velocities, and this effect is immediately apparent in surface elevation measurements. The cause of the observed slowdown is not clear, but the mass-balance measurements do not show a clear difference in the amount of melt in 2005 (Fig. 10). However, Reference Motyka, Truffer, Kuriger and BuckiMotyka and others (2006) point to spatially heterogeneous excavation, which would be expected to lead to changes in basal water routing and could affect surface velocities. Regardless of the cause, a slowdown of near-terminus velocities with near-steady surface ablation must be accompanied by thickening ice upstream, or through excavation. This suggests that the processes leading to terminus thickening and advance can be episodic, due to an evolving subglacial environment. Reference Kuriger, Truffer, Motyka and BuckiKuriger and others (2006) also observed this for the activation of motion in proglacial moraines.
Acknowledgements
Funding for this work was obtained through US National Science Foundation grant NSF OPP-0221307, and the modeling work was also supported by NSF OPP-0414128. We thank Veco Polar Resources for logistical support and Era for helicopter support. Numerous people helped in the field: J. Amundson, A. Arendt, E. Boyce, A. Bucki, L. Cox, E. Kuriger and M. Lüthi. Thanks to all of them. We appreciate insightful comments from B. Hubbard (scientific editor), and from A. Vieli and an anonymous referee that led to an improved manuscript.

















