Introduction
The study of ice cores from the large ice sheets of Greenland and Antarctica is one of the most powerful tools for gaining knowledge about past climate (Reference Lorius, Merlivat, Jouzel and PourchetLorius and others, 1979; Reference RobinRobin, 1983; Reference Yiou, Jouzel, Johnsen and RögnvaldssonYiou and others, 1995). In order to investigate a possible ongoing or future climatic change and to distinguish between natural and anthropogenic climate variations we need to fully understand the changes in climate that occurred in the past. Physical and chemical properties of the ice and the air contained in polar ice cores yield information about former temperature and composition of the atmosphere (Reference DansgaardDansgaard, 1964; Reference Dansgaard, Johnsen, Clausen and GundestrupDansgaard and others, 1973; Reference Johnsen, Dansgaard, Clausen and LangwayJohnsen and others, 1972; Reference Jouzel, Merlivat, Petit and LoriusJouzel and others, 1983, Reference Jouzel1997; Reference Mosley-ThompsonMosley-Thompson and others, 1995; Reference Delmotte, Raynaud, Morgan and JouzelDelmotte and others, 1999).
However, since the information recorded in the ice is affected by precipitation processes, the reliability of interpretations of ice cores depends on a thorough understanding of the atmospheric processes that produced the snow found in the cores. Measurements of precipitation in Antarctica are sparse and difficult to make, due to the remoteness and size of the Antarctic continent and its climatic extremes. In the coastal areas, where precipitation rates are relatively high, measurements are problematic because of the strong winds. Standard precipitation gauges fail, and so far no reliable method for measuring precipitation under such conditions has been developed, thus the surface accumulation is usually used as a measure for precipitation. This approach neglects the influence of sublimation, which is comparably small, and of snowdrift, which can be large. At high-altitude inland stations like Vostok or South Pole the amount of accumulation often is so low that high-time-resolution measurements are not yet feasible.
To investigate the spatial and temporal variability of Antarctic accumulation in spite of the lack of data, models are useful tools for deriving the accumulation distribution (Reference Connolley and CattleConnolley and Cattle, 1994; Reference Krinner and GenthonKrinner and Genthon, 1997; Reference Krinner, Genthon and JouzelKrinner and others, 1997; Reference Cullather, Bromwich and WoertCullather and others, 1998; Reference Genthon and KrinnerGenthon and Krinner, 1998; Reference Genthon, Krinner and DéquéGenthon and others, 1998; Reference Turner, Connolley, Leonard, Marshall and VaughanTurner and others, 1999; Reference Van LipzigVan Lipzig, 1999). Accumulation maps (Reference Giovinetto and BentleyGiovinetto and Bentley, 1985; Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others, 1999) are often used to evaluate the surface mass balance of these atmospheric models, but there are hardly any studies on the temporal variation of the net accumulation on time-scales of weeks or months because so few data are available.
At the German Antarctic base Neumayer (until 1992: Georg-von-Neumayer), extensive glacio-meteorological measurements have been carried out since 1981. Accumulation has been measured weekly at an array of stakes. To our knowledge, these are the only available accumulation measurements with high temporal resolution for such a long time period at a location where meteorological data are also available. Accumulation data from automatic weather stations (AWSs) in Dronning Maud Land are available with much higher resolution, but only for periods of 3–5 years. The data from two of these AWSs were compared to European Centre for Medium-Range Weather Forecasts (ECMWF) model precipitation by Reference Reijmer and van den BroekeReijmer and Van den Broeke (2001). The ECMWF precipitation is lower than the AWS-derived accumulation. The AWSs measure snow-height changes, which can be due to snowfall, snowdrift, settling of the snow cover and sublimation, whereas the ECMWF gives only the amount of precipitation. This might partly explain the differences, but also the model precipitation represents the mean precipitation rate over the area of a gridcell rather than at one location within the cell.
In this study, the data from Neumayer are used to investigate whether the Regional Atmospheric Climate MOdel (RACMO) is able to represent the temporal variations in accumulation for the period 1981–93. The model is driven at the lateral boundaries by data from the ECMWF re-analysis (ERA; Reference Gibson, Kållberg, Uppala, Hernandez, Nomura and SerranoGibson and others, 1997). Due to this realistic forcing, the model is also suitable for case-studies. Here we describe to what extent the model is able to represent the precipitation events observed at Neumayer. A case-study for 1987 is described to explain the differences between model results and stake data. The comparison between measurements and model output also gives an answer to the question whether the precipitation events at Neumayer are due mainly to local effects or whether they are determined by the general synoptic conditions and thus representative of a larger area.
Especially with regard to the deep drilling planned in Dronning Maud Land as part of the European Project for Ice Coring in Antarctica (EPICA), it is important to study the precipitation conditions in the Atlantic sector of Antarctica, particularly the areas that are influenced by the cyclogenesis east of South America and the Antarctic Peninsula.
Surface Mass-Balance Measurements
The German base “Georg-von-Neumayer” was constructed in 1981 (Fig. 1a). In 1992 a new base, now called “Neumayer”, was built about 7 km southeast of the old one.

Fig. 1. (a) Model domain covering the Antarctic continent and a large part of the Southern Ocean (122 × 130 points). The relaxation zone (lateral boundary zone where the model variables are a linear combination of the fields supplied by ERA-15 and the prognostically calculated fields) is shown by dots; each dot is a model gridpoint. Locations of Neumayer station (NM) and the EPICA drilling site are shown. (b) Enlargement of the small grey square showing model gridpoints, coastline and model elevation in the Neumayer area. The grey dots are sea orsea-ice gridpoints, and the black dots are land-ice gridpoints. The gridpoint closest to Neumayer is S1. L1 and L2 are two of the surrounding ice-shelf gridpoints. Variations in elevation and in the position of the coastline on a scale smaller than the gridpoint spacing (55 km) are not resolved by the model. The numbers on the isohypses are given in decameters.
An array of 25 stakes was set up 600 m southeast of the base in March 1981. The location of the array and the number of stakes were slightly modified twice. From 1987 the stake array was situated about 1500 m southeast of the Georg-von-Neumayer station and consisted of 25 (5 × 5) metal stakes 2 m long and with a spacing of 5 m. When the new base Neumayer was built, a similar new stake array was set up and both stake arrays were run simultaneously until 1994; afterwards only the measurements at the new array were continued. The shifting of the array did not lead to inhomogeneities in the data series, except that accumulation at the new base was higher than at the old one during the first 3 years after the construction of the base. Accumulation rates from a firn core that had been taken at the construction site before the new base was built are well correlated with accumulation rates derived from the old stake array. Thus it is assumed that the higher amounts of accumulation during the first years are due to the influence of the building, which quickly damped out; the station was close to the level of the surrounding surface after only 3 years (Reference Schlosser, Oerter and GrafSchlosser and others, 1999). Except in 1983, the stakes were read weekly, sometimes even more frequently. Although some melting snow was observed close to the surface during summer, the stakes remained frozen to the surrounding snow at deeper levels and thus did not melt in. Once a year, usually at the end of summer, the stakes were taken out and set afresh next to the old holes. They could be removed only by using a plumber’s wrench, which shows that they were firmly frozen into position.
Settling of the snow can be estimated by observing the changes at the stake array during quiet-weather periods. The amount of settling depends strongly on amount and initial density of the fresh snow and on temperatures after the snowfall. On average, it reaches only 2% of the amount of initial accumulation, which is probably smaller than, or the same order of magnitude as, the mean error in the measurements. In summer, especially after major snowfall events, settling can sometimes reach extreme values of a few cm snow per week. For comparison: erosion due to wind removes, on average, about 30% of the initial accumulation (corresponding to about 30 cm snow) (Reference SchlosserSchlosser, 1999).
The snow surface was usually fairly rough, with sastrugi of different sizes, which caused differences in the accumulation measured at individual poles. The length of the sastrugis seldom exceeded 2–3 m, so it is unlikely that the › majority of the stakes could have been in a single drift structure or in a single zone of scour. Therefore the mean height change of the 25 stakes should give a representative mean accumulation value.
Additionally, at irregular time intervals, snow pits were dug and shallow firn cores taken. These were analyzed with regard to physical and chemical properties (e.g. Reference Reinwarth, Graf, Stichler, Moser and OerterReinwarth and others, 1985; Reference Schlosser, Oerter and GrafSchlosser and others, 1999). Dating of cores and pits was achieved using stable-isotope profiles (δ 18O, δ 2H), which show relatively clear seasonal variations.
These snow pits and cores were used to estimate the snow density for converting the snow-height changes to water equivalent, since no density measurements of freshly fallen snow are available. The density of freshly fallen snow is usually lower than that of the snow in pits (dug mostly in summer). Of course, the density varies between different snowfall events, depending on wind speed and temperature, so this estimate always includes a certain error.
We have thus collected a wealth of glaciological data at Neumayer, which are complemented by meteorological data that include climate and boundary-layer measurements, upper-air data (radiosondes and ozone sondes) and so-called SYNOP measurements (Reference König-Langlo, Marx, Lautenschlager and ReinkeKönig-Langlo and Marx, 1997). These are standard 3 hourly meteorological observations that consist of measured variables like air temperature, pressure, wind speed and direction, and the records of observers (“eye observations”) like cloud cover, visibility, snowfall and snowdrift (WMO, 1995). Four different types of snowdrift are distinguished: slight or moderate drifting snow, heavy drifting snow (both below eye level), slight or moderate blowing snow and heavy blowing snow (above eye level). In the last two cases, the observer is unable to distinguish between blowing snow and precipitation.
Detailed information on the glaciological data at Neumayer can be found in Reference SchlosserSchlosser (1999) and Reference Schlosser, Oerter and GrafSchlosser and others (1999).
The Regional Atmospheric Model
RACMO (Reference Christensen and van MeijgaardChristensen and Van Meijgaard, 1992; Reference Christensen, Christensen, Lopez, van Meijgaard and BotzetChristensen and others, 1996) uses the calculation of the dynamical processes from the High-Resolution Limited Area Model (Reference GustafssonGustafsson, 1993) and the parameterization of the physical processes from the ECHAM4 model (Reference RoecknerRoeckner and others, 1996). Some adjustments were made in the original code in order to improve the model for the Antarctic region (Reference Van LipzigVan Lipzig, 1999; Reference Van Lipzig, van Meijgaard and OerlemansVan Lipzig and others, 1999). An important adjustment for this study is that the ice shelves are treated as land ice, rather than as sea ice which is the case in some state-of-the-art atmospheric models like the ECHAM model (Reference Van den BroekeVan den Broeke, 1997).
The model is driven from the lateral boundaries by the ECMWF re-analyses (ERA-15; Reference Gibson, Kållberg, Uppala, Hernandez, Nomura and SerranoGibson and others, 1997). The fields in this lateral boundary zone of the model (see Fig. 1a) are a linear combination of the fields supplied by ERA-15 and the prognostically calculated fields, using a technique proposed by Reference Dickinson, Errico, Giorgi and BatesDickinson and others (1989). The distance between Neumayer station and the lateral boundary zone is 840 km. The calculated weather systems at Neumayer are expected to be strongly influenced by the ERA-15 fields. Sea-surface temperature and sea-ice extent are prescribed from observations and are identical to the values used in ERA-15.
The model was integrated for a period of 14 years (1980–93) using a horizontal grid spacing of 55 km. In the vertical, the model has 20 levels, with the lowest levels centered at about 7, 35, 130 and 330 m. The 7 m level, which was not present in the original formulation, was inserted in order to improve representation of the shallow katabatic layer.
Accumulation in the model is defined as precipitation (P) minus sublimation (E). Runoff is ignored, because this term is very small, since temperatures are generally below the freezing point. Snowdrift, the transport of snow from one place to another by the wind, is also ignored. However, snowdrift can be important especially on small scales and for investigations of short time periods, as in our study.
The 14 year mean spatial distribution of the modelled net accumulation corresponds closely to compilations of in situ measurements (Reference Van LipzigVan Lipzig, 1999). The two large ice shelves, Ross and Filchner–Ronne, are relatively dry. The high plateau of East Antarctica is also very arid, with accumulation values of <50 mm w.e. a−1. The largest difference between model output and the compilation of measurements is found in Marie Byrd Land, but measurements in this area are sparse. During the 14 year integration, the model shows no serious climate drift (Reference Van LipzigVan Lipzig, 1999). Sensitivity to initial conditions is small, but the results are very sensitive to the fields supplied by ERA-15 at the lateral boundaries.
The model grid in the Neumayer area is shown in Figure 1b. Neumayer is located on the ice shelf, 7 km from the edge. A model gridbox covers an area of 55 × 55 km2. Most of the gridbox in which Neumayer is located is sea ice, so the gridpoint closest to Neumayer (S1 in Fig. 2b) is a sea-ice gridpoint. Two of the surrounding ice-shelf gridpoints are L1 and L2 at an elevation of 38 and 75 m, respectively. The elevation of Neumayer is 36 m. Sublimation over sea ice (93 mm w.e. a−1 at S1) is much larger than over land ice (58 mm w.e. a−1 at L1 and L2), due to the vertical heat flux from the ocean to the sea ice which increases the temperature at the ice surface. Precipitation is largest at L2 (485 mm w.e. a−1), where the local slope is steepest and the orographical lifting of air is largest. Precipitation at L1 is 413 mm w.e. a−1, and precipitation over the flat sea ice (S1) is only 389 mm w.e. a−1.

Fig. 2. Modelled annual mean P − E (P: precipitation; E: evaporation) normalized by the 14 year mean value for P − E for gridpoints S1, L1 and L2.
Although the mean accumulation is different for the three gridpoints (296, 355 and 427 kg m−2 a−1 at S1, L1 and L2, respectively), the relative year-to-year variability is similar (Fig. 2). For comparison with Neumayer data we use the closest ice-shelf gridpoint (L2), because Neumayer is located on the ice shelf and it is unrealistic to use a sea-ice gridpoint.
Figure 3 shows the 14 year mean annual cycle of P, E and P − E for gridpoint L2. Precipitation is largest during austral autumn (58 mm w.e. month−1), with a secondary maximum in November. Twelve per cent of the annual precipitation is removed by sublimation, mainly during summer. Therefore, the net accumulation (P − E) is somewhat smaller than the precipitation, especially in the summer months, when a strong minimum of (P − E) is found due to a minimum in P and a maximum in E.

Fig 3. Fourteen-year calculated mean annual cycle of precipitation P, evaporation E and P − E at gridpoint L2 for the period 1980–93.
Comparison of Model and Data
Figure 4 shows annual accumulation rates for 1981–93 derived, respectively, from the stake array, the model (L2) and from a shallow firn core. Accumulation rates are normalized by the mean of the 13 years. The range in interannual variability of accumulation is similar in the model and the measurements. There is, however, no significant correlation between the modelled time series of annual mean accumulation and the observed time series.

Fig. 4. Normalized annual accumulation, 1981–93, derived from model, stake-array measurements and a shallow firn core, respectively.
The model does not take into account snowdrift, which is important at Neumayer and can lead to net ablation measured at the end of a storm that produced much precipitation, as well as to accumulation higher than the amount of precipitation. Therefore we cannot decide whether the low correlation is due to the influence of the snowdrift or to a low correlation between modelled and actual precipitation. At present, this problem cannot be solved. It is impossible to calculate the snowdrift at Neumayer using a model with a spatial resolution of 55 km. On a larger scale using a model gridbox of 40 km, Reference Gallée, Guyomarc’h and BrunGallée and others (2001) calculated transport and sublimation due to snowdrift above the Antarctic ice sheet. They found a strong sensitivity of snow erosion to snow-surface properties, indicating that the history of the snowpack should be taken into account in realistic studies. This was done on a smaller scale by Guyomarc’h and Reference Guyomarc’h and MérindolMérindol (1998) who combined a snow model with an atmospheric model in order to predict snowdrift events. Implementing the state of the snow cover and the different transport processes in a large-scale model remains a challenge.
The impact of snowdrift on mass balance becomes smaller with increasing scale. For an infinite ice sheet it would be zero, since the snow would only be redistributed. We do not know how important snowdrift is on the scale of a model gridcell. No measurements are yet available to answer this question with certainty. At present, it is not known on what scale snowdrift transport can be neglected in mass-balance calculations. For our study this means we cannot expect good quantitative agreement between the amounts of accumulation from model and stake measurements, since accumulation at Neumayer is highly influenced by snowdrift. We can, however, use the weekly data to investigate whether the temporal distribution of precipitation events, and thus the synoptic situation, is represented correctly by the model.
In Figure 5 the monthly accumulation rates are shown for the years 1981–93. Correlation coefficients for each year are given in the plots. The correlation varies greatly from year to year; the best correlation is found in 1987 with a correlation coefficient of 0.87, and the worst year is 1982 with a correlation coefficient of 0.15. The correlation between the measured and the modelled time series is significant on the 95% confidence level for the periods 1985–87 and 1989–92.

Fig. 5. Monthly accumulation derived from model calculation (P − E) and stake-array measurements for 1981–93. Correlation coefficients are given for each year.
Possible reasons for the differences between model and stake data are:
accumulation or erosion of the snow surface due to wind influence which is not accounted for in the model
underestimation or overestimation of precipitation and/or sublimation by the model for particular precipitation events
deviation of the dynamics of the atmospheric flow in the model from the “real dynamics”, which in most cases means that low-pressure systems, and thus precipitation events, were represented by the model at a different time or location.
uncertainties in the stake measurements
uncertainties in the calculation of water equivalent from snow-height change
the stake measurements not being representative of the gridcell.
Precipitation at Neumayer is closely connected to cyclonic activity in the circumpolar trough (Reference BromwichBromwich, 1988; Reference King and TurnerKing and Turner, 1997; Reference König-Langlo, King and PettréKönig-Langlo and others, 1998). Usually, low-pressure systems with their corresponding frontal systems, which pass north of the coast in an eastward direction, cause the precipitation. At a later stage, precipitation can also be due to so-called cut-off lows or upper lows. These are systems that are not connected to fronts and can be identified, not in the surface pressure maps, but in the geopotential fields at higher levels (Reference BluesteinBluestein, 1993). They are often stationary and can bring large amounts of precipitation. Clear-sky precipitation occurs very seldom at Neumayer: in the 3 hourly SYNOP observations, it is found on average about four times per year. It is not measurable, but from the frequency of its occurrence alone it can be said that it is negligible compared to the rest of the precipitation.
Because of this strong connection between precipitation and cyclonic activity we also compared the monthly mean surface pressure measured at Neumayer with the results derived from the model (Fig. 6). The correlation between measured and calculated pressure is very high. Correlation coefficients vary between 0.7 and 0.9. This supports the assumption that the model correctly shows the low-pressure systems that pass Neumayer and cause precipitation there.

Fig 6. Monthly mean sea-level pressure derived from the model (S1) and measured at Neumayer. (The gridpoint S1 was chosen here because it is the closest gridpoint to Neumayer.)
Temporal pressure variations are similar at the surrounding eight gridpoints (not shown here), which indicates that the precipitation conditions found at Neumayer are not due to local effects but mainly depend on the large-scale synoptic weather situation.
A Case-Study for 1987
The year 1987 was chosen for a closer investigation of the agreement between model and measurements, because the correlation between model and measurements is highest for this year. We want to investigate whether the good correlation is caused by a correct representation of the single precipitation events.
Figure 7 shows mean daily accumulation rates derived from the model and the stake measurements for 1987. The measurement interval for the stake measurements was usually 1 week; in 1987 it was often shorter. In order to calculate the mean daily accumulation rate, for each period we first looked at the SYNOP data to determine the number of days on which snowfall or drift was observed. For the remaining days, accumulation was zero. Then we divided the accumulation measured during the relevant period by the number of accumulation days, in order to obtain the mean daily accumulation rate. The modelled accumulation rate was calculated for the same time intervals.
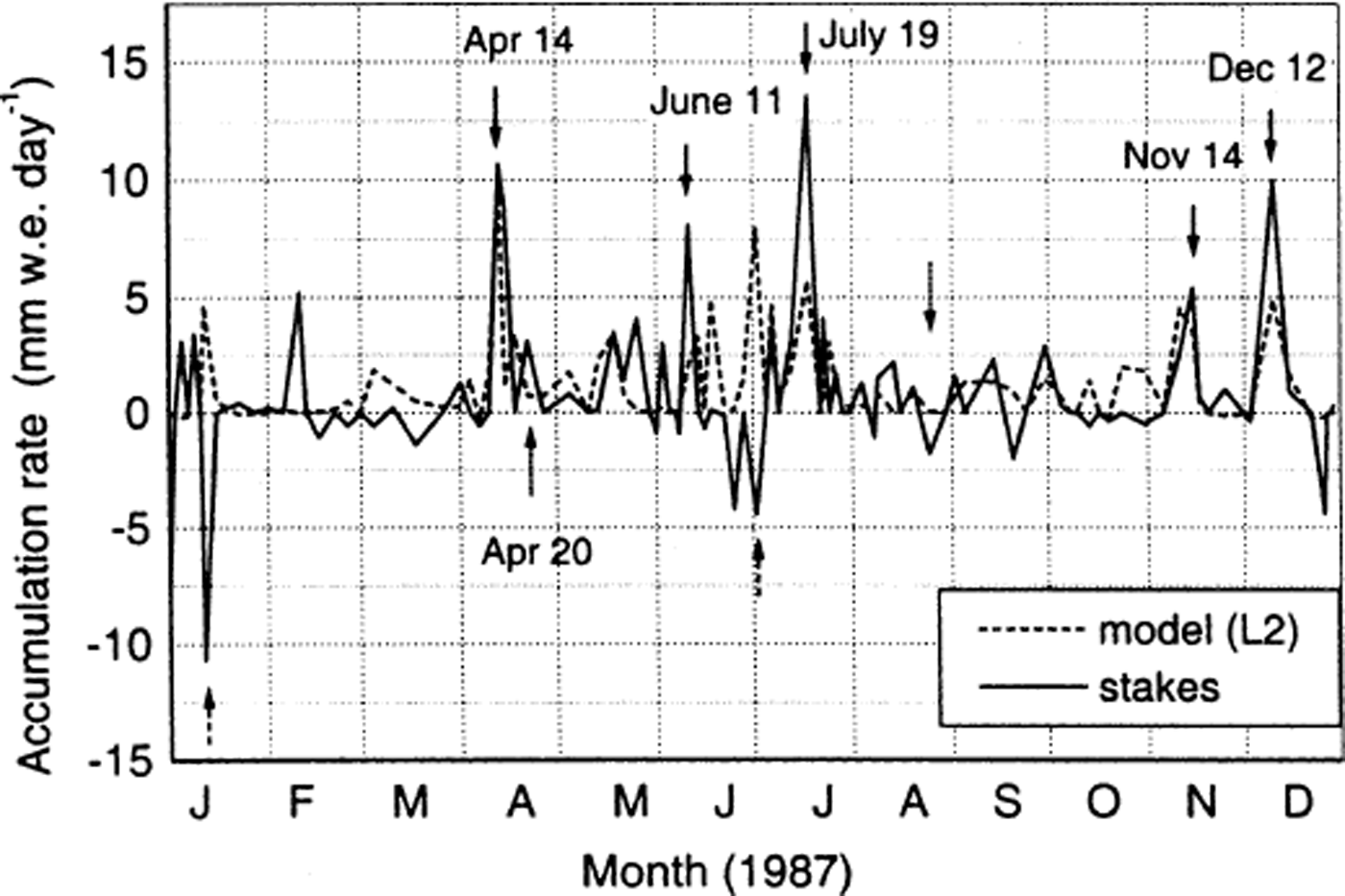
Fig. 7. Measured and modelled (gridpoint L2) accumulation rate for 1987.
At Neumayer, major accumulation events are usually connected to a low-pressure system passing the area in the north, with prevailing strong easterly winds. Such events occurred in 1987 around 14 April, 11 June, 19 July, 14 November and 12 December (indicated in Fig. 7 with black arrows).
With the exception of 11 June, these major precipitation events are represented clearly by the model, but the amounts of accumulation are generally lower in the model than in the stake data. It cannot be determined whether the model underestimates precipitation or whether this effect is due to drift influence. However, such easterly storms can also lead to net ablation at the stake array. In this case, the wind erosion is larger than precipitation, which usually accompanies strong easterly winds. Whether the storm results in net accumulation or net ablation depends on the amount of precipitation, the divergence of the wind field and the history of the snow cover. Of course, the agreement with the model result is poor in the case of net ablation (wind erosion). The model shows a certain precipitation amount caused by the same low-pressure system that caused net ablation at Neumayer. This occurred, for example, around 10 January and in early July (dashed arrows in Fig. 7).
The second typical case for disagreement between model and measurements is a southwesterly flow combined with a high-pressure system to the west of Neumayer. The south-westerly winds are strong enough to cause snowdrift and thus a small amount of accumulation (20 April; dotted arrow in Fig. 7) at Neumayer, although the SYNOP data show no major precipitation. They can also lead to ablation (wind erosion) (27 August; dotted arrow in Fig. 7).
Two cases are investigated in more detail using ERA. We first study the 19 July event. Figure 8a and b show the weather situation on 19 July. On the surface pressure map of ERA (Fig. 8a) a low-pressure system with a core pressure of 950 hPa is situated to the northwest of Neumayer. The corresponding trough at the 500 hPa level can be seen in Figure 8b. Neumayer lies in a northwesterly flow, which advects relatively warm and moist air towards the coast. At the surface the flow is more northeasterly. RACMO (Fig. 8c and d) shows much the same picture, although the low is less deep and there are more closed isohypses in the ECMWF 500 hPa map. However, the resulting flow above Neumayer is the same in RACMO and ERA, and both model and stake measurements show high accumulation values for this precipitation event, but accumulation in the model is lower than the observed value.

Fig. 8. Mean sea-level pressure and geopotential height of 500 hPa level for 19 July 1987 derived from RACMO (a, b) and from ERA (c, d).
A different picture is seen on 20 April (Fig. 9). Neumayer is situated on the southeastern side of a high-pressure system lying above the north and eastern Weddell Sea. The corresponding southwesterly flow, which is found at the surface as well as at higher levels, is strong enough to cause snowdrift from the southwest, which leads to accumulation at Neumayer, although no precipitation was observed on 20 April: the SYNOP data showed that there was only drifting snow below eye level. Since the model does not take into account the effect of drifting snow, no accumulation is seen in the model on that day. We thus find a disagreement between model and stake accumulation here. Nevertheless, the weather was correctly represented by the model.

Fig. 9. Mean sea-level pressure and geopotential height of 500 hPa level for 20 April 1987 derived from RACMO (a, b) and from ERA (c, d).
Conclusions
In this study we investigated the ability of a state-of-the-art atmospheric model to represent the temporal variations of Antarctic accumulation using the high-time-resolution accumulation dataset from Neumayer station. The 13 year mean accumulation and the range of interannual variability of accumulation derived from model and stake measurements are similar. However, there is no significant correlation between the time series of annual mean accumulation derived from model and observations, respectively. The correlation of the monthly mean values varies for different years; the correlation coefficients lie between 0.15 (1982) and 0.87 (1987). A closer investigation for the year 1987 shows that four out of the five major precipitation events were represented clearly by the model. The amounts of accumulation are, however, generally lower in the model than in the stake data. For these cases, it cannot be determined whether the model underestimates precipitation or whether this effect is due to drift influence, which is not taken into account in the model. The drift influence is certainly the main reason for disagreement between model results and measurements in cases where a storm caused net ablation at Neumayer or where accumulation was due to snowdrift from the southwest under high surface pressure influence without precipitation being observed. To try to investigate to what extent snowdrift causes disagreement between model and measurements, we studied the relationship between wind speed and the difference between model output and measurements. We found no significant correlation. However, both wind speed and the state of the snow surface are important for the amount of snowdrift.
On the positive side, the model does show most major precipitation events, and the pressure variations calculated by the model correspond closely to the pressure variations measured at Neumayer. This means that the model satisfactorily represents the synoptic situations that lead to precipitation and thus the temporal distribution of accumulation.
More measurements of snow redistribution and a thorough parameterization of snowdrift in a regional atmospheric model are needed for a quantitative comparison of calculated and observed accumulation.
Acknowledgements
This study was funded by the Austrian Science Fund (FWF) (grant No P13429-GEO) and the Netherlands Organization for Scientific Research (NWO). The meteorological data were kindly provided by the Alfred Wegener Institute for Polar and Marine Research, Bremerhaven; we would like to thank G. König-Langlo. We would also like to thank the wintering meteorologists for operating the stake array and the meteorological observatory over the years. The authors are grateful to ECMWF for providing the re-analysis fields. D. G. Vaughan and an anonymous reviewer contributed constructive and useful comments. Thanks are also due to our editors, M. R. van den Broeke and M. Sturm.
This is EPICA publication No. 44. This work is a contribution to the European Project for Ice Coring in Antarctica (EPICA), a joint European Science Foundation (ESF)/European Commission (EC) scientific programme, funded by the EC and by national contributions from Belgium, Denmark, France, Germany, Italy, the Netherlands, Norway, Sweden, Switzerland and the United Kingdom.











