1. Framework

The impact of sea ice on the ocean–atmosphere–biosphere interactions in the polar regions is well recognized. Annual growth of a continuous sea-ice cover is considered to impede gaseous exchanges with the atmosphere so efficiently that global coupled models either assume a yes/no scenario, respectively, for absence/presence of sea ice (Reference England, Garçon and MinsterEngland and others, 1994; Reference Dixon, Bullister, Gammon and StoufferDixon and others, 1996), or, more recently (Reference Goosse, Deleersnijder, Fichefet and EnglandGoosse and others, 1999), reduce winter exchanges to the “lead” areas (open-water fraction, generally <10%, of the total area covered with sea ice in mid-winter). However, since for temperatures higher than roughly −5°C a marked transition is assumed to occur toward increased permeability for inclusions in sea ice (Reference Weeks, Ackley and UntersteinerWeeks and Ackley, 1986; Reference Golden, Ackley and LytleGolden and others, 1998), this should allow, in both autumn and spring, gas transfer between the ocean and the atmosphere across the sea-ice cover mainly via the brine-channel network. On the other hand, recent studies of the biogeochemistry of the sea-ice habitat (Reference Gleitz, van der Loeff, Thomas, Dieckmann and MilleroGleitz and others, 1995, Reference Gleitz, Kukert, Riebesell and Dieckmann1996) have shown that under favourable circumstances such as summer algal blooms, biological activity can profoundly affect the brine geochemistry, including the gaseous components. This has important implications for pathways of algal carbon acquisition (and therefore ice-algal species succession during summer blooms), carbon isotope fractionation and species distribution in the open-water phytoplankton. These two examples point to the need for a better understanding of the behaviour of the gaseous components of sea ice, both as gas bubbles and dissolved in brines.

Datasets on total gas content and gas composition of sea ice are scarce. To our knowledge, only two attempts, both in the mid-1960s, have been made to measure gas properties of sea ice (Reference Miyake and MatsuoMiyake and Matsuo, 1963; Reference Matsuo and MiyakeMatsuo and Miyake, 1966). Although these measurements were performed on only four samples and were obtained using a “melting–refreezing” extraction method (suspected to be sensitive to CO₂ contamination by calcium carbonate equilibration reactions during the procedure), they provided us with valuable first estimates of total gas contents (2.2–21.2 mL STP (standard temperature and pressure) of air per kg of ice) and atmospheric gas compositions (N₂ = 54.2−76.8% per unit volume of total gas; O₂ = 20.6−29.0%, Ar = 0.93−1.1% and CO₂ = 0.98−24.3%). Reference Matsuo and MiyakeMatsuo and Miyake (1966) noted that the total gas content of their samples was much lower that would be expected from “instant freezing” of sea water (23–24 mL STP of air kg⁻¹). They suggested that this was due to diffusion of soluble gases away from the ice as it forms, a process that is now much better understood for other impurities in frozen sea water (mainly bulk salinity; see, e.g., Reference Weeks, Ackley and UntersteinerWeeks and Ackley, 1986; Reference Eicken and JeffriesEicken, 1998). However, they also noted that the CO₂ and O₂ concentrations were quite variable and that ratios between species concentrations could not be explained by differential diffusion alone. They suggested a biological bias, but could not see any correlation with indicators of biological activity in their samples.

Reference TsurikovTsurikov (1979) gave a more detailed, theoretical account of the impact of the various genetic and evolutive processes in sea ice on its total gas content and gas composition. He set out to quantify the contribution of each of the processes to the total porosity, and only briefly discussed the consequences for individual gas concentrations and ratios. The mechanisms invoked led to calculated gaseous porosities up to ten times higher than those measured by Reference Matsuo and MiyakeMatsuo and Miyake (1966) or calculated using Reference Cox and WeeksCox and Weeks’ (1988) equations.

In this paper, we report gas measurements in experimental sea ice collected during the interdisciplinary ice-tank experiment INTERICE II. The use of an “environmental test basin” at the Hamburg Ship Model Basin (Hamburgische Schiffbau-Versuchsanstalt (HSVA)) in Germany provided us with a unique opportunity to test the physico-chemical controls on gas content and composition of sea ice in the absence of biological activity. However, later data analysis revealed some problems. We discuss them and recommend that they be taken into account in planning future experiments.

2. The Interice II Tank Experiment

Experiments were performed in the Arctic Environmental Test Basin of the HSVA, an indoor tank that is 30 m long, 6 m wide and 1 m deep (Fig. 1). Ice formation can be forced by air temperatures as low as −25°C (roof-cooling elements). The tank was used for the 1996–98 sea-ice growth experiments of the INTERICE I–II programmes (Reference Eicken and ShenEicken and others, 1999; Reference HaasHaas and others, 1999). The present work took place during the freeze–melt–refreeze experiment of INTERICE II, in November–December 1998 (Reference HaasHaas and others, 1999).

Fig. 1. Map (above) and general view (below) of the Arctic Environmental Test Basin, HSVA. The map shows the Quiet and Current zones and the location of the biogeochemical compartments (B1–B6). Also shown are the two thermistor strings (T) the conductivity–temperature–depth profiler (CTD) the acoustic Doppler current meter (ADC) the thickness profiles (dots 1–10 in the Quiet zone, dots 1–9 in the Current zone) and the sample locations (triangles).

The tank was subdivided into Quiet and Current zones (Fig. 1). In the Current zone, laterally homogeneous currents of 0.085–0.065 m s⁻¹ were induced by impellers. The basin was filled with Hamburg tap water with added NaCl (>99.8% pure) at a final bulk salinity of approximately 35‰. In the Quiet zone, biogeochemical studies were conducted in 1 m closed polyethylene (PE)-foil compartments filled with artificial sea water made of a solution of “Instant Ocean Salt” (Aquarium Systems Ltd; chosen to provide a closer similarity to natural sea water) in Hamburg tap water, also brought to an initial bulk salinity of approximately 35‰. These studies examined the fate of dissolved organic matter (DOM) and other specific biochemical compounds (algal-derived DOM, lipid, amino acid and carbohydrate) in sea water when ice forms and consolidates in the absence of any biological activity (Reference Giannelli, Thomas, Haas, Kattner, Kennedy and DieckmannGiannelli and others, 2001).

The experiment was designed to simulate a growth–melt–growth cycle over a 14 day period, 9–22 November 1998. The thermal forcing is shown as open circles in Figure 2. The temperature was kept at about −15°C during the initial growth period, 9–14 November. The cooling system was switched off at 0800 h on 15 November, and restarted at full power on 17 November, to ensure a mean air temperature of −21° to −23°C. On 22 November the cooling was switched off again and the sea-ice cover left to warm up until 24 November.

Fig. 2. Twelve-hour mean air-temperature profile and daily ice thicknesses in the Quiet and the Current zones during experiment 1 of INTERICE II. Dates: dd.mm.yy.

Ice-thickness and ice-salinity profiles were determined daily along given transects (numbered grey dots in Fig. 1) in both the Quiet and Current zones. Figure 2 shows the mean ice thickness in the Quiet (black dots) and Current (black triangles) zones. Although both areas were seeded simultaneously (“ice-fog” seeding procedure; Reference Evers and JochmannEvers and Jochmann, 1993), ice growth started only on 10 November in the Quiet zone because that side of the tank was in connection with an external, slightly warmer tank. As shown by the striking parallelism of both thickness curves in Figure 2 and by the textural characteristics of the ice discussed below, this delay led to no significant difference in growth rate between the Quiet and the Current zones. During the melt phase, ice growth proceeded for a day and a half, and then ice thickness decreased (Fig. 2).

The water temperature, salinity (CTD in Fig. 1) and current (ADC in Fig. 1) were measured continuously in the Current zone throughout the experiment. During the growth phase, salinization of the tank water occurred (from about 35.5‰ to 39.5‰) due to salt rejection at the freezing front; it was not compensated for by dilution with fresh water. The volumetric increase due to ice growth was compensated for by pumping off the excess water volume daily, to avoid pressure build-up or upward forcing of brine during the experiment.

Vertical ice-temperature profiles (Fig. 3) were measured continuously using two thermistor strings frozen into the ice and protruding both above the air–ice and below the ice–water interfaces. Each of the periods in the cycle is clearly identified. During the growth phase a strong, regularly increasing and downward-progressing gradient existed. At the end of the warming phase the ice was quasi-isothermal. At the end of the regrowth phase the strong gradient was re-established, with complete freezing of the thermistor string. The effect of the final shut-off of the cooling system is also clear in the last profile (23 November 1998), still very cold at the base, but warming up slowly from the surface.

Fig. 3. Air and ice/water temperature profiles from the thermistor string in the Current zone during the growth–warming–cooling cycle of experiment 1. Dates: mm.dd.yy.

3. Sampling Procedure and Analytical Techniques

Sample blocks were collected from both the Quiet and Current zones every other day and from each of the biogeochemical tanks at the end of the initial growth cycle. For this study we have selected six samples that appeared to best represent the situation at the end of each phase in the different zones. Sample blocks C14, C17 and C20 (Fig. 1) were from the Current zone and corresponded to the end of the initial growth phase, the end of the warming phase and the end of the regrowth phase, respectively. Sample blocks Q14 and Q17 (Fig. 1) were both from the Quiet zone and were retrieved at the end of the initial growth phase and at the end of the warming phase, respectively. Finally, for comparison, one block corresponding to the end of the initial growth period from the biogeochemical tank 3 (BIO-3, Fig. 1) was selected.

The samples were approximately 20 × 20 cm in surface area and were collected following the procedure described by Reference CottierCottier (1999) and Reference Cottier, Eicken and WadhamsCottier and others (1999) to minimize brine drainage from the sample and surface flooding. A large plastic box was submerged under the ice via an access hole cut into the ice cover; then the sample was cut away from the ice cover and carefully floated over the box. After the box was lifted from the tank with the sample floating inside it, the water surrounding the sample was drained from the bottom of the box until the ice just remained floating. Finally, the whole box and its contents were shock-frozen at −40°C. After 24 hours the blocks were extracted from the containers, packed into PE bags and transported to Brussels in a −30°C chest freezer. In the −30°C cold-room laboratory, the relatively rough surface ice (typically a few millimetres height difference) was trimmed off the top of each block. The outer part of each sample block (including the frozen tank water and about 5 cm of the sides of the sample block itself) was cut away, and various adjacent vertical sub-blocks were cut for multi-parametric analyses. These included ice textures, bulk salinity, total gas content, gas composition, bacterial counts and detection of carbonate precipitates. Details on analytical procedures, precision and accuracy are given in Appendix A.

4. Results and Discussion

4.1. Ice textures

Figure 4 shows vertical thin sections from each of the sample blocks together with one characteristic horizontal thin section (except for the BIO-3 sample). The Current zone samples (C14, C17) clearly show an upstream deflection of the columnar crystals into the current (heavy arrows) that is absent from the other set of samples where no current existed (Q14, Q17, BIO-3). This has been previously described by Reference Langhorne and RobinsonLanghorne and Robinson (1986) for sea-ice growth in the presence of surface water currents. It is not surprising to find a similar behaviour here because the current velocity in the experiment (0.065–0.085 m s⁻¹) was considerably higher than 0.010 m s⁻¹, the predicted characteristic velocity above which the flow is expected to have a significant influence on the sea-ice texture (Reference Langhorne and RobinsonLanghorne and Robinson, 1986).

Fig 4. Vertical (V) and horizontal thin sections (H), photographed between crossed polarizers, from, the block sampled at the end of the growth period (14.November), at the end of the warming period (17.November) and at the end of the cooling period (20 November), in the Current, Quiet and biogeochemical tank 3 areas. Heavy arrows indicateflow direction in the Current zone. Thin arrows indicate the location of horizontal thin sections.

Another salient feature of Figure 4 is the contrast in textures in the Current area after growth (C14) and warming (C17), compared to that observed at the end of the regrowth phase (C20). Recrystallization close to the pressure-melting point after the isothermal warming phase has totally erased, in a few days, the textural imprint from the initial growth phase in the lower half of the ice cover. These changes occurred along with a major reduction in the areal pore fraction as described by Reference HaasHaas and others (1999). This suggests that such drastic textural changes could be efficiently used as indicators of isothermal phases in the growth history of natural columnar sea ice. Reference Tucker, Gow and WeeksTucker and others (1987) observed such a process in arctic sea ice, referring to it as “retexturing”, and indeed used it to discriminate between first-year and multi-year ice.

4.2. Bulk salinity

All bulk-salinity measurements acquired on initial growth (black circles in Fig. 5) displayed an inverse J-shaped profile with similar salinity ranges between 7–8‰ (top) and 11–16‰ (bottom). However, at a given depth the salinity was slightly higher in the Quiet than in the Current zone (direct comparison with the BIO-3 tank is not pertinent given the difference in initial conditions). This is understandable if one considers the “boundary-layer concept” as being valid for impurity inclusions in sea ice. In this approach (see, e.g., Reference Eicken and JeffriesEicken, 1998 for a full discussion), salt impurities are rejected at the ice–water interface. They accumulate in a thin water layer (the “boundary layer”, generally on the order of 1 to a few mm) wherein chemical-species transport occurs by diffusion only, in this case from the interface toward the water reservoir. Beyond that layer, the reservoir is considered to be homogenized at all times through compositional and mechanical convection. If significant currents are present, the boundary layer is thinner due to increasing external flow speed, the salinity gradient is higher in this layer (all other conditions being equal) and the export of chemical species towards the reservoir is more efficient. The net result is a lower incorporation of salt into the Current zone ice on freezing, as observed here.

Fig. 5. Bulk salinity in the blocks sampled at the end of each period of the growth (14)–warming (17)–cooling (20) cycle of experiment 1 in the three zones investigated.

In most natural and experimental sea-ice salinity measurements (including INTERICE I experiments under similar conditions: Reference Eicken and JeffriesEicken, 1998; Reference CottierCottier, 1999; Reference Cottier, Eicken and WadhamsCottier and others, 1999), C-shaped profiles were described. The observed higher salinity in the top 10 cm (see the first in the series of natural sea-ice profiles (4 November 1977) in Reference Nakawo and SinhaNakawo and Sinha, 1981) can be attributed to the combination of upward brine expulsion during freezing, wicking of brines into the frost flowers and decreasing freezing rate as growth progresses. During the INTERICE I experiment, higher salinities only typically occurred in the first sample (Reference Cottier, Eicken and WadhamsCottier and others, 1999, fig. 4) immediately at the surface (upper 2 cm), and most probably mainly resulted from the first two processes and possibly from contamination. Since in this study we trimmed the surface irregularities from the sea-ice blocks, we probably eliminated the highest concentration spots and therefore the salinity maximum of the top layer.

The observed inverse J-shaped profiles reflect both the progressive enrichment of the reservoir, and the large ice salinity increase due to brine/sea-water storage near the ice–water interface in the very porous skeletal layer, particularly well preserved given the special sampling technique used. Both processes obviously overcompensated, in this experimental 3 day young sea-ice cover of a closed reservoir, the expected decrease of initial salinity entrapment due to the decreasing freezing rate observed in the upper 20 cm of natural sea ice (Reference Nakawo and SinhaNakawo and Sinha, 1981).

At the end of the warming phase (open circles in Fig. 5) a clear release of brine had occurred in both the Current (C17) and Quiet zones (Q17). Bulk salinity had decreased by about 2‰ over the whole thickness, with the exception of the very bottom layers. This is comparable to the shift observed by Reference Cottier, Eicken and WadhamsCottier and others (1999) during INTERICE I. The enrichment of the bottom layers certainly reflected brine percolation downwards since there was no net growth (Figs 2 and 5) between 14 November (C14) and 17 November (C17) in the area of the Current zone investigated. Following Reference AssurAssur’s (1958) phase equilibrium table, the brine salinity at the −2°C temperature observed in the isothermal ice of C17 should be 37.6‰. This was within the range of the tank water salinity during the experiment and was only slightly lower than the observed mean salinity on 17 November in the Current zone (38.8‰).

The net effect of re-establishing a strong temperature gradient on regrowth in the Current zone ice (black triangles in Fig. 5) was a homogenization of the bulk salinity, with enrichment of the upper half and depletion of the lower half of the pre-existing ice cover, and further growth of a rather porous bottom layer. This new salinity profile in the Current zone ice raises some interesting questions on the processes at work during the transition from isothermal ice (C17) to the recooling phase (C20). Using the mean temperature (−2.41°C) and the mean bulk ice salinity (6.57‰) for the 1–11 cm depth range of C17 (to avoid surface- and skeletal-layer bias effects), we can apply Reference Cox and WeeksCox and Weeks’ (1983) equations to reconstruct the mean relative brine volume (V _b/V, where V _b is the brine volume and V is the bulk ice volume). This yields a value of 0.134, using a total gas content of 10 mL STP kg⁻¹ ice and a pure ice density of 0.917. With a mean bulk ice salinity of 6.57‰, one obtains a brine salinity of 48.99‰, which is about 10‰ higher than the reservoir water salinity at that time (38.8‰; Reference HaasHaas and others, 1999, fig. 2a). The mean bulk ice salinity in the same depth interval after 3 days of recooling is 7.74‰ (C20). This is only conceivable if there has been a net salt input into the system between 17 and 20 November. Indeed, mere freezing of the channel walls on recooling, without vertical salt transfer through diffusion or brine convection, should have resulted in identical bulk ice salinities. Salt input from the top layers is precluded since higher salinities than in C17 are observed in C20 from the very top (Fig. 5). Salt input from the skeletal layer or the reservoir is also unlikely since the water salinity there (38.8‰) is lower than the brine salinities calculated for C17 (48.99‰). Upward forcing of enriched brines on freezing of the bottom layers is, however, not precluded.

Another plausible scenario is that at some stage between the C17 sampling event and the effective recooling of the ice, the ice porosity has increased above that calculated for C17. For example, reapplying Reference Cox and WeeksCox and Weeks’ (1983) equation with a mean bulk ice temperature of −1.65°C gives a relative brine volume of 0.201 and a brine salinity of 32.60‰. If, in the early stages of recooling, this brine volume is filled with water at reservoir salinities (through diffusion or mechanical mixing in the widely interconnected brine channels, including the disturbance from walking on the ice surface), a bulk ice salinity of 7.82‰ could be achieved. This implies that subsequent freezing reduces the channel interconnectivity fast enough to prevent any significant loss of salt through diffusion or brine convection towards the reservoir.

There is some clue that lower-salinity water has been drained into the reservoir during the melt phase, as hypothesized above. Indeed, as shown in Reference HaasHaas and others (1999, fig. 2a), a slight decrease of the reservoir salinity has been observed between 16 and 18 November, with a minimum value about 8 hours after C17 was sampled. Maximum temperature profiles were also recorded in the ice at the same moment (1700 h, 17 November), but only in the top 5 cm of the Quiet area were temperatures higher than −2°C, with an interface air temperature of −1.5°C. The question may thus be raised how efficiently thermistor chains measure temperature fields in a highly heterogeneous medium, and integrate heat-transfer processes occurring locally, in areas possibly relatively remote from the sensors.

Lower freezing rates at greater depths favour salt fractionation, and result in lower salinities, whilst the increasing porosity of the newly formed ice drives salinity up again in the bottom layers.

4.3. Total gas-content and gas-concentration profiles

Figure 6a–c summarize the results from the gas measurements in the sample blocks from the Current (Fig. 6a), the Quiet (Fig. 6b) and the BIO-3 tank (Fig. 6c) areas. The total gas-content (total volume) measurements, expressed as mL STP of gas per kg of ice, are plotted as profiles vs depth in the first column of Figure 6 (solid line, no symbols). Columns 2–4 show gas concentrations as a percentage of the total gas content (solid line with open circles, bottom scales) and individual gas contents in mL STP per kg of ice (solid line with no symbol, top scale) for CO₂, O₂ and N₂, respectively. Individual gas contents were calculated by multiplying total gas content by the appropriate gas concentration. Finally, O₂/N₂ ratios are also shown as a solid line with dotted circle symbols in the first column of graphs. For reference, the first row of graphs shows corresponding values for “instantly frozen sea water” (IFSW; 35‰ sea water frozen in closed system at a high freezing rate, preventing chemical fractionation) and for the atmosphere above the tank.

Fig. 6. Gas properties of the samples from experiment 1. Total gas contents are plotted in column 1 (solid line, top scale), together with the O₂/N₂ ratio (solid line with symbols, bottom scale). Concentration in % in volume of the gases extracted (solid line with white dots, bottom scale) and in mL STP of gas per kg of ice (solid line, top scale) for CO₂, O₂ and N₂ is plotted in columns 2, 3 and 4, respectively, (a) Current zone at the end of each period of the growth–warming–cooling cycle; (b) Quiet zone at the end of the growth and the warming period, respectively; (c) biogeochemical tank 3 at the end of the initial growth period. In columns 2–4, the numbers quoted for IFSW are (a) concentration of the species in mL STP per kg of sea water and (b) concentration in parts per volume of the total gas content (from Reference Riley and SkirrowRiley and Skirrow, 1975). In column 1 the numbers are (a) total gas content in mL STP per kg of frozen sea water and (b) O₂/N₂ ratio. Equivalent numbers are also given for the atmosphere when applicable.

The range of total gas-content values for all the samples is 3.5–18 mL STP kg⁻¹, which is comparable to the range obtained by Reference Matsuo and MiyakeMatsuo and Miyake (1966) in their four samples (2.2–21.2 mL STP kg⁻¹) and to various other direct or indirect estimates from the literature (5–30 ppt in volume) summarized by Reference Weeks and LeppärantaWeeks (1994). It is coherent with the range calculated from Reference Cox and WeeksCox and Weeks (1983, equation 24), neglecting the solid-salts contribution. Taking as an example the isothermal (−2°C) C17 sample block with a mean salinity of 6.5‰ (ignoring the surface and bottom layers, Fig. 5), calculations give 5.33‰ for the relative air volume at a bulk ice density of 930 kg m⁻³. This is in good agreement with the mean value of about 6 mL STP kg⁻¹ measured in the sample block.

The total gas content was always lower than the 23.75 mL STP kg⁻¹ value that would be expected in IFSW (Fig. 6a). This shows that gases, like other impurities in sea water, are preferentially expelled from the growing ice.

4.3.1. Acquisition of the gas content during initial ice growth

The total gas-content profile was generally similar in the Current and Quiet zones (Q14 and C14): an initial increase in the surface layers, a stable value in most of the ice cover and a final increase in the bottom layer. However, the ice from the Quiet zone reached its “plateau value” faster (about 1.5 cm depth) than ice from the Current zone (about 4 cm depth), and the mean value of the “plateau” was twice as high in the Current (10–11 mL STP kg⁻¹) as in the Quiet (4–5 mL STP kg⁻¹) zone.

To understand these features, we need to look at individual gas-content profiles C14 and Q14 in the light of the boundary-layer concept, described above for salt transport but equally valid for other types of solute impurities like gases. During downward freezing, the layer close to the ice–water interface in which solutes are transported only by diffusion is truncated by convection at its base and is reduced to a thickness of millimetres to form what is usually called a boundary layer. Eventually a steady state is reached when the incoming solutes flux associated with the downward movement of the boundary layer (of constant thickness) is compensated for by the outcoming diffusional solutes flux driven by the rejection of these solutes at the ice–water interface. Fick’s first law of diffusion, in the case of moving coordinates, applies:

(1)

where C _bw is the solute concentration in the bulk water reservoir, C _iw is the solute concentration at the ice–water interface, V is the linear rate of advance of the freezing front, D is the diffusion coefficient of the solute species (1.18, 1.61 and 2.08 × 10⁻⁵ cm² s⁻¹ for CO₂, N₂ and O₂, respectively (Reference Stauffer, Neftel, Oeschger, Schwander, Langway, Oeschger and DansgaardStauffer and others, 1985)) and z _bl is the boundary-layer thickness. In Table 1 (lines 1–4) we use Equation (1) to calculate the enrichment factor (C _iw/C _bw) at the interface for both C14 and Q14, assuming a near-constant freezing rate for 12–14 November (Fig. 5) and a z _bl value of 0.29 cm (Reference Weeks, Ackley and UntersteinerWeeks and Ackley, 1986; a). It was then possible to estimate the “close-off” individual gas concentrations in the sea ice, for brine volumes ≤5%, i.e. for temperatures of about −5°C, when connectivity is assumed to be lost between the brines (and gas inclusions) and the reservoir water (Reference Golden, Ackley and LytleGolden and others, 1998). This is done in Table 1 (lines 5–7), assuming that the brine concentration on “close-off” equals C _iw. For the present experimental settings there was not much difference between the Current and Quiet zones, and the values were around 1.1 and 0.60 mL STP kg⁻¹ for N₂ and O₂, respectively. These calculated values are very close to the observed initial and “baseline” values (Table 1, line 8) in both C14 (1.1 and 0.48 mL STP kg⁻¹) and Q14 (1.42 and 0.60 mL STP kg⁻¹). It is, however, interesting to note that the observed values were slightly lower in the Current zone, probably because of the thinner boundary layer due to increased external flow speed as was hypothesized for bulk salinity (section 4.1).

Table 1. Calculation of “close-off” gas contents in experiments C14 and Q14 and observed values. A value of 930 kgm⁻³ has been used for sea-ice density

The main difference, nevertheless, between C14 and Q14 was that the whole profile in the Quiet area did not significantly depart from the baseline (mean values were 1.56 and 0.66, respectively, which is very nearly within the precision of the measurements), whilst the Current area showed an ice enrichment by a factor of 3 in both species (Table 1, line 9). We propose, as a possible mechanism to explain this contrast, that the gas enrichment at the interface of the C14 sample had reached the critical necessary value for bubble nucleation.

Once it started, bubble nucleation further enriched the ice by pumping into the gas phase what would otherwise have diffused as a solute towards the bulk water reservoir. Eventually, all other conditions being equal, the situation evolved towards an equilibrium between the rate of transfer of solutes into the gas phase and their rate of diffusion from the ice–water interface towards the bulk reservoir, across the boundary-layer gradient, resulting in the observed “plateau” at C14. The slight decrease observed in this “plateau” may reflect the impact of the freezing-rate decrease on the solute transfer in the boundary layer.

It is interesting to note that observations from previous experimental work (Reference CarteCarte, 1961; Reference Killawee, Fairchild, Tison, Janssens and LorrainKillawee and others, 1998) suggested that much higher supersaturation levels (12–30 vs 2–3) were necessary for initial bubble nucleation when the conditions were closer to convection-free, i.e. higher boundary-layer thickness. This might explain why the critical supersaturation does not seem to have occurred significantly in the Quiet area (Q14). Thin sections examined under the microscope clearly showed a high density of bubbles in sample C14 and their scarcity in sample Q14, lending strong support to the hypothesis developed above.

As observed for bulk salinity, the final increase of the total gas content observed in the bottom layers, at both C14 and Q14, results from the “shock-freezing” of the large amount of reservoir water trapped into the very porous (V _b/V > 20%) skeletal layer.

4.3.2. Origin of the CO₂ signal

Extremely high CO₂ concentrations and contents were observed in all the experiments (Fig. 6). CO₂ concentrations are in the range 18–57%, which almost excludes the highest observation of Reference Matsuo and MiyakeMatsuo and Miyake (1966; 24.3%) for natural sea ice. This results in CO₂ contents of 1–8 mL STP kg⁻¹, 30–250 times higher than the “close-off” concentration value (0.03 mL STP kg⁻¹; Table 1). There are two possible main paths leading to such CO₂ enrichments in the water reservoir at the ice–water interface: a geochemical one (equilibrium in the carbonate system) and a biological one (bacterial activity).

4.3.2.1. The geochemical source

Reference Killawee, Fairchild, Tison, Janssens and LorrainKillawee and others (1998) studied the effect of freezing on solutions with various supersaturation levels with respect to calcium carbonate. This was measured by a saturation index S _i, defined as the logarithm of the ionic activity product divided by the solubility product for calcite; positive values thus indicated supersaturation. In their set of experiments, S _i of the initial waters varied between −0.90 and +0.65. On completing each experiment, the authors sampled the ice for gas measurements and major-ion chemistry. Thin sections were observed under the binocular to detect in situ secondary calcite formation, and the precipitates were studied with a scanning electron microscope (SEM). Since these were closed-system experiments, CaCO₃ precipitation always occurred, but at different relative depths, depending on the initial saturation index (Table 2). In all the experiments, first CaCO₃ precipitation was accompanied by a drastic rise of the CO₂ concentration in the gas phase from a few per cent to 55–65%, whilst equivalent test runs with demineralized water typically showed a plateau at a few per cent, for relative depths of up to 0.9. Clearly, the initiation of calcium carbonate precipitation enhanced preferential CO₂ degassing at the ice–water interface in accordance with the approximated reaction (for pH < 9):

Table 2. Relative depths (depth of sample/reservoir depth) at which first CaCO₃ precipitate was recovered from the ice (Reference Killawee, Fairchild, Tison, Janssens and LorrainKillawee and others, 1998)

(2)

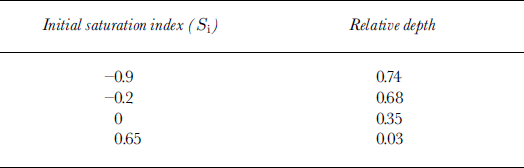
It was therefore of interest to calculate the saturation index for the tap, the tank and the biogeochemical-tanks waters at INTERICE II, using the available chemistry. This was done using PHREEQM, a modified version of the U.S. Geological Survey PHREEQE program (Reference Appelo and PostmaAppelo and Postma, 1994). Calcite saturation indices were −0.14 for the tap water, −0.65 for the Current and Quiet zones (lowering of ion activities by the increased salinities) and +0.24 for the biogeochemical tanks (added Ca²⁺ and HCO₃ ⁻ overcompensating the effect of increased salinities on activities). This implies, following the results of Reference Killawee, Fairchild, Tison, Janssens and LorrainKillawee and others (1998) summarized in Table 2, that supersaturation could not be reached in the Quiet and Current zones, given the limited thickness of the sea-ice cover relative to the tank depth (<0.2; see Table 2). On the other hand, it is quite likely that calcite precipitation occurred soon after freezing in the biogeochemical tanks, given their initial saturation index.

To test this further, we checked selected samples with high CO₂ levels, both from the Current (C17; 6–8 cm, CO₂ = 45%) and from the BIO-3 tank (BIO-3; 6–9 cm, CO₂ = 49.7%), for the presence of CaCO₃ precipitates as described above (Reference Killawee, Fairchild, Tison, Janssens and LorrainKillawee and others, 1998). Figure 7 shows selected grains as seen under the SEM. Sample C17 (Fig. 7h) was completely examined, and only two calcite grains were found that did not show typical features of fast-crystallizing calcite as seen in Reference Killawee, Fairchild, Tison, Janssens and LorrainKillawee and others’ (1998) samples (Fig. 7e–g). They most probably resulted from contamination of the sample. In contrast, calcium carbonate was easily detected in larger amounts on the BIO-3 tank sample filter (Fig. 7a–d). The grains showed many features, in terms of size, geometry and aggregation, in common with the carbonates from Reference Killawee, Fairchild, Tison, Janssens and LorrainKillawee and others’ (1998) experiments. These observations thus support the occurrence of active CaCO₃ precipitation (and associated CO₂ degassing) in the biogeochemical tanks but not in the Current and Quiet zones. Calculations based on Richardson’s work on phase relationships in sea ice (Reference RichardsonRichardson, 1976) give a maximum possible CO₂ concentration of 77% in the gas phase (see Appendix B), which compares well with the observed 40–53% CO₂ in the BIO-3 tank.

Fig. 7. SEM photographs of calcium carbonate precipitates centrifuged with the brines (a–d, h), as compared to those produced in Reference Killawee, Fairchild, Tison, Janssens and LorrainKillawee and others’ (1998) experiments (e–g). (a–d) are from the 6–8 cm depth interval in sample C17 from the Current zone; (h) is the only precipitatefound in the filtered sample from the biogeochemical tank 3 (depth interval 6–9 cm), (d) is similar to (b), but with clear dissolution features resulting from the extraction procedure. Lower right scale in (h) applies to all photographs. See details in the text.

4.3.2.2. The bacterial source

Three samples were selected from each zone (BIO-3 tank, C17 and Q17) to check for bacteria as another source of CO₂. Typical densities and morphologies are illustrated in Figure 8. The BIO-3 tank contained low levels of bacteria, with a mean value of 1.42 × 10⁴ cells mL⁻¹. Bacteria were mostly very small cocci (<1 μm), some loose and some in fluffy aggregates. The Current and the Quiet zones were both much richer, with mean values of 5.56 × 10⁵ and 3.92 × 10⁵ cells mL⁻¹, respectively. In the Current zone, bacteria were mostly short rods and cocci about 1 μm in size, often grouped in three-dimensional clumps that had to be sonicated before counting. There were also “crescent-shaped” items about 5–8 μm long and 1 μm in diameter that were not full of DNA (usually one sphere in the centre or one at the end). The sample also contained debris, appearing as wispy irregular material staining pale blue. The Quiet zone sample looked similar to that of the Current zone, but with smaller and fewer “crescent-shaped” items and less debris.

Fig 8. Enlarged photographs of typical bacterial populations in each of the zones investigated: (a) biogeochemical tank 3 (BIO-3; depth 9–12 cm), (b) Current zone (C17; depth 12–14 cm) and (c) Quiet zone (Q17; 9–10.5 cm). Individual bacteria cells are between 0.5 and 1 μm.

Bacterial abundances in natural sea ice from the Weddell and Ross Seas range from approximately 0.6 to 2.7 × 10⁶ cells mL⁻¹ (e.g. Reference Kottmeier, Grossi and SullivanKottmeier and others, 1987; Reference Kottmeier and SullivanKottmeier and Sullivan, 1990; Reference GrossmannGrossmann, 1994; Reference Grossmann and DieckmannGrossmann and Dieckmann, 1994). Abundances in the BIO-3 tank were lower than these and were about half the minimum abundance observed on a May–June 1998 winter cruise of the Nathaniel B. Palmer in the Ross Sea (M. Gowing, unpublished information). Abundances in the Current and Quiet zones were slightly below the low end of the range of published observations and were near the maximum of 5.3 × 10⁵ cells mL⁻¹ observed on the winter cruise (M. Gowing, unpublished information).

Bacterial activity is thus a plausible alternative to explain the high CO₂ levels in the Current and Quiet zones where CaCO₃ precipitation was precluded. It should be noted, however, that most of that activity must have been located close to the ice–water interface since there was no apparent inverse correlation between CO₂ and O₂ concentrations in the samples. The tank water would then act as the oxygen source. This is in accordance with the findings of Reference Sullivan and PalmisanoSullivan and Palmisano (1984) that 47% of the bacterial numbers and 93% of the biomass were located within 20 cm of the bottom of the ice cover in McMurdo Sound. Bacteria also require nutrients. A possible nutrient source may have been contamination of the water tank during oil degradation tests from previous studies in the Arctic Environmental Test Basin.

One could estimate (Appendix C) the daily amount of CO₂ that might have been produced by the bacteria in the Current tank, using our bacterial abundance values and bacterial production rates in autumn Antarctic ice from Reference Kottmeier and SullivanKottmeier and Sullivan (1990). Hypothesizing that 5% of the interfacial brine would have entered the ice before connectivity was lost (“law of five”: Reference Weeks, Ackley and UntersteinerWeeks and Ackley, 1986; Reference Golden, Ackley and LytleGolden and others, 1998), the daily input of CO₂ to the bulk ice would have been 0.062 mL kg⁻¹. This value is only twice the “close-off” concentration calculated (in the absence of biology) in Table 1, and about 30- to 50-fold lower than the mean values of 2–3.25 effectively measured in the Current zone (C14; Table 1). However, the bacterial production calculated in Appendix C is probably a serious underestimate for at least four reasons:

1. (1) Samples were counted during March 2000, so there was undoubtedly loss of the original populations over time. The magnitude of loss over time for bacteria stored frozen in ice is unknown, but loss over time in preservative solutions has been documented (Reference Spinrad, Glover, Ward, Codispoti and KullenbergSpinrad and others, 1989). Loss can be up to 75% within 39 days and is different for different samples (Reference Turley and HughesTurley and Hughes, 1992).

2. (2) Bacteria were likely to have been producing CO₂ for 2 or 3 days before the CO₂ was sealed into the ice above the skeletal layer, based on the first temperature profile (Fig. 3).

3. (3) There could have been much higher densities of bacteria at the ice–water interface; samples counted were taken several cm away from this interface. A profile of bacterial abundance in Arctic sea ice showed bacterial concentrations an order of magnitude higher within 0.5 cm of the ice−water interface than those 1.5–4 cm higher in the ice (Reference Maranger, Bird and JuniperMaranger and others, 1994).

4. (4) If bubble nucleation occurred, all the CO₂ produced at the interface may have ended up in the ice because of buoyancy. In that case, the final drastic reduction coefficient of 5% (amount of interfacial water actually incorporated into the ice brine volume) in the calculation would be erroneous.

If all or some of these factors occurred together, it is clear that the bacteria could have produced the CO₂ amount measured in the ice.

4.3.3. Trends of individual gas-concentration profiles developed on initial ice growth

The CO₂ concentration profile in sample C14 (Fig. 6a) is C-shaped; this is mirrored by the O₂ and N₂ concentration profiles. Although the trends are consistent with the effect of a decreasing freezing rate as the ice cover builds up in the upper part of the profile, we will now demonstrate that neither the observed range nor the relative amplitude is plausible. Table 3 indeed shows the calculated effect of the decreasing freezing rate on the expected gas concentrations in the ice. Mean freezing rates for the depth ranges corresponding to the observed values were interpolated from a best-fit power regression across the daily observed freezing-front positions between 10 and 14 November (r² = 0.997). From Equation (1), with z _bl = 0.29 cm (Reference Weeks, Ackley and UntersteinerWeeks and Ackley, 1986; Reference Eicken and JeffriesEicken, 1998) and appropriate diffusion coefficients, enrichment factors at the ice–water interface were calculated for each species. Using solubility values for O₂ and N₂ (IFSW values in Fig. 6a) and realistic “close-off” brine volumes (5%), the CO₂ level was adjusted (since it is believed to result from bacterial activity at the interface) so that the calculated percentage concentrations were close to those observed in the first 0–2 cm depth interval. Appropriate mean freezing rates were then used to proceed with the same calculation to obtain the expected gas concentrations for the following depth intervals, in the case where they would be solely controlled by the balance between the growth rate and diffusion in the boundary layer. CO₂ decreased by 2.27% in concentration, which was compensated by a 1.35% and a 0.93% increase for O₂ and N₂, respectively.

Table 3. Effect of the freezing rate on the gas concentration in the ice

The concentration variations calculated above (Table 3) were, however, only roughly 1/10 of those measured (Fig. 6a top, columns 2–4, open circles). On the other hand, although calculated O₂/N₂ ratios (0.497–0.527) were lower than those in air dissolved in water at 0°C (0.56), which reflected faster diffusion of oxygen ahead of the ice–water interface (Reference Killawee, Fairchild, Tison, Janssens and LorrainKillawee and others, 1998), the trend with depth was opposite to the observed one (Fig. 6a, first column, solid line with dotted open circles), and the range was much lower. We therefore need another (dominant) process to explain the observed trends.

Reference CarteCarte (1961) suggested that, on bubble nucleation, the composition of the gas phase would be controlled by diffusion processes between the water close to the interface and the air bubble. One can therefore surmise the existence of the following process:

1. (a) Rejection during the first stages of ice growth leads to gas supersaturation in the solution at the interface, with typical enrichment factors of 1.3–1.6 in the present experimental conditions, as suggested by the values in Table 1.

2. (b) On nucleation, the bubbles show gas concentrations and ratios close to those of the air dissolved in the water at the interface, reflecting the combined effect of supersaturation and diffusion ahead of the freezing front, towards the bulk of the reservoir, as calculated in Tables 1 and 3

3. (c) However, these initial concentrations in the bubbles (e.g. 64%, 34% and 2% for N₂, O₂ and CO₂ (in the absence of biological bias), respectively, if we use the C _iw values in Table 1) strongly differ from those in equilibrium with saturated sea water at 0°C (atmospheric values in Fig. 6a: 78.08%, 20.95% and 0.034%, respectively). Diffusion thus occurs, according to differences in partial pressures between the air in the bubbles and the air dissolved in the interface water. Therefore, whilst the total gas content of the bubbles eventually further increases to reduce supersaturation, N₂ diffuses from the interface towards the bubbles, and the reverse applies to O₂ and CO₂. This process continues as long as the bubbles are not isolated into the ice cover, i.e. for longer times at deeper levels, where freezing is slower. It results in strongly decreasing CO₂ levels and O₂/N₂ ratios, as observed during growth in the Current area. This, in turn, supports the idea that the marked increase in total gas content in the sample was indeed linked with bubble nucleation as hypothesized above.

Similarly, observed O₂/N₂ ratios in sample Q14 are all in the range 0.38–0.45, with a mean value of 0.42, which is consistent with negligible bubble nucleation.

An interesting exercise is to reconstruct the O₂ and N₂ concentrations in sample C14, hypothesizing that CO₂ and other minor gases are “negligible” and using the observed O₂/N₂ ratios. This is done in Table 4. In the 0–6 cm depth range, O₂ concentrations decrease and N₂ concentrations increase. The reverse trend, although somewhat dampened, occurs in the lower 8–14 cm depth range. The kinetic effects of the processes discussed above are clearly shown: in the upper half, gas concentrations span the range between solubility values in sea water (34.80% and 61.40% for O₂ and N₂, respectively) and atmospheric values (20.95% and 78.08% for O₂ and N₂, respectively), with an intensity that depends on their relative diffusion rates. N₂, which has a lower diffusion coefficient, takes longer to approach atmospheric values. However, the atmospheric values are never reached in the bubbles, due to the limited final thickness of the sea-ice cover. Indeed, for depths over 7 cm (where the ice temperature was above −5°C before sampling), connectivity between the brines and the water below was still efficient, and “shock-frozen” brines on sampling and storage have slightly shifted gas compositions towards water-solubility values again. This has the important implication that any natural thermodynamically growing sea-ice cover will most likely show, on bubble nucleation and above the skeletal layer, a gas composition close to atmospheric, provided that no biological activity has taken place.

Table 4. Reconstructing O₂ and N₂ concentrations in sample C14, in the absence of the other gases (the −5°C isotherm is located at about 7 cm; see Fig. 3)

4.3.4. Alteration of total and individual gas contents on warming/melting

On warming of the ice, the brine salinity thermodynamically readjusts by melting ice on the walls of the channels and pores. This should result in partial redissolution of the bubbles. Since our technique measured both the air existing as bubbles and that dissolved in the brines, the process alone should not have changed the measured gas properties at a given depth level. However, when full connectivity is achieved between the water reservoir and the atmosphere through the channel network, gas species will diffuse away from or into the ice, depending on their concentration in the brine as compared to the atmosphere above and the water below.

Comparison of the individual gas-concentration profiles in samples Q14 and Q17 (Fig. 6b) illustrates this. Since both the air and the saturated-water CO₂ concentrations were lower than the level in the ice, diffusion occurred both upwards and downwards. The reverse was true for O₂ and N₂. It is interesting to note that the gradient in the ice was strongly reduced on the water side, suggesting that water values close to the interface were much higher (around 30% for CO₂) than the solubility limit (2.5% for CO₂). Since ice was not growing at the time of sampling, geochemical production of CO₂ via the carbonate equilibrium is definitely precluded, and the idea of a biologically mediated input is supported.

A similar behaviour prevails for C17. Diffusion at the ice/atmosphere interface lowered the CO₂ level in the surface layers, and the initial gap in the intermediate layers was filled from both top and bottom. Concentrations in the bottom layers, however, instead of decreasing, rise to the maximum observed value of about 57% CO₂. This could be, as above, the result of a diffusion process from the locally biologically enriched interface water, or it could result from brine transport from the upper layers, with simultaneous “passive” entrainment of gaseous and dissolved CO₂ downwards. The net result of the combined dilution and diffusion processes described above was an impoverishment of the total gas content, apart from the top and surface few centimetres. This impoverishment was particularly well marked in the Current zone where bubble nucleation had occurred on initial growth.

4.3.5. Impact of cooling and further growth

Sample C20 (Fig. 6a) illustrates the effect on the gas impurities of recooling and further growth of the ice cover. Generally, the total gas content had considerably increased, and the individual gas profiles were much more homogeneous. We suggest that this was due to increased water transport in the channel system as the ice approached the isothermal state, upward movement of saturated reservoir water mixing and partially replacing the initial brines. Relatively sudden resumption of the thermal forcing would result in a certain amount of “mass freezing” in the channels (as clearly indicated by the texture showing freezing of small crystals in formerly broader brine channels and brine layers) which was less efficient in terms of impurity rejection than the initial freezing process in the bottom skeletal layer. This scenario would explain acquisition of individual gas concentrations at intermediate levels between those acquired on initial entrapment and further modified by diffusion and gravity transport in the channels during the warming phase, and those existing in the underlying water when resuming the growth process. Since freezing rates were faster (only the water in the brines had to partially freeze), supersaturation at the ice–water interface was higher, and bubble nucleation resumed with its characteristic signature of a lower O₂/N₂ ratio.

4.3.6. Behaviour of the biogeochemical tank 3

Profiles in the biogeochemical tank 3 (BIO-3, Fig. 6c) were very similar to those observed in the Quiet area (Fig. 6b) on initial ice growth, with limited (if any) bubble nucleation. The evolution of the CO₂ concentration profile looked more regular than in the Q14 sample, a possible result of the hypothesized difference in the origin of the enhanced CO₂ signal.

5. Summary and Conclusions

Our dataset provides the first detailed study of acquisition and alteration processes of gas properties in experimental sea ice. Ice textures showed typical features of congelation ice growth, with the predicted upstream deflection of columnar crystals towards the current on initial growth in the Current zone. This textural imprint was, however, strongly erased on a subsequent warming/cooling cycle, demonstrating the adequacy of using “retexturing” to detect isothermal phases in the growth history of natural sea ice (e.g. in multi-year sea ice (Reference Tucker, Gow and WeeksTucker and others, 1987)).

Progressive salt enrichment of the reservoir in these closed-system experiments resulted in downward increasing porosity and a typical invertedj-shaped bulk-salinity profile. The strongly increasing salinity of the bottom layers reflected impeded brine drainage on sampling, due to the special technique used. At the end of the warming phase, a clear redistribution of the brine downwards had occurred in both the Current and the Quiet zones. Bulk salinities shifted down by about 2‰ over nearly the whole thickness, apart from the bottom layers showing the effect of brine percolation downwards. On subsequent cooling, the bulk salinity homogenized at an intermediate level between initial-growth and warming-phase profiles, suggesting a net salt input into the system during the warming–cooling transition.

The range of total gas-content values (3.5–18 mL STP kg⁻¹) is comparable to the range measured directly by Reference Matsuo and MiyakeMatsuo and Miyake (1966) in a limited number of natural sea-ice samples. It is also coherent with those calculated using the Reference Cox and WeeksCox and Weeks (1983) formulation.

On initial growth, in both the Current and Quiet zones, the observed baseline values for O₂ (0.55 mL STP kg⁻¹) and N₂ (1 mL STP kg⁻¹) were very close to estimates of the “close-off” values. However, whilst the whole profile in the Quiet zone had not significantly departed from the baseline, the one in the Current zone showed enrichment factors of about 3 in both species. This is thought to be due to bubble nucleation at the interface. The behaviour of the O₂/N₂ ratio in the Current zone, steadily decreasing to minimum values, as expected in a scenario where concentration levels in the bubbles were governed by selective diffusion processes from the water at the interface towards the bubble, supports this assertion. The fact that bubble nucleation does not seem to have occurred in the Quiet zone is coherent with the observation from previous work that much higher supersaturation levels are needed for initial bubble nucleation when convection is lower, which would be the case in the absence of current.

Extremely high CO₂ concentrations were observed in all the experiments (18–57%), nearly exclusive of the range observed in natural sea ice, resulting in CO₂ contents of 1–8 mL STP per kg of ice, that is 50–250 times the calculated “close-off” value. This appeared to be the (unfortunate) result of two major biases in the experimental settings:

1. (a) the use of CaCO₃-rich “tap” water as a solvent for the “Instant Ocean Salt” in the biological tanks, which resulted in CaCO₃ precipitation and correlative CO₂ degassing at the ice–water interface, and

2. (b) uncontrolled sustained bacterial activity in the Current and Quiet zones.

The individual profiles of O₂, N₂ and CO₂ concentration, developed in the Current zone on initial growth, could not be explained solely by the dependence of the apparent segregation coefficient on the balance between the freezing rate and diffusion across the boundary layer. We suggest that these profiles originated from a double kinetic effect, linked with bubble nucleation, that combines diffusion across the boundary layer with diffusion from inside that layer towards the bubbles and vice versa. In the absence of biological activity, this process would result in a transition between solubility values in sea water and atmospheric values in the first decimetre of the sea-ice cover, excluding the skeletal layer. Sampling the skeletal layer is indeed likely to shift gas composition toward water-solubility values, given the fast in situ freezing of sea water in this highly porous medium. It should be stressed that the rationale for the above relies on the assumption that the bacterial CO₂ input at the ice–water interface was constant, which is a major unknown. It is, however, unlikely that the drop in CO₂ concentrations at intermediate depth in the Current zone corresponded to a decrease in bacterial activity. It would indeed be difficult to explain with the same scenario the simultaneous increase in total gas content and decrease in the O₂/N₂ ratio.

Warming the whole ice cover to isothermal at −2°C resulted in an impoverishment of the total gas content; melting ice on the walls of the channels eventually induced redissolution of the gas phase; and channel connectivity allowed diffusional exchanges with the atmosphere above and the water below.

Recooling of the ice cover homogenized the profiles and considerably increased the total gas content on rapid freezing of the brines after exchange with saturated reservoir water during the warming phase. Bubble nucleation resumed in the process, as was also shown by the decreasing O₂/N₂ ratio.

Although the experimental setting partially failed to deliver reference background levels (in the absence of biological activity) for sea ice in natural environments, the dataset proved to be useful in demonstrating the processes involved in the acquisition and alteration of the gas properties of sea ice on a typical growth–warming–cooling cycle. Furthermore, it has highlighted some limitations of tank studies on sea-ice growth of which we were previously unaware. In particular, it is clear that when semi-quantitative studies of biological processes in experimental sea ice are carried out, extreme care will need to be taken in preparing the reservoir water to avoid biases from “parasitic” geochemical or biological processes.