Introduction
According to the overall trend of increasing air temperatures in High Asia over several decades, most glaciers on the Tibetan Plateau (TP; Reference YaoYao and others, 2012) and in the Himalaya (Reference BolchBolch and others, 2012) are retreating. Nonetheless, regional patterns are contrasting in some cases (Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others, 2012, Reference Kääb, Treichler, Nuth and Berthier2015; Reference Neckel, Kropacek, Bolch and HochschildNeckel and others, 2014). Due to their remoteness, their high altitude and the harsh climatic conditions, little is known about the state of ice caps on the TP. However, understanding the influence of the spatial and temporal heterogeneity of climate and climate variability on glacier melt requires analysis of the surface energy balance (SEB) and mass balance (MB). Due to its large area and remote location, Purogangri ice cap (PIC) was chosen as one benchmark region of the research project ‘Variability and Trends in Water Balance Components of Benchmark Drainage Basins on the Tibetan Plateau (WET)’ which aims to combine numerical models and satellite observations for the monitoring of relevant atmospheric, glaciological and hydrological variables on the TP. In a previous study, Reference Neckel, Braun, Kropacek and HochschildNeckel and others (2013) estimated the geodetic MB from TanDEM-X data acquired in 2012 and SRTM-X data acquired in 2000. Reference Spieß, Maussion, Möller, Scherer and SchneiderSpieß and others (2015) estimated changes in the snowline and equilibrium-line altitude (ELA) between 2001 and 2011 from data acquired by the Moderate Resolution Imaging Spectroradiometer (MODIS; Reference Hall, Riggs, Salomonson, DiGirolamo and BayrHall and others, 2002).
Ground observations at PIC are scarce. Reference ThompsonThompson and others (2006) collected two ice cores from PIC to reconstruct the palaeoclimate. Reference LeiLei and others (2012) attempted to relate the lake-level rise of Linggo Co (40 km west of PIC) to glacier retreat at PIC based on remote-sensing techniques and field investigations.
In this study we apply a steady-state physically based ‘COupled Snowpack and Ice surface energy and MAss balance model’ (COSIMA; Reference HuintjesHuintjes and others, 2015) to the whole PIC to overcome the need for a site-specific calibration as is the case for, for example, empirical index models. The model is forced by high-resolution atmospheric model data from the High Asia Refined analysis (HAR; Reference Maussion, Scherer, Mölg, Collier, Curio and FinkelnburgMaussion and others, 2014). We analyse the derived SEB and MB components to understand the influence of atmospheric conditions on PIC. Furthermore, we focus on the question whether the surface elevation change and MB over the past decade at PIC can be reproduced without any observational data from the ground. The results of Reference Neckel, Braun, Kropacek and HochschildNeckel and others (2013) and Spieß and others (2014) are used to evaluate the performance of COSIMA. When comparing COSIMA results with remote-sensing based calculations we focus on surface-elevation changes because the common method to apply an average ice density for the conversion from geodetic height changes to mass changes introduces uncertainties (e.g. Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others, 2012; Reference Neckel, Braun, Kropacek and HochschildNeckel and others, 2013). Surface-elevation changes are related to glacier MB and glacier flow (e.g. Reference FischerFischer, 2011). Glacier flow balances the elevation changes through accumulation (glacier thickening) and ablation (glacier thinning; Reference PatersonPaterson, 1994). At glaciers with high surface velocities a steady-state SEB/MB model like COSIMA will produce a steepening of the surface elevation gradient over time, with increased glacier thickening in the accumulation areas and increased glacier thinning in the ablation areas. Thus, results from steady-state SEB/MB models can only be compared directly to geodetic surface elevation changes when glacier flow is close to zero. In order to show that surface velocities are small at PIC, data of the European Remote-sensing Satellites (ERS-1 and -2) are analysed.
Study Area
PIC is the largest ice cap on the TP, covering an area of ∼400 km2 (Reference LeiLei and others, 2012; Reference Neckel, Braun, Kropacek and HochschildNeckel and others, 2013). It consists of 13 glacier catchments (Fig. 1) and its altitude ranges between 5350 and 6370 m a.s.l. The ice cap is located in the north-central part of the TP, characterized by a cold and relatively dry continental climate. Climate conditions at PIC are derived from the HAR dataset (Fig. 2). For detailed information on HAR we refer to the following section. Winter months at PIC are dominated by strong westerly winds, whereas wind directions in summer show the influence of the Indian summer monsoon. Moreover, the effect of the northward shift of the westerly jet in spring (Reference Schiemann, Lüthi and SchärSchiemann and others, 2009) is evident from highest wind speeds and significant precipitation amounts in spring (Fig. 2). However, precipitation amounts associated with monsoonal air masses regularly dominate the annual cycle. Around 70% of the annual total falls between May and September. Including March and April this proportion rises to 86%. Due to the low air temperatures (Fig. 2) all spring precipitation falls as snow. According to Reference Maussion, Scherer, Mölg, Collier, Curio and FinkelnburgMaussion and others (2014), PIC is therefore a mixed ‘spring- and summer-accumulation type’ glacier. Daily mean air temperature generated by HAR generally rises above zero from June to September in the lower regions of PIC, whereas positive daily mean temperatures in the middle parts are limited to July and August. Shortwave incoming radiation reaches its maximum around May and decreases in summer, when monsoonal cloud cover increases. The monsoon season is associated with annual maxima in air pressure and decreasing wind speeds associated with the thermally induced high-pressure system in the upper troposphere over the southern TP (Reference Boos and KuangBoos and Kuang, 2010; Fig. 2).

Fig. 1. InSAR-derived line-of-sight (LOS) displacement of Purogangri ice cap (PIC). Look direction of the satellite is indicated by the black arrow. Glacier outlines (solid black lines) are from 2000 (Reference Neckel, Braun, Kropacek and HochschildNeckel and others, 2013). Numbers indicate single glaciers. Digitized glacier centre lines are shown in solid and dashed red. For profiles of selected glaciers (solid red lines) see Figure 7. The dashed white box indicates the location of the HAR gridcell (10 km × 10 km) used to force COSIMA. Ice-core drill sites of the Byrd Polar Research Center (Reference ThompsonThompson and others, 2006) are shown as yellow triangles. Figure 5 shows contours.

Fig. 2. Monthly means or sums (precipitation) of meteorological variables at the highest (5734 m a.s.l) atmospheric gridcell containing PIC (Fig. 1), October 2000–September 2011. Dashed lines indicate the beginning of April and October. COSIMA is forced with hourly values of this gridcell. The scaling factor of 0.56 is already applied on precipitation amounts.
Data
High Asia Refined analysis (HAR)
For the simulation of SEB and MB for PIC between October 2000 and 2011 we use hourly HAR data (Reference Maussion, Scherer, Mölg, Collier, Curio and FinkelnburgMaussion and others, 2014) to force the distributed COSIMA. The HAR is a high-resolution atmospheric dataset generated using the advanced research version of the Weather Research and Forecasting (WRF-ARW) model. The WRF model is forced with the GFS operational model global tropospheric analyses from the US National Centers for Environmental Prediction (NCEP) (final analysis (FNL); dataset ds083.2; Reference Maussion, Scherer, Mölg, Collier, Curio and FinkelnburgMaussion and others, 2014). The HAR spans a period of >11 years (October 2000 to December 2011) and comprises a 30 km and a 10 km resolution dataset. The latter covers most parts of High Asia including the TP (Reference Maussion, Scherer, Mölg, Collier, Curio and FinkelnburgMaussion and others, 2014) and is used within this study. Incoming shortwave radiation (W m−2), air temperature (°C; 2 m), relative humidity (%; 2 m), air pressure (hPa), wind speed (m s−1; 10 m), all-phase precipitation (mm) and cloud cover fraction are extracted from the uppermost HAR gridcell located on the ice cap (Figs 1 and 2). The cloud cover fraction is determined from the occurrence of clouds around the HAR glacier gridcell. A HAR gridcell is considered cloudy when the cloud, water and ice in at least one atmospheric level exceeds a threshold value of 10−6 kg kg−1 (CLDFRA variable in the WRF model; Reference Skamarock and KlempSkamarock and Klemp, 2008). The cloud cover fraction for each glacier gridcell is the ratio of cloudy gridpoints to all gridpoints found within a field of view of radius 50 km.
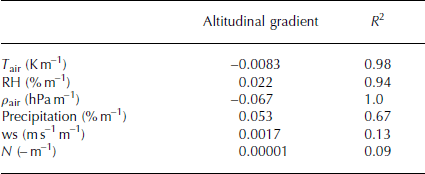
Altitudinal gradients of most input parameters are required to run the distributed model for the total ice cap (Reference HuintjesHuintjes and others, 2015). The altitude dependency is calculated from the 15 HAR gridcells contributing to PIC. The altitude of the gridcells ranges from 5.366 to 5.734 m a.s.l. Resulting gradients are −0.0083 K m−1 for air temperature (T air), 0.022% m−1 for relative humidity (RH), −0.067 hPa m−1 for air pressure (ρ air) and 4 × 10−5 mm m−1 or 0.053% m−1 for precipitation (Table 1). The altitude dependency of wind speed (ws) and cloud cover fraction (N) is not significant. Considering the spatial extent of the ice cap, vertical gradients of, for example, ws may differ depending on the exposition to, for example, main wind direction. In this study we do not account for this and apply no altitudinal gradient for ws and N but use constant hourly values for the entire ice cap.
Table 1. Altitudinal gradients for COSIMA input parameters determined from 15 HAR gridcells including correlation coefficients. T air: air temperature; RH: relative humidity; ρ air: air pressure; ws: wind speed; N: cloud cover fraction
From in situ measurements at Zhadang glacier, southeastern TP, Reference Mölg, Maussion, Yang and SchererMölg and others (2012) and Reference HuintjesHuintjes and others (2015) revealed that the HAR very likely overestimates total precipitation amounts. Reference Mölg, Maussion, Yang and SchererMölg and others (2012) applied a precipitation scaling factor (psf) of 0.56 to HAR precipitation to correct for possible HAR overestimation, as well as for measurement errors from the precipitation gauge and/or the loss of snow on the glacier by wind drift (Reference HuintjesHuintjes and others, 2015). The psf was successfully applied in the HAR-forced COSIMA runs 2001–11 for Zhadang glacier (Reference HuintjesHuintjes and others, 2015). Although there is a lack of precipitation measurements around PIC, we assume that the scaling factor determined at Zhadang glacier is also applicable on HAR precipitation at PIC. The resulting mean annual precipitation total of 377 mm is reasonable compared to values determined by Reference LeiLei and others (2012) around Linggo Co (150–200 mm a−1), 40 km west of the ice cap. However, precipitation amounts can vary significantly over a distance of 40 km. Therefore, these values can only be considered a rough estimate.
Remote sensing
At any specific point on a glacier, surface-elevation changes are related to glacier MB and glacier flow (e.g. Reference FischerFischer, 2011). In order to show that glacier flow is near to zero at PIC, surface velocities were derived from two passes of the ERS-1/-2 satellites. The data were acquired on 14–15 January 1996 on a descending satellite pass. Both satellites were separated by a 116 m perpendicular baseline. This satellite configuration (i.e. short temporal and spatial baseline) is preferable for deriving glacier velocities by means of interferometric synthetic aperture radar (InSAR).
Further, two digital elevation models (DEMs) were employed in this study to obtain information about surface elevation and topography. Both DEMs were acquired during the Shuttle Radar Topography Mission (SRTM) in February 2000 (Reference Rabus, Eineder, Roth and BamlerRabus and others, 2003; Reference FarrFarr and others, 2007). One DEM was acquired in C-band (hereinafter SRTM-C DEM) with a swath width of 225 km while the other DEM was acquired in X-band with a swath width of 45 km. Due to the smaller swath width of the latter, large data gaps are present in the X-band DEM (hereinafter SRTM-X DEM; Reference Rabus, Eineder, Roth and BamlerRabus and others, 2003). Fortunately, 90% of PIC is covered by the X-band DEM, which comes at a grid spacing of 1 arcsec (∼30 m on the ground; Reference FarrFarr and others, 2007). The SRTM-C DEM is sampled to a grid spacing of 3 arcsec ( 90 m on the ground; Reference FarrFarr and others, 2007) and covers the whole ice cap. While the SRTM-C DEM is referenced to the Earth Gravitational Model 1996 (EGM96) geoid, the SRTM-X DEM is referenced to the World Geodetic System 1984 (WGS84) ellipsoid. The mean and standard deviation of the EGM96 geoid is estimated to −37.57 ± 0.17 m for the area of the ice cap. This difference has to be considered when comparing elevations of both DEMs.
The distributed COSIMA runs on the SRTM-C DEM resampled to 450 m resolution. The DEM pixels are resampled from 90 m to 450 m to reduce computation time. The size of the ice cap is kept constant throughout the modelling period and is based on the 2000 glacier extent (Reference Neckel, Braun, Kropacek and HochschildNeckel and others, 2013). As the area change between 2000 and 2012 is small (−1.81 ± 0.04 km2; Reference Neckel, Braun, Kropacek and HochschildNeckel and others, 2013) the influence is negligible.
Methods
Surface velocities
Surface velocities were calculated by repeat-pass InSAR, employing the GAMMA SAR and interferometric processing software (Reference Werner, Wegmüller, Strozzi and WiesmannWerner and others, 2000). For this, an interferogram was calculated from the two descending ERS-1/-2 passes described in the Data section. As the interferometric phase of a repeat-pass acquisition is a mixture of the surface displacement between the dates of data acquisition and the surface topography, a ‘topography-only’ interferogram was simulated from the SRTM-X DEM and subtracted from the ERS interferogram. This way we received a ‘motion-only’ interferogram, representing the surface displacement in the line of sight (LOS) of the ERS SAR sensor (e.g. Reference Joughin, Kwok and FahnestockJoughin and others, 1996). After unwrapping the interferogram via the GAMMAs MCF algorithm (Reference CostantiniCostantini, 1998) an artificial linear phase ramp was detected and removed from the interferogram. Absolute surface velocities were calculated from the relative interferometric phase using a ‘no-motion’ seedpoint in a flat off-glacier region of the interferogram assuming negligible surface displacement in off-glacier regions. The final one-dimensional velocity field was then translated into ground range and geocoded via the SRTM-X DEM.
In order to show glacier surface velocities along selected centre lines, centre lines were digitized manually following the identification scheme described in Reference Kienholz, Rich, Arendt and HockKienholz and others (2014).
COSIMA model
COSIMA is described in detail in Reference HuintjesHuintjes and others (2015), so we only provide a brief summary. The physically based COSIMA couples a SEB to a multilayer subsurface snow and ice model. COSIMA consists of several modules for, for example, solving the heat equation, calculating surface temperature and energy balance, calculating meltwater percolation, refreezing and densification (Reference HuintjesHuintjes and others, 2015). The model computes the MB at an hourly time step as the sum of mass gains by solid precipitation and refreezing of liquid water in the snowpack, and of mass losses by surface melt, subsurface melt and sublimation (Reference HuintjesHuintjes and others, 2015). The SEB equation governs the calculation of the mass fluxes:
The SEB consists of incoming shortwave radiation (SWin), surface albedo ( α), incoming and outgoing longwave radiation (LWin and LWout), the turbulent sensible and latent heat flux (Q sens and Q lat) and the ground heat flux (Q G). Q G consists of energy fluxes of heat conduction (Q C) and penetrating shortwave radiation (Q PS). Q PS is always negative because it transfers energy from the glacier surface into the snow or ice. Heat flux from liquid precipitation is neglected. Energy fluxes towards the surface have a positive sign. The resulting flux F is equal to Q melt only if the surface temperature (T s) is at the melting point (273.15 K). T s is calculated iteratively through Eqn (1) from the energy available at the surface. In order to downscale HAR SWin (10 km) to the COSIMA model resolution (450 m) we first derive potential SWin at any pixel of the DEM (x,y; SWin,x,y,pot) from a radiation model after Reference Kumar, Skidmore and KnowlesKumar and others (1997) that computes clear-sky direct and diffuse SWin in response to geographical position and terrain effects (Reference HuintjesHuintjes and others, 2015). SWin,x,y,pot does not consider the effect of clouds. The radiation model is independent of COSIMA and runs on the identical DEM (SRTM-C DEM; 450 m). For each time step, we average SWin,x,y,pot over all DEM pixels that lie within the uppermost HAR gridcell (i,j) that contributes to the ice cap (Fig. 1; SWin,i_HAR,j_HAR,pot). Thus, SWin from HAR and from the radiation model are available for the same area. Then we calculate the ratio of SWin,x,y,pot to SWin,i_HAR,j_HAR,pot for every DEM pixel (rix,y ). Finally, HAR SWin (SWin,i_HAR,j_HAR) is downscaled to the DEM by
SWin,x,y thus includes effects from both cloud coverage and terrain shading and serves as input for COSIMA (Reference HuintjesHuintjes and others, 2015).
The subsurface model of COSIMA uses a vertical layer structure that consists of layers with an equal thickness of 0.2 m (Reference HuintjesHuintjes and others, 2015). Each subsurface layer is characterized by a temperature, density, liquid water content and depth. The initial temperature profile is linearly interpolated between T air (=T s) and a constant bottom temperature of −5°C adopted from measurements at Zhadang glacier (Reference HuintjesHuintjes and others, 2015). The initial water content is assumed to be zero. The density profile of the initial snowpack is calculated by a linear interpolation between 250 kg m−3 for the uppermost snow layer and 550 kg m−3 for the lowermost snow layer as estimated from the snow pits at Zhadang glacier. Below the snowpack, glacier ice with a constant density of 917 kg m−3 is assumed (Reference HuintjesHuintjes and others, 2015). In the first year of simulation, COSIMA is initialized assuming a snow depth that increases linearly from 0 cm at the ELA to 20 cm in the uppermost regions. On average, the ELA is estimated between 5700 and 5750 m a.s.l. (Reference YaoYao and others, 2012; Reference Neckel, Braun, Kropacek and HochschildNeckel and others, 2013). We chose these initial conditions because studies on surface-elevation changes of PIC between 1974 and 2012 found a surface lowering in the glacier tongue regions whereas the ice cap thickens in the interior (Reference LeiLei and others, 2012; Reference Neckel, Braun, Kropacek and HochschildNeckel others, 2013). This thickening implies that the uppermost regions are permanently covered by snow.
The HAR spans a period from October 2000 to December 2011. However, COSIMA results within the first months suffer from errors that stem from the spin-up time of the model. Therefore, only model output for the MB years 2001–11 is discussed in the following.
Uncertainty assessment
COSIMA has been verified at Zhadang glacier for the point location as well as for the spatially distributed model run (Reference HuintjesHuintjes and others, 2015). Since no atmospheric or glaciological in situ measurements are available for PIC, the structure of COSIMA, the applied parameterizations, constants and assumptions set for Zhadang glacier remain unchanged. This introduces an uncertainty that can hardly be quantified. We address uncertainties in the subsurface temperature, water content and snow density by including a model spin-up period of 1 year. Mölg and others (Reference Mölg, Maussion, Yang and Scherer2012, Reference Mölg, Maussion and Scherer2014) conducted extensive uncertainty and sensitivity estimations for a point MB model of similar structure at Zhadang glacier. The authors stress the importance of incorporating stability corrections of turbulent fluxes, snow compaction, refreezing and subsurface melt. In the COSIMA model these processes are accounted for (Reference HuintjesHuintjes and others, 2015). Through the evaluation of the results from COSIMA against multi-annual MB measurements using the glaciological method Reference HuintjesHuintjes and others (2015) determined a glacier-wide model uncertainty of 600 kg m−2 a−1. Uncertainty at PIC is assumed to be larger because COSIMA cannot be calibrated towards observations, so model settings derived from Zhadang glacier remain unchanged.
To account for uncertainties in total precipitation amounts and to obtain a model uncertainty for further MB calculations at PIC, we perform three model runs with varying precipitation-scaling factors (0.56 ± 0.25). The model run with a psf of 0.56 is called the reference run. Then HAR precipitation amounts are decreased by 25% (psf 0.31) and increased by 25% (psf 0.81) relative to the reference run. The lower psf (0.31) leads to a mean annual precipitation total of 209 mm at the highest HAR gridcell (Fig. 1). The application of the higher psf (0.81) results in a mean annual precipitation sum of 545 mm a−1. It is very likely that the uncertainty in the SEB and MB results is dominated by the precipitation scaling.
Results
Surface velocities
LOS surface velocities range from no motion at ice divides to >0.05 m d−1 for glacier 7 in the eastern part of the ice cap. For the elevation band between 5700 and 5800 m a.s.l. (i.e. near the approximate ELA) we calculated a mean surface velocity and standard deviation of 0.026 ± 0.012 m d−1 along the eight centre lines shown in Figure 1. Surface velocities of four selected centre lines are shown in Figure 3. As the centre lines are almost in the LOS direction of the satellite, surface velocities along the profiles are assumed to be representative for the actual surface velocities. Peak velocities reach from 0.02 to 0.05 m d−1 at an elevation between 5950 and 6100 m a.s.l. for the selected profiles.

Fig. 3. Centre-line velocities and elevations of four selected glaciers. Centre lines are in the approximate LOS direction of the satellite and are indicated as solid red lines in Figure 1.
Surface energy and mass balance
Annual cycles of glacier-wide mean monthly SEB and MB components at PIC as calculated by COSIMA for the reference run for the period 2001–11 are illustrated in Figure 4. Unless otherwise stated, the given energy and mass fluxes refer to the reference run. In both the summer (s: April–September) and winter seasons (w: October–March), SWin (s: +292 W m−2; w: +190 W m−2) and LWin (s: +234 W m−2; w: +168 W m−2) dominate the energy input over the considered period, followed by Q sens (s: +26 W m−2; w: +30 W m−2). Q G is an energy source in winter (+3 W m−2). Energy is removed from the glacier surface by LWout (s: −268 W m−2; w: –212 W m−2), Q lat (s: −24 W m−2; w: −21 W m−2) and Q melt (s: −3 W m−2; w: 0 W m−2). Outgoing shortwave radiation (SWout; s: −253 W m−2; w: −160 W m−2) is shortwave radiation reflected by the surface, and thus unavailable for temperature increase or melt. Q G is negative in summer (−6 W m−2). Net shortwave radiation (SWnet; s: +39 W m−2; w: +30 W m−2) is the most important energy source for PIC in summer. In winter SWnet and Q sens are of equal importance for energy input. Similar patterns of energy fluxes are observed or simulated over other glaciers in High Asia, such as Zhadang glacier (Reference Mölg, Maussion, Yang and SchererMölg and others, 2012; Reference HuintjesHuintjes and others, 2015) and Baltoro glacier, Karakoram (Reference Collier, Mölg, Maussion, Scherer, Mayer and BushCollier and others, 2014), and elsewhere, such as Storbreen, Norway (Reference Andreassen, Van den Broeke, Giesen and OerlemansAndreassen and others, 2008), glaciers at Kilimanjaro (Reference Mölg and HardyMölg and Hardy, 2004) and glaciers in Greenland (Reference Van den Broeke, Smeets and Van de WalVan den Broeke and others, 2011). Figure 4a shows that the period between December and February is characterized by lowest values of SWnet. This regular pattern is caused by the seasonal cycle of the position of the sun and is strengthened by a high albedo resulting from small precipitation amounts but frequent precipitation events during winter. The seasonal cycle of net longwave radiation (LWnet) is less pronounced than that of SWnet (Fig. 4a). The average annual cycle of LWnet reveals that LWnet plays a smaller role as energy sink in summer than in winter. This can be explained by the seasonal patterns of LWin and LWout. LWin is higher in summer depending on T air, N and water vapour pressure. LWout reaches largest negative values in summer depending on T s. Averaged over the whole period, Q C is very small. In winter, when the surface is colder than the underlying snow layers, Q C becomes positive. In spring, Q C is a significant energy sink (Fig. 4a), when the surface warms but subsurface layers are still cold from the winter season. Q PS is always negative, with larger values when is low and SWnet is large. The generally dry conditions on the TP lead to negative Q lat and significant sublimation (Fig. 4) with largest values in spring and autumn when RH is small and high wind speeds favour turbulence (Fig. 2). Generally, monthly means of Q sens and Q lat are of opposite sign and sometimes cancel each other out. Absolute values of Q sens are slightly larger than Q lat, especially in winter when T s decreases. In summer daily mean T air can rise to 11°C, increasing the importance of Q sens for surface melt (see also Reference Braun and SchneiderBraun and Schneider, 2000). Nevertheless, mass loss through sublimation plays an important role for PIC because surface melt is small (Fig. 4b). Surface melt occurs dominantly in July–September when LWnet, Q lat and Q C cannot compensate the energy input through SWnet and Q sens (Fig. 4a).

Fig. 4. Glacier-wide monthly (a) SEB components and (b) MB components from October 2001 to September 2011 at PIC (reference run). Dashed lines indicate the beginning of April and October.
The glacier-wide annual mean MB estimate of the reference run for the period 2001–11 is −44 kg m−2 a−1 (Table 2). The average annual ELA is 5790 m a.s.l. The surface elevation change is calculated at each time step within COSIMA from the derived MB without refreezing and by applying the respective density of the snow or ice. Surface-elevation change over the total ice cap is −0.58 m. Figure 5 shows that glacier thinning occurred in the lower parts of the ice cap while a slight thickening appears in the upper regions around 6000 m a.s.l. Uncertainties in the conversion from mass changes to height changes are introduced through the initial temperature and density profiles and density changes calculated within COSIMA. The update of the profiles with each time step mostly depends on simulated snowpack, surface and subsurface melt, and refreezing (Reference HuintjesHuintjes and others, 2015). At Zhadang glacier, simulated density profiles and in situ measurements are in good agreement. However, simulated density profiles at PIC cannot be evaluated because in situ measurements are not available. Thus, COSIMA is validated against satellite-derived surface elevation changes. Results are discussed in the following section.

Fig. 5. Spatial distribution of modelled surface height change of PIC for the reference run of COSIMA, 2001–11. Contours (m) are at 200 m spacing.
Table 2. Glacier-wide mean annual mass-balance components over the period October 2001–September 2011 for three different precipitation scaling factors (psf) at PIC
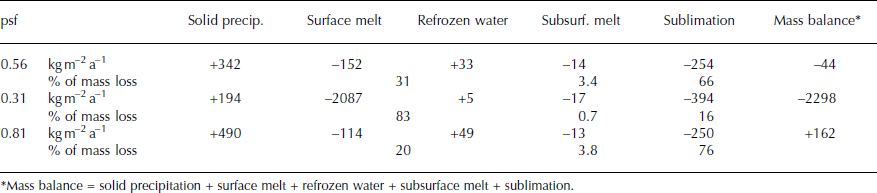
In general, sublimation is the largest factor in glacier-wide mass loss (−254 kg m−2 a−1), followed by surface melt (−152 kg m−2 a−1), and clearly dominates ablation in winter, spring and autumn, when air temperatures are <0°C and surface melt is absent (Figs 2 and 4b). Subsurface melt (−14 kg m−2 a−1) is insignificant. Solid precipitation (+342 kg m−2 a−1) and refreezing (+33 kg m−2 a−1) contribute to mass gain of the glacier. Maximum snowfall amounts occur in spring and summer (Fig. 4b). Absolute amounts of refreezing at PIC are largest in summer, when meltwater is produced at the surface and percolates through the snow layers that are still cold from the winter and spring seasons. Air temperatures at PIC are <0°C until June (Fig. 2). Therefore, subsurface temperatures above the ELA are well below the melting point throughout the summer and allow the refreezing of considerable amounts of meltwater. The reference run implies that 20% of the surface and subsurface meltwater refreezes within the snowpack between 2001 and 2011. The proportion exceeds 70% from November until May. However, absolute amounts are small during this period because surface melt is nearly absent. Locally the absolute amount of refreezing is largest near the ELA where decent amounts of surface melt, low temperatures and a sufficient thickness of the snowpack are present.
Table 3 lists the absolute and relative contributions of the energy flux components to the overall energy turnover for the considered period 2001–11. The energy turnover is calculated as the sum of energy fluxes in absolute values. For the reference run, LWnet accounted for 30%, followed by SWnet (28%), Q sens (21%), Q lat (17%) and Q G (4%). The relative contribution of SWnet and LWnet, as well as of Q sens and Q lat, to the total energy budget is nearly balanced. Therefore, simulated Q melt is generally low at PIC over the period 2001–11 (Table 1). Low Q melt results in low surface melt and only slightly negative MB (Table 2). Over the total simulation period, effective melt (surface melt + subsurface melt + refreezing) accounts for only 34%, and sublimation for 66%, of the total mass loss (Table 2).
Table 3. Mean values of energy-flux components as modelled for October 2001–September 2011 for three different psf, with proportional contribution to total energy flux at PIC
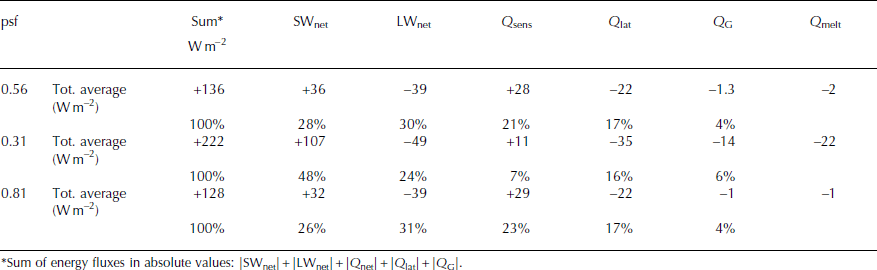
The importance of the various SEB and MB components to surface melt and MB differs greatly within the three model runs. With decreasing precipitation compared to the reference run (psf 0.31) the relative contribution of SWnet to the total energy flux increases from 28% to 48% through decreasing (Table 3). More energy from SWnet is available at the glacier surface, which increases surface melt considerably (Tables 2 and 3). In this case, the MB becomes more negative and is more closely linked to surface melt because the contribution of effective melt to total mass loss increases to 84% (Table 2). However, increasing SWnet also yields increasing surface temperature which in turn results in larger negative LWnet through larger LWout, smaller positive Q sens and higher negative Q lat. The latter increases mass loss through sublimation. Decreasing snow accumulation and increasing mass loss from surface melt further increase overall mass loss because in consequence the amount of refreezing decreases as well. Furthermore, the altitude of maximum amounts of refreezing rises. The feedback processes affect all regions of PIC besides the uppermost areas. In the uppermost regions differences in MB are solely forced by varying snowfall amounts. A precipitation increase relative to the reference run (psf 0.81) causes overall positive MB at PIC. However, the differences in the SEB and MB components of the reference run are less distinct than for a precipitation decrease by 25% (Tables 2 and 3). The differences in sensitivity of PIC to precipitation changes of ±25% can be explained through the link between solid precipitation and albedo. A precipitation increase has a strong effect only in the ablation area, where the difference between snow and ice albedo is large. In other words, only the lowest regions of PIC are affected by enhanced sensitivity through positive snow–albedo feedback for an increase in precipitation by 25%, whereas the inverse effect of snow–albedo feedback through a decrease in precipitation by 25% affects much larger areas. Therefore, compared to the reference run the overall mass-balance response in absolute values for a 25% increase in precipitation is smaller than for a 25% decrease in precipitation.
The accumulation area ratio (AAR) is the ratio of the accumulation area to the total area of a glacier (Reference CogleyCogley and others, 2011). On most glaciers the AAR correlates well with the climatic MB and is closely linked to the ELA (Reference CogleyCogley and others, 2011). The average AAR over a number of years indicates the state of the MB of a glacier when compared to the balanced-budget AAR (AAR0; Reference Dyurgerov, Meier and BahrDyurgerov and others, 2009; Reference CogleyCogley and others, 2011). The AAR0 is the AAR of a glacier with MB = 0. The relation between AAR and annual MB at PIC for the period 2001–11 for the reference run is visualized in Figure 6. At PIC the linear relationship between AAR and MB is significant (R 2 = 0.74; Fig. 6). Annual AAR varies between 28% in 2003/04 and 91% in 2002/03. For the total simulation period of the reference run the AAR is 58%. AAR0 is estimated to be 69%. The index α d after Reference Dyurgerov, Meier and BahrDyurgerov and others (2009) is a measure of the glacier’s displacement from its equilibrium and directly related to glacier area change. The index is defined as [(AAR – AAR0) AAR0 –1] × 100. For PIC α d is −16%. Thus, the ice cap has to decrease its area by 64 km2 to reach its equilibrium state for the climate conditions of the simulation period and according to the reference run.

Fig. 6. Relation between annual MB and AAR at PIC, 2001–11, for the COSIMA run with a psf of 0.56 (reference run). The AAR at MB = 0 denotes AAR0.
A precipitation decrease of 25% compared to the reference run results in an AAR of 1.5% and α d of −98%. This implies that PIC would have to decrease its area greatly to reach its equilibrium. Only 8 km2 would remain in steady state with contemporary climate forcing when assuming a psf of 0.31. A precipitation increase of 25% compared to the reference run leads to an AAR of 94% and α d of +36%. Thus, the ice cap would increase its area and advance in order to reach its equilibrium state when applying a precipitation scaling factor of 0.81. In conclusion, the ice cap is in imbalance according to the climate conditions of the reference run. Assuming precipitation changes by ±25% reveals that the feedback mechanisms within COSIMA result in a high sensitivity of the MB to the amount of precipitation input.
Discussion
In this study, glacier MB and surface-elevation changes of PIC are calculated by the HAR-driven COSIMA between 2001 and 2011. Furthermore, surface velocities were measured by ERS SAR interferometry. The surface velocities were calculated for a 1 day time interval in January. Therefore, velocities are given in m d−1 throughout the text. However, for comparison with other studies the mean surface velocity of 0.026 ± 0.012 m d−1 corresponds to 9.5 ± 4.4 m a−1. In a recent study Reference Yasuda and FuruyaYasuda and Furuya (2013) estimated seasonal surface velocities in the west Kunlun Shan, a mountain range ∼750 km northwest of PIC. For Duofeng glacier, a glacier with normal flow, they estimated average winter and summer velocities of 70 ± 7 and 92 ± 10 m a−1 respectively. However, for seven glaciers with stable terminus positions, Reference Yasuda and FuruyaYasuda and Furuya (2013) could not observe significant summer speed-up signals. As we do not have information about summer velocities at PIC, we can only speculate about summer speed-up, having in mind the results of Reference Yasuda and FuruyaYasuda and Furuya (2013). As terminus positions at PIC were stable between 2000 and 2012 (Reference Neckel, Braun, Kropacek and HochschildNeckel and others, 2013) and the ice cap is assumed to be cold-based (Reference ThompsonThompson and others, 2006) we assume no significant summer speed-up. Even a summer speed-up of ∼24%, as observed by Reference Yasuda and FuruyaYasuda and Furuya (2013) for Duofeng glacier, would result in a low average summer velocity of 11.8 ± 5.5 m a−1 for PIC. Considering the spatial resolution of COSIMA (450 m) the dynamical change due to derived small surface velocities can be neglected for simulations at decadal timescales when comparing COSIMA to remote-sensing derived surface-elevation changes. Overall, the modelled surface elevation change agrees well with a surface height change determined by Reference Neckel, Braun, Kropacek and HochschildNeckel and others (2013) for a similar time period. Respective surface height change of the three COSIMA runs with varying psf (0.56; 0.31; 0.81) over the total ice cap is −0.58 m (−26 m; +2.1 m) within this study and −0.59 ± 2.4 m in Reference Neckel, Braun, Kropacek and HochschildNeckel and others (2013). Figure 7a shows a comparison between the results of COSIMA within this study and the results from Reference Neckel, Braun, Kropacek and HochschildNeckel and others (2013). Employing an average ice density of 900 ± 17 kg m−3 for the conversion from height changes to mass changes, Reference Neckel, Braun, Kropacek and HochschildNeckel and others (2013) estimated an annual MB of −44 ± 15 kg m−2 a−1 for the period 2000–12. Results for both surface elevation change and MB are totally within the assumed uncertainty ranges and confirm the reasonable performance of COSIMA at PIC. Additionally, Reference Neckel, Braun, Kropacek and HochschildNeckel and others (2013) give surface-elevation changes and MB for the single glaciers of PIC (glacier identification numbers are shown in Fig. 1). The given values are again compared to the COSIMA calculations. The results for surface-elevation changes are shown in Table 4. For all glaciers the results from both studies are within the limits of uncertainties. Considering the spatial pattern of differences between both studies reveals a north–south gradient with positive discrepancies (COSIMA is more positive or less negative) for the southern glaciers and negative discrepancies (COSIMA is less positive or more negative) for the glaciers at the northern PIC (Table 4). Glaciers with highest negative differences between both studies concentrate in the northeast of PIC. Regional differences in the applied altitude-dependent gradients of HAR variables (Table 1) probably cause this pattern. In particular, local differences in the gradients of T air and precipitation would modify the spatial patterns. The location of PIC making it subject to the influence of the westerly jet suggests a connection between the observed differences and the glaciers’ exposition to the main wind direction. The highest regions of the ice cap are located in the northeast (Fig. 5). Assuming the formation of orographic-induced precipitation in the highest regions, it is very likely that enhanced precipitation occurs in this area and is shifted to the glaciers east of these summits by wind drift. The added mass leads to positive surface elevation changes on these glaciers as derived by Neckel and others (Reference Neckel, Braun, Kropacek and Hochschild2013; Table 4). Since in COSIMA an overall average precipitation lapse rate for the whole PIC is applied, COSIMA cannot resolve spatial patterns resulting from orographically induced precipitation. We speculate that this is why negative discrepancies between the surface-elevation changes calculated by COSIMA and those observed by Reference Neckel, Braun, Kropacek and HochschildNeckel and others (2013) are largest for the northeastern parts of PIC.

Fig. 7. (a) Histogram of differences of the surface elevation changes of PIC estimated from COSIMA for 2001–11 and from Reference Neckel, Braun, Kropacek and HochschildNeckel and others (2013) by means of differential synthetic aperture radar interferometry (DInSAR). (b) Ice-cap hypsometry in 100 m elevation bins. (c) Surfaceelevation changes of PIC as estimated from COSIMA for 2001–11 and from Neckel and others (Reference Neckel, Braun, Kropacek and Hochschild2013; TDX) are shown as a function of elevation; third-order polynomial fits are shown as solid lines.
Table 4. Mean surface-elevation changes estimated by COSIMA and by DInSAR (Reference Neckel, Braun, Kropacek and HochschildNeckel and others, 2013) for the single glaciers shown in Figure 1.
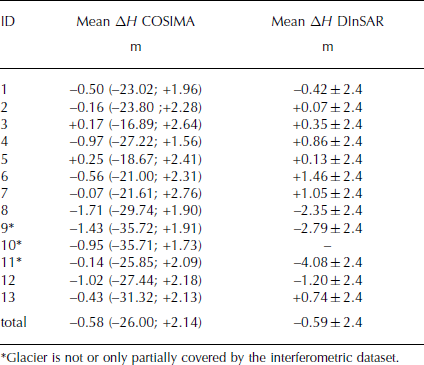
Figure 7c shows that glacier thinning occurred in the lower parts of the ice cap, while a slight thickening is found in the upper regions around 6000 m a.s.l. where a large proportion of the glacier area is located (Fig. 7b). This spatial pattern agrees well within the two datasets. The results of Reference Neckel, Braun, Kropacek and HochschildNeckel and others (2013) indicate a stronger thickening in some upper parts, which might be compensated through stronger thinning in the lowest regions compared to this study (Fig. 7a).
From the HAR data no simple altitude dependency of wind speed could be determined at PIC. However, it is very likely that the wind-induced redistribution of snow is important in the windward and leeward regions of the ice cap. Snowdrift influences the spatial variability of snow accumulation and ablation and also affects the energy budget of a snowpack (Reference Barral, Genthon, Trouvilliez, Brun and AmoryBarral and others, 2014). SEB/MB models that do not account for snowdrift are probably affected by a dry bias and overestimate surface sublimation because blowing snow enhances boundary layer sublimation (Reference Barral, Genthon, Trouvilliez, Brun and AmoryBarral and others, 2014). Moreover, the development of katabatic winds in the glacier boundary layer introduces an uncertainty in the modelled SEB and MB at PIC. These processes are not resolved in COSIMA. However, it has been observed that they modify the spatial pattern of near-surface air temperature and vapour pressure (e.g. Reference Oerlemans and GrisogonoOerlemans and Grisogono, 2002; Reference Shea and MooreShea and Moore, 2010) and therefore influence turbulent energy fluxes.
At glacier 7 Reference Neckel, Braun, Kropacek and HochschildNeckel and others (2013) found a thickening at the terminus and a thinning in the upper regions. They interpreted this result as an indication of a surging event. However, COSIMA is a steady-state SEB/MB model and can only be applied to compute climatic surface MB. The MB can only be translated into elevation changes if glacier dynamics are assumed to be negligible. The result from Reference Neckel, Braun, Kropacek and HochschildNeckel and others (2013) regarding glacier 7 suggests that this assumption may not hold for all outlet glaciers of PIC.
The annual ELA for PIC is calculated from the annual MB at the end of September. The average ELA for 2001–10 is 5790 m a.s.l. for the reference run. This value agrees with the altitude given by Reference Neckel, Braun, Kropacek and HochschildNeckel and others (2013) and Reference YaoYao and others (2012). Reference Spieß, Maussion, Möller, Scherer and SchneiderSpieß and others (2015) present annual ELA for PIC for a similar period derived from the evaluation of the MODIS snow product. Figure 8 shows the comparison between the annual ELA derived within this study and the results of Reference Spieß, Maussion, Möller, Scherer and SchneiderSpieß and others (2015). Generally, the interannual variability is similar (Fig. 8a). However, the ELA calculated from COSIMA shows larger amplitude of the interannual variability. Reference Spieß, Maussion, Möller, Scherer and SchneiderSpieß and others (2015) derived the annual ELA from the snowline at the end of the ablation season (July–September). Reference BrunBrun and others (2015) applied a similar method to a winter and a summer accumulation-type glacier in the Himalaya. They showed that the relation between MB and annual minimum albedo is poorly constrained for summer accumulation-type glaciers because accumulation and ablation occur simultaneously and a clear annual cycle of the albedo is missing. This might be the reason for the small interannual variability in Reference Spieß, Maussion, Möller, Scherer and SchneiderSpieß and others (2015). COSIMA results for PIC show that spring and summer accumulation keeps albedo high throughout the summer and causes a minimum of the albedo in October/November. Nevertheless, the discrepancies between this study and Reference Spieß, Maussion, Möller, Scherer and SchneiderSpieß and others (2015) are small concerning the coarse horizontal resolution of both datasets (Fig. 8b; MODIS: 500 m).

Fig. 8. Annual ELA at PIC, 2002–11. Comparison of the COSIMA results within this study and the results of Spieß and others (Reference Spieß, Maussion, Möller, Scherer and Schneider2015; MODIS). The uncertainty of COSIMA is calculated assuming different psf (0.56 ± 0.25) The uncertainty of COSIMA is calculated assuming different psf (0.56 ± 0.25)
The slightly negative MB as calculated within this study applying COSIMA is in agreement with several other studies. Gardelle and others (Reference Gardelle, Berthier, Arnaud and Kääb2013a,Reference Gardelle, Berthier, Arnaud and Kääbb), Reference GardnerGardner and others (2013), Reference Neckel, Kropacek, Bolch and HochschildNeckel and others (2014) and Reference YaoYao and others (2012) estimated almost balanced MB for glaciers and ice caps in the northwestern TP for a similar period. The findings contrast with those from the southern and eastern regions of the TP (Reference YaoYao and others, 2012; Reference Neckel, Kropacek, Bolch and HochschildNeckel and others, 2014) and the Himalaya (Reference BolchBolch and others, 2012; Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others, 2012; Reference Gardelle, Berthier, Arnaud and KääbGardelle and others, 2013a,Reference Gardnerb) where glacier MB are predominantly negative.
In 2000 two ice cores 118.4 and 214.7 m in length were drilled near the main ice divide of PIC (Reference ThompsonThompson and others, 2006). The locations of the drill sites are shown in Figure 1. Reference ThompsonThompson and others (2006) could not reveal a firn layer and suggest that the surface consists of bare ice caused by increasing T air. This finding implies that the drill sites are at or below the ELA, where no snow cover from previous years remains. Modelled surface-height changes within this study show that the ice-core drill sites are located close to the ELA in a region of stable to slightly positive mass gain (Fig. 5). Thus, model results of this study are in accordance with the observations of Reference ThompsonThompson and others (2006).
The application of COSIMA to PIC allows the interpretation of possible mechanisms for the glacier MB variability observed during the past decade. Due to the low air temperatures at PIC, all spring precipitation falls as snow, positively affecting glacier MB both through increasing accumulation and increasing albedo. The applied altitudinal lapse rates for air temperature and precipitation result in ∼86% of total HAR-simulated precipitation falling as snow between 2000 and 2011. Even in July and August the proportion is 73% on average. This is reasonable since large parts of PIC are located at higher altitudes between 5800 and 6000 m a.s.l. (Fig. 7c) above the ELA, experiencing low temperatures throughout the year (Fig. 2). As the positive effect of an early monsoon onset and associated snow accumulation on glacier MB could already be revealed at Zhadang glacier (Reference KangKang and others, 2009), regular spring accumulation associated with the northward shift of the westerly jet might be a reason for the observed below-average mass loss at PIC during 2001–11 in this study and by Reference Neckel, Braun, Kropacek and HochschildNeckel and others (2013). Spring accumulation causes an increase of the winter snowpack that can persist over a longer period during summer. This affects both accumulation and ablation of the ice cap through the snow–albedo feedback. The results also indicate that a significant amount of snowfall in spring is responsible for a relatively high surface albedo throughout the year. The high albedo of snow-covered areas restrains the energy supply from SWin to the glacier surface and thus affects most SEB/MB components through the influence on surface temperature. SWnet at PIC is small. The average surface energy gain by SWnet is smaller (average +35.6 W m−2; see Table 2) than the energy loss by LWnet (average −39.1 W m−2). Therefore, simulated Q melt and surface melt are generally low at PIC over the period 2001–11, resulting in small mass turnover and only slightly negative MB.
Conclusions
The distributed and physically based COSIMA (Reference HuintjesHuintjes and others, 2015) reproduces the surface elevation change and MB determined by remote-sensing techniques for PIC very well. The comparison with the MODIS-derived ELA leads to satisfying results even though interannual variability is larger within COSIMA compared to the remote-sensing data. The reason for this might be the weak annual albedo cycle at summer accumulation-type glaciers, which limits the relation between albedo and ELA at the end of the ablation period. The small surface velocities measured for the ice cap and its outlet glaciers support the application of a steady-state MB model with a spatial resolution of 450 m to estimate spatially distributed surface-elevation changes.
Comparing the derived SEB and MB components at PIC to other studies on glaciers in High Asia allows the conclusion that the results of this study are reasonable for a glacier in a cold and dry continental climate. Significant amounts of snowfall in spring and summer are responsible for a high surface albedo and low SWnet throughout the year. Thus, the contribution of SWnet to the total energy turnover during the simulation period (28%) is slightly lower than the contribution of LWnet (30%). The dry continental climate favours mass loss through sublimation, which accounts for >60% of the total mass loss of the ice cap. The analysis of the AAR and AAR0 for the varying precipitation scaling factors reveals that the area and volume of PIC are already in imbalance for the reference run. PIC would have to decrease its area by 16% to reach its equilibrium state for the climate conditions of the simulation period. Assuming precipitation changes by ±25% reveals that the feedback mechanisms within COSIMA result in a high sensitivity of the MB to the amount of precipitation input. Absolute values of energy and mass fluxes as well as their proportions to the total flux cannot be independently confirmed because in situ measurements are not available so far.
With respect to the thematic focus of this study, our results confirm that the applied COSIMA can reproduce the surface elevation change and MB of PIC over the last decade to a very high degree. The deviation from the mean surface elevation change derived by the interferometric approach (Reference Neckel, Braun, Kropacek and HochschildNeckel and others, 2013) is only 0.01 m even though discrepancies for individual outlet glaciers may be large. The mean annual MBs of this study (−44 kg m−2 a−1) and Reference Neckel, Braun, Kropacek and HochschildNeckel and others (2013) are similar. The experimental set-up behind this study (e.g. forcing of COSIMA by high-resolution atmospheric model data and the evaluation of the results of COSIMA by satellite-based data products) fulfils the expectation that significant results can be obtained independently of ground observations. The combination of numerical models and satellite observations yields convincing results for PIC and provides new possibilities for the analysis of glacier changes in data-sparse regions. However, the results are highly sensitive to the precipitation amount and thus to uncertainties in HAR precipitation data. Uncertainties in the timing of precipitation events and in the amount of precipitation from HAR are documented by Reference Maussion, Scherer, Finkelnburg, Richters, Yang and YaoMaussion and others (2011). The simulation of precipitation on the TP using an atmospheric model is not trivial because the atmospheric processes behind the generation of precipitation are complex. Furthermore, permanent weather stations on the TP are scarce and limited to lower altitudes (Reference Qin, Yang, Liang and GuoQin and others, 2009). These facts and the difficulty in measuring precipitation in mountainous regions in general limit the availability of validation data for atmospheric model output, resulting in large uncertainties of COSIMA output.
COSIMA is applied to PIC with parameter settings determined at Zhadang glacier because glaciological measurements are not available for the region of PIC itself. The evaluation of COSIMA results for PIC suggests that the parameter settings of Zhadang glacier are indeed also suitable for glacier SEB/MB modelling for the PIC region. However, generally it is advisable to adjust model settings based on observations from a nearby glacier. The validation of model results against glaciological or remote-sensing based field observations is a strict requirement due to the constraints and limitations inherent in the driving atmospheric reanalysis data and overall model deficiencies and model uncertainties.
Author Contributions
E.H. and N.N. designed the study and wrote the paper, E.H. and C.S. developed COSIMA, E.H. conducted the numerical modelling, N.N. performed the remote-sensing analysis and calculation of surface velocities, C.S. and V.H. helped in writing the paper. All authors continuously discussed the results and developed the analysis further.
Acknowledgements
This work was supported by the German Federal Ministry of Education and Research (BMBF) Programme ‘Central Asia – Monsoon Dynamics and Geo-Ecosystems’ (CAME) within the WET project (‘Variability and Trends in Water Balance Components of Benchmark Drainage Basins on the Tibetan Plateau’) under the codes 03G0804E, 03G0804D, and by the German Research Foundation (DFG) Priority Programme 1372, ‘Tibetan Plateau: Formation – Climate – Ecosystems’ within the DynRG-TiP (‘Dynamic Response of Glaciers on the Tibetan Plateau to Climate Change’) project under the codes SCHN 680/3-1, SCHN 680/3-2, SCHN 680/3-3. ERS data were provided by the European Space Agency through project 12538. SRTM data were provided by the US Geological Survey and the German Aerospace Center (DLR). We thank Dieter Scherer and Julia Curio (Technical University of Berlin) and Fabien Maussion (University of Innsbruck) for providing hourly HAR data. We thank two anonymous reviewers for valuable suggestions that improved the manuscript.














