Introduction
The nature of the flow field in marginal zones of polar ice sheets has been a subject of interest to glacial geologists since Reference ChamberlinChamberlin (1895) and Reference SalisburySalisbury (1896) first described ice-cored moraines on the Greenland ice sheet a few hundred meters up-glacier from the margin. No supraglacial source for the morainal debris was apparent, and in ice beneath the moraines, debris bands dipped steeply up-glacier. Thus it was inferred that the debris had been eroded from the bed and carried englacially until finally melting out at the surface (Fig. 1). These observations raise a problem of some importance in glacial geology: namely why is there clean ice beneath the dirty ice at the margin? This problem is discussed further in another paper (Hooke, in press), but the flow field and structure herein described place certain constraints on the solution.

Fig. 1. Schematic sketch of a glacier margin showing moraines and inferred distribution of dirt-bearing ice.
Field Observations and Measurements
Between 1969 and 1972 a detailed investigation of the margin of the Barnes Ice Cap, Baffin Island, Canada (Fig. 2) was undertaken. In the area studied, the margin is relatively straight and foliation is parallel to it, suggesting that flow is nearly two-dimensional and that complex flow patterns will not complicate the analysis.

Fig. 2. South dome of the Barnes Ice Cap showing location of study area.
The ice contains a perceptible but small (<c. 0.01 weight per cent) concentration of fine black silt. No effect of this debris on the flow or structure has been detected. There is no moraine present, but the geometry of the dirt bands is such that a moraine would form about 150 m up-glacier from the margin (Fig. 3A, cross-section) if the dirt concentration were higher and the debris coarser. Thus we are here considering an “initial condition” such as might exist prior to moraine development but with approximately the flow field necessary for moraine formation.

Fig. 3(a).

Fig. 3(b). Cross-section of the ice-cap margin showing velocity distribution in bore holes, foliation attitudes, fabric diagrams, and line drawings of crystal boundaries. Foliation traces are based on measured dips at the glacier surface and in the tunnel. No attempt has been made to identify in the tunnel a particular foliation plane observed at the surface. Fabric diagrams in the same row are from approximately the same foliation band. For location see Figure 2.
Because previous investigators (Reference GoldthwaitGoldthwait, 1951; Reference BishopBishop, 1957; Reference SouchezSouchez, 1967, Reference Souchez1971) have suggested the possibility that debris is carried to the surface in discrete shear zones, the structure and flow near the dirt bands and at about mid-depth in the glacier is of interest. A 125 m tunnel was excavated in this zone, and four bore holes were drilled through it (Fig. 3A). The tops of two of the bore holes, bo and bix, are in the tunnel. These two holes bottomed on rocks which are believed to be subglacial, as they lie on the plane defined by the outwash surface in front of the glacier.
All bore holes were cased with aluminum casing and the inclination of the casing was measured with an inclinometer (Series 200-B) rented from the Slope Indicator Company, Seattle, Washington, U.S.A. This inclinometer runs in tracks in the casing, and on separate runs down the hole first measures the E–W inclination of the casing and then the N–S inclination. A pendulum in the inclinometer moves across a resistance coil and the change in resistance is measured with a bridge circuit at the surface. The inclinometer can resolve changes in inclination of 0.001 radians.
Cores were obtained from the bore holes and from several locations near the glacier surface. Thin sections were cut from these cores and fabric diagrams were prepared (Fig. 3) using standard techniques (Reference LangwayLangway, 1958). Generally 100 c-axes were measured in each thin section; each c-axis measured was then assumed to be representative of the crystal orientation in one per cent of the volume of the core (Reference HookeHooke, 1969). Where crystals were large, several thin sections were cut from the same core segment. The interval between thin sections was always greater than 0.05 m, even though this meant measuring less than 100 c-axes in some of the shorter core segments. Photographs of the thin sections were taken through crossed polaroids and were used to prepare sketches showing crystal boundaries (Fig. 3).
In one wall of the tunnel two continuous lines of 68 wooden pegs each were set. The pegs are 1.6 m apart horizontally, and one line is 1.6 m vertically below the other. Thus any two adjacent pegs in the top row together with the corresponding pegs in the bottom row form a square strain net. Lengths of the sides and diagonals of each net were determined with a specially-designed telescoping bar graduated in millimeters. Conical pins on the ends of the bar fit snugly into conical holes in the wooden pegs. Lengths were recorded to the nearest 0.2 mm and were reproducible to about 0.3 mm. To estimate the error in measurement, the length of one diagonal of each net was calculated from the lengths of the four sides and the other diagonal. The closure error, or difference between the calculated and measured lengths of this diagonal, was distributed among the six dimensions. The median closure error was 0.4 mm.
On the glacier surface immediately above the tunnel, nineteen aluminum poles were set at 50 m intervals in a straight line perpendicular to the margin. Eight additional poles were offset laterally from the main line to form strain diamonds at four places. Distances between poles were chained to the nearest millimeter, and positions of the poles were determined by theodolite triangulation from a 1 567 m base line in front of the ice cap. Pole elevations were determined by leveling from a fixed point on a large boulder in front of the ice cap. Movement and strain data for selected poles are given in Table I and pole locations are shown in Figure 3A (cross-section). More detailed movement data are presented elsewhere (Hooke, in press).
Table I. Movement of selected poles in pole line B

Structure in the Margin
Foliation
As in most glaciers, the marginal zone of the Barnes Ice Cap has a banded or foliated appearance due to small changes in bubble or dirt content of the ice. This foliation generally dips up-glacier. At the glacier surface, dips decrease from about 50° within 75 m of the margin to less than 8° 450 m from the margin, and then remain close to 7° out to about 850 m. Dips also decrease rapidly with depth. For instance a dip of 38° was measured at the surface near pole 2 (Fig. 3), but in the tunnel, about 4 m vertically beneath pole 2, the dip was only 15°.
About 160 m from the margin there is a band of bubbly white ice with an outcrop width of approximately 30 m (Fig. 3). Due to its high bubble content, this ice is less dense than adjacent blue ice (Table II), and it deforms more rapidly (see velocity profile for hole b2, Fig. 3A). Contacts above and below the white ice band are sharp, and the band itself is continuous along the glacier margin. It is usually underlain by bluish-gray debris-bearing ice and overlain by 2 to 4 m of light-blue clean ice. The latter grades upward into darker bluishgray ice. The upper boundary of the white ice band tends to be ragged, with white folia 5 to 15 m wide branching from the main band and continuing parallel to it for a few hundred meters before grading into blue ice along strike. Englacial debris is only rarely seen in, or upglacier from, the white ice band. Preliminary oxygen isotope analyses suggest that this bubbly white ice is of Pleistocene age.
Table II. Density measurements

Fabric analyses
Ice above the white ice band is coarse grained and has a diamond-shaped four-maximum fabric (Fig. 3A, Sections A and B). The center of the diamond is generally offset from the pole to the foliation plane. Such fabrics are common in temperate glaciers (Reference KambKamb, 1959; Reference RigsbyRigsby, 1960) and have also been found in polar ice on the Greenland ice sheet (Reference RigsbyRigsby, 1960) and in Antaretica (Reference KizakiKizaki, 1969).
The white ice band and blue ice immediately beneath it are fine grained and have an unusually strong single maximum fabric with up to 72% of the c-axes in one per cent of the area of an equal-area net (Sections C, D, and E). Beneath this there is a layer of moderately coarse ice which has an elongate single maximum fabric at the surface and in hole b1 (Sections F and G), and a multiple maximum fabric in hole b2 (Section H). Sections F and G may be from a foliation horizon slightly above or below that of Section H so a lateral change in fabric along a foliation horizon is not demonstrated.
Beneath this moderately coarse ice, crystal size again decreases and fabrics have a single maximum with c-axes perpendicular to the foliation plane (Sections I, J, and K, Fig. 3B). This fine ice is underlain by several meters of moderately coarse ice with either an elongate single maximum or a two-maximum fabric (Sections L through P), Fine ice with a single-maximum fabric reappears at the base of the glacier (Sections Q and R).
Although the bands of fine ice alternate with bands of coarser ice in a seemingly random manner, there is a systematic change in fabric with increasing crystal size. Fabrics in fine ice (Section C) have a single very strong maximum. In somewhat coarser ice (Section G) the fabric pattern becomes elongate perpendicular to the direction of bubble elongation, which is presumed to lie in the plane of the foliation and to parallel the direction of shear in that plane. In slightly coarser ice (Section M) the elongate pattern splits into two distinct maxima, and with a further increase in crystal size a third (Section H) and finally a fourth (Section A) maximum appears. Reference KizakiKizaki (1969) has observed a similar systematic increase in the number of maxima with increasing crystal size in Antaretica. These last maxima are always weaker than the first two, and fall on a line approximately parallel to the direction of bubble elongation, characteristics which are also observed in multiple-maximum fabrics in temperate ice (Reference KambKamb, 1959, p. 1904).
Tunnel Strain-Net Analysis
In each of the tunnel strain nets, the strain-rate components ![]() , and
, and ![]() , and the principal strain-rates
, and the principal strain-rates ![]() and
and ![]() were calculated (Reference NyeNye, 1959). The x′ and y′ axes are directed down-glacier and vertically downward respectively. The effective strain-rate in each net was then determined by assuming that
were calculated (Reference NyeNye, 1959). The x′ and y′ axes are directed down-glacier and vertically downward respectively. The effective strain-rate in each net was then determined by assuming that ![]() was perpendicular to the tunnel wall, thus:
was perpendicular to the tunnel wall, thus: ![]() .
.
Reference Shreve and SharpShreve and Sharp (1970, p. 82–83) have shown that the constants n and A in Glen’s flow law, ![]() , can be determined if one knows the effective strain-rate, one component of the deviatoric-stress tensor (say τ
x′y′), and the corresponding component of the strain-rate tensor
, can be determined if one knows the effective strain-rate, one component of the deviatoric-stress tensor (say τ
x′y′), and the corresponding component of the strain-rate tensor ![]() .
. ![]() is then plotted against the viscosity,
is then plotted against the viscosity, ![]() , on a double logarithmic graph (Fig. 4). Straight lines on such a graph have a slope −(n−1)/n and intercept A/2.
, on a double logarithmic graph (Fig. 4). Straight lines on such a graph have a slope −(n−1)/n and intercept A/2.

Fig. 4. Relationship between viscosity and effective strain-rate. Arrowheads show values calculated from 1971 and 1972 survey and inclinometry data. Point near middle of arrow is calculated from 1970 and 1972 data, and perpendicular line at other end of arrow shows value from 1970 and 1971 data. Bend in arrow is due to fact that ablation rate was much less in second year than in first, so calculated shear stress decreased non-linearly through time, but variation in strain-rate was nearly linear.
Unfortunately, the stress distribution in a wedge-shaped glacier margin containing a tunnel is complex, and a solution to this problem is not available. Herein we will consider two approximate shear stress distributions:
and
where ρ is the ice density, g is the acceleration due to gravity, h is the vertical depth below the glacier surface, and τ 0 and m are empirically determined parameters which in the general case are functions of x′, the distance from the margin. Equation (1) is valid only where α is small (Reference NyeNye, 1967), so it is not strictly applicable near the margin. Equation (1a) is based on a slip line field analysis by Reference NyeNye (1967, p. 707), and is a reasonable approximation to the theoretical stress distribution in the margin of a perfectly plastic glacier. However, it contains two parameters, τ 0 and m, which must be determined empirically in the quasi-plastic case. Nye’s analysis indicates that τ 0 ⩽ k, the yield strength of the perfectly plastic glacier, and that m ⩽ 1. τ 0 → 0 and m → 1 as x′ increases (or α decreases), so Equation (1a) reduces to Equation (1) far from the margin.
Viscosities calculated using values of τ
x′y′ from Equation (1) are plotted in Figure 4 (dots without arrows). Near the tunnel entrance shear strain-rates are relatively high despite the low calculated shear stresses; thus calculated viscosities are low. However, where h exceeds 5 to 10 m, calculated viscosities are higher, and they decrease systematically with increasing ![]() . The rate of decrease indicates a value for n of 1.65±0.12. A ranges from about 4.5 to 5.5 bar year1/n
.
. The rate of decrease indicates a value for n of 1.65±0.12. A ranges from about 4.5 to 5.5 bar year1/n
.
The high shear strain-rates near the tunnel entrance suggest that the shear stress does not go to zero at the surface as suggested by Equation (1). This difficiency is not present in Equation (1a). However a rigorous determination of the four parameters τ 0, m, n, and A, including the variation in τ 0 and m with x′, is not mathematically straightforward. Furthermore, trial calculations suggested that the actual shear stress distribution, while obeying neither Equation (1) nor Equation (1a), is most readily studied by contrasting it with the distribution given by Equation (1) (Fig. 5C). Therefore this approach is adopted.
A value of 1.65 for n is reasonable for ice deforming under low stresses (τ x′y′ ⩽ 0.4 bar). Reference BuddBudd (1969, p. 21) compiled data from a number of sources and found that n was consistently between c. 1.2 and c. 1.8 at stresses between 0.2 and 0.5 bar, and Reference Holdsworth and BullHoldsworth and Bull (1970) found that n was between 1.6±0.1 and 1.9±0.2 for shear stresses below 0.5 bar on the Meserve Glacier, Antaretica.
The values of A are also generally consistent with those of previous investigations. Laboratory studies (Reference BuddBudd, 1969, p. 21; Reference Hooke, Hooke, Dahlin and KauperHooke and others, 1972) give values of about 6 bar year1/n at −10° C, the temperature of this part of the Barnes Ice Cap (Hooke, in press). The laboratory studies were on very fine-grained, bubble-free, polycrystalline ice with a random c-axis orientation, so values somewhat higher than those in glacier ice are perhaps to be expected. In addition the local stress field was modified by excavation of the tunnel, and ice fabrics are no longer necessarily in equilibrium with the flow. Thus better agreement between laboratory and field data is not to be expected.
Bore-Hole Analysis
Bore-hole inclinometry data were analyzed with the use of a modified version of a computer program written by R. L. Shreve. The theoretical basis for the program was presented by Reference Shreve and SharpShreve and Sharp (1970). The theory applies to two bore holes separated by distances which are small compared with distances over which strain-rates change noticeably. Because strain-rates do change significantly between the holes discussed herein, some error (probably systematic) has been introduced in the analysis.
The program utilizes a local right-handed cartesian coordinate system with x and y directed down-glacier and downward perpendicular to the bed respectively, and z horizontal (Fig. 3A, cross-section). The x, y, and z components of the ice velocity are u, v, and w respectively.
The bore holes lie approximately on the same flow line, so data from two holes in two successive years can be used to calculate the longitudinal strain-rate, ∂u/∂x (Fig. 5A), using equation (12) of Reference Shreve and SharpShreve and Sharp (1970). (The convection term in equation (12) was calculated using v measured at the surface and assuming that it decreased linearly with depth. The term is small, so the more refined values of v calculated below need not be used).
The glacier margin is gently convex outward at this location (Fig. 2), so there is a small transverse strain rate, ∂w/∂z, which was measured at the surface near each bore hole (Table I). Because the glacier is frozen to its bed (Hooke, is press) ∂w/∂z must be zero at the base, as is ∂u/∂x (Fig. 5A). ∂w/∂z is therefore assumed to decrease with depth in proportion to the decrease in ∂u/∂x, thus:

where the subscripts refer to the surface, s, and depth, y. Assuming incompressibility, the vertical strain-rate at any depth is then given by

and the v component of the velocity at any depth can be calculated by numerical integration of ∂v/∂y, starting at the bed where v = 0. The upward velocities at the tops of the bore holes calculated in this way are compared with the measured upward velocities in Table III. The agreement is satisfactory for bore holes b1 and b2, but measured values of v seem high at the tops of holes bo and bix. This probably reflects tunnel closure with upward movement of the tunnel floor. Values of v at corresponding heights above the bed in the two bore holes were used to calculate ∂v/∂x. ∂u/∂z and ∂w/∂x were assumed to be zero. The remaining three velocity derivatives, ∂u/∂y, ∂w/∂y and ∂v/∂z were calculated from equations (5) of Reference Shreve and SharpShreve and Sharp (1970), assuming that ∂v/∂z decreased linearly with depth and adjusting it so as to make the shear strain-rate component ![]() zero at the surface.
zero at the surface.
Table III. Comparison between calculated and measured velocities and strain-rates at tops of bore holes

The values of ∂u/∂x and ∂v/∂x calculated above are average values for ice between the two holes. Because strain-rates change between the holes, the actual values of these derivatives at the holes are somewhat different from the values used in the calculations. Although these errors are substantial in some instances, they do not result in significant uncertainty in other calculated parameters (Figs. 4, 5B, and 5C), as in the present experiment these parameters depend predominantly on changes in inclination of the holes.
As a check on the procedure, the relation

(Reference PopovPopov, 1952, p. 204) was used to calculate shear strain-rates parallel to the tunnel axis at the tops of holes bo and bix. θ is the angle that the x-axis makes with the tunnel axis. Calculated values of ![]() are in reasonable agreement with values measured in the tunnel strain nets near the tops of these holes (Table III).
are in reasonable agreement with values measured in the tunnel strain nets near the tops of these holes (Table III).
Effect of fabric on A
If a shear-stress distribution is assumed, the parameters n and A can be studied as above (Fig. 4). ![]() is calculated from the velocity derivatives using the definitions
is calculated from the velocity derivatives using the definitions ![]() and
and

and the shear stress is approximated by
which is identical to Equation (1) except for the cos2 β term. This term arises from the fact that the x-axis is parallel to the bed which has a slope β of about 2° (Fig. 3A). Calculations were carried out at depth intervals of 1.5 m in each bore hole (Fig. 5).

Fig. 5. Variation in longitudinal strain-rate, r, flow law parameter, A, and shear stress, τxy, with depth. For meaning of arrows see caption of Figure 4. Lengths of arrows in diagram B give indication of reproducibility of measurements. However, in diagram A length of arrow also reflects, in part, a decrease in /r/ through time. Open circles in diagram A are assumed values of r. Above highest point where bore holes overlapped r was assumed to be constant. Below lowest point of overlap, r was assumed to decrease linearly with depth toward zero at the bed. Points in diagram B are calculated with the use of an assumed shear stress distribution (shown by solid lines in diagram C), and points in diagram C are calculated with the use of assumed values of A (A = 2.8 in white ice band and 5 bar/year1/n (elsewhere). 1971 survey data not used in calculating values in diagram C.
The data show considerable scatter (Fig. 4) so meaningful values of n cannot be determined. However, if n is assumed to be 1.65, A can be calculated from the relation

(Reference Shreve and SharpShreve and Sharp, 1970, p. 83). Lines of equal A have been drawn on Figure 4, and the variation of A with height above the bed is shown in Figure 5B. Owing to the uncertainty in the shear stress distribution and to the possibility of systematic errors in ![]() , only relative values of A between adjacent parts of the same hole will be considered.
, only relative values of A between adjacent parts of the same hole will be considered.
Where hole b2 passes through the white ice band, A averages about 2.8 bar year1/n (Fig. 4). In the coarser ice above and below the white ice band A is approximately 5 bar year1/n (Sections B and H). These relative values are quantitatively consistent with earlier work on the relation between strain-rate and density in snow and ice (Reference Mellor, Smith and ŌuraMellor and Smith, 1966, as interpreted by Reference BuddBudd, 1969, p. 30) which suggest that a value of 2.8 bar year1/n in ice with a density of 0.87 Mg/m3 (Table III) corresponds to a value of about 4.7 bar year1/n in bubble free ice.
The relative value of A in the bubble-free fine ice is less reliably determined. Near the bottom of hole bix A appears to be about 10% lower in the fine ice than in overlying coarser ice (Sections M, P, and R), but the fine-grained ice in hole bo simply decreases the rate at which A increases with depth (Fig. 5B). Moderately coarse ice continues to the bottom of hole bo (Hooke, in press).
Shear-stress distribution
By assuming values for n and A, τ xy may be calculated from Equation (2) and the shear-stress distribution may be studied. A is assumed to be 5 bar year1/n in the blue ice and 2.8 bar year1/n in the white ice, and n is assumed to be 1.65. The resulting shear stresses are plotted in Figure 5C, together with the stress calculated from Equation (1b) for each bore hole.
Near the surface τ xy is non-zero, in agreement with the predictions of Nye’s perfectly plastic model (Equation (1a)), but it is apparently independent of depth, in contrast to those predictions. Deeper in the glacier, τ xy increases approximately linearly with depth. However, in hole bo the rate of increase is less than given by Equation (1b) and in hole bi the stress appears to be higher than given by Equation (1b).
In conclusion, neither the flow law nor the shear stress can be determined independently from the field data presented herein. However if one is assumed, some insight into possible variations in the other may be gained. It seems reasonable, for instance, to suggest that (1) τ xy is non-zero and independent of depth near the surface; (2) n is about 1.65; (3) A is 40 to 50% lower in the fine bubbly white ice than in the coarse blue ice; and (4) A may be 10% lower in the fine blue ice than in the coarse blue ice.
Foliation Attitude in an Ice-Cap Margin
As noted, the dip of foliation planes decreases rapidly with depth in the margin (Fig. 3, cross-section). To gain some insight into possible causes of this change in attitude consider an idealized perfectly plastic two-dimensional ice cap with a surface profile ![]() (Reference NyeNye, 1951, p. 571) where h is the height of the glacier surface, x is the distance from the margin, and c is a constant which depends on the yield strength of the ice. We assume that: (1) foliation originates near and parallel to the base of the glacier; (2) after formation foliation is transported passively and deformed with the ice; (3) the horizontal velocity is independent of depth; (4) the ablation rate, Ȧ
b, is constant over the ablation area; (5) the mass budget is balanced; and (6) ice is incompressible. For convenience, the y axis will now be directed vertically upward and the x-axis will be directed up-glacier.
(Reference NyeNye, 1951, p. 571) where h is the height of the glacier surface, x is the distance from the margin, and c is a constant which depends on the yield strength of the ice. We assume that: (1) foliation originates near and parallel to the base of the glacier; (2) after formation foliation is transported passively and deformed with the ice; (3) the horizontal velocity is independent of depth; (4) the ablation rate, Ȧ
b, is constant over the ablation area; (5) the mass budget is balanced; and (6) ice is incompressible. For convenience, the y axis will now be directed vertically upward and the x-axis will be directed up-glacier.
The amount of ice lost from the glacier surface down-glacier from a point a distance x from the margin is A b x. This equals the ice discharge through a vertical section at x. Hence the horizontal velocity, u, at x is

where ![]() , and the minus sign indicates that u is in the negative x direction.
, and the minus sign indicates that u is in the negative x direction.
The assumption of incompressibility can be expressed as

Differentiating Equation (3) and using the result to integrate Equation (4), yields:
Intuitively one might not expect the factor of ![]() because at y = h, Equation (5) makes
because at y = h, Equation (5) makes ![]() rather than A
b. However for a balanced budget the ablation rate must equal the emergence velocity, v+u tan θ, where θ is the surface slope. This indeed is the case because u tan θ also equals A
b/2.
rather than A
b. However for a balanced budget the ablation rate must equal the emergence velocity, v+u tan θ, where θ is the surface slope. This indeed is the case because u tan θ also equals A
b/2.
We now determine the coordinates of an element of ice as a function of time (x = ξ(t), y = ƞ(t)). Making use of u = dξ/dt and the initial condition ξ(0) = ξ 0, Equation (3) may be integrated to obtain
Then using v = dƞ/dt, Equations (5) and (6), and the initial condition ƞ(0) = ƞ 0 we obtain
where ƞ is the height of the element of ice above the bed after it has traveled a distance ξ from its initial position at (ξ
0, ƞ
0). A plot of ƞ versus ξ defines the path of the particle, and by setting ![]() , the x coordinate of the point where the particle reaches the glacier surface is obtained. The path is observed to be hyperbolic with a rapid increase in slope near the margin.
, the x coordinate of the point where the particle reaches the glacier surface is obtained. The path is observed to be hyperbolic with a rapid increase in slope near the margin.
We now consider an initially horizontal foliation plane in the element of ice that follows this path. Two processes tend to change the slope of this foliation plane with time: (1) shear in the vertical direction, ∂v/∂ξ, and (2) the vertical strain-rate ∂v/∂ƞ. The problem is similar to that solved by Reference Shreve and SharpShreve and Sharp (1970, equation 7) for the deformation of a bore hole, except that the convection term does not appear in the Lagrangian coordinate system used herein. The appropriate equation is thus

where ζ is the tangent of the angle of dip of the foliation plane, and the two terms on the right represent respectively the two effects identified above, ∂v/∂ξ and ∂v/∂ƞ are evaluated from Equation (5), making use of Equation (7). The term on the left is evaluated by using the chain rule

and obtaining dξ/dt from Equation (6). The resulting differential equation is

which has the solution

(Reference FordFord, 1955, p. 34). Dips of foliation planes at different positions in the ice are plotted in Figure 6. ξ 0 was taken as 1 250 m, and ζ and ƞ were calculated from Equations (7) and (11) for different values of ƞ 0 and ξ. The rapid increase in dip of foliation planes near the glacier surface observed in the ice tunnel (Fig. 3A) is clearly present in the model.

Fig. 6. Foliation attitudes in the margin of an idealized perfectly plastic glacier with parabolic surface profile,  (Reference NyeNye, 1951). Foliation is assumed to have been parallel to the bed at a point ξ
0 = 1 250 m from the margin. An element of ice containing the foliation plane then followed the path defined by Equation (7), and the dip of the foliation plane at various points along this path was determined from Equation (11). The six paths shown are for six different values of ƞ
0, the height of the element of ice at ξ = ξ
0. The values of ƞ
0, used were 0.5, 1, 2, 6, 15, and 25 m.
(Reference NyeNye, 1951). Foliation is assumed to have been parallel to the bed at a point ξ
0 = 1 250 m from the margin. An element of ice containing the foliation plane then followed the path defined by Equation (7), and the dip of the foliation plane at various points along this path was determined from Equation (11). The six paths shown are for six different values of ƞ
0, the height of the element of ice at ξ = ξ
0. The values of ƞ
0, used were 0.5, 1, 2, 6, 15, and 25 m.
Note also that the dip of a foliation plane near the margin is considerably steeper than the slope of the path followed by the element of ice containing that foliation plane. Thus the foliation plane which comes to the surface with a dip of 72° about 50 m from the margin is not continuous with the plane which is 15 m above the bed and 200 m from the margin, despite the fact that the element of ice containing the former plane passed through the latter position at one time. In other words, foliation planes do not (necessarily) parallel flow lines in the ice.
The assumption, that the horizontal velocity is independent of depth maximizes the terms ∂v/∂ξ and ∂v/∂ƞ, and thus maximizes Dζ/Dt. If instead one were to assume a linear decrease in u with depth, as suggested by velocity profiles in holes bo and b1 (Fig. 3), the mean horizontal velocity is given by Equation (3), but u at the surface is twice the mean. Thus

∂u/∂ξ is now seen to be zero, so v = 0, ∂v/∂ξ = 0, and ∂v/∂ƞ = 0. Hence Dζ/Dt = 0.
A more serious problem with the model arises from the fact that the surface profile near a glacier margin is best described not by ![]() , but rather by
, but rather by ![]() where a and b are constants (Reference NyeNye, 1967). As a limiting case we might, for example, assume a linear increase in thickness with distance from the margin. Thus Equation (3) becomes:
where a and b are constants (Reference NyeNye, 1967). As a limiting case we might, for example, assume a linear increase in thickness with distance from the margin. Thus Equation (3) becomes:

which again is independent of x and hence again leads to Dζ/Dt = 0.
Comparison with Barnes Ice Cap foliation
Because the surface profile of the Barnes Ice Cap differs from the profiles assumed in the models, quantitative comparison of predicted and observed foliation attitudes is made with the use of the original differential equation (8) and values of the velocity derivatives obtained from the bore-hole deformation analysis. Making use of Equation (9) and the fact that u = dξ/dt, Equation (8) becomes

Taking dv/dξ, dv/dƞ, and u constant between the bore holes and using the initial condition ζ = 0 at ξ = ξ 0, Equation (8a) may be integrated to yield

where v ξ = dv/dξ and v ƞ = dv/dƞ. v ξ , v ƞ and u were evaluated at the top of hole bi and at a depth of 11.4 m in b2 (Table IV). These two points are the same height above the bed and lie approximately on the same foliation plane. Using the mean values from Table IV in Equation (12) we obtain tan−1 ζ = 3.7°; the observed increase in dip of foliation at this level between holes bi and b2 is about 30°.

It seems clear, therefore, that the observed foliation attitudes could not have developed under the present flow field, primarily because v ξ is much too small. However, the flow field may well have been different in the past.
Between August 1969 and August 1972 the average local mass balance (emergence velocity minus net ablation) was −0.28 m of ice per year along the 1 km pole line above the tunnel. Earlier mass-balance measurements (Reference Løken and SagarLøken and Sagar, 1968), lichen trim lines at various places along the margin, and geomorphological studies of moraines (Reference Løken, Andrews and IslandLøken and Andrews, 1966) suggest that the mass balance has been negative for many years.
This negative mass balance is not uniform over the margin because down-glacier from the white ice band, drifting snow accumulates to greater depths than elsewhere (Reference HookeHooke, 1970, p. 318; Reference Hookein press), and melt water percolating through this snow refreezes along the snow-ice contact. During cooler summers some of this wind-drift snow may persist, through the ablation season, resulting in a positive mass balance within a few tens of meters of the margin. For instance between late August 1969 and early June 1972, 0.5 m of ice formed around the base of pole 1 which is 50 m from the margin (Fig. 3). Thus the present negative mass balance has probably resulted in thinning of the glacier without appreciable retreat of the margin.
It is thus hypothesized that the observed foliation pattern probably developed under a flow field more or less comparable to that found from the perfectly plastic model with a parabolic surface profile and parabolic increase in the longitudinal velocity with distance from the margin (Equation (3)). Subsequent thinning resulted in the present ice-cap margin configuration with a nearly linear increase in thickness and velocity (Equation (3b)). The theoretical model (Equation (3b)) predicts that the flow field in an ice-cap margin with the present configuration could not be responsible for the observed foliation pattern, and substitution of observed velocities and velocity derivatives into Equation (12) supports this prediction.
The amount of thinning since the time of development of the observed foliation pattern is not known, but a loss of 5 to 10 m of ice is probably sufficient. The thinning cannot have been too great, as ice with steeply dipping foliation near the surface would then have been lost. However the steepest dips are observed near the margin where drifting snow reduces net ablation, so considerable thinning may have occurred up-glacier without loss of the steeply dipping foliation down-glacier. At the same time, due to the high value of n in the flow law, a relatively small decrease in thickness could cause a substantial change in the flow field. For example v ξ , and hence tan−1 ζ, increased by a factor of 10 during this study, apparently in response to a general improvement in the mass balance over the past three years. Thus the fact that steeply dipping foliation is observed does not necessarily mean that the thinning has not been sufficient to produce the postulated change in the flow field.
One further possibility should be considered: namely that the foliation developed in its present position under the existing local flow field. The foliarion is approximately parallel to the direction of maximum shear strain-rate determined from the bore-hole analysis. However the maximum shear strain-rate is on the order of 0.01 year−1, so several tens of years would be required to produce significant finite strain, while only a few tens of years are required for the ice to move to the glacier surface from a position where foliation is presently horizontal. Thus the observed foliation probably did not develop under the local flow field in which it is at present, but small irregularities and thrust offsets in foliation planes are observed and these may have developed under the present local flow field.
Acknowledgements
I am particularly indebted to R. L. Shreve for his patience in explaining to me many basic principles of glaciology, and for use of a computer program which formed the basis for my bore-hole deformation analysis. B. B. Dahlin, P. J. Hudleston, R. G. Oakberg, R. L. Shreve, and an anonymous reviewer contributed valuable suggestions during preparation of the manuscript. Logistical support from the Glaciology Subdivision, Department of the Environment, Ottawa, Canada, was essential for the study, and the cooperation of O. Løken and G. Holdsworth in this regard is gratefully acknowledged. Financial support was provided by the National Science Foundation and the University of Minnesota Graduate School.


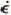 was determined from the bore-hole and tunnel deformation data, and possible variations in the other three parameters in Glen’s flow law,
was determined from the bore-hole and tunnel deformation data, and possible variations in the other three parameters in Glen’s flow law, 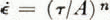 , were studied. It appears that
, were studied. It appears that 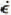 a été déterminée à partir des données sur la déformation des trous de sondage et du tunnel; des variations possibles dans les trois autres paramètres de la loi de Glen
a été déterminée à partir des données sur la déformation des trous de sondage et du tunnel; des variations possibles dans les trois autres paramètres de la loi de Glen 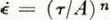 ont été étudiées. Il semble que
ont été étudiées. Il semble que 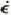 wurde aus den Deformationen der Bohrlöcher und des Tunnels bestimmt; die möglichen Veränderungen der drei anderen Parameter in Glen’s Fliessgesetz
wurde aus den Deformationen der Bohrlöcher und des Tunnels bestimmt; die möglichen Veränderungen der drei anderen Parameter in Glen’s Fliessgesetz 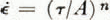 wurden untersucht. Es scheint, dass
wurden untersucht. Es scheint, dass 










