Historical Background
The effect of stresses on the phase equilibrium between a solid and an adjacent fluid has been a rich source of theoretical speculation for the past century. It appears in the evolution of thermodynamics as a recurring theme which has engaged the attention of leading contributors to the science. The subject was introduced by Reference ThomsonJ. Thomson (1849), who showed theoretically that hydrostatic pressure on a solid-liquid system would change the equilibrium temperature of the system. W. Thomson (later Lord Kelvin) proved this by reducing the freezing point of water under pressure, one of the earliest confirmations of thermodynamic theory. In 1861, Reference ThomsonJ. Thomson (1860–62) generalized his theory. He deduced the following axiom, by reasoning from specific chemical, mechanical and thermodynamical examples:
“If any substance, or any system of substances, be in a condition in which it is free to change its state, and if mechanical work be applied to it as potential energy, in such a way as that the occurrence of the change of state will make it lose that mechanical work from the condition of potential energy, without receiving other potential energy as an equivalent, then the substance or system will pass into the changed state.”
Thomson chose the two-phase system ice-water for an example, as did many of his successors. For this, he rephrased the axiom:
“…any stress whatever, tending to change the form of a piece of ice in ice-cold water, must impart to the ice a tendency to melt away, and to give out its cold, which will tend to generate, from the surrounding water, an equivalent quantity of ice free from the applied stresses.”
In his 1861 paper, Reference ThomsonThomson (1860–62) examined the question of whether the newly-generated ice could form on the surface of the strained ice, and concluded that it could not. He reasoned that if each molecular layer of ice formed on the strained ice adopted the state of strain, removing the stress would release more potential energy than was stored, an impossibility. He visualized instead the formation of an ice “spiculum” in the liquid which was attached only lightly to the ice or container surface. Because this spiculum would be a single crystal and less plastic than polycrystalline ice, it would tend to resist deformation under the stress of its buoyancy. Thomson also suggested the following experiment to demonstrate the postulated recrystallization of stressed ice:
Consider two cylinders, one within the other and both filled with a mixture of ice and water. The inner cylinder is fitted with a moveable piston attached to a shaft which extends outside the outer cylinder. Heat can flow between the two ice baths, across the walls of the inner cylinder. Potential energy is now stored in the inner cylinder by tension on the shaft which pulls the piston to a fixed displacement. The pressure is lowered within the inner cylinder, the equilibrium temperature rises, and heat flows outward to the outer cylinder. Water freezes within and ice melts without the inner cylinder. Part of the tension is relieved as the freezing water expands, the phase changes thus taking place at the expense of the stored potential energy.
Thomson does not seem to have tested his ideas in the laboratory, but the question was taken up by Reference Helmholtz and HelmholtzHelmholtz (1865, see also Reference Helmholtz and HelmholtzHelmholtz, 1885). He adopted the viewpoint suggested by Thomson and championed the theory of plasticity for glacier ice based on it by the latter (Reference ThomsonThomson, 1856–57). He also performed Thomson’s experiment. For a cylinder stressed by tension on its piston, he substituted a sealed flask half-filled with ice and water from which the air had been partially evacuated. This was immersed in an ice bath at normal atmospheric pressure. Within an hour, ice within the flask had begun freezing to the walls. After eight days “bildeten sich … sehr regelmässige und scharf begrenzte Eiskrystalle aus”. Helmholtz’s account is sketchy; there are no more details. Curiously, this experiment is not mentioned in later German versions of this lecture (e.g. Reference HelmholtzHelmholtz, 1896).
Thomson’s axiom was couched in general terms of “any stress whatever”. Apparently he thought in terms of hydrostatic stress; the experiment he proposed was based on two different hydrostatic stresses. The phase equilibrium of a solid under non-hydrostatic (oriented) stress was first examined by Reference GibbsGibbs (1877), who carefully established the thermodynamic principles involved. Gibbs based his calculation on work done by straining the solid and displacing the contacting liquid. His conclusions concerning strained solids were stated in general terms without reference to specific examples:
“… the fluids in equilibrium with the solids are all supersaturated with respect to the substance of the solid, except when the solid is in a state of hydrostatic stress; so that if there were present in any one of these fluids any small fragment of the same kind of solid subject to the hydrostatic pressure of the fluid, such a fragment would tend to increase.”
Gibbs went on to point out that even in the absence of such a fragment, a solid under hydrostatic stress would still start to form at the expense of the solid subjected to distorting stress. He adduced these conclusions for amorphous substances, but expressed caution about crystalline solids, admitting only for the latter that the same phase changes would occur within certain limits, especially for fluids easily supersaturated. The solid product of such phase changes (Thomson’s “spiculurn”) he termed “crystals of hydrostatic stress”.
The first development of specific examples and magnitudes of the effect produced by strained solids was left to Reference PoyntingPoynting (1881). He based his argument on the premise that pressure on both solid and liquid would increase the rate at which molecules are given off from the surfaces, but would do so more rapidly for the less dense phase. This accounts for the pressure depression of the melting point if the solid is less dense. But if pressure were applied to the solid alone, much less pressure would be required to reach the same lower equilibrium temperature. Taking water as an example, he calculated that for a given melting point depression the ratio of required pressure, p′, on the ice alone to the pressure p applied to water and ice together would be given by

where v′ is the specific volume of ice and v the specific volume of water.
p′ thus can be 11·5 times smaller than p to produce the same melting-point change. This result is based on the assumption that the melted ice generated by pressure is immediately relieved of the pressure and is free to depart as unstressed water. Poynting attempted experimental verification of this ratio with inconclusive results.
Reference JohnstonJohnston (1912) and Reference NiggliNiggli (1915) both equated the free energy of the solid to that of the liquid before and after stress was applied to the solid. From this assumption they both reached the same magnitude of the melting-point depression as Poynting.
Reference TammannTammann (1925) pointed out the fallacies in these theories and similar ones (e.g. Reference OstwaldOstwald, 1896–1902, p. 374). Poynting’s fallacy was a hidden assumption concerning the nature of the hypothetical thermodynamic engine on which he had based his deductions, those of Johnston and Niggli were equating the free energies for an indefinite number of equilibrium states, which therefore “asserts nothing definite, and its mathematical transformations can lead to no definite results”. Tammann cited the correct thermodynamic approach to the problem made by Gibbs and Riecke.
In the meantime, Reference RieckeRiecke (1895) had published a paper in which he calculated the temperature depression to be expected from a uniaxially stressed solid. The temperature depression was due only to the release of elastic strain energy when some of the solid melted. Like Gibbs, Riecke assumed a reversible process operating within the elastic limit of the solid. This led to a much smaller temperature depression than that obtained by Poynting and his successors. In fact, at small pressures this depression was also much smaller than that predicted for hydrostatic stress by Thomson and by the Clausius–Clapeyron equation. Riecke also chose ice for an example, and gave the relation
for the depression of the ice melting point t in degrees Celsius due to uniaxial pressure p in kg mm−2, although the equation and values of the physical constants given in his paper actually lead to −0·018 as the coefficient of p 2. He published a second paper (Reference RieckeRiecke, 1912) on this same topic in which he introduced, without explanation, the expression
where p was the uniaxial pressure in kg cm−2, a result which leads to a melting point depression two orders of magnitude larger than that derived in 1895. Riecke based his theory on an amorphous solid, but was also reluctant to extend its validity to crystalline solids, even though he constantly returned to ice for an example. About the latter substance he observed (translation into English by the present author):
“Of especial interest is the fact that ice and uniaxially stressed ice cannot exist in equilibrium with one another. In one and the same vessel filled with water, two ice prisms under equal hydrostatic stress can exist in equilibrium with water. If one is now subjected to uniaxial stress, its melting point is lowered and a certain quantity of ice is melted away; this same quantity will recrystallize on the other prism.”
Riecke’s successors were not so inhibited. Both his theory and Poynting’s enjoyed a vogue among mineralogists who tried to apply them to recrystallization and crystal reorientation in rocks. The fact that the former’s theory was formulated for reversible thermodynamic processes did not deter such investigators from embracing the so-called “Riecke Principle”. Aside from the question of whether one of his calculated magnitudes for the temperature depression of stressed ice is correct, or whether these are applicable to irreversible processes, the fact that the passage from Riecke’s 1912 paper quoted above is nothing more than a restatement of Thomson’s axiom for the special case of uniaxial stress would point to the justice of using instead the term “Thomson’s Principle”.
Recent Developments
A number of investigators in recent years have re-examined the nature of phase equilibrium between a non-hydrostatically stressed solid and the adjacent fluid. Each advanced a different theoretical approach. Reference KambKamb (1961) undertook a critical review of the subject by expressing several of the recent theories in a common mathematical format, pointing out the existence of several errors, and developing his own theory based on the foundation established by Gibbs. He rejected the intervening theories as incorrect. Reference KumazawaKumazawa (1963) advocated a different theory. Most recently, Reference McLellanMcLellan (1966) supported Kamb’s position, generalized his theory, and termed Kumazawa’s approach inadequate. In the meanwhile, Reference ShumskiyShumskiy (1955, p. 38) and Reference Barnes and TaborBarnes and Tabor (1966) have given respectively −0.000 004 85 and −0.000 000 435 as the coefficient for ice in Rieckc’s equation if the pressure is in kg cm−2. These figures presumably are based on more recent values for the physical constants for ice (Shumskiy says so), but they differ from one another by an order of magnitude. The theory of non-hydrostatic thermodynamics obviously has not yet been laid to rest.
Although this topic has provided a fertile medium for theoretical inventiveness, experiment and observation have trailed far behind. The very common system of ice-water was chosen for examples by many of the theorists, but there have been surprisingly few reports in the glaciological literature of experiments along the lines initiated by Helmholtz and Poynting. Tammann demonstrated by experiment the invalidity of Poynting’s theory, but detection of the very small temperature change predicted by Riecke is difficult. Both the flow of glacier ice and the recrystallization of minerals in rock under stress involve irreversible processes, with the stress distributions apt to be complex and crystal growth severely constrained. The phase equilibrium of stressed solids envisioned by early investigators was in simpler terms of a fluid experiencing only its own hydrostatic stress in an environment permitting free crystal growth. That the local relief of hydrostatic pressure in a temperate glacier will cause new ice to appear is an obvious consequence of Thomson’s axiom. if Thomson’s “spicula” are to appear anywhere in nature, it ought to be in cavities deep within a temperate glacier. Evidence has been at hand for some time that such crystals do appear.
Field Observations
Reference SchneiderSchneider (1939) appears to have been the first to mention the existence of an unusual type of ice crystal in water-filled glacier cavities. He reported observing such crystals on the Unterer Grindelwaldgletscher in 1938. By dropping stones down a cavity in the glacier, he was able to dislodge crystals from its walls. They floated to the surface after a time delay which suggested that they had originated deep within the glacier. These crystals were flat, up to 30 cm diameter, and exhibited an intricate, branching structure. They bore resemblance to the arms of giant snow crystals, or to dendritic ice growth, but were 1–2 cm thick. A few thin, structureless disks were also observed. Schneider did not offer any theories about their origin. There does not seem to be any further mention since of such crystals in the literature, except another short note by Reference SchneiderSchneider (1948). M. F. Meier (personal communication) reports finding this same type of crystal in similar circumstances on the lower Blue Glacier.
During the summer of 1966 an ice tunnel 43 m long was excavated in the upper Blue Glacier (Mt. Olympus, Washington), as a pilot project to develop improved tunneling techniques. For convenience, this tunnel was excavated in a nearly stagnant ice face (annual motion 3–4 m/year) close to the station buildings of the Blue Glacier Project. At its head it was about 20 m below the surface of the snow dome, one of the principal accumulation areas of the Blue Glacier. This tunnel intersected several water-filled cavities.
These varied in size from small pockets to a large cavern at the tunnel head from which many cubic meters of water were drained. Attached to the walls of the three innermost cavities (profusely in the large cavern), crystals identical to those described by Schneider were found in situ, as well as many crystals of other unusual morphologies. For reasons to be discussed below, these crystals appear to be Thomson’s “spicula”.
The following were observed in the tunnel:
-
The size and number of the crystals appeared to be directly proportional to the size of the cavity.
-
The crystals all grew from the cavity walls into the water. The larger ones tended to slope downward, but there was little preferred spatial orientation. In places the crystals occurred in rows aligned with foliation in the cavity walls.
-
Crystal growth was found only in the innermost cavities intersected by the tunnel, at depths 15 m or more beneath the surface. This is beyond the normal penetration of winter chill in the ice face of the snow dome, which has been noted by previous observations to be about 10 m. (The diffuse heat source in the ice, due to the heat of fusion of the water, will always lead to a reduced chill penetration and a sharp boundary between freeze and non-freeze, in contrast to the case of cold wave penetration in a single-phase medium, where slight temperature changes could be expected to a greater depth.)
-
All such cavities apparently communicated with the surface, as shown by the character of water drainage when they were first tapped. Especially in the case of the smaller cavities, this communication was intricate and obscure. In one instance crystals were found in the re-entrant part of a cavity which did not communicate with the surface.
-
Number and size of the crystals increased toward the tops of the cavities.
-
Four principal types of ice crystals were found:
-
A. Large, irregular plates, up to 40 cm across and 2–3 cm thick (Fig. 1). The edges showed occasional crude dendritic structure, or were vaguely lobate. Step variations in thickness sometimes occurred. All those examined were single crystals with c-axis perpendicular to the plane of the plate. The larger plates tended to be oriented horizontally.
-
B. Small, thin, clear disks of ice, nearly circular, with diameters up to 6–7 cm. They had smooth, featureless, parallel faces, and practically no inclusions. c-axis was perpendicular to the plane of the disk. They were attached with random orientation to other, larger crystals.
-
C. Intricate, branched single crystals up to 20 cm long and 1–2 cm thick, growing at random orientations from the cavity walls (Figs. 2 and 3). The two flat, parallel faces were smooth, but the edges were crenelated. c-axis was perpendicular to the plane of the smooth faces. Dendritic structures of this type are distinguished in mineralogy by the term arborescent. Natural silver, for instance, occurs in very similar forms (Reference PearlPearl, 1964, p. 33).
-
D. Small “mushrooms” (Fig. 4), which were most common in the lower part of the large cavern. It is not clear whether these represent a separate morphology or are the early growth stage of Type A. They increase in diameter outward from the point of origin on the cavity walls, have fluted or sculptured sides, and each has a flat, smooth face parallel to the ice surface from which it grows. c-axis is perpendicular to the flat face.
-
-
The walls of the cavity where crystals were not attached exhibited a pattern of faceted ice in the form of irregularly arranged planes with dimensions of the order of a centimeter.
-
Although the tunnel traversed white, bubbly glacier ice, the ice surrounding the large cavern was bubble-free for a distance of 25–30 cm in from the cavern walls. Examination of this clear zone by means of a thin section between crossed polaroid screens showed it to be fine-grained and polycrystalline, similar to the surrounding bulk of white glacier ice. Only the first two centimeters next to the cavity wall had a different structure of crystals elongated parallel to the walls.
The tunnel mouth was sealed during the winter of 1966/67 by normal snow accumulation. This accumulation was dug away and the tunnel re-entered late in July 1967. Refreezing of flowing melt-water from internal streams exposed during the 1966 excavation had added 30 cm of ice to the tunnel floor for about 10 m back from the mouth. Other evidence of ice frozen from flowing melt water was found for another 10 m. Beyond this the tunnel appeared unchanged from the previous year. There was no evidence of either freezing of melt at the tunnel head: water standing in the bottom of the large cavity was unfrozen, while saw marks in the ice made to procure specimens in 1966 were still clearly visible.
Numerous ice structures had developed on the tunnel and cavity walls during the intervening year. These were confined to the large cavity and innermost 10 m of the tunnel; they were absent from the outer part of the tunnel where refrozen melt water clearly indicated the presence of sub-freezing temperatures.
The following were observed:
-
Numerous small bumps, dimensions under 1 cm, formed on previously smooth ice walls of the tunnel. These had a marked tendency to form rows along the intersection of tunnel wall with foliation planes in the ice. ‘Their scattered and irregular occurrence suggested formation by accretion on the existing ice surfaces, rather than by melt erosion of the walls.
-
Scattered larger ice structures formed on tunnel and cavity walls since the previous summer (Figs. 5 and 6). Icicle-like figures from some of these generally irregular structures in the cavity hung parallel to the slanting cavity wall rather than vertically.
-
Larger, flattened ice structures formed parallel to foliation planes intersecting the cavity walls (Fig. 7). These bore resemblance to the large crystals described under (6A) above, but had not developed any recognizable structure. There is a strong temptation to call them an initial stage in growth of the large crystals.
-
Long, slender “icicles” suspended approximately in the vertical from the tunnel roof. Diameters were in the order of 0·5 cm (Fig. 8). Unlike normal icicles, many of these were almost perfect cylinders and were single ice crystals. The bottom end of each was a smooth plane, oriented at random in respect to the cylinder axis. The cylinders were remarkably strong. They required far more force to break from the roof than conventional icicles of this size.
-
The faceted character of the cavity walls mentioned under (7) was no longer visible. Instead, a striated pattern of irregular ridges had formed in places. Ridge spacing was 1–3 cm. The striations were not aligned with foliation of the surrounding glacier ice.

Fig. 1. Large. irregular, single crystal formed in the water-filled Blue Glacier ice cavity

Fig. 2. Branched single ice crystal from the Blue Glacier ice cavity

Fig. 3. Branched ice crystals in situ after water was drained from the cavity intersected by the 1966 Blue Glacier ice tunnel

Fig. 4. “Mushroom” ice crystals growing from the Blue Glacier cavity wall. These are single crystals with c-axis parallel to the “stems”

Fig. 5. Ice accretion formed over the winter on wall of 1966 Blue Glacier tunnel. Smaller accretions, or bumps, are seen in the foreground. Scale is given by pick of an ice-axe

Fig. 6. Ice accretions with suspended icicles on wall of the large cavity intersected by the 1966 Blue Glacier ice tunnel. Photograph token in July 1967

Fig. 7. Large ice accretions along. foliation plane in wall of cavity intersected by the 1966 Blue Glacier ice tunnel. The ice formations developed over a period of nearly a year while the cavity was empty of water. Photograph taken in July 1967
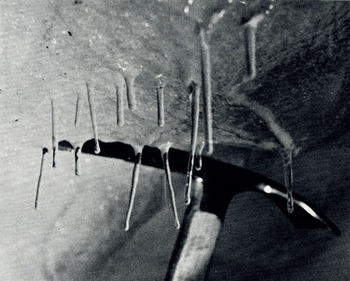
Fig. 8. Cylindrical, single-crystal icicles hanging from roof of the 1966 Blue Glacier tunnel. These icicles formed over the winter and were photographed in 1967
Laboratory Tests
I have repeated the Helmholtz version of Thomson’s experiment. Air was evacuated from a “Pyrex” flask with a spherical body 9 cm in diameter and half-filled with water. The water was then frozen and allowed to remelt until only a disk of ice 0·5 cm thick was left floating on the surface. The sealed flask was then kept in an ice bath at atmospheric pressure for 8 days. Large crystals of ice formed over the walls of the flask beneath the water surface, while ice crystals deposited from the vapor formed a fine-grain pattern on the upper flask walls. The sub-surface crystals were coarsely dendritic. They covered most of the flask walls to a thickness from 2 to 5 mm. Although water both inside and outside the flask was drawn from a common source (tap water of low ion content), the possibility could not be ruled out that depression of the ice bath melting point by solutes introduced along with ice added during the experiment could have produced the same effect. This test was repeated under similar conditions, but with the ice-water mixture in the flask at atmospheric pressure (flask unsealed). No crystals formed.
For an evacuated “Pyrex” sphere 9 cm in diameter, with a wall 1 mm thick, even the slight temperature difference of approximately 0·007°C between the ice baths inside and out will produce a daily heat flux through the walls of about 3×103 cal (12·5 kJ). This is enough to freeze about 300 g of ice during the eight-day experiment. In fact, about one-tenth this amount froze, a discrepancy possibly duc to minute traces of solutes altering the freezing point. Although the temperature difference may be small, the amount of heat which can be transferred by the arrangement Thomson proposed and Helmholtz executed turns out to be comparatively large.
Discussion
The interior of a temperate glacier beneath the zone of winter chill penetration must be the most nearly isothermal environment to be found in nature. In static ice there exists only the extremely minute vertical temperature gradient (6·4 × 10−6 deg cm−1) imposed by the pressure dependence of the melting point. Yet the evidence of crystal formation within deep, water-filled cavities, and refreezing deep in bore holes (which constantly plagues drillers in temperate glacier ice but has received little attention in the literature) clearly indicates that phase changes do take place within this apparently isothermal environment.
While the transient penetration of winter chill can lead to heat loss from cavities at appreciable depths, and quite possibly contributes to ice crystal formation, this process is not necessary for the crystals to form. New ice will appear whenever hydrostatic stress is locally relieved in ice at the pressure melting point. The steady-state heat flux out of a glacier cavity is a result of the temperature gradient generated by differential hydrostatic stress. This situation is precisely the Thomson–Helmholtz experiment performed by nature on a large scale. The heat flow can be considerable. if a glacier cavity is partly filled with water and air at external atmospheric pressure, equilibrium temperature of any unstressed ice at this water surface is 0°C (T 0) regardless of its depth beneath the glacier surface. The ice–water interface temperature at a non-hydrostatically stressed cavity wall may not be exactly 0°C (see below), but is assumed so for a first approximation. Some distance x into the ice the equilibrium temperature of the ice undisturbed by the cavity is given by T i = T 0−0.0075p where p is the hydrostatic stress in bars. Due to this temperature difference, heat flows outward through the cavity walls. If a spherical cavity, radius r, is assumed, this becomes the hollow sphere problem in heat conduction discussed by Reference Carslaw and JaegerCarslaw and Jaeger (1959), who give the following solution:

where Φ is the heat flux out of cavity, λ the thermal conductivity of ice (5 × 10−3 cal deg−1 cm−1 s−1) and b = r+x. In the case of the idealized glacier cavity, the cavity wall is the inner surface of the hollow sphere, radius r; the surrounding ice at the undisturbed pressure melting point is the outside surface, radius b. If r = 1m and the ambient hydrostatic pressure from the ice overburden is 1 bar, values approximating those for the cavity at the head of the 1966 Blue Glacier tunnel, Φ as a function of x is given by Figure 9. If x = 5r, a reasonable figure, the heat flux out of the spherical cavity is nearly 5×103 cal/day (20 kJ/day), enough to freeze about 25 kg of ice a year. Thus there is no difficulty in disposing of the heat of fusion from crystal formation even with such slight temperature differences distributed over several meters of ice. The basic condition for ice crystal formation in an “isothermal” glacier, a mechanism to remove the liberated heat of fusion, can thus be explained by simple thermodynamics. More complex is the question of why these crystals take the form they do, and what is the role, if any, played by oriented stresses at the cavity walls.

Fig. 9. Heat flow from a spherical ice cavity two meters in diameter, in ice under 1 bar overburden pressure, if zone of undisturbed hydrostatic pressure is distance x from cavity wall
The 1967 Blue Glacier observations (paragraphs 9–12) suggest that a mechanism in addition to simple heat conduction in stressed ice may be at work. New ice in various shapes and in substantial quantities formed on the tunnel and cavity walls under circumstances where external sources of liquid water and a heat sink seem very unlikely. There was a marked relationship between these accretions and foliation of the surrounding ice. The only logical cause of these accretions appears to be the refreezing of slightly supercooled water extruded through interstitial passages of glacier ice by the ambient hydrostatic stress. This process occurs preferentially, but by no means exclusively, along foliation planes. The pressure melting point within the wet ice is lowered by the hydrostatic stress, but if the water is mobile adjacent to the cavity walls, the stress on it vanishes at the ice-air interface and part of it refreezcs to form unstressed accretions. A regelation process is at work which leads to latent-heat transport by the interstitial water in a direction opposite to heat flow by conduction out of the cavity. A heat circulation thus exists around a glacier cavity, driven by stress differences and leading to mass transfer with ice deposition in the cavity.
The Blue Glacier observations have borne witness to this phenomenon in an air-filled glacier cavity. Just what transpires in a water-filled cavity lies closer to the realm of speculation. Presumably the same basic mechanisms must be at work. But the intricate, branched form of many of the crystals found when the cavity was drained in 1966 can only have formed through growth into the melt—that is, loss of the heat of fusion to the water. It is difficult to conceive that heat conduction through the crystal base and into the wall could have led to such structures as the one in Figure 3. Inevitably, the conclusion must be reached that water in such a glacier cavity is persistently or recurrently supercooled in respect to these crystals. The most ready source for supercooling is the interstitial water expelled from the cavity walls. The supercooling of this water is slight and only a small fraction can refreeze. If only part of this fraction refroze at the wall at the instant of expulsion, then the temperature of the body of water filling the cavity would eventually be lowered by addition of the remainder.
But water does not normally persist in a supercooled state within an ice-walled container. An additional factor must be present which contributes to or sustains the supercooling. Though presence of an unsealed cavity eliminates local hydrostatic stresses and oriented stresses perpendicular to the cavity wall, the latter can exist parallel to the wall. I suggest that these stresses must lead in some fashion to a depression, however slight, of the equilibrium temperature at the ice-water interface. Even if this depression is due directly to the effect of oriented stress predicted by theory, its magnitude is difficult to specify in the light of theoretical uncertainties. The situation within the ice at and near the interface may well be more complex. Water at the equilibrium temperature of this interface must in any case be slightly supercooled in respect to the unstressed crystals growing into it. This supercooling does not detract from the existence of a heat flux out of the cavity, but only from its magnitude. Growth of unstressed crystals into the liquid, instead of on the stressed cavity walls (preference for the lower energy state) also fits the previously cited postulates of Gibbs and Riecke.
Why these crystals growing into the water assume the varied forms that they do is an unsolved problem, as it is for crystal growth from liquids in general. Undoubtedly their growth regime is complex, being subject to the fluctuations of water level and even alternate inundation and exposure to air. The steady-state hydrostatic heat flux could occasionally be altered by winter chill penetration if the cavity is sufficiently near the glacier surface. This would immobilize the interstitial water and completely alter the freezing process to the more conventional one of direct congelation on the cavity walls. If a cavity persists for years, an extremely complicated thermal and crystal-growth history can ensue. The crystals themselves could experience gradual metamorphism even after the generating influences are removed. In the ablation zone of a glacier, surface wastage will eventually expose a formerly deep cavity or its connecting water passages to the surface. This apparently led to the situations reported by Schneider and Meier. The large cavity encountered in the 1966 Blue Glacier tunnel is beneath an accumulation zone in a location where it probably had existed for years.
Additional observations bearing on the subject of ice regelation in a deep glacier cavity were made in another (1967) tunnel driven into intensely stressed ice beneath an active ice fall of the Blue Glacier. These and other observations about the deformation of ice under stress will be discussed in a separate paper now in preparation by Kamb and LaChapelle.
Conclusions
Large and varied ice accretions will grow in unsealed cavities in certain depth zones of temperate glaciers. Intricate crystal forms develop when growth takes place in water. These zones are demarcated above by the maximum penetration of normal freezing processes due to surface cooling. Below, they are limited in actively flowing ice by stress domains leading to rapid cavity closure. Growth into the water in the form of complex, unstressed crystals is promoted by differential hydrostatic stress, by movement of interstitial melt water, and possibly by oriented stresses at the cavity walls. The effect of the latter stresses on the melting point has received diverse theoretical treatment for nearly a century and cannot be specified with confidence even today. The heat flux from a cavity necessary to remove the heat of fusion can readily be explained in terms of Thomson’s experiment with different hydrostatic stresses. The cycle of heat and mass transfer is completed by regelation of interstitial water expelled from the cavity walls. If these interpretations are correct, the rise of internal pressure in sealed cavities can reduce or eliminate crystal formation. Cavities connecting to the surface can generate crystals in inverse proportion to the depth to which they are filled with water. If the water depth exceeds nine-tenths of the ice depth, melting instead of freezing will occur.
The unusual form of these glacier crystals suggests the need for an identifying name. Because J. Thomson predicted a century ago that “spicula” would be generated by hydrostatic stress difference in ice, the name “Thomson crystal” is proposed.
Acknowledgements
This work has been supported by National Science Foundation Grant GA-466. Field work on the Blue Glacier is made possible by permission of the Superintendant, Olympic National Park. K. O. Bennington, P. V. Hobbs, C. Knight, and N. Untersteiner have contributed valuable suggestions.











