1. Introduction
1.1. Background
The equilibrium equations for an ice mass concern stress gradients at a point. The integral of these equations through the ice thickness provides the fundamental equation for the mean stress of a column along a flow line in terms of the boundary dimensions. Through the introduction of a flow law this fundamental “one-dimensional" stress equation provides the mechanism for studying the motion of the ice along the flow line. The resulting velocities and strain-rates, together with the continuity equation allow the history of change of the ice mass to be calculated as a one-dimensional problem. In addition there are many other uses of this equation.Reference Robin de.Robin 1967) showed that surface slope variations along a line of flow in Greenland could be interpreted in terms of varying longitudinal stress gradients. Reference BuddBudd (1968) showed that surface slope deviations along a flow line of the Wilkes ice cap were proportional to the measured surface strain-rate gradients, and thereby calculated effective flow-law parameters of the ice. Reference CollinsCollins (1968) analysed the derivation of the expression for the longitudinal stress deviator to investigate the conditions under which Robin's results apply.Reference NyeNye (1969[b]) showed that a simpler form of the equation could be derived with respect 10 a variable longitudinal axis parallel to the surface for each point. Nye examined the hypotheses of Robin and Budd that the surface slope varied with longitudinal stress or strain-rate gradients and posed the question: why should the basal stress of the ice remain at its regional value while the longitudinal stress gradient varies with local slope deviations? The following analysis provides an answer to this question.
The results of two previous papers by the author Reference Budd(Budd, 1970[a], [b]) are combined to show how the various stress components are distributed in a simple model of flow over undulations. As before we restrict our study to two dimensions.
1.2. The longitudinal stress equation
It was shown byReference BuddBudd (1970[b]) that for an arbitrary homogeneous medium for which the quasi-static equilibrium stress equations under gravity hold viz.:
where ρ is the density of the medium and ρgx and ρgz are gravitational weight components in the x and z directions for any orthogonal axes system; that the following general integral equation holds

where z1 and z2(x) are any smooth, single-valued, distinct boundary curves in the medium,
and τxz1 and τxz2 are the (x, z) shear-stress components at. these boundaries.
This equation may be used to study the motion of an ice mass along its longitudinal profile by choosing z1 , for the upper boundary, z2 , for the bed, and the axis x in the general longitudinal direction (cf. Fig. l). It was also shown that for small slopes and stress gradients, a good first-order approximation was the equation of Reference BuddBudd (1968)

Fig. 1. Coordinate system mid boundaries for longitudinal stress equation.
where

is the mean stress deviator through the column, a is the surface slope, x is the basal shear stress (parallel to the bed), and x is taken generally along the glacier and it is not very important whether it is along the surface or bed provided the inclinations are small.
Equations (3) and (5) in effect represent the total longitudinal stresses on a column from the surface to the bed. Similarly to Reference NyeNye (1969[b]) we shall examine the four individual terms of Equation (5).
-
(i)
is the stress-deviator gradient term and represents the net longitudinal stress on the column of the ice up- and down-stream. It determines whether the column will extend or compress in the line of motion.
-
(ii)
is the down-slope stress and represents the down-slope component of the gravitational stress on a uniform slab resting on an inclined plane of slope α.
-
(iii) τb is the basal stress, or friction, term which, for the uniform slab on the inclined plane, would balance the slope term.
-
(iv)
may be termed the variational stress since it represents the resistance
of the medium to a varying stress gradient in the line of motion. It is usually associated with curved particle paths. For slowly varying stresses or long waves it becomes negligible (irrespective of the magnitude of τxz ) but for short-wave fluctuations it becomes very important.Reference BuddBudd (1968) indicated that for variations of wavelength about four times the ice thickness or shorter this term should be considered.
We note here that Equations (3) and (5), having been derived directly from the equilibrium equations, apply whatever the flow law.
1.3. Ice flow over sinusoidal bedrock perturbations
Reference BudaBudd (1970[a]) considered the motion of a medium of uniform thickness ![]() down a uniform slope α on which small harmonic perturbations
down a uniform slope α on which small harmonic perturbations
were superimposed, cf. Figure 2. The method used was to consider the perturbations to the flow down a uniform slope caused by the bedrock undulations. The model chosen was one in which most of the horizontal shear occurred near the bed so that for the perturbations the velocity in the upper region could be taken as approximately uniform. Also for this section of the medium a constant viscosity was taken so that the longitudinal strain perturbations were proportional to the longitudinal stress deviators.
This model is a simpler and more restrictive medium than the general medium for which Equations (3) and (5) for stresses apply.
We adopt the same simple model here as used in Budd (a]) (cf. Fig. 2) and the same axes system and boundary conditions, viz.
(1*) Upper boundary. The vertical stress for the perturbed upper surface is taken as
where h is the height above the unperturbed surface ![]() The sign has been chosen negative here (as opposed to positive in Reference BudaBudd 1970[a]) to keep tensile stresses positive.
The sign has been chosen negative here (as opposed to positive in Reference BudaBudd 1970[a]) to keep tensile stresses positive.
(2*) Lower boundary. The vertical velocity at the lower boundary υb is taken as
(3*) Steady-state condition. For the upper boundary the steady-state surface condition for the vertical velocity at the surface (υz) leads to
Where α1 and α2 are to be determined.
The stress function to be found to fit these boundary conditions is taken as
The previous paper used a viscous flow law defined by:
(where ƞ is the effective mean viscosity parameter) to determine the Ai
of Equation (11) which satisfy the boundary conditions Equations (8), (9) and (10), for the purpose of obtaining the surface profile, i.e. α1 and α2 in terms of the bed profile, b = b1
cos ωx, the ice thickness ![]() , the velocity V and the mean viscosity parameter ƞ.
, the velocity V and the mean viscosity parameter ƞ.

Fig. 2. Flow down uniform slope with simsoidal perturbations.
1.4. Aim of the present paper
The aims of the present analysis can now be given specifically:
-
First we wish to derive a general result for the stresses in the longitudinal stress equation. The individual components of stress follow from the stress function (11) and the surface slope from the stress boundary condition (1*). Hence the individual terms of Equation (5) can be calculated and the relations between them obtained. This will be quite general and independent of the flow law or the state of balance.
-
Using in addition the further conditions of (i) uniform velocity and flow parameter and (ii) the steady-state continuity, i.e. boundary conditions (2*) and (3*), a solution for this special case can be obtained which allows the magnitudes of the various terms to be assessed.
-
Finally the condition of steady state can be relaxed to show that the motion is independent of the state of balance provided the surface variations are small.
2. General Stress Equation
We begin by simply evaluating the stress components from the stress function in terms of the constants Ai which in general are determined by additional boundary conditions (e.g. 2* and 3*).
We note that without loss of generality we may chose A3 = A4 , i.e. make the cos ωx component of the base shear stress perturbation τxz zero when z = o and x = o . This is merely specifying the zero of the x axis with respect to φ, and in addition makes this context compatible with the next section and the steady-state flow over undulations of Reference BudaBudd (1970[a]).
The stress function is then
The stress components follow directly from the definition of the. stress function cf. Reference BudaBudd (1970[a])
The next step is to determine the terms G and T as integrals through the ice thickness. For Equation (5) the limits of the integration were the irregular upper and lower boundaries, and the equation is not exact.
Equation (3) is exact and we note that although z1(x) and zl(x) may in general be irregular functions of x, they are arbitrary, and this generality allows an important simplification lo be made here. In this case we choose the limits to be the straight-line means of the surface and the bed of Figure 2, viz. z = 0 and ![]() They could of course be taken at any other two levels in the medium, e.g. cf. Figure 4.
They could of course be taken at any other two levels in the medium, e.g. cf. Figure 4.
Now Equation (3) becomes

Also we note that for the unperturbed flow this equation becomes simply (cf.Reference BudaBudd 1970[a])
all other terms being zero.
Furthermore from Equation (8) for the surface

where α is the perturbation slope difference from the mean.
Equation (18) now becomes, for the perturbations noting that with the constant limits 0 and ![]() we can simply interchange the differentiation and integration,
we can simply interchange the differentiation and integration,

where

is the mean longitudinal stress deviator through the column.
Equation (21) is now the fundamental relation for which we wish to examine the part played by its various terms. Using a similar notation to that introduced in section (1.3) we may write for brevity
The first term is found from Equation (16) by performing the integration and differentiation viz.
The term s is found from Equations (20) and (15) as
For the surface Ts is found from Txz of Equation (17) by putting z = Z, is
Similarly for the base Txz )o = Txzwhen z = o
Using (17) we evaluate T as follows:


Finally

This completes the evaluation of the individual terms of Equation (22). To aid the comparison of the terms the same brackets have been used for the same expressions in each term. These terms are now combined together inTable I.
Table I. Separate Terms of the Longitudinal Stress Equation

It may not be surprising that the terms do all combine to satisfy Equation (23) exactly since this was derived more generally in Reference BuddBudd (1970[b]), but it is quite interesting to see the various relationships between the terms. The essence of the coefficient 2 of G is that each of the terms of G occur twice (in different terms) on the right-hand side. It may be surprising to some that G and s in fact have no terms in common. T has a term in common with all others. Some simple sub-relations may be written down which are also exact, e.g.
The first of these, Equation (31), simply expresses the equilibrium of the column in the line of motion. When τs is small, as we shall see is the case for small slopes (cf. next section), this gives
The second relation, Equation (32), shows that for small T (as we shall see is the case for long waves) G ≃ s, (not½s).
Already we begin to see the answer to Nye's question. The Robin-Budd hypothesis may be simply expressed as
where the bar represents the large scale regional average along the line of flow (≈ 20
(ii)
where G and s are the variations in the longitudinal stress gradient and the surface slope stress ![]()
The above analysis suggests
(i)
and
(ii)or
This will be more clearly brought out, in the next section, in terms of actual magnitudes, for the simple model described in section 1.3.
3. Special Solution For Steady-state Flow
3.1. Determination of stress terms
It is an easy matter to determine the values of the constants Ai of the stress function, Equation (13), and Table. for the special case of steady-state flow, and uniform velocity (V) and flow parameter (η) through the thickness.
It was shown in BuddReference BudaBudd (1970[a]) that the continuity equation for the perturbations with uniform velocity V implied
where υb and υz are the velocity components perpendicular to x at the base and surface respectively, cf. Figure 2;
and
is the given bedrock slope variation.
These together with the flow law
where ƞ is assumed uniform through the thickness, are sufficient conditions to determine the constants Ai of the stress function and the steady-state surface α in terms of β, V, and η, using Equation (16), viz.
and the stress boundary condition at the surface Equation (8):
The steady-state surface was determined byReference BudaBudd (1970[a]). A similar algebraic process is required to determine explicitly the values of the Ai This is given in the Appendix. Here we require only the specific terms appearing in the stress terms ofTable I. There are only five different terms and the required expressions are also derived in the Appendix, viz.
Where
This directly allows us to construct a Table II corresponding toTable I, showing the precise values of each term of the longitudinal stress equation.
Table II. Longitudinal Stress Equation for Steady-State Flow

3.2. The longitudinal stress equation
For typical ice flow conditions the ratio ψ of the surface variations to the bed variations is small, cf. Budd (1970[a]), Reference Budd and CarterBudd and Carter (1971).
Some conditions may exist (e.g. where ![]() is small), for which this factor is not large in which caseTable II gives the complete terms. In other cases
is small), for which this factor is not large in which caseTable II gives the complete terms. In other cases

Thus for small surface variations the term τ s may be neglected and the longitudinal stress equation may be written as
or
i.e.
This last equation shows that for long waves (ω
as a function of relative wavelength ![]() is shown in Figure 3.
is shown in Figure 3.
This indicates that for wavelengths ![]() or less the term T cannot be neglected, nor can the higher-order terms in the expressions for G and τb
.
or less the term T cannot be neglected, nor can the higher-order terms in the expressions for G and τb
.
3.3. Surface strain-rate variations
In order to relate the stresses to measured surface strain-rates we note that the longitudinal stress deviator at the surface, or rather for ![]() is given by:
is given by:
therefore

This equation is exact and may be used directly to associate the surface strain-rate ![]() with the surface slope variations α a through
with the surface slope variations α a through

Fig. 3. Relative magnitude of variational stress, T, to slope stress, pgZa, different wavelengths.
This gives for the surface strain-rate variations
which differs from the relation of Reference BuddBudd (1968) by a factor of 2 since the parameter B used there is related to the viscosity here. ƞ, by
Secondly the term on the left concerns surface values and not averages through the column. However for small slopes and long waves it is apparent from the above that this also becomes approximately the same as the average through the column. Again Figure 3 indicates the magnitude of the error.
3.4. Calculation of surface slopes from steady-state flow
For calculations of the type made byReference Robin de.Robin (1967) where the continuity equation for average velocity through the column is used to obtain longitudinal strain-rates, Equations (54)
(55)) (56) are relevant. Again there is a correction of a factor 2 required to Robin's formula and in addition for the higher frequencies the term T is required. For example for the second half of the southern line from Camp Century the mean ice thickness is c. 1100 m and the predominant mean wavelength c. 3.6 km. This gives ![]() From Figure 3 this indicates an increase in stress (or decrease in calculated slope deviation) of about 70%. Both these features together may explain why Robin's calculated surface slope variations were much larger than the measured surface slope deviations, and thus further support his use of the laboratory Bow parameters extrapolated to lower strain-rates.
From Figure 3 this indicates an increase in stress (or decrease in calculated slope deviation) of about 70%. Both these features together may explain why Robin's calculated surface slope variations were much larger than the measured surface slope deviations, and thus further support his use of the laboratory Bow parameters extrapolated to lower strain-rates.
3.5. Variation of longitudinal and base stress with surface slope
Nye's question can now be answered explicitly as follows. The empirical evidence for the Robin-Budd hypothesis was one of proportionality, i.e. the longitudinal stress (or strain-rate) variations G are proportional to the surface slope variations s or
The hypothesis was to make the assumption that the base stress. stays at its regional value while the surface slope variations caused variations in the longitudinal stress deviator gradient. i.e.
In fact we find for small surface variations
and in addition for long waves where T may be neglected
The factor 2 difference between the relations was absorbed in the case of Reference BuddBudd (1968) in the calculated flow parameter. In the case of Reference Robin de.Robin (1967), higher calculated surface slopes. The reason for the presence of the factor of 2 is that the base stress does not stay constant at its regional value but varies similarly to the surface slope for long waves. For short waves the expressions for both the base stress and average longitudinal stress gradient through the column require the addition of the higher-order term T.
4. Generalizations And Extensions
4.1. Relaxation of steady-slate condition
If the surface variations are small the surface stresses (for ![]() ) are also small and so if they may be neglected it docs not matter much whether they are in a steady state or not. If the surface stresses are neglected the base stress and longitudinal stress gradient are given by
) are also small and so if they may be neglected it docs not matter much whether they are in a steady state or not. If the surface stresses are neglected the base stress and longitudinal stress gradient are given by
Using Equation (47) this can be expressed in terms of ß1, η and V as
This result still applies whether the surface slope is in exact balance or not. In this case the surface slope variations are irrelevant. Or in other words for small surface variations compared to the bed variations the base stress and longitudinal strain-rates are governed by the deformation of the stream-lines of the ice to conform to the bedrock profile. It so happens that for a steady state a particular surface shape is formed which is simply related to the bed profile and the motion, and thereby provides a further means of calculating the base stress or longitudinal stress variations, directly from the surface. The stress effect and motion of non-steady state or transient surface waves was indicated in Reference BudaBudd (1970[a]).
4.2. Relaxation of uniform viscosity and velocity conditions
The generalization of the above discussion to take into account the variation of the flow parameter with stress, temperature or crystal type etc. may be studied in the following way. The stress solution still applies but the strain-rate solution will be somewhat modified. We start from the expression for the modified stress deviator and the flow law. viz.
and
where η is now a function of stress and temperature etc.
Since the stress analysis carried out in section 2 applies for any two boundaries z1
and z2
, parallel to the mean bed and distance ![]() apart, we may divide the ice mass up into a number of thin layers of thickness
apart, we may divide the ice mass up into a number of thin layers of thickness ![]() cf. Figure 4.
cf. Figure 4.
For the type of model considered here the viscosity and velocity may be expected to vary considerably with depth but not appreciably in the longitudinal direction.

Fig. 4. Treatment of variable viscosity and variable velocity with depth.
Hence by considering a sequence of increasing viscosities η1 η2 . . . . . and velocities V1 , V2 …. from the base upwards the boundary conditions
analogous to Equation (40) may be used where now the bi refer to the stream lines between the various layers, [n this way the decrease in amplitude and degree of phase shift of the waves as well as the magnitudes of the stress variations at various levels may be traced through the ice by repetition of the previous analysis using the sequence of specified velocity and viscosity variations with depth. If a continuous analytical expression is available for η and V the strain-rate variation is given by
and the velocity variations can be found by integration.
The expression for the damping factor
with η and V in the denominator indicates that for typical profiles of velocity and viscosity decreasing towards the bed the damping there of the high frequency bedrock variations is even more greatly enhanced.
For the long waves which do penetrate to the surface. Equation (74) with η in the denominator indicates that it is the high resistance of the upper layers that is most relevant to the surface variations i.e. the appropriate average viscosity is a weighted mean of the reciprocals similar to a harmonic mean, or we may say that the resistances of different layers to the ice motion combine somewhat like electrical resistances in series in that the highest resistances are the most important.
The results of this section indicate that where the greatest shear is taking place near the bed then both the high-frequency bedrock variations and the lower viscosity near the bed become unimportant in determining the major stress variations through the ice which are primarily governed by the higher and more uniform velocity and viscosity of the upper layers. This indicates that the simple analysis of the previous sections with uniform velocity and viscosity will not be much affected by decreasing velocity and viscosity with depth except for the high frequency variations near the bed. For the present study the base z = o can be chosen at any level and in particular above the high shear layer near the bed.
4.3. Stress variations on a flat base
Suppose instead of undulations superimposed on a Hat base we consider harmonic variations of the basal shear stress about its mean value on a flat bed according to Equation (70). In this case the same solution describes the motion that takes place. The stream lines are the same as before with undulating motion near the base being formed by the varying longitudinal stress and strain-rates associated with the varying shear stresses.
It is obvious from Equation (70) that longitudinal stress gradient variations go hand in hand with basal stress variations and vice versa. Both are involved with the resultant steady-state surface slope variations. More complex variations of basal stress can of course be studied by means of Fourier series or integrals. An interesting case of the basal stress varying on a Hal. base is the situation where ice flows across a smooth but abrupt transition from grounded to floating ice. This corresponds to a simple step function variation of basal stress. These positions are often associated with a surface slope variation. It would be valuable also to have measurements of the corresponding longitudinal strain-rate variations over such a transition.
4.4. Small-scale variations at the base
So far the study has been concerned with flow over the large-scale undulations which have some influence on the surface. As we have seen the small-scale irregularities are quickly damped out in the lower layers, and are not relevant to the study of surface variations. Several studies of the effects of small-scale irregularities however have been made e.g.Reference LliboutryLliboutry (1968), Reference WeertmanWeertman (1964), Reference NyeNye (1969[a]), so it is necessary to indicate here the transition between large and small irregularities.
To do this we go back to the velocity distribution through the ice for the uniform flow of the unperturbed state, cf. Reference BudaBudd (1970[a]). Here the velocity profile is given by
where we have taken a power law for flow with parameters n and B and B is in general dependent on the ice temperature etc., α is the mean regional slope, and ![]() is the distance below the surface.
is the distance below the surface.
Suppose for the moment the simplest case in which n = I and B is constant
Here Vb is an unspecified boundary condition—the sliding velocity of the base. Now the perturbations to the basal stress are given by Equation (70) as
If we average this value along the x axis for a distance large compared with the wavelength ![]() we find it has negligible effect on the average basal stress, even though the variations become very high as the frequency ω increases (ƞ, V, ß1
, assumed constant). What is more relevant to the effect on the motion is the energy dissipation throughout the ice. Consider a stress variation near the base given by
we find it has negligible effect on the average basal stress, even though the variations become very high as the frequency ω increases (ƞ, V, ß1
, assumed constant). What is more relevant to the effect on the motion is the energy dissipation throughout the ice. Consider a stress variation near the base given by
The energy dissipation for constant viscosity is given by
Now we integrate this expression throughout the ice over distances large compared with the wavelength
For η, V, ß1 , constant this expression increases indefinitely with ω. However if we take the integral in the vertical, instead of from zero, from some arbitrary small distance, say b, (the amplitude of the variations) from the base then the expression for the energy dissipation in the majority of the ice is given by
Considering variations in wavelength for constant amplitude this may be written
We notice that this expression tends to zero for very high ω.
If we consider a uniform spectrum of bedrock amplitudes we find that the expression b3ω3e-ωb has a maximum for ωb = 3/2 or
indicating that for the ice above z = b the effect of the perturbations starts to decrease for ![]() .
.
For the region below this level the energy dissipation still increases with ω but becomes increasingly concentrated at the base. In spite of this the average base stress remains constant.
From Equation (77) we notice that the magnitude of the sliding velocity does not effect the basal stress. The energy dissipation at the base due to sliding is τ b V b. So if this is to decrease while τb remains constant Vb must decrease. Thus the increasing frequency in Equation (81) for the dissipation of energy can only go along with a decreasing sliding velocity Vbs so that as ω →o, Vb→o and Wb→o with the basal material in contact with the bed motionless. In effect the motion can be described as the layer below z = b becoming sheared off as λ→o. Real beds however are much more complex but in two dimensions may be approximated by Fourier series or integrals in which case steep edges or fronts in the bedrock are features which may be described as having a strong concentration of high-frequency terms. It is here that shearing of the ice may take place.
However it is at this stage that any simple treatment becomes somewhat academic, because of the many complications that need to be considered, e.g.
-
regelation cf. Reference LliboutryLliboutry (1968), Reference NyeNye (1969[a]),
-
water production and lubrication cf.Reference WeertmanWeertman (1962),
-
effects of moraine on the bed and in the ice cf. Reference Lister, Lister, Pendlington and ChorltonLister and others (1968),
-
enhanced horizontal shear caused by the non-linearity of the flow law and the high longitudinal strain-rates near the bed associated with the irregularities.
This latter does not appear to have been dealt with but may be a feature of apparent very high flow-law exponents found in borehole shear near the bed, cf.Reference Kamb and ShreveKamb and Shreve (1966).
In this paper we have taken a given ice thickness ![]() , an average surface and bed slope α.and a mean down-slope velocity V, to calculate the effect of undulations in the bed on the motion. This docs not gloss over the effect of small-scale irregularities but finds they are only important in so far as their average over the larger scales determines the large-scale motion including the mean velocity
V
surface slope α, the ice thickness α, and regional base stress
, an average surface and bed slope α.and a mean down-slope velocity V, to calculate the effect of undulations in the bed on the motion. This docs not gloss over the effect of small-scale irregularities but finds they are only important in so far as their average over the larger scales determines the large-scale motion including the mean velocity
V
surface slope α, the ice thickness α, and regional base stress ![]() Reference NyeNye (1969[a]) also found that il is the average bed spectrum of variations that is relevant to the average base stress and velocity.
Reference NyeNye (1969[a]) also found that il is the average bed spectrum of variations that is relevant to the average base stress and velocity.
Since the large-scale base stress can be determined from Equation {59) for steady-state flow of uniform thickness or more generally Equation (5) which requires only large-scale data—ice thickness, surface slope, surface strain-rates, then it suggests that a theory of sliding and basal stress can be developed from a macroscopic point of view.
5. Summary And Conclusions
Harmonic solutions of the stress function provide a relatively simple means of analysing sinusoidal stress or strain-rate variations in a quasi-static moving medium.. Applied to the How of ice over undulations this method enables each term of the longitudinal stress equation to be determined and the relations between the stress terms evaluated. As a result, some simple expressions are obtained for the relations between these various stress terms. In addition to the longitudinal stress equation
an exact sub-relation for the longitudinal stress gradient term G in terms of the surface slope term s = ![]() and the variational stress term T is
and the variational stress term T is
An exact sub-relation between G and the base stress τb , and surface stress τb is
These apply whatever the flow law and whether or not the ice mass is in balance.
For small surface variations, τs is negligible compared with the other terms giving
For a simple model whose velocity and viscosity are uniform with depth in the upper layers. and whose surface is in steady state, the variational stress is given by
and its variation with wavelength (λ = 2π/ω) is shown in Figure 4. For long waves T is negligible giving
but for high frequencies it becomes very important and explains the absence of the effect of any high-frequency bed variations in the surface. The main effect of high-frequency bed variations is to impair basal sliding by energy dissipation until the wavelength becomes so small that other effects such as regelation or lubrication become important.
For typical velocity and viscosity profiles which decrease with depth the high-frequency bed variations become even less important and the ice reacts to the long waves with an effective harmonic mean viscosity which places most weight on the upper layers.
Appendix
Determination Of The Stress Function Constants Ai For Steady-state Flow With Uniform Velocity And Viscosity
To avoid excessive repetition or back reference yet maintain satisfactory completeness the following decimal numbered equations are taken directly fromReference BudaBudd (1970[a], section 4).
The argument runs as follows. Starting from the harmonic stress function (Ai ) the longitudinal stress deviator (A2) is found from the definition of the stress function in terms of the stresses σx
and σz
. Equation (A3) expresses the flow law generally. The vertical velocity (A4) is found by integration and here the assumption of constant if is introduced. (A5) expresses the basal boundary condition which gives A1
, in terms of A2
and A3
in terms of. A4
, Two further conditions are required. (A9) expresses the steady-state surface criterion and here introduces an assumption of uniform velocity i.e. the F of (A5) and (19) is the same. The other condition results from the prescribed vertical boundary stress at ![]() (A11). Here to preserve the convention of tensions being positive, h must represent the distance below
(A11). Here to preserve the convention of tensions being positive, h must represent the distance below ![]() Equation (A12) makes the steady-state surface correspond to the prescribed surface stress distribution. (A13) makes this also agree with the surface stress derived from the stress function (A1) at
Equation (A12) makes the steady-state surface correspond to the prescribed surface stress distribution. (A13) makes this also agree with the surface stress derived from the stress function (A1) at ![]() Finally these two are equated giving (A14) and (A15) which together with (A6) make a set of three equations in three unknowns.A1
, A2
and. A3
.
Finally these two are equated giving (A14) and (A15) which together with (A6) make a set of three equations in three unknowns.A1
, A2
and. A3
.
These equations were not solved explicitly inReference BudaBudd (1970[a]) since only the ratio of the surface to bed velocity was being sought.
The following results ofthat work are noted (with a sign correction)
Here the object is to determine the constants A i explicitly and the specific combinations of them occurring in the individual stress terms ofTable 1.
From Equation (A6)
Using this to eliminate A 2 from (A14) and (A15) yields
Eliminating. A3 , from these gives
or
or using (A7)
Substituting in (A19) gives

Using (A7)
Substituting A1 from (A23) yields for A3

Therefore
or using (A7)
With these values of the Ai the various combinations required forTable 1 may now be easily obtained. Using (A23) and (A26)

or using (A7)
and using (A17)
Similarly
or using (A7)
and using (A17)
We write
and
where the negative sign is introduced to make h1 and h2 height above z = Z
Now the various terms ofTable 1 tan be easily evaluated, From (A35) and (A38)
From (A6), (A7) and (A18)
From (A29) and (A17) and (A38)
From (A32)
From (A29) and (A17)
This completes the evaluation of the five different terms required forTable I. Equations (A40), (A44), (A47), (A48) and (A50) now allow (he stress of Table 1 to be expressed simply in terms of the steady-state surface parameters the ice thickness and wavelength of the undulations.


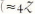 or less) requires the addition of the fourth term
or less) requires the addition of the fourth term 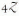 ou moins) il faut ajouter le quatrième terme
ou moins) il faut ajouter le quatrième terme 





