Introduction
The electromagnetic response of a given medium is generally described by a complex dielectric constant ε* = ε′ – iε”, with the familiar index of refraction ![]() The attenuation length
The attenuation length ![]() is the frequency- (f-)dependent inverse of the loss, which is related to the ‘loss tangent′ tan δ = ε”/ε′ via (Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others, 1985): loss
is the frequency- (f-)dependent inverse of the loss, which is related to the ‘loss tangent′ tan δ = ε”/ε′ via (Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others, 1985): loss ![]()
Here, c0 is the electromagnetic wave speed in vacuum, and ω (= 2πf) is the angular frequency. The absorption of radio-frequency (RF) electromagnetic radiation can result in either bulk conductivity (in ice, due to the mobility of proton defects (Reference Petrenko and WhitworthPetrenko and Whitworth, 1999), and growing with frequency) or polarization of the medium itself (due to rotation of the ice molecules at their fixed sites, having a resonance pole at f ~ 103 Hz and a magnitude decreasing with frequency away from the resonance pole). In the frequency regime 0.1–2 GHz, due to the dominant polarization and lattice vibration effects, we expect that ε” ~ 1/f, or Lα ~ constant.
Free of impurities, in situ measurements have demonstrated that enclathrated glacial ice will transmit visible photons over ~200m (Reference Woschnagg and PriceWoschnagg and Price, 2001). At longer wavelengths, attenuation lengths for pure ice in the laboratory Lα (f = 300MHz)~6km (Reference Matsuoka, Fujita and MaeMatsuoka and others, 1996; Reference Fujita, Matsuoka, Ishida, Matsuoka, Mae and HondohFujita and others, 2000) have been derived, at T = –50°C. Using laboratory samples, the temperature dependence of the RF attenuation length has been found to be significant, with the attenuation length decreasing by a factor of ~3, for example, as the ice temperature warms from –50 to –20°C. In situ measurements at radio frequencies have, however, resulted in a wide range of values for the attenuation length (Fig. 1). This variation presumably reflects differences in impurity and contaminant levels, and may also reflect difficulties in separating scattering from true absorption effects in assessing their relative contributions to effective attenuation. Reference EvansEvans (1965) and Reference Evans and SmithEvans and Smith (1969) performed some of the earliest in situ dielectric constant measurements, obtaining losses (dBm–1) of 0.3 dB (100 m)–1 at T = –50°C, and ~1dB(100m)–1 at T = –30°C, in the frequency regime below 500MHz, but with sharply increasing attenuation above that value.

Fig. 1. Previous attenuation length measurements; data are taken from Reference EvansEvans (1965), M. Walford (unpublished data), Little America, Antarctica (Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others, 1985), and Westphal (cited in Reference JiracekJiracek, 1967), as shown.
Recently, dielectric profiling (DEP) measurement data have been made available from Antarctic ice cores from Siple Dome and Dronning Maud Land (core B2). In these measurements, two probes slide along the vertical length of a core, and the conductivity across the core is measured directly. Figure 2 (using data taken from http://nsidc.org/data/waiscores/pi/taylor.html) compares the raw conductivity from four different cores extracted from Siple Dome, as well as the extracted value of tan δ (250 kHz) for Siple core A compared to Dronning Maud Land (Reference Eisen, Wilhelms, Nixdorf and MillerEisen and others, 2003). The Siple data correspond to T≈ — 25°C (see, e.g., http://skua.gps.caltech.edu/hermann/tsiple.gif). These loss tangents correspond to field absorption lengths well in excess of 1 km; we note the decrease in loss tangent with depth, which highlights the need for such high-precision conductivity measurements on deeper cores.

Fig. 2. (a) Raw conductivity, comparing four different cores taken from Siple Dome. (b) Extracted value of tan(<5) for core A, compared with data taken from Dronning Maud Land.
The remarkably long RF attenuation length of cold ice has enabled experimental initiatives aimed at detection of neutrinos via radio coherence. Several neutrino telescopes (Reference AhrensAhrens and others, 2004a, Reference Ahrensb; Reference SokalskiSokalski, 2004; C. Spiering for the BAIKAL collaboration, http://arxiv.org/abs/astro-ph/0404096) currently either operating or under construction have the potential to detect high-energy cosmic-ray neutrinos of energies Ev > 10 GeV. These detectors are based on photomultiplier tube detection of the optical Cherenkov radiation which results when a muon neutrino collides with an ice molecule, producing a muon traveling at velocities faster than the local velocity of light. Such instruments have limited sensitivity in the regime Ev >1 PeV.
The innovative Soviet physicist G. Askaryan (Reference AskaryanAskaryan, 1962, Reference Askaryan1965) suggested over 40 years ago that detection of the longer-wavelength components of (broadband) Cherenkov radiation could offer a more advantageous strategy for detecting electromagnetic showers (cascades) at >PeV energies. Within the last few years, the Askaryan effect was dramatically demonstrated in a SLAC (Stanford Linear Accelerator Center) test beam experiment (Reference SaltzbergSaltzberg and others, 2001). In tandem, there has been significant progress in modeling the signals from electromagnetic showers. Despite the numerical intricacies of such modeling, recent calculations of the expected field strengths have converged (Reference Halzen, Zas and StanevHalzen and others, 1991; Reference Zas, Halzen and StanevZas and others, 1992; Reference Alvarez-Muniz, Marques, Vazquez and ZasAlvarez-Muniz and others, 2003; Reference RazzaqueRazzaque and others, 2004).
The balloon-borne ANITA (Antarctic Impulsive Transient Apparatus;Reference Silvestri, Shapiro, Stanev and WefelSilvestri and others, 2005) project, the RICE (Radio Ice Cherenkov Experiment) project at the South Pole (Reference Kravchenko, Besson and MeyersKravchenko and others, 2003a, Reference Kravchenkob), the GLUE (Goldstone Lunar UHE neutrino Experiment) project (searching for radio signals from neutrino interactions in the lunar regolith) (Reference Gorham, Hebert, Liewer, Naudet, Saltzberg and WilliamsGorham and others, 2004), and the FORTE (Fast On-orbit Recording of Transient Events) search for neutrino interactions in the Greenland ice cap (Reference Lehtinen, Gorham, Jacobson and Roussel-Dupre.Lehtinen and others, 2004) build on initial measurements in Antarctica of natural and man-made radio impulse background for the RAMAND (Radio wave Antarctic Muon And Neutrino Detector) experiment near continental station Vostok in 1985–90 (Reference Markov and ZheleznykhMarkov and Zheleznykh, 1986; Reference Butkevich, Kaidalov, Zheleznykh and KrastevButkevich and others, 1988; Reference Dagkesamansky and ZheleznykhDagkesamansky and Zheleznykh, 1989; Reference Provorov and ZheleznykhProvorov and Zheleznykh, 1995) to achieve unprecedented sensitivity to neutrinos at energies in excess of 1017 eV. Following a successful test flight in 2003/04 which enabled shake-down of the essential electronics and hardware, radio receivers mounted on the ANITA gondola during a 2006/07 circumpolar flight will synoptically scan the Antarctic ice for evidence of radio waves produced by cosmic neutrinos crashing into the ice cap. For all these experiments, the number of neutrino detections depends on the volume to which the detectors are sensitive, which depends primarily on the local temperature- and impurity-dependent radio wavelength attenuation length.
Experimental Approach
Two measurements of the RF attenuation length were attempted in December 2003–January 2004, at Amundsen–Scott (South Pole) Station. In one, RF signals were broadcast horizontally from a distant transmitter (Tx) lowered into an ice hole to a depth (z) of 125 m to the RICE array of under-ice receivers (Rx), located ~3 km away horizontally and consisting of dipole receivers at depths of 100–350 m. For the case where z(Tx) = z(Rx), and both transmitter and receiver are located below the firn, this measurement offers the possibility of directly probing ice attenuation at a uniform ice density and temperature. However, due to the vertical variation of the index of refraction (n(z)) with depth in the ice (Reference KravchenkoKravchenko and others, 2003c) and the consequent curvature of rays emitted by such a shallow transmitter, the RICE array is located in the ‘shadow zone’ for this particular geometry;the nonobservation of clear RICE receiver signals therefore merely verified (qualitatively) the presence of a gradient in the index of refraction, and this approach was subsequently abandoned. Future measurements, with both Tx and Rx well below the firn, should yield more directly useful results.
As an alternative, signals were broadcast vertically from a horn antenna on the surface down through the 2.8km thick ice cap at the South Pole and reflected upwards off the bedrock to a surface receiver. The surface receiver is attached, by a short coaxial cable, to a digital oscilloscope, which records waveforms. This measurement has the disadvantage of integrating over ice of varying temperature, and also requires a sufficiently strong bed echo to produce a measurable signal. Nevertheless, this approach offers simplicity of experimental set-up and triggering and avoids large cable losses to both receiver and transmitter. In the rest of this paper, we focus on results from this second approach.
To maximize experimental sensitivity, the signal was broadcast as a single-frequency tone burst, of duration 40 ns to 8μs, triggered by a 1 pps TrueTime global positioning system receiver output. The selection of a tone was a compromise between a fast pulse (characterized by a fast, distinctive rising edge in the time domain, but having a somewhat complicated Fourier spectrum which must be separated from the noise) and a continuous wave signal (clearly evident in the time domain, but subject to multipath interference effects). The GPS output was split into two copies: one copy was fed directly into one channel of the LeCroy digital oscilloscope (4 GSas–1, 1 GHz bandwidth) to monitor the signal start time; the other was sent to the transmitting horn antenna (Fig. 3). A sample signal generator output showing the monochromatic tone (in this case, 200ns duration) sent to the transmitter is shown in Figure 4.

Fig. 3. Sketch of experimental method. One TEM horn antenna transmitter (‘Tx horn’) broadcasts RF signal through the ice cap, off the underlying bedrock and up to an identical TEM horn antenna receiver (‘Rx horn’). A 52 dB, 1 GHz bandwidth low-noise amplifier (not shown) is used to boost the signal at the output of the Rx horn into the dynamic range of the LeCroy digital oscilloscope. The horizontal distance between the horns is of order ~25 m.

Fig. 4. Signal generator output, showing monochromatic signal ‘tone’ sent by cable to transmitter and broadcast to receiver.
Signal Detection and Observables
Signals are measured in three ways. After sufficient averaging, the signal is directly observable in the time domain. Figure 5 displays the voltage, as a function of time (V(t)) obtained after averaging 40 000 samples. Each sample consisted of one 400 ns signal, broadcast at a frequency of 380 MHz. The figure clearly shows shallow internal reflections early in the waveform, as well as the 400 ns duration signal ~33.8 μs later, corresponding to the bedrock reflection at ~2800m depth. (The times have been converted into distances using an average index of refraction through the firn of n = 1.5, and an index of refraction below the firn of 1.78.) This location of the bottom echo is consistent with other measurements of the bedrock echo. The corresponding signal is also clearly evident in the frequency domain. Figure 6 shows the fast Fourier transform (FFT) intensity, as one scans in 500 ns windows across the waveform. The 380 MHz signal is clearly strongest in the time interval corresponding to the observed V(t) signal.

Fig. 5. Search for bottom echo (as a function of implied depth) using horn broadcasting to horn, 40K samples, f = 380MHz. Horizontal axis has been converted into distance, as described in the text. Note the enhancement at ~2800m depth.

Fig. 6. Search for bottom echo (as a function of time delay relative to surface signal) in the frequency domain, based on Figure 5 (40 K samples). Time intervals of FFTs are as indicated; no cable-time delay corrections have been applied. Signal is clearest at the known broadcast frequency (380 MHz).
Most succinctly, one can cross-correlate a monochromatic, 400 ns width, 380 MHz ‘template’ with the measured Rx-horn signal. This allows observation of the turn-on of the return signal, and gives a more quantitative measure of the reflected signal. Figure 7 shows the magnitude of crosscorrelation (arbitrarily normalized to the saturated outgoing pulse) between the measured data and the template, as a function of the center time of the correlation template. The correlation function has been digitally down-converted to baseband (0–5 MHz based on the 400 ns tone burst used here). The bedrock return is distinct at 33.8 μs in this echogram.

Fig. 7. Search for bottom echo (as a function of implied depth) using horns, using cross-correlation. The locations of significant returns prior to the bedrock reflection are indicated.
Extraction of Attenuation Length from Horn Measurements
Absolute determination of the average attenuation length 〈Lα〉
Figure 8 shows the echograms for various frequencies, showing the exponential decay of the incoherent back-scattering, which meets the noise floor at about 2000 m depth. Bottom echoes rise above this noise floor at the 2810 m South Pole ice depth.

Fig. 8. Search for bottom echo (as a function of implied depth) for several different frequencies, and also time duration of broadcast signal. Dashed vertical line indicates bed location.
Figure 9 shows a zoomed version of the same data as in Figure 8, centered on the expected location of the bottom reflection at ~2810 m. Here we have rescaled the plots vertically in terms of the measured signal-to-noise ratio (SNR) above the noise floor, which is at 0dB in each pane. The values of the SNR range from 9 to 25 dB, giving detection levels which are about 3.5–4σ in terms of Gaussian confidence levels, for the weakest reflections. The majority are, however, much stronger, and statistical errors are negligible in determining the associated attenuation length.

Fig. 9. Zoom of Figure 8, renormalized, and showing signal region in greater detail.
It is interesting to note that a region of higher reflectivity from 2200 to 2500 m appears in many of the bands;there appears to be some tendency for its strength to be correlated to a weakening of the bottom reflection. This is not surprising since such reflections, probably due to narrowband interference effects of a group of ice layers, must scatter power from the beam. Their location within 500 m of the bottom also means that the strength of the bottom echo is apparently intrinsically weaker in several cases than the echo from these layers, since the distance correction is only about 20% in field strength, or <2dB in power. Such effects are of course well known in optics: when a series of dielectric layers with thicknesses smaller than a wavelength are applied to a plate, very large reflection coefficients can be obtained over narrow bands even when the reflectivity of any individual layer is small (Reference Born and WolfBorn and Wolf, 1997). The loss of power due to constructive interference effects of several layers leads to a further underestimate of the bulk attenuation length for these frequencies. Although the layers do have an important effect for narrowband signals, extremely broadband signals such as coherent radio Cherenkov radiation would be largely unaffected.
Signals are evident across the frequency range 250–700 MHz. To extract Lα, we compare the measured power to the power that would be expected in the absence of attenuation through the ice. The Friis equation relates the ratio of the measured power in a receiver antenna to the transmitted power via P Rx/P Tx = G Tx G Rxλ2/(16π2d2 L), with PTx the power input to the transmitter, GTx the gain of the transmitter relative to an isotrope, CRx the gain of the receiver relative to an isotrope, d the distance from transmitter to receiver, A the broadcast wavelength, and L the known system loss factor, taking into account cables, etc. In our case, PTx ~ 50 W, d~ (2 ×2.81) km, and A ~ 1m, depending on the broadcast frequency. The gain of the TEM horn antennas is based on a calibration originally performed on the roof of the University of Kansas Physics Department, and later verified during the course of our measurements, yielding GTx ≡ CRx ~ 12dBi at boresight. Using the Friis equation, the voltage measured in the receiver horn (V(scope), measured) can be compared to the expected signal strength in the absence of any attenuation (V(scope), no loss), and the number of absorption lengths traversed through the distance d correspondingly extracted. A summary of the absolute gain calculations is presented in Table 1.
Table 1. Data used in extraction of attenuation lengths

Measurement relative to direct (in-air) transmission
Measurements were also made with the horns pointed directly at each other, and broadcasting through the air. Knowing the distance between the horns in-air (dair), as well as the round-trip distance of the signal path through ice dice, considering the air to be non-absorptive, and attributing all in-ice losses greater than 1/r amplitude spreading to ice attenuation, we can use
to extract the ‘average’ attenuation length 〈Lα〉, with V ice and V air the measured voltages for the in-ice and in-air signal paths, respectively. Table 2 summarizes the experimental differences between the in-air and in-ice measurements.
Table 2. Comparison of in-air vs in-ice measurements

Check of thermal noise floor
Although there are other evident signal returns in the echogram for depths up to 2000 m, below this depth the V(t) spectrum is largely featureless (Fig. 5). We have quantitatively verified that the signal return, below 2 km, is roughly consistent with the expected thermal ‘floor’. The thermal noise power PT ~ kTB, with B the bandwidth of the system, corresponding to –174dBm Hz–1, –114 dBm (-144 dB)MHz–1. Since the pulse duration is 400 ns, the effective bandwidth is 2.5 MHz. The 52 dB amplifier used at the output of the Rx horn gives an expected value (in units of dB rather than dBm) of ~–88 dB. The scope average over N coherent samples (N = 40 000) should result in a reduction of the noise power by a factor of ![]() approximately commensurate (within ~8dB) with the background levels shown in the echogram in the vicinity of the bedrock echo.
approximately commensurate (within ~8dB) with the background levels shown in the echogram in the vicinity of the bedrock echo.
Determination of the attenuation length as a function of temperature
Since the attenuation depends on temperature, and since the temperature gradient is positive with increasing depth (dT/dz> 0), the ice near the bottom of the ice cap is most absorptive. To extract the temperature-dependent attenuation length, we relate the measured average attenuation length to the integrated attenuation length along a vertical chord: ![]() We use the parameterization of Lα
(T) from Reference Matsuoka, Fujita and MaeMatsuoka and others (1996), and use the measured temperature profile (Reference PricePrice and others, 2002) at the South Pole obtained by the AMANDA (Antarctic Muon And Neutrino Detector Array) experiment. Figure 10 shows the results of this exercise, displaying the average attenuation length under various assumptions for R, as well as the attenuation lengths extracted at –50°C. At a frequency of 380 MHz, we find Lα
~ 1450 m, at –50°C. The open pentagonal points in the figure represent the average attenuation lengths obtained by normalizing the inair measurements to the in-ice measurements.
We use the parameterization of Lα
(T) from Reference Matsuoka, Fujita and MaeMatsuoka and others (1996), and use the measured temperature profile (Reference PricePrice and others, 2002) at the South Pole obtained by the AMANDA (Antarctic Muon And Neutrino Detector Array) experiment. Figure 10 shows the results of this exercise, displaying the average attenuation length under various assumptions for R, as well as the attenuation lengths extracted at –50°C. At a frequency of 380 MHz, we find Lα
~ 1450 m, at –50°C. The open pentagonal points in the figure represent the average attenuation lengths obtained by normalizing the inair measurements to the in-ice measurements.

Fig. 10. Extracted attenuation lengths, as a function of frequency. Lower set of lines correspond to ‘average’ attenuation lengths obtained from the Friis equation, under various assumptions for the bedrock reflectivity. Results depicted by open pentagonal symbols are obtained by normalizing Tx → Rx signal (in-air) relative to Tx → Rx signal (in-ice), assuming R = 1. Upper set of lines show derived attenuation lengths, at T = –5Ü°C, taking into account the measured T (z) profile at the South Pole (Reference PricePrice and others, 2002), combined with the Reference Matsuoka, Fujita and MaeMatsuoka and others (1996) estimate of Lα (T).
Possible birefringent effects
Over the last three decades, several studies of RF birefringence in the ice sheets have been conducted (Reference HargreavesHargreaves, 1977, Reference Hargreaves1978; Reference MatsuokaMatsuoka and others, 2003). Two types of birefringence are, in principle, possible. In the case where the transmitting medium exhibits a particular asymmetry, or chirality, the left- and right-circular polarizations (LCP and RCP, respectively) may propagate with different velocities. In such a case, (a) the polarization of the propagating signal varies with distance from the transmitter, and (b) there is a time delay ∆f between reception of LCP vs RCP, given by Δt=(nLCP – nRCp)d/c0, where nLCp and nRCp are the indices of refraction of the LCP and RCP, d is the total distance traveled by the ray, and c0 is the velocity of light in vacuum. Alternately, in media such as polar ice without rotational asymmetry, birefringence may result from the different propagation velocities of the two orthogonal projections of a linearly polarized wave (e.g. ‘x-’ and ‘y-’, or ‘ordinary’ and ‘extraordinary’). In such a case, ∆t = (nx – ny )d/c, where nx and ny are the indices of refraction along the orthogonal basis axes. Vertical asymmetries in ice properties might be expected to result from gravitational effects;horizontal asymmetries are expected to result from ice-flow effects. In order to properly probe birefringence, one should in principle map out all possible orientations relative to both the horizontal and vertical. Furthermore, one would ideally measure the interference effects which might result when the two linearly polarized projections recombine at the receiver, which we have not done. We would expect that proper inclusion of such birefringent effects would only tend to increase our estimated attenuation length, since we currently assume our received signal to be a coherent sum of two in-time polarizations. Correcting for any mitigation of the detected signal due to birefringent effects would therefore increase our estimated L α.
We did, nevertheless, probe propagation asymmetries by rotating the receiver horn by 90° relative to the default (‘copolarized’, or parallel) orientation, so that the long axis of the receiver horn was perpendicular to the long axis of the transmitter horn on the surface (‘cross-polarized’). If there are large depolarization effects due to basal scattering, we might expect considerable signal measured in the perpendicular orientation (e.g. as much as in the parallel orientation). We find that the cross-polarized signal is a factor of 5 smaller than the co-polarized received signal, consistent with little basal depolarization, as well as the expected absence of measurable circular birefringence effects.
Systematic Errors and Biases
Our goal is to estimate the attenuation length in situ and compare with laboratory measurements. Since the latter are made for pure ice, at a predetermined temperature, there are systematic differences which (generally) bias our measurement towards an underestimate relative to the laboratory results. We are most sensitive to the assumed value for the reflection coefficient at the bedrock interface. Attributing any reduction in measured signal to ice absorption rather than effects such as R < 1 will obviously result in an underestimate of the extracted attenuation length. Given an estimate of the dielectric contrast between ice and the underlying bedrock, one can calculate R. A reasonable assumption is that the underlying rock has an index of refraction of order 3 (silicate-based rock), corresponding to a reflectivity of order 0.3 (~6dB). We note that ground-penetrating radar measurements made in Greenland have observed variations in the bedrock reflectivity over two orders of magnitude (personal communication from P. Gogineni, 2004). Other estimates bracket the reflectivity between 3 and 11 dB (Reference Herique, Kofman, Bauer, Rémy and PhallipouHerique and others, 1999), depending on whether there is an underlying layer of water (3 dB) or an ice/rock transition (11 dB). Based on the deviation between the R = 1 values and the R = 0.3 values shown in Figure 10, we estimate a corresponding (asymmetric) systematic uncertainty of +250 m in L α.
We have also noted that the V(t) trace shown in Figure 5 shows loss of signal from returns prior to the bedrock reflection. This could be due to the effect of discrete internal scattering layers, as well as semi-continous Rayleigh scattering in the ice itself. Some of the observed reflected signal could also be due to returns off the AMANDA phototube array, located in the ice directly beneath the horns. Again, we have neglected the effects of such reflections in extracting the attenuation length. Including such effects, as well as birefringence (previously discussed), would increase our estimated value of L α.
It is reasonable to assume that, for pure ice, the attenuation length should vary monotonically over the range 200–800MHz. Local impurities and inhomogeneities are, of course, expected, and may account for the scatter observed in Figure 1. Nevertheless, we conservatively assign a symmetric systematic error of 150 m in L
α, which should also incorporate systematics in the attenuation length extraction. We note that this is also the typical deviation between the in-air/in-ice normalized measurements to the entirely in-ice-based extractions of L
α. Adding in quadrature, the asymmetric error due to the uncertainty in R, the total systematic error is then assessed at ![]()
Summary
Measuring the signal transmitted from a horn antenna above ice, and reflected back off the underlying bedrock to a surface receiver, we have estimated the attenuation length Lα of cold polar ice, in the regime 200–700 MHz. Our measurements confirm that the attenuation length at radio frequencies is approximately an order of magnitude larger than the attenuation length at optical frequencies (Reference AndresAndres and others, 2000), but less than what is expected for pure ice by a factor of 2–3. Our results are also at variance with previous assertions that the ice attenuation increases steeply above 500 MHz (Reference Evans and SmithEvans and Smith, 1969), or even above 100MHz (Reference WalfordWalford, 1968). By comparison, a University of Kansas group has recently performed a very similar measurement, substituting a network analyzer for our signal generator, and obtained a minimum path-length-averaged attenuation length of ~600m (Reference Paden, Allen, Gogineni, Dahl-Jensen, Larsen and JezekPaden and others, 2005) over the range 100–500 MHz, based on data taken at the North Greenland Icecore Project (NorthGRIP) ice hole. Given the generally warmer ice in Greenland, we might expect smaller, rather than larger, attenuation lengths. We reemphasize that our extraction relies on prior estimates of the dependence of the absorption length with temperature, and, very importantly, an extraction of the temperature profile at the South Pole down to the bedrock. To directly measure the temperature dependence of the attenuation length in situ requires broadcasting horizontally along a chord of constant depth and, therefore, uniform temperature.
Acknowledgements
We thank our ANITA and RICE collaborators for providing very useful suggestions, ideas and instructive comments, as well as the AMANDA and SPASE (South Pole Air Shower Experiment) collaborations for their logistical support since 1995. We are indebted to the logistical support provided by Raytheon Polar Services at the South Pole, and particularly A. Baker, B. Bergeron, D. Braun, S. Churchwell, J. Corbin, Ji Woo Nam, A. Thompson, D. Schwieder, P. Sullivan, V. Peyton and J. Vineyard, without whom this effort would not have been possible. This material is based upon work supported by the US National Science Foundation’s Office of Polar Programs under grant No. 0085119.


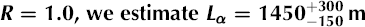 for
for 











