Introduction
In mountainous terrain, blowing snow (taken as the combination of high-level snow-fall drift processes and low-level scoring processes) causes many problems through irregular, often excessive snow deposits. Because previous snow-drift investigations have been almost exclusively concerned with snow-drift on extended horizontal surfaces (Reference DyuninDyunin, 1959; Reference MellorMellor, 1965; Reference Budd, Budd, Dingle and RadokBudd and others, 1965; Reference RadokRadok, 1977), a study of the rather complex subject of mountain snow-drift problems has been initiated.
Our plan was to simulate the two-phase mass flux over an extended, modelled mountain crest, and, in order to achieve this, we had to design or to adapt suitable instrumentation to measure the airflow, the roughness parameters, and the snow-particle flux over a mountain crest in order to gain appropriate boundary conditions. Particle size and mass distribution also had to be measured in a separate study (Reference PopePope, 1979) as it seemed that the combination of high- and low-level snow-drifting (large snow-fall particles) would influence the catch efficiency of snow-drift gauges and hence the measured flux rates. Finally, we tried to answer an urgent question raised by avalanche forecasters over the years: “How much additional wind-blown snow is deposited during a snow-storm on steep lee-slopes, given the wind data on ridge-top locations?”
The main emphasis during the first phase of work was given to crest-line locations, where the eroded drift-snow of the windward slopes is passed to the leeside slopes. Thus, estimated and measured ridge-top flux rates may be compared with measured mass-balance differences on adjacent slopes yielding the possibility of cross-checking the two measuring procedures.
Test sites and instruments
All detailed wind profile, drift flux, or drift density measurements have been completed on a small crest line north of the Eidg. Institut für Schnee- und Lawinenforschung (2 670 m a.s.l.). During major snow-storm or snow-drifting periods the wind blows from the north-west across this crest line. However, because the leeside slope is disturbed by the Institut building, the areal snow re-distribution features could not be investigated on the slopes of the same ridge, but were measured on a ridge similar in orientation, shape, and slope roughly two kilometres away, the so-called Gaudergrat ridge. A cross-section of this ridge is represented in Figure 1. These two ridges show rather sharp crest lines, slope angles between 28-38°, and might be regarded as quite typical for our Alpine topography.
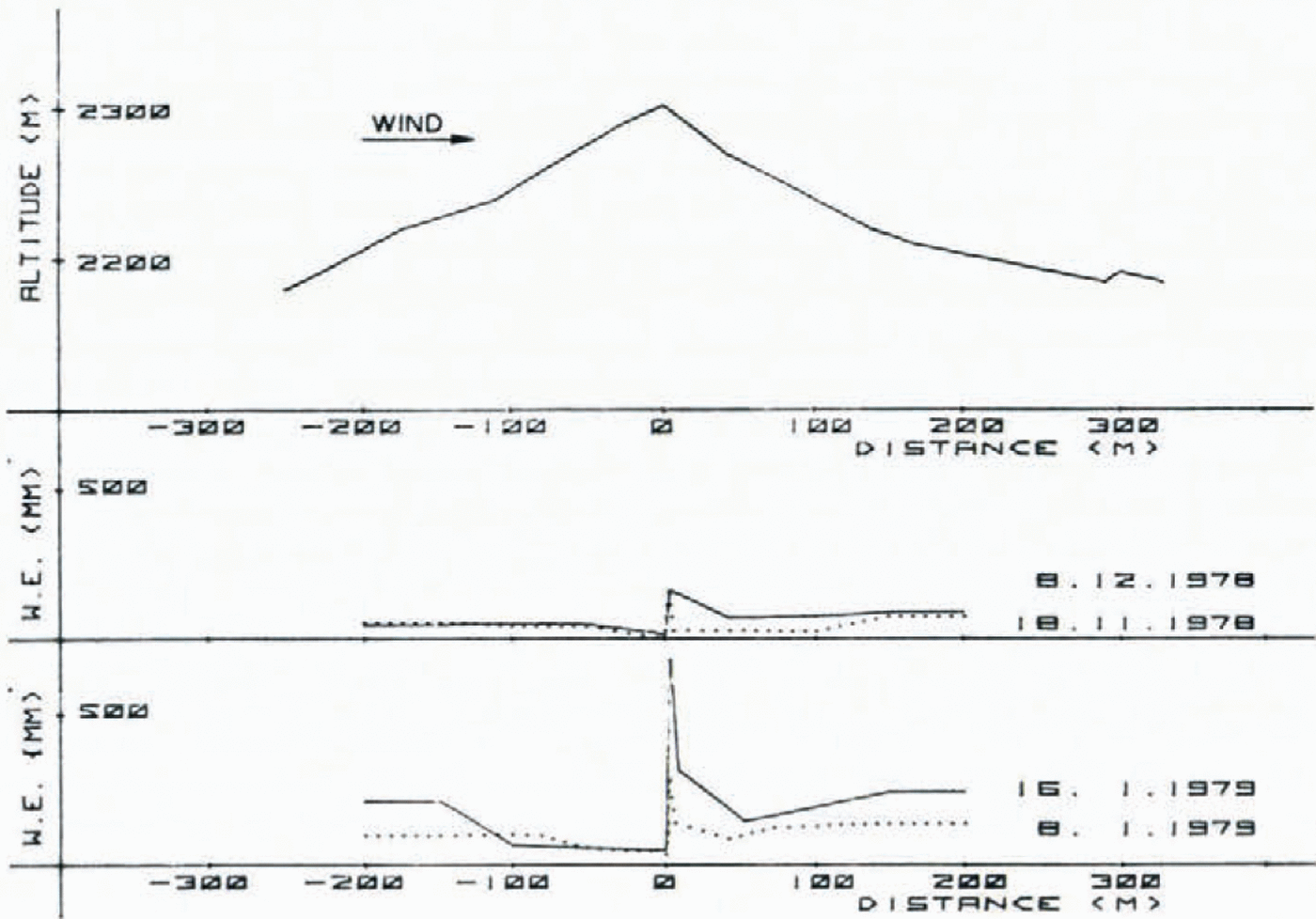
Fig. 1. Cross-section of Gaudergrat ridge (W.N.W.-E.S.E.) and mean areal mass balance for two surveyed periods. Surplus snow deposition on lee slope and irregular snow accumulation pattern may clearly be observed.
The wind profiles were measured with small cup-anemometers (accuracy ±0.3 ms -1) mounted on one side of a vertical mast, the drift-snow gauges were installed on the other side of the mast. Drift flux measurements were generally made at three heights above the snow surface (between 0.1-2 m) with a slightly modified rocket-type drift gauge first constructed and tested by Reference MellorMellor (1960). The exterior shape has only been changed slightly to retain the calibrated flow efficiency ratio of 0.78 (the ratio of wind-speed through the inlet nozzle to speed in front of the nozzle). The central section of the gauge has been elongated by 10% in order to settle nearly all particles in this central region which was constructed of clear “Plexiglass” cylinders so that exposure times (0.5-2 h) could be determined visually. The sharpened inlet tube had an internal diameter of 8 mm and the separable fin section was Constructed from thin aluminium sheet. (The gauges could freely turn in the vertical and horizontal plane to match the air flow.) The nose-to-centre velocity ratio is 306 : 1. Because the calibration measurements reported by Mellor showed that wail smoothness and windspeed fluctuations appreciably influence the “collection” efficiency of such gauges, no corrections have been applied to the drift measurements. On a few occasions a small glass gauge of reduced size and without fins was used to gauge heights smaller than 0. 1 m above snow surface.
Airflow over ridge crests
The snow-drift over crests is mainly determined by small-scale airflow, which is rarely described in the literature. Most of the theoretical work is concerned with the effects of stratification, with lee-wave phenomena, and with upper-level winds. We need measurements and a simple analytical theory which describes the interrelations between terrain shape and the turbulent boundary layer, which carries most of the suspended snow during drift conditions.
Measured wind profiles
Figure 2 shows several profiles of the horizontal wind-speed component which do not follow the usual logarithmic form. The right-hand profiles were measured almost exclusively during blowing snow periods, whereas the left-hand ones were recorded during rather sunny weather (warm-air advection). They all show a hump in the lowest metres, increasing with higher wind-speeds. Although the incomplete matching of the anemometers may account for some profile deviations, it is believed that the general trend is correct, because similar profiles, recorded with the same instruments on the adjacent windward slope during blowing snow conditions (when the wind was blowing tangentially along the slope), show a nicely logarithmic shape as one might expect for a shear flow along an inclined plane during neutral stability conditions.
In order to calculate the friction velocity u ★ and the roughness length z 0 over the eroded snow surfaces, all profiles which are almost logarithmic have been analysed. Assuming the logarithmic law

Fig. 2. A variety of vertical profiles of horizontal wind-speed measured at the Weissfluhjoch ridge crest. The wind-speed maximum is more pronounced and at a lower height if the wind approaches the ridge from N.W. than from S.E., due to terrain differences.
where u is the wind-speed at height z and k is the von Kármán constant, the mean values for u★ and z 0 have been determined. The mean roughness length was
whereas for the friction velocity a mean value of
was evaluated. The wind-speed range was 5-15 m s_1 at a height of one metre. The number of “logarithmic” wind profiles was rather limited due to the special measuring locations (N = 12), and so no attempt was made to derive a general relationship of the form z 0= f (u★); similarly a simple linear expression:
was chosen for the relationship between u ★ and a reference velocity u z, a form often quoted in the literature (Reference MellorMellor, 1965; Reference Shiotani and AraiShiotani and Arai, 1967).
The mean value of z 0 corresponds to the larger values reported previously (Reference DeaconDeacon, 1953; Reference Budd, Budd, Dingle and RadokBudd and others, 1965; ōReference Ōura, Ōura, Ishida, Kobayashi, Kobayashi and Yamadaura and others, 1967), the value of ū ★ is, according to Reference MellorMellor (1965), two to four times smaller than those usually reported. These divergences could indicate that even the selected profiles had a small hump-like deviation at lower heights, thus increasing z 0 and reducing u ★The Sutton criterion for aerodynamically rough flow

where v is the kinematic viscosity of air, was always fulfilled.
Theoretical approach
Strong airflow (u1 > 7 m s-1) seems to cause an accelerated, hump-shaped wind profile on ridge-top locations. It is well known that neither potential flow nor viscous flow theories describe the boundary layer flow adequately, but such theories may describe the contribution of the various forces which are important for the flow of snow particles in the air stream.
According to Prandtl (1965, p. 523) a boundary-layer equation may be derived from the hydrodynamic equations of motion and continuity. A sketch of the flow field and the coordinate-system appears in Figure 3. Beginning from an incompressible fluid moving in the x-direction with a mean velocity u or U 0, the equation may be written for steady two-Figure 3 dimensional flow (assuming a predominance of the x-direction terms over those in the direction):
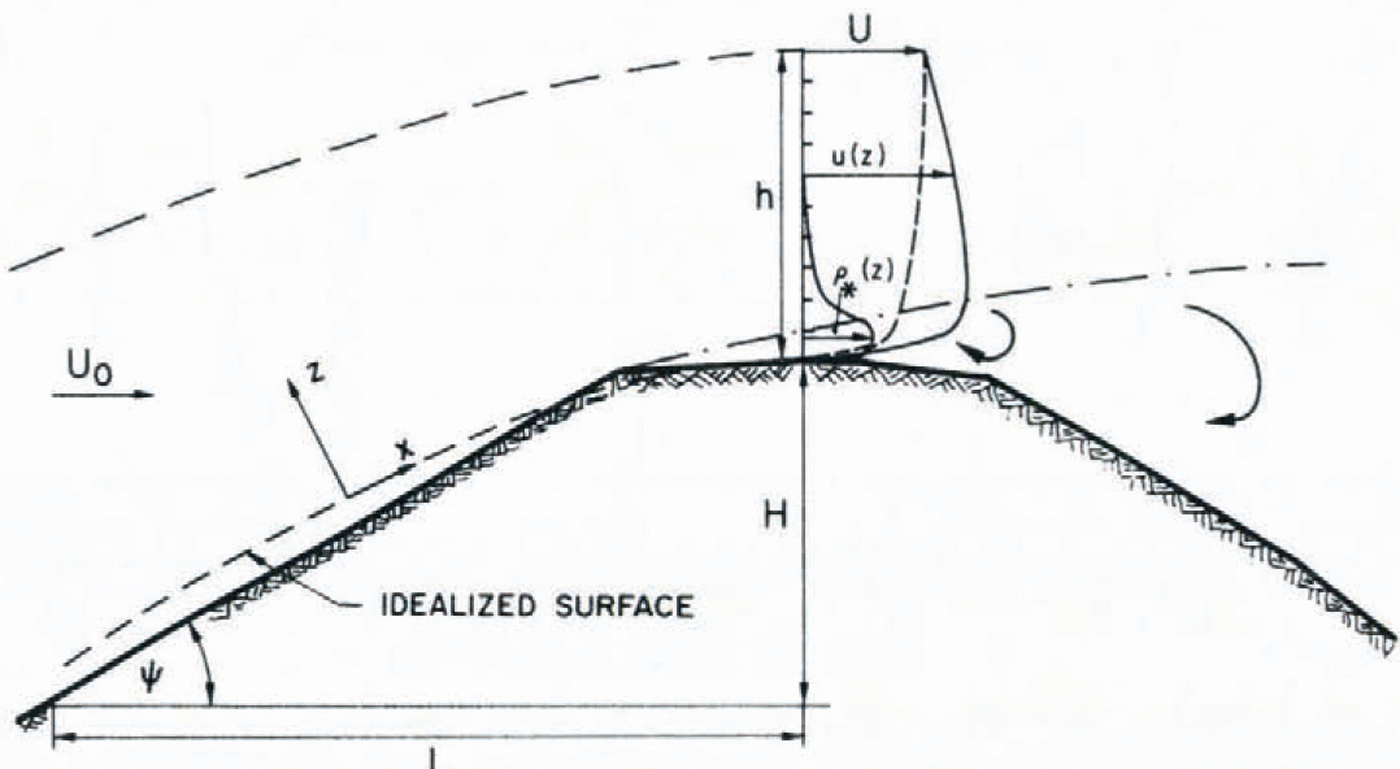
Fig. 3. Schematic diagram of lurbulent-flow regime and snow-drift concentration on a ridge crest.

where u and v are the x- and the z-velocity components, g is the acceleration due to gravity, ρ' is the air density including drifting snow, and p and τxz the pressure and Reynolds stress, respectively. If no abrupt slope changes occur, the local curvatures of the boundary layer of depth h may be neglected, i.e. the x-coordinate is positioned along the slope.
The first term on the right-hand side represents the effect of the weight, the second a volume force (the Bernoulli pressure-gradient force), and the third the frictional forces; the left-hand-side terms represent the inertial forces.
We can see that mainly inertial forces (almost frictionless flow) are experienced in the uppermost air layer above the ridge, whereas in the lower layer (between the two dashed lines in Fig. 3) predominantly frictional forces are present despite the fact that air is a medium of low viscosity. Because the major snow-transport phenomena take place in this lower layer, special attention is given to this layer in what follows. For the upper boundary, applying Bernoulli’s equation:

and we may write:

where U is the speed of the upper, almost frictionless flow.
At the lower boundary (where u = v = o) the equation may be written as:

Generally speaking, the boundary conditions are :

Knowing that the atmospheric boundary-layer equations may only be solved analytically provided the specific problem can be formulated in terms of ordinary differential equations, we try to find a solution for the ridge-top wind profile with appropriate simplifications.
If we consider only the much larger turbulent part of the frictional stresses, the term τzx, following Prandtl’s theory of momentum transfer, may be written as

We set

and for the new coefficient of eddy viscosity µ' the expression
can be derived where l is a distance known as the mixing length
Equation (3) may be rearranged to formulate an equation for the ridge-top location, where all horizontal gradients of the mean velocity are much smaller than the vertical ones; gravity forces are negligible due to the small density differences:

This equation may be solved for u(z) by introducing for µ the values given in Equation (7) by assuming that v is a small and constant term on ridge-top locations and by applying for ∂p/∂x a numerical value derived from the specific ridge dimensions.
A solution which satisfies the boundary conditions is of the form:

where h is the boundary-layer height and ΔP/ Δx is the local “Bernoulli” pressure gradient.
The local pressure gradient may be approximated by Equation (4) using for U an empirical relation for a wedge-shaped surface given by Reference ManglerMangler (1948) in the form

and further

where U 0 stands for the free-air flow speed, L is the windward base distance of the ridge, and ψ the mean slope angle.
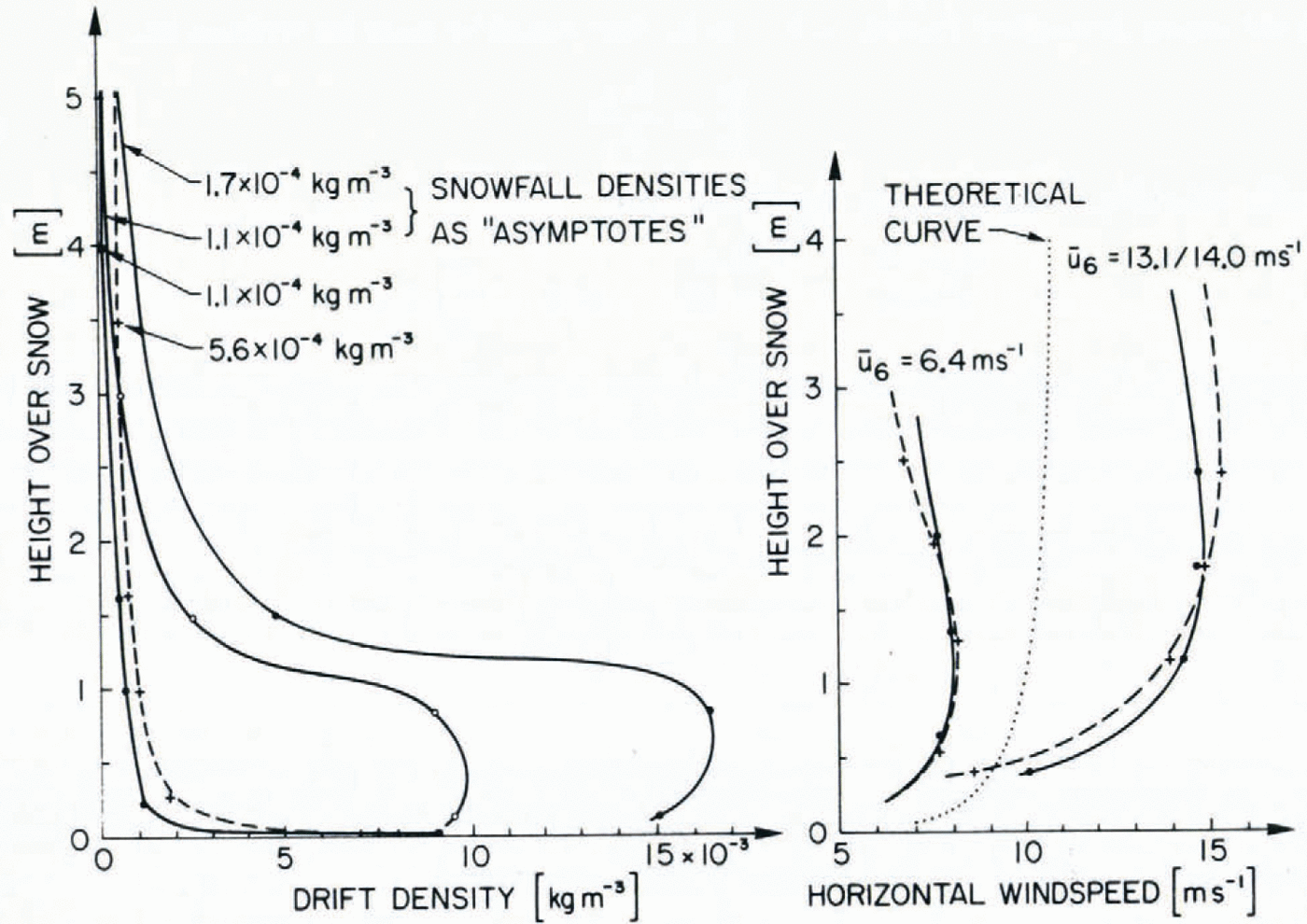
Fig. 4. Typical drift density profiles are shown on the left together with corresponding wind profiles measured on the ridge crest on the right. The theoretical wind-profile curve, calculated using Equation (9) bulges less than the measured ones andyields a flat maximum at a height of about 4 m.
In order to simulate the mean measured wind conditions of Figure 4 a free-flow speed U 0 = 10 m s-1, a ridge length of x = 180 m and a boundary-layer height of 8 m were used. The theoretical curve of Figure 4 shows, in comparison with the measured wind profiles, that part of the humped-shaped profiles may be explained by theory, but that the measured profiles bulge even more, perhaps an indication that additional small-scale geometrical effects may be involved (e.g. small surface edges caused by cornices).
Measurements of blowing snow
A theoretical analysis of the transport of blowing snow over a mountain ridge, combining the equations of motion, continuity, and the diffusion equations, could not be accomplished, so in the following section only the measured drift-flux profiles converted to drift-density profiles will be discussed. Figure 4 shows on the left-hand side four selected drift-density profiles, recorded on the same ridge-top location during snow-storms with low to moderate snow-fall densities. The corresponding wind profiles are given in the right-hand side of Figure 4.
The “low wind-speed” density profiles (two additional ones are presented in detail on Figure 5) conform approximately to the theoretical steady-state snow-drift relation first published by Reference Shiotani and AraiShiotani and Arai (1967)

where ρ★, ρ★ 1 are snow-drift densities at the levels z, z 1 respectively, and w is the terminal velocity of the particles, chosen according to literature (Reference HobbsHobbs and others, 1973) as 0.5 m s-15.
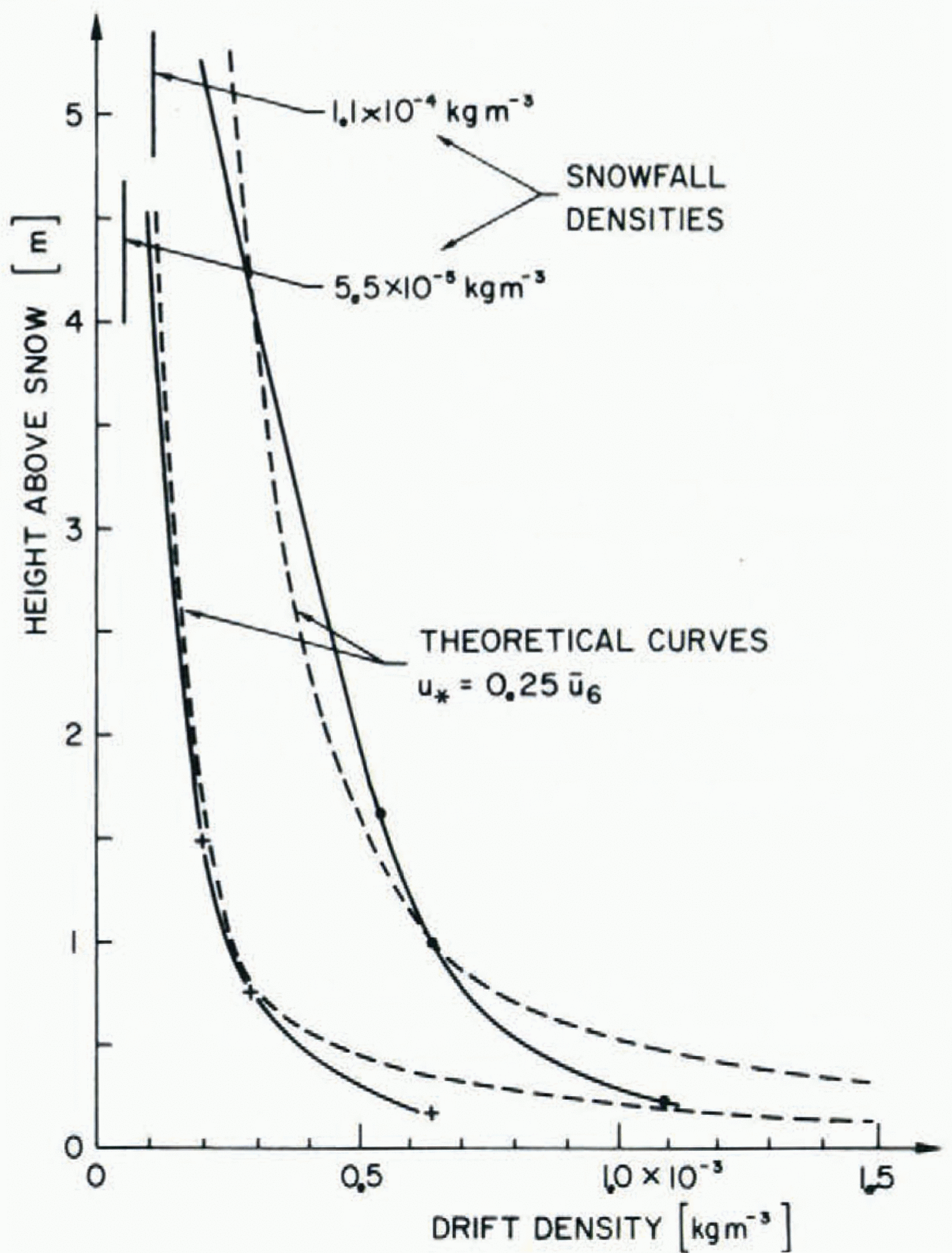
Fig. 5. Two measured drift-density profiles, which show similar shape to the theoretical steady-state drift profiles, if friction velocity u⋆(obtained by wind measurements) is enlarged by an order of magnitude.
However, the two detailed profiles of Figure 5 could not have been matched with theoretical curves if the mean measured friction velocities relationship for the wind profiles
had been used, where u 6 represents the wind-speed at a height of 6 m above snow surface. A u★enhanced approximately by a factor of ten
was required to match the curves roughly. It is interesting to note that Reference Sommerfeld and BusingerSommerfeld and Businger (1965) have shown that the ratio of the eddy diffusivity for blowing snow Ks and the eddy viscosity K m derived from wind profiles is also 10:1.
As indicated in the previous sections, one objective of the present study was to estimate the areally measured transport rates over the ridge crest (mass balance between windward and leeward slopes) by measured drift transport rates on the crest line.
The calculation of the drift transport

or the specific drift transport

which yields the mean transport rate per unit area, readily comparable with areal measure-ments, is straightforward once the height limits are chosen:

where zu is the upper and z 0 the lower height limit.

where a = w/ku ★', a term defined in now slightly modified for blowing snow with u ★' in the denominator, ρ★1 corresponds to the measured drift density at the one-metre level.
The specific drift transport rates and the drift density p★0 at the height z 0 = 10-3 m have been calculated for the two drift profiles represented in Figure 5 and are given in Table 1. For the main calculations the “pure” drift densities (ρ★1', ρ★0'), i.e. snow-fall densities subtracted first, have been considered (e.g.ρ★1 '= ρ★1 — ρp) where ρp is the precipitation density).
Calculated z odrift densities(p ★0'),specific drift transport rates for various layer HEIGHTS(

A comparison with measured values by Reference Budd, Budd, Dingle and RadokBudd and others (1966) shows that for rather low wind-speeds on the ridge (6-12 m s-1) the extrapolated z 0 drift densities (p★ 0') are an order of magnitude smaller than on flat Antarctic snow-fields. In addition Table I illustrates that the specific drift transport rate depends strongly on the upper height limit, especially for low wind speeds. If we choose an upper height limit of 40 m as adequate based on visual observations, we see that the specific drift transport rates may be doubled through slight snow-fall drift (0. 1-0.2 mm water equivalent h-1). Snow-fall densities have been calculated with the aid of three snow-fall precipitation recording gauges, positioned on a flat sheltered experimental plot in the vicinity of the ridge.
More typical drift density profiles on crest-line locations are shown in Figures 3, 4, and 6. As soon as the crest wind-speed reaches a threshold velocity of u1 = 7-10 m s-1, the drift density profiles also show a hump-shaped course. The left side of Figure 6 demonstrates the 6 transition from a steady-state snow-drift profile to a typical crest-line drift profile with increasing velocities. The right side of Figure 6 illustrates the fact that snow-fall, i.e. an additional precipitation snow flux may be superimposed on low-level scoring processes, thus the measured drift profiles are only translated by the snow-fall.

Fig. 6. Measured drift-density profiles ; left-hand side shows the effect of increased winds; right-hand side illustrates translatoryshift by increased snow-fall rates. (A snow-fall density of 5.5 X I0 -4 kg m -3 corresponds to about 1 mm water equivalent snow per hour.)
The hump-shaped density profiles may be caused by the flow acceleration over the top of the ridge (cf. wind profiles) leading to reduced pressure and therefore increased particle lift. Another explanation for a uniform snow-filled ground layer of 1-1.5 m depth above snow surface could be based on the presence of a separation layer, starting at the edge of the ridge as illustrated in Figure 3. Drift measurements on ridges of different microshapes and theoretical approximations, e.g. turbulent motion theories of buoyant jets and plumes, may clarify this point in future.
Determination of snow transport by areal mass balances
In connection with a study into the influences of slope aspect on the stability of seasonal snow cover, re-distribution of loose surface snow and the deflection of suspended snow have been analysed on an extended ridge similar in shape and orientation to the one described in the previous sections. It is obvious that the measured snow mass-balance differences between an extended windward slope and the adjacent lee slope may help to approximate the total transport over the crest as well as to localize typical avalanche-prone snow deposits.
During the winter 1978-79 more detailed areal measurements have been initiated in anticipation of suitable snow-storm conditions (steady winds from W.N.W.—N.W., lasting for a few days and dumping enough snow for the measuring error to be small). Unfortunately such periods occurred rarely this winter, the wind regime was unsteady in direction, and speed and snow-fall rates were low compared with previous winters. However, a few periods could be analysed separating time spans with low wind-speeds and no drift phenomena from those with blowing snow conditions.
There are basically three possibilities involved in estimating the specific transport rate from the windward onto the lee slope and, as a consequence, the windborne mean snow deposition in the lee slope D. Either the snow loss in the windward slope ΔWw or the snow gain on the lee slope ΔWl compared with a horizontal, drift-free snow plot ΔW is determined during blowing snow periods; furthermore a mean value of both may be chosen as an even better estimate counterbalancing the measuring errors.
Assuming that a snow-storm without wind would deliver to all slopes the same amount of snow and that, by definition, on the windward slope snow erosion and on the lee slope snow deposition occur, we may write:


The arithmetic mean of the two terms in is equivalent to the net mass gain on the horizontal snow plot and may be used as a measure for the tightness of the whole system. If the measured mass increase (ΔW) on the horizontal plot shows values within ±10% of the above mean, we may conclude that no essential gain or loss of snow mass takes place from or towards areas outside the surveyed slope areas.
If(ΔWL+ΔWW)/2 < ΔW mass losses are likely, if (ΔWL+ΔWW)/2 >ΔW mass gains must be assumed.

Fig. 7. Mean areal snow-cover water equivalent in the upper part of Gaudergrat ridge on two consecutive dates. Windward slope (left to crest-line) stores appreciably less snow than leeward slope (right side of crest line).
Figure 7 shows an example of such areal mass balance measurements in the immediate vicinity of the crest-line. The whole outlined time interval consisted of three blowing-snow periods with moderate winds (mean daily wind speeds between 5 and 13 m s_1) and yielded the following total mass gains:

Consequently mean lee-slope snow deposition by blowing snow amounts to D = 87.5 kg/m2, whilst for the specific drift transport rate Q a mean value of 1.04 X 10-3 kg m-2 s-1 results. This amount compares favourably with the values of Q ,z 040 in Table 1.
Two additional examples, where the slopes have been surveyed further up- and down-wind are represented in Figure 1. Using these two representative periods as a basis for discussion, the following features may be of interest:
A horizontal distance of about 200 m on both sides of the crest-line seems to contain in most cases the blowing-snow processes caused by the ridge.
If the mass ratio

(system not closed), then it is rather smaller than one, indicating that mass losses are mainly on the lee side (sublimation and/or drifting snow further down-wind).
In the wind shadow of the ridge there is a strong reverse eddy flow of the order of 50 to 150 m long (measured horizontally, Fig. 1), resulting in a large depression or cavity in the snow-pack. Where snow-pack depth is substantially decreasing, zones of increased stresses develop, often giving rise to snow-slab failure. Surveying the mass balance on ridge slopes before and after snow-storm periods and including the ridge-crest wind data, quantitative relationships for the surplus deposition of snow in the upper parts of lee slopes may be derived. The wind power, the expression of the ability of the wind to transport snow is, theoretically, proportional to the cube of the wind-speed, thus an empirical relationship of the form
may be established. HNs represents an average areal “wind-snow” depth, i.e. the surplus snow accumulation by wind on lee slopes compared with drift-free horizontal areas. The coefficient k = 8x 10-5 s3d-1 m-2 is determined empirically. The relation holds for snow-storm conditions and for periods of 24 h, consequently for ū the mean daily wind-speed on the crest has to be inserted. The introduction of a threshold velocity, above which snow transport is said to begin (cf, Reference DyuninDyunin, 1959) was not adequate, because during snow-storms snow particles are fed into the air flow from upper air layers even at very low wind speeds.
Equation 17 has been derived from mass-balance measurements over three winters (1972/73-1974/75) on the ridge described here and it may be of interest that the few short- interval measurements of the past winter (1978/79) confirmed the validity of this approximation.
Conclusions
The problem of snow erosion or drift accumulation by natural topographical features is great, a primary requirement for its solution is a quantitative estimate of air-flow patterns over various terrain structures. It has not been possible here to do more than mention a few problems, however the measurements and theoretical approximations presented may help to begin further work in mountainous terrain.
The most important points can be summarized as follows:
Profiles of the horizontal wind-speed measured on a ridge show a hump-shaped course close to the ground with a wind-speed maximum between 1 and 4 m height. Mean measured surface roughness z 0 amounts to 1.3 mm and seems to be independent of snow surface features. Mean friction velocity ū ★ equals 0.1 ms-1 or in terms of the wind speed at 6 m,ū★ = 0.22u 6, on the other hand the blowing-snow friction velocity u ★' seems to be an order of magnitude larger, consequently the relationship u ★' = 0.25u6 may be used.
A theoretical solution of Prandtl’s boundary-layer equation adapted for the specific ridgecrest conditions shows that the negative pressure gradient towards the ridge crest might be the main cause for the special wind profile.
An elongated rocket-shaped drift gauge (Reference MellorMellor, 1960) is well suited for drift-flux measurements on ridge crests. Riming occurred rarely and the large snow particles of Alpine snow storms could easily enter the inlet nozzle.
Drift-density profiles measured at the ridge crest conform roughly with theoretical steady- state drift profiles providing wind speeds are low (u1 ≤ 7—10 ms-1), at greater windspeeds a snow plume of 1-1.5 m depth develops above the snow surface. It may be explained partly by accelerated air (low and/or by small-scale geometric effects (flow separation by small surface edges).
Areal mass balance measurements of storm periods yield the possibility of cross-checking measured or theoretically approximated ridge-crest flux rates. At the same time they may be used to derive much needed quantitative relationships between crest winds and drift-snow deposition on lee slopes.
Acknowledgements
I am very grateful to R. Meister and M. Pope for their assistance in the field and for executing various computer studies.









