Introduction
In the tropical Andes, the retreat of glaciers since the Little Ice Age (LIA) has been documented at a few sites, most of them located in the Cordillera Blanca, Peru (Reference Ames and FrancouAmes and Francou, 1995; Reference Hastenrath and AmesHastenrath and Ames, 1995b; Reference Kaser and GeorgesKaser and Georges, 1997). Some studies in the Central Andes have pointed out the strong acceleration in glacier recession since the early 1980s (Reference Brecher and ThompsonBrecher and Thompson, 1993; Reference Ames and FrancouAmes and Francou, 1995; Reference Francou, Ribstein, Saravia and TiriauFrancou and others, 1995), an evolution also recorded in Central Africa (Reference Hastenrath and KrussHastenrath and Kruss, 1992) and in other low- or mid-latitude mountain ranges (Reference CaoCao, 1998; Reference Haeberli, Haeberli, Hoelzle and SuterHaeberli, 1998). The rapid glacier recession in the Andes is probably related to important changes occurring in mid-tropospheric conditions, such as the widely recognized rapid increase in temperature during recent decades (Reference Diaz and GrahamDiaz and Graham, 1996). As a result of this rapid evolution, many small glaciers located at low elevation could disappear in the next few decades. These small glaciers are the most common in the tropical Andes and, despite their size, make an important contribution to the water resources of many high-elevation basins (Reference Ribstein, Tiriau, Francou and SaraviaRibstein and others, 1995). Understanding these glacier fluctuations is of great interest for diagnosing future water availability in the Andean watersheds. Continuous monitoring on these glaciers is required, along with the collection of mass-balance data and evaluation of ongoing area and ice-volume changes over decades. Such data are now available in the Andes (Reference Haeberli, Hoelzle and FrauenfelderHaeberli and others, 1999; Reference Francou, Ramírez, Cáceres and MendozaFrancou and others, 2000). Energy-balance investigations have been undertaken on some Andean glaciers (e.g. Glaciar Zongo, Bolivia, and Glaciar Antizana 15, Ecuador), in order to quantify the factors responsible for increasing melting rates during the present decade (Reference Wagnon, Ribstein, Francou and PouyaudWagnon and others, 1999, Reference Wagnon, Ribstein, Francou and Sicart2001).
The case-study of Glaciar Chacaltaya, Bolivia (16° S), representative of small glaciers, is a rare example of long-term documentation of the evolution of a glacier in the Central Andes. The available data include mass-balance measurements, mappings of the surface topography and a map of the glacier bed given by ground-penetrating radar (GPR) survey. The objective of the present study is to compile and evaluate this information in order to reconstruct the area and volume changes of Glaciar Chacaltaya since the LIA maximum. We present in this paper a probable scenario for the future, based on extrapolation of the mass balance measured over the present decade. This study is motivated by the need for quantitative information to analyze the climate forcing and to anticipate the glacier evolution and the related water resources in the near future. Glaciers in the high mountains of the tropics are very sensitive to changing meteorological conditions, so glacier signals are key elements for early detection of climatic change.
Site Description
Glaciar Chacaltaya is a south-facing cirque glacier, located in the Cordillera Real (16°21′ S, 68°07′ W), approximately 20 km northeast of La Paz (Fig. 1). In 1998, its area was approximately 0.06 km2, extending from 5360 to 5140 m a.s.l., with a maximum width of 230 m. This glacier is included in the Ghoqueyapu basin which supplies part of the water resources of La Paz. It is directly accessible by road all year round, being used as a ski area during part of the wet season. Its accessibility from La Paz makes it very suitable for longterm monitoring.
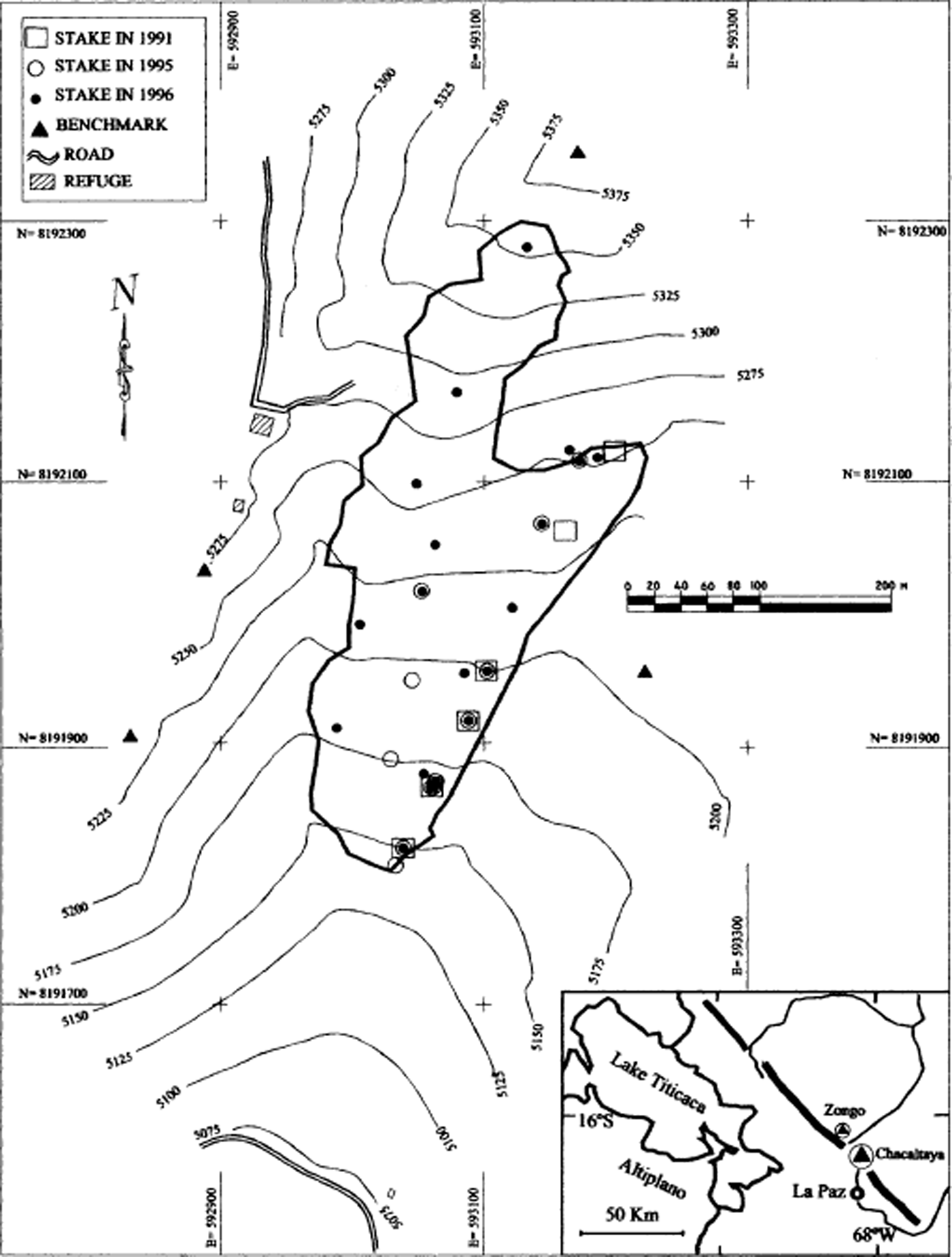
Fig. 1. Map of Glaciar Chacaltaya (ice extension of 1998), showing the location of the mass-balance stakes in 1991, 1995 and 1996. N and E indicate north and east UTM coordinates, respectively, in m.
Although high-resolution measurements (glaciological stakes and rain gauges, both surveyed every month) have been performed since 1991, other equipment was installed on the glacier in 1999, including an automatic energy-budget station and a hydrometric station at 4870 m a.s.l. on the proglacial stream, for a basin surface of 0.53 km2. At the astronomic observatory (5260 m a.s.l), located 500 m north of the glacier, daily air temperature and precipitation have been recorded since 1953 (Reference Francou, Ramírez, Mendoza, Guereca, Miranda and NoriegaFrancou and others, 1998). For 45 years (1953–98), mean annual temperature has been −1.1°C, the average monthly values ranging between −0.3°C (November) and −2.5°C (July). In these conditions, the glacier is temperate and all precipitation is solid. Annual precipitation totals 518 mm, around 65% of it falling from December to March during the austral summer. This accumulation season coincides with the period of higher ablation and melt rates at the glacier surface. The hydrological year is defined from 1 September to 31 August.
Data and Methods
Observations to monitor the evolution of the glacier and to reconstruct past areas and volumes involve (in descending order of accuracy) direct mass-balance records since 1991, topographic measurements since 1992, stereo-photogrammetric restitutions from air photographs taken in 1940, 1963 and 1983, a reconstruction of the LIA maximum using the well-preserved external moraines and a GPR survey in 1998.
Mass-balance records
Since September 1991, Glaciar Chacaltaya’s mass balance has been surveyed every month with stakes (Fig. 1). The stake measurements are performed on the first day of each month. The network includes a minimum of six PVC stakes inserted into 10 m drilled holes. Before 1995, the stakes were installed at 5230–5125 m a.s.l. on the left part of the glacier, 20–100 m from the central axis. The network was extended in 1995, with three stakes located on the central axis, and in 1996, with five stakes along the right axis, in order to survey the whole glacier surface. Considering that the number of stakes was increased after 1996, the mass-balance values calculated from the six previous stakes and those including the new stakes after 1996 correlate well (R 2 = 0.90). When snow covers the glacier surface, soundings and pits allow estimation of the accumulation in metres of water equivalent. The net mass balance is estimated between the beginning and the end of the hydrological year using a density of 0.9 g cm−3 for the ice.
Topography and stereo-photogrammetric restitution
Every year since 1992, the glacier has been topographically surveyed. The survey is performed between September and November, depending on the presence of snow on the glacier limits. From 1992 to 1995, only the glacier contour and the stake positions were measured. We tried to obtain the ice velocity by repeated surveys of the stake positions, but the displacements of the stakes are insignificant (<1 m a−1), indicating that the horizontal component of the surface flow is nearly zero within the ±1 m accuracy of the measurement. Such small and low-stress glaciers have been called “glaciers réservoirs” (Reference LliboutryLliboutry, 1965). The precise surface topography of the glacier was mapped by terrestrial triangulation in 1996 and 1998. The technique consisted of double-theodolite triangulation of a target rod, using four precision-surveyed control points (benchmarks) definitively installed in 1996 on the bedrock outside the glacier. These reference points are tied into the global positioning system used for the Bolivian maps (Provisional South American 1956). The accuracy of all these surveys is to within 1 m.
A mark, painted on a rock at the contact of the glacier snout, gives an accurate position of the terminus in October 1982. Oblique air photographs were taken in 1940 by the Servicio Nacional de Aerofotogrametría and in 1982 by W. Reinhardt (from Reference JordanJordan, 1991) (Fig. 2). We used the high-resolution 1940 oblique photograph to reconstruct the glacier limits for this date. The accuracy of this method is estimated to be around 10 m. Two vertical air photographs, taken in 1963 and 1983 by the Instituto Geográfico Militar of Bolivia, were processed by stereo-photogrammetric analysis at the University of Düsseldorf. The accuracy of this analysis is to within 10 m. A maximum ice extent was determined from the ground topographic survey of the well-preserved moraine located at 4730–5000 m a.s.l. The morphology and the position allow this moraine to be related to the LIA maximum (Reference MüllerMüller, 1985; Reference JordanJordan, 1991). In the upper part, the glacier covered all the cirque area during this last maximum. With reference to the information existing in Peru (Reference BroggiBroggi, 1945), this stage is hypothetically labelled “1860”.

Fig. 2. Oblique aerial photographs of Glaciar Chacaltaya. (a) Photograph taken in 1940 by the Servicio Aerofotogramétrico Nacional (Bolivia), and (b) photograph taken in April 1982 by W. Reinhardt (Reference JordanJordan, 1991).
Geophysical survey
In 1997, we used the seismic refraction method to evaluate the glacier thickness along a longitudinal line situated in the centre of the glacier (Reference Francou, Ramírez, Mendoza, Guereca, Miranda and NoriegaFrancou and others, 1998). The velocity contrast between the surficial layer (∼3000 m s−1) and the bed (∼5000 m s−1) was significant and confirmed that the maximum ice thickness is <20 m. It was impossible to calculate small thickness values, however, because of the lack of resolution of this method. Furthermore, seismic refraction does not permit an extensive survey over the entire area without considerable field time. Consequently, we decided to perform another geophysical survey using a GPR in order to obtain high-resolution topography of the glacier bed (for a review of the GPR method carried out on permafrost and glaciers, see, e.g., Reference Annan and DavisAnnan and Davis, 1976; Reference Arcone, Lawson and DelaneyArcone and others, 1995). This method was also regularly used by Reference ThompsonThompson (1992) on tropical ice caps in order to locate ice-core drillings.
We used a “Pulse Ekko 100” (Sensor and Software Company) GPR operating at a frequency of 50 MHz (Reference Descloitres, Guérin, Ramírez, Gallaire, Ribstein and VallaDescloitres and others, 1999). This equipment includes a portable computer, a radar control unit and two identical transmitter and receiver antennas connected to the control unit by fiber-optic cables that maintain the signal-to-noise ratio to a high level. The GPR equipment is light (<20 kg), easy to carry at high elevation and can be handled by three persons. Two longitudinal and eight transverse profiles were performed in 4 days, covering the whole surface of the glacier (Fig. 3). GPR traces were collected every 0.50 m along the profile in order to obtain the radargram sections presented on Figure 3 as a three-dimensional perspective. The vertical axis of those diagrams has been converted from time to metres considering a mean velocity of the electromagnetic wave in temperate ice of 0.16 m ns−1. This velocity value, determined by migration analysis (Reference StoltStolt, 1978), is consistent for ice (Reference ReynoldsReynolds, 1997). The maximum thickness deduced from the GPR is 16 m in the northwest part of the glacier. A kriging technique was applied to the radar data, using a grid with a 5 m spacing to interpolate the values of ice thickness between the profiles, assuming that the glacier bed topography variations between profiles remain smooth as observed along the GPR profile (Fig. 4). A topographic map of the glacier bed was then obtained by subtracting the ice thickness from the surface elevation determined by the topographic survey.

Fig 3. Location map of the 50 MHz GPR profiles. The eight transverse and two longitudinal profiles are represented in perspective without taking account of surface topography.
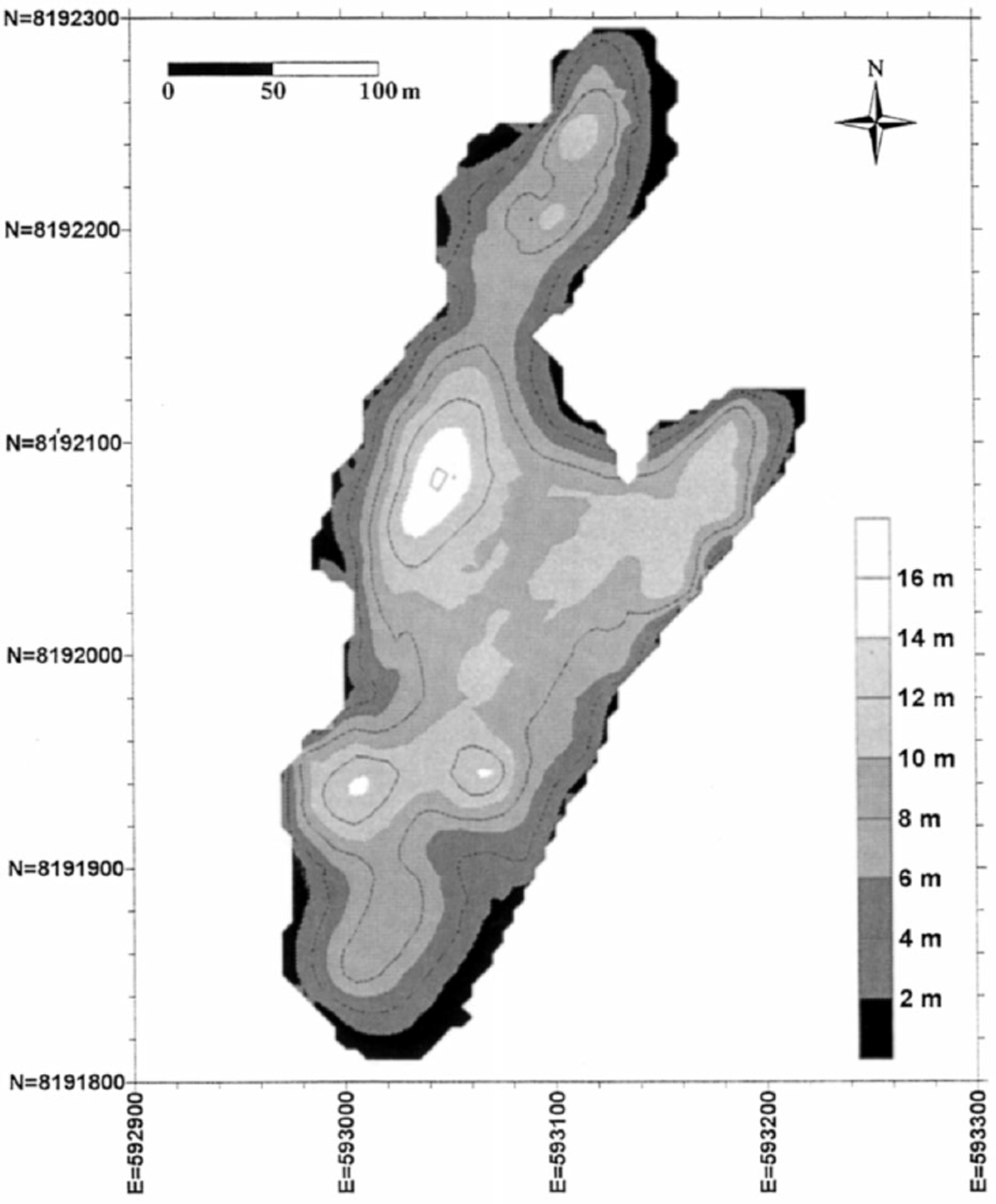
Fig. 4. Map of Glaciar Chacaltaya thickness in 1998.
Reconstruction of the 1992–95 glacier topography from the stake network
The determination of ice-volume changes requires precise mapping of the surface topography of the glacier for each selected date. From 1992 to 1995, the topographic survey includes glacier contour and stake positions but does not include the relief of the glacier surface. Using a more accurate topographic survey carried out in 1996 as reference and considering that the stake positions have not moved significantly during the 1992–96 period, we used the stakes as fixed points to reconstruct the glacier surface from the net mass balance. The method of reconstruction is presented in Figure 5, valuable in this case because of insignificant horizontal velocities (<1 m in the considered period). The glacier was subdivided into eight sections of 25 m elevation range, and the stakes located in each section were considered representative of the whole section. The surface topography estimated for each selected date (between 1992 and 1995) was parallel to the 1996 surface topography (reference), with a variation in elevation determined by the net mass balance measured on the stakes (ΔH measured in Fig. 5). For sections without stake measurements during the selected year, we assumed a similarity in the mass balance of the nearest sections.
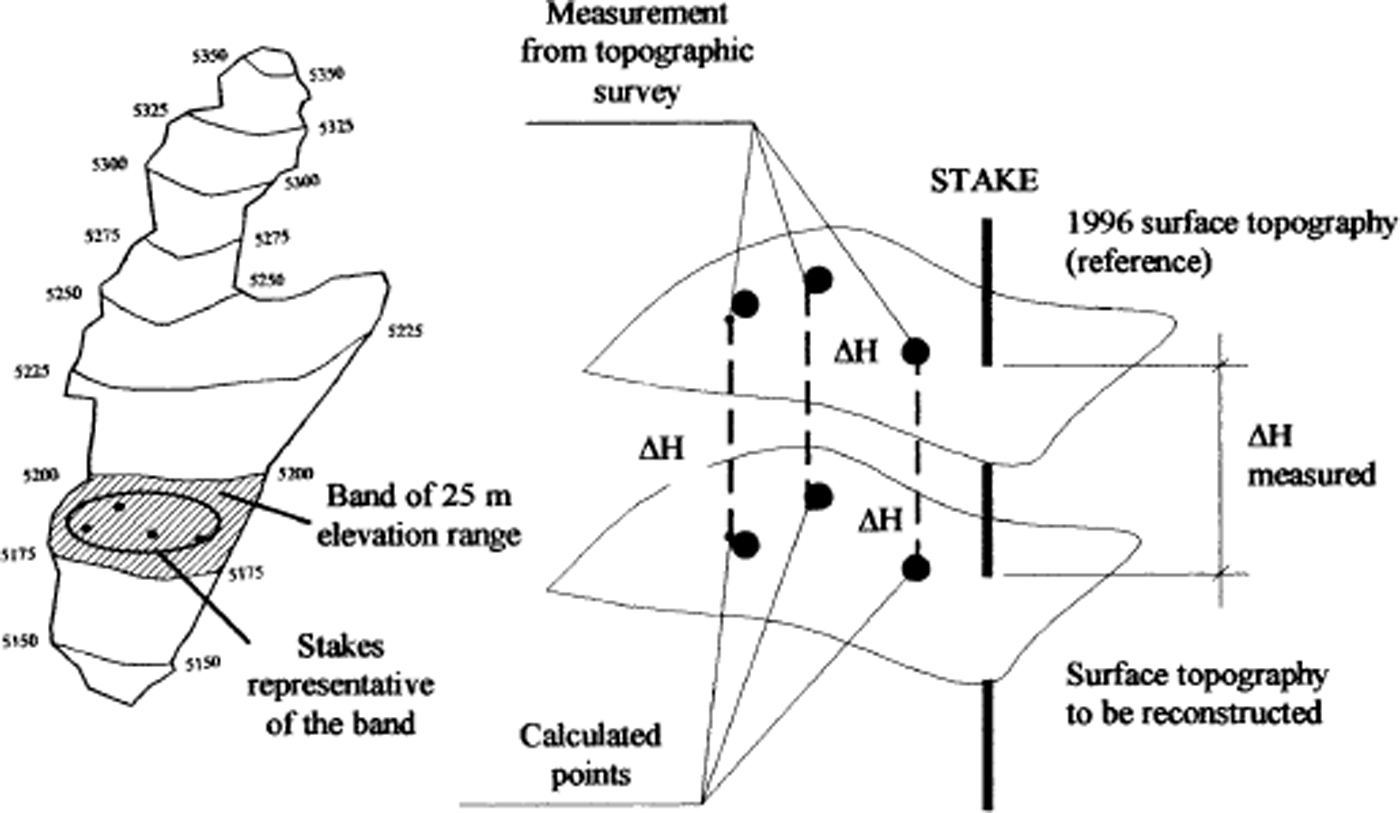
Fig. 5. Reconstruction of the 1992–95 surface topography based on the stake measurements. The high-resolution topography of 1996 is considered as the reference of the glacier surface. ΔH measured is the mean mass balance surveyed on the stakes representative of each 25 m elevation-range section.
Data reduction into a digital terrain model
All the data collected by the direct topographic surveys and by the stereo-photogrammetric restitution were processed into a digital terrain model (DTM). The reference map of the glacier and of the surrounding area was generated from the 1996 topographic survey. The map of non-glacierized areas was produced by stereo-photogrammetric restitution. The DTM was based on the topography of the cirque above 4730 m a.s.l., including the glacier bed mapped by the GPR survey. The maps of the glacier from 1992 to 1998 were introduced into the DTM as a multi-layer system, and the areas and volumes were calculated from the DTM (Ramírez, unpublished).
For “1860” and 1940, the volume could not be directly estimated. Based on the data from 1963 to 1998, a logarithmic relation between area and volume was found, as commonly observed on the glaciers in the world (Reference Meier and BahrMeier and Bahr, 1996; Reference Bahr, Meier and PeckhamBahr and others, 1997). The high coefficient of correlation (R 2 = 0.99) allows estimation of the volume using the volume–area equation.
Results
Changes in ice extent, volume and net balance
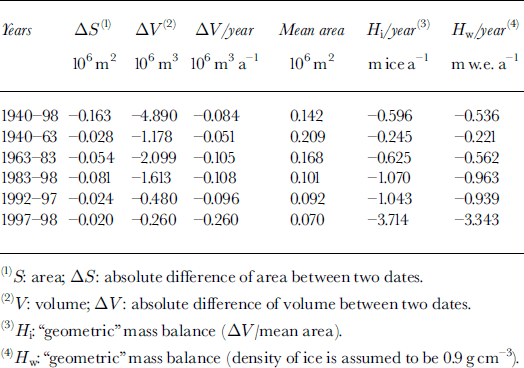
In Figure 6, the different stages of the glacier since the LIA (identified as “1860”) are mapped, whereas in Table 1 and Figure 7 the corresponding areas and volumes are quoted (the volume before 1963 has been estimated using the glacier volume–area relationship). In Table 2, the area/volume evolution was converted into average mass balances. The average loss of ice volume was 0.051 × 10 m a−1 during the 1940–63 period, and was twice that amount (0.108 × 106 m3 a−1) from 1983 to 1998. During the 1990s, the glacier lost two-thirds of its total volume (reduced from 1.114 × 106 m3 in 1992 to 0.374 × 106 m3 in 1998) and the surface area was reduced by >40% (from 0.104 × 106 m2 in 1992 to 0.060 × 106 m2 in 1998). Despite a large information gap during the 1970s, it is obvious that the retreat of the glacier has been continuous since 1940, with an acceleration since at least the early 1980s.
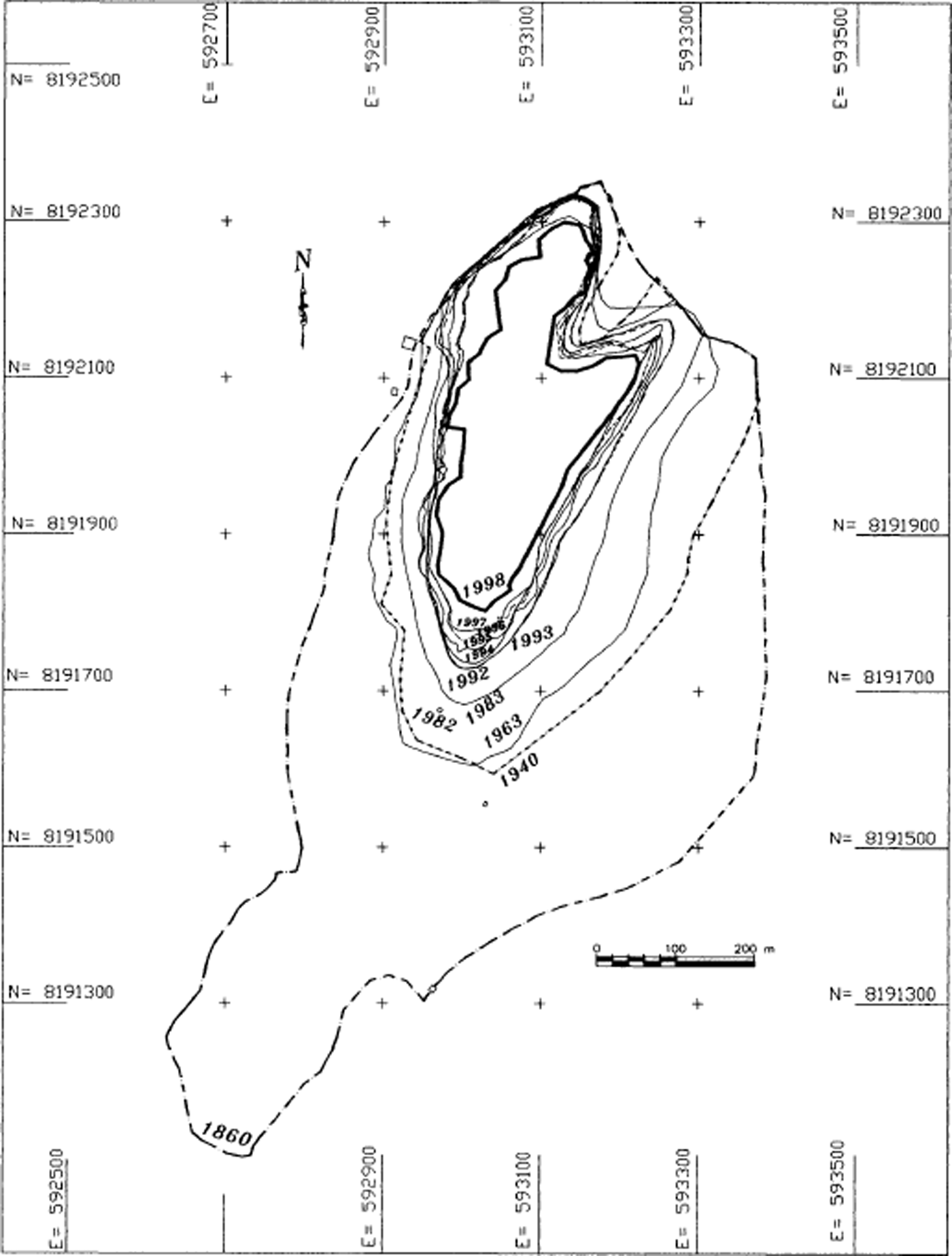
Fig. 6. Map of the ice extent of Glaciar Chacaltaya during the LIA maximum (“1860” inferred from external moraines), and for 1940, 1963, 1983 and 1992–98. The mark painted on the bedrock indicating the position of the glacier terminus in April 1982 is noted by a small open circle.
Table 1. Glacier area and volume evolution from “1860” to 1998.
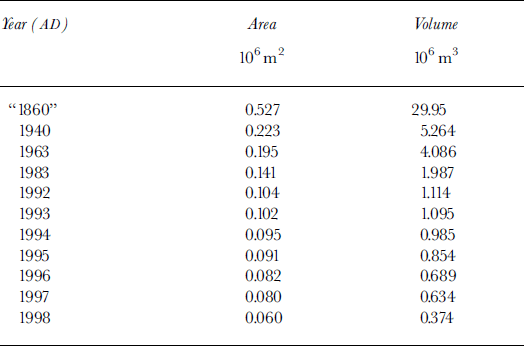
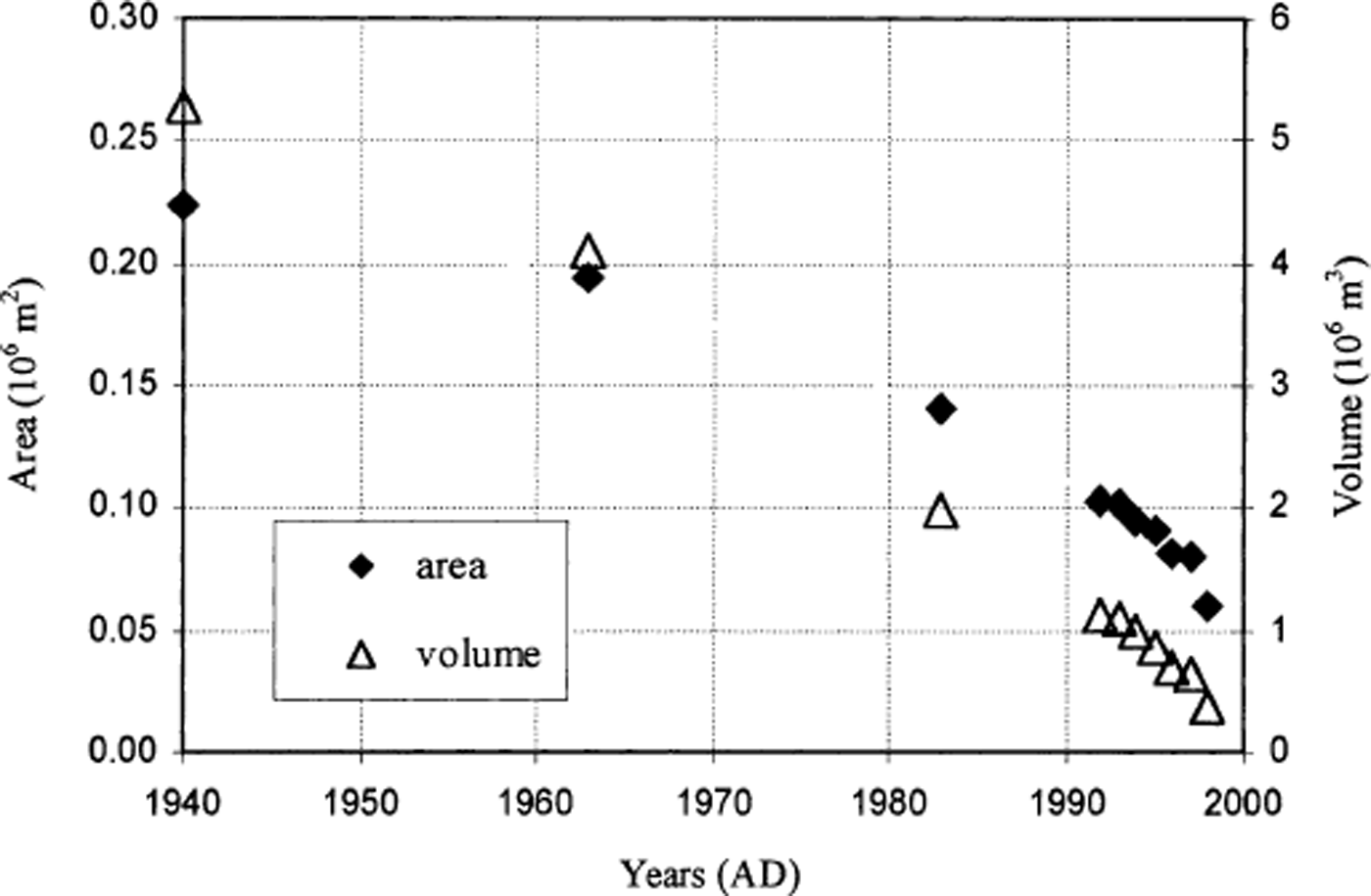
Fig. 7. Glacier-area (lefthand scale) and ice-volume (right-hand scale) evolution since 1940.
Table 2. Area/volume evolution and mass-balance reconstruction since 1940.
The net balances from the stake network (Table 3) show the strong mass deficit of this glacier during the 1990s. Except for 1992/93, the yearly net balance for the glacier was always negative, with the ELA lying above the upper reaches. The total loss for 7 years (1991–98) was nearly 10 m w.e., a considerable loss when compared with the maximum ice thickness of 16 m calculated by the GPR survey in 1998.
Table 3. Specific net balance measured on the stake network, 1991–98.

Given the area and the volume changes accurately obtained since 1940, it was possible to reconstruct the mean mass-balance values (volume/area) over the last six decades (Table 2). This “geometric” mass balance (−0.61 m w.e. in 1996/97; −3.34 m in 1997/98) is close to the net balance measured on the stake network (−0.66 m w.e. in 1996/97; −3.58 m in 1997/98). Before 1996, the comparison is not possible because the stake measurements were used to reconstruct the glacier topography. The first two decades (1940–63) show a moderate mass-balance deficit, whereas the last two, since 1983, are marked by a strong increase in water loss (≥1m a−1).
The mass-balance deficit was greatly amplified during 1997/98 due to one of the strongest El Niño–Southern Oscillation (ENSO) events of the century. The 1996/97 shrinkage corresponds to a mass loss of only 0.66 m, whereas in 1997/98 it was 3.58 m. The energy balance measured on Glaciar Zongo (location indicated in Fig. 1), only 20 km north of Glaciar Chacaltaya, allows an understanding of the fluxes responsible for the increased ablation on tropical glaciers during ENSO events (Reference Wagnon, Ribstein, Francou and SicartWagnon and others, 2001). The deficit of precipitation, worsened by the temperature increase, decreases the albedo, leading to very negative mass balance during ENSO warm events. As the ice thickness is <16 m, a single year with a very strong negative balance, such as 1997/98, can significantly affect the total mass of the glacier.
Hydrologie impact of glacier shrinkage
For annual mean conditions, the liquid-water budget of a glacierized basin can be written, in approximate form (modified from Reference Hastenrath and AmesHastenrath and Ames, 1995a), as:
where A g is the area of the glacier (m2), A ng is the catchment area without glacier (m2), P and B are liquid-water-equivalent precipitation and net balance (m a−1), respectively, K r is the runoff coefficient (0–1) of the surface without glacier, E is the sublimation (m a−1) and R is the water runoff in the proglacial stream (m3 a−1).
The mean precipitation is 0.52 m a−1. The mean sublimation E estimated at 5150 m a.s.l. on Glaciar Zongo is around 0.165 m a−1 for 1996–98 (Reference Wagnon, Ribstein, Francou and SicartWagnon and others, 2001). From the preliminary measurements at the hydrometric station of Glaciar Chacaltaya in 1999, we estimate K r = 0.66 in the area without glacier. The glacier surfaces are given in Table 1, and the net balance inTable 3. We treat the glacier in 1940 as the reference basin (A g = 0.223 × 103 m2) and we compare the hydrologic budget in 1940 and 1998, assuming no change in precipitation, sublimation, K r and a mean net balance reconstructed according to Table 2 for the considered decade. We find, in units of 103 m3, A g P = 116, K r A ng P = 0, A g B = −49 (1940–63 net balance = −0.221 m a−1), A g E = 37, and hence R = 128 for the 1940 budget. By comparison, for the same basin in 1998, the results are A g P = 31, K r A ng P = 56, A g B = −83 (1992–98 net balance = −1.39 m a−1), A g E = 10, and hence R = 160 for the 1998 budget. Given error tolerances of about 10% in all terms, we conclude that there is a small but significant increase of runoff in the proglacial stream supplied by the progressive thinning of the glacier. In the past decade, about half of the water discharge is not renewed by precipitation but supplied by the shrinkage of the glacier. Nevertheless, in the case of a complete disappearance of the glacier, the runoff will decrease in the future to R = K r A ng P = 116 × 103 m3 for this basin.
In other respects, the retreat of glaciers should change not only the runoff volume but also the hydrologic regime due to the regulating nature of glaciers compared with basins with entirely pluvial runoff. Glacier runoff is less seasonal than pluvial runoff, and the highest monthly discharges do not coincide with the highest precipitations (Reference Ribstein, Tiriau, Francou and SaraviaRibstein and others, 1995).
Discussion
Comparing the mass balances at Glaciar Chacaltaya with those at Glaciar Zongo, a more extensive glacier both in size (2.1 km2) and in elevation (summit at 6000 m a.s.l.), the same kind of response to climatic variability can be observed (Fig. 8). However, Glaciar Chacaltaya has experienced a more dramatic mass deficit during the present decade; we believe that this result points to the specific evolution of the small-sized glaciers and their stronger sensitivity to the present climatic conditions above 5000 m a.s.l.. Since 80% of the glaciers of the eastern cordilleras in Bolivia are <0.5 km2 in size (Reference JordanJordan, 1991) and since many have the same aspect and altitude features, an evolution similar to that of Glaciar Chacaltaya is expected on these glaciers. Thus, the future of these small glaciers can be extrapolated from the Chacaltaya case-study.
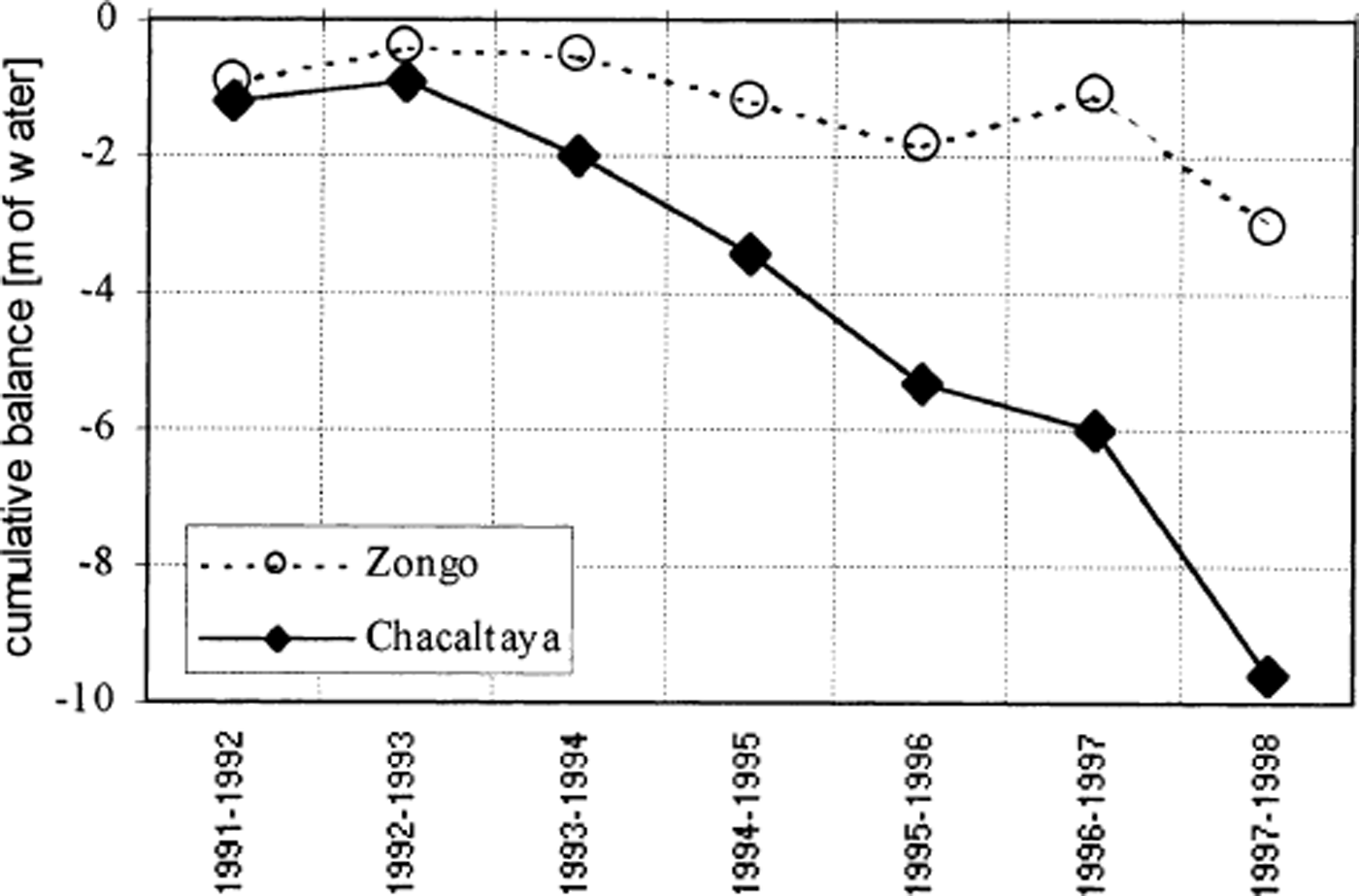
Fig. 8. Cumulative net balance (m w.e.) of Glaciar Chacaltaya and Glaciar Zongo, 20 km north of Glaciar Chacaltaya in the Cordillera Real. On Glaciar Chacaltaya, the net balance was estimated from the stake network. On Glaciar Zongo, measurement points included pits in the upper zone (6000–5200 m a.s.l.) and a stake network in the lower zone (5200–4900 m a.s.l).
Referring to the 16 m maximum ice thickness measured in 1998 and the insignificant mass transfer from the upper to the lower zone due to the absence of accumulation zone and negligible horizontal velocities, the future of Glaciar Chacaltaya can be estimated from the mass-balance evolution over a given period of time. This simple calculation leads to a glacier extinction in around 10 years extrapolating the mean 1991–98 mass balance (−1.54 m ice a−1); around 15 years for 1983–98 (−1.07 m ice a−1); around 20 years for 1963–98 (−0.815 m ice a−1); and around 27 years for 1940–98 (−0.596 m ice a−1). It is most probable that the glacier will completely disappear in the 10–15 year range.
The drastic imbalance of the glacier since 1983 (−0.96 m a−1 of water loss) translates to an average departure of heat supply for ice melting of 10 W m−2. For a similar case-study analyzed in Peru by Reference Hastenrath and AmesHastenrath and Ames (1995a), sensitivity analyses indicate that the stabilization of the glacier (net balance = 0) could be produced by a cloudiness increase of less than one-tenth (reducing solar radiation), by an air-temperature decrease of about 1.5°C (reducing sensible-heat transfer to the glacier), by a decrease in specific humidity of about 0.5 g kg−1 (enhancing the sublimation), or by some combination of these heat-budget processes. Based on the equilibrium-line altitude (ELA) calculated for the 1991–98 period, the stabilization of the glacier would imply a reduction in the ELA of about 200 m (ELA1991–98 = 5400 m a.s.l. vs ELA0 = 5200 m a.s.l).
Conclusion
Glaciar Chacaltaya is representative of small glaciers of the Bolivian cordilleras. The large amount of high-resolution information collected makes this glacier particularly suitable for diagnosing the glacier recession in this part of the tropical Andes. The principal results are :
The glacier has experienced a major recession since the LIA maximum, losing 89% of its surface area.
The recession was moderate from 1940 to 1963, with an average mass deficit of 0.221 m w.e. a−1; the recession rate increased to 0.563 m a−1 in the period 1963–83.
Since 1983, the glacier has lost 0.963 m a−1. Considering the total volume of ice remaining, determined by high resolution GPR measurements, and with no change in the present shrinkage rate, the glacier would disappear within 10–15 years.
Assuming no changes in the different terms of the hydrologic balance, a complete extinction of the glacier would reduce by about 30% the total runoff of the proglacial stream. Furthermore, its regime would become completely dependent on the precipitation variability.
Such imbalance translates to an average departure of heat supply for glacier melting of 10 W m−2. The stabilization of Glaciar Chacaltaya could require a cloudiness increase of less than one-tenth, an air-temperature decrease of about 1.5°C, a decrease in specific humidity of about 0.5 g kg−1, or some combination of these processes. Such a stabilization would imply a 200 m reduction of the present average ELA.
In a forthcoming paper, the fluctuations of Glaciar Chacaltaya will be analyzed in the context of recent climatic changes in the Andean mid-troposphere.
Acknowledgements
The authors thank R. Naruse, G. Casassa and W. Haeberli for valuable comments that led to improvements in the manuscript, and W. D. Harrison, Co-Chief Editor, for assistance with the English.













