1. INTRODUCTION
Assessing the contribution of polar ice sheets to future sea level rise (SLR) is a major challenge that ice-sheet models are intended to address. Most of the ice loss from the Antarctic ice sheet, which constitutes the largest potential source of future SLR, occurs through solid ice discharge into the ocean and is controlled by marine terminating glaciers (Church and others, Reference Church2013). In this context, accurate knowledge of the position of the grounding line (GL), the limit beyond which grounded ice starts floating, is critical for reliable calculations of the current mass budget (Rignot and others, Reference Rignot, Velicogna, Van den Broeke, Monaghan and Lenaerts2011) and proper modelling of its dynamics is required for future SLR projections (Durand and Pattyn, Reference Durand and Pattyn2015).
In the recent years, particular concern has arisen regarding large parts of the West Antarctic ice sheet, which are known to be lying on upward sloping beds (Fretwell and others, Reference Fretwell2013), and thus potentially prone to a marine ice-sheet instability (MISI). First proposed by Weertman (Reference Weertman1974) from theoretical arguments and later confirmed by Schoof (Reference Schoof2007a ) using an analytical approach based on asymptotic expansions, the MISI hypothesis states that marine-based ice sheets resting on upward-sloping beds, also called reverse slopes, are inherently unstable. Although it has been controversial for many years, the MISI theory is now largely accepted within the community in the absence of buttressing. However, Gudmundsson and others (Reference Gudmundsson, Krug, Durand, Favier and Gagliardini2012) have shown that stable sections of GL located on a reverse slope can be obtained when lateral buttressing is sufficient. Experiment 3 of the marine ice-sheet intercomparison exercise MISMIP (Pattyn and others, Reference Pattyn2012) was designed to test the ability of 1HD numerical models to accurately simulate GL migration on a reverse slope. The experimental set-up prescribed the commonly used non-linear Weertman law (Weertman, Reference Weertman1957) as a basal boundary condition to account for basal slip at the ice/bed interface.
A large part of the flow of fast-flowing ice streams draining ice from Antarctica is due to basal slip (Cuffey and Paterson, Reference Cuffey and Paterson2010), which is governed by various, complex and poorly observed processes such as deformation of subglacial sediments (Tulaczyk and others, Reference Tulaczyk, Kamb and Engelhardt2000) or ice flowing over rigid obstacles by a combination of viscous creep and regelation (Weertman, Reference Weertman1957) with potential formation of water-filled cavities (Lliboutry, Reference Lliboutry1968). Observational evidence has established the existence of an active subglacial drainage system (Gray and others, Reference Gray2005; Fricker and others, Reference Fricker, Scambos, Bindschadler and Padman2007) made of water-laden till and interconnected subglacial lakes linked by water channels (Wingham and others, Reference Wingham, Siegert, Shepherd and Muir2006; Fricker and Scambos, Reference Fricker and Scambos2009). Subglacial water exiting the grounded ice sheet and entering the sub-ice-shelf cavity at the GL has notably been reported by several authors (Carter and Fricker, Reference Carter and Fricker2012; Le Brocq and others, Reference Le Brocq2013) suggesting a connectivity between the basal hydrological network and the ocean. By reducing the effective pressure, i.e. the difference between ice overburden pressure and water pressure, the liquid water flowing through this basal network enhances basal slip (Zwally and others, Reference Zwally2002; Stearns and others, Reference Stearns, Smith and Hamilton2008).
Ice flow models account for basal slip via the use of a friction law, i.e. the relationship between the basal drag τ b and the sliding velocity u b. Effective pressure N has been included in several friction laws over the last 30 years (Budd and others, Reference Budd, Jenssen and Smith1984; Schoof, Reference Schoof2005; Tsai and others, Reference Tsai, Stewart and Thompson2015) to represent the effect of water at the ice/bed interface. Computing basal drag then requires a hydrological model to evaluate the basal water pressure. Several hydrological models have been proposed over the last years. The most complex ones simulate the subglacial drainage processes with a high level of detail (Schoof, Reference Schoof2010; Hewitt and others, Reference Hewitt, Schoof and Werder2012; Werder and others, Reference Werder, Hewitt, Schoof and Flowers2013; Fleurian and others, Reference Fleurian2014). However, the characterisation of the subglacial system being ill-defined, these models usually rely on a set of poorly constrained parameters. For this reason, although empirical parameterisations of basal water pressure have been developed (Pimentel and others, Reference Pimentel, Flowers and Schoof2010; Martin and others, Reference Martin2011), authors using effective pressure-dependent friction laws usually adopt the assumption of perfect hydrological connectivity to the ocean (Morlighem and others, Reference Morlighem2010; Tsai and others, Reference Tsai, Stewart and Thompson2015; Gladstone and others, Reference Gladstone2017).
Inverse methods are now routinely used when forecasting the evolution of real ice sheets in order to initialise the model, and in particular the basal friction field, from available observations of surface velocities. Because the inferred basal stress must satisfy the global stress balance, the form of the friction law cannot be determined from a unique set of observations. For this reason, most models use the classical Weertman friction law (Weertman, Reference Weertman1957) and infer a unique field, the basal friction coefficient C(x,y), from observed surface velocities (Vieli and Payne, Reference Vieli and Payne2003; Arthern and Gudmundsson, Reference Arthern and Gudmundsson2010; Gillet-Chaulet and others, Reference Gillet-Chaulet2012; Larour and others, Reference Larour, Seroussi, Morlighem and Rignot2012b ). The complexity of the underlying physical processes, in particular the dependence on effective pressure, is then hidden in the inferred spatial distribution of C. Due to the lack of constraints on its temporal evolution, one adopted solution is to keep the friction coefficient field stationary for transient prognostic simulations (Favier and others, Reference Favier2014). Nevertheless, several attempts have been made to account for temporal evolution of basal conditions. Shannon and others (Reference Shannon2013) proposed a parameterisation of the annual speed-up, implemented through fractional changes of the basal friction, as a function of the meltwater run-off. Calibrated from observations in Greenland, the parameterisation allows for both continuously increasing or bounded lubrication. Studying the southern Basin 3 of the Austfonna ice cap (Svalbard), Gong and others (Reference Gong2016) linearly extrapolated in time the friction coefficient field using the values inferred from observations made in 1995 and 2011. They were not able to reproduce the 2012 surge with this simple procedure, leading them to the conclusion that more physically based models are required.
The inferred spatial distribution of C usually exhibits a smooth decrease over a certain distance upstream of the GL (Vieli and Payne, Reference Vieli and Payne2003), which supports the hypothesis of a locally reduced effective pressure due to the connectivity between the subglacial drainage system and the ocean. This area of reduced friction is of major importance from a mechanical point of view as it constitutes the transition zone within which ice flow switches from basal-drag-controlled ice stream flow to drag-free flow of floating ice shelves onto the ocean. Some authors have proposed ad hoc methods to account for the basal drag decrease occuring in this transition zone independently of the GL position (Pattyn and others, Reference Pattyn, Huyghe, De Brabander and De Smedt2006; Gagliardini and others, Reference Gagliardini2016), but the typical length scale of the decay is chosen arbitrarily without considering the actual physical mechanisms behind it. Using an effective pressure-dependent friction law is a physically motivated way to account for the transition zone. By definition, the effective pressure is zero at the GL and wherever ice is floating. Further inland, ice thickness increases while water disponibility tends to decrease. Consequently, the ice overburden pressure progressively overcomes water pressure causing effective pressure to increase over a certain length scale upstream of the GL, which is determined by the surface profile as well as the spatial distribution of basal water pressure and corresponds to the transition zone.
Using a combination of numerical and analytical results Schoof (Reference Schoof2007a ) developed a boundary layer theory enabling to predict steady ice-sheet profiles and providing stability criterion under Weertman friction regime. Tsai and others (Reference Tsai, Stewart and Thompson2015) extended this work, assuming that the friction should shift from a Weertman friction regime at high effective pressure to a Coulomb friction regime at low effective pressure. However, the implications on the GL dynamics of such a shift were not investigated. Based on an experimental setup adapted from experiment 3 of MISMIP, the aim of this work is to study the sensitivity of the GL dynamics to different friction regimes. To this end, we compare four friction laws that mainly differ in their dependence on N. These laws can be calibrated to give the same initial solution, but will differ in their response to a perturbation. The first section is an overview of these friction laws. A precise description of the experiments and of the model used to conduct them is given in the second section. In the following section, results are presented both in terms of steady states and transient responses. Finally, these results, as well as their implications, are discussed in the last section.
2. OVERVIEW OF FRICTION LAWS
The original theory of sliding was formulated assuming that the bedrock is rigid, ice is clean and temperate and that a thin film of water separates ice and bedrock. At the local scale, ice is assumed to slide perfectly on the bedrock, but bedrock roughness induces a mean resistance to basal motion which is referred to as basal drag. Weertman (Reference Weertman1957) demonstrated that in such a case the relation between τ b and u b takes the form of a power law:
$$\tau _{\rm b} = C_{\rm W} u_{\rm b}^m, $$
where C W is a friction parameter, hereafter called Weertman friction parameter, and m a positive constant. This is the most commonly used relation in ice flow models and projections in terms of sea level rise have been shown to be highly sensitive to the value of m (Ritz and others, Reference Ritz2015). Given that Eqn (1) was initially developed to account for the creep of ice over hard beds, the exponent m is often related to the creep exponent n of the Glen's flow law as m = 1/n and, therefore, usually set to m = 1/3 (Weertman, Reference Weertman1974; Schoof, Reference Schoof2007b ; Gudmundsson and others, Reference Gudmundsson, Krug, Durand, Favier and Gagliardini2012; Pattyn and others, Reference Pattyn2012; Pattyn and others, Reference Pattyn2013). However, the case of ice sliding over soft beds can also be represented through Eqn (1) provided that the value of m is correctly chosen in order to account for the underlying till deformation. For example, Joughin and others (Reference Joughin, Smith and Holland2010) tried three different parameterisations of m to reproduce the observed speedup of ice flow at the GL of Pine Island Glacier between 1996 and 2010; they concluded that assuming m = 3 over hard-bedded areas and a quasi-plastic behaviour (m → 0), where till is likely to be present, gives the best match to observed flow speeds and thinning rates. This result was later confirmed by Gillet-Chaulet and others (Reference Gillet-Chaulet2016) and extended to the main trunk of the glacier. A linear relationship, i.e. m = 1 in Eqn (1), is nevertheless the most commonly adopted in ice flow models making use of inverse methods to constrain the basal friction from observed surface velocities (Larour and others, Reference Larour, Seroussi, Morlighem and Rignot2012b ; Schäfer and others, Reference Schäfer2013; Gladstone and others, Reference Gladstone2014). The inferred friction parameter can then be seen as an ‘effective friction parameter’ accounting for all the unknown underlying physics.
Budd and others (Reference Budd, Keage and Blundy1979) carried out laboratory experiments for studying temperate-ice sliding over rock surfaces with a wide range of roughnesses, for normal and shear stresses comparable to those expected under real ice masses. They concluded that τ b exhibits a strong dependence on N which led them to modify the Weertman law as follows:
$$\tau _{\rm b} = C_{\rm B} u_{\rm b}^m N^q, $$
where C B is a friction parameter, hereafter called Budd friction parameter, N the effective pressure and q a positive constant. Original values proposed by the authors were m = 1 and q = 2 (Budd and others, Reference Budd, Jenssen and Smith1984), but more recent modelling studies adopt q = 1 (Morlighem and others, Reference Morlighem2010; Larour and others, Reference Larour2012a ; Gladstone and others, Reference Gladstone2017). In the particular case q = 0, the Budd law reduces to the Weertman law (Eqn (1)).
The form of Eqns (1) and (2) directly implies that basal drag can reach arbitrary high values. However, considering ice sliding over a rigid and undulated bedrock made of rectangular steps, Iken (Reference Iken1981) demonstrated that the presence of water-filled cavities induces the existence of an upper bound for basal drag determined only by the maximum up-slope of the bed. Schoof (Reference Schoof2005) validated this result for more general bed geometries and analytically derived a new friction law for a linear ice rheology. This law was numerically extended to non-linear rheologies by Gagliardini and others (Reference Gagliardini, Cohen, Råback and Zwinger2007), and the general relationship writes:
$$\tau _{\rm b} = \displaystyle{{C_{\rm S} u_{\rm b}^m} \over {(1 + \left( {C_{\rm S} /C_{{\rm max}} N} \right)^{1/m} u_{\rm b} )^m}}, $$
where C
S is a friction parameter, hereafter called Schoof friction parameter, and C
max a positive value corresponding to the maximum value of τ
b/N which is bounded by the local maximum up-slope of the bedrock (more details in Gagliardini and others (Reference Gagliardini, Cohen, Råback and Zwinger2007)). The Schoof law exhibits two asymptotic behaviours. At large N, Eqn (3) reduces to
$\tau _{\rm b} {\rm \sim} C_{\rm S} u_{\rm b}^m $
which corresponds to a Weertman-type friction regime. On the other hand, when N → 0 water-filled cavities open, decreasing the apparent roughness of the rigid bedrock and inducing a Coulomb-type regime with τ
b ~ C
max
N. This latter situation is a particular case of plastic basal rheology, i.e τ
b = τ
0, with a yield stress τ
0 proportional to N.
The Coulomb-type plastic rheology has also been suggested as the most appropriate to account for glacial till deformation in the case of ice sliding over soft beds (Iverson and others, Reference Iverson, Hooyer and Baker1998; Tulaczyk and others, Reference Tulaczyk, Kamb and Engelhardt2000; Truffer and others, Reference Truffer, Echelmeyer and Harrison2001). Arguing that basal motion is a combination of both mechanisms, i.e. ice deformation around and across the bedrock rugosity and deformation of the underlying soft till, Tsai and others (Reference Tsai, Stewart and Thompson2015) proposed a friction law which accomodates the two friction regimes:
$$\tau _{\rm b} = \min [C_{\rm W} u_{\rm b}^m, \;fN]$$
with f a solid friction coefficient. While the Schoof law induces a continuous transition from a Coulomb-type basal rheology to a Weertman-type basal rheology, the Tsai law is characterised by a cut-off; the cross-over from the former regime to the latter occurs when f N gets higher than
$C_{\rm W} u_{\rm b}^m $
. Consequently, although the two formulations are intended to describe different physical processes, for properly chosen friction parameters (i.e. C
S = C
W and f = C
max), the Tsai and Schoof laws present the same limit regimes.
Contour plots of τ
b given in the plane (N, u
b) are represented in Fig. 1 for the four friction laws (Eqns (1)–(4)) using m = 1/3, q = 1, C
W = C
B = C
S = 7.624 × 106 S.I. and f = C
max = 0.5; with this choice the four laws give the same τ
b for the value N = 1 MPa (highlighted by the black vertical dashed lines in Figs 1a–d). By definition, τ
b is independent of N with the Weertman law, and isovalues are given by horizontal lines (Fig. 1a). Isolines obtained with the Tsai law (Fig. 1d) are divided into two parts: high effective pressures correspond to the Weertman-type regime, whereas a Coulomb-type regime applies at low effective pressures. The switch from one regime to the other being governed by a cut-off, contour lines form a corner at the threshold value. With the Schoof law (Eqn (3)), the transition between the two regimes is continuous, and τ
b asymptotically tends towards the Weertman and Coulomb regimes at, respectively, low sliding velocity and low effective pressure (Fig. 1c). The range of effective pressure over which the Schoof law shifts from a Weertman-type regime to a Coulomb-type regime gets narrower as τ
b gets higher (Fig. 1d). As an example, for
$\tau _{\rm b} = 0.2\;{\kern 1pt} {\rm MPa}$
, the Schoof law is numerically close to a Weertman-type friction law for
$N \ge 1{\kern 1pt} \;{\rm MPa}$
, whereas it is numerically close to a Coulomb-type friction law for
$N \le 0.4\;{\kern 1pt} {\rm MPa}$
. For intermediate values of N, the dependence of basal drag on basal velocity gets weaker for decreasing values of N. The Budd law does not have limit regimes and iso-contours, in a log–log plot, are given by straight lines of slope proportional to −q/m (Fig. 1b). With the chosen coefficients, it always gives larger (resp. lower) τ
b
than the Schoof law for N > 1 MPa (resp. N < 1 MPa). As an example, for
$N{\rm \sim} 0.3{\kern 1pt} \;{\rm MPa}$
and a basal drag of 0.04 MPa, velocities are ~36 times larger with the Budd law than with the Schoof one. These general features prefigure very different ice flow dynamics.
Fig. 1. Iso-values of τ b ranging from 0.04 to 0.2 MPa given in the basal velocity-effective pressure log–log plane with: (a) Weertman, (b) Budd, (c) Schoof and (d) Tsai laws (Eqns (1)–(4)), for m = 1/3, q = 1, C W = C B = C S = 7.624 × 106 S.I. and f = C max = 0.5. Dotted black lines reported on each plot are the iso-values of τ b given with the Schoof law. The vertical black dotted line corresponds to N = 1 MPa.
The main objective of this work is to evaluate the sensitivity of the GL dynamics depending on the chosen friction law.
3. METHODS
3.1. Model description
We use the finite-element ice flow model Elmer/Ice (Gagliardini and others, Reference Gagliardini2013) to solve the shallow shelf approximation (SSA) equation (MacAyeal, Reference MacAyeal1989) in 1HD. This vertically integrated model neglects vertical variations of horizontal velocities and is an asymptotic approximation of the Stokes equations when the aspect ratio and the basal friction are small (Schoof and Hindmarsh, Reference Schoof and Hindmarsh2010). The 1HD velocity field is restricted to the component u only which is the solution of the equation:
$$4\displaystyle{\partial \over {\partial x}}\left( {\bar \eta \displaystyle{{\partial u} \over {\partial x}}} \right) - \tau _{\rm b} = \rho _{\rm i} gH\displaystyle{{\partial z_{\rm s}} \over {\partial x}},$$
where ρ
i is the ice density, g the gravity norm, H = z
s − z
b the ice thickness, with z
s and z
b the top and bottom surface elevations, respectively. The vertically integrated effective viscosity
$\bar \eta $
is given by
$$\bar \eta = \int_{z_{\rm b}} ^{z_{\rm s}} \displaystyle{1 \over 2}A^{ - 1/n} D_{\rm e}^{(1 - n)/n} dz,$$
where D e is the second invariant of the strain-rate tensor, A the fluidity parameter and n the Glen's law exponent set to n = 3.
The evolution of ice thickness is governed by the vertically integrated mass conservation equation:
$$\displaystyle{{\partial H} \over {\partial t}} + \displaystyle{{\partial (uH)} \over {\partial x}} = a_{\rm s}, $$
where a s is the surface mass balance only, as melting/refreezing at the base is neglected.
The bottom surface elevation can be deduced from the bedrock topography b(x) by applying the no-penetration condition and the floating condition. Assuming a constant sea level set to z sl = 0, these conditions write:
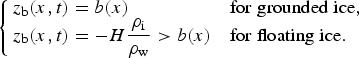$$\left\{ {\matrix{ {z_{\rm b} (x,t) = b(x)} \hfill & {{\rm for}\;{\rm grounded}\;{\rm ice},} \hfill \cr {z_{\rm b} (x,t) = - H\displaystyle{{\rho _{\rm i}} \over {\rho _{\rm w}}} \gt b(x)} \hfill & {{\rm for}\;{\rm floating}\;{\rm ice}.} \hfill \cr}} \right.$$
In the SSA, the GL position x G is directly evaluated from the flotation criterion, i.e. by solving the equation:
$$H(x_{\rm G} ) + b(x_{\rm G} )\displaystyle{{\rho _{\rm w}} \over {\rho _{\rm i}}} = 0.$$
Therefore, the GL can be located at any point of the domain and does not necessarily have to fall at a mesh node.
Solving Eqn (5) requires an explicit formulation of the potential dependence of τ b on u. Because we use a 1HD vertically integrated model, u = u b. Ice shelves do not experience basal drag, therefore τ b is set to zero wherever ice is floating. For grounded ice, τ b is related to u b via one of the friction laws given by Eqns (1)–(4). Three of these friction laws, i.e. the Schoof, Tsai and Budd laws, are effective pressure dependent (Eqns (2)–(4)). Here we adopt a simple hydrological model and make the common assumption of perfect hydrological connectivity to the ocean, which leads to
$$N = \left\{ {\matrix{ {\rho _{\rm i} gH + \rho _{\rm w} gz_{\rm b}} \hfill & {{\rm if}\;z_{\rm b} \lt 0,} \hfill \cr {\rho _{\rm i} gH} \hfill & {{\rm if}\;z_{\rm b} \ge 0.} \hfill \cr}} \right.$$
The upstream end of the domain is a symmetry axis (ice divide) for which the Dirichlet boundary condition u(x = 0) = 0 applies. The downstream end of the domain is a calving front, where the difference between the ice pressure and sea-water pressure leads to the following Neumann boundary condition:
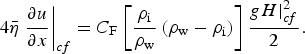$$4\bar \eta \left. {\displaystyle{{\partial u} \over {\partial x}}} \right \vert _{cf} = C_{\rm F} \left[ {\displaystyle{{\rho _{\rm i}} \over {\rho _{\rm w}}} \left( {\rho _{\rm w} - \rho _{\rm i}} \right)} \right]\displaystyle{{gH \vert _{cf}^2} \over 2}.$$
Following Drouet and others (Reference Drouet2013), C F is a buttressing factor; C F = 1 implies no buttressing, whereas C F<1 reduces the driving force, and thus simulates buttressing at the calving front. This parameterisation is used in the numerical experiments to induce dynamical pertubations and thus GL migration and is not a physical representation of lateral buttressing as in Gagliardini and others (Reference Gagliardini, Durand, Zwinger, Hindmarsh and Le Meur2010).
Extensive work has been published showing the importance of mesh resolution to accurately model GL dynamics (Vieli and Payne, Reference Vieli and Payne2005; Durand and others, Reference Durand, Gagliardini, De Fleurian, Zwinger and Le Meur2009a , Reference Durand, Gagliardini, Zwinger, Le Meur and Hindmarsh b ; Pattyn and others, Reference Pattyn2012; Seroussi and others, Reference Seroussi, Morlighem, Larour, Rignot and Khazendar2014; Durand and Pattyn, Reference Durand and Pattyn2015; Gagliardini and others, Reference Gagliardini2016). To ensure a sufficient and constant resolution of 100 m around the GL for all the experiments, the domain is meshed with 9080 linear elements, 9000 of which are regularly distributed between x = 525.0 and 1425.0 km. The size of the remaining 80 elements increases upstream and downstream following a geometric progression. In Elmer/Ice, friction coefficients are estimated at mesh nodes and linearly interpolated at quadrature points. The flow dynamics is particularly sensitive to the numerical scheme used to integrate the friction in the elements close to the GL (Seroussi and others, Reference Seroussi, Morlighem, Larour, Rignot and Khazendar2014; Gagliardini and others, Reference Gagliardini2016). Here, the GL position being evaluated with a subelement precision (Eqn (9)), the friction can be set to 0 at floating quadrature points (subelement parameterisation SEP3 in Seroussi and others (Reference Seroussi, Morlighem, Larour, Rignot and Khazendar2014)) allowing coarser mesh resolution at the GL. The number of quadrature points is set to 10 in the element containing the GL.
3.2. Experimental setup
The experimental setup is adapted from MISMIP experiment 3 (Pattyn and others, Reference Pattyn2012). The domain stretches along a flow-line in the x-direction from a dome at x = 0 km to a calving front kept at x = 2000 km. The bedrock topography is given by Eqn (16) in Pattyn and others (Reference Pattyn2012). It exhibits an overdeepening with a retrograde bed slope between x = 973.7 and 1265.7 km; elsewhere, the bed slopes downward towards the ocean.
All the experiments start from a steady-state geometry obtained using the Schoof friction law (Eqn (3)) and setting the buttressing factor to C F = 0.4 in Eqn (11). Values of the model parameters are given in Table 1. The spatially uniform fluidity parameter A = 1.61166 × 10−25 Pa−3 s−1 has been chosen to get an initial steady-state position of the GL downstream but sufficiently close to the reverse slope area (x = 1267.7 km).
Table 1. List of parameter values used to obtain the steady state for the reference case (Schoof friction law)
From this steady state, a reference simulation is obtained by releasing the buttressing, i.e. C F = 1 in Eqn (11), and running the model forward in time for 20 ka. As for the initial state, the friction law for the reference simulation is given by the Schoof friction law (Eqn (3)). The GL position as a function of time is shown in Fig. 2 (green solid curve). The GL retreats across the MISI region and reaches a new steady-state position located at x = 680.0 km.
Fig. 2. Grounding line position as a function of time for the four friction laws. The reference case (green solid line) corresponds to the retreat obtained with a Schoof friction law after buttressing is released at t = 0 a. The red dash-dotted line is the GL retreat obtained with the Tsai law. Black circles along the green solid line correspond to the seven different initial states used for inversion (respectively after 0, 100, 300, 500, 700, 900 and 1100 years of GL retreat for the reference case). Blue dotted and magenta dashed lines are the GL retreats obtained with, respectively, a Budd and a Weertman friction law starting from each of the seven initial states. The dotted black lines are the unique steady GL positions obtained with a Weertman and a Schoof law (x = 759.5 and 680.0 km, respectively) and the most retreated steady GL position obtained with a Budd law (x = 529.3 km). The grey-shaded area corresponds to the zone of reverse slope.
The objective of the following experiments is to illustrate the sensitivity of the GL dynamics to the form of the friction law. At a given time t
i, the flow solution depends only on the boundary conditions, the ice-sheet topography and the basal stress field. We assume that the reference experiment is perfectly observed at time t
i, and denote by
$u_{{\rm bS}}^{t_{\rm i}} $
and
$N_{\rm S}^{t_{\rm i}} $
, the corresponding basal velocity and effective pressure fields, respectively. The friction coefficients of the Weertman and Budd laws,
$C_{\rm W}^{t_{\rm i}} $
and
$C_{\rm B}^{t_{\rm i}} $
, that would lead to the same reference stress field
$\tau _{{\rm bS}}^{t_{\rm i}} $
, calculated from Eqn (3), can be identified analytically using Eqns (1) and (2) as:
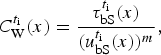$$C_{\rm W}^{t_{\rm i}} (x) = \displaystyle{{\tau _{{\rm bS}}^{t_{\rm i}} (x)} \over {(u_{{\rm bS}}^{t_{\rm i}} (x))^m}}, $$
and
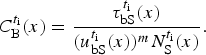$$C_{\rm B}^{t_{\rm i}} (x) = \displaystyle{{\tau _{{\rm bS}}^{t_{\rm i}} (x)} \over {(u_{{\rm bS}}^{t_{\rm i}} (x))^m N_{\rm S}^{t_{\rm i}} (x)}}.$$
Under the shelf,
$C_{\rm W}^{t_{\rm i}} $
and
$C_{\rm B}^{t_{\rm i}} $
are undetermined as the ice is not in contact with the bedrock, and we set
$C_{\rm W}^{t_{\rm i}} = C_{\rm B}^{t_{\rm i}} = 0$
for floating ice. This choice does not affect the results as the chosen perturbation is expected to induce GL retreat only. Similarly, because of the Dirichlet boundary condition at x = 0,
$C_{\rm W}^{t_{\rm i}} (x = 0)$
and
$C_{\rm B}^{t_{\rm i}} (x = 0)$
are set to the value determined for the first node downstream.
Computing again the flow velocities at time t
i (i.e. solving Eqn (5)), using
$C_{\rm W}^{t_{\rm i}} $
and
$C_{\rm B}^{t_{\rm i}} $
and their corresponding friction law, leads to the same solution with a mean relative difference of <1.5 × 10−5. The transient experiments are then continued with the Weertman and Budd laws to the end of the 20 ka, assuming that the friction coefficient fields
$C_{\rm W}^{t_{\rm i}} $
and
$C_{\rm B}^{t_{\rm i}} $
are constant in time. As illustrated in Fig. 2 (black circles), this procedure is applied at seven discrete times t
i = 0, 100, 300, 500, 700, 900, 1100 years. For each time t
i, the experiments with the three different friction laws start from the same initial state, but will differ in their transient evolution as the three laws have a different dependence on effective pressure N. In the following, the experiments using the Weertman and Budd friction laws, with initialisation performed at t
i, are denoted, respectively,
${\rm W}^{t_{\rm i}} $
and
${\rm B}^{t_{\rm i}} $
.
The Tsai law can be seen as an end-member case of the Schoof law and, therefore, is expected to give similar GL behaviour as the latter. To confirm this hypothesis, an additional experiment is carried out with the Tsai law starting from the ice-sheet topography and basal velocity of the reference case at t
i = 0 a. The parameters C
W and f of Eqn (4) are set to, respectively, C
S and C
max (Table 1). Note that, the Schoof and Tsai laws giving slightly different τ
b in the range of effective pressure within which the Schoof law continuously switches from a Coulomb-type regime to a Weertman-type regime (Fig. 1d), the initial basal stress field obtained with the Tsai law is not exactly identical to the reference basal stress field at initial time
$\tau _{{\rm bS}}^{0\;{\rm a}} $
.
4. RESULTS
GL positions against time are shown in Fig. 2 for the various simulations. The maximum GL migration rates dx G/dt over the whole simulation and the distances covered by the GL over the first 100 years following the initialisation Δx G are summarised in Table 2. Because it corresponds to the reference simulation, the maximum GL migration rate obtained for the Schoof law is only given for t i = 0 a. The same holds for the Tsai law for which the only simulation that has been run starts with the topography and velocity field of the reference simulation at t i = 0 a.
Table 2. Maximum GL migration rate dx G /dt in m a−1 over the whole simulation and distance covered by the GL Δx G in km over the first 100 years following the initialisation for the four friction laws and the seven initial states (the highest value obtained for each friction law is in bold)
With the Schoof law (reference simulation), buttressing release is immediately followed by a retreat of the GL across the MISI region at a slowly growing rate. The GL reaches a maximum retreat speed of 495 m a−1 before slowing down and stabilising at x = 680.0 km. It takes 14 680 years from t i = 0 years for the GL to reach its new steady position. As expected, the Tsai law (dash-dotted red curve in Fig. 2) gives very similar GL dynamics with a maximum retreat speed of 465 m a−1 and a steady GL position reached after 14 550 years of simulation and located at x = 683.3 km. The Budd law (dotted blue curves in Fig. 2) gives GL migration rates one order of magnitude faster with values ranging from 3260 to 9180 m a−1. It takes between 6610 and 8085 years for the GL to reach its new steady position which differs slightly depending on the initial state t i. The different steady positions are ranging from x = 529.3 km for B0 a to x = 532.6 km for B1.1 ka. The Weertman law (dashed magenta curves in Fig. 2) gives much slower retreat rates spanning from 45 to 105 m a−1 (Table 2). Two different behaviours can be distinguished depending on the initial state. For W300 a, a first period of ~7000 years of very slow GL retreat is followed by a period of accelerated retreat before the migration rate decreases to zero as the ice sheet tends to a new steady state. The same type of behaviour is observed for every W≥300 a, except that the first period of very slow GL retreat gets shorter and shorter. The fastest migrations rates are always almost one order of magnitude smaller than those obtained with the Schoof friction law. It takes between 16 050 and 29 560 years after the initialisation for the GL to reach its new steady state located at x = 759.5 km. In contrast to what is obtained with the Budd law, this new steady-state position is the same for every W≥300 a with an accuracy of 50 m. For W0 a and W100 a, the second phase of accelerated GL retreat accross the MISI is never reached. In the first case the GL, initially located at x = 1267.7 km, starts to retreat during 160 years only before stabilizing at x = 1265.4 km. Similarly, for the simulation W100 a, it takes 4380 years for the GL to retreat from an initial location x = 1235.5 km to a new steady position located at x = 1233.2 km. Because of the small amplitudes and short durations of these retreat phases, they are not distinguishable on Fig. 2. The retreat rates given in Table 2 for these two cases correspond to these small retreats. Importantly, the two obtained steady GL positions are located in the area of retrograde slope (grey-shaded area in Fig. 2). This point will be discussed in more detail in the following section.
The thickness rates of change ∂H/∂t after 0, 20 and 40 years of GL retreat are shown in Fig. 3 for the reference simulation as well as the simulations W0 a and B0 a. The corresponding u b, τ b and ice-sheet profiles are given in the vicinity of the GL in Figs 4b–d. Buttressing release at initial time induces a dynamical response of the ice sheet: the whole ice shelf thins as well as the ice sheet over ~30 km upstream of the GL causing the latter to retreat. The initial peak of thinning occurs at x = 1265.3 km, only 2.4 km upstream of the GL. By construction, the initial responses obtained with the Weertman and Budd laws are identical to the one obtained with the Schoof law for the reference simulation (black lines in Fig. 3).
Fig. 3. Initialisation at time t i = 0 years. Thickness rate of change at initial time (black solid lines), 20 years after initialisation (colored solid lines) and 40 years after initialisation (colored dashed line) for the Schoof (green), Weertman (magenta) and Budd (blue) friction laws. The GL positions are highlighted by black dots at initial time, diamonds 20 years after initialisation and triangles 40 years after initialisation. The black dashed line corresponds to zero thickness rate of change.
Fig. 4. Initialisation at time t
i = 0 years. (a) Spatial distribution of the friction parameters C
S (dash-dotted green line), C
W (dash-dotted magenta line) and C
B (dash-dotted blue line) at initial time. Basal velocities (b), basal drags (c) and ice-sheet profiles (d) at initial time (black solid lines), 20 years after inversion (colored solid lines) and 40 years after inversion (colored dashed lines) for the Schoof (green), Weertman (magenta) and Budd (blue) friction laws. The asymptotic behaviours of the Schoof law, i.e.
$\tau _{\rm b} = C_{\rm S} u_{\rm b}^m $
and τ
b = C
max
N are highlighted in (c) by dotted and dashed cyan lines, respectively. Basal drags obtained with the Tsai law at initial time (dash-dotted line), 20 (continuous line) and 40 (dashed line) years after inversion are represented in red in (c). The vertical black dotted line is the dowstream bound of the reverse slope. The GL positions are highlighted by black dots at initial time, diamonds 20 years after inversion and triangles 40 years after inversion. The brown solid line in (d) is the bedrock.
Figure 4a shows the uniform friction parameter C S as well as the inferred spatial distribution of C W and C B for initialisation performed at t i = 0 a. Note that since these friction parameters have different units, their absolute values should not be compared directly. Rather, the general shape of their spatial distributions is of interest. Note also that these distributions are the initial ones; as the GL retreats, they keep the same shape except that the value of the friction parameter at a node which starts floating is switched to zero. The inferred Weertman friction parameter C W is quasi-identical to the Schoof friction parameter C S under the whole ice sheet except in the close vicinity of the GL within which the former continuously decreases to zero (magenta dash-dotted lines in Fig. 4a). The Budd friction parameter C B exhibits a totally different spatial distribution; from low values far upstream of the GL, it gets higher and higher as getting closer to the GL and reaches a maximum located at 1.1 km upstream of the GL. Then it slightly decreases down to the GL within an area where the Schoof law reduces to a Coulomb law and, as such, is free from any dependence on basal velocity. With these distributions of C W and C B, the transition zone due to the dependence of the Schoof law on effective pressure and within which τ b goes smoothly from a maximum beneath the ice sheet to zero at the GL, is well reproduced by the Budd and Weertman laws at initial time (black line in Fig. 4c). In contrast, because the parameters of the Tsai law were not inferred from the reference simulation but simply set to C W = C S and f = C max, the initial τ b obtained with this law is slightly different. Indeed, the point where τ b reaches its maximum is a tipping point; upstream of this point the Tsai law is perfectly equivalent to a Weertman law while it is perfectly equivalent to a Coulomb law downstream of this point. Consequently, the Tsai and Schoof laws give quasi-identical τ b under the whole ice sheet except in a narrow area located a few kilometers upstream of the GL and within which the transition from one regime to the other occurs in a continuous manner for the Schoof law. In this area, the Tsai law gives a slightly larger τ b than the Schoof law (black/green and red lines in Fig. 4c). Despite this difference, both laws show very close GL behaviours all along the experiment. Therefore, in order to facilitate the reading of Figs 3, 4, the results obtained with the Tsai law are not shown, except in Fig. 4c.
Although the Schoof, Weertman and Budd laws all give the same initial response, they rapidly induce very different behaviours. For the reference simulation, the thinning of the domain slows down while spreading further upstream (green lines in Fig. 3). Meanwhile, the whole domain sees an increase of the flow velocities. In particular, the flow velocity at the GL increases of 50% during the first 20 years. This increase reduces to only 5% between t = 20 and 40 years (green lines in Fig. 4b). The asymptotic friction regimes associated with the Schoof law, i.e. the Weertman-type regime at high N and the Coulomb-type regime at low N, are highlighted in Fig. 4c by, respectively, dotted and dashed cyan lines. Note that the reference simulation uses the same values for C
S and C
max as the ones used to plot the Schoof friction law behaviour in Fig. 1c. Sufficiently upstream of the GL, N is high and the Schoof law reduces to a Weertman law with
$\tau _{\rm b} = C_{\rm S} u_{\rm b}^m $
(superimposed continuous black/green lines and dotted cyan lines in Fig. 4c). Closer to the GL, the dependence of basal drag on basal velocity gets weaker until vanishing completely for sufficiently low N leading to a pure Coulomb-type regime with τ
b = C
max
N (superimposed continuous black/green lines and dashed cyan lines in Fig. 4c). The above mentioned increase of flow velocities for the reference simulation is associated with an increase of basal drag in the area where the Schoof law induces a dependence of τ
b on u
b, i.e. where it is not purely equivalent to a Coulomb law (green lines in Fig. 4c).
Simulation W0 a shows very limited thinning over the grounded ice sheet with a maximum thinning rate of 0.2 m a−1 at t = 20 years. This maximum thinning rate decreases to <0.1 m a−1 at t = 40 years (magenta lines in Fig. 3). During the first 20 years of this simulation, there is a small increase in flow velocities far from the GL down to the area of smoothly decreasing C W; in this area, the flow velocities are slightly lower than the initial ones. Between t = 20 and 40 years, these flow velocities barely evolve (magenta lines in Fig. 1b). The associated τ b shows very little evolution over the 40 years following the perturbation except at nodes becoming afloat over this time window for which C W is switched to zero (magenta lines in Fig. 1c). Consequently, the zone of smooth decrease of τ b is progressively taken away as the GL retreats.
In contrast, the response to the perturbation for simulation B0 a is much stronger: The peak thinning rate has more than doubled within the first 20 years and keeps increasing between t = 20 and 40 years, while the region affected by the thinning spreads further upstream (negative blue peaks in Fig. 3). Meanwhile, large amounts of ice are transferred from the grounded region right upstream of the GL to the neighbouring region on the ice shelf, which corresponds to a surge-type behaviour (positive blue peaks in Fig. 3). The flow velocities are multiplied by a factor of ~5 between t = 0 and 20 years and ~2 between t = 20 and 40 years (blue lines in Fig. 4b). In the close vicinity of the GL, τ b becomes significantly lower than the ones obtained with the other laws and the area of reduced basal drag propagates further upstream.
As shown in Fig. 4d, ice-sheet profiles differ substantially depending on the chosen friction law. In line with the analytical solution derived by Tsai and others (Reference Tsai, Stewart and Thompson2015), our reference simulation shows a nearly exponential tapering off of the ice-sheet surface profile towards the GL (black and green lines in Fig. 4d). For the simulation W0 a, this tapering off vanishes rapidly as the GL retreats and 20 years after initialisation the ice sheet already exhibits the classical steep surface gradient as predicted by Schoof (Reference Schoof2007a ) for a Weertman law with a constant friction parameter (magenta lines in Fig. 4d). In contrast, simulation B0 a gives rise to a concave ice-sheet profile (blue lines in Fig. 4d), which shows a surface slope at its steepest ~30 km upstream of the GL and smoothly tapering off towards the GL. This result is similar to steady-state profiles obtained by Gladstone and others (Reference Gladstone2017) with various Budd-like friction laws.
Because SLR estimations are usually given for the end of the 21st century, it is of great interest to investigate wether the substancial differences in GL dynamics obtained with the three friction laws over millenial time scales are still significant over shorter time scales. To this end, the distance Δx G covered by the GL over the first 100 years following initialisation is given for each friction law in Table 2. With a Weertman law, the GL retreats of a few kilometers only (3 km at most) over a century, while the Budd law predicts GL retreats ranging from 69 to 316 km over the same time window. Once again, the Schoof law gives intermediate projections with GL retreats ranging from 24 to 47 km. The dynamical contribution of real marine-terminated ice sheets to SLR can be determined by assessing the temporal evolution of the volume above flotation (VAF): a decrease of the VAF means that ice has been released into the ocean inducing SLR. Figure 5 shows the relative evolution over a century of the ice stored above flotation as the GL retreats for the Schoof, Weertman and Budd friction laws starting from different t i . Once again, the result obtained with the Tsai law for t i = 0 years is not represented here because it is almost superimposed on the one obtained with the Schoof law. Although the present study is based on a synthetic two-dimensional geometry, it gives some insight about the sensitivity of SLR projections at a 100-year time horizon depending on the friction law. After a century, the Schoof law gives losses ranging from 1 to 5% of the total amount of ice stored above flotation. Because the new steady state is reached very rapidly for the simulation W0 a, the corresponding ice loss is neglectable. For W500 a and W1.1 ka, the ice losses represent, respectively, 1% and 3% of the total amount of ice stored above flotation. The Budd law gives much higher contribution to SLR with a relative loss of ice above flotation ranging from 15 to 29% after a century of GL retreat.
Fig. 5. Relative evolution in % of the ice stored above flotation over 100 years with initialisation at t i = 0 years (continuous), 500 years (dashed) and 1100 years (dotted) for the Schoof (green), Weertman (magenta) and Budd (blue) friction laws. The result obtained for the Tsai law at t i = 0 years (not shown) is almost superimposed on the continuous green line.
5. DISCUSSION
Different friction laws induce different GL responses to buttressing release at the calving front. In order to satisfy the global stress balance, the loss of buttressing at the calving front must be compensated by an increase of the total basal drag. As the ice-shelf/ocean interface is friction-free, the perturbation is transmitted to the GL and progressively vanishes within the grounded ice sheet. The initial thinning associated with the perturbation causes a change in the effective pressure distribution (Eqn (10)), which is dealt with differently by the different friction laws giving rise to different GL dynamics over the following time steps. In the case of the reference simulation, there is a narrow region right upstream of the GL where the basal drag is proportional to N and does not increase despite an increase of basal velocities. Consequently, the perturbation propagates further upstream in regions where the Schoof law implies a dependence of τ b on u b. The distance over which the perturbation propagates is determined by the amount of basal drag increase required for the total basal drag to compensate the loss of buttressing. As the GL retreats in deeper waters, the water pressure in the GL vicinity gets higher while the ice thickens at the GL causing an increase of ice overburden pressure. The two effects compete and the increase of water pressure slightly outweigh the increase of ice overburden pressure and leads to a local decrease of effective pressure; the basal drag C max N furnished by the region governed by a Coulomb-type friction law decreases causing the perturbation to propagate further upstream which creates a positive feedback (green curves in Figs 3, 4b, c). After the GL has retreated beyond the reverse slope area, further GL retreat induces an increase of effective pressure in the GL vicinity; the mechanism is reverted and the GL can progressively reach a new steady position. Nevertheless, because of the assumption of perfect hydrological connectivity to the ocean, the Schoof law always exhibits a narrow zone of smoothly decreasing basal drag causing locally high velocities at the GL (i.e. ~400 m a−1 for the steady velocity at the GL). Consequently, the GL has to retreat down to a position where ice is thin enough so that the ice flux becomes sufficiently low to be entirely balanced by surface accumulation on the grounded area.
On the other hand, for the simulation W0 a, τ
b is given by the Weertman law and so depends on u
b for the whole ice sheet, including the region immediately upstream of the GL. As a result, only a small increase in flow velocities is required to satisfy the global force balance. As a consequence, the perturbation is confined to the vicinity of the GL and does not spread further upstream. Furthermore, by construction, the inferred spatial distribution of the Weertman friction parameter is such that the friction parameter
$C_{\rm W}^{{\rm 0}\;{\rm a}} (x_{\rm G} )$
at the GL increases as the latter retreats within the transition zone, i.e. the zone of smoothly decreasing
$C_{\rm W}^{{\rm 0}\;{\rm a}} $
(magenta line in Fig. 4a). Consequently, for a given basal drag required to satisfy the global stress balance, the velocity at the GL decreases as the latter retreats (Eqn (1)). This mechanism has a stabilizing effect, which leads the velocities to converge (superimposed magenta lines in Fig. 4b) and the GL to rapidly reach a steady state located within the area of reverse slope.
Starting from the SSA equations with a Weertman friction law, Schoof (Reference Schoof2007b ) applied the boundary layer theory for sheet-shelf interactions with rapid sliding and showed that the ice flux q B(x G) at the GL can be written as
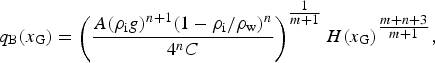$$q_{\rm B} (x_{\rm G} ) = \left( {\displaystyle{{A(\rho _{\rm i} g)^{n + 1} (1 - \rho _{\rm i} /\rho _{\rm w} )^n} \over {4^n C}}} \right)^{\textstyle{1 \over {m + 1}}} H(x_{\rm G} )^{\textstyle{{m + n + 3} \over {m + 1}}}, $$
where C is the friction parameter. Because the surface mass balance a s is assumed to be spatially uniform, possible steady GL positions x G can then be found by solving:
$$q_{\rm B} (x_{\rm G} ) = a_{\rm s} x_{\rm G}. $$
When a s x G>q B(x G), the ice-sheet thickens and the GL advances. Conversely, when a s x G<q B(x G), the ice sheet thins and the GL retreats.
Figure 6 shows the integrated accumulation rate a
s
x and the ice flux q
B as a function of the horizontal distance x for different spatial distributions of the friction coefficient: C = C
S = Cste (black line),
$C = C_{\rm W}^{{\rm 100}\;{\rm a}} (x)$
(magenta line) and
$C = C_{\rm W}^{{\rm 300}\;{\rm a}} (x)$
(brown line). The green dots/star highlight possible stable GL steady positions, whereas the red dot corresponds to an unstable steady position. The transition zones correspond to the parts of the brown and magenta lines, which are not superimposed to the black line in Fig. 6. Note that these zones are located within the reverse slope area. As demonstrated by Schoof (Reference Schoof2007a
), when the friction coefficient is assumed to be spatially uniform, unbuttressed marine ice sheets are unconditionally unstable on retrograde slopes (black line in Fig. 1). This is because q
B increases as the GL retreats within the reverse slope area causing thinning at the GL and further retreat, i.e. a positive feedback. This result was later numerically confirmed by a wide range of models (Pattyn and others, Reference Pattyn2012). Replacing the friction coefficient C in Eqn (14) by the spatial distribution
$C_{\rm W}^{t_{\rm i}} (x)$
inferred at a given time t
i induces a modification of the ice flux. Indeed, as the GL retreats within the transition zone, the decrease of the flow velocity at the GL competes with the increase of H(x
G) related to the bedrock topography. As it can be seen in Fig. 6, the former effect outweights the latter and q
B decreases as long as the GL retreats over the transition zone. In other words, the local minimum of q
B is shifted upstream giving rise to possible stable steady states located within the area of reverse slope (green star in Fig. 6). A steady GL located on the reverse slope is possible only if the ice flux at the upstream bound of the transition zone (local minimum of q
B) is smaller than the accumation rate at this location. Graphically, it is easy to see that prescribing a surface mass balance a
s larger than 0.3 m a−1 (steeper blue line in Fig. 6) would have extended the zone of stability further upstream. In this respect, the horizontal position x
tp = 1195.3 km (red dot in Fig. 6) turns out to be a tipping point for the parameters of these experiments: if inversion is performed after the GL has retreated beyond this point, the only stable GL steady position is located upstream of the reverse slope region at x = 760.3 km (brown line in Fig. 6). The stable steady positions predicted by the boundary layer theory, i.e. x = 1232.7 and 760.3 km for W100 yr and W≥300 a, respectively, are in very close agreement with the ones obtained numerically, i.e. x = 1233.2 and 759.5 km. Note that for the reference case, the GL reaches the tipping point x
tp at about t
tp = 273 years. In other words, every W≤273 yr are expected to give rise to steady states located within the region of retrograde slope, whereas every W>273 yr will induce GL retreat to the steady position located at x = 760.3 km, which is consistent with the behaviour observed with a Weertman law (magenta lines in Fig. 2). This underlines the fact that considering the MISI region as being exactly the section of reverse slope in the 1HD case might be too restrictive: the instability of the GL does not depend on the bedrock geometry only but also on the spatial distribution of the friction parameter.
Fig. 6. Plot of a
s
x (blue) and q
B(x) as a function of horizontal position. q
B(x) is represented for different distributions of friction coefficient C (Eqn (14)): C = C
S (black line),
$C = C_{\rm W}^{{\rm 100}\;{\rm a}} $
(magenta line) and
$C_{\rm W}^{{\rm 300}\;{\rm a}} $
(brown line). The green dots are possible stable GL steady positions. The green star is the stable GL position located within the reverse slope area. The red dot is an unstable GL steady position. These positions are highlighted by the vertical black dotted lines. The grey shaded area corresponds to the zone of reverse slope.
Based on the work of Schoof 477 (Reference Schoof2007b ), Tsai and others (Reference Tsai, Stewart and Thompson2015) have derived an equivalent of Eqn (14) for their law:
$$q_{\rm B} (x_{\rm G} ) = Q_0 \displaystyle{{8A(\rho _{\rm i} g)^n (1 - \rho _{\rm i} /\rho _{\rm w} )^{n - 1}} \over {4^n f}}H(x_{\rm G} )^{n + 2}, $$
where Q 0 ≈ 0.61 is a numerical coefficient and f the solid friction coefficient. Using this expression of q B with f = C max to solve Eqn (15) results in a stable steady GL position predicted at x = 688.3 km, while our numerical experiment with the Tsai law leads to a steady GL located at x = 683.3 km.
Similarly to the reference simulation, for the simulation B0 a the effective pressure keeps decreasing in the GL vicinity as the latter retreats within the reverse slope area. However, unlike the reference simulation for which N plays a role only in a narrow area, for the Budd law the basal drag depends on N under the whole ice sheet. Therefore, the local decrease of N causes the perturbation to propagate far upstream of the GL (blue lines in Fig. 3). As a consequence, the velocities increase, which results in two opposite effects: it induces an increase of basal drag and it enhances dynamical thinning leading to further decrease of effective pressure and, therefore, of basal drag. In other words, when the GL is retreating, there is a competition between the decrease of N and the increase of u b. Despite a dramatic increase of basal velocities, the region of reduced basal drag extends further upstream of the GL as the latter retreats (blue lines in Figs 1b, c). This unstable behaviour is responsible for the observed surge-type behaviour obtained with the Budd law.
Whereas the steady GL positions obtained with a Budd law are slightly different depending on the time of inversion, the Weertman law gives a unique steady GL location for every W≥300 a. Because the Schoof law is equivalent to a Weertman law on most of the grounded ice sheet, the inferred spatial distribution of Weertman friction coefficient at any t
i is such that
$C_{\rm W}^{t_{\rm i}} (x) \approx C_{\rm S} $
except in the narrow transition zone (magenta line in Fig. 4a). As the GL retreats beyond the latter for every W≥300 a, the steady GL positions differ by <50 m. Conversely, as N plays a role on the whole grounded ice sheet in the case of the Budd law and as the distribution of N evolves with GL retreat, the inferred distribution of friction coefficient
$C_{\rm B}^{t_{\rm i}} (x)$
differs substantially on a large distance uptream the GL depending on t
i
. Even if the GL retreat ends up in areas where the
$C_{\rm B}^{t_{\rm i}} (x)$
are almost identical for every
${\rm B}^{t_{\rm i}} $
, the initial difference between the
$C_{\rm B}^{t_{\rm i}} $
depending on t
i is sufficient to lead to GL steady positions a few hundreds of meters away from each others (3.3 km between the most retreated and the most advanced steady GL positions).
In a context where projections of future sea level rise rely in great part on the ability of ice-sheet models to deal with GL dynamics, the different transient responses obtained with these different laws are of great concern. At a 100-year time horizon, the domain has lost <3% of the amount of ice stored above flotation with the Weertman law, whereas Schoof/Tsai and Budd laws predict losses reaching 5% for the former and up to 29% for the latter. This emphasises the importance of choosing an appropriate friction law. Observational evidences of the presence of water at the ice/bedrock interface support the use of effective pressure-dependent friction laws. However, the present work shows that, assuming perfect hydrological connectivity to the ocean, three effective pressure-dependent laws, i.e. the Budd and the Schoof/Tsai laws, can give significantly different results both in terms of transient behaviour and steady states. We suggest to rather use the Schoof law as it transitions continuously between two asymptotic regimes, i.e. the Weertman and Coulomb regimes, which have been shown to be the most appropriate ones to describe the sliding mechanisms in their respective domain of validity. Moreover, contrary to the Budd law for which basal drag can reach arbitrary high values, the Schoof law satisfies the Iken's bound (Iken, Reference Iken1981).
In the present study, we have assumed perfect hydrological connectivity to the ocean. Leguy and others (Reference Leguy, Asay-Davis and Lipscomb2014) proposed a method to parameterise the quality of this connectivity; they introduced an ad hoc parameter p enabling to reduce the basal water pressure to a fraction of the ocean pressure at a given position. Although it improves the description of basal hydrology, such a model does not allow to account for more complex features of the basal hydrological networks such as water-laden till, meltwater channels or interconnected subglacial lakes potentially prone to drainage events (Gray and others, Reference Gray2005; Wingham and others, Reference Wingham, Siegert, Shepherd and Muir2006; Fricker and others, Reference Fricker, Scambos, Bindschadler and Padman2007; Fricker and Scambos, Reference Fricker and Scambos2009). Several authors have developed physically based subglacial hydrological models accounting for some of these features (Schoof, Reference Schoof2010; Hewitt and others, Reference Hewitt, Schoof and Werder2012; Werder and others, Reference Werder, Hewitt, Schoof and Flowers2013; Fleurian and others, Reference Fleurian2014), but constraining them against observations is an arduous task as glacier beds are usually out of reach and traditionally used instruments, such as borehole pressure sensors (Schoof and others, Reference Schoof, Rada, Wilson, Flowers and Haseloff2014), provide limited spatial and temporal coverage. Although still at its premise, cryoseismology appears as a promising method to tackle this shortcoming in the near future (Gimbert and others, Reference Gimbert, Tsai, Amundson, Bartholomaus and Walter2016; Podolskiy and Walter, Reference Podolskiy and Walter2016). At the same time, assuming that basal friction is governed by the Schoof law, observations of surface slopes at the GL and of GL retreat rates over a sufficiently large time window could give some insight on the distribution of basal water pressure.
6. CONCLUSION
The experimental setup used in this work was designed in order to reproduce what is done when studying real glaciers. Our reference case can be seen as an equivalent to ‘observations’, except that, unlike real observations which are usually sparse in time and space, the velocity field, the effective pressure field and, consequently, the basal drag, are perfectly known at any time of the reference simulation. Whatever the chosen friction law, it is always possible to infer a spatial distribution of the friction parameter enabling to perfectly recreate the ‘observed’ state at any fixed time t. However, although the Schoof, Weertman and Budd laws are all starting from identical initial states, simulations with these different friction laws show thoroughly different transient behaviours. On the other hand, for correctly chosen parameters, the GL dynamics obtained with the Tsai law is very similar to the one obtained with the Schoof law.
The steady GL positions obtained after 20 ka of simulation are significantly different depending on the friction law. Remarkably, some of the inferred spatial distributions of the Weertman friction parameter induce a modification of the flux at the GL such that the latter reaches a steady position located within the zone of retrograde slope. Consequently, even in a flow-line case, the bed shape alone is not sufficient to determine whether an area is prone to MISI when using a Weertman law.
Furthermore, we have also demonstrated that SLR projections over a 100-year time horizon vary greatly depending on the chosen law; the commonly used Weertman law appears to forecast more limited SLR than the two other laws. However, evidence of the presence of water at the base of ice sheets rather support the use of effective pressure-dependent frictions laws such as the Budd or the Schoof/Tsai laws. We suggest to use the Schoof law because of its stronger physical basis.
Finally, coupling an ice flow model using an effective pressure-dependent law to a physically based subglacial hydrological model could greatly improve our confidence in the simulated GL dynamics and in the associated SLR forecast. Although such models are already available, the lack of observations to constrain them hampers the generalisation of their use. However, the recent development of innovative measurement techniques such as cryoseismology gives promising results and could address this shortcoming in the near future.
ACKNOWLEDGEMENTS
We would like to thank the editor, F. Pattyn, as well as the two anonymous referees for their insightful and helpful comments. This study was funded by the Agence Nationale pour la Recherche (ANR) through the SUMER, Blanc SIMI 6-2012.
Open access
