Introduction
The Greenland ice sheet (GrIS) is losing mass through increases in both meltwater runoff (Reference BoxBox and others, 2006; Reference HannaHanna and others, 2008; Reference Mernild and HasholtMernild and others, 2009, Reference Mernild, Liston, Steffen and Chylek2010; Reference Van den BroekeVan den Broeke and others, 2009) and ice discharge from outlet glaciers (Reference Rignot and KanagaratnamRignot and Kanagaratnam, 2006; Reference Howat, Joughin and ScambosHowat and others, 2007; Reference Pritchard, Arthern, Vaughan and EdwardsPritchard and others, 2009). These changes are being driven by a recent increase in temperatures across the Arctic of 0.72 ± 0.10°C (10 a)-1 since 1981 (Reference ComisoComiso, 2003, 2006) and, in particular, along the Greenland coast where summer temperatures have increased by 1.7°C between 1991 and 2006 (Reference HannaHanna and others, 2008). Observed increases in the melt extent of the GrIS and the subsequent increases in meltwater runoff (Reference Abdalati and SteffenAbdalati and Steffen, 2001; Reference BoxBox and others, 2006; Reference Hall, Williams, Luthcke and DigirolamoHall and others, 2008; Reference HannaHanna and others, 2008; Reference Mernild and HasholtMernild and others, 2009) are believed to be a result of the coastal warming and an increase in advection of warmer air masses from the south. Surface mass loss is further compounded by increased ice discharge from fast-flowing outlet glaciers, through a combination of changing boundary conditions at the floating termini (Reference Howat, Joughin and ScambosHowat and others, 2007; Reference Holland, Thomas, de Young, Ribergaard and LyberthHolland and others, 2008; Reference Nick, Vieli, Howat and JoughinNick and others, 2009) and increased basal lubrication from surface meltwater production (Reference Zwally, Abdalati, Herring, Larson, Saba and SteffenZwally and others, 2002; Reference Shepherd, Hubbard, Nienow, McMillan and JoughinShepherd and others, 2009;Reference Bartholomew, Nienow, Mair, Hubbard, King and SoleBartholomew and others, 2010), although recent observations find this process is limited to regions of ice-sheet flow rather than fast outlet glacier flow (Reference Joughin, Das, King, Smith, Howat and MoonJoughin and others, 2008; Reference Van den Broeke, Smeets, Ettema, van der Veen, van de Wal and OerlemansVan de Wal and others, 2008). The current mass loss from the ice sheet increases the freshwater flux to the ocean, contributes to the present global eustatic sea-level rise of +3.4 ± 0.1 mm a-1 (Reference Prandi, Cazenave and BeckerPrandi and others, 2009) and possibly will alter global thermohaline circulation in decades or centuries to come (Jung-Reference Jungclaus, Haak, Esch, Roeckner and Marotzkeclaus and others, 2006; Reference Chu, Smith, Rennermalm, Forster, Box and ReehHu and others, 2009). It is imperative to improve understanding of the current freshwater runoff from the GrIS in order to better model the future mass loss of the GrIS.
Although meltwater runoff is an important component of GrlS mass balance, it is poorly constrained due to a lack of in situ measurements. This scarcity can be attributed to the difficulty of installing and maintaining a network of gauging stations around the remote periphery of the ice sheet. Many rivers in Greenland have braided channels with unstable banks, making accurate gauging extremely difficult. One exception is the Watson River gauging station that measures river discharge at a bedrock constriction in Kangerlussuaq, West Greenland, since 2007 (Reference Mernild, Hasholt, Tidwell and KaneMernild and others, 2008; Reference Mernild and HasholtMernild and Hasholt, 2009). All other published runoff estimates from the GrIS directly are derived from regional surface mass-balance models which use either energy-balance or positive degree-day (PDD) methodologies, and rely on sparse input data, especially in the ablation zone (Reference BoxBox and others, 2006; Reference HannaHanna and others, 2008; Reference Mernild and HasholtMernild and others, 2009). Although the complex processes of meltwater percolation and refreezing have been treated theoretically (Reference Pfeffer, Meier and IllangasekarePfeffer and others, 1991; Reference Janssens and HuybrechtsJanssens and Huybrechts, 2000), it is unclear, due to a void in observations, whether there is agreement between modeled and actual meltwater retention (Reference Van den Broeke, Smeets, Ettema, van der Veen, van de Wal and OerlemansVan den Broeke and others, 2008).
Our present study develops a methodology for estimating the onset, duration and cumulative runoff from a localized basin of the GrIS based on sediment plume characteristics in the downstream fjord. Sediment plumes respond sensitively to river discharge, which is primarily meltwater runoff and thus is directly tied to the ablation rate on the ice. We show that sediment plume formation and cessation, derived from Moderate Resolution Imaging Spectroradiometer (MODIS) satellite imagery, is a viable record of ice-sheet ablation onset and cessation, as measured by in situ automatic weather station (AWS) records. Satellite observations of the duration of plume presence can be used to estimate the duration of runoff from the ice sheet, independent of in situ observations, if a sequence of cloud-free satellite images is available.
Due to limited measurements of ablation and meltwater runoff in the marginal zones of the GrIS and the need to quantify surface mass loss, we utilize sediment plumes and their temporal variability as observed from satellite imagery to infer ablation variability in the hydrological basin of the ice sheet. To verify our assumptions, we first correlate daily ablation rates with discharge measurements to confirm that variations in river discharge are primarily due to changes in the ice ablation rate. We then develop a statistical relationship between plume length and river discharge over the 2007 and 2008 melt seasons and apply this relationship to the observed plume-length time series (2001-08). Hence, a time series of plume length can be used to estimate ablation variability, and, if plume length can be calibrated to discharge measurements, then both instantaneous and cumulative runoff can be reconstructed.
Sediment Plumes and River Discharge
Sediment plumes form when sediment-rich rivers flow into a receiving basin (i.e. ocean, fjord or lake) and undergo a dramatic deceleration and lateral spreading (Reference Syvitski, Asprey, Clattenburg and HodgeSyvitski and others, 1985). Most marine plumes are hypopycnal, meaning the fresh or brackish river water flows over the top of the marine water due to its lower density (Reference Syvitski, Asprey, Clattenburg and HodgeSyvitski and others, 1985). In the upper prodelta, river discharge dominates the plume characteristics, while, in the lower prodelta, external forces including wind, tides, topographical constraints and the Earth’s rotation influence the plume (Reference Syvitski, Burrell and SkeiSyvitski and others, 1987).
Wind stress has been shown to influence the structure and distribution of buoyant coastal plumes over daily and seasonal timescales (Reference Stumpf, Gelfenbaum and PennockStumpf and others, 1993; Reference Whitney and GarvineWhitney and Garvine, 2005). Reference Stumpf, Gelfenbaum and PennockStumpf and others (1993) observed a 10-30 km shift in the location of the Mobile Bay plume over 2 days, with observed motion aligned with wind direction and moving at speeds ˜10% of the wind speed, suggesting a decoupling of the plume from the marine waters below. Over seasonal timescales, Reference Whitney and GarvineWhitney and Garvine (2005) found that wind stresses constitute a primary forcing on plumes due to changes in plume thickness and subsequent mixing and buoyancy with underlying marine water. Alongshore winds drive a net offshore Ekman transport, and subsequent upwelling results in plume spreading and thinning, allowing for wind-induced shear to thoroughly mix the plume and reduce the plume buoyancy (Reference Whitney and GarvineWhitney and Garvine, 2005).
Semi-diurnal, diurnal and biweekly tidal cycles introduce currents in the coastal environments that can move the plume location and drive mixing of surface waters (Reference Stumpf, Gelfenbaum and PennockStumpf and others, 1993; Reference Halverson and PawlowiczHalverson and Pawlowicz, 2008). The tidal influence is often modulated by river discharge, such that during periods of high flow the estuarine stratification is too strong for the tides to produce enough shear to mix layers (Reference Halverson and PawlowiczHalverson and Pawlowicz, 2008). At the head of a fjord, the tide is primarily a standing wave and thus produces little residual flow, reducing the impact on the plume (Reference Syvitski, Burrell and SkeiSyvitski and others, 1987). Accordingly, Reference Chu, Smith, Rennermalm, Forster, Box and ReehChu and others (2009) find that the tidal influence on plume area is negligible in Kangerlussuaq Fjord based on nearly identical plume-area probability functions for ebb and flood tides.
Visible/near-infrared imagery has been used to quantify suspended sediment concentration (SSC) in coastal waters, although established empirical relationships are site- dependent and suffer from reflectance saturation at higher sediment concentrations (Reference Doxaran, Froidefond and CastaingDoxaran and others, 2002; Reference Miller and McKeeMiller and McKee, 2004; Reference WarrickWarrick and others, 2007;Reference Chu, Smith, Rennermalm, Forster, Box and ReehChu and others, 2009). Alternatively, measurements of plume area, length and mean reflectance have been used to elucidate river discharge and coastal currents (Reference Nezlin and DiGiacomoNezlin and DiGiacomo, 2005; Reference Thomas and WeatherbeeThomas and Weatherbee, 2006; Reference Halverson and PawlowiczHalverson and Pawlowicz, 2008; Reference Lihan, Saitoh, lida, Hirawake and lidaLihan and others, 2008). Reference Lihan, Saitoh, lida, Hirawake and lidaLihan and others (2008) showed a strong correlation between discharge of the Tokachi river, Japan, and plume area during the April-October season from 1998 to 2002, using a 1 day time lag (r2 = 0.40-0.66). The relationship is driven by a very rapid discharge increase from ˜150m3s-1 to ˜750m3s-1 in late spring, resulting in a substantial increase in plume area from ˜100km2 to ˜550km2. Reference Nezlin and DiGiacomoNezlin and DiGiacomo (2005) found a robust linear correlation (r2 = 0.73) between plume area and cumulative precipitation during storm events, a proxy for river discharge, in southern California, USA, using the satellite Sea-viewing Wide Field-of-view Sensor (Sea-WiFS) optical radiometer. Reference Thomas and WeatherbeeThomas and Weatherbee (2006) found that the Columbia River (Oregon, USA) plume responds sensitively to interannual variability in discharge, using an 8day discharge average and the SeaWiFS nLw555 mean reflectance over a 30 km2 region immediately offshore from the river mouth. Reference Halverson and PawlowiczHalverson and Pawlowicz (2008) found that the surface area of the Fraser River plume in British Columbia, Canada, is proportional to river discharge over longer timescales (tens of days) using MODIS imagery (band 12, 1km resolution).
Reference Chu, Smith, Rennermalm, Forster, Box and ReehChu and others (2009) found that plume area in Kangerlussuaq Fjord reflected the seasonal development of surface melt on the ice sheet between 2000 and 2007 (R = 0.64) using MODIS and passive microwave imagery. Plume onset closely followed melt onset, except during years when sea ice remained in the fjord after melt onset, which delayed plume identification (Reference Chu, Smith, Rennermalm, Forster, Box and ReehChu and others, 2009). Plume area responded to changes in supraglacial water supply, as identified by changes in melt-area extent passive microwave imagery and the drainage of supraglacial lakes. The system shows a seasonal hysteresis resulting in a smaller plume area late in the melt season relative to a continued large melt extent which is attributed to a reduction in river discharge due to meltwater retention on the ice sheet and/or a decrease in transportable sediments as the melt season evolves (Reference Chu, Smith, Rennermalm, Forster, Box and ReehChu and others, 2009).
Study Area
This study focuses on the Russell Glacier-Watson River-Kangerlussuaq Fjord system in West Greenland (Fig. 1). The ice-sheet basin covers 6130 km2, with an average equilibrium-line elevation of 1530 m (Reference Van den Broeke, Smeets, Ettema, van der Veen, van de Wal and OerlemansVan den Broeke and others, 2008; Reference Mernild and HasholtMernild and Hasholt, 2009;Reference Mernild, Liston, Steffen and ChylekMernild and others, 2010). It is a region of high ablation (-1.5 to -3.5 m w.e. a-1) and low annual snow accumulation (0.07-0.36 m w.e. a-1), and all glaciers are land-terminating (Reference Van de Wal and RussellVan de Wal and Russell, 1994; Reference Van de WalVan den Broeke and others, 2008).

Fig. 1. Landsat 7 image detailing Kangerlussuaq-Watson River-GrIS study region, West Greenland.
There are two major river systems that transport meltwater from the GrIS into the head of Kangerlussuaq Fjord. The Watson River (Sandflugtdalen river) runs 31 km from the ice margin before converging with the 0rkendalen river, prior to entering Kangerlussuaq Fjord. The 0rkendalen river flows 41 km from the GrIS margin before the convergence. The combined discharge of the rivers, measured at the town of Kangerlussuaq, ranges between 30 and 500m3s-1 over the 2007 and 2008 runoff seasons (Reference Mernild and HasholtMernild and Hasholt, 2009). A third river system, the Aussivigssuit, enters Kangerlussuaq Fjord ˜10km from the head of the fjord. This system is ungauged. At elevations below 500 m, the Watson River basin is 26% bigger than the Aussivigssuit river basin area. At 1000 m elevation, the Aussivigssuit is 19% larger and expands to be 105% larger than the Watson River basin at 1500 m.
Kangerlussuaq Fjord is 165 km long and runs approximately west-southwest. It is 4.5 km wide at its head, gradually widening to 6-8km over the first 60 km length, before narrowing to 2 km over the next 100 km. It has a relatively simple elongated box-like geometry, facilitating plume analysis. At the head of the fjord, the maximum tidal range is 3.2 m (Reference TapagerTapager, 1955; Meteo365.com Ltd, http://www.tide-forecast.com).
Data Sources and Methods
AWS Data
In 2003, three AWSs were installed along an elevation profile in southwest Greenland by Utrecht University/IMAU. The K-Transect consists of stations at 6, 38 and 88 km from the ice margin at 490, 1020 and 1520ma.s.l. (Reference Van den Broeke, Smeets, Ettema, van der Veen, van de Wal and OerlemansVan den Broeke and others, 2008). Stations 5 and 6 (S5 and S6) are in the ablation zone, with net annual ablations of -3.6 and -1.5 m w.e., respectively, while station 9 (S9) is close to the equilibrium line (Reference Van den Broeke, Smeets, Ettema, van der Veen, van de Wal and OerlemansVan den Broeke and others, 2008). The average lengths of the ablation season are 126, 90 and 73 days along the elevation gradient. Initial height loss at the upper-elevation stations (S6 and S9), as measured with a sonic height ranger, is the result of ablation and/or densification of the seasonal snowpack, while at S5, where there is little winter snow accumulation, height loss is mainly from ice ablation and a minor amount of sublimation (Reference Van den Broeke, Smeets, Ettema, van der Veen, van de Wal and OerlemansVan den Broeke and others, 2008). S5 is used in this study because of its high ablation rates, low snow accumulation and proximity to the ice edge, which allows for a rapid (hours-days) transfer of meltwater from the ice to the fluvial-fjord system.
Watson River discharge
As part of another project, a gauging station was installed in 2007 at a bedrock constriction on the Watson River in Kangerlussuaq, ˜30km from the ice-sheet margin (Reference Mernild, Hasholt, Tidwell and KaneMernild and others, 2008). It is located ˜1 km downstream of the Watson and Ørkendalen river convergence. River-stage height measurements are taken every 20min between late May and mid-September. Stage measurements were converted to a discharge time series from measurements of crosssectional area and velocity using the float method (r2 = 0.91, n = 21) and have a 10-15% uncertainty (Reference Mernild, Hasholt, Tidwell and KaneMernild and others, 2008; Reference Mernild and HasholtMernild and Hasholt, 2009). The observation period covers the majority of the melt season, although runoff in the basin begins in mid- to late April and extends through late September. Local snowmelt largely constitutes early river discharge and has been observed to flow over and beneath the frozen river surface. River discharge during this period is usually <30m3s-1, the minimum discharge that can be measured by the Watson River instrumentation. Likewise, runoff that extends into late September to mid-October is below these thresholds for measurement. Assuming a continuous discharge of 30 m3 s-1 for an additional 30 days, the cumulative volume is equivalent to <5% of total observed flux during the 2007 melt season.
Total runoff during the observation period (June-mid-September) was 1.77 km3 in 2007, ˜27% greater than the total observed runoff of 1.28km3 for 2008 (Reference Mernild and HasholtMernild and Hasholt, 2009). Due to the short observation period, it is not clear whether the 2007 runoff reflects the satellite-observed record melt extent throughout southern Greenland (Reference Tedesco, Serreze and FettweisTedesco and others, 2008).
MODIS imagery
The MODIS aboard the NASA Terra and Aqua satellites provides near daily coverage of Greenland in visible to infrared (400-1440nm) wavelengths. This study utilizes band 1 (620-670 nm) due to its sensitivity to suspended sediment and higher spatial resolution (250 m) than other bands (Reference Miller and McKeeMiller and McKee, 2004; Reference Chu, Smith, Rennermalm, Forster, Box and ReehChu and others, 2009). MODIS imagery is available through the NASA Earth Observing System (EOS) data gateway from the Goddard Earth Sciences Distributed Active Archive Center (DAAC) and through the MODIS Rapidfire website (http://rapidfire.sci.gsfc.nasa.gov/). A subset of MODIS images with ‘clear sky’ coverage of southwestern Greenland was retrieved for the April-October period in 2001-08. Images were geo-referenced and corrected using standard bow-tie procedures (Reference Miller and McKeeMiller and McKee, 2004).
The river plume was characterized by two parameters: plume area, A, and plume length, L. A 270 km2 region of interest was defined within the fjord and each pixel was classified by its reflectance value into one of the following classes: clear water (1-2.9%), mildly turbid water (3.04.9%), plume periphery (5-9.9%) and plume core (>10%). The latter two classes were summed to calculate the plume area. An alternative metric, plume length was measured as the furthest continuous extent of the plume (pixel with ≥5% reflectance) from a fixed location at the head of the fjord. This reflectance value was chosen from in situ SSC measurements and visual inspection of MODIS imagery (Reference McGrathMcGrath, 2009).
Kangerlussuaq Fjord is frequently under partial cloud cover that hinders calculations of plume area while permitting observations of plume length. This restriction, coupled with the simple box-like dimensions of Kangerlussuaq Fjord and the decay in plume velocity and SSC along the center line, suggests that plume length is the optimal metric for this study. We find a strong linear relationship between plume length and plume area, for a subset of MODIS images that are completely cloud-free, further justifying this suggestion (Fig. 2). Frequent cloud cover results in an average image interval of 9days, with a maximum spacing of 33 days in 2002 (Table 1).
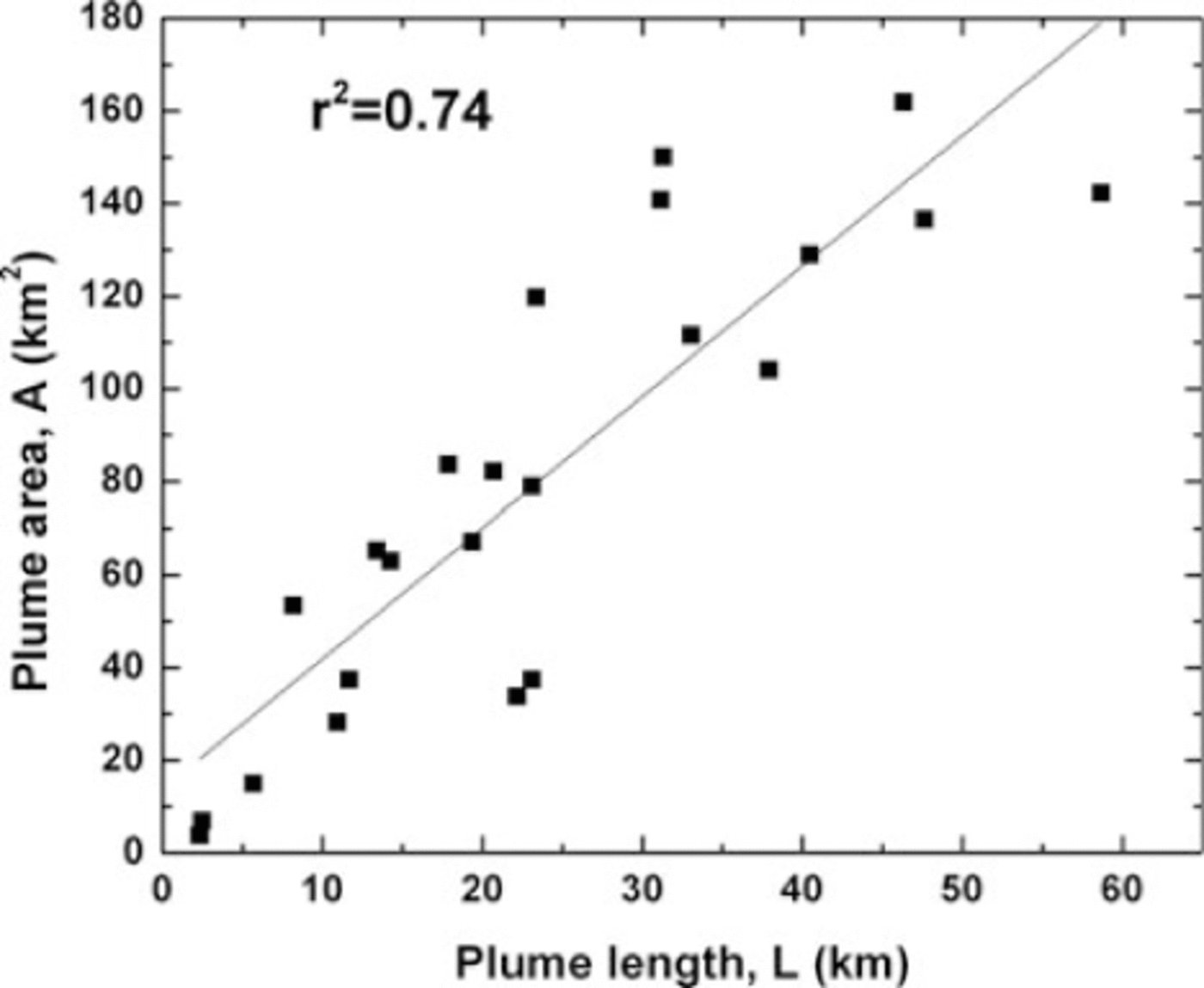
Fig. 2. Plume area as a function of plume length for the 2007 and 2008 melt seasons.
Table 1. Days of year (where 1 January is day 1) for all MODIS imagery used in this study

Results
Ice-sheet to river to plume linkages
The first step in the proxy development is to examine whether ice ablation on the GrIS drives discharge of the Watson River. The discharge hydrograph displays a strong diurnal cycle, reflecting diurnal variations in incoming radiation, and a seasonal pattern driven by changes in both the ice ablation rate and total melt area. To remove the diurnal and seasonal cycle, a daily rate of change of discharge was computed by subtracting the previous mean daily discharge from the current day’s mean discharge (Reference Willis, Richards and SharpWillis and others, 1996). The resulting term is positive on rising discharges and negative during falling discharges. The short time-step (1 day) minimizes the influence of changes in melt extent and emphasizes changes in the ablation rate. Daily ablation rate (dH/dt) at S5 is positively correlated with the daily change in discharge, dQ/dt, of the Watson River throughout the melt season with no lag time introduced (r2 = 0.61, n = 88, p<0.01 (2007); r2 = 0.59, n = 96, p<0.01 (2008)) (Fig. 3).

Fig. 3. Time series of K-Transect S5 dH/dt and Watson River dQ/dt for the 2007 and 2008 melt seasons.
The sediment plume in Kangerlussuaq Fjord forms shortly after ablation begins, and grows and recedes in extent and SSC throughout the melt season in response to discharge fluctuations. Plume length tracks river discharge volume for 2007 and 2008 as shown in Figure 4. Plume length from 35 images (2007 and 2008) was correlated with corresponding river discharge values; a 4 day lag (3 days prior to and the day of satellite image acquisition) resulted in the strongest correlation (r2= 0.52, n = 35, p<0.01; L (km) = 0.112Q (m3 s-1) + 6.29, where Q is discharge) (Fig. 5). This statistical relationship was subsequently applied to the plume length observed with MODIS satellite images during the 2001-08 melt seasons to infer the instantaneous discharge estimates at discrete times throughout the melt season. The derived discharge values were integrated to obtain the cumulative Watson River discharge estimates (∫ Qdt) for each melt season.

Fig. 4. Plume length, L, and instantaneous discharge, Q, for 2007 and 2008 melt seasons. Squares indicate satellite observations of plume length.
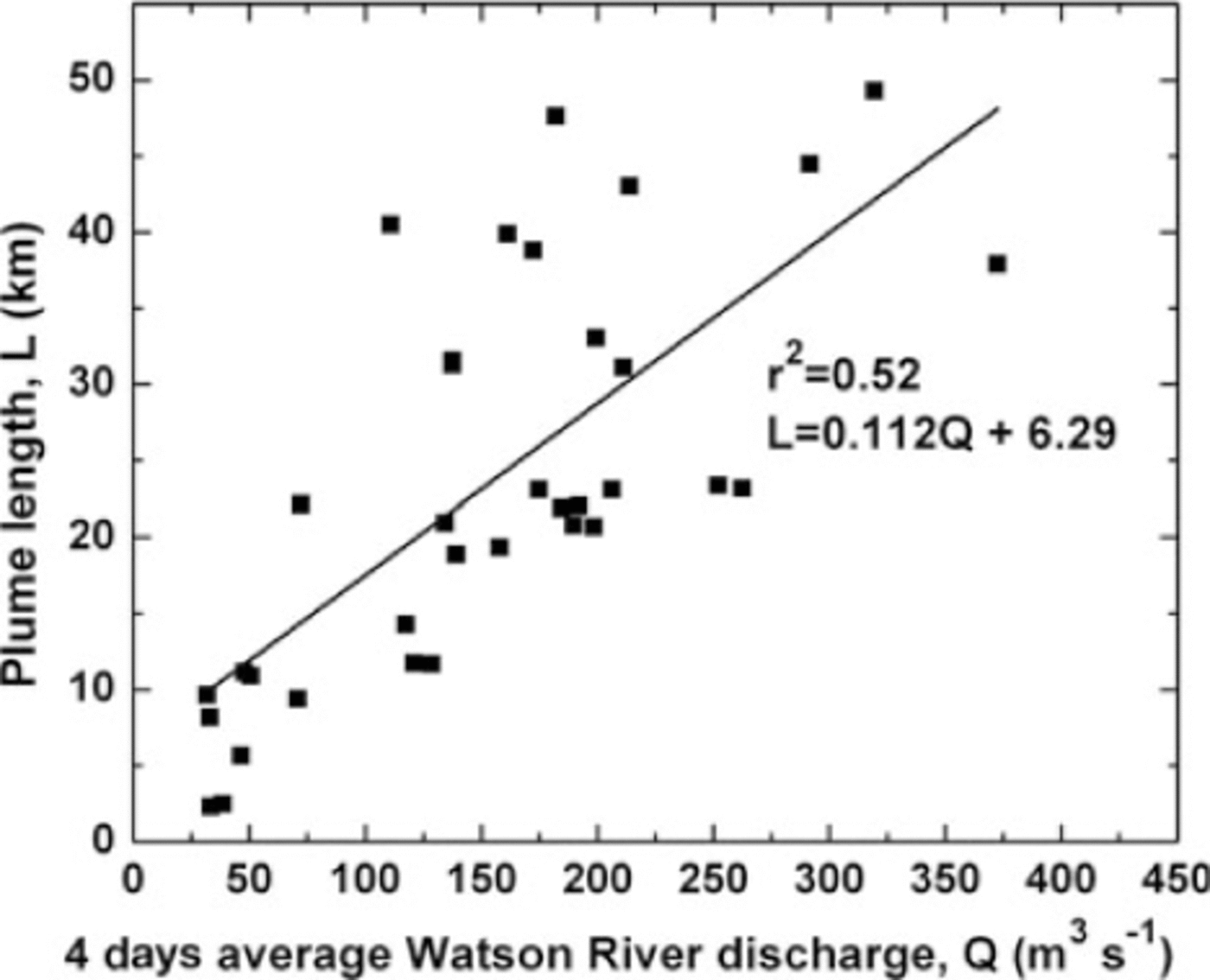
Fig. 5. Plume length in Kangerlussuaq Fjord as a function of a 4 day average Watson River discharge, Q (r 2 = 0.52, n = 35).
Instrumental error for the ablation measurement is estimated at 1%, stage discharge error estimate is 15% and plume length from MODIS is 5% (250 m pixel resolution on a 5 km plume). The unexplained variance (1-r2) of the ablation discharge proxy is 40% and for the discharge plume-length proxy is 48%. Thus, the combined root-meansquare error for this methodology is 29%.
Plume duration and reconstructed meltwater volume
The dates of onset and cessation of ablation and plume occurrence are strongly correlated (r2 = 0.88, p < 0.05, n = 5; r2 = 0.93, p < 0.05, n = 5) and are shown in Figure 6. Ablation onset precedes plume formation by an average of 6 ± 4 days, and ablation cessation precedes plume cessation by an average of 7 ± 8 days at the end of the melt season. A 1.25 daysa-1 (p>0.05) trend in both plume onset and plume cessation was observed over the 8 year study period, suggesting a forward shift in the melt season in this basin. Yearly reconstructed cumulative discharge for the Watson River basin for 2001-08 is shown in Figure 7, with a mean discharge of 1.87 km3, a minimum discharge of 1.44 km3 in 2006 and a maximum discharge of 2.06 km3 in 2003.
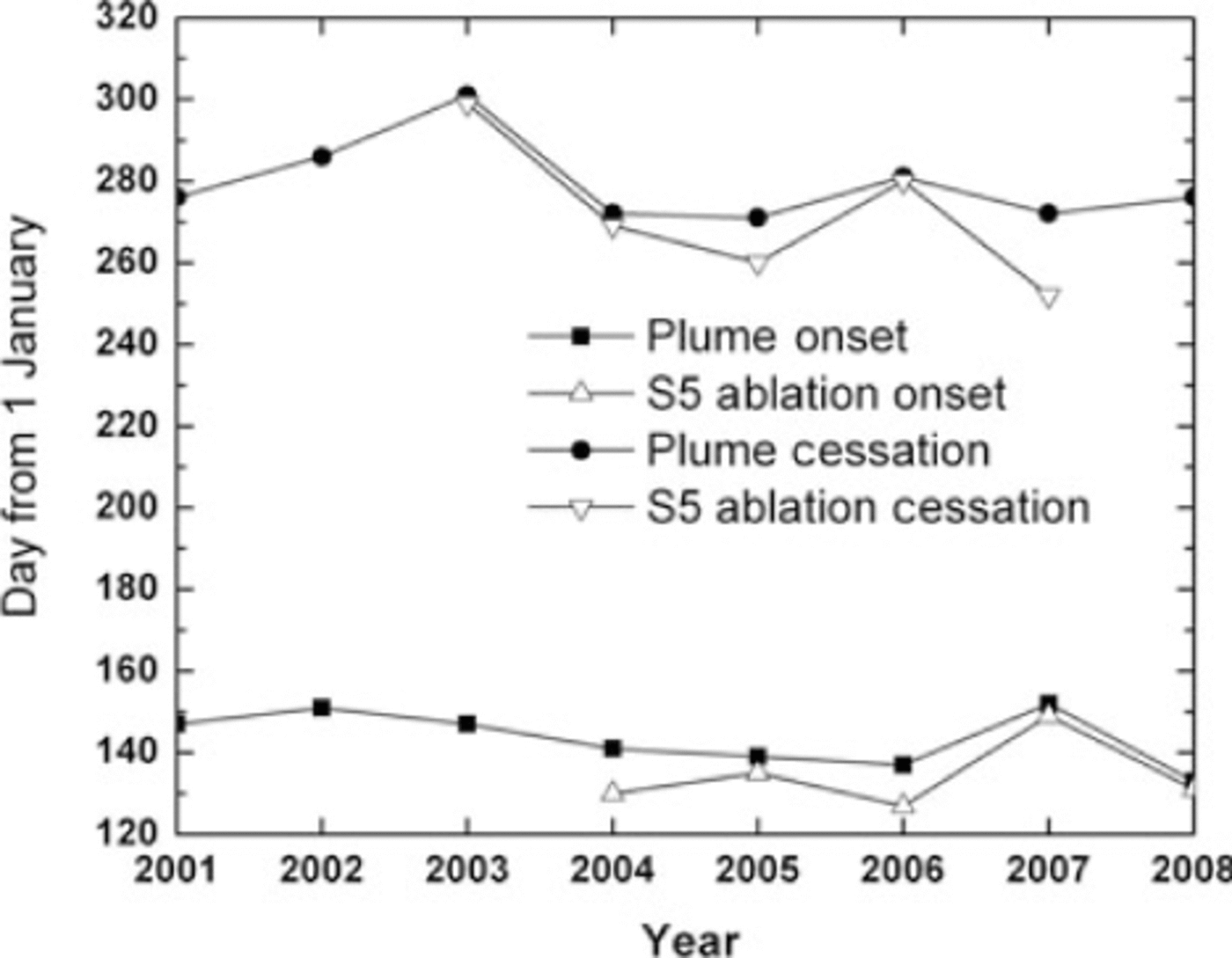
Fig. 6. Plume onset and cessation compared with S5 ablation onset and cessation.

Fig. 7. Reconstructed cumulative discharge from Watson River for each melt season 2001-08. Reconstructed discharge overestimates measured discharge in 2007 and 2008 by 15% and 29%, respectively.
Discussion
One of the biggest gaps in current knowledge of the surface mass balance of the GrIS is meltwater runoff. Best estimates of this component are modeled using in situ but sparse climate data, especially in the ablation zone where meltwater is produced (Reference BoxBox and others, 2006; Reference HannaHanna and others, 2008; Reference Mernild and HasholtMernild and others, 2009). Further, theoretical work suggests that 20-25% of meltwater is retained on the ice sheet (Reference Janssens and HuybrechtsJanssens and Huybrechts, 2000; Reference Mernild and HasholtMernild and others, 2009), but the spatial and temporal variability in this term is largely unconstrained. Numerous studies have quantified melt extent through active and passive microwave and infrared satellite imagery with great success, providing a useful metric for interannual comparison but little quantification of the meltwater flux ultimately draining to the ocean (Reference Abdalati and SteffenAbdalati and Steffen, 2001; Reference ComisoComiso, 2006; Reference Hall, Williams, Luthcke and DigirolamoHall and others, 2008, 2009). Interannual cumulative melt extent for the entire ice sheet has been broadly correlated with modeled meltwater runoff (Reference HannaHanna and others, 2008; Reference Mernild and HasholtMernild and others, 2009), although it is unlikely that this relationship extends to finer spatial scales.
The use of sediment plumes as a proxy for meltwater runoff provides a method for constraining runoff-season duration and for quantifying both ablation variability and cumulative meltwater volume. Both runoff season and ablation variability are independent of in situ observations and thus can be applied to the ˜325 meltwater outlets that reach the ocean around the periphery of the GrIS (Reference Lewis and SmithLewis and Smith, 2009). Differences in fjord shape, sediment supply and plume dynamics can all affect plume characteristics, necessitating a site-specific plume length relationship.
Runoff season, as determined from sediment plumes, integrates numerous poorly constrained processes, including meltwater refreezing and supra- and englacial water storage, and thus captures meltwater that actually exits the ice sheet. It must be noted that runoff onset and cessation determined from sediment plumes adds a systematic shift in the runoff season because of the lag between meltwater production and plume development. Plume development lags ablation onset by 6days on average, likely reflecting the development of supra- and englacial channels, transport in the terrestrial fluvial system and plume development in the fjord. The short lag between meltwater production and plume formation in the fjord suggests limited englacial storage and agrees with observations of a rapid transfer of meltwater from the surface to the ice-bed interface at the peak of the melt season, resulting in localized uplift and enhanced ice flow shortly after peak meltwater production (Reference Shepherd, Hubbard, Nienow, McMillan and JoughinShepherd and others, 2009; Reference Bartholomew, Nienow, Mair, Hubbard, King and SoleBartholomew and others, 2010). We hypothesize that the lag at the end of the melt season reflects the settling time of sediment in the fjord.
Runoff-season duration from this study differs substantially from other studies that constrain the ‘melt season’ by the temporal duration of snowmelt. On average, the runoff season determined from sediment plumes extends 70days beyond the melt season that Reference Hall, Williams, Luthcke and DigirolamoHall and others (2008) found using MODIS land-surface temperature. In situ ablation data confirm this result, with ablation lasting 63, 23 and 18days longer (at S5, S6 and S9, respectively) than in the Reference Hall, Williams, Luthcke and DigirolamoHall and others (2008) study. One cause of this discrepancy is differences between measuring snowmelt over large regions, including high elevations above the equilibrium line included in the Reference Hall, Williams, Luthcke and DigirolamoHall and others (2008) study, and runoff, which is driven by ablation along the lower-elevation margins of the ice sheet and is of longer duration.
Reconstructed discharge values are in good agreement with in situ discharge measurements in 2007 and 2008. The reconstructed value in 2007 overestimates cumulative measured discharge by 15%, while in 2008 it overestimates measured discharge by 29%. We hypothesize that the overestimation is due to a systematic error introduced by the discharge of the Aussivigssuit river. The statistical relationship between plume length and discharge was developed using solely the Watson River discharge record, while the length of the sediment plume, once the plumes merge, reflects the discharge and sediment load of both river systems. This contribution results in the observed plume length being longer than the discharge value of the Watson River suggests, leading to an overestimation of reconstructed discharge values compared with observed values. Basin hypsometry suggests that the basins are of similar size at elevations below 1000 m but that the Aussivigssuit basin is substantially larger at higher elevations. Even assuming that the runoff contributions are comparable from the two river basins, the plume dynamics in the fjord are too complicated to warrant a simple doubling in plume length once they combine. Thus, the plume-length-discharge relationship is solely based on the Watson River discharge, with substantial uncertainty due to variable contributions of runoff from the Aussivigssuit river. Future work is thus necessary to constrain the Aussivigssuit’s contribution to the sediment plume in Kangerlussuaq Fjord.
This study presents a methodology using sediment plumes as a proxy to quantify the runoff season duration and reconstruct meltwater runoff from a specific drainage basin of the GrIS. At this time, the methodology to determine runoff volume is validated for a specific river system, meaning that the statistical relationship between plume length and river discharge is only valid for this system. The empirical relationship is not a direct measurement. The controlling processes are complicated and integrate a large number of meteorological, hydrological and oceanographic variables, which cannot be fully constrained (local snowmelt, rainfall, supra-and englacial water storage, sediment supply, discharge-sediment rating, wind and tidal currents and the addition of an ungauged river down-fjord). A discussion of critical assumptions and sources of uncertainty follows, beginning with water supply, moving to sediment supply and concluding with fjord processes.
We assume that meltwater from the ice sheet is the main constituent of water in the Watson River throughout the melt season. Other possible sources of water include proglacial snowmelt early in the melt season, rainfall throughout the season and groundwater. Snowfall in the proglacial region is minimal and almost completely melts by mid-May, before the onset of melt on the ice sheet. However, it is possible that this contributes to plume formation early in the melt season, confounding the ablation onset signal. Other potential complications to this relationship include the presence of sea ice in the fjord when ablation begins, which occurred in 2002, 2005 and 2006 (Reference Chu, Smith, Rennermalm, Forster, Box and ReehChu and others, 2009) and/or high snow accumulation, which can retain meltwater and delay runoff (Reference HannaHanna and others, 2008). However, other observations using passive microwave melt onset rather than in situ ablation measurements also find that plume onset is tightly coupled to melt onset on the ice sheet (Reference Chu, Smith, Rennermalm, Forster, Box and ReehChu and others, 2009).
Rainfall is measured at the Danish Meteorological Institute’s (DMI) station in Kangerlussuaq (http://www.dmi.dk/dmi/vejrarkiv-gl), ˜30km from the ice edge. To constrain the potential contribution of rainfall to river discharge, we examined the largest rain event of the 2007 melt season, during which 42.5 mm of rainfall were measured between 24 and 26 July 2007. Watson River discharge declined during this period, with no noticeable impact from the rainfall (Fig. 8). For comparison, during this same 3 day period ˜150mm of ice ablated at S5. One possible explanation for a limited hydrographic response is that a decrease in temperature following frontal passage reduces ablation rates and meltwater production, smoothing the impact of the increased hydrologic input.

Fig. 8. Daily precipitation at the DMI weather station in Kangerlussuaq and instantaneous Watson River discharge, Q, for the 2007 melt season. Sediment plume characteristics are directly tied to the concentration and particle size of sediment carried by the river as it enters the fjord.
Supra- and englacial storage and subsequent rapid drainage can influence meltwater supply throughout the melt season. There are approximately 60 lakes located on the ice sheet within the Watson River catchment basin between 1000 and 1600 m a.s.l., at a distance of 40-100 km from the ice edge. These lakes fill with meltwater throughout the melt season and can drain completely in a matter of hours (Reference DasDas and others, 2008), with important implications for enhanced glacier flow and sediment transport (Reference Box and SkiBox and Ski, 2007). A large proglacial lake drainage event occurred on 31 August 2008 (Reference Mernild and HasholtMernild and Hasholt, 2009) and was observed in the Watson River hydrograph, but was not observed with MODIS imagery 1 day later. This suggests that large but rapid meltwater pulses have little effect on plume characteristics. Possible reasons include either a muting of the pulse by the subglacial system, especially if lake drainages occur on the GrIS, or in the case of ice-marginal lakes the plume may become hyperpycnal and dive beneath the surface waters in the fjord. Similarly, Reference Chu, Smith, Rennermalm, Forster, Box and ReehChu and others (2009) found that <40% of observed lake drainages resulted in noticeable changes to plume area in Kangerlussuaq Fjord.
Sediment supply is not constant and varies spatially and temporally as the subglacial drainage network evolves over diurnal and seasonal timescales. Much work has been done on alpine glaciers to understand subglacial hydrology, glacier motion and sediment transport (Reference CollinsCollins, 1990; Reference Willis, Richards and SharpWillis and others, 1996; Reference Harper, Humphrey, Pfeffer and LazarHarper and others, 2007; Reference Bartholomaus, Anderson and AndersonBartholomaus and others, 2008). Theory and observations suggest that the subglacial drainage network evolves seasonally from a high-pressure distributed network to a low-pressure arborescent channelized system, with both reduced basal water pressure and sediment transport. Importantly though, meltwater pulses that overwhelm the channelized system, through increased melt, lake drainage or rainfall, will likely revert to pressurized distributed flow. This will result in enhanced glacier flow and greater meltwater-bed interaction, yielding greater sediment transport (Reference CollinsCollins, 1990; Reference Harper, Humphrey, Pfeffer and LazarHarper and others, 2007; Reference Bartholomaus, Anderson and AndersonBartholomaus and others, 2008). Recent work on Russell Glacier, within the study area of this project, finds localized uplift and accelerated velocities ˜2 hours after peak meltwater production, suggesting that the basal hydrology network cycles between pressurized and channelized flow in response to diurnal variations in meltwater input (Reference Shepherd, Hubbard, Nienow, McMillan and JoughinShepherd and others, 2009;Reference Bartholomew, Nienow, Mair, Hubbard, King and SoleBartholomew and others, 2010).
Meltwater that exits the ice sheet must first travel through a sediment-rich ˜30km fluvial system. Reference Hodson, Gurnell, Tranter, Bogen, Hagen and ClarkeHodson and others (1998) found that the proglacial sandur evolves seasonally from a minor net sediment source at the beginning to a net sediment sink later in the season. Our preliminary measurements (July 2008) show a fourfold increase in suspended sediment in the Watson River along a transect from the ice margin to the Kangerlussuaq gauging station, thus suggesting the river increasingly entrains sediment as it travels downstream through the sandur. This process will buffer and mute variations in SSCs present in meltwater streams as they exit the ice sheet.
Hysteresis in sediment supply has been observed over daily, weekly and seasonal timescales for proglacial streams of alpine glaciers worldwide, owing to previously described subglacial drainage evolution and the exhaustion of sediment (Reference Gurnell, Gurnell and ClarkGurnell, 1987; Reference CollinsCollins, 1990; Reference Willis, Richards and SharpWillis and others, 1996; Reference Haritashya, Singh, Kumar and GuptaHaritashya and others, 2006). The Watson River system shows seasonal hysteresis in sediment supply, with longer plume lengths (and hence more sediment) early in the melt season compared to later in the melt season for the same discharge value. This anticlockwise hysteresis is likely due to the large quantities of sediment accumulating over winter, both beneath the ice and in the proglacial fluvial environment, which are easily entrained on the rising limb of the hydrograph. A similar hysteresis may be overlaid on this seasonal hysteresis operating over intermediate timescales (days to week). Falling discharges and reduced velocities will deposit sediment on the riverbank that will be entrained and transported during the next major increase in discharge. Five examples of this rising and falling discharge cycle can be observed during the 2007 melt season (Fig. 8). Other work in Kangerlussuaq Fjord found a similar seasonal hysteresis when comparing mean plume area with mean melt extent between 2000 and 2007 (Reference Chu, Smith, Rennermalm, Forster, Box and ReehChu and others, 2009). The hysteresis is attributed to a decrease in river discharge due to increased englacial storage during the latter half of the season and/or a decrease in sediment supply (Reference Chu, Smith, Rennermalm, Forster, Box and ReehChu and others, 2009). Additional suspended sediment measurements, both at the ice margin and at the river mouth, are needed to quantify the spatial and temporal evolution of sediment supply.
Plume dynamics are primarily controlled by river velocity and tidal cycle (Reference Syvitski, Asprey, Clattenburg and HodgeSyvitski and others, 1985), but as they extend longitudinally, external forces (e.g. wind stresses and tidal currents) increasingly affect them. To constrain the impact of wind on the sediment plume in Kangerlussuaq Fjord, we utilized the DMI station in Kangerlussuaq (http://www.dmi.dk/dmi/vejrarkiv-gl). The primary wind direction during the 2007 and 2008 melt seasons was 128°, with a mean speed of 3.9 ms-1. The mean wind direction is offset from the fjord orientation by 75°, reducing the fetch of the wind and thus its ability to affect the plume. We find no relationship between wind direction/speed and the residuals of the plume-length-discharge relationship (Fig. 5), suggesting a negligible influence of wind forcing on plume length (Fig. 9). Further, Reference Chu, Smith, Rennermalm, Forster, Box and ReehChu and others (2009) showed that the tidal influence can be neglected in Kangerlussuaq Fjord based on nearly identical plume area probability functions for ebb and flood tides.

Fig. 9. Wind direction and wind speed compared with plume-length-discharge residuals (Fig. 5). There is no relationship between residuals and either variable.
The use of sediment plumes as a proxy for runoff from the ice sheet encompasses numerous glaciological, meteorological, fluvial and oceanographic processes, many of which are poorly understood and unconstrained. Despite these complications, their use as a proxy for ice-sheet melt is promising, but the method needs further in situ observations to reduce uncertainties.
Conclusion
Meltwater runoff is one of the largest uncertainties in constraining the surface mass balance of the GrIS. This study demonstrates the use of satellite observations of sediment plume length in Kangerlussuaq Fjord as a proxy for ice ablation on, and runoff from, a 6130 km2 basin of the GrIS. Plume formation can be used to estimate runoff onset and duration. This provides an alternative metric to the commonly used melt season, which primarily reflects the large regions of the ice sheet that undergo surface melting but do not contribute to mass loss from the ice sheet. We show that ice ablation drives terrestrial river discharge, which in turn drives plume length in the fjord. This tightly coupled relationship makes it possible to resolve ablation variability throughout the melt season from satellite observations of plume length without direct ablation measurements and can be established for, and applied to, any fjord without in situ measurements. Plume length can be further calibrated with in situ discharge measurements and then used to reconstruct basin-scale runoff. Results from this test study find that reconstructed values agree with but overestimate observed cumulative discharge values for 2007 and 2008 by 15% and 29%, respectively.
Acknowledgements
This work was supported by NASA grant NNX08AT85G. W. Colgan assisted in the field and provided valuable suggestions on the manuscript. M. Berlin provided basin hypsometry data. C. Roesler contributed useful discussions during project development. CH2M HILL Polar Services provided excellent field support. F. Tweed and an anonymous reviewer provided constructive comments that greatly improved the manuscript.












