Introduction

Knowledge of the surface roughness of a glacier, interpreted as small-scale topographic variation, is important for a number of reasons. The surface roughness is an important control on turbulent heat exchange between the glacier surface and the atmosphere (Reference MunroMunro, 1990; Reference Brock, Willis, Sharp and ArnoldBrock and others, 2000; Reference Denby and GreuellDenby and Greuell, 2000) and hence on the surface energy balance and, ultimately, the mass balance. The size of the roughness elements that are significant in this regard is typically of the order of 0.1 m. Glacier albedo has also been shown to vary at small spatial scales (Reference Arnold and ReesArnold and Rees, 2003), and given the anisotropic reflectance of ice and snow surfaces at high solar zenith angles (Reference Knap and ReijmerKnap and Reijmer, 1998), typical for high-latitude ice masses, small-scale topographic variation and the resulting variation in the local incidence angle of the solar beam, may also play a role in glacier surface energy balance via the flux of shortwave radiation at the surface (Reference König, Winther and IsakssonKönig and others, 2001).

Surface roughness also modulates the response of an imaging radar to the surface of a glacier. In situations where surface scattering dominates over volume scattering, which, in the context of a glacier, means where the surface is either free of snow or the snow cover is sufficiently wet (Reference ReesRees, 2006), the backscattering coefficient is controlled by three factors: the local incidence angle, the dielectric constant of the surface and the roughness at a scale comparable with the radar wavelength. The local incidence angle is determined by the larger-scale topography (slope and aspect) of the surface and the viewing geometry of the radar. In the case of a snow-covered surface the dielectric constant is determined by the density and liquid-water content of the snow, while in the case of a bare ice surface it is simply that of ice itself. Thus, knowledge of the radar backscattering coefficient and the incidence angle has the potential to yield information on the surface roughness of a bare ice surface, and on a combination of surface roughness and snowpack parameters in the case of a snow-covered surface.

A particularly interesting possibility is that the surface roughness properties retrieved from a radar image can be related to those relevant to the thermodynamic and optical properties of the surface. The idea of seeking a link between radar backscatter and surface roughness, as it affects aeolian processes, has been investigated for desert (Reference GreeleyGreeley and others 1991, Reference Greeley2006; Reference Blumberg and GreeleyBlumberg and Greeley, 1993; Reference Greeley and BlumbergGreeley and Blumberg, 1995) and vegetated (Reference Rasmussen, Wall, Greeley, Blumberg, Mikkelsen, Rasmussen, Wall, Greeley, Blumberg and MikkelsenRasmussen and others, 1993) surfaces. No similar studies have been performed for glacier surfaces, to the best of our knowledge. Furthermore, it is not obvious at what spatial scale the roughness properties should be described. In the case of radar imagery the relevant scale is less than that of the spatial resolution, while for aerodynamic interactions the answer is not clear. Models of surface roughness usually assume that it can be characterized by some definite horizontal and vertical scale, while there is increasing evidence that many natural surfaces, including those of glaciers (Reference ReesRees, 1992; Reference Arnold and ReesArnold and Rees, 2003), should be described as consisting of a spectrum of scales.

The aim of this paper is to assess the extent to which glacier surface topography can be described as ‘scale-free’ or alternatively as having a definite scale of roughness elements. Roughness and topographic data will be related to considerations of radar backscattering and aerodynamic modelling. Then, to the extent that it is possible to identify the range of scales contributing most significantly to these phenomena, the paper will attempt to identify the optimal data collection strategy for topographic data capable of being applied to both radar backscattering and aerodynamic modelling.

Characterization of Surface Roughness

Various measures of surface roughness have been proposed. These include the root-mean-square (rms) height deviation σ, the correlation length l and the rms slope deviation m. Definitions of these terms are given below.

The first three of these measures can be defined in terms of a topographic transect z(x) from which any linear variation has been subtracted, i.e. one for which 〈z(x)〈 and 〈xz(x)〉 are both equal to zero, where the angle brackets (·) denote averaging over the transect. In this case, the rms height deviation is simply defined as

The correlation length l is defined in terms of the autocorrelation function of the transect

as the smallest value of x’ for which ρ = 1/e. The rms slope deviation m is defined as

and it is related to the rms height deviation and the autocorrelation function through

Even if the rms height deviation and autocorrelation function of a surface can be defined, it does not follow that the rms slope deviation m has a well-defined value. For Equation (4) to yield a meaningful value of m, it is necessary that

This condition is satisfied by a surface having a Gaussian autocorrelation function, but not (for example) a negative exponential autocorrelation function.

In practice, these measures of surface roughness must be estimated from a discrete, rather than a continuous, topographic transect. This can be represented as z_i , where i is an integer 1,2,..., n that numbers the samples. If the horizontal sampling interval is s, the total length of the transect is

Again we assume that any linear variation has been subtracted from the transect so that

where the sums are taken from i = 1 to n (this convention is adopted here wherever the limits of the sum are not specified). The expression for the rms height deviation becomes

The autocorrelation function is defined as

and the rms slope deviation m is defined as

An alternative approach to the characterization of surface roughness is based on consideration of the aerodynamic roughness length z ₀. This is an aerodynamic parameter that is a function of the surface roughness (Reference BagnoldBagnold, 1941) and is essentially the height above the surface at which the wind- speed profile falls to zero For example, for an adiabatic atmosphere with fully turbulent flow, the surface-parallel component u_h of the air speed varies with the height h above the surface according to the von Kármán-Prandtl logarithmic law (Reference SchlichtingSchlichting, 1968; Reference Plüss and MazzoniPlüss and Mazzoni, 1994) as

for h > z ₀, where u* is a constant (the friction velocity) and k is von Kármán’s constant, approximately 0.40. This equation, or more complicated variants of it that apply when the adiabatic and fully turbulent criteria do not apply (Reference Rasmussen, Wall, Greeley, Blumberg, Mikkelsen, Rasmussen, Wall, Greeley, Blumberg and MikkelsenRasmussen and others, 1993; Reference King and AndersonKing and Anderson, 1994), defines the aerodynamic roughness length z ₀, which can thus in principle be deduced from the air-speed profile above the surface. However, in many studies of the surface energy balance of ice masses, the value of z ₀ is estimated by measurements of the surface topography itself, rather than the air-speed profile. This is partly due to the difficulties of maintaining the complex instrument suite needed to obtain z ₀ from atmospheric measurements in the hostile environment of a glacier surface, but also because the atmospheric conditions over glacierized surfaces (strong katabatic flow and temperature inversions) make such an approach theoretically difficult (Reference Denby and GreuellDenby and Greuell, 2000). Typically, z0 is estimated from a topographic transect. Several approaches have been proposed (Reference SellersSellers, 1965; Reference LettauLettau, 1969). We adopt the approach of Reference MunroMunro (1989, 1990) which involves counting the number N of positive zero-crossings in the transect represented by the values z_i:

Since t/N is an estimate of the correlation length l, Equation (12) is equivalent to estimating z ₀ as proportional to σ ²/l. It is important to recognize that the quantity defined by Equation (12) is merely an estimate of the quantity defined by Equation (11), and it would perhaps be appropriate to use different symbols for the two quantities. However, we retain the symbol z ₀ for convenience, since it will be obvious from the context which quantity is being referred to.

All four of these topographically defined measures of surface roughness (σ, l, m and z ₀) can be regarded as functions of the horizontal sampling interval s and the transect length t. If the surface can be represented as consisting of ‘typical’ roughness elements of width w, the roughness measures will not in fact depend on the values of s and t provided that s is sufficiently smaller than w and t is sufficiently larger than w.

This assumption of single-scale roughness underlies the simpler models (Reference Ulaby, Moore and FungUlaby and others, 1982) that are used to predict microwave scattering from rough surfaces, and to relate topographically derived aerodynamic roughness (e.g. through Equation (12)) to the aerodynamic definition implied by Equation (11). However, there is increasing evidence (Reference BurroughBurrough, 1981; Reference GilbertGilbert, 1989; Reference ReesRees, 1992; Reference Arnold and ReesArnold and Rees, 2003) that the roughness of many natural surfaces is better described by a spectrum of scales. In particular, natural surfaces are often well modelled as showing random but statistically self-affine behaviour resulting in a power-law dependence of the Fourier transform of the surface profile on the spatial frequency q. Specifically, the power spectrum of the surface profile is described by

over some range of spatial frequencies, where c is a constant. Equivalently, the semivariogram of the surface profile, defined as

is given by the power-law expression

between some inner scale s ₁ and some outer scale s ₂; a is a constant related to c and H. The value of H in Equations (13) and (15) is the Hurst exponent, related to the fractal dimension D of the surface transect through (Reference MandelbrotMandelbrot, 1985; Reference Voss, Peitgen and SaupeVoss, 1988)

Since the value of D lies between 1 and 2 for any possible transect z(x), it follows that the Hurst exponent lies between 0 and 1. Values of H above 0.5 indicate persistent behaviour, whereby above-average values of z tend to be succeeded by more above-average values, and conversely. Most natural surfaces that satisfy Equation (15) (or equivalently Equation (13)) exhibit this persistent behaviour, and hence show H > 0.5, D < 1.5.

For a surface that satisfies Equation (13), the rms height deviation can be shown (Reference ChurchChurch, 1988) to be given by

and the correlation length by

Thus, the calculated values of σ, l and z ₀ will all exhibit a power-law dependence on the transect length t, with exponents of H, 1 and 2H – 1 respectively. The rms height deviation and correlation length both increase with t, while the estimated aerodynamic roughness length increases with t provided that the surface shows persistent (H > 0.5) behaviour. From Equations (10) and (15), the rms slope deviation m is given by

so it is a power-law function of the sampling interval s and decreases with increasing s.

These power-law dependencies of the roughness measures on transect length t or sampling interval s are characteristic of scale-free behaviour of the type represented by Equation (13) or (15), and hence point to the need for more sophisticated models of radar scattering and of aerodynamic flow over the surface. In the case of radar scattering, such models have been proposed by Reference Mattia and Le ToanMattia and Le Toan (1999). The aim of this paper is to investigate the roughness of a glacier surface from this point of view, and hence to determine whether there appears to be a need to invoke such models.

Data Collection

Topographic data were collected from the snow-free surface of the glacier midre Lovénbreen, Svalbard, in August 2003. Heavy rain at the beginning of the month had removed the remaining snow from most of the glacier’s surface (Fig. 1). Almost the entire glacier was mapped on 9 August using an Optech ALTM 3033 LIDAR (light detection and ranging) system, mounted in a Dornier Do228 aircraft. The topographic data were gridded to a horizontal resolution of 2 m, which is coarser than the sampling interval of the LIDAR, with an estimated vertical accuracy of 0.1 m. The details of the LIDAR data acquisition and processing are described by Reference Arnold, Rees, Devereux and AmableArnold and others (2006).

Fig. 1. Midre Lovénbreen viewed from the north on 4 August 2003.

Finer-scale topographic profile data were collected during fieldwork on 6 and 8 August 2003. Two specific locations were selected for these measurements, close to stakes for which accurate GPS (global positioning system) locations were determined. One stake (‘stake 2’) was located close to the glacier terminus, at an altitude of approximately 80 m, while the other (‘stake 5’) was approximately halfway up the glacier, at an altitude of about 250 m (Fig. 2). Both were located close to the centre line of the glacier. The two sites provided a range of surface slopes, needed for comparison with radar data, but otherwise no obvious differences were apparent between the two sites, nor indeed over any other parts of the glacier surface that we were able to explore. Visually, the most obvious characteristic of the glacier surface at scales up to a few tens of metres was the presence of relict meltwater channels, a few tens of centimetres deep and a few metres apart, which can be seen in Figures 2 and 3.

Fig. 2. Study sites near stake 2 (top) and stake 5 (bottom). A Kipp & Zonen albedometer on tripod is shown for scale at each location.

Fig. 3. Metre-long back plate inserted into the ice surface for microtopographic roughness measurement.

At each site, two kinds of roughness profile were collected. The first consisted of transects 10–20m long, defined by string tautly stretched between ice screws. The depth of the ice surface below the string was measured at intervals of 0.5 m (chosen for convenience and to provide some overlap with the second method of sampling), with an estimated precision of 0.01 m. The second kind of roughness measurement was performed by carefully pushing and sliding a metre-long black metal plate vertically into the ice and photographing the ice surface with a digital camera (Fujifilm Finepix S5000). Considerable care had to be exercised to avoid disturbing the ice surface while inserting the back plate (Fig. 3). The method described by Reference ReesRee (1998) was used to retrieve the surface profiles from the resulting images. Since the length of the plate was typically represented by 1600 pixels in the digital photographs, this resulted in an effective sampling interval of 0.0013 m over a 1 m transect, giving a precision of better than 0.0007 m. At each site and with each method, several transects were recorded in both the cross-glacier and along-glacier directions. The LIDAR data were used to extract profiles approximately 300 m long, in the cross-glacier and along- glacier directions, centred on the two stakes. Representative surface profiles collected by the three methods are shown in Figure 4.

Fig. 4. Representative surface profiles (stake 2, cross-glacier direction) after removal of linear trends. Top: from digital photography; middle: from taut string; bottom: from LIDAR.

Analysis

The transect data were processed to generate values of the four roughness parameters σ, l, m and z ₀ as functions of the transect length t (0.014-280 m) and the sampling interval s (0.0014–8 m). The results of this analysis for stake 2 in the cross-glacier direction are shown in Figure 5. Results for stake 5 and for the along-glacier direction were broadly similar, as demonstrated in Figure 6. This figure shows the average binned semivariograms for the roughness profiles measured at the two stakes and in the two directions. The semivariograms are virtually identical for sampling intervals below 0.3 m, while for intervals above 0.5 m they show rather more divergence but the same general trend. The maximum difference between the semivariograms is equivalent to a factor of 2 in the variability of the height.

Fig. 5. Log-log plots (to base 10) showing roughness parameters (stake 2, cross-glacier direction) as functions of transect length t and sampling interval s, both expressed in metres.

Fig. 6. Mean semivariograms for the roughness profiles at the two sites in two directions. ‘2’ and ‘5’ denote the stake numbers, while ‘L’ and ‘X’ denote along and across the glacier, respectively.

The results in Figure 5 show clearly that the rms height deviation σ and the correlation length l are well described as functions of the transect length t. The same is true of the estimated aerodynamic roughness z ₀, although with rather more scatter. The rms slope deviation m is well described as a function of the sampling interval s. These dependencies are in general accord with the principles of scale-free roughness discussed in the preceding section. However, it is also clear that the roughness parameters do not depend on t and s in the simple manner implied by the power laws of Equations (13) and (15). There is evidence for power-law behaviour at scales shorter than about 0.1 m and longer than a few metres, but these regimes are characterized by different values of the Hurst exponent H and there is a transition in behaviour between these two scales. This would appear to constitute evidence for a definite roughness scale which can be investigated using the microtopographic data collected by digital photography, and possibly also using the string profiles.

The values of σ, l and z ₀ were recalculated from the microtopographic transects (i.e. effectively for t = 1 m and s ≈ 1 mm). Since no significant differences were observed between the data from stake 2 and stake 5, these were averaged, giving six independent measurements for each variable. Values were also calculated for the string profiles (s = 0.5 m, t = 5–10 m). Again, data were combined from stakes 2 and 5, giving a total of 40 independent transects (14 cross-glacier and 26 along-glacier). The results are shown in Table 1. The table shows little evidence for anisotropy of the surface roughness over the range of scales explored by the microtopographic transects, but perhaps a little more over the scales explored by the string profiles. Examination of the autocorrelation functions of the microtopographic transects shows them to be well described by negative exponential functions. As discussed in the previous section, this implies that no meaningful value can be assigned to the rms slope deviation m. The autocorrelation functions of the string profiles are harder to characterize: as Table 1 suggests, the correlation length is often less than the sampling interval and hence rather poorly defined by the data. Nevertheless, the table suggests the existence of features with a definite size in the range 70–500 mm in horizontal extent, 6–65 mm in vertical extent, and with an estimated aerodynamic roughness length of 0.3–2 mm (these values are simply rounded values of σ and l estimated by the two methods). As demonstrated by Figures 2 and 3, there are no obvious discrete features of the surface that can be identified with this range of scales. It is tempting to associate the outer scale with the relict meltwater channels, but the fact that no significant difference was observed in the correlation length between the cross-glacier and along-glacier directions argues against this.

Comparison with Radar Data

In this section we investigate the extent to which the surface roughness parameters measured in the previous section can be related to the microwave backscattering behaviour of the glacier surface.

Unfortunately, no suitable SAR (synthetic aperture radar) image was available for the period of the field investigations reported in this paper. However, an ERS-2 (European Remote-sensing Satellite-2) SAR image (C-band (wavelength 57 mm), VV-polarized) covering midre Lovénbreen was available for 20 July 1999 (Fig. 7). Field observations on the glacier in 1999 showed that the snowline had retreated to an altitude of above 250 m by 16 July and was continuing to retreat rapidly, so by the date of the SAR acquisition, certainly the two stake sites, and probably much of the glacier, were clear of snow. We thus believe that this SAR image will be very similar to a hypothetical one collected in August 2003.

Fig. 7. Extract of ERS-2 SAR image (acquired 20 July 1999) centred on midre Love´nbreen. Up corresponds approximately to south. © European Space Agency 1999.

Three simple models of microwave surface scattering are well known (Reference Ulaby, Moore and FungUlaby and others, 1982). These are the geometric optics (GO), scalar (S) and small perturbation (SP) models. Approximate conditions for the validity of these three models are summarized in Table 2. Figure 8 shows the regions of validity of the three models (for the GO model, the incidence angle is assumed to be 28°). It also shows the range of values of σ and l deduced in the previous section. Both pairs of values, i.e. those derived from the microtopographic and string profiles, appear to be consistent with the requirements of the S model, while the values derived from the string profiles are also consistent with the GO model. We therefore begin by investigating whether the radar backscattering observed from the glacier can be explained by the S model using either or both of these pairs of roughness parameters.

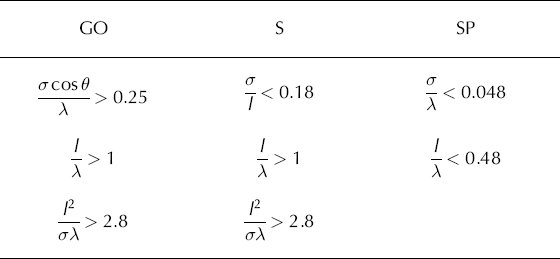
Fig. 8. Regions of validity of the three simple surface scattering models (SP, S and GO), shown in shades of grey. The crosses ‘m’ and ‘s’ show the range of values of σ and l measured from the microtopographic and string profiles, respectively. The quadrilateral area delineated by black lines shows the limits of the region in l-σ space for which the scalar model is capable of explaining the observed SAR backscatter values.

Three regions of the SAR image were investigated, each roughly 500 m square, located near the margin, the middle and the top of the glacier. No attempt was made to correct the radar imagery for terrain distortion effects, but since the slope of the glacier is reasonably constant over the area studied the three regions defined in the SAR image could be located sufficiently accurately to define the corresponding regions within the LIDAR dataset. The local incidence angle was calculated for each pixel in the SAR regions, using the LIDAR data to define the direction of the surface normal, and the header data provided with the SAR image to determine the viewing geometry of the radar. Statistics of the backscattering coefficient were extracted from the radar data. The results were analyzed for 2° bins in incidence angle, and three bins, centred at 26°, 28° and 30°, were found to be well enough populated with data for the results to be statistically meaningful. We found mean and standard- deviation backscattering coefficients as follows: 26°: –14.7 ± 3.0 dB;28°: –16.9 ± 4.2 dB;30°: –15.2 ± 3.1 dB. It is well known that SAR images are subject to noise-like variations in backscattering coefficient called speckle (Reference GoodmanGoodman, 1976), and some of the observed variation is attributable to this cause. For the three-look imagery that we used, the expected value of the standard deviation of the decibel value of the backscattering coefficient for a homogeneous region with fully developed speckle is 2.7 dB (Reference Rees and SatchellRees and Satchell, 1997), so the scattering conditions in the areas contributing to the bins centred at 26° and 30° can be inferred to have been close to uniform. The data contributing to the bin centred at 28° show rather more variability. This could, of course, be reduced by averaging, but at the expense of altering the spatial dependence of the backscattering coefficient. We therefore elected not to attempt any averaging of the data.

The scalar approximation gives the backscattering coefficient as (Reference Ulaby, Moore and FungUlaby and others, 1982)

where k is the wavenumber (= 2π/λ), σ is the rms height variation, θ is the incidence angle, r is the Fresnel amplitude reflection coefficient evaluated for the appropriate polarization and at the incidence angle θ, p is the normalized autocorrelation function of the surface variations, J₀ is the zero-order Bessel function and ξ is a dummy variable with dimensions of length. In the case of a negative exponential autocorrelation function with correlation length l, this can be evaluated to

This expression was used to determine combinations of σ and l consistent with the observed backscattering coefficients, assuming that r was determined by the dielectric constant of pure ice at microwave frequencies (taken to be 3.17). The results of this analysis showed that values of σ²/l between about 0.42 and 7.3 mm, when inserted into Equation (21), could explain the observed values of the backscattering coefficient. These limits are shown in Figure 8, from which it is clear that the radar backscatter values are consistent, through the scalar model, with the measured roughness properties whether derived from the microtopographic or string transects. This suggests that these properties are the appropriate ones to determine the microwave backscattering behaviour of the glacier surface.

The GO model gives the backscattering coefficient as

where r(0) is the Fresnel amplitude reflection coefficient at normal incidence and m is the rms slope deviation defined in Equation (3). Again assuming that r is governed by the dielectric constant of pure ice, we find that the radar data are consistent with a narrow range of values of m, between 0.184 and 0.194. If the surface autocorrelation function is taken to be Gaussian, Equation (4) thus implies that 0.130 ≤ σ/l ≤ 0.137. This range of values is consistent with the measurements of σ and l from the string profiles.

Comparison with estimated Aerodynamic Roughness Length

No aerodynamic data were collected from midre Lovénbreen, so it is not possible to make a direct comparison between the topographically estimated values of z ₀ reported above and the model represented by Equation (11). However, results collected from the literature by Reference BrockBrock (1996) show typical values of z ₀ for glacier ice between 1 and 10 mm; values below 1mm are rarely recorded (although values of ~0.05mm have been reported for non-melting snow surfaces in Antarctica (Reference King and AndersonKing and Anderson, 1994)). Reference BrockBrock (1996) investigated spatio-temporal variations of z ₀ on Haut Glacier d’Arolla, Switzerland, finding values of around 1 mm early in the ablation season, rising to around 4mm in mid-August before declining again. He also investigated the effect of transect length (3–15 m) on the topographic profile method of estimating z ₀ and concluded that it had no significant effect. These results show that the estimated values of z ₀ of around 0.3 mm using our 1 m microtopographic transects, up to 1.5 mm using the string profiles, are plausible. As Figure 5 indicates, the sampling strategy proved not to be ideal for estimating the value of z ₀, and it is not possible to resolve the question of whether the estimate based on the microtopographic profiles or the string profiles is more likely to be correct, although the balance of evidence is in favour of the higher estimate.

Conclusions and Suggestions for Further Work

The surface roughness characteristics of the snow-free surface of midre Lovénbreen have been investigated on scales from 1 mm to around 300 m. We find that they are characterized by two more-or-less scale-free domains, below about 0.1 m and above a few metres. It is not particularly meaningful to attempt to specify these values more precisely, since they merely indicate a decreasing tendency for the scale-free descriptions to represent reality. In between these domains is a region characterized by a definite scale. Our measurements do not permit a particularly precise estimate of this scale, but we can place lower and upper limits on it based on the microtopographic and string profiles, respectively. These limits are around 70mm in horizontal extent and 6 mm vertically, and 500 mm horizontally and 70 mm vertically, respectively. The corresponding topographic estimates of the aerodynamic roughness length z0 are 0.33 mm and 1.5 mm, respectively. Comparison of these estimates with field measurements of z ₀ supplied by other investigators suggests that the size of the features responsible for our observations is towards the upper end of the range of values. However, the full range of values appears to be consistent with the observed values of the radar backscattering coefficient, and thus to imply that, in this case at least, it is not necessary to consider the scale- free behaviour of the surface in selecting suitable radar scattering models. We also note that the spatial extent of the surface roughness features is between about one and nine wavelengths of the C-band radiation used in forming the SAR image, and hence optimal for contributing to the scattering. This strongly suggests a relationship between z ₀ and the backscattering coefficient σº, similar to that for desert surfaces established by Reference Blumberg and GreeleyBlumberg and Greeley (1993), Reference Greeley and BlumbergGreeley and Blumberg (1995) and by Reference GreeleyGreeley and others (1991, 2006). Although we do not have the data to pursue this possibility, and indeed no reason to suspect that z ₀ varied significantly over the glacier, this analogy may well be worth pursuing. The dielectric constant of dry sand is quite similar to that of ice (Reference MätzlerMätzler, 1998) and suitable aerodynamic measurements are available (personal communication from D. Blumberg, 2006).

One difficulty identified by this investigation is that of obtaining topographic transects with sufficient spatial extent and resolution to encompass the necessary range of scales. This is manifested by the gaps in Figure 5, which occur in the transition region between the short- and long- scale behaviour. The results presented here suggest that, for adequate sampling of the roughness properties as they relate to C-band microwave backscattering, a sampling interval of at most 1 cm would be required, with a transect length of a few metres. The sampling interval needed for adequate representation of the aerodynamic roughness length can be somewhat coarser (perhaps 10 cm), but again a transect length of a few metres would be needed. In both cases, the necessary vertical accuracy would be of the order of a millimetre. This will clearly be rather challenging.