Introduction: Glacier Hydrology Before Channelized-Flow Theory
Channelized drainage versus distributed drainage; slow versus fast drainage system; seasonal switching from one drainage type to the other; the link between glacier surging and basal drainage system; maps of hydraulic potential and drainage divides at the glacier bed; the physics of jökulhlaups: these concepts, familiar to us circa 2010, trace their development to a pair of papers that appeared in sequence in issue No. 62 of the Journal of Glaciology in 1972. In those two papers, Hans Röthlisberger and Ron Shreve applied the conservation laws of physics to draw general conclusions about the nature of water flow through glaciers. These were the first steps in developing the various theoretical models that now inform all of glacier hydrology. Röthlisberger’s and Shreve’s conclusions about water flow at the glacier bed have stood the test of time; their picture of englacial drainage has been significantly modified not owing to errors on their part, but rather owing to data collected by methods (notably hot-water borehole drilling) that had not even been developed in 1972.
Röthlisberger first presented his version of channelized- flow theory at the Symposium on the Hydrology of Glaciers, held in Cambridge, UK, in September 1969, the same year that the first English-language glaciology textbook was published. The contents of that book – the first edition of Stan Paterson’s The physics of glaciers (Reference PatersonPaterson, 1969) – provide some useful context for viewing Röthlisberger’s contribution. Not only did Paterson’s text nowhere use the phrase ‘glacier hydrology’, but it mentioned water in glaciers only in the context of Hans Weertman’s then-recent papers on the effect of basal water on glacier sliding. Reference WeertmanWeertman (1962, Reference Weertman1964, Reference Weertman1966) had argued that a water layer covered much of the glacier bed and that a layer thickness of only a few mm could substantially ‘lubricate’ the bed and lead to enhanced sliding. In commenting on Weertman’s claims, Paterson wrote:
-
Whether such a water layer can even exist is a controversial question … It is uncertain whether an appreciable quantity of the surface water which penetrates to the glacier bed can flow as a layer rather than in channels. The water is certainly in channels when it emerges from under the terminus. Further up the glacier, however, where the ice is much thicker than at the terminus, the hydrostatic pressure of the ice may largely control the flow of water at the bed. This flow will then depend on the slope of the glacier surface rather than on the topography of the bed, and in this case the water might flow as a layer. (Reference PatersonPaterson, 1969, p. 126)
The reader needs to bear in mind the meager data about glacier-bed conditions available when Paterson wrote these words. Aside from descriptive reports of subglacial caverns near glacier margins, the only data on bed conditions available to Paterson were the more-or-less serendipitous measurements made by Reference MathewsMathews (1964), who obtained some basal water-pressure measurements at South Leduc Glacier, British Columbia, Canada, where a tunnel associated with mine workings had reached the bed ~2 km from the terminus beneath ~150 m of ice. Hot-water drilling to the glacier bed and borehole instrumentation would not be achieved for several more years (Reference HodgeHodge, 1976, Reference Hodge1979). As Paterson wrote his book and pondered the importance of channelized subglacial flow away from the terminus, he truly had little data and no theoretical framework to guide him.
Looking beyond The physics of glaciers for historical perspective, it is natural to turn first to the pages of the Journal of Glaciology from its inception in 1947 through 1969, but one finds there practically nothing of a hydrological nature aside from a few descriptive papers on ice-dammed lakes. To the extent that glacier hydrology was even being studied in that era, it was as an aspect of surface-water hydrology rather than as a discipline within glaciology. The key insights of that time about water flow through glaciers – for example, the fact that glaciers could store and then release water, and that the timescales of storage and release changed seasonally – came from surface-water and meteorological records for glacier- ized basins, along with glacier mass-balance studies (see, e.g., Reference Meier and TangbornMeier and Tangborn, 1961;Reference StenborgStenborg, 1970; Reference EllistonElliston, 1973; Reference LangLang, 1973). English- and French-language papers on such themes commonly appeared in publications of the International Association of Scientific Hydrology (IASH), now known as the International Association of Hydrological Sciences (IAHS). Indeed, the proceedings of the Symposium on the Hydrology of Glaciers were published by the IASH rather than by the Glaciological Society-with, of course, the notable exception of Reference RöthlisbergerRöthlisberger (1972).
In retrospect, one can say that the 1969 Cambridge symposium, the first ever to focus on glacier hydrology, came at a time when glacier hydrology was shifting from being part of surface-water hydrology to being part of glaciology. Reference StenborgStenborg’s (1968) study of the evolution of moulins, and their relationship to glacier structures, is a good example of this shift. Once glaciologists became interested in how water moved through glaciers and affected glacier dynamics, field methods had to change: systematic dye tracing, for example, began with Reference StenborgStenborg (1969), who reviewed his results at the Cambridge symposium (Reference StenborgStenborg, 1973). Observations and data from subglacial sites associated with hydropower projects (Reference Bezinge, Perreten and SchaferBezinge and others, 1973; Reference Vivian and ZumsteinVivian and Zumstein, 1973) first reached a wide audience in Cambridge. (To the best of my knowledge, Vivian and Zumstein were the first to refer explicitly to the concept of subglacial hydrology – ‘hydrologie sous-glaciaire’ in the original French.) As for theoretical studies, Röthlisberger’s presentation was in fact only one of several delivered at the Cambridge symposium: Reference MathewsMathews (1973) discussed the physics of jöikulhlaups (more about this paper below); Reference NyeNye and Frank (1973) discussed water movement through intergranular veins;and Reference NyeNye (1973) explored the paradoxical roles attributed to water-sheet drainage at the glacier bed.
The Core of Channelized-Flow Theory
Channelized-flow theory applied the key earlier insight (Reference LiestølLiestøl, 1956; Reference RöthlisbergerRöthlisberger, 1968; Reference StenborgStenborg, 1969; Reference MathewsMathews, 1973) that frictional energy dissipated by flowing water tends to enlarge passageways in ice. Reference MathewsMathews (1973) was the only one of these investigators to present any mathematical analysis: in discussing the drainage of an ice-dammed lake, he considered the case of water at a temperature of 0°C entering an ice-walled channel and wrote a differential equation for water temperature as a function of distance downstream in the steady state, with the water assumed to be warmed by frictional dissipation and cooled by heat loss to the ice walls. Mathews’ primary interest seems to have been in estimating how large the channel would become during lake drainage, but somewhat perplexingly he did not attempt to calculate how the enlargement process would be offset by ice creep, rather remarking simply that ‘should the walls of the tunnel be squeezed inward mechanically, notwithstanding the outward pressure of the contained water … a higher input of heat energy would be required to enlarge the tunnel by melting than has been assumed in the simple model adopted here’.
The theory of channelized water flow through ice was eventually developed in three papers published independently in 1972: in addition to Röthlisberger’s and Shreve’s back-to-back papers in the Journal of Glaciology, Weertman offered a treatment of channelized flow within the context of a broader theoretical analysis of water flow at the glacier bed. (The usages ‘Röthlisberger channel’ and ‘R channel’ were in fact originally recommended by Weertman to reflect precedent: Röthlisberger’s 1969 presentation in Cambridge.) All three papers have been widely cited in subsequent years, but arguably Röthlisberger’s has had the greatest impact owing to the simplicity of his presentation.
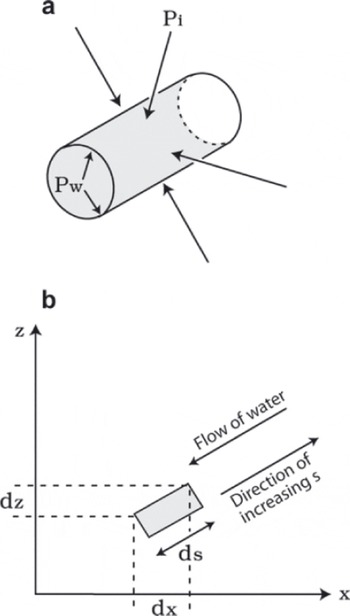
R-channel theory follows from a straightforward application of conservation principles. Conservation of H2O mass is expressed as a balance between inward creep of ice, which shrinks the channel, and melting of the ice walls, which enlarges the channel (Fig. 1). The channel is assumed to have a circular cross section if englacial, or semicircular if at the glacier bed. Conservation of energy is expressed as a balance between a source (frictional dissipation of gravitational potential energy within the flowing water) and two sinks (energy absorbed by the water and energy that goes into melting the ice walls). Conservation of momentum for the flowing water reduces to a relationship between discharge, channel size and hydraulic gradient. As the water flow is turbulent except for tiny channels or very small hydraulic gradients (Reference WeertmanWeertman, 1972), momentum conservation amounts to an empiricism of the sort long used in hydraulics and associated with names such as Chézy, Manning, and Darcy (Reference ChansonChanson, 2004, p. 69-80). The conservation relations have to be supplemented by two additional constitutive relations: (1) An expression is required to compute inward ice creep. Reference NyeNye’s (1953) analysis of borehole closure and generalization of Glen’s flow law provided the method, giving the rate of ice creep in terms of the ice flow-law parameters, ice pressure p i and water pressure p w. (2) Generally, water and ice are at different temperatures, and heat exchange between the two phases has to be parameterized in terms of, say, water temperature, ice temperature and characteristics of the turbulent flow. Röthlisberger (explicitly) and Shreve and Weertman (implicitly) instead made two key simplifying assumptions: first, energy dissipated by friction was assumed to be absorbed locally and instantaneously; second, the water temperature was assumed to be locally at the pressure-melting temperature of ice. These assumptions meant that not only was there no need for a heat-transfer empiricism, but more importantly there was no need to solve a differential equation for water temperature. Channelized- flow theory was thereby reduced to a single differential equation, and in the special case of steady-state flow, the theory made an important prediction: channels should form an arborescent network. Röthlisberger and Shreve took rather different approaches to making this prediction, however. (Weertman did not comment on the form that a channel network should take.) Reference RöthlisbergerRöthlisberger (1972, p. 180) considered the special case of a horizontal channel and showed that the steady-state pressure p w is given by

Fig. 1. Schematic of a Röthlisberger channel (after Reference RöthlisbergerRöthlisberger, 1972). (a) The channel tends to close by creep of ice at overburden pressure p i but opened by melting as flowing water at pressure p w dissipates energy. (b) In general, the coordinate s following the channel is inclined at some angle to the horizontal x axis, and the simple expression (Equation (1)) for pressure gradient dp w/dx is replaced by a more complicated expression for the variation of total hydraulic potential with s.
where Q is discharge; A and n are the usual parameters in Glen’s flow law for ice, A being the ‘softness’ and n(≈ 3) the exponent; and x is distance along the channel, increasing upstream. He then went on to state:
-
The dependence on Q is fundamentally important. It is such that the greater the discharge the lesser the pressure gradient, and therefore, after integration over the distance x, the lesser the water pressure at a given distance from the snout. If two channels side by side should compete with each other, the larger one of the two would show the lower head of water and consequently drain the water away from the smaller one. This is taken as proof that intra- and subglacial water flows in discrete conduits with a tendency to form main arteries.
Reference ShreveShreve (1972, p.207-209) reached the same conclusion about the tendency of channels to form an arborescent network, but because he never wrote a differential equation for water pressure, his line of argument involved a long series of mathematical manipulations and detailed discussion of the Reynolds-number dependence of hydraulic roughness, covering about one and a half pages in the Journal. Röthlisberger’s approach has become the preferred one for pedagogical purposes (see, e.g., Reference Cuffey and PatersonCuffey and Paterson, 2010, ch. 6).
Röthlisberger and Shreve also drew conclusions from their theory as to where channels should be found and how they should be oriented. Both writers made clear that in general, water flow depends not upon the gradient of water pressure but rather upon the gradient of total potential Φ. This is, of course, not a revolutionary principle – groundwater flow is always expressed in terms of ∇Φ – but because p i and p w are related by Nye’s expression for channel closure rate, there are interesting consequences when one works in terms of total potential. Shreve argued that ice was soft enough that the creep response would tend to track changes in p w, leading to a situation in which p w barely differs from p i. One then finds that, for englacial conduits (Fig. 2),

Fig. 2. Fluid equipotentials (dotted curves) and hypothetical arborescent network of englacial channels (after Reference ShreveShreve, 1985a). Reprinted from Geological Society of America Bulletin by permission of Geological Society of America, Boulder, Colorado.
-
The general direction of drainage will be perpendicular to the equipotentials of Φ, which in turn will dip up- glacier at an average angle
(2)
-
… that is, they will slope downward in the up-glacier direction with a gradient approximately 11 times that of the surface.
(Note: h i is ice-surface elevation, ρi is the density of ice and ρw is the density of water.)
Shreve wrote that this englacial drainage would be accomplished by
-
literally tree-like systems of passages penetrating the ice from bed to surface. Some of the larger passages will reach all the way to the surface as moulins to receive the superglacial run-off, but most will divide and redivide upward to drain the water percolating downward through the anastomosing three-dimensional network formed by the very smallest passages …
Shreve’s phrasing here is evocative of the fact that during this same period of time, he was deeply involved in studies of the topology of subaerial stream-channel networks (Reference ShreveShreve, 1975, and papers cited therein). As for channels at the glacier bed, Shreve used the same argument leading to Equation (2) to make a connection between channelized- flow theory and geomorphology:
-
The subglacial passages will follow the lines of steepest rate of decrease of Φ on the glacier bed … Thus, on a level bed they will trend in the direction of surface slope, and hence the direction of flow, of the ice. Where the bed is not level, they will still trend in the general direction of ice flow, but will tend to follow valley floors and to cross divides at their lowest points. These inferences exactly describe the behavior of eskers …
Finally, Röthlisberger showed that a valley glacier could plausibly have, in addition to a main trunk channel at or near the thalweg (the deepest part of the valley), what he termed ‘gradient conduits’, which ‘would probably not be located in an arbitrary position somewhere in the glacier, but most likely along the borders. Since that is where large amounts of water are collecting, there is little doubt that lateral channels must exist.’
Criticisms and Limitations Of The R- Channel Concept
Reference WeertmanWeertman’s (1972) lengthy paper on subglacial water flow served not only to codify his ideas about sheet flow of water at the glacier bed – ideas that Weertman had developed in conjunction with his seminal work on glacier-sliding theory (Reference WeertmanWeertman, 1962, Reference Weertman1964, Reference Schoof1966) – but to offer a contemporaneous critique of R-channel theory. Weertman did not dispute that R channels exist, but he stated rather forcefully his belief that ‘these channels are not good collectors of the water produced at the bottom surface of a glacier or ice sheet’. He maintained that the nonlinear rheology of ice should produce a stress field at the bed that blocks inflow of water except in a relatively narrow strip bordering a channel, and furthermore that very small channels could not be maintained owing to the effect of geothermal heating and heat conduction through the ice away from channels, and because they would tend to be destroyed by sliding of the glacier over its bed. Weertman’s argument about the stress field at the bed derived from an idealized model of a semicircular channel over a planar glacier bed and is problematic for an actual glacier bed, which is rough and commonly covered by permeable sediment (Reference Cuffey and PatersonCuffey and Paterson, 2010). His point about maintenance of very small channels has merit, but seen from nearly 40 years later, is perhaps moot. Even if very small R channels are unstable, basally derived meltwater must be delivered to the main drainage paths (R channels and perhaps linked cavities) via some sort of passageways, and, given the fact of material heterogeneity and the limits of observational data, worrying whether those passageways constitute a Weertman-style sheet, a permeable layer or a macroporous horizon seems like an exercise in gilding the lily: regardless of the details, on a macroscopic level, discharge through unchannelized domains, and exchange between such domains and R channels, is likely be governed by an expression akin to Darcy’s law for porous media (Reference Flowers, Björnsson, Pálsson and ClarkeFlowers and others, 2004; Reference FlowersFlowers, 2008; Reference Hewitt and FowlerHewitt and Fowler, 2008).
A major limitation of R-channel theory is the focus on steady-state conditions. If one envisages rapid increase in flux through a channel, say, the channel size cannot adjust quickly enough, water backs up, and rather than an inverse relationship between flux and water pressure, one finds that water pressure and flux changes are in phase, as they would be in a rigid pipe. Reference RöthlisbergerRöthlisberger (1972, p. 198) recognized this fact and suggested that the actual water pressure in a channel would fluctuate about the value indicated by the steady-state theory. Transient flow conditions have subsequently been explored in the context of jökulhlaups (Reference NyeNye, 1976; Reference Spring and HutterSpring and Hutter, 1981, Reference Spring and Hutter1982; Reference ClarkeClarke, 1982, Reference Flowers2003) and time-dependent meltwater forcing (Reference ClarkeClarke, 1996; Reference Flowers and ClarkeFlowers and Clarke, 2002a, Reference Flowers and Clarkeb).
Another well-known issue is the limited value of R-channel theory for making quantitative predictions: if the theory is applied to calculate water pressure in basal channels, one sometimes finds negative values of p w. Two remedies have been suggested for this conundrum: (1) the flow law parameter A is much larger than the generally accepted value, perhaps owing to the fact that basal ice commonly has a relatively high water content and, as a result, is relatively soft (Reference Cuffey and PatersonCuffey and Paterson, 2010, p.201). (2) Channels are not in fact semicircular in shape but rather broad and low (Reference Hooke, Laumann and KohlerHooke and others, 1990; Reference CutlerCutler, 1998).
Channels are assumed to be semicircular and full of water in the standard R-channel theory. Röthlisberger recognized that channels near the terminus would not be full, but did not discuss the likely extent of open-channel flow, nor circumstances that would favor this condition. Reference LliboutryLliboutry (1983) and Reference HookeHooke (1984) argued on theoretical grounds that open-channel flow would be common even for ice thicknesses of 200-300 m. A dye-tracing study by Reference KohlerKohler (1995) at Storglaciären, Sweden, did not support the theoretical prediction, however. This discrepancy between theory and data may also have to do with values assigned to the ice flow-law parameters.
The heat-transfer assumptions of the standard R-channel theory – namely, instantaneous heat transfer between water and ice, and water everywhere at the pressure-melting temperature – were relaxed by Reference NyeNye (1976) and other investigators who adapted the theory to model jökulhlaups. However, all jökulhlaup models predict water temperature substantially greater than values measured where flood- waters discharge from beneath the ice; this discrepancy possibly arises because important phenomena, such as the melting of ice mechanically scoured from channel walls by sediment, have not been factored into the models, or because the heat-transfer empiricisms developed by engineers from pipe-flow studies are incorrect at the large values of Reynolds number in subglacial channels (Reference BjörnssonBjörnsson, 1992; Reference ClarkeClarke, 2003). Unfortunately, data from the single published experimental study of water flow through a channel in ice (Reference Isenko, Naruse and MavlyudovIsenko and others, 2005) are not able to resolve this issue.
Developments in Glacier Hydrology that Built Upon Channelized-Flow Theory
Limitations of the theory notwithstanding, it is not an exaggeration to state that the Röthlisberger-Shreve model transformed the study of glacier hydrology by providing, for the first time, a theoretical basis for thinking about how and where water would flow. Reference PatersonPaterson (1981), in the second edition of The physics of glaciers, assured that students would learn about channelized-flow theory by presenting a summary of the basic theory, as well as Reference NyeNye’s (1976) extension of the theory to the study of jökulhlaups. Nye was the first to build upon R-channel theory in a significant way. He followed Röthlisberger by starting with the fundamental conservation laws for channelized flow, but then adapted his approach to address an intrinsically transient phenomenon: jökulhlaups from Vatnajökull, Iceland. Nye retained the time-dependent terms in the conservation equations and dropped the assumption that the water was always at the local pressure-melting temperature, so the energy-conservation equation became a differential equation for water temperature. Heat flux from water to ice was expressed (as Reference MathewsMathews (1973) had previously done) by an engineering empiricism appropriate for turbulent flow in a pipe. Nye then focused attention on a small section of the subglacial channel that was thought to be located at a hydraulic ‘seal’: essentially, a hump in the basal hydraulic potential field that had to be overtopped for lake drainage to begin. (The concept of the seal, and data bearing on its location, had been previously presented by Reference BjörnssonBjörnsson (1974).) By using some judicious approximations, such as an expression for average hydraulic potential gradient along the channel, he was able to avoid explicitly considering spatial dependence and wound up with a set of equations describing time-dependent channel evolution at the seal. Reference ClarkeClarke (1982) extended Nye’s analysis by taking into account the volume and shape of the reservoir, thereby permitting computation of complete model hydrographs. A detailed derivation of the governing equations for channelized water flow through ice, with all time- and space-dependent terms included, was presented by Reference Spring and HutterSpring and Hutter (1982), although productive application of their results awaited Reference ClarkeClarke’s (2003) development of appropriate computational methods. Detailed mathematical analysis of the Nye-Clarke model has also yielded important insights about jökulhlaup triggering and floods beneath ice sheets (Reference FowlerFowler, 1999; Reference Evatt, Fowler, Clark and HultonEvatt and others, 2006).
Reference ShreveShreve’s (1972) view of englacial drainage as involving an arborescent channel network is still commonly cited, although in recent years observational evidence from boreholes has indicated that englacial conduit orientations are not accurately predicted by Equation (2). This discrepancy has to do with a fact revealed by borehole, speleological and geophysical studies: namely, that fractures play a key role in englacial water transport and delivery of water to the glacier bed (Reference Fountain and WalderFountain and Walder, 1998; Reference Fountain, Jacobel, Schlichting and JanssonFountain and others, 2005a, Reference Fountain, Schlichting, Jansson and Jacobelb; Reference DasDas and others, 2008; Reference Gulley, Benn, Screaton and MartinGulley and others, 2009; Reference Catania and NeumannCatania and Neumann, 2010; Reference Harper, Bradford, Humphrey and MeierbachtolHarper and others, 2010). It is in the analysis of esker patterns on the landscape that Shreve’s contribution to channel theory has been primarily recognized and applied. The first such applications were by Shreve himself (Reference ShreveShreve, 1985a, Reference Shreveb), with many subsequent investigators applying Shreve’s insights (e.g. Reference Clark and WalderClark and Walder, 1994). The method that Shreve used to come up with maps of (paleo)subglacial hydraulic potential has also been used to delineate drainage basins at the bed of extant glaciers and ice sheets (Reference BjörnssonBjörnsson, 1986, Reference Björnsson2003; Reference Vaughan, Corr, Smith, Pritchard and ShepherdVaughan and others, 2008).
R-channel theory has contributed to discussions of sediment entrainment at the glacier bed through freeze-on. Reference RöthlisbergerRöthlisberger (1972, p. 186) recognized that if the glacier bed slopes upward in the down-glacier direction at a steep enough angle – on the down-glacier side of an overdeepened basin, say – the steady-state theory leads to p w > p i sufficiently far upstream. Physically this means that frictional dissipation is not enough to warm the water to the pressure-melting point, and that water must therefore freeze to the channel wall and release latent heat. Generally this is not a stable situation, and alternate drainage configurations include englacial conduits (Reference Hooke, Miller and KohlerHooke and others, 1988) or subglacial gradient conduits along the valley walls (Reference LliboutryLliboutry, 1983), where bed slope is not conducive to freeze-on. It might also be that freeze-on truly occurs, as suggested by some field evidence, and that layers of sediment-laden ice at the glacier bed reflect fluctuating water pressure in subglacial channels (Reference Alley, Lawson, Evenson, Strasserand and LarsonAlley and others, 1998; Reference Lawson, Strasser, Evenson, Alley, Larson and ArconeLawson and others, 1998).
Within a few years of Röthlisberger’s Cambridge presentation and the publication of his and Reference ShreveShreve’s 1972 papers, channelized-flow theory became central to the interpretation of field experiments such as tracer studies (e.g. Reference BurkimsherBurkimsher, 1983; Reference Seaberg, Seaberg, Hooke and WibergSeaberg and others, 1988; Reference Willis, Sharp and RichardsWillis and others, 1990; Reference FountainFountain, 1993) that probed the glacier drainage system. Tracer studies done previously had not had the benefit of a theoretical interpretive framework: for example, Reference StenborgStenborg (1969), who did the first systematic investigation of glacier hydrology using tracers (at Mikka- glaciären and Storglaciären in northern Sweden), demonstrated the existence of an internal drainage divide, and speculated about the geometry of flow paths, but lack of a physically based theoretical framework certainly constrained his interpretations.
Tracer studies provide another sort of historical benchmark, because such studies from about the late 1980s onward invariably include discussion of the contrast between flow in an R-channel network and flow in some sort of more convoluted ‘distributed’ network. The fundamental observation behind this perceived dichotomy is the difference between dye-return curves peaked in time, with relatively high average flow speeds, and dye-return curves smeared out in time and indicative of slow transit (Fig. 3). The channelized/distributed dichotomy can be not only spatial – that is, with different parts of the bed exhibiting different drainage regimes – but also temporal, with the drainage system switching from mainly distributed to mainly channelized as the ablation season progresses (Reference Nienow, Sharp and WillisNienow and others, 1998). Historically, the first sort of distributed drainage system to be considered was the linked-cavity system, comprising a connected network of cavities formed on the down-glacier side of bed irregularities. Reference LliboutryLliboutry (1968) seems to have been the first to suggest that a linked- cavity system might exist, and subsequently detailed mapping of recently deglaciated carbonate bedrock surfaces revealed the complex topology of such systems (Reference Walder and HalletWalder and Hallet, 1979; Reference Hallet and AndersonHallet and Anderson, 1980; Reference Sharp, Gemmell and TisonSharp and others, 1989). The hydraulics of linked-cavity systems was elucidated by Reference WalderWalder (1986) and Reference KambKamb (1987), whose analyses borrow from R-channel theory insofar as they consider competing processes that either enlarge or constrict openings. Cavity theory departs from R-channel theory by taking into account geometrical constraints provided by the glacier bed and the role of glacier motion in enlarging cavities. Having theories for alternate sorts of drainage networks, of course, begged the question of how, exactly, the drainage system could potentially switch between an arborescent R- channel network and a non-arborescent linked-cavity network. Reference KambKamb (1987) showed that large pressure perturbations would destabilize a linked-cavity network and presumably trigger development of an R-channel network, but until the recent work of Reference SchoofSchoof (2010), there was no theoretical framework for understanding the switch from an R-channel network to a linked-cavity network.

Fig. 3. Drainage network morphology and its effect on dye-tracer returns. (a) Idealized plan view of (left) a ‘fast’ arborescent drainage system composed of channels and (right) a ‘slow’ non-arborescent drainage system composed of cavities and other non-R-channel components. After Reference Fountain and WalderFountain and Walder (1998). Reprinted from Reviews of Geophysics by permission of the American Geophysical Union. (b) Records of discharge and dye concentration from experiments conducted at South Cascade Glacier, Washington State, USA, by Reference FountainFountain (1993). Dye return from an injection into the ‘Stream 2’ drainage basin shows a relatively slow onset and a slow decline from the peak, whereas the dye return from an injection into the ‘Stream 3’ drainage basin shows a rapid onset and rapid decline from the peak.
A linked-cavity network is not the only possible configuration for ‘distributed’ drainage at the glacier bed. If the ice is underlain by a fairly continuous layer of sediment, then that sediment may act as an aquifer (Reference Engelhardt, Harrison and KambEngelhardt and others, 1978; Reference ClarkeClarke, 1987). Commonly, however, such subglacial aquifers are not thick enough and permeable enough to convey all meltwater, in which case some sort of channelized drainage is expected to develop. One possibility is the formation of a non-arborescent network of ‘canals’ at the sediment/ice interface (Reference Walder and FowlerWalder and Fowler, 1994; Reference NgNg, 2000). Canal theory (Reference Walder and FowlerWalder and Fowler, 1994; Reference NgNg, 2000) builds upon R-channel theory, but then considers sediment input and removal as well as H2O input and output.
Röthlisberger Channels and the State of Glacier Hydrology in 2010
Reference PatersonPaterson (1969), writing in the first edition of The physics of glaciers, wondered whether channelized drainage existed except near glacier margins. Forty-one years later, direct evidence for R channels remains a rare commodity. A few investigators (e.g. Reference Hubbard, Sharp, Willis, Nielsen and SmartHubbard and others, 1995; Reference Fudge, Humphrey, Harper and PfefferFudge and others, 2008) have collected borehole water-level data that strongly suggest the boreholes either connected directly with low-pressure R channels or reached the bed quite close to such channels. Observations of this sort are atypical, however, probably unsurprisingly so, as the likelihood of a borehole intersecting a conduit is not great.
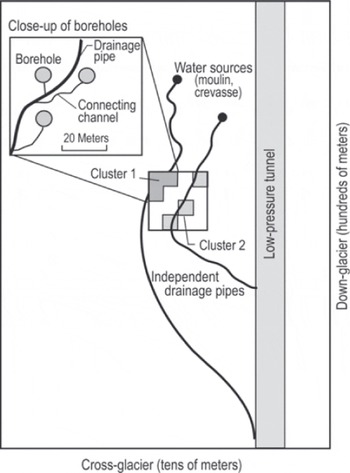
The central theoretical concepts in glacier hydrology, including the R-channel model, emerged from a background of alpine-glacier investigations. Glaciology in 2010 is, relatively speaking, much more focused on ice sheets, but alpine-glacier studies are still refining our understanding of glacier hydrology and providing some surprises. Studies at Bench Glacier, Alaska, USA, are of particular interest because of the extremely dense array of boreholes that has been drilled along the entire length of the glacier. Borehole water-pressure data collected by Reference Harper, Humphrey, Pfeffer, Fudge and O’NeelHarper and others (2005) and Reference Fudge, Humphrey, Harper and PfefferFudge and others (2008) suggest a modification to the usual conception of an arborescent-channel network (Fig. 4): it appears that the drainage system may involve a large, low-pressure channel fed by moulins or crevasses, with small ‘feeder’ channels essentially independent of each other and extending for long distances down-glacier, but very little cross-glacier connectivity. More recent work at Bench Glacier has revealed another unexpected phenomenon: the apparent existence of hydraulically active fractures at the glacier bed (Reference Harper, Bradford, Humphrey and MeierbachtolHarper and others, 2010). The long-term success of Bench Glacier studies no doubt reflects the fact that a core team of investigators has been involved with research conducted there since the early 1990s.

Fig. 4. Conceptual model (after Reference Fudge, Humphrey, Harper and PfefferFudge and others, 2008) of the basal drainage system of Bench Glacier. Low-pressure channels are fed from the glacier surface by moulins. Water in individual boreholes connects to low-pressure channels by small ‘pipes’, which are independent of one another and do not branch.
An important recent research direction in glacier hydrology has been the development of models that integrate R-channel theory with analyses of distributed drainage. These models trace water flow from the surface to the bed and thence to the terminus, with physically reasonable ‘rules’ to represent flow through channelized and distributed components of the drainage system, as well as interactions between those components (Reference ClarkeClarke, 1996; Reference Flowers and ClarkeFlowers and Clarke, 2002a,b; Reference Flowers, Björnsson, Pálsson and ClarkeFlowers and others, 2004; Reference FlowersFlowers, 2008). The rules can be modified to reflect changing knowledge: for example, crevasses factor into the models of Flowers and co-workers as storage units, but as borehole videography has revealed the ubiquity of hydraulically active fractures both englacially (Reference PohjolaPohjola, 1994; Reference Harper and HumphreyHarper and Humphrey, 1995; Reference Fountain, Jacobel, Schlichting and JanssonFountain and others, 2005a, Reference Fountain, Schlichting, Jansson and Jacobelb) and at the glacier bed (Reference Harper, Bradford, Humphrey and MeierbachtolHarper and others, 2010), there may be scope for a model version in which flow through crevasses is represented. These integrated models have been applied to the relatively large-scale problem of jökulhlaups (Reference Flowers, Björnsson, Pálsson and ClarkeFlowers and others, 2004) and have been shown to be promising tools for investigating one of the longest-standing problems in glaciology: the relationship between glacier sliding and basal hydrology (Reference Kessler and AndersonKessler and Anderson, 2004). These integrated models, as well as Reference SchoofBjörnsson (2010) recent contribution on channel/cavity switching, may also provide a path to improving our understanding of what we now know to be the complicated, time-dependent hydrology of ice streams and ice sheets (Reference Fricker, Scambos, Bindschadler and PadmanFricker and others, 2007; Reference PattynPattyn, 2008; Reference Carter, Blankenship, Young, Peters, Holt and SiegertCarter and others, 2009).
Acknowledgements
I am honored to have been asked to write this retrospective, especially as glaciological research has been a distinctly part-time effort for me for many years. Writing this paper was a pleasure, as it gave me the opportunity to revisit some classic scientific literature (including a well-worn copy of the IASH ‘red book’ with papers from the Cambridge symposium) that I first encountered while doing research for my Master’s thesis under the able supervision of Bernard Hallet, himself a student of Ron Shreve. I also thank Andrew Fountain, Bob Anderson and Ian Willis for carefully reviewing earlier versions of this paper. Any oversights or misinterpretations of the historical record are, of course, entirely my responsibility.