Introduction – History and Essence of the Problem

The problem of the surface thawing of glaciers covered with moraine has been discussed in a number of papers (e.g. Reference AvsyukAvsyuk, 1953; Reference Kreiter and TikhanovskayaKreiter and Tikhanovskaya, 1964; Reference TronovTronov, 1966; Reference Dolgushin, Dolgushin, Lebedeva, Osipova and RototayevaDolgushin and others, 1972; Reference KhodakovKhodakov, 1972[a], Reference Khodakov[b]; Reference KonovalovKonovalov, 1979). Correct understanding and description of the physical processes accompanying heat and mass exchange on a glacier surface will permit estimations of alterations to its thermal regime and run-off to be made either under conditions of natural moraine cover or when the surface is blackened by external processes, such as glacier soiling by tephra material after volcanic eruptions and anthropogenic influences.

The main qualitative results of the works mentioned above are as follows. When the thickness of moraine cover is small, of the order of several centimetres, the rate of ice thawing increases. This effect was discovered experimentally (Reference Østremøstrem, 1959) by artificially covering a representative area on a glacier surface with dust. This effect also takes place with snow (Reference Higuchi and NagoshiHiguchi and Nagoshi, 1977). Use of a rather simple model shows (Reference ZotikovZotikov, 1982) that the increase of the thawing rate is related to changes (an exponential decrease during the melting season) in the surface albedo of ice covered by a thin layer of dust. However, moderate thicknesses of moraine cover result in a shielding (armouring) effect; the ice thawing rate decreases and when the thickness of moraine reaches about 1.5–2 m melting practically ceases (Reference Dolgushin, Dolgushin, Lebedeva, Osipova and RototayevaDolgushin and others, 1972). Experimental data obtained from glaciers in the Caucasus and in Central Asia, which have been summarized by Reference Khodakov(Khodakov (1972[a]) and Reference Dolgushin, Dolgushin, Lebedeva, Osipova and RototayevaDolgushin and others (1972)), show a hyperbolic dependence between the thawing rate decrease and moraine-cover thickness. A theoretical basis for this relationship was given by Reference Khodakov(Khodakov (1972[a]), who obtained an approximate solution for the stationary heat conduction equation within the moraine layer. More recently, some theoretical attempts have been made to construct the curve describing the variation in ice thawing rate over a wide range of moraine thicknesses. This has been done by using a quasi-stationary model of the interaction between solid, liquid, and gaseous phases (Reference DenisovDenisov, 1980), and also by proceeding from purely geometric considerations concerning the shape of the curve (Reference KonovalovKonovalov, 1979). Reference Khodakov(Khodakov (1972[b]) also gave an approximate description of the non-steady problem.

A complete theoretical treatment of the non-steady thawing of ice containing particles of morainic material does not yet exist. This paper gives such a treatment and applies the model to Djankuat glacier, a high-alpine valley glacier of the Central Caucasus. In addition, quantitative relationships characterizing the effect of the most intensive glacial thawing under debris cover are obtained. Thoughts about the advisability of employing this effect for the artificial adjustment of summer glacier run-off in different regions are given and some practical recommendations are also presented.

On the Formation of Moraine Cover

Superficial moraines on mountain glaciers form as a result of three processes: the deposition of colluvial material on the glacier surface, the melting-out of englacial moraine, and the widespread development of thrust moraines (transfer of debris from the glacier bed to the surface along shear planes). The formation of medial moraine is a particular case of the first or second formation mechanism depending on whether the convergence point of glacier tributaries is above or below the firn line.

Moraine cover, i.e. a form on a glacier where concentrations of debris do not manifest themselves as strongly pronounced lengthwise relief features but cover the snout surface by a continuous lithogenic envelope, may arise as a result of any of the three mechanisms mentioned above.

The most frequent type of continuous moraine-cover formation is caused by the confluence of a number of medial moraines or the junction of medial moraines with lateral ones. Both of these types of moraines are usually well pronounced in glacial relief as longitudinal ramparts. However, proximity to a glacier terminus and slow ice-flow velocities induce the sprawling of moraine ramparts; in their axial parts, where debris thickness is greatest, one can observe the near cessation of ice thawing. However, as adjacent areas of clean ice lower progressively and the steepness of lateral slopes and the relative height of the rampart increases, lithogenic material undergoes gravitational re-distribution. Debris accumulates along the foot of the rampart, so that the flank steepness tends to its angle of natural repose. The strips of clean ice between adjacent ramparts gradually taper off and sometimes completely pinch out. The closer the ramparts, the sooner this pinching out occurs, and this is therefore especially characteristic of large glaciers with a complicated structure in their upper reaches and with long and narrow snouts. Afterwards, the relief vanishes, since morainic material accumulating between the ramparts creates an armouring envelope while debris slipping down the flanks of the ramparts periodically exposes the substrate ice, which resumes its melting. Thus, the superficial moraine plays the role of a self-developing system tending towards the minimization of relief, and the transformation of linear features into a continuous debris envelope.

Of course, explaining the formation of moraine cover solely as a result of the confluence of several medial moraines is too simplistic. On some glaciers, a significant role is played by ablation moraine, and a continuous cover arises from the areal melting-out of debris dispersed randomly inside a glacier body. However, the existence of a continuous moraine cover seems to be a characteristic feature of the retreating phase of large glaciers and essentially governs mass and heat transfers in their lower reaches.

The processes of debris thawing out from glacier ice is described below. For simplicity, the composition of the moraine cover is supposed to be homogeneous.

Formulation of the Problem

The mathematical problem of moraine thawing out of debris-containing ice is now formulated.

Let μ be the bulk debris concentration in the uniform ice debris. Attention is confined to the one-dimensional case neglecting horizontal effects. Such a schematization is applicable provided the horizontal dimension of the object is much greater than the vertical one, i.e. the moraine layer is relatively thin. The coordinate z is directed downwards (Fig, 1), the origin being coincident with the initial surface of the debris-containing ice layer. After thawing out, the debris-bearing layer has a thickness

where z = ξ(t) is the position of the phase boundary of ice melting, p is the porosity of the debris cover, and t is the elapsed time. The process of debris consolidation is not examined here; the moraine is assumed to remain homogeneous in time and therefore the porosity is constant. Melt water is also assumed to leave the moraine layer practically instantaneously. The latter assumption can be justified for two reasons: first, the process of thawing out is too prolonged for melt water to trickle down the glacier slope; secondly, natural observations show that the debris layer throughout its thickness does not contain free water, except as a thin film at the contact with the ice. The moraine and the ice-moraine are assumed to be devoid of heat sources.

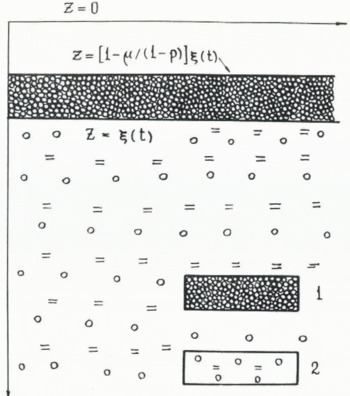
Fig. 1. The coordinate system for the problem. 1, moraine; 2, ice.

The temperature T _m within the moraine layer is governed by the heat-transfer equation

Here, C _m, ρ_m, and λ_m denote the specific heat, density, and heat conductivity of the debris cover, respectively, and t is time.

The temperature T of the debris-containing ice is also determined by the heat-transfer equation

Thermophysical parameters in Equations (2) and (3) can be estimated from the volume-weighted averages of the corresponding constituent parameters, i.e.

where symbols with subscripts i correspond to pure ice, g to debris material, and a to air.

We now define the boundary conditions for the problem. On the upper boundary of the moraine cover the heat flux can be set as

where q_j (j = 1–4) are heat fluxes caused by solar radiation, evaporation/condensation, radiation from the surface and convective heat exchange with the air, respectively. More detailed estimates of these terms are given below.

The lower boundary of the moraine z = ξ(t) represents a phase boundary. Two conditions are set on this boundary: the temperature at ice melting-point T _h and a condition that defines the movement of the boundary itself (Reference Tikhonov and SamarskiyTikhonov and Samarskiy, 1972)

where Q is the latent heat for the phase transition and the square brackets signify the jump in heat flux at the phase boundary. Equation (6) shows that the rate of movement of the phase boundary in debris-containing ice depends only on the difference between the heat fluxes across the interface.

The layer of debris-containing ice is assumed to be infinitely thick, and so the condition

is set.

Since the thermal problem is evolutional, the initial state has to be fixed. Let us assume that initially the moraine layer is absent, i.e. the whole area z ⩾ 0 corresponds to the uniform mixture of debris and ice with constant temperature

The third condition in Equations (8) requires that the initial heat flux on the free surface of debris-containing ice be given.

Equations (1)–(8) completely define the mathematical problem of debris thawing out of ice. This problem is non-linear by virtue of the second condition in Equations (6). Its solution also permits the determination of the ablation rate immediately beneath the moraine; from Equations (6) it can be found to be

In the particular case when T _i = T _h = 0°C (debris-containing ice is at its melting point), the formula cited by Reference Khodakov(Khodakov (1972[b])

can be obtained from Equation (9).

This formulation of the equations governing the thawing out of debris from ice and its concentration on the surface can be extended by altering Equation (1) to take into account the mass influx of debris material from outside or its outflow as a result of slipping:

where h _int is defined by Equation (1) and the function h _ext represents external sources of debris.

Before proceeding further, it is necessary to consider in more detail the heat transfer at the free surface. We estimate the orders of all the terms on the right-hand side of Equations Equation (5) and (8); to that purpose we deduce formulae for each summand.

The heat influx to the surface due to solar radiation is defined by

Here, Q _s is the total radiation flux (direct plus scattered solar radiation) and α_m is the moraine albedo. As a rule, in a high mountain belt, Q _s reaches a value of about 120 Wm⁻²

The remaining terms are evaluated relative to q ₁ The heat flux caused by evaporation and condensation, q ₂, comprises a relatively small part of the total radiation flux, no more than 10% (Reference KotlyakovKotlyakov, 1968; Reference LebedevaLebedeva, 1972), and therefore this term is disregarded in Equation (5).

The heat flux caused by radiation from the surface, q ₃, is determined by the following expression on the basis of heat-transfer theory (Reference Mikheyev and MikheyevaMikheyev and Mikheyeva, 1977):

in which T _a is the air temperature measured here in degrees absolute (as is T _m); σ_o is the emission coefficient of an absolutely black body which equals 5.67 × 10⁻⁸ W m⁻² K ⁻⁴; ϵ is the reduced degree of blackness of the system “gas-solid boundary” that is defined in thermal physics as

where ϵ _a and ϵ _m are the degrees of blackness of gas and boundary correspondingly. The degree of blackness characterizes the total or integral emission of a body embracing all wavelengths: 0 ⩽ ϵ ⩽ 1 (1 is the degree of blackness for an absolutely black body) (Reference Mikheyev and MikheyevaMikheyev and Mikheyeva, 1977). For solid non-granular materials, the degree of blackness is usually ϵ _m ≈ 0.5–0.6; for the air, ϵ _a depends on the spectral degrees of blackness of its components and for usual temperatures does not exceed 0.1, subject to water-vapour content. Consequently, from Equation (13), the reduced degree of blackness

Since the difference between air and moraine temperatures does not exceed 20 deg, the term in Equation Equation (12), using these parameter values, is only a few per cent of q ₁. Hence heat flux caused by radiation is negligible when temperatures are low.

The last term in condition (5) describes the convective heat exchange at the system gas–boundary interface. Heat flux is represented by

where b is the eddy-heat emission factor defined as (Reference Mikheyev and MikheyevaMikheyev and Mikheyeva, 1977)

In Equation (15) Nu signifies the Nusselt number, which defines the intensity of convective heat exchange between the body surface and the gas stream; λ _a is the heat conductivity of the gas; and l is the characteristic size of the surface the gas is flowing past. When the gas flow past the solid surface is turbulent, the Nusselt number is defined as (Reference Mikheyev and MikheyevaMikheyev and Mikheyeva, 1977):

Here, Re is the Reynolds number which depends on the characteristic gas velocity w, the characteristic size l, and the kinematic viscosity of the gas ν (Reference Mikheyev and MikheyevaMikheyev and Mikheyeva, 1977)

Taking an average wind velocity over the glacier surface, w = 5 m/s, the characteristic size of the moraine surface l ⩾ 100 m, and assuming that at a temperature of about 10–20°C the heat conductivity, λ_a, is equal to 0.024 Wm⁻¹ deg⁻¹, and its kinematic viscosity (Reference VagaftikVagaftik, 1963), one can obtain from Equations (15)–(17) that

When |T _a-T _m|≈ 10–20 deg, the term in Equation (14) has the same order of magnitude as the first term in Equation (11), as in Equation (5).

Thus, retaining the dominant terms in Equation (5) leads to the relationship:

It should be noted that a similar expression is cited in Reference Khodakov(Khodakov (1972[a]) for the approximate computation of heat flow through a moraine surface, but Khodakov’s formulation uses too many undetermined parameters to be useful.

The initial condition in Equation (8) is simplified in the same way:

α here denotes the debris-containing ice albedo, i.e. initially the heat flux on the free surface is defined by thermo-physical parameters of the initial mixture of ice and moraine; after the appearance of the first elementary debris layer (ξ(t) > 0), heat flux on the free surface is also affected by the moraine properties. In reality, such an abrupt jump could not occur because the surface albedo changes gradually from the value α representative of debris-containing ice to the value α _m representative of moraine cover. Field observations indicate that the albedo of debris-containing ice decreases with the increase in the concentration of lithogenic matter. The dependence of the glacier-surface albedo on the weight content of fine-grained matter and on the fractional coverage by spheroidal particles has been investigated by Reference Tikhanovskaya(Tikhanovskaya (I970[b]) and Reference Zotikov(Zotikov (1982)), respectively. It would appear that the albedo of a surface with a moraine cover can be defined as a function of cover thickness h including in it dependence on debris concentration and also on the degree of blackness by the following relationship:

Here, γ is the albedo decrement which has to be determined empirically and α_g is the albedo of morainic material. The dependence of α_m on debris-layer thickness h is shown in Figure 2.

Fig. 2. Surface-albedo dependence on moraine-cover thickness.

Consequently, the initial condition in Equation (20) that defines heat exchange on the surface, with Equation(21) taken into account, enters into the condition in Equation (19); similarly, λ _m should be expressed in a form similar to Equation (21):

where the prime corresponds to the moraine layer. This equation is supposed to exclude the jump in the thermal diffusivity in Equation Equation (19). The exponential coefficient γ in Equations (21) and (22) is the same for simplicity.

The initial condition can now be simplified to the following expressions:

Hence, the final formulation of the problem of thawing-out of moraine-bearing ice comes to a Stephan-type non-linear problem consisting of Equations (2) and (3) with defining expressions in Equations (1) or (1a), (4), (21), and (22), boundary conditions in Equations (6), (7), and (19), and the initial condition in Equation (8a). The eddy heat-transfer coefficient is determined with the help of formulae (15)–(17) that give the opportunity to take temporal changes into consideration if the necessary meteorological data are available.

The proposed system of equations and expressions is closed and represents a one-dimensional mathematical model describing the process of thawing-out of moraine-bearing glacier ice and debris-cover formation on its surface.

Djankuat Glacier and Derived Parameters of its Debris Cover

The non-steady mathematical model of debris-cover formation was applied using numerical techniques to the valley glacier of Djankuat (Dzhankuat).

This glacier is one of the best explored mountain glaciers in the U.S.S.R. Glaciological investigations began here in 1965 and have continued uninterrupted from 1968 up to the present. Djankuat glacier was chosen as a representative I.H.D. basin for the Central Caucasus. Besides the glaciological observations, a vast complex of hydrological, meteorological, geophysical, and other kinds of research was also established there with the main purpose of determining the mass, liquid, and heat balances. The raw factual data obtained here are sufficient to evaluate all input parameters to the model.

Djankuat glacier Fig. 3 is situated on the northern slope of the Great Caucasus central section. It occupies an area of 3.2 km² and flows north-west from the main Caucasus Range; its length is 3 km (Reference BoyarskiyBoyarskiy, 1978). The subglacial bed of Djankuat glacier is complicated by rock ledges that give its longitudinal profile a stepped character. Because they are subjected to erosion, these ledges serve as a principal source of subglacial moraine. The glacier flow can be divided into three main branches with independent catchments. The contact zone between adjacent tributaries is marked by medial moraine ramparts. The left-hand margin of the snout in particular is covered by a continuous envelope of debris on the final kilometre of its length.

Fig. 3. Djankuat glacier. (Photograph by E.A. Zolotaryov.)

At present, Djankuat glacier, like the majority of Caucasian glaciers, is retreating but the rate of retreat has been decreasing slightly in the last decade. Growing piles of debris on the snout surface can be seen, as is typical of the retreat phase. The total area occupied by the debris cover increased from 0.10 km² in 1968 to 0.22 km² in 1983. The appreciable fraction (6.9%) of superficial moraine over the total glacier area, as well as a number of special investigations undertaken in 1982–83, led to the choice of Djankuat glacier as a convenient natural object for validation of the mathematical model.

As was shown in the previous section, solution of the equations that determine the influence of debris cover on heat exchange near the glacier surface requires the determination of a large number of parameters.

Debris Thawing-Out

To investigate changes in debris-cover thickness with time and the influence of moraine on ablation rate, a series of numerical calculations, using the formulation described in the section previous but one, were undertaken. Calculations deal only with that part of the ablation period after the disappearance of the seasonal snow cover on the snout, i.e. during the 3 months from 15 June to 15 September, thus dealing solely with melting of glacier ice.

For comparison, computations using a formulation based on an assumption of quasi-stationary temperature distributions within the moraine layer were also made. This assumption contradicts the non-steady nature of Stephan problems which arises as a result of the phase-boundary transition condition (6). The assumption may be admissable if the rate of establishment of the thermal regime in the moraine considerably exceeds the rate of moraine-thickness change, which is related to the movement of the phase boundary, i.e. if

For values of thermophysical parameters of debris cited in Table III and an ablation rate of approximately 4 m per melting season of mean length of about 3 months, the condition (23) is observed even for rather high values of h. It should be borne in mind, however, that the establishment of a stationary thermal regime in the moraine is quite impossible even at the end of the ablation season owing to temporal fluctuations in the insolation and the air temperature.

The ablation rate under the moraine layer a_m can be computed by

if the function h(t) is known. In the case of a quasi-statinary regime, balance ratios give:

This expression, with the initial temperature of debris-containing ice T _i = 0°C, is identical to that cited by Khodakov (1973[a]). Equation (25) allows for properties of already formed moraine cover after the initial stage of its development. Use of Equation (25) in the limit when h → 0 is incorrect if the moraine albedo does not tend to the ice albedo continuously. Use of Equation (21) permits analysis of the dependence of a _m on h.

The values of input parameters cited in Tables II and III were used for calculations with the proposed model which were done on a computer. Besides using the inferred debris concentration μ = 0.12% evaluated for Djankuat glacier, other cases where μ was set to 0.5%, 1%, and 5% were also run, bringing to light some of the thermophysical features of the debris thawing-out process.

An explicit numerical method with a non-uniform grid was used for calculations. The grid is deformable to take account of ice melting. This method is convenient for calculation of a Stephan-type problem with moving boundaries (Reference Grigoryan, Grigoryan, Krass, Lovchuk and MikhaylovGrigoryan and others, 1982).

Figure 4 illustrates the temporal dependence of moraine-cover thickness h as a result of this process. For comparison, model results based on the quasi-stationary temperature formulation are also plotted using dashed lines. This formulation, using Equations (24) and (25), requires step integration

where ∆t is the time step. Figure 4 shows that the quasi-stationary formulation underestimates h, the deviation increasing in time. However, the relative deviation between stationary and non-stationary solutions declines with µ and elapsed time. As calculations show, every curve has an inflection point near the start; this point corresponds to the critical value

that coincides with the maximum rate of increase of the debris-layer thickness and hence of the sub-moraine ablation rate α_m. The value h _cr conforms to observed effects of ablation intensification beneath the moraine layer (Reference Østremøstrem, 1959; Reference Kreiter and TikhanovskayaKreiter and Tikhanovskaya, 1964; Reference KreiterKreiter, 1965; Reference KamalovKamalov, 1967; Reference Dolgushin, Dolgushin, Lebedeva, Osipova and RototayevaDolgushin and others, 1972; Reference KhodakovKhodakov, 1972[a]; Reference Demchenko and SokolovDemchenko and Sokolov, 1982). The time elapsed until h _cr is reached diminishes with the concentration. For a debris concentration of µ = 0.12% (Djankuat glacier case), h_cr is attained by the third year; in 30 years the thickness of the moraine layer caused by debris thawing out should reach ~30 cm, which is accompanied by deceleration of moraine-cover growth. Its growth sharply increases with increase of µ; thus, when µ = 1%, the half-metre thick moraine layer is reached after 12 years, but when µ = 5% it takes only 2.5 years. The computation suggests that the stabilization of debris-cover thickness occurs when

Fig. 4. Moraine-cover thickness dependence on time. I, non-steady solution; II, quasi-stationary solution. 1, 2, 3, and 4 correspond to µ = 0.12%, 0.5%, 1%, and 5%.

The dynamics of debris-cover growth are connected intimately with the sub-moraine ablation rate. The temporal relationships of α_m are shown in Figure 5. Use of Equation (21) relating surface albedo to moraine-layer thickness is shown to lead to the appearance of maxima corresponding to a moraine thickness of 2–3 cm. When µ rises, these maxima move to the left, i.e. the time required to reach them decreases. Diminution of the sub-moraine ablation rate with the growth of h is due to the shielding effect of the debris cover which is also affected by its relatively low heat conductivity. The dashed line marks the ablation rate for clean ice in the melting season. This quantity can be estimated from the balance equations, so:

where t ₀ and t ₁ are the beginning and the end of the ice ablation season. Results using Equation (27) for conditions appropriate to Djankuat glacier give an average seasonal ice-ablation rate

Thermal shielding of the debris cover begins when the sub-moraine ablation rate decreases back to a_i . The equivalent time elapsed until the beginning of the shielding effect, t _e, diminishes abruptly with increases in the debris concentration. Thus, when µ = 0.12% (Djankuat glacier case) corresponds to t _e = 8 years but for µ = 5%, t _e = 0.6 years only. The dependence of the equivalent time on µ is shown in Figure 6. These results are extremely interesting because by estimating the debris concentration in the ice it is possible to estimate the time span during which an augmentation of liquid run-off from a glacier should be expected. Furthermore, when t > t _e, the shielding stage commences. In this way, a glacier covered with a well-developed moraine envelope serves as a self-controlling system with respect to run-off under natural conditions.

Fig. 5. Sub-moraine ablation-rate dependence on time. I, curves α_m(t); II, ablation rate a _i on a clean-ice surface. 1, 2, 3, and 4 correspond to µ = 0.12%, 0.5%. 1%, and 5%.

Fig. 6. Equivalent time t_e dependence on debris concentration.

During the shielding stage the development of the moraine cover leads to a rapid diminution of sub-moraine ablation. This effect can be observed not only in Figure 5 but also in Figure 7 where the temporal dependence of the relative sub-moraine ablation rate is illustrated. For glaciers with a comparatively small debris content, it takes rather a long time to achieve the self-armouring effect and there is a relatively slight decrease in the surface ice-melting rate later on. When the debris content is high (µ > 1%), thermal development evolves rapidly; the self-armouring effect is reached in the first few years and is followed by the formation of a thick debris cover, and in 20–30 years by the practical cessation of sub-moraine ablation due to atmospheric heat penetration.

Because of the faint thermal inertia, the maximum of a _m/a _i higher for small values of µ than for high concentrations; thus, when µ = 0.12% the maximum sub-moraine ablation rate is 1.35 times higher than the ablation rate for clean ice. This ratio decreases considerably with increases in µ. In other words, debris concentration appears in the role of a regulator of not only the duration of augmentation of the glacial run-off period but also of the amplitude of this augmentation.

Fig. 7. Non-dimensional ablation rate a_m/a_i dependences on time (lower scale) and on moraine-cover thickness for the Djankuat glacier case with µ = 0.12% (upper scale). 1, 2, 3, and 4 correspond to µ = 0.12%, 0.5%, 1%, and 5%.

Figure 8 shows curves for temperature against depth for different seasons, e.g. in the thirtieth year after the commencement of debris thawing out when the concentration µ = 1%. It is clear that the temperature does not become fixed in the upper 80 cm corresponding to the moraine layer. In the ablation season, by 15 August (curve 1) the moraine surface is heated up to 16 °C, more than twice the average monthly air temperature (see Table II). A seasonal heat wave moving through the moraine cover pushes the winter cold wave downward and creates a temperature maximum in the ice. A similar phenomenon has been observed for the migration of the lower limit of the seasonal thawing layer within the permafrost zone (Reference Grigoryan, Grigoryan, Krass, Lovchuk and MikhaylovGrigoryan and others, 1982). In winter, the moraine temperature is below zero (curve 2). Both temperature curves join up in the ice at a depth of about 8 m, where seasonal fluctuations fade away. For Djankuat glacier, in the thirtieth year of debris thawing out the summer temperature of the surface ~30 cm moraine cover is about +10 °C; due to the relatively small moraine-cover thickness, the major part of the heat supply in summer is expended on sub-moraine ablation, as is evident from Figures 4, 5, and 7.

Fig. 8. Moraine- and ice-temperature dependence on depth, for µ = 1%. I. temperature curves with depth; II. lower limit of debris layer. 1. temperature by 15 August; 2. temperature by 1 March.

All the calculations using a value of µ = 0.12% match well with observations from Djankuat glacier. Thus, the mean thickness of moraine cover formed during 1968–83 on the representative area was found to be 13 cm according to the direct moraine survey, while from Figure 4 after 14 years the accumulated debris layer is computed to be 13.3 cm thick. Furthermore, direct stake measurements of sub-moraine ablation over the representative area where debris thickness was about 12 cm showed a 10% decrease in ablation relative to the adjacent areas of clean ice; a _m/a _i is found to be equal to 1 in areas where the debris cover is about 8 cm thick. Both of these results agree with Figure 7 (curve 1) quite well with only a slight tendency towards overestimation of values of a_m/a_i . Figure 8 illustrates the considerable attenuation of seasonal temperature fluctuations to practically zero below 7–8 m. Stabilization of negative T _i values in the lower horizons to within a few tenths of a degree as was indicated by bore-hole thermometry. Hence, the proposed model may also be used in a predictive mode, in the first instance for mass-balance calculations on glaciers.

The Shielding Role of the Debris Cover

When its thickness increases, the moraine cover on the ice surface begins playing the role of a heat screen (when t > t _e). The growth of the debris-layer thickness leads to the expansion of the frequency spectrum of oscillations caused by external heat influences that attenuate within it. An harmonic air-temperature wave with a frequency ω

is known to cause thermal perturbations in an homogeneous medium with a free surface (Reference Tikhonov and SamarskiyTikhonov and Samarskiy, 1972):

where k = λ/cp is the thermal diffusivity of the medium. As can be seen from Equation (29), the attenuation decrease defines the depth h* of the medium layer at which the amplitude of an initial wave diminishes by a factor of e:

Using the thermophysical parameter values listed in Table III for granitic moraine in Equation (30) daily temperature oscillations (ω = 2π/24 h⁻¹) fade out strongly in a debris layer of thickness

Seasonal oscillations of external genesis (ω = 2π/2160 h⁻¹) fade out in a layer of thickness

Annual temperature oscillations (ω = 2 π /8720 h⁻¹) fade out in a moraine layer of thickness

Estimates from Equations (31)–(33) depend considerably on the moraine thermal conductivity determined with the help of formulae (4); in the Djankuat glacier case it is equal to 1.6 W m⁻¹ deg⁻¹. If moraine consists of macro-clastic material, λ_m may be much higher and then the corresponding values for Equations (31)–(33) should be increased by 20–25%. A debris layer of several metres thickness thus isolates the underlying ice from the thermal influence of the atmosphere almost completely. Nevertheless, even in such cases, sub-moraine ice melting during the summer season may occur because of the filtration of melt and rain water through the debris cover. According to various hydrological estimates, the rate of water filtration through different materials, including coarse-grained materials with high permeability, does not exceed 0.005–0.01 m/s under low heads. Then, according to Equations (14) and (15), and using a kinematic viscosity for water of ν = 1.3 × 10⁻⁶m²/s (Reference VagaftikVagaftik, 1963), sub-moraine ablation caused by heat transfer by filtering melt water with temperature ~0.2 °C comes approximately to 0.05 m per Summer season of about 3 months. This value does not exceed 2% of the seasonal ablation rate from a clean ice surface as in Equation (28). After a time the thick debris cover consolidates and densifies which is accompanied by granulometric fractionation (Reference SmallSmall, 1983). Thus, the moraine roof insulates the ice not only from heat but also from rainfall. Indeed, the existence of buried and stagnant glaciers through dozens and hundreds of years would not be possible without this effect.

So, the thawing out of ice from a moraine serves to “self-armour” Reference Khodakov(Khodakov, 1972[a]) a glacier during its thermal evolution. Debris cover, acting as a heat screen, cuts off separate glacier surface sections from participation in the thermal evolution and also promotes its insolation from mechanical activity.

The glacial degradation leads to geomorphological levelling of parts of the glacier surface shielded by moraine. At first, they differ from other glacier areas as they look like raised areas armoured by the debris cover and afterwards like insulated ice having no connection with the dynamics of the main glacier. Such features may be classified as dead ice (Reference ShumskiyShumskiy, 1955; Reference VtyurinVtyurin, 1981).

Glacier advances lead to the burial of stagnant glacier parts and to the formation of dead-ice cores inside the glacier body. Such cores, in Shumskiy’s opinion, may even play the role of a bed over which a glacier moves. Furthermore, under certain conditions, dead-ice cores may turn into a stage of “buried glacial ice” (Reference VtyurinVtyurin, 1981) with changes in texture and structure Reference Shumskiy(Shumskiy, 1955). That stage can last a rather long time, of the order of thousands of years.

As was mentioned above, morainic “armour” is able to preserve buried ice from rainfall of usual intensity; anomalous showers considerably exceeding the precipitation norm may still move the debris cover away. Thus, on 18–19 July 1983, extremely intense showers in the Caucasus caused many mudflows that caused slumping and mudflow removal of the thick debris cover from stagnant parts of the marginal moraine ramparts of Djankuat glacier dating back to the maximum of the Fernau stage (seventeenth century), and from the steep part of the terminus. As a result, these processes exposed buried ice of azure hue which resumed thawing at its surface.

Blackening of a Glacier Surface

One of the most important aspects of glacial activity in the alpine zone is liquid run-off. This is governed in the summer mainly by ablation from glacier surfaces. Due to the irregular distribution of morainic matter within the ice and on its surface, the ice-thawing rate can vary greatly over a glacier. Here, technical and scientific problems arise concerning the influence of glacier-surface blackening on the augmentation of its run-off and the economic impact of this effect. These problems are closely connected with the question of an artificial influence on natural objects which is itself within the bounds of general problems of the rational utilization of natural resources and the protection of the environment.

In order to estimate the sub-moraine ice-thawing rate, let us use the quasi-stationary approximation for the thermal regime in the moraine layer; in this case, the ablation rate is expressed by Equation (25). Assuming that all the absorbed radiation is used only for melting, the clean ice-thawing rate a _i is defined by

For the values cited in Table I, a_m/a_i = 1.3–1.5, i.e. the maximum sub-moraine ablation rate can be one and a half of that for clean-ice surfaces (Fig. 7). On high-latitude and high-mountain glaciers, where the total solar radiation Q_s is relatively high and the air temperature T _a in summer is low, the ratio a _m/a _i can be still higher, reaching 2–3 for snow-covered surfaces with a very high albedo.

Aspects of the artificial blackening of a glacier surface can now be discussed. In this case, the cover thickness generally is so small that the thermal state within the layer can be ignored; instead we let the free surface have the same albedo α_c as the covering material. Then the ablation rate a_c is calculated according to a formula similar to Equation (34) and the ratio a_c/a_i is determined by the expression:

Suppose that a black substance with a very low albedo α _c << 1 is distributed over the clean-ice surface. In this case Equation (35) becomes:

Ablation will thus be augmented by artificial blackening when the following natural conditions are observed:

1. The surface-ice albedo under natural conditions should be comparatively high. Glaciers in high-latitude and high-mountain zones with solid precipitation during the summer seasons satisfy this condition.

2. Air temperature should be rather low; this is found in alpine belts.

3. Shearing in the wind flow promoting convective heat exchange between the ice surface and the air should be relatively small. This factor depends mainly on local meteorological conditions, the topography, and the orography of the non-glacierized area.

Proceeding from these conditions, it is possible to subdivide existing alpine glacierization into separate areas with respect to their potential run-off augmentation arising from artificial surface blackening. If multi-year average distributions of the parameters of formula (36) in the ablation season (say, decade means) are known, the prediction of expected glacial run-off augmentation can be made by using

where R _c and R _i are the liquid run-off volumes from the unit area during the ablation period for blackened ice and clean ice, respectively; N is the number of time steps ∆t _k comprising the ablation period; the bar denotes values averaged over the corresponding time span ∆t _k. Equation (37) may be used as a basis for dividing glacierization into areas of differing potential for liquid run-off augmentation caused by blackening.

In previous papers Reference Avsyuk(Avsyuk, 1953; Reference Kreiter and TikhanovskayaKreiter and Tikhanovskaya, 1964; Reference KreiterKreiter, 1965; Reference KamalovKamalov, 1967; Reference TikhanovskayaTikhanovskaya, 1970[a]), blackening has been discussed in terms of surface soiling or distribution of thin layers of dust or powdery matter with a low albedo over a glacier surface. Such experiments have been carried out (Reference Kreiter and TikhanovskayaKreiter and Tikhanovskaya, 1964; Reference KreiterKreiter, 1965) but this method is of limited effectiveness for the following reasons. First, the soiling process is difficult to execute when the substance has to be dispersed from a helicopter. Secondly, because of the peculiarity of highland conditions, it is almost impossible to ensure effective distribution of the blackening substance over large areas since the major part of the substance is carried by wind beyond the glacier limits and on the glacier itself the black cover has an extremely irregular thickness. Thirdly, in melt seasons, the blackening substance is removed by surface streamlets very soon after its deposition, meaning that its influence is only transitory. Fourthly, the distribution of the blackening layer with a thickness of even 1 cm over sufficiently large areas demands an enormous mass of the blackening substance and consequently titanic volume of aircraft work. For example, blackening over 1 km² of a glacier surface by a substance with a density ρ _b = 1000 kg/m³ would require 10⁴ tonnes of such a substance!

However, there is another method of blackening the glacier surface – that of spreading a thin plastic film. Such a film must be purpose-made and possess the following qualities. It must be durable, thin, black, and it must adhere well to an icy surface. The first two requirements are quite feasible since the technology for manufacturing thin and durable film exists. The third one may be fulfilled by using soot as a filler in the manufacturing process. The fourth requirement is indispensable so as to prevent the film from warping and parting from the ice under wind action. This requirement may be easily satisfied by producing a film of wettable material, in which it will adhere to the ice by surface-tension forces arising as a result of the presence of melt water acting on the bottom surface of the film.

The thinness of the film permits a considerable reduction in the expenditure on material required for blackening glacier surfaces. The covering for an area of 1 km² by a film 50 µm thick and with polymer density ρ _p = 1200 kg/m³ would weigh only 60 tonnes. This can be manufactured in the form of separate rolls; a single roll of such a film 2 m wide and 300 m long should weigh about 20 kg. Helicopters could easily deliver such rolls to places where they are needed on the chosen glacier, and then specially trained teams of mountaineers and glaciologists would be able to spread the film cover over the surface. Here the problem of fastening film edges at some points so as to avoid slip arises, but it is technically surmountable without any particular trouble.

The film thinness also allows the short-wave part of the solar spectrum to penetrate through it and hence to increase the effect of insolation on ice thawing.

An absolute run-off value calculation of superficial ablation beneath the film over an area S can be made, according to Equation (37) with the expression

For instance, film blackening of an area 1 km² with initial surface albedo α ≈ 0.4–0.5, when average insolation is approximately 230 W m⁻², b = 12Wm⁻²deg⁻¹ and T _a = 5°C, leads to doubling of the ablation (in comparison with clean-ice ablation) during a melting season of 100 d long and produces an extra 5 ×10⁶ m³ of water. A common irrigation requirement for agriculture is ~1 m/m² per season Reference Kharchenko and Shestakov(Kharchenko, 1981); this quantity of water should be sufficient for watering an additional area of 500 ha.

The suitability of a glacier for artificial blackening of its surface is constrained by the requirements of environmental protection. Briefly, these requirements can be formulated as: preservation of the affected object; maintenance of mudflow security conditions; preservation of channels of mountain streams.

These conditions show the preliminary work that needs to be done before the development of plans for the artificial augmentation of ablation. In particular, it is desirable to affect simultaneously relatively small areas of a number of glaciers so that fluctuations in the run-off from each glacier do not differ greatly from the natural discharge of their rivers. The total effect of obtaining the additional volume of melt water in these cases should not cause a strongly marked divergence from natural equilibrium conditions. In order to retrieve ice resources on affected glaciers, objects that can be influenced by engineering work may be changed or alternated from season to season.

Conclusions

A non-steady mathematical model of debris thawing out on to the surfaces of mountain glaciers has been formulated which can be used not only for the estimation of possible run-off augmentation from glaciers in different regions, but also for predicting moraine-cover evolution and sub-moraine ablation due to climatic changes over 30–50 years. Further development of the model requires the representation of additional processes affecting the moraine-cover thickness. These are due first to mass influx from valley walls, marginal moraines, and mass outflow due to debris sliding along the ice surface, and secondly to the re-distribution of morainic mass with glacier movement Reference Khodakov(Khodakov, 1974). Here, a coupled problem relating debris thawing out and glacier surface-layer kinematics has to be solved because the velocities of ice ablation under the moraine and debris-particle displacement along the surface are comparable.

It ought to be emphasized that all the processes mentioned are essentially non-steady. Also, for a glacier as a whole, it is advisable to consider three-dimensional formulations in order to ascertain the influence of non-uniformity not only on debris concentration but also on glacier-surface velocities; non-uniformity of moraine content with depth is also of importance.

Finally, the effect on sub-moraine ablation and, consequently, glacier run-off “self-control” or “self-armouring” by debris-cover development Reference Khodakov(Khodakov, 1972[b], Reference Khodakov1974) is delicate enough to show how complicated glaciological objects are and at the same time how susceptible they are to any kind of exterior, and in particular anthropogenic, influence.