Introduction
Ice, like other materials, can sustain damage in the form of non-propagating cracks that result from irreversible, localized strain. This kind of damage interests us because it alters the properties and behavior of the ice, which are important to understand for engineering applications, as well as for insight into the underlying physics of materials. One of the challenges in advancing this understanding is the difficulty of quantifying damage. Before we review various ways to measure damage, suffice it to say that they typically involve some laborious task of counting cracks. If we know that the presence of cracks changes certain material properties that are more readily measurable, to what extent can we rely on those properties instead to quantify the damage? This question (as it pertains to elastic properties in damaged ice) underlies the new experiments that we present here.
These experiments demonstrate that damage imparted by compression of ice can significantly (and anisotropically) reduce its Young’s modulus, on which this paper is focused, and can also cause an increase in the critical strain rate that marks its ductile-to-brittle transition, which will be the subject of a future paper. Under the conditions we tested, recrystallization accompanied damage but appeared to play a lesser role than cracking in producing the observed effects, as we will show. Before describing our experimental procedure and results, we begin here with a synopsis of damage quantification.
Damage due to non-propagating cracks may be measured in different ways. One approach is to use a continuous variable, , to represent the undamaged fraction of material remaining as damage evolves (Reference KachanovKachanov, 1999). The damage variable, D = 1 − ψ, varying from 0 to 1, measures the deterioration of effective stress-resisting materials. The effective stress concept allows constitutive equations for macroscopic strain in a damaged body to be written in the same terms as for an undamaged body, but replacing the applied stress, σ, with an effective stress, 
, modified by damage (Reference LemaitreLemaitre, 1984).
A different approach, conceptually if not practically simple, is just to count the number of cracks, N, that cross a unit cross-sectional area, A, perpendicular to the plane of the cracks (Reference SinhaSinha, 1989a). However, the discrete variable, N/A, does not account for crack lengths. The dimensionless crack damage measure of π/2 N/A incorporates a mean length, l, for cracks (Reference Sammis and AshbySammis and Ashby, 1986). To account for a distribution of lengths, summation over individual cracks in a two-dimensional (2-D) cross section of area A gives the dimensionless scalar crack density
where ci is the half-length of the ith crack (Reference BristowBristow, 1960). As noted in early usage (Reference WalshWalsh, 1965), ρ c assumes crack lengths are uniformly represented across all crack orientations. Because ci 2 scales in proportion to the area of influence surrounding each crack, a value of ρ c >1/4 may suggest significant crack interaction.
In three dimensions (3-D) the corresponding crack density becomes
where ai is the radius of the ith circular-shaped crack in representative volume, V.
Extending the concept of ρ c to describe the orientations of cracks as well as their spatial extent, Reference KachanovKachanov (1980) developed a crack density tensor, given in 2-D as
where 
is a unit vector normal to the ith crack trace of length 2c. In the summation, 
denotes the dyadic, or outer product, yielding a second-rank tensor.
α
is a generalization of the damage parameter that simplifies (when crack orientations are isotropic or random) to the scalar ρ
c, which equals the first invariant of the tensor, i.e. tr(
α
) = ρ
c. Further sophistications pertain, for example, to cases in 3-D or where crack interactions become significant (Reference KachanovKachanov, 1992).
Asserting the broad applicability of a non-interacting crack model, Reference KachanovKachanov (1992, Reference Kachanov1993) shows how emerges α through analysis of the stress fields, σ , around isolated cracks and their impact on the elastic potential, f , which comprises two terms: f ( σ , α ) = f 0( σ )+ f( σ , α ), of which the first term, f 0, describes the undamaged material; damage affects only the second term, Δf, the effective elastic potential increment. The tensor components of the change in compliance due to damage are given by
with symmetries about permutations of the subscripts in braces (i ↔ j, k ↔ l, ij ↔ kl). The Kronecker delta δij , etc., equals 1 if its two indices are equal (i = j) and 0 if not. E 0 denotes the Young’s modulus of undamaged material.
Any choice of metric involves balancing the required accuracy with the practicality of making measurements. The scalar crack density, ρ c, is one of the commonly used measures of damage and encapsulates information in a convenient number that can be generated (in 2-D, at least) from thin-section analysis. Another important consideration in the choice of damage measure is its appropriateness to the material property of interest. Reference Kachanov and SevostianovKachanov and Sevostianov (2005) provide a rigorous comparison of approaches to the quantification of damage (including cracks, pores and other inhomogeneities). As they explain, depending on the property at hand, certain aspects of damage may not contribute to an effect on that property, and such aspects can be ignored in the damage parameter. At the same time, the parameter should account for all aspects of damage that do affect the properties of interest.
Here those properties of interest are the elastic moduli in addition to the mass density or porosity. For ice in particular, few studies exist of the elastic moduli of damaged ice (Reference Schulson and DuvalSchulson and Duval, 2009). One of our goals is to test how well damage parameters (c, ) relate to elastic properties as measured at the macroscopic scale of bulk specimens. A novel feature of this study is that we compare freshwater ice and saline ice tested under identical conditions.
Experimental Methods
The test procedure involved (1) growing and preparing specimens of S2 columnar ice, (2) loading the specimens in uniaxial compression at a constant strain rate to impart damage, then (3) obtaining elastic properties using ultrasonic transmission techniques. All tests were conducted at −10°C. (S2 refers to a type of columnar-grained ice in which the crystallographic c-axes are randomly oriented within, but essentially confined to, the horizontal plane, i.e. normal to the long axis of the columns. S2 ice commonly occurs in natural ice covers (Reference Michel and RamseierMichel and Ramseier, 1971)).
Ice preparation
Columnar S2 ice was produced in the laboratory to simulate both naturally grown freshwater ice and sea ice. Following the procedures of Reference Golding, Snyder, Schulson and RenshawGolding and others (2014), freshwater ice was prepared by freezing filtered tap water, and saline ice by freezing from a solution of 17.5 ± 0.2‰ salinity. Both types of ice were grown in a cylindrical 800 L polyethylene tank. After filling the tank, the water or solution was allowed to equilibrate to +4°C. The sides of the tank were wrapped with insulation to promote unidirectional freezing from the top. The liquid surface was seeded with a layer of <4 mm equiaxed freshwater ice grains. The tank was then capped with a cooling plate of aluminum, which was maintained at −20°C until ice had formed to a depth of 22–30 cm.
To prepare for testing, blocks of the ice were machined into 152 mm cubes, taking care to align one edge of the cube parallel to the long axis of the columnar grains, identified as the x 3-direction. Machining tolerance was 0.076 mm.
Straining procedure
The cubic specimens at a temperature of −10.0 ± 0.2°C were loaded in uniaxial compression in an across-column direction (defined henceforth as x
1) to a specified level of strain, ε
p, at a constant strain rate, 
. Figure 1a shows the loading configuration with respect to the columnar grains in a parent specimen.
Fig. 1. Typical geometry (a) with respect to uniaxial loading by across-column compression along x 1 to impart strain, ε p, in parent specimen, which yields (b) two pairs of subspecimens oriented lengthwise in either the x 1- or x 2-direction.
Loading was performed using a servohydraulic multi-axial test system (MATS), with its opposing pair of vertical actuators. (The stiffness of the loading frame in the vertical direction is 8 MN mm−1.) The specimen was placed between polished brass brush platens fastened to the load cell attached to each actuator. The x 2 and x 3 faces of the specimen were unconfined. The MATS load-control mode allowed the platens to make initial contact on the specimen with as little as 0.2 kN force, after which the load was incrementally stepped up to 2.0 kN. The specimen was seated in the platens under this load for ∼15 min before being compressed at the specified constant strain rate.
To explore the effect of , we compressed specimens at both one and two orders of magnitude below the ductile-to-brittle transition strain rate, 
, for undamaged material. At −10°C this rate has been reported (Reference Schulson and BuckSchulson and Buck, 1995) to be 1 × 10−4 s−1 for freshwater ice, ten times lower than for saline ice (1 × 10−3 s−1). Levels of strain were specified from ε
p = 0.003 to 0.20, a range in which the specimen would permanently deform but remain intact. Table 1 lists the levels of ε
p at each tested. We recognize that imparting damage at strain rates below the ductile-to-brittle transition presents challenges for isolating the effects of microcracking, due to attendant processes (such as recrystallization, which we describe below) that occur during ductile deformation. However, had we chosen to load specimens at strain rates 
, they would not have withstood strains beyond ∼0.004, severely limiting the range of damage we could explore.
Table 1. Uniaxial compressive strain conditions tested for fresh-water ice (F) and saline ice (S)
After being shortened at , the specimen was unloaded at the same rate (this is an important point) in order to avoid imparting additional cracks that can occur upon rapid unloading (Reference Couture and SchulsonCouture and Schulson, 1994). The specimen was then re-milled to square its faces; the x
2 faces, particularly, had noticeable deformation after the compression. The mass density, ρ, of each specimen was recorded before straining and again after re-milling. ρ was calculated by weighing the specimen and dividing by its volume as the product of measured lengths in each direction. The bounding volume included any porous space of cracks imparted through straining. Porosity was calculated as
where ρ 0 = 917.45 kg m−3 is the expected density of damage-free ice at −10°C (Reference HobbsHobbs, 1974). Next, the specimen was sectioned into rectangular prisms, machined to 60 mm × 60 mm × 120 mm, with the long dimension running across the columnar grains either parallel (x 1) or perpendicular (x 2) to the initial loading direction (Fig. 1b).
Microstructural analysis
Microstructural changes were visually assessed from thin sections sliced parallel to the faces of the strained parent specimen. Each thin section was mounted on a glass slide and planed using a microtome to a uniform thickness of 3 ± 0.2 mm, if possible. Photographs of the 3 mm thin sections under visible light recorded cracks and grain-boundary decohesions. The thin sections were planed again to <1 mm thickness until the crystal grains became distinctly visible between cross-polarizing filters in transmitted light. Figure 2 depicts thin sections of undamaged freshwater ice and saline ice. Cross-polarized light revealed the grain structure in both materials. The mean column diameter of grains based on the linear intercept method was 5.6 ± 1.9 mm for freshwater ice and 4.4 ± 1.5 mm for saline ice.
Fig. 2. Thin sections of undamaged saline ice (left column) and undamaged freshwater ice (right column) at −10°C taken normal to (a–d) the across-column x 1-direction and (e–f) the along-column x 3-direction. Grid paper was placed behind the freshwater ice thin section (b) in order to better show its transparency and the absence of bubbles and cracks. Cross-polarized light revealed the grain structure in the lower four photographs.
Measurement of elastic properties
The dimensions and mass density, ρ, of each subspecimen were measured in a similar manner. Elastic properties in both the x 1- and x 2-directions were then determined from and from P-wave (longitudinal) and S-wave (transverse) ultrasonic velocities. We focused on the x 1- and x 2-directions because of practical considerations and our interest in across-column loading scenarios.
Ultrasonic measurements were performed using a through-transmission set-up that placed the specimen under a load of 400 N between transducer platens containing crystals of 200 kHz resonant frequency. A thin layer of ultrasonic coupling gel was spread at the specimen/platen interface to improve contact. The apparatus was calibrated using aluminum samples of both prismatic and cylindrical shapes, as well as using undamaged ice. P-wave and S-wave speeds, c P and c S, respectively, were found by manually determining the first-arrival times of a pulse transmitted through the specimen between the transducers, and dividing into the specimen length. This measurement method depends on the accuracy of choosing the pulse first-arrival times, which is subject to signal noise that may increase with damage, as well as to user error. The uncertainty in the measured wave speeds was estimated to be ∼5%.
Using ρ and the ultrasonic transmission wave speeds measured along direction xi , it is possible to calculate Young’s modulus, E, shear modulus, G, Poisson’s ratio, ν, and bulk modulus, K, using the following relationships:
Equations (6–9) are derived assuming a fully isotropic homogeneous material (Reference Timoshenko and GoodierTimoshenko and Goodier, 1951). In contrast, in S2 ice the along-column x 3-direction is slightly anisotropic with respect to elastic constants relative to the x 1-x 2 plane, although within this horizontal plane the polycrystal is essentially elastically isotropic. Thus the number of independent elastic compliances, Sij (i, j = 1,…,6), is reduced to 6 from 9 in the general orthotropic case (Reference Gagnon, Jones, Levy, Bass and SternGagnon and Jones, 2001). Given that the Sij are aggregate properties, the polycrystalline parent specimens and subspecimens were made as large as the loading apparatus and ultrasonic transducers could accommodate, in order to minimize orientation effects of any single grain within the bulk sample, whose cross section contained ≳300 grains. Aggregate elastic compliances for undamaged S2 ice are related to independent Young’s moduli, shear moduli and Poisson’s ratios as follows (Reference Schulson and DuvalSchulson and Duval, 2009, eqns (4.11–4.15)):
Appendix A gives more detail of how Gi and νi relate to Eqns (11–13).
Results and Discussion
We detected four primary changes in the ice specimens as a result of the applied strain:
-
Damage, in the form of non-propagating cracks
-
Recrystallization
-
Increased porosity
-
Increased elastic compliance
In the following subsections we present our experimental results for each of these items. The first two (cracking and recrystallization) were quantified by inspecting thin sections, examples of which appear in Figures 3–6. Figure 7 shows stress–strain curves recorded during the uniaxial compression of representative specimens of both types of ice.
Fig. 3. Thin sections and crack patterns of freshwater ice after 0.003 strain at 1 × 10−5 s−1 at −10°C. Sections were taken normal to (a, b) x 1 or (d, e) x 3. Cross-polarized light revealed the grain structure (top row), which at this level of strain contained essentially no evidence of recrystallization. Evidence of cracking, in contrast, appeared in images photographed under scattered light (middle row). Along with relatively short transgranular cracks, rather long cracks (visible in (b)) occurred at some grain boundaries and tended to align with the x 1-direction of loading (as viewed in the across-column section, (e)). The cracks seen in (b) and (e) were digitally traced to produce the corresponding fracture patterns shown in (c) and (f). Orthogonal vectors (in red) show the principal directions of the crack density tensor, α (Eqn (3)), each scaled to the Young’s modulus derived from the corresponding component of α .
Fig. 4. Thin sections of freshwater ice after (left column) 0.035 and (right column) 0.100 strain at 1 × 10−5 s−1 at −10°C. Sections were taken normal to x 1. Cross-polarized light revealed the grain structure in (a) which contained relatively little recrystallization, and in (d) where more recrystallization was evident. The cracks seen under scattered light in (b) and (e) were digitally traced to produce the fracture patterns shown in (c) and (f).
Fig. 5. Thin sections of freshwater ice after (a–c) 0.035 and (d–f) 0.100 strain at 1 × 10−6 s−1 at −10°C. Sections were taken normal to x 1. Cross-polarized light in (a) and (d) revealed recrystallization, the area fraction of which increased with ε p. Fracture patterns are shown in (c) and (f).
Fig. 6. Thin sections comparing recrystallization in saline ice after strains of 0.035 (a, c) and 0.100 (b, d) imparted at 1 × 10−4 s−1 (a, b) and at 1 × 10−5 s−1 (c, d) at −10°C. Sections were taken normal to x 3.
Fig. 7. Typical stress–strain curves for freshwater ice (blue) and saline ice (green), recorded during uniaxial compression at −10°C at the strain rates, , indicated in each panel.
Damage did not occur immediately. Beginning at ∼0.001 strain, decohesions appeared along columnar grain boundaries. Decohesions were followed by transgranular cracks occurring by 0.002 strain, both of which are visible in Figure 3b. The grain-boundary decohesion and initial cracking activity were similar to that observed by Reference Weiss and SchulsonWeiss and Schulson (2000) at similar stages in constant-strain-rate tests. After strains of 0.003 and greater, long intergranular cracks were also observed that had either nucleated separately or evolved from decohesions. In our examination of thin sections, we found no practical way to reliably differentiate such cracks from decohesions. We counted traces of both features, and the following subsection on quantifying damage explains how we filtered out long traces oriented parallel to near-vertical grain boundaries. In this work, we use the term ‘crack’ loosely, referring to fracture features that include transgranular and intergranular cracks, and grain-boundary decohesions.
Damage
Crack density was estimated by counting individual cracks in the thin sections photographed under scattered light. Counting cracks accurately proved to be challenging, especially in highly strained specimens and in saline ice in general. In preparing some thin sections, additional cracks were observed to occur during the planing process, as a result of the stress applied by the microtome blade itself. In some specimens pre-shortened by 10% or more, the thin sections disintegrated before they could be planed to the desired thinness, even following the high-precision double-microtoming technique (Reference SinhaSinha, 1977) of removing very thin (<5 μm) layers at a time. In this technique, ice is mounted on a glass slide with just a few beads of water pipetted at the perimeter of the thin section. An alternate way to mount thin sections involves melting the surface of the section briefly (<10 s) on a warm clean surface to create a smooth flat interface with a liquid layer, then freezing that directly to the glass. This ensured a strong bond to the glass, which reinforced the fragile ice section along its full surface and made it less susceptible to fracturing in the microtome. The surface melting procedure, however, could introduce water into any cracks open to the glass interface, potentially obliterating them. This was a particular problem in saline ice, with a lower melting point and higher porosity, where cracks were further obscured by the presence (even without strain) of brine platelets and air bubbles. Lacking confidence in any method to unambiguously count cracks in saline ice, we made crack density measurements for freshwater ice only.
By tracing and measuring the individual crack lengths, 2ci
, within a given area, A (typically 50 cm2), the scalar crack density, ρ
c, was calculated according to Eqn (1)
.
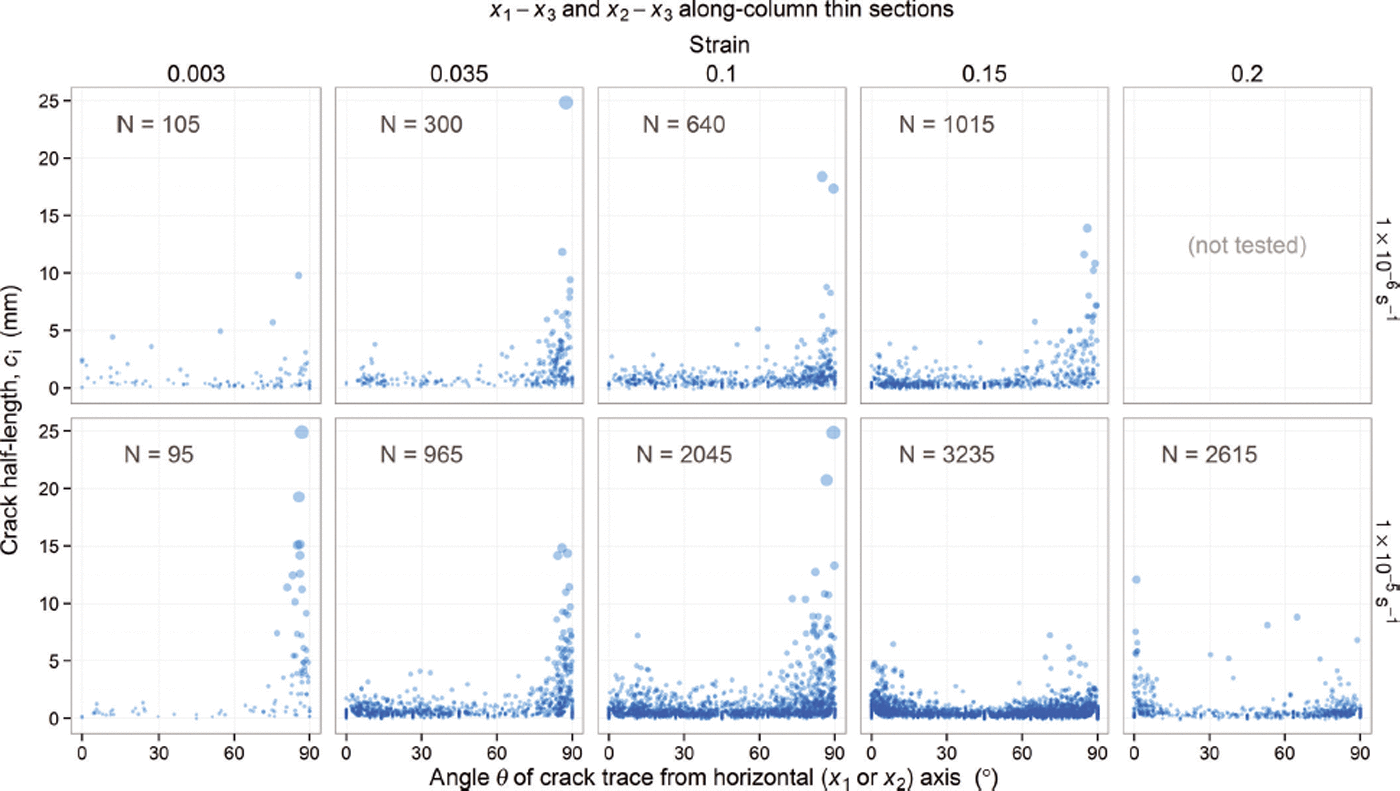
We also measured the angle, θ, from the horizontal axis (x 1 or x 2) of each crack trace in the plane of the thin section, as shown in Figure 8. Figure 9 plots the half-length versus inclination angle of crack traces measured in along-column thin sections.
Fig. 8. Common coordinate system, xu -xv , used in analysis of thin sections cut across and along columnar grains, as shown. The angle θ measures the inclination of crack traces within the thin-section plane.
Fig. 9. Distribution of sizes and angles of crack traces in along-column thin sections of strained freshwater ice. The level of strain increases from left to right, as indicated above the panels, imparted at 1 × 10−6 s−1 (top row) or 1 × 10−5 s−1 (bottom row). Each panel plots the half-length versus inclination angle for a random sampling of N crack trace measurements, where N is the mean number of cracks counted in a 50 cm2 thin-section area for each condition (except for ε p = 0.2, for which the thin-section area was only 12.5 cm2).
Vertically oriented cracks, i.e. θ = 90°, lie in a plane parallel to x 3. Using thin sections, which reveal only the 2-D traces of cracks, it was impossible to know the unique, 3-D crack orientations, as defined by vectors normal to the plane of each crack. At best we could assume that a crack normal was inclined no more than 45° out of the plane of the thin section if the trace of that crack had an apparent width less than the finite (3 mm) thickness of the thin section.
From the angle, θ, the components of were calculated for each crack as nu
= −sin and nv
= cosθ for thin sections oriented in the xu
-xv
plane, using a common coordinate system for all thin sections (Fig. 8). For along-column thin sections, xv
= x
3 always; for across-column thin sections, xu
= x
1 and xv
= x
2 always. The crack density tensor,
α
, was then computed from Eqn (3) (Appendix B).
For thin sections cut parallel to the columnar grain axis (x
3), Figure 10 shows mean values of ρ
c as a function of strain for all cracks with θ ≤ θ
t, a threshold angle in the interval 0–90°. The vertical spacing between points on the graph reveals the relative contribution to ρ
c of cracks oriented within that interval of θ
t. For example, at 
, for ε
p > 0.003 there were many more cracks inclined <15° than ∼45°. As may be expected, a strong trend of ρ
c increasing with strain is demonstrated, but only up to θ
t = 75°. When near-vertical cracks are included, the relationship between ρ
c and ε
p becomes less clear, with high variation among thin sections of similarly strained specimens.
Fig. 10. Crack densities, ρ c, measured in strained freshwater ice, for groups of cracks inclined up to the threshold angle, θ t.
One explanation for the lack of clear correspondence between crack density and strain when near-vertical fracture features are included may be due to the geometry of columnar ice. The long vertical grain boundaries facilitate the nucleation of highly attenuated cracks. These may nucleate more easily than transgranular cracks, and, as already noted, during straining we observed grain-boundary decohesions that appeared before other visible damage. Even though there are relatively few grain boundaries compared with sites for transgranular cracks (which can nucleate anywhere along the length of the grains), the long intergranular cracks get disproportionately weighted in the summation for ρ c based on crack half-length squared. Thus, specimens strained as little as 0.003 may have cracks at many of their grain boundaries yet very few cracks elsewhere (Fig. 3a), and still have a high ρ c (for all θ), which would not change significantly with the addition of many more short cracks.
Another observation from the thin sections (Figs 3–5) and the data in Figure 10 is that the damage in strained freshwater ice was not uniformly distributed. This non-uniformity raises the issue of size effects, as well as the possibility that clustering may produce locally significant crack interactions.
The size of the specimen could affect the distribution of damage, to the extent that cracks may populate differently near the edges of the specimen, perhaps due to stress gradients. Boundary layers will be relatively smaller in larger specimens, affecting the damage distribution less than in smaller specimens.
As mentioned in the procedural description, constraints of the experimental apparatus prevented us from exploring effects of specimen size. The possibility of a size effect thus falls beyond the scope of this work. Except for those following grain boundaries, the majority of cracks were shorter than the typical column diameter. Regarding local effects of crack clustering, we defer that issue until we present our results on damage-reduced elastic moduli in the context of non-interacting crack models, below.
In order to generate some useful relationships between crack density, ρ c, and strain, ε p, we can filter out the near-vertical cracks and decohesions that form a distinct population (Fig. 9) within the overall damage. Figure 11 shows ρ c, as a function of ε p, computed from along-column thin sections for only non-vertical cracks (θ ≤ 75°), fitting these data by simple linear regression. At the higher strain rate, ρ c increases with respect to strain about three times more rapidly:
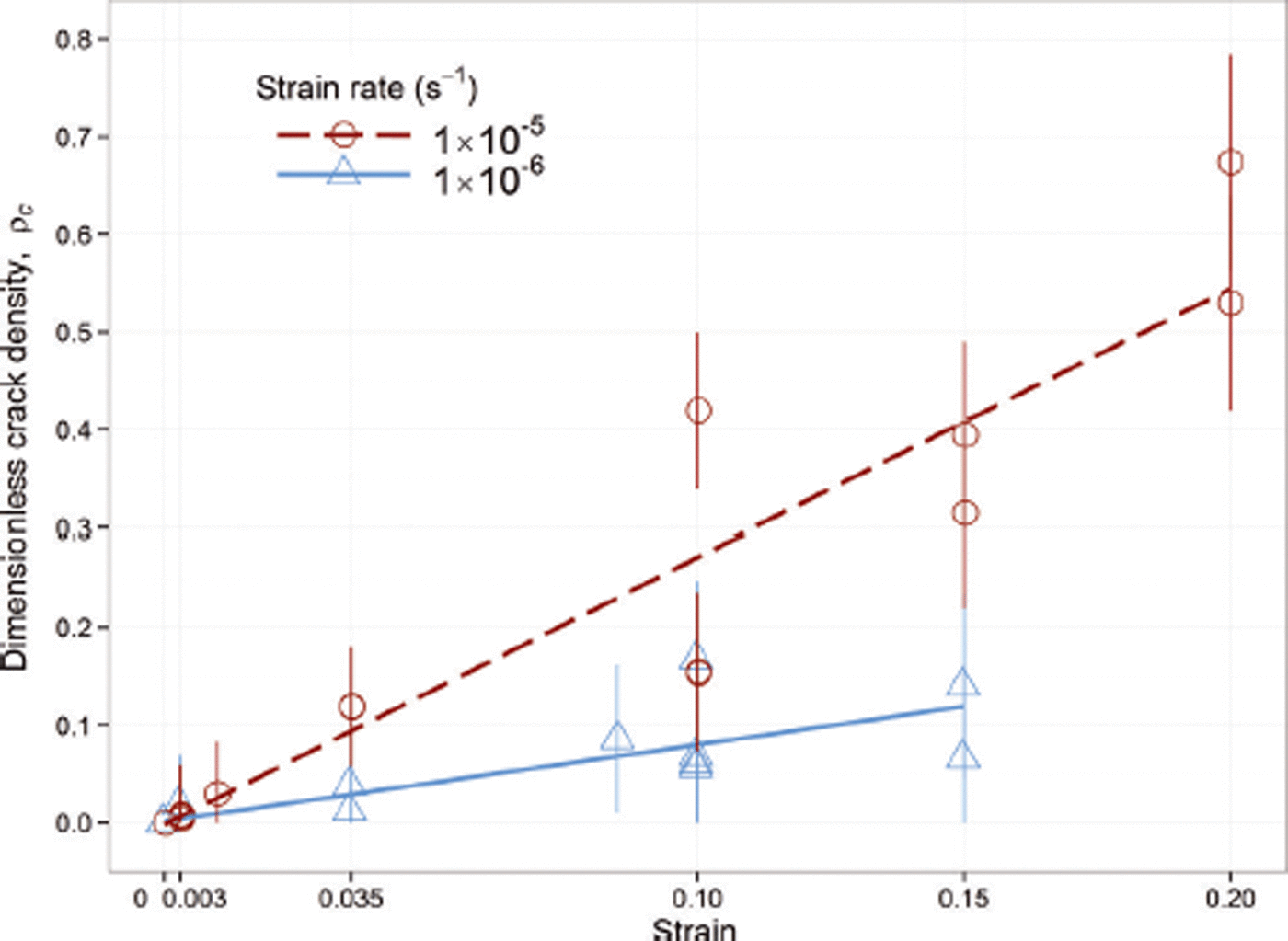
Fig. 11. Crack density, ρ c (θ ≤ 75°), in freshwater ice as a function of strain, ε p, with a linear fit. Vertical lines indicate estimated uncertainty in ρ c measurements, that reflects the possibility of failing to count some cracks, on the one hand, and on the other, of over-counting features such as bubbles, scratches or cracks caused by microtoming.
As given in the simple terms above, ρ c provides a basic measure of damage to allow some comparison among various strain conditions. However, as described in the Introduction, the scalar ρ c does not take into account crack orientations. When crack orientations are non-random, a better damage parameter is the crack density tensor, α .
When comparing thin sections in both of the along-column planes (x
1-x
3 and x
2-x
3), we found the components of
α
in the across-column directions, i.e. α
1 and α
2, to be similar. The magnitudes of α
1 and α
2 were similar to ρ
c values obtained from along-column thin sections for corresponding conditions of strain. However, in across-column (x
1-x
2) thin sections, the magnitude of the α
1 component was consistently less than that of α
2, capturing the fact that cracks tended to align with the x
1-direction of initial loading. For 
, ∂α
1/∂ε
p was 0.3 compared with ∂α
2/∂ε
p of 1.0. For 
, the derivatives for the two components were 0.6 and 1.5, respectively. In the x
1-x
2 sections, cutting across the short dimension of grains, all crack density parameters were naturally lower than those describing crack traces in thin sections cut along the length of the grains. In all cases, however, the higher strain rate produced greater crack density.
As an aside, we present one further damage parameter that expands the generality of this work on ice, given that many of the damage concepts we incorporate were developed in the context of rock mechanics. This parameter, the ratio σ
cd/σ
peak, can be found using stress–strain curves (Fig. 7). The crack damage stress threshold, cd, is located where the near-linear portion of the ascending (axial) stress-strain curve ends (Reference Martin and ChandlerMartin and Chandler, 1994). Dividing σ
cd by the peak stress, σ
peak, we get a ratio of 0.82 ± 0.03 for freshwater ice 
and 0.71 ± 0.04 for saline ice 
. Both of these values are near the same average ratio of σ
cd /σ
UCS = 0.80 ± 0.10, where σ
UCS is the uniaxial compressive strength, reported for different types of rock in research establishing that ratio as an intrinsic property useful for predicting material strength (Reference Xue, Qin, Sun, Wang and QianXue and others, 2014). In that same work, material of higher porosity had lower σ
cd/σ
UCS ratios, consistent with our findings for saline ice. We will not dwell further on this parameter, but it points to an interesting similarity in damage development between ice and rock.
Recrystallization
The thin sections photographed under cross-polarized light revealed recrystallized grains. We assume this recrystallization occurred dynamically although, in this work, our goal was not to examine recrystallization itself as a phenomenon. The subject has been treated in previous experimental studies of ice creep (e.g. Reference Kamb, Heard, Borg, Carter and RaleighKamb, 1972; Reference DuvalDuval, 1981) and in ongoing efforts to numerically model ice deformation (Reference MontagnatMontagnat and others, 2014). The area fraction, f rx, of recrystallized grains relative to the thin-section area, A, was measured and is shown in Figure 12 as a function of strain. f rx increased with strain in both saline and freshwater ice.
Fig. 12. Recrystallized area fraction, f
rx, versus strain in (a) saline ice and (b) freshwater ice. The freshwater ice data for each were fitted with an Avrami-type function (Eqn (15)).
The uncertainty in recrystallized area fraction, indicated by vertical error bars on the graphs in Figure 12, was estimated to be ±0.05, based on the average discrepancy between counts of the same thin sections made by two different researchers. Although the data have some scatter that increases with strain, the trend appears in both types of ice that less recrystallization occurs for the same ε
p when imparted at the higher strain rate. This inverse relationship of f
rx to suggests that the kinetics of recrystallization depend significantly on duration of loading at the scale of these compression tests. For example, shortening by 10% at 1 × 10−6 s−1 requires >30 hours. In freshwater ice, this was sufficient time to allow 50–90% of the area to recrystallize, compared with only 25–50% when the same strain was imparted in just 3 hours, i.e. 10 times faster, at 1 × 10−5 s−1. At that strain rate, strain of ε
p = 0.100 resulted in similar amounts of recrystallization to (but much more cracking than) strain of ε
p = 0.035 imparted at the lower strain rate.
For freshwater ice, the f rx data for each strain rate were fitted with an Avrami-type function:
The curves of these relationships are shown in Figure 12b.
Interestingly, and for reasons not yet understood, recrystallization was greater in saline ice than in freshwater ice compressed at the same strain rate. At 0.035 and 0.100 strain, f
rx measured in saline ice at both rates, , that were tested was comparable to that in freshwater ice at a strain rate one order of magnitude lower. Why might recrystallization occur more readily in saline ice? On the one hand, pores and brine pockets in saline ice should allow it to accommodate more strain, but on the other hand they may provide sites for grain nucleation that are absent in freshwater ice. The grain boundaries appear more inter-digitated in saline ice, possibly impeding grain-boundary sliding as a process to accommodate strain and instead creating local stress concentrations that become additional nucleation sites. These aspects of microstructural change due to strain, and the related material differences, warrant further study.
Porosity
The bulk mass density, or more directly the porosity, provides another indicator of damage. In all specimens that we tested, the mass density decreased and porosity increased with increasing strain (Fig. 13). Porosity, φ, was calculated using Eqn (5). Due to the presence of brine pockets and pores, even in undamaged saline ice φ was typically measured as ∼1–2% porosity, with some samples, perhaps containing larger brine channels, as high as 6–7% porosity. The porosity of undamaged freshwater ice always measured very near zero. Despite this difference in the two types of ice, the linear trends relating to ε
p are remarkably similar for both, although the corresponding strain rates, , are shifted higher in saline ice by one order of magnitude. Table 2 lists the values of ∂φ/∂ε
p calculated using a weighted linear regression. Note that the ratio of the higher to lower value of ∂φ/∂ε
p is 2.5, the same for both types of ice.
Table 2. Values of the slopes of weighted linear regression predicting porosity, φ, as a function of strain, ε
p (Fig. 13), applied at the strain rate indicated for each type of ice. Slope values are in units of % porosity ± standard error of the mean
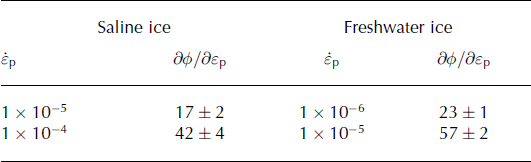
Fig. 13. Porosity, φ, of columnar (a) saline ice and (b) freshwater ice, measured at −10°C, as a function of strain, ε p. Labels indicate the number of data points measured in each group. Shaded zones indicate 95% confidence intervals about the linear fits, weighted for heteroscedasticity.
Crack density correlated to porosity
The strong correlation between scalar crack density (Fig. 11) and porosity (Fig. 13b) in freshwater ice allows us to estimate crack density in saline ice, which we were unable to measure directly. Figure 14 plots this correlation explicitly, fitting a weighted linear regression to crack density as a function of the change in porosity, Δφ = (ρ(0) − ρ(ε p))/ρ 0, where the numerator is the difference in mass density before and after strain, ε p. The x-coordinate of each point represents a mean Δφ for each parent specimen, averaging 1 bulk plus 4 subspecimen measurements. The horizontal error bars span the range of values from subspecimens (indicating precision error in measurement and that damage was somewhat non-uniformly distributed). Vertical error bars are located at the group mean, 〈Δφ〉, for each strain condition, and their height indicates an estimated uncertainty based on the range of average crack densities over all (along- and across-column) thin-section orientations from which ρ c was calculated for each group. When the same strain level appears twice on the graph, the lower-valued data represent the lower (1 × 10−6 s−1) strain rate; the higher-valued data represent 1 × 10−5 s−1. The linear regression equation was found to predict crack density in terms of % units of porosity as
Fig. 14. Scalar crack density, ρ c, as function of change in porosity, Δφ. At each strain condition, ρ c is averaged over measurements made using across-column and along-column thin sections of freshwater ice.
The regression coefficients are given with ± standard error terms. The high statistical significance (p < 0.001) suggests that porosity can be a useful indicator of damage. Is it as good an indicator for saline ice, which is innately more porous, as it is for freshwater ice? The next subsection presents elastic properties and relates them to porosity, showing similar trends for both materials.
Before leaving Figure 14, we note the positive y-intercept. This implies an initial period of damage activity in which porosity does not change much, that essentially coincides with the ascending portion of the stress–strain curve. During this period, as noted above, we observed the emergence of grain-boundary decohesions as well as initial cracks.
Elastic properties
The ultrasonic transmission method was used to measure the velocities of P- and S-waves in subspecimens of the strained ice in order to obtain the dynamic elastic properties. Table 3 lists the mean properties for undamaged ice and strained ice, and the direction in which they were measured. The velocities, c
P and c
S, both decreased with ε
p and with (Table 3), implying a reduction in stiffness of damaged ice that is not merely due to its lower density. A standard deviation in calculated properties of ∼4% was typical of specimens tested under identical conditions, and likely reflects some natural material variation, as well as experimental error. Our use of the ultrasonic technique was validated by the close match between results from our calibration tests on as-grown specimens and previously published properties of freshwater ice (Reference Gammon, Kiefte and ClouterGammon and others, 1983) and sea ice (Reference SinhaSinha, 1989b). In undamaged ice, the mean of >30 measurements of Young’s modulus was 9.5 GPa. This is close to 9.7 GPa, the across-column value expected for S2 freshwater ice at −10°C, based on the compliances collected by Reference Schulson and DuvalSchulson and Duval (2009, table 4.4).
Table 3. Elastic properties measured at −10°C in freshwater ice and saline ice after various levels of strain, ε p. Mean values ± sample standard deviation of N samples are tabulated for mass density, ρ, Young’s modulus, E, shear modulus, G, Poisson’s ratio, ν, P-wave speed, c P, and S-wave speed, c S
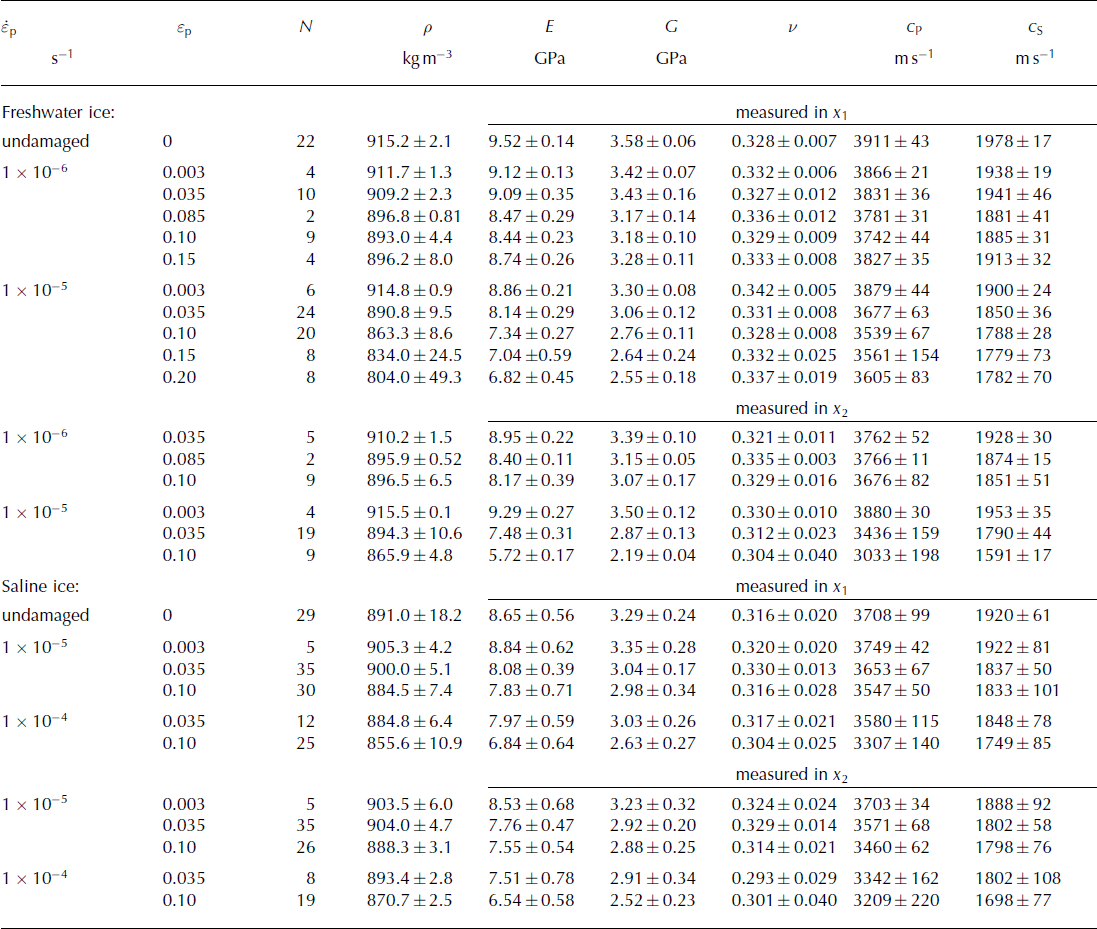
Figure 15 shows Young’s modulus, Ei (measured in the xi -direction at −10°C), versus strain, ε p, in both freshwater ice and saline ice. Young’s modulus decreased with increasing levels and rates of strain; similar trends were seen in shear modulus, G (Table 3), and bulk modulus, K (not listed in the Table 3, but calculated using Eqn (9)).
Fig. 15. Young’s modulus of columnar (a, c) saline ice and (b, d) freshwater ice, measured along one of the two across-column directions, x 1 (top row) and x 2 (bottom row), at −10°C as a function of strain, ε p, applied by uniaxial compression in x 1. Curves connect mean values for each strain group, and error bars indicate 95% confidence intervals about the means.
We measured little or no detectable effect of damage on Poisson’s ratio, ν. This does not necessarily contradict findings for rocks (e.g. Reference Heap, Vinciguerra and MeredithHeap and others, 2009) that indicate damage may increase the static or apparent Poisson’s ratio (of radial strain to axial strain). Unlike our measurements of the dynamic elastic moduli, these static elastic properties were ascertained from stress–strain curves (Reference Heap and FaulknerHeap and Faulkner, 2008) and therefore may likely include inelastic effects on the deformation of the bulk material. Hence values for the apparent Poisson’s ratio >0.3 (as in Reference Heap, Vinciguerra and MeredithHeap and others, 2009) are not unexpected. Static and dynamic elastic moduli often differ significantly for many materials, such as metals (Reference BristowBristow, 1960). Under the assumptions of the non-interacting crack model, ‘the impact of cracks on Poisson's ratio (in the principal axes of [crack density tensor] α) is small, as compared to the impact on the shear and Young’s moduli’ (Reference KachanovKachanov, 1992, emphasis in original).
We observed that strain reduced the elastic moduli (other than ν) by a greater amount in freshwater ice than in saline ice under the same strain conditions. Furthermore, mass density and Young’s modulus were reduced by a greater amount when compression occurred at the higher strain rate in either type of ice. As mentioned in the straining procedure, recall that 
is higher for saline ice than freshwater ice. These observations indicate that for both materials the effects of damage on elastic behavior are more pronounced the closer to .
The influence of damage, of course, may be modified by the presence of other factors, such as recrystallization, that accompany microcracking during ductile deformation. The negative correlation of f
rx with and the strong positive correlation of ρ
c and 𝜙 with suggest that cracking is the major contributor to reduction in elastic moduli.
Strain-induced anisotropy
Elastic moduli differed, depending on whether strained ice was measured in a direction either parallel (x 1) or perpendicular (x 2) to initial loading. The same level of strain imparted along the x 1-direction tended to cause a greater reduction in E measured along x 2, ranging from slightly more than to up to twice as much as that measured along x 1. To our knowledge, such strain-induced anisotropy has not previously been reported in ice.
When using the ultrasonic transmission technique to measure the elastic moduli of the strained ice, specimens were loaded under a typical force of 0.4 kN (corresponding to a compressive stress of 0.1 MPa) in the direction of the transmitted pulse. We investigated whether the measured elastic moduli are sensitive to the load applied on the specimen at the time of measurement. This question has particular relevance in the presence of what appears to be damage-induced anisotropy (i.e. greater compliance in the transverse x 2-direction than in the longitudinal x 1-direction). If such anisotropy were primarily due to cracks aligning preferentially parallel to the direction of applied strain, would we find the anisotropy to diminish upon closure of those transverse cracks under sufficient compression? We tested this idea by increasing the load on the specimen slowly, at 10 N s−1, and holding at 1, 2, 3 and 4 kN to take ultrasonic readings. Upon reaching 4 kN (∼1.1 MPa), the specimen could not support the load for more than a few minutes before fracturing. We found no significant difference in the elastic moduli measured at any of the stresses from 0.1 to 1.1 MPa in either direction (x 1 or x 2). Although these tests did not support the hypothesis that crack closure would reduce the anisotropy, they do not rule it out conclusively, as we observed additional cracks nucleating during the process of applying the higher loads (>1 kN). However, these results suggest that other factors (perhaps the development of a crystallographic texture through dynamic recrystallization) in addition to cracks are responsible for this strain-induced anisotropy, which persists even after further compression.
The nature of the observed strain-induced anisotropy warrants further study.
Young’s modulus versus porosity
The relationship between Young’s modulus, E, and porosity, φ, is illustrated in Figure 16. In these graphs, data from individual subspecimens tested at all levels of strain are plotted together, regardless of strain rate. The colors indicate the level of strain, ε p, where ‘0’ refers to undamaged, asgrown specimens. Young’s modulus appears to decrease linearly with porosity over the range of conditions we have tested, represented by a relationship such as
where E 0 refers to the Young’s modulus of undamaged ice of zero porosity. Table 4 lists values for the constant slope, ∂E/φ∂ , calculated from a least-squares regression for each type of ice and in each direction (x 1 and x 2). For E measured in the x 1-direction, the trends are nearly indistinguishable between saline ice (Fig. 16a) and freshwater ice (Fig. 16b) up to 10% porosity, although the saline ice data show greater scatter. In the x 2-direction, compared with x 1, the slope of the fitted line drops slightly to −0.46 from −0.36 in saline ice (Fig. 16c) and more substantially to −0.63 from −0.35 in freshwater ice (Fig. 16d), again showing evidence of strain-induced anisotropy.
Fig. 16. Young’s modulus, E, versus porosity, φ, in freshwater ice and saline ice, at −10°C, after the level of strain indicated in the legend. E was measured along x 1 (top row) or along x 2 (bottom row) in the two materials. Shaded zones indicate 95% confidence intervals about the linear fits, excluding in (b) data for φ > 10% and in (a) and (c) data from the anomalous damage-free saline ice with φ > 6%.
Table 4. Values of the slope, ∂E/∂φ, of the linear regression describing Young’s modulus as a function of porosity (Eqn (17); Fig. 16). Young’s modulus was measured either parallel (x 1) or perpendicular (x 2) to the direction of strain applied to the type of ice as indicated. Slope values are in units of GPa ÷% porosity
Although we were unable to directly measure crack density in saline ice, we have described how porosity may serve as an approximate measure of damage. According to Eqn (16), a change in porosity of Δφ = 8% corresponds to a dimensionless scalar crack density, ρ c, of 0.30. Thus the results (Fig. 16) could be translated in terms of crack density, albeit tentatively with regard to saline ice.
Again plotting Young’s modulus versus porosity, Figure 17 combines the means of x 1 measurements from common parent specimens (i.e. each of the data points here represents the average over two to four subspecimens cut from the same initial block of strained ice; Fig. 1) of both freshwater and saline ice with an aggregate trend line, along with previously reported measurements of sea ice from the sources noted in the legend. Error bars on the previous data, in gray, extend between original and newly adjusted values. The top of each error bar marks the value originally published by Reference Langleben, Pounder and KingeryLangleben and Pounder (1963) who, lacking S-wave velocity measurements, calculated E by assuming a value for the Poisson’s ratio of ν = 0.295, based on other tests. Except for the highest strain cases, our data generally follow the same trend but slightly below the original field data. Equations (6) and (7) can be solved for the S-wave velocity in terms of P-wave velocity and Poisson’s ratio:
Fig. 17. Young’s modulus versus porosity. Data from current work (circles) are compared with previous field data (squares) from Reference Langleben, Pounder and KingeryLangleben and Pounder (1963).
This allows Young’s modulus to be written as
Using this formulation, the original Young’s modulus values were rescaled using an alternative analysis of the dynamic Poisson’s ratio for sea ice (Reference Timco and WeeksTimco and Weeks, 2010), which at −10°C gives ν = 0.34, close to our measurements (Table 3). The adjusted values are shown as the bottom of each error bar in Figure 17, with the square symbols at the midpoints. Linear fits through the original and adjusted sea-ice data closely match the slope of our laboratory data and bound them on either side. The field measurements were made from vertical ice cores, placing transducers at the ends for ultrasonic transmission along their lengths, which corresponds to what we have defined as x 3. This direction is marginally stiffer than across-column directions, possibly another factor contributing to slightly higher moduli in the original field data. At the highest levels of strain in our tests, the nature of damage was different, with large crack openings observed, so it was not surprising that those data (φ ≳ 10%) departed from the trend.
Comparison with the non-interacting crack model
Returning to our quantification of damage in terms of crack density, we tested the non-interacting crack model against our elastic modulus data. In choosing this model, we assume that cracks do not interact significantly at strain levels ε p ≤ 0.10 (i.e. before cracks begin to open substantially). We emphasize that the model does not require the absence of interactions altogether, but rather that stress amplifications and stress-shielding effects mutually cancel each other.
For the 3-D case of randomly oriented penny-shaped cracks, in which α simplifies to α 11 = α 22 = α 33 = ρ c/3, Reference KachanovKachanov (1992) derived the effective Young’s modulus
as a result of damage measured by ρ c and in terms of E 0 and ν0, the Young’s modulus and Poisson’s ratio, respectively, of the corresponding undamaged material. For the extreme situation in which all cracks are parallel (say, normal to x 1 such that α 22 = α 33 = 0), the effective Young’s modulus in the common normal (xi ) direction is
In the 2-D case, for randomly oriented non-interacting cracks, α is isotropic and the effective Young’s modulus simplifies to (Reference KachanovKachanov, 1992)
and for parallel cracks normal to xi ,
These models all have in common a reduced modulus inversely proportional to (1 + Cρ ), where C is a constant, because the additional compliance due to damage is a linear function of crack density. Compare these models to the effective stress model, which gives
a linear function in damage variable D (Reference LemaitreLemaitre, 1984), which may be equated with ρ c,3-D.
Figure 18 plots the theoretical E 1 eff, 3-D (dotted curve) and E 1 eff, 2-D (solid curve) predicted according to Eqns (21) and (23), as functions of the dimensionless crack density tensor component, α 11, and E eff, 2-D (dashed curve) and E effσ (dash-dot curve), from Eqns (22) and (24), as functions of the crack density scalar, ρ c. On the same graph are the data obtained by ultrasonic transmission for Young’s modulus, Ei , of the strained specimens of freshwater ice as a function of αii ≈ αi , the principal component of the crack density tensor in the direction xi , quantified from thin sections cut in the x 1-x 2 plane. Off-diagonal components of α were essentially zero, meaning that the principal axes aligned closely with the specimen edges, with the first principal direction coinciding with the x 2-direction. Note that for all strains >0.003, the E 2 value is less than, and 22 is greater than, the corresponding E 1 and 11 values at the same strain condition (Fig. 18).
Fig. 18. Comparison of measured and theoretical Young’s modulus of damaged freshwater ice as a function of dimensionless crack density. The ‘2-D’ and ‘3-D’ theoretical curves are based on the non-interacting (NI) crack model. The dash-dot curve is based on the effective stress model (Eqn (24)). The data points show the mean data for Ei obtained by ultrasonic transmission at each strain condition, as indicated in the legend, against the crack density tensor component, αii , measured in the corresponding direction, xi (using closed symbols for x 1 and open symbols for x 2). Lines across data points extend two standard deviations in Ei , and show an estimated uncertainty in crack density ascertained from those cases where αii values were taken from multiple thin sections.
The theoretical (solid) curve of E 1 eff, 2-D follows the trend in experimental values of E 1 for strains up to ε p = 0.10. E is nonlinear according to Eqn (23), but its reciprocal, the compliance, is linear in crack density and can be expressed as
in the x 1-direction for parallel cracks. A least-squares fit to the data in terms of S 11 gives coefficient s 0 = (9.540 GPa)−1 and s 1/s 0 = 6.178, which is within 2% of 2π, the value expected from the 2-D model.
At higher crack densities, resulting from strain ε p > 0.10, the 2-D model underpredicts Young’s modulus compared with our measurements (which also had greater scatter; note the large error bar at the point near α 11 = 0.15 for strain ε p = 0.15). The model fares worse with the x 2-direction, considering measurements of E 2 as a function of α 22 ≈ α 2 (Fig. 18, open symbols). At the lowest strains tested, the data lie near the 3-D model (Eqn (20)), which predicts a much lesser effect on E than the 2-D model, because cracks are averaged over volume instead of area. At most strain levels, however, E 2 falls somewhere between the two models.
These discrepancies may be explained by a host of factors, including (1) the limitations of our experimental instruments, (2) asymmetric crack shapes and (3) the evolving nature of damage. Regarding the first factor, the resonant frequency of the ultrasonic transducers (200 kHz) implies an upper bound on the length of detectable cracks. For c P = 3800 m s−1 the corresponding wavelength is 19 mm, thus cracks with half-lengths ci ≳ 1cm may not contribute to the measured elastic properties. This bias may explain the higher-than-predicted E 1 value at ε p = 0.15; it is only at that level of strain that we begin to see half-lengths longer than ∼1 cm in across-column (x 1-x 2) thin sections.
It is important to remember that what we see in x 1-x 2 thin sections are just traces of cracks that primarily run parallel to the columnar grains (x 3), so the measurements often represent the shorter dimension of cracks that are clearly not penny-shaped. The first implication of asymmetric crack shape is that crack densities ( α or ρ c) are generally lower by a factor of 3 or more when computed using x 1-x 2 thin sections compared with x 1-x 3 or x 2-x 3 thin sections.
To illustrate one source of uncertainty involved in measuring crack traces in thin sections, Figure 19 shows a diagram of damaged material containing tall, narrow cracks with a thin section cut across the horizontal plane above. In the thin section, the traces reveal only the narrow dimension of the cracks, so the characteristic areas (solid red circles) about each crack would underestimate the 3-D crack density. In contrast, areas based on the tall dimension of cracks (dotted red circles) will overestimate crack density.
Fig. 19. Diagram of tall, narrow cracks, illustrating the potential error in characteristic areas determined from traces in a horizontal plane (solid red circles) or in a vertical plane (dotted red circles). Ellipses give a better approximation, but their dimensions remain difficult to ascertain.
So far, we have assumed circular crack shapes in our discussion of damage models, conceptually extrapolating from crack half-length in 2-D to crack radius in 3-D. To remove this assumption, generalizing to an elliptical crack shape modifies the definition (Eqn (2)) as
in which Ai = πab is the area and Pi = 4aE(k) is the perimeter of the ith crack, with a and b the major and minor semi-axes of the ellipse, respectively (Reference Budiansky and O’ConnellBudiansky and O’Connell, 1976). The perimeter term includes
a complete elliptic integral of the second kind, where k 2 = (1 − b 2/a 2) (Reference Budiansky and O’ConnellBudiansky and O’Connell, 1976). For circles, k = 0 ⇒ E(k) = π/2 and Eqn (26) simplifies to Eqn (2). At the other extreme, k → 1 ⇒ E(1) = 1 for highly attenuated ellipses.
We could reasonably approximate some of the cracks that form along grain boundaries as ellipses having aspect ratios a/b as high as 5 or more. Solving Eqn (27) for this aspect ratio 
givesc, ρ
c, 2-D (a = 5b) ≈ 2.4πρ
c, 3-D(a = b). In other words, if we treat short crack traces (as in x
1-x
2 thin sections) as minor semi-axes of long ellipses instead of as radii of circles, the crack density will increase by a factor of 7.5. Certainly, not all the cracks in our ice specimens were so attenuated, but some additional correction seems required in order to compare 2-D and 3-D cases on any equivalent terms. The non-interacting (NI) crack model predicts a substantially weaker reduction of stiffness for cracks in 2-D than in 3-D, but Reference Kachanov, Hutchinson and Yao-tsu WuKachanov (1994) notes that that ‘conclusion is somewhat relative, though, since each of the definitions [of crack density] can always be made to incorporate an arbitrary multiplier.’
We might expect a scaled 3-D crack model to be a better fit for similar tests on granular ice, in which, up to moderate levels of damage, cracks would remain confined within the equiaxed grains and thus would be better approximated as penny-shaped. None of the damage models can fully account for the diversity of crack geometries, made of irregular surfaces or composite shapes, such as wing crack extensions.
The second implication of asymmetric crack shape is that the long dimension (only) of many of these cracks may exceed the ultrasonic detectable length. In all x 1-x 2 thin sections analyzed, crack density was greater in x 2 than in x 1, as expected, given the tendency for cracks to align along the direction of uniaxial strain. Thus, instrumental bias error (contributing to artificially high E values) may be exacerbated in the x 2-direction, in which the relative quantity of attenuated cracks is greater. Moreover, we observed attenuated cracks and decohesions along grain boundaries occurring and saturating earlier (in terms of strain) than shorter transgranular cracks (compare Fig. 3b with Fig. 4e; also Figs 10 and 9). In other words, the average crack geometry looks more penny-shaped as strain increases, which may help to explain why the divergence of x 2 data from the 2-D model also improves as strain increases.
Complicating this issue is our conflation of decohesions resulting from grain-boundary sliding and intergranular cracks. Consider Figure 20, where long narrow cracks are represented as arrays of shorter penny-shaped cracks (dotted circles). Discontinuities along attenuated fracture surfaces, as observed previously in decohesions (Reference Weiss and SchulsonWeiss and Schulson, 2000), may occur at intervals along a length that otherwise might have exceeded detection by certain acoustic pulses. At this time, we do not know exactly how the different fracture features influence ultrasonic transmission measurements. These speculations deserve further study.
Fig. 20. Diagram of long attenuated cracks represented by arrays of shorter penny-shaped cracks (dotted circles).
Another factor to consider is the observed change in the nature of damage, namely the preponderance of large cracks opening as wide as 2 cm at a strain of 0.10 or more, and therefore the difficulty of measuring representative intact subspecimens. These higher levels of damage may exceed either the valid range in which cracks can be assumed to be non-interacting, or (perhaps more fundamentally) the range in which the material can be considered as a continuum.
An altogether separate question is whether crack clustering plays a significant role in affecting the elastic properties. To explore interactions among N cracks that are not randomly located requires manipulating an N × N matrix to transmit the influence of each individual crack to the rest of the array, accounting for crack lengths, positions and orientations (Reference KachanovKachanov, 1993). This is challenging to implement, so other approximations are often employed, as in a crack-matrix-effective-medium approach to model damage evolution (Reference Paliwal and RameshPaliwal and Ramesh, 2008). Compared to the scale of error due to the other factors we have discussed, we suspect that crack clustering would have negligible, if any, effect on bulk elastic properties, although the effect on other properties and processes, such as brittle fracture, could be very significant (Reference KachanovKachanov, 1992). Whereas crack interactions can strongly influence macroscopic resistance to rupture, due to their local effect on stress intensity factors, this does not contradict the NI crack hypothesis regarding elastic properties, based on the mutual cancellation, on average, of amplification and shielding effects of cracks overall (Reference Kachanov, Hutchinson and Yao-tsu WuKachanov, 1994). Notwithstanding the various sources of uncertainty, the general trend of elastic measurements in strained freshwater ice supports the applicability of the non-interacting crack model.
Further discussion
The physics underlying the damage models deserves further discussion. Formulations for effective moduli (Eqns (21–23)) that we have borrowed from the non-interacting crack model are derived from considerations of crack mechanics involving Mode-I openings only. Reference Kachanov, Hutchinson and Yao-tsu WuKachanov (1994) describes how the model can handle compressive loading conditions, including frictional sliding, in which Mode-II and Mode-III stress fields also apply. The major modification is that compressive loading becomes path-dependent and invalidates the elastic potential from which Eqn (4) is derived for the additional (due to damage) compliance, ΔSijkl . A fourth-rank tensor term enters the crack density, since elastic anisotropy, in general, as opposed to orthotropy, is induced under applied compressive stress (Reference KachanovKachanov, 1992).
The current work can be extended in several directions, and we caution the reader that different effects of damage may occur under conditions that depart from those producing the results presented herein. The ultrasonic transmission method creates a condition equivalent to loading at very high rates but very low stresses. Thus we do not expect tension/compression asymmetry or frictional effects to be significant in our elastic property measurements. However, under compressive stress states, friction may have an influence on elastic compliance that is not yet fully understood. In this connection, possible temperature and rate effects are also worth considering, as sliding resistance in ice depends upon both temperature and sliding speed (Reference Schulson and DuvalSchulson and Duval, 2009). The effects of damage under dynamic loading scenarios (e.g. at high strain rates or in the absence of creep) have not yet been addressed, but are worthy of investigation.
Conclusions
Experiments on columnar ice have demonstrated that the effective elastic compliance of the bulk damaged material correlates strongly with measurable crack density and porosity, up to a critical level of damage. Beyond a strain of ε p ≈ 0.10, the damage evolves to take on a different character, with cracks opening to form voids, sometimes much wider than the grain diameters. At this level, possibly departing the realm of continuum damage mechanics, the relationship between damage and effective properties becomes indeterminate. Increasing damage also increases the variability in porosity and elastic properties. Nevertheless, for porosity up to ∼10%, our Young’s modulus measurements (in x 1, the direction of strain) correspond well with the values predicted by a non-interacting crack model (Fig. 18), as well as with previous field measurements on ice with that range of porosity (Fig. 17). Although we were unable to directly quantify crack density in saline ice, its porosity and elastic properties followed similar trends to freshwater ice, so it is reasonable to infer that damage and its effects evolve comparably in the two materials.
We imparted damage by uniaxial compression at two fixed strain rates: one and two orders of magnitude below the ductile-to-brittle transition strain rate of the undamaged material. The results show that increasing strain rate enhances the effects of damage. As measured by scalar crack density, damage itself also evolves more rapidly with strain at higher strain rates. In contrast, we see less recrystallization, although it, too, increases with strain, as strain rate increases. Furthermore, Young’s modulus nearly coincides in specimens with similar crack densities or porosities, even if they contain quite different amounts of recrystallization (compare specimens in Fig. 3a and Fig. 5a, both with E ≈ 9.0 GPa). Therefore we conclude that recrystallization plays a minor role compared with damage in columnar ice regarding its elastic properties. Consistent with this conclusion, we detected in freshwater ice a strain-induced anisotropy, in which Young’s modulus measured was lower in the x 2-direction than in the x 1, the direction along which cracks preferred to align and, thus, normal to which the crack density tensor component was higher. Within a limited but useful range, the bulk elastic properties provide a quantitative indication of damage. Moreover, even simple measures of damage, such as porosity, can be useful for predicting bulk elastic properties.
Acknowledgements
We thank Stephen Nodder for his assistance analyzing thin sections. The reviewers are thanked for their comments and suggestions, which improved the quality and clarity of the paper. This work was supported by the US Department of the Interior–Bureau of Safety and Environmental Enforcement (BSEE), contract No. E12PC00033.
Appendix A: Aggregate Elastic Properties
Equations (11) express the shear modulus with two subscripts to articulate its definition as the stress-to-strain ratio under simple shear acting in direction j:
where σij denotes stress and γij denotes engineering shear strain (i ≠ j). However, the ultrasonic method we used was unable to distinguish a unique shear wave direction. Thus when we speak of measuring G 1 (Eqn (8)), for example, this quantity actually reflects some combination of G 12 and G 13, which generally have different values. Similarly for G 2. Likewise, the definition of the independent Poisson’s ratio:
involves a specific direction, j, of lateral strain relative to the direction, i, of an applied uniaxial stress, σi . Of the quantities obtained by ultrasonic measurements, we might say that Gi and νi are aggregates of aggregate properties, in this way:
and
where χ is a weighting coefficient, in the spirit of Reference Nanthikesan and Shyam SunderNanthikesan and Sunder (1994), who calculated aggregate elastic moduli and compliances based on the spatial distribution of grain orientations in polycrystalline ice. Here, the two contributions to the weighted averages in Eqns (A1) and (A2) represent the transverse across-column and along-column directions perpendicular to the longitudinal across-column direction of the long axis of subspecimens (Fig. 1b).
Appendix B: Thin-Section Digital Analysis
This appendix explains how digital images of thin sections were analyzed and describes some of the subtleties involved in computing the crack density tensor, α, using fracture patterns traced from those images. Digital photographs of thin sections were viewed and traced using imageJ (Reference RasbandRasband, 1997–2014) open-source software. ImageJ allows images to be scaled to real units if a feature of known length appears in the frame. Thus when photographing a thin section, we placed a scale marked in millimeters alongside it within the field of view. As the first step in analyzing each thin-section image, the ‘line selection’ tool in imageJ was used to trace, along the marked scale, a line segment extending from 65% to 90% of the image width, in order to reduce error due to both resolution and lens distortion. Most thin-section photographs captured an area greater than 100 mm × 50 mm with image sizes exceeding 2000 × 1000 pixels, giving resolutions finer than 20 pixels mm−1. Tick marks on the scale appeared to be a few pixels in thickness; in tracing along 100 mm, we might conservatively expect an uncertainty of 4 pixels, or 0.2 mm. After drawing this line segment in imageJ, the ‘set scale’ tool was used to define the physical length that it represented. Then the scaled image was cropped to a standard area of 5000 mm2, if possible, and saved as a separate file to preserve the original.
The images taken in cross-polarized light were analyzed in imageJ to assess the extent of recrystallization. Polygon or freehand selections were made around the perimeters of regions containing recrystallized grains, identifiable by virtue of being smaller (and in along-column thin sections, equiaxed) compared to typical parent grains. Each selection was added to the ‘ROI manager’ list. The ‘measure’ command then automatically tallied the scaled areas of all regions in the list to a results table to be exported to a file. The sum of these areas was divided by the total image area to obtain the recrystallized area fraction, ρ rx.
The images taken in scattered light were used to trace cracks, again using the line selection tool in imageJ. For cracks that curved or consisted of multiple segments a single trace was drawn. After each crack was traced, the selection was added to the ROI manager list and, this time, their lengths as well as angles were measured and tallied automatically. It is important to understand the particular way that imageJ measures line segments. The pixel coordinate system in imageJ locates the origin at the top left corner of the image. ImageJ defines the angle, , of a line segment in a positive-counterclockwise sense, relative to a baseline that is parallel to the horizontal axis of the image. However, that baseline can emanate from either endpoint of the line segment, depending on the direction in which it was drawn. Figure 21 illustrates the possible situations. For example, if a line is drawn from a lower left point diagonally up to the right (Fig. 21a), then 0° ≤ θ ≤ 90°, naturally enough. But if the same line is traced in the reverse manner, starting from the upper right (Fig. 21b), then the reference baseline is also put at the upper right, imageJ returns a negative angle, −180° < θ< −90°.
Fig. 21. Image coordinate system (x, y) with parameters Bx , By , w, h and angles, θ, describing line segments as reported by imageJ software (Reference RasbandRasband, 1997–2014). Note the orientation of θ depends on the direction in which the line segment was drawn (indicated by the arrows).
For our purposes (computing crack density tensors), it would be convenient to define crack angles such that −90° ≤ θ ≤ 90°. If one could remember always to trace cracks from left to right, this would ensure |θ| ≤ 90°. Otherwise, if one (like this author) failed to anticipate the peculiarities of the software, one can transform the θ that imageJ returns by using its range to deduce the direction in which the line segment was drawn – a property that imageJ does not save or report explicitly. Neither does imageJ report the coordinates of the line segment endpoint, which would also be convenient to know. Other useful properties can be reported directly, however, by selecting ‘bounding rectangle’ in the ‘set measurements’ menu. This provides the height, h, and width, w, of the bounding rectangle of which the line segment forms the diagonal, along with coordinates Bx and By . The point (Bx , By ) is always anchored at the top left corner of the rectangle, regardless of the direction in which the line segment was drawn. Thus, (Bx , By ) may not always lie on the line segment. Working with these reported values and keeping in mind the upside-down coordinate system, the following transformations give the endpoints of the line segment and its angle, θ, in the desired range:
In addition to these angle transformations, the reference point can be translated to coincide with the lower-left endpoint of the line segment:
This makes it easier to locate the individual crack traces (e.g. for plotting the crack patterns), particularly if the coordinate system needs to be transformed (e.g. to flip the x- and y-axes), which was useful in maintaining consistent thin-section orientations (see Fig. 8). With respect to horizontal (xu = x) and vertical (xv = −y) coordinates, thin-section images were always oriented such that, for along-column sections, x 3 was vertical, and for across-column sections, x 2 was vertical. That is, x 1 was never vertical.
In the 2-D image coordinate system, the components of the unit vector, ni , normal to the ith crack trace are
These are the vectors used in Eqn (3) to compute the crack density tensor α ,
Open access
