1. Introduction
The time required for transformation of polar firn to glacial ice is generally from 100 years to >1000 years depending on the in situ accumulation rate and temperature (Reference Cuffey and PatersonCuffey and Paterson, 2010). The rate of firn compaction depends inversely on firn density (Reference Cuffey and PatersonCuffey and Paterson, 2010), with lower-density firn layers compacting faster than higher-density layers. Thus, during the transformation, firn layers with anomalous densities caused by variations of the surface weather conditions are continuously adjusting towards a long-term density–depth profile. This implies that surface-height changes due to variations in compaction rates will take some time to decline, but this time should be effectively shorter than the firn–ice transition time. A principal characteristic of the compaction process is that the resulting surface-height changes occurring at any particular time are very much dependent upon the time history of the surface conditions.
Detailed information on the compaction process is needed, because a primary purpose of satellite observation of surface-height changes, dH/dt, of the polar ice sheets has been to estimate the corresponding mass changes, dM/dt. Estimation of dM/dt from dH/dt requires corrections for the firn compaction (FC) height changes that do not involve changes in mass (e.g. Reference Li and ZwallyLi and Zwally, 2011; Reference ZwallyZwally and others, 2011; Reference ShepherdShepherd and others, 2012; Reference WoutersWouters and others, 2015). Calculation of FC height changes requires information on surface temperature and accumulation variations for some time prior to and during the observations of dH/dt. Therefore, a primary purpose of this paper is to derive the response times of the firn to typical short-term variations of surface accumulation A s(t) and temperature T s(t), so the length of the needed time series prior to (as well as during) the period of dH/dt measurements can be determined. Prior investigations of the response time of firn compaction are limited. Reference Arthern and WinghamArthern and Wingham (1998) used an early version of their numeric model with less temperature sensitivity and examined the surface height (H(t)) response to two examples of step changes in A s(t) and T s(t). Reference Kuipers Munneke, Ligtenberg, Suder and Van den BroekeKuipers Munneke and others (2015) recently examined the response time of dry and wet firn to the 1°C step temperature changes at different accumulation rate levels using the model developed by Reference Ligtenberg, Helsen and Van den BroekeLigtenberg and others (2011). In this paper, we review characteristics of several FC models including their functional dependencies on firn temperature and accumulation that affect the response times. We examine the firn responses to perturbations of A s(t) and T s(t) by performing sensitivity experiments with our model for selected sites on the Antarctic ice sheet, using sample perturbations and data on time series of A s(t) and T s(t).
2. The Rate of Surface Height Change (dH/dT) Components
The rate of surface height change dH/dt of polar ice sheets consists of a number of components from different processes. The complete perturbation form of the rate equation was given by Reference Li and ZwallyLi and Zwally (2011) and Reference ZwallyZwally and others (2011),
where the first three terms are caused by surface accumulation anomalies, δA s(t) = A s(t) − A m, and surface temperature anomalies, δT s(t) = T s(t) − T m, with respect to their long-term means, A m and T m. dH a/dt is the direct height change from δA s(t), and dC A/dt and dC T/dt are the changes in firn compaction rates driven by δA s(t) and δT s(t) respectively. dH d/dt is the ice-dynamic term caused by imbalance between the ice flow and the long-term average surface balance. dH b/dt is the component due to surface melt in the ablation zone, which for most of Antarctica is not significant. dB/dt is the vertical motion of the bedrock. The direct and indirect effects of δA s(t) on surface-height change are combined as
Although the direct-height change, dH a/dt, and its FC response, dC A/dt, are separately of interest, we focus here primarily on their sum, dH a CA/dt, as the combined effect of the accumulation anomalies, δA s(t). The rationale for this focus is that dH a CA/dt can be considered as an observable quantity, based on Eqn (1) and altimetric measurements of dH/dt along with independent estimates of the other terms in the equation. We perform the numerical experiments under A m and T m conditions for sample sites in Antarctica to examine the characteristics of H a CA(t) and C T(t) and, more importantly, their rate changes, dH a CA(t)/dt and dC T(t)/dt, in response to selected perturbations of δA s(t) and δT s(t).
3. Firn Compaction Model
Our FC model is based on a one-dimensional time-dependent formulation of firn densification coupled with the heat-transfer equation. The model includes an explicit time dependency on surface accumulation rate A s(t) as well as temperature T s(t). The initial development of the model was described by Reference Zwally and LiZwally and Li (2002) and was later improved by incorporating melt and refreezing processes (Reference Li, Zwally and ComisoLi and others, 2007). The model is based on the steady-state densification relation given by Reference Herron and LangwayHerron and Langway (1980):
The parameter A m in this steady-state formulation is a measure of the change of the overburden pressure, and K is the Arrhenius-type rate constant that was dependent on temperature given by
E1 and E2 in Eqns (4) and (5) were empirically derived activation energies with respective values of 10.16 and 21.40 kJ mol−1, lower than the commonly used values, 40–42 kJ mol−1 for grain growth (Reference Cuffey and PatersonCuffey and Paterson, 2010) as discussed by Reference Herron and LangwayHerron and Langway (1980). In Eqns (3–5), both T m and A m are constant mean values. The power index α had values of 1.1 and 0.5, respectively, for firn relative density ρ< 0.55 and ρ> 0.55 (relative to 1 gm cm−3 density of water).
For the time-dependent case, our modification of Eqn (3) is
where the temperature-dependent factor K used by Reference Zwally and LiZwally and Li (2002) and Reference Li and ZwallyLi and Zwally (2011) is
The model was initially (Reference Li and ZwallyLi and others, 2002; Reference Zwally and LiZwally and Li, 2002) made time-dependent on T s(t) by coupling with the heat-transfer equation
to calculate T(z, t). We later (Reference Li and ZwallyLi and Zwally, 2011; Reference ZwallyZwally and others, 2011) made the model time-dependent on A s(t) by replacing A m in Eqn (6) by the average accumulation rate above depth z, i.e.
where tz is the time taken for the layer to propagate from the surface to depth z. A L(z, t) reflects the average change of the overburden pressure applied to a firn element at depth z that gradually propagates downward in time with changes in A s(t), which is similar to the use of A m in the time-independent formulation (Eqn (3)).
A principal advancement in Reference Zwally and LiZwally and Li (2002) was that Eqn (7) made the densification rate more strongly dependent on temperature than Eqns (4) and (5). The stronger temperature dependence resulted from incorporating nonlinear temperature dependences, for both the activation energy and the rate constant in the densification equation, that were based on laboratory and field experiments of ice deformation and grain growth. This stronger dependence on temperature significantly increased the rate of firn compaction, particularly for the higher summer temperatures due to the time dependence of T s(t) and the nonlinear temperature dependence of the compaction rate. The model produced seasonal cycles in compaction that explained observed seasonal variations in surface height (Reference Zwally and LiZwally and Li, 2002; Reference Li, Zwally and ComisoLi and others, 2007) and seasonal layers in density profiles (Reference Li and ZwallyLi and Zwally, 2002; Reference Morris and WinghamMorris and Wingham, 2014).
Our initial model was adopted by others (e.g. Reference HelsenHelsen and others, 2008), and the stronger temperature dependence was also confirmed by field measurements in the Antarctic Peninsula (Reference Arthern, Vaughan, Rankin, Mulvaney and ThomasArthern and others, 2010). Reference Arthern, Vaughan, Rankin, Mulvaney and ThomasArthern and others (2010) re-parameterized the rate constants from their previous formulation (Reference Arthern and WinghamArthern and Wingham, 1998) and incorporated grain growth process to further increase the temperature sensitivity. However, comparisons with the field data show that their increased temperature sensitivity is too high for other locations in Greenland and Antarctica (e.g. Reference Ligtenberg, Helsen and Van den BroekeLigtenberg and others, 2011; Reference Simonsen, Stenseng, Aðalgeirsdóttir, Fausto, Hvidberg and Lucas-PicherSimonsen and others, 2013). Their formulation cannot be directly applied to the large regions of polar ice sheets without re-parameterization of the rate constants. In fact compared with Eqn (7), the functional part of the temperature dependence in Reference Arthern, Vaughan, Rankin, Mulvaney and ThomasArthern and others (2010) has higher temperature sensitivity mainly for lower temperatures. For temperatures above −15°C or so, Eqn (7) still provides significantly higher-temperature sensitivity, implying our model compacts firn relatively less during winter and more during summer, which causes larger seasonal variations in density and surface height as a consequence.
An important aspect of our model is the time-dependent treatment of the accumulation rate, which is essential for determining the proper time response of the firn to accumulation variations. Simply substituting A s(t) for A m in Eqn (3) causes the model densification to cease at all depths during times of zero A s(t) at the surface, which clearly would not be realistic. Also, during periods of a positive (or negative) δA s(t), the densification rate would increase (or decrease) at all depths during the anomaly, and then immediately change to the mean rate afterward. In general, there would be no dependence on the time history of the perturbations, as there necessarily is in a time-dependent treatment. In the model of Reference Ligtenberg, Helsen and Van den BroekeLigtenberg and others (2011), the accumulation rate appears as a constant in their equations 5, 8 and 9. Therefore, it is not clear whether they used a time series of A s(t) in their formulation as well as a time series of T s(t).
For Antarctica, we calibrate our model by choosing values of β in Eqn (7) that are a function of A m and T m similar to that described by Reference Li and ZwallyLi and Zwally (2011) for Greenland, with β=β 1 from the surface to the density of 0.55, and β= β 2 for densities greater than 0.55. We first calculate two firn ages of t 0.55 and t 0.83 corresponding to the densities of 0.55 and 0.83 according to Reference Herron and LangwayHerron and Langway’s (1980) density–age relation, in which the ages are functions of A m and T m with the selected typical surface density of 0.3. Herron and Langway’s density–age relation was constrained by density data from 17 ice-core sites and has been widely used for steady-state firn densification over Antarctica. We calculate t 0.55 and t 0.83 for 21 locations that essentially cover the entire ranges of A m and T m in Antarctica. We use the long-term values of A m from Reference Giovinetto and ZwallyGiovinetto and Zwally (2000) and the T m that is the mean annual temperature for the first 3 years (1982–84) from satellite-observed temperatures from the Advanced Very High Resolution Radiometer (AVHRR) (Reference Li, Zwally and ComisoLi Antarctica and others, 2007) For each site with its pair of A m and T m, we first run the FC model by iterating the β=β 1 value until the model-produced density of 0.55 and the corresponding age are in agreement with the values of t 0.55. The results for 1 as a function of T m for the 21 locations are shown in Figure 1a.The coefficients for the linear relation between β1 and Tm with a correlation of 0.993 are

Fig. 1. (a) Plot of the iterated β 1 versus T m at 21 sites in Antarctica for the model calibration. Equation (10) is given by the fitted line (R = 0.993) in the diagram. (b) Plot of the iterated β 2 as a function of A m and T m. Equation (11) is determined from the multivariant linear regression on both A m and T m. (c) Plot of the calculated β 2fit (i.e. β 2) according to Eqn (11), versus the iterated β 2 with linear correlation 0.981.
We then run the model using the determined β1 and iterating values of β = β 2 for the further depths until the model-produced density of 0.83 and the corresponding age are in agreement with the values of t 0.83. The results in Figure 1b show that β 2 is a function of A m as well as T m. We therefore write β 2 as a function of β 1 times a linear function of A m and T m. From a multivariant linear regression we obtain
The relation between the parameterized β2 according to Eqn (11) and the iterated β2 with a correlation of 0.981 is shown in Figure 1c. Finally, we note that because the β-calibration parameters are functions of constant A m and T m, there is a possible undetermined higher-order time dependence on accumulation and temperature that is not accounted for in our and other similar FC models. We also performed experiments using the surface density of 0.33 at these 21 sites. The impact to the density profiles is rather small, within ±0.4% on average in terms of firn–ice transition depth.
A comprehensive comparison of FC models was performed by the Firn Model Intercomparison Experiment (FirnMICE) group (Reference LundinLundin and others, 2013). Six models including Reference Li and ZwallyLi and Zwally (2011) were used to calculate the values of t 0.83 over a wide range of A m and T m (Reference Yoon, Stevens, Vo and WaddingtonYoon and others, 2014). All six models are accurate within ±5% of the observed t 0.83. Calculations of the deviation of t0.83 from the mean of the six models showed our model was the closest to the average of the six models.
4. The numerical experiments
In order to examine the response time of the surface height to δA s(t) and δT s(t) perturbations, we perform numerical experiments with our FC model using monthly time steps and the climate conditions for several locations on the Antarctic ice sheet representing a wide range of T m and A m. For the perturbation experiments shown by Figures 2–5 for Byrd and Vostok, we initialize the model to steady-state conditions under constant T m and A m using the values described in Section 3, and then use the perturbations to drive the model. We first apply impulse variations of δA s(t) at constant temperature T m, and then impulse variations of δT s(t) at constant accumulation A m. The sample perturbations (δA s(t) = ±0.5A m and δT s(t) = +2°C) are chosen to be typical, in magnitude, of the larger short-term (e.g. monthly) natural variations, but of longer duration (5 years) in order to clearly illustrate the response characteristics. We find the functional forms of the responses of surface height, H(t), and of the rate of change of surface height, dH(t)/dt, after a perturbation, to be similar to exponential. Therefore, we use the time for H(t) to change by 63% to within 1/e = 37% of the new value after the perturbation, and the time for dH(t)/dt to recover to within 37% of the initial value, as estimates of the time constants of the responses. Although similar to exponential, the differences between the estimated time constants for H(t) and those for dH(t)/dt indicate that the responses are not exactly exponential. Generally, half-time response estimates (e.g. used by Reference Arthern and WinghamArthern and Wingham, 1998) would be ∼0.7 of our 63% response time estimates for the same experiments (cf. Fig. 2b).
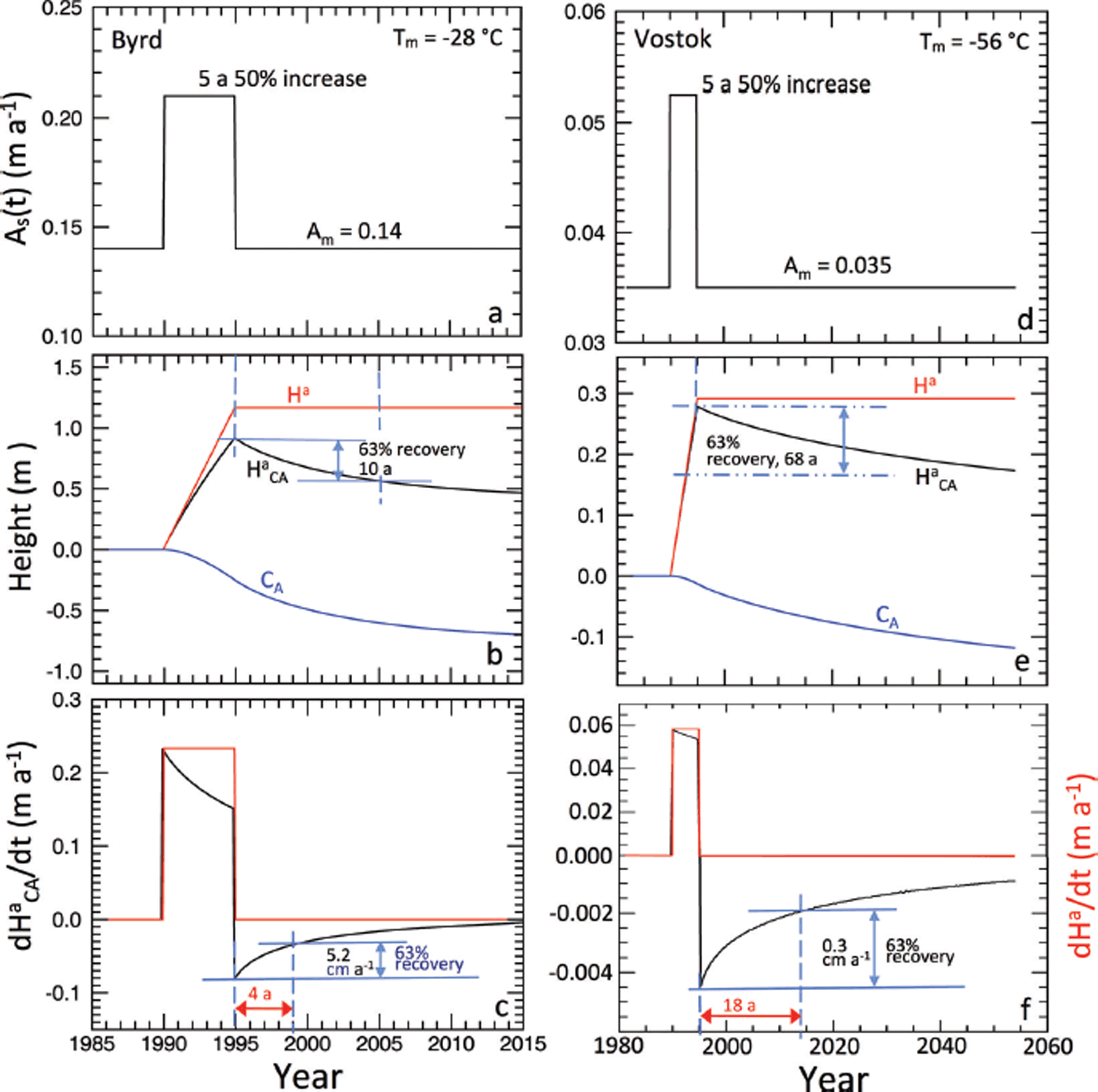
Fig. 2. Sensitivity test of the time response to a single-impulse perturbation in accumulation rate under the climate conditions at (a–c) Byrd, West Antarctica, and (d–f) Vostok, East Antarctica. (a, d) The driving accumulation rates A s(t) for the two locations. (b, e) The corresponding changes in modeled surface height components of H a CA(t), H a(t) and CA(t). (c, f) The rates of the total height change dH a CA(t)/dt and the rates of direct height change dH a(t)/dt, showing the time constants are 4 years for Byrd and 18 years for Vostok, which are shorter than the 10 years and 68 years for the height changes in (b) and (e).

Fig. 3. Sensitivity test of the time response to a double-impulse perturbation in accumulation rate under the climate conditions at Byrd (a−c) and Vostok (d−f). (a, d) the driving accumulation rates A s(t) for the two locations; (b, e) the corresponding changes in modeled surface height components of H a CA(t), H a(t) and C A(t); and (c, f) the rates of the total height change dH a CA(t)/dt and the rates of direct height change dH a(t)/dt, showing the time constants are 4 years for Byrd and 18 years for Vostok (not marked due to negligible amount of the residual), shorter than the 12 years and 70 years for responses of the height changes in (b) and (e). In contrast to the single-pulse perturbations, the magnitudes of both the height changes and the rates of height change are smaller after the double pulse due to the offsetting effect of opposite fluctuations.

Fig. 4. Modeled depth–density profiles for Byrd Station at the three different times of 20, 43 and 68 years (red, green and black), showing how the fluctuations of the density caused by a double-impulse perturbation in accumulation rate for 5 years and ±50% of A m (as given in Fig. 3a) propagate into the firn.
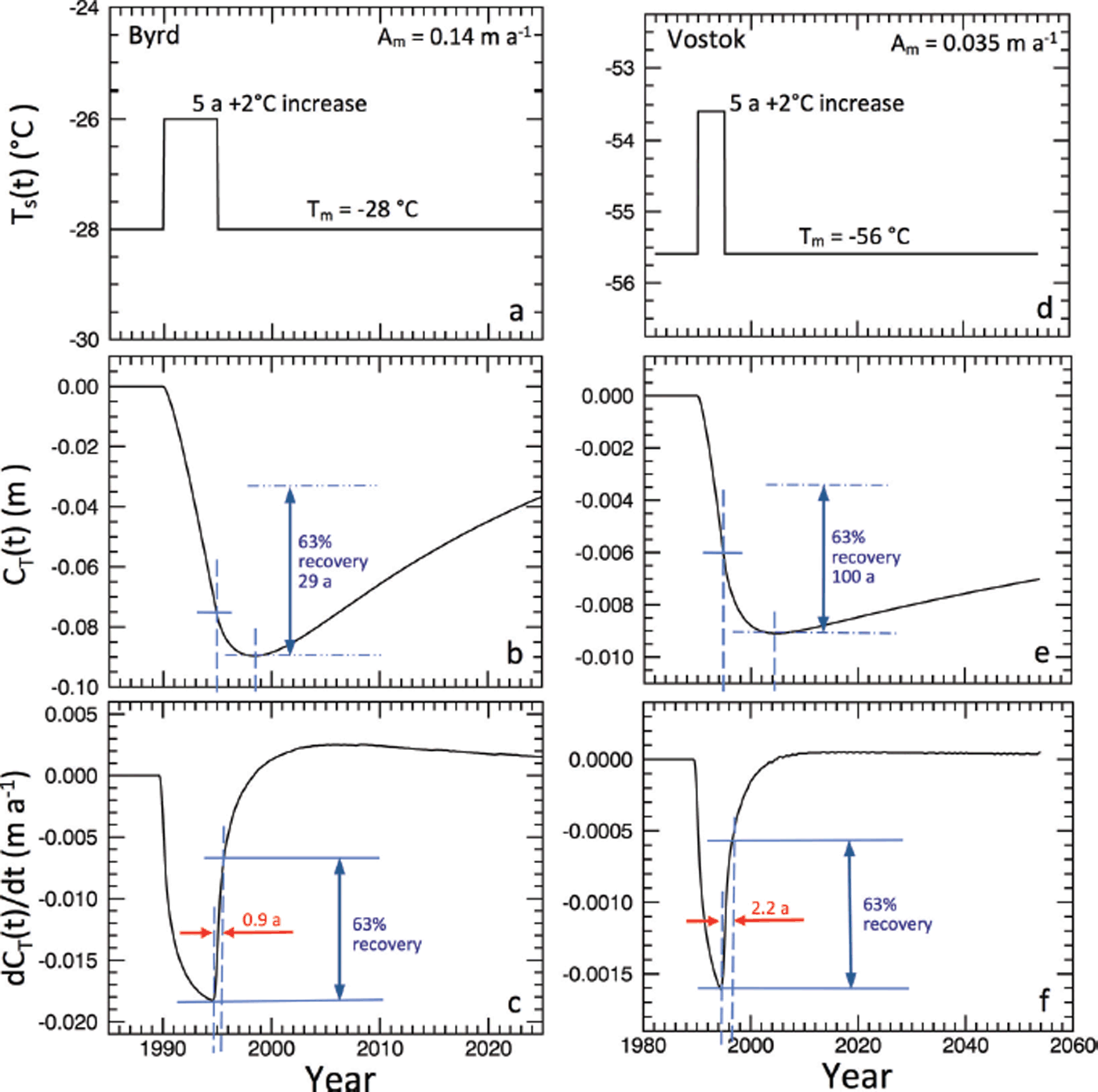
Fig. 5. Sensitivity test of the time response to a single-impulse perturbation in temperature under the climate conditions at Byrd (a−c) and Vostok (d−f). (a, d) The driving temperatures T s(t) for the two locations; (b, e) the corresponding changes in modeled surface height C T(t); and (c, f) the rates of height change dC(t)/dt, showing the time constants are 0.9 year for Byrd and 2.2 years for Vostok, much shorter than the 29 years and 100 years for the height changes in (b) and (e).
For the experiments driven by the climate data shown in Figure 6 for Law Dome and South Pole, we initialize the model to steady-state conditions in 1982, determined by the constant A m, as previously, and the background monthly temperatures that are the average monthly T s(t) for the first 3 years (1982–84) from the AVHRR temperature data. Continuity of the temperature and accumulation forcing data between the initialization to steady state and the continuation with the numerical experiments is especially important to avoid the introduction of an artificial change in the rate of firn compaction and consequently an artificial response of the surface elevation. Beginning in 1982, we apply time series of climate variations for 1982–2008 using the average monthly T s(t) and δA s(t) as described in Section 4.4.

Fig. 6. The surface height response to the monthly variations in accumulation rate A s(t) from ERA-Interim and the surface temperature T s(t) from AVHRR for 1982–2008 at Law Dome Summit, East Antarctica (a−f), and South Pole, Antarctica (g−l). (a, g) The driving accumulation rates A s(t) for the two locations. (b, h) The driving temperatures T s(t). (c, i) The temperature-driven height changes, C T(t), showing clear seasonal variations along with significant interannual changes and trends. (d, j) The components of the accumulation-driven height change; the total change, H a CA(t), the direct change, H a(t) and the FC change, C A(t). (e, k) The rates of total accumulation-driven height change, dH a CA(t)/dt, and the direct height change, dH a(t)/dt, showing that the two rates are closely correlated. (f, l) the slope of dH a CA(t)/dt versus dH a(t)/dt is 0.816 at Law Dome and 0.988 at South Pole, indicating that the observable accumulation-driven height changes reflect the accumulation-rate variations by approximately 82% and 99% for the two sites.
4.1. Experiments with single pulses in accumulation rate
The long-term accumulation rate A m and temperature T m for the Byrd site in West Antarctica are 0.14 m a−1 and −28°C, higher than the 0.035 m a−1 and −56°C at the Vostok site, inland in East Antarctica. The time variations of the driving accumulation rate A s(t), the modeled surface height H a CA(t) with its direct and indirect components, and the rate of change dH a CA(t)/dt with its direct component dH a(t)/dt are shown in Figure 2a–c for Byrd and in Figure 2d–f for Vostok.
Figure 2a shows the A s(t) series with a positive δA s(t) pulse of 50% increase for 5 years at Byrd Station. As soon as the A s(t) increases, the height starts increasing relative to the steady-state surface height, which is taken to be zero (Fig. 2b). Initially, the increase in H a CA(t) is only the direct change, H a(t), but then includes a gradual increase in the negative compaction component, C A(t). During the 5 years of the step increase in A s(t), the H a CA(t) continues rising to a maximum of 0.92 m, which is lower than the value of 1.17 m (calculated from the δA s(t) = 0.07 m a−1 at ρ s = 0.3 for 5 years) because of the increasing rate of compaction. At the end of the pulse, the increased compaction continues (i.e. C A(t)<0) and total accumulation-driven H a CA(t) declines toward an asymptotic value. After the perturbation, the H a CA(t) decreases 63% in ∼10 years.
The response to a sustained step change in A s(t), as might be caused by abrupt climate change, would be immediate and sustained, with H a(t) increasing linearly with time as long as the perturbation lasts and with an increasing C A(t) reducing the total H a CA(t) as shown in Figure 2b and e.
In practice, we are more concerned with the rate of surface height change (i.e. dH/dt) and the associated rate of mass change dM/dt and its rate of contribution to sea-level change. As shown, after A s(t) increases, the dH a CA(t)/dt immediately increases by the maximum amount of dH a(t)/ dt = 0.23 m a−1 (δA s(t)/ρ s) as shown in Figure 2c. The subsequent reduction in dH a CA(t)/dt during the pulse is due to the increase in firn compaction throughout the firn column from the extra amount of the snow added at each time step. In response to the decrease of A s(t) to the regular value A m at the completion of the perturbation, dH a CA(t)/dt drops by the same amount as the initial increase to a negative value, followed by recovery to the value before the perturbation. As indicated in Figure 2c, the time for the 63% recovery in dH a CA(t)/dt is ∼4 years, 60% shorter than the >10 years for H a CA(t), illustrating how the rate recovers faster than the height.
Figure 2d–f show the results for positive δA s(t) pulse of 50% for 5 years at Vostok, East Antarctica, where the climatic conditions are extreme with low accumulation rate and lower temperature (A m = 0.035 m a−1 and T m = –56°C). The features of the change in H a CA(t) and the rate of the change in dH a CA(t)/dt are similar to those for Byrd, but with much smaller magnitudes due to the low accumulation rate. The response time of 68 years for the 63% change in H a CA(t) is much longer at Vostok than the 10 years at Byrd, mainly due to the lower temperature. Although the response time of 18 years for dH a CA(t)/dt is also longer than the 4 years at Byrd, it is also much shorter than the 68 year response time of H a CA(t).
4.2. Experiments with double pulses in accumulation rate
Natural accumulation rates fluctuate, with both positive and negative variations around their long-term means. Therefore, successive opposite fluctuations should partially offset the impacts on the surface height change and reduce the magnitude of the variations. To illustrate the offsetting responses from opposite fluctuations, we perform numerical experiments driven by two opposite pulses of δA s(t), equal to +50% of A m for 5 years followed by −50% for 5 years as shown in Figure 3a for Byrd and Figure 3d for Vostok. The corresponding changes in H a CA(t) together with H a(t) and C A(t), dH a CA(t)/dt, and dH a(t)/dt are also shown in Figure 3b, c, e and f. The first pulse causes the same positive response as the single-pulse case, followed by a similar response in the opposite direction. The negative pulse quickly drives the height to a value below zero, followed by a gradual recovery to the steady-state value of zero. The time for the 63% recovery of the height, H a CA(t), is ∼12 years for Byrd (Fig. 3b) and ∼70 years for Vostok (Fig. 3e). In contrast to the single-pulse case, the total amount of mass added is zero.
Figure 3c shows the corresponding rate changes in dH a CA(t)/dt and dH a(t)/dt for Byrd Station. The changes in both the height and rates of height change are asymmetrical, in contrast to the symmetrical perturbations of A s(t) (Fig. 3a). The positive pulse of the δA s(t) drives a dH a CA(t)/dt increase as described for the single pulse. When δA s(t) decreases from +50% to -50% values, the rate drops by 2 × δA s(t)/ρ s=0.47ma−1 (from 0.15ma−1 to −0.32ma−1) and then gradually increases during the 5 years due to the reduced amount of compaction caused by the decrease in added snow. In response to the change of A s(t) back to the regular value of A m, the dH a CA(t)/dt becomes slightly positive (0.04 m a−1) and then gradually recovers to zero with a time constant of ∼4 years, similar to the single-pulse case. However, the amplitude of the residual perturbation in dH a CA(t)/dt is 50% smaller than the corresponding rate at the completion of perturbation for the single-pulse case (Fig. 2c), indicating that the opposite perturbations of the accumulation rate offset the impacts of the changes in firn compaction on the surface height change as well as offsetting the direct height changes. A response for a negative pulse followed by a positive pulse would be very close to a reflection of the simulation shown for the positive–negative pulse, because the compaction rate equation (Eqn (6)) is a linear function of accumulation. For offsetting perturbations of durations shorter than 5 years, compared to the recovery time (4 years in this case), the fraction of the residual amplitudes of both H a CA(t) and dH a CA(t)/dt would be smaller.
At the colder Vostok location, the H a CA(t) response (Fig. 3e) is a near-linear rise during the positive pulse and a near-linear fall during the negative pulse, reflecting mostly the changes in H a(t) with only minor modifications by the compaction component, C A(t). The small changes in dH a CA(t)/dt during the pulses indicate the minor changes in the compaction rate (Fig. 3f). While the response times of the residuals after the double pulse are similar to the single-pulse cases for both Byrd and Vostok, the amplitudes of the residuals are very small, especially at Vostok. Similar response characteristics are illustrated in the experiments using climate data in Section 4.4. For these experimental cases of symmetrical double pulses of the same magnitude and duration, both direct components H a(t) and dH a(t)/dt are zero after the pulses, which is not always the case for natural fluctuations for which height increases or decreases can accumulate with time.
Variations in compaction rate cause variations in the density profile that propagate into the firn with time as illustrated in Figure 4 for the case of double pulse in A s(t) at Byrd (Fig. 3a). The density fluctuations caused by the two opposite pulses are obvious, with the density variation of ∼0.10 over 3.8 m depth at 20 years gradually reduced to 0.074 over 2.8 m at 43 years and to 0.048 over 2.3 m at 68 years. These density variations induced by accumulation variations are analogous to those previously modeled and observed for seasonal temperature variations (Reference Zwally and LiZwally and Li, 2002; Reference Morris and WinghamMorris and Wingham, 2014). Although seasonal accumulation-induced variations in density may be relatively small, their probable existence should be considered in interpretation of density variations in firn as annual layering.
4.3. Experiments with single pulses in surface temperature
Parallel to the perturbation experiments in accumulation rate, we model the surface height response to temperature perturbations. Figure 5a–c show the results for Byrd, and Figure 5d–f for Vostok. The experiments are performed under constant A m and are driven by a 2°C increase in T s(t) above T m of −28.0°C for 5 years at Byrd and above T m of −56°C for 5 years at Vostok. The increase in T s(t) causes a continuous decrease in the temperature-driven surface height, CT(t), from zero to −0.075 m at the end of the 5 years at Byrd to a minimum of −0.09 m 3 years later. During the 5 years, the rate of decrease, dC T/dt, continues to increase as the temperature pulse propagates deeper into the firn, thereby affecting the rate of compaction of more firn layers. After the warming pulse ends, the dC T(t)/dt rate abruptly decreases (less negative; Fig. 5c) with a 63% recovery in only 0.9 year as the cooling quickly reduces the compaction in the uppermost firn layers and the prior warming pulse continues to propagate to deeper layers. The dC T(t)/dt becomes positive as the positive effect of the cooling at the end of the pulse exceeds the negative effect of the prior warming, reaching a broad maximum ∼10 years later when the positive and negative effects balance. In contrast, the recovery of the C T(t) height is much slower than the dC T(t)/dt recovery, with 63% of the decrease still remaining after∼29 years (Fig. 5b).
At Vostok, the surface height, C T(t), decreases from zero to −0.0064 m at the end of the 5 years and to a minimum of −0.0091 m ∼5 years later (Fig. 5e). These decreases are ∼1/10 of the corresponding decreases at Byrd for the same temperature perturbation, because of the much lower temperatures and the nonlinear dependence of the compaction rate on temperature. As expected, the C T(t) response time of 100 years for 63% recovery time is also much longer than at Byrd, but again dC T(t)/dt recovers much faster, in ∼2.2 years for 63% recovery (Fig. 5f). The results show that variations of surface temperature have short sustained impacts on the rate of the surface height change, but much longer impacts on the surface height.
The response to a sustained step change in T s(t), as might be caused by abrupt climate change, would be immediate, with C T(t) decreasing nearly linearly for the first 5 years with the rate of elevation change approaching a minimum of approximately −0.02 m a−1 (Fig. 5a–c) in ∼5 years as the firn warms to the new T m.
4.4. Experiments driven by climate data
To examine height variations caused by natural variations in A s(t) and T s(t), we model the changes produced by monthly time series of A s(t) and T s(t) for the period 1982–2008. The model runs in monthly time steps using T s(t) and A s(t) =A m +δA s(t), where δA s(t)= A s(t)−〈A s(t)〉 using A s(t) from European Centre for Medium-Range Weather Forecasts ERA-Interim reanalysis data (Reference DeeDee and others, 2011) and 〈As (t)〉27 is the 27 year mean. The temperature-driven component of the surface height change, C T(t), is obtained by first running the model under constant accumulation rate A m forced by T s(t). C T(t) is then subtracted from the modeled height change, H a CAT(t), which is driven by both A s(t) and T s(t), to obtain the accumulation-driven component, H a CA(t), as was done previously (Reference Li and ZwallyLi and Zwally, 2011; Reference ZwallyZwally and others, 2011). Two sites with contrasting climate conditions are the summit of Law Dome with high A m and T m and South Pole with low A m and T m. Figure 6 shows the monthly time series of the driving A s(t) and T s(t), the modeled temperature-driven height change C T(t), the accumulation-driven height change H a CA(t) with associated components of C A(t) and H a(t), and a comparison of the rate of the accumulation-driven height change dH a CA(t)/dt with its direct-height change component dH a(t)/dt. The H a CA(t) curve is the time integral of the accumulation anomaly, i.e. H a(t) = δA s(t)/ρ s Δt, modified by C A(t) and represents the cumulative height change resulting from the accumulation anomaly, taking into account the corresponding anomaly in compaction. The near-continuity of the temperature forcing that we apply between the initialization and the run with climate data is illustrated in Figure 6c and i by the lack of significant change in the C T(t) (other than the seasonal response) until about 1988 or 1990. Similarly, the dH a CA/dt in Figure 6e and k closely mirror the A s(t) forcing beginning in 1982.
From 1982 through 2008 the temperature-driven change C T at Law Dome (Fig. 6c) is about −0.3 m, with an average rate of −0.01 m a−1. As previously noted (Reference Li, Zwally and ComisoLi and others, 2007), this height decrease in East Antarctica is from increased firn compaction caused mainly by a rise in winter temperatures (cf. Fig. 6b). At South Pole, the warming is less (Fig. 6h) than at Law Dome, and the C T change is very small at −0.02 m, with an average rate of −0.0007 m a−1.
The effect of short-term fluctuations in temperature is demonstrated by the seasonal cycles of C T(t) in Figure 6c and i that lag the seasonal cycles in T s(t). The peak-to-peak variation of the seasonal cycle is ∼0.07 m at Law Dome and 0.004 m at South Pole. Another example is the interannual variation at Law Dome, with a rise in C T(t) peaking at the beginning of 2002, following a cooling of summer temperatures centered around 2000. That rise, and a smaller similar variation ∼8 years earlier, interrupted the longer-term temperature-driven surface lowering over the 27 years.
As shown in Figure 6a and g, A s(t) has strong interannual variations, up to ∼140% of the long-term value of 0.45 m a−1 from a minimum of 0.18 m a−1 to a maximum of 0.82 m a−1 at Law Dome, and up to ∼67% of the long-term value of 0.07 m a−1 from a minimum of 0.051 m a−1 to a maximum of 0.098 m a−1 at South Pole. At Law Dome, the total accumulation-driven height, H a CA(t), exhibits strong variations with a range of 1.2 m (Fig. 6d). From 1982 to 1991, A s(t) is on average >10% lower than the long-term A m of 0.45 m a−1, causing a significant decrease in the surface height from the initial zero level to −0.7 m. The drop in H a(t) to its minimum of −1.3 m in 1991, due to a deficiency in accumulation, is partially mitigated by a rising C A(t), due to a slowing of the firn compaction. Between 1992 and 1997 the A s(t) are on average >10% higher than A m, raising the height back to near zero in 1997. The subsequent sharp negative anomaly in A s(t) to a minimum of 0.2 m a−1 during 1999, followed by a sharp positive anomaly up to 0.7 m a−1 during 2001, are reflected in a minimum in H a CA(t) of −0.80 m followed by a maximum of 0.40 m. Comparing three curves in Figure 6d shows that the H a CA(t) is dominated by H a(t), but the compaction component C A(t) is generally in the opposite direction on H a(t), which reduces the total height change caused by the accumulation anomaly.
At South Pole, the total accumulation-driven height, H a CA(t), varies from a maximum in 1986 of 0.09 m above the initial value of zero to a minimum of −0.05 m at the end of the period (Fig. 6j). These changes in H a CA(t) at South Pole are ∼1/10 the magnitude of the changes at Law Dome, mainly because of the smaller magnitude of the δA s(t) anomalies. As shown in Figure 6j, the C A(t) has a relatively minor impact on the total H a CA(t) at this location.
The effects of accumulation variations, δA s(t), are clearly illustrated by comparison of the rate of the total accumulation-driven height change, dH a CA(t)/dt (black), with the rate of direct height change, dH a(t)/dt (red), in Figure 6e for Law Dome and Figure 6k for South Pole. The direct dH a(t)/dt and the input anomaly δA s(t) differ only in their ratio, which is the surface relative density, 0.3. However, dH a CA(t)/dt includes the compaction term, dC A(t)/dt, which depends on the integral of prior variations in δA s(t) and lags behind the direct dH a(t)/dt. As more or less snow is added to the surface during anomalies, the firn responds by compressing faster or slower with a time delay. For Law Dome, the effect of the variation in compaction is shown in Figure 6e by the intermittent separation of the black and red lines. For South Pole, the effect of the variation in compaction is minimal as shown by the near overlap of the lines in Figure 6k.
The effect of the compaction variations is also shown by the fitted slopes of dH a CA(t)/dt versus dH a(t)/dt in Figure 6f and l, which are 0.816 at Law Dome and 0.988 at South Pole. In addition, the correlation coefficients are 0.952 at Law Dome and 0.995 at South Pole. Since firn compaction at South Pole, with its low accumulation rate and temperature, is much slower than at Law Dome, the direct height change driven by δA s(t) more strongly dominates the changes in surface height, with only minor modification by the slower-responding change in the rate of firn compaction, dC A/dt. Therefore, as noted in the experiments with double pulses, the degree of offsetting of effects of opposite fluctuations in δA s(t) depends on the fluctuation frequency relative to the response time of the firn compaction. If the fluctuation frequency is fast (e.g. monthly) relative to the response time (e.g. 14 years), as it is at South Pole, then the firn is, in effect, inelastic (stiff) with respect to the alternating changes in the compressive loading.
5. Discussion and Conclusions
Both the 10 year firn-compaction response time to A s(t) variations at Byrd Station for surface height H a CA(t) and the 29 year response time of C T(t) to variations of T s(t) are approximately twice as fast as those from a previous model (Reference Arthern and WinghamArthern and Wingham, 1998). The primary reason for the faster response is the increased temperature dependence introduced in Reference Zwally and LiZwally and Li (2002), as discussed in Section 3. At the colder Vostok location, the respective response times of 68 years and 100 years are much slower than at Byrd due to lower firn temperatures.
However, our principal result is that the response times of the rates of surface height changes, dH a CA(t)/dt and dC T(t)/dt, caused by accumulation and temperature anomalies and their associated variations in the rate of firn compaction, are faster than the responses times of the corresponding height changes, H a CA(t) and C T(t). The importance of this finding is that studies of elevation change (e.g. with altimeter data) are inherently based on the differences in surface heights between successive measurements, commonly referred to as dH/dt. The basis for making corrections to the observed dH/dt for dC A(t)/dt and dC T(t)/dt, which do not involve changes in mass, is given by Eqn (1). Although H(t) time series are sometimes constructed from altimetry data, the series are essentially based on sequences of differential height measurements (e.g. height differences at orbital crossovers) (Reference Zwally, Brenner, Fu and CazenaveZwally and Brenner, 2001). Therefore, we have focused on the response of the rates of surface height change.
As shown in Figure 2, the impact on dH a CA(t)/dt from the perturbation of 50% increase in A s(t) for 5 years is reduced by 63% in only 4 years at Byrd, with the maximum close to 20 years at the cold extreme of Vostok. In addition, the double-pulse perturbation experiment shows that opposite fluctuations of A s(t) counteract and reduce the magnitude of the impact (Fig. 3). At Byrd, dH a CA(t)/dt after the double pulse is ∼50% less in magnitude at the 63% point than for the single-pulse case and at Vostok it is negligible. The extent to which successive A s(t) fluctuations of opposite signs offset in the magnitude of the response depends on the rapidity of fluctuations relative to the response time. For example, at Vostok where the response time for dH a CA(t)/dt is 18 years, successive 50% perturbations in A s(t) of opposite sign for 5 years leave a negligible residual height response.
The response of the rate of surface height change to T s(t) perturbations is even faster than the response to A s(t) perturbations, probably due to the near-exponential dependence of the compaction rate on temperature compared to the linear dependence on accumulation rate. As shown in Figure 5, the response time for dC T/dt to the temperature perturbation is only 0.9 year for the Byrd conditions and 2.2 years for the cold Vostok conditions.
The impacts of climatic variations in A s(t) and T s(t) on monthly to decadal timescales are shown in Figure 6. The C T(t) variations (Fig. 6c and i) show that over 27 years the temperature-induced surface lowerings of 0.3 m (0.01 m a−1) at Law Dome and 0.02 m (0.001 m a−1) at South Pole are small, but nevertheless need to be accounted for in mass-balance studies based on dH/dt changes. In addition, the temperature-induced seasonal cycle (e.g. peak-to-peak variations of 0.07 m at Law Dome and 0.004 m at Vostok) should be accounted for if height comparisons use data from differing seasons (Reference Ligtenberg, Horwath, Van den Broeke and LegrésyLigtenberg and others, 2012). The importance of the application of dC T(t)/dt corrections to observed dH/dt was shown for Greenland observations (Reference ZwallyZwally and others, 2011), for which the average dC T(t)/dt values were −0.002 m a−1 for 1992–2002 and −0.041 m a−1 for 2003–07 as a result of the increase in warming. Those dC T(t) corrections changed the respective mass estimates by −3 and −54 Gt a−1, without which an incorrect conclusion about Greenland mass loss at high elevations in the latter period might have been made.
The H a CA(t) curves over 27 years in Figure 6d and j represent the cumulative height changes resulting from the δA s(t) anomalies in Figure 6a and g taking into account the corresponding anomalies in compaction. The rates of direct height change, dH a/dt, in Figure 6e and k track the δA s(t) anomalies, and the rates of the total accumulation-driven height change, dH a CA(t)/dt, also include the corresponding modifications from the changes in rates of firn compaction. However, the direct components clearly dominate in the rate at Law Dome (Fig. 6e), and to a lesser extent in the rate at South Pole (Fig. 6k). The slopes (0.816 and 0.988 for Law Dome and South Pole) and the correlation coefficients (0.952 and 0.995) for dH a CA(t)/dt versus dH a(t)/dt in Figure 6f and l provide measures of how the monthly values of the two parameters differ in their short-term variabilities.
The relationship of dH a CA(t)/dt to dH a(t)/dt is of practical importance for extracting information on the values of dH a(t)/dt, which is a parameter of interest, from observable dH a CA(t)/dt. In ice-sheet locations with slow FC response times (i.e. much of Antarctica), the near-unity slopes and correlation coefficients indicate that observation of dH a CA(t)/dt on monthly timescales can provide estimates of dH a(t)/dt and δA s(t) directly, using only an estimate of ρ s. At warmer locations with faster response times, knowledge of the response times from firn compaction modeling as functions of A m and T m can provide a basis for parameterization and estimation of the deviations between dH a(t)/dt and the observed dH a CA(t)/dt. The required observations of surface elevation changes on monthly timescales are expected from the multi-beam laser altimeter measurements on Ice, Cloud and Land Elevation Satellite-2 (ICESat-2) beginning in 2017. Extracting estimates of the dH a(t)/dt and δA s(t) variability also requires information on the ice-dynamic component of the observed dH/dt, as has been obtained from European Remote-sensing Satellite (ERS) and ICESat measurements from 1992 to 2008 (Reference ZwallyZwally and others, 2011, Reference Zwally, Li, Robbins, Saba, Yi and Brenner2015) including information on the decadal-scale stability of the ice dynamics (e.g. in East Antarctica) or sub-decadal changes (e.g. West Antarctica).
Understanding the time response of ice-sheet surface heights to short-term changes in temperature and accumulation rate is essential for deriving accurate ice-sheet mass changes from altimeter measurements of dH/dt. Calculation of both dC T(t)/dt and dH a CA(t)/dt with a firn compaction model, using data on T s(t) from satellite (AVHRR) observations since 1982 and A s(t) from atmospheric reanalysis since 1979, provides essential corrections to the measured dH/dt. For dC T(t)/dt, the response time of only several years or less to temperature variations, as shown by the single-pulse experiment and by the seasonal cycle in dC T(t)/dt using observed T s(t), indicates that just a few years of temperature data prior to the dH/dt period of measurements, as well as during the measurements, is sufficient to correct a dH/dt time series. In the case of an abrupt continued step in temperature rather than a temperature fluctuation, or for correcting an H(t) time series, a longer prior record of temperature is needed.
For dH a CA(t)/dt with its longer response time compared to the temperature response, a longer period of A s(t) is needed prior to the dH/dt measurements. For example, 5–20 years would be needed considering the results from the single-pulse experiment, which applies to a positive or negative accumulation anomaly persisting for several years. However, the more typical cases are illustrated by the double-pulse experiment, for which the response time is similar to the single-pulse experiment, but the amplitude of the residual height change is small or negligible. The examples using 27 years of A s(t) variations at Law Dome and South Pole show that frequent anomalies lasting ∼1 year are typically followed by similar anomalies of opposite sign, in addition to the higher-frequency monthly fluctuations. Therefore, for a regular random climate change the A s(t) data beginning in 1979, i.e. 13 years before the ERS-1 radar altimeter measurements began in 1992, is sufficient for use with ERS-1 and subsequent satellite altimeter measurements of dH/dt.
Acknowledgements
We thank the Scientific Editor Ralf Greve and three anonymous reviewers for thoughtful reviews that significantly improved the manuscript.








