Disclaimer
Oak Ridge National Laboratory is managed by UT-Battelle, LLC. This submission was written by the authors acting in their own independent capacity and not on behalf of UT-Batelle, LLC, or its affiliates or successors.
1. Introduction
Observations show that the microstructure of ice records aspects of climate history (e.g. Reference PatersonPaterson, 1991; Reference GowGow and others, 1997; Reference DurandDurand and others, 2007; Reference PettitPettit and others, 2011). However, understanding if and how the climate ‘memory’ is preserved and evolved through time is challenging (Reference Kennedy, Pettit and Di PrinzioKennedy and others, 2013). Reference PatersonPaterson (1991) showed that ice-age ice typically consists of smaller grains and stronger fabric (statistically preferred orientation of the ice crystal lattice) than Holocene ice, providing the first hint of a connection between paleoclimate and microstructure in an ice sheet. More recently, both thin-section data and sonic-velocity data from Dome C, East Antarctica, show an abrupt transition in the ice rheology at 1750 m depth, which corresponds to a transition between the warm MIS-5 (marine isotope stage 5) and the cool MIS-6 ∼150 ka ago (Reference DurandDurand and others, 2007; Reference Gusmeroli, Pettit, Kennedy and RitzGusmeroli and others, 2012). Many microstructural features (e.g. dust particles, grain size, fabric) correlate with climate history (e.g. Reference Durand, Gagliardini, Thorsteinsson, Svensson, Kipfstuhl and Dahl-JensenDurand and others, 2006a). This correlation is caused by a number of interdependent microstructural processes (e.g. Reference AlleyAlley, 1992; Reference Faria, Weikusat and AzumaFaria and others, 2014b).
Classically, three main processes account for the observed grain and fabric structure throughout the depth of the ice sheet (e.g. Reference Alley, Perepezko and BentleyAlley and others, 1986; Reference AlleyAlley, 1992; Reference De La Chapelle, Castelnau, Lipenkov and DuvalDe La Chapelle and others, 1998; Reference Cuffey and PatersonCuffey and Paterson, 2010). Normal grain growth is the temperature-controlled coarsening of grains through grain-boundary migration, in order to reduce the total grain-boundary energy stored in the ice. Large grains consume small grains in such a way that the average grain cross-sectional area increases linearly with time (Reference Alley, Perepezko and BentleyAlley and others, 1986). This process is considered to be active throughout the depth of the ice sheet, but is counterbalanced by polygonization at intermediate depths of the ice sheet, where a steady grain-size profile is observed (Reference AlleyAlley, 1992). Strain energy builds in a grain during deformation, and bending or twisting stresses cause dislocations to form a ‘wall’, which eventually divides (polygonizes) the grain and causes a small misorientation between the grains' crystal lattices. At the greatest depths of an ice sheet, where the temperature is >−10°C, migration recrystallization becomes active. Here temperatures are great enough for grain boundaries to move easily, driven by differences in stored strain energy (Reference AlleyAlley, 1992). With high enough stored strain energy, it becomes energetically favorable to nucleate a new strain-free grain, which rapidly migrates through neighboring grains and has an orientation that is dependent on the applied stress (Reference Duval and CastelnauDuval and Castelnau, 1995). With sufficiently high rates of migration recrystallization, an inverse power-law relationship between grain size and stress forms (Reference Jacka and JunJacka and Jun, 1994) and an entirely new fabric structure results. Because fabric and grain structure are a result of recrystallization processes, conventional wisdom is that fabric will not maintain any past climate information.
Although the classic three-process model, or ‘tripartite paradigm’, has successfully described the average grain size and fabric in ice cores, observations in the last decade have led to new perspectives on these processes (e.g. Reference Faria, Weikusat and AzumaFaria and others, 2014a,Reference Faria, Weikusat and Azumab; cf. Reference De La Chapelle, Castelnau, Lipenkov and DuvalDe La Chapelle and others, 1998). Techniques that allow observations on the scale of micrometers or smaller (e.g. Reference KipfstuhlKipfstuhl and others, 2006; Reference Obbard, Baker and SiegObbard and others, 2006; Reference Weikusat, Miyamoto, Faria, Kipfstuhl, Azuma and HondohWeikusat and others, 2011) are now common, whereas classical observations typically were on the scale of millimeters or larger (Reference Faria, Weikusat and AzumaFaria and others, 2014a). Some observations from these high-resolution techniques cannot be accounted for under the tripartite paradigm if it is considered a description of the actual microstructural physics. For example, in Dronning Maud Land, Antarctica, the firn grain-boundary structure appears to have been dominated by migration recrystallization during the firn–ice transition, even though it is much colder (annual mean temperature −46°C) than where migration recrystallization is considered to be a dominant process (≲−10°C; Reference KipfstuhlKipfstuhl and others, 2009). However, due to its success in describing the microstructure observed in ice (summarized by Reference Faria, Weikusat and AzumaFaria and others, 2014a,Reference Faria, Weikusat and Azumab), the tripartite paradigm provides a robust phenomenological model of the average grain size and especially the fabric evolution (as discussed in the next section), despite its imperfections.
Observations of more recrystallization in the firn and ice of an ice sheet than expected under the tripartite paradigm (e.g. Reference KipfstuhlKipfstuhl and others, 2009) would seem to reinforce the conventional idea that fabric cannot preserve a memory of past climate. Indeed, the memory is unlikely to be stored directly in the grain structure or fabric strength of a particular layer of ice, as they are continually evolving. The relative differences in the fabric between layers, however, can be preserved under certain conditions (Reference Kennedy, Pettit and Di PrinzioKennedy and others, 2013).
Because the microstructural processes active in the firn are sensitive to climatic variables (Reference Alley, Saltzman, Cuffey and FitzpatrickAlley and others, 1990), layers of firn experiencing different climate regimes may have observable variations in the fabric which can be preserved. For example, in polar regions, vapor deposition is the primary method of grain growth in the upper firn and it is anisotropic: deposition will favor either the basal or prism faces of the ice-crystalline lattice, depending on the temperature (Reference Nelson and KnightNelson and Knight, 1998). This process causes grains with the preferred face parallel to the vapor-pressure gradient to grow more than grains in a less favorable orientation. Because these grains grow at the expense of other grains (Reference ColbeckColbeck, 1983), the well-oriented grains are more likely to remain (Reference Carns, Waddington, Pettit and WarrenCarns and others (2010) are developing a model to explore this process). Variations in texture and fabric in the firn may reflect variations in temperature and vapor-pressure gradients (Reference Adams and MillerAdams and Miller, 2003). While measuring fabric in firn is difficult, several studies have reported non-isotropic fabric measurements from firn (Reference DiPrinzio, Wilen, Alley, Fitzpatrick, Spencer and GowDiPrinzio and others, 2005; Reference Fujita, Okuyama, Hori and HondohFujita and others, 2009; Reference MontagnatMontagnat and others, 2012). Reference MontagnatMontagnat and others (2012) found that using non-isotropic initial fabrics was required during simulations of the fabric evolution in Talos Dome, East Antarctica, for a good quantitative match to observed fabrics. Therefore, fabric variations may arise from climatic variations and these variations may be present beneath the firn–ice transition. Fabric variations then may preserve memory of past climate, as long as the fabric variation is observable. (A loose analogy can be drawn to the familiar climate proxy, δ18O; it is the variation in δ18O, not the particular amount of the oxygen isotope present, that allows us to extract a temperature history.)
Here, we ask how long a subtle fabric variation (of any origin), just below the firn–ice transition, can be preserved within an ice sheet. Reference Kennedy, Pettit and Di PrinzioKennedy and others (2013) used a model based on the tripartite paradigm to show that a subtle variation in fabric can persist throughout the depth of an ice sheet when the ice is in a vertical uniaxial-compression or pure-shear regime and experiences polygonization events typical of ice divides. We build on this work to show that it is possible to preserve a subtle variation in fabric in a simple-shear stress regime and subject to migration recrystallization. Ice flows dominantly by simple shear on the flank of an ice sheet, while ice at the divide may experience some simple shear, especially in the case of divide migration. We also show that for any of the modeled stresses or temperatures, migration recrystallization does not ‘erase’ the fabric variation. Together, the combination of uniaxial compression, pure shear, simple shear, polygonization and migration recrystallization account for the dominant processes within an ice sheet that affect the fabric evolution.
2. Fabric
A sample of ice can display a statistically preferred orientation of its crystal lattices called fabric. The statistical measure of this preference is often reported as eigenvalues and eigenvectors of the (volume-weighted) average orientation tensor of the sample. The grain volume can be determined from the measurement of the two-dimensional grain area in a cross section of the sample (Reference WoodcockWoodcock, 1977; Reference Gagliardini, Durand and WangGagliardini and others, 2004).
The orientation tensor is calculated from a sample of N grains:
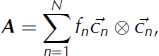
where fn
is the estimate of the grain’s volume fraction, ![]() is a unit vector describing the grain’s c-axis orientation and ⊗ is the vector direct (outer) product. The eigenvalues, ei
, for i = 1, 2, 3, of
A
then represent the spatial distribution of the orientations, and how tightly the crystals are aligned to the eigenvectors,
is a unit vector describing the grain’s c-axis orientation and ⊗ is the vector direct (outer) product. The eigenvalues, ei
, for i = 1, 2, 3, of
A
then represent the spatial distribution of the orientations, and how tightly the crystals are aligned to the eigenvectors, ![]() . The eigenvalues are labeled in descending order (e
1 > e
2 > e
3) and sum to unity (e
1 + e
2 + e
3 = 1). For a single-maximum fabric, the statistically preferred orientation is the first eigenvector,
. The eigenvalues are labeled in descending order (e
1 > e
2 > e
3) and sum to unity (e
1 + e
2 + e
3 = 1). For a single-maximum fabric, the statistically preferred orientation is the first eigenvector, ![]() . The first eigenvalue, e
1, measures the fabric strength. Fabrics typically strengthen throughout the depth of an ice sheet in response to stress-induced velocity gradients driving grain rotation in the ice (e.g. Reference PatersonPaterson, 1991; Reference Arnaud, Weiss, Gay and DuvalArnaud and others, 2000; Reference DiPrinzio, Wilen, Alley, Fitzpatrick, Spencer and GowDiPrinzio and others, 2005; Reference DurandDurand and others, 2007; Reference Gow and MeeseGow and Meese, 2007).
. The first eigenvalue, e
1, measures the fabric strength. Fabrics typically strengthen throughout the depth of an ice sheet in response to stress-induced velocity gradients driving grain rotation in the ice (e.g. Reference PatersonPaterson, 1991; Reference Arnaud, Weiss, Gay and DuvalArnaud and others, 2000; Reference DiPrinzio, Wilen, Alley, Fitzpatrick, Spencer and GowDiPrinzio and others, 2005; Reference DurandDurand and others, 2007; Reference Gow and MeeseGow and Meese, 2007).
Microstructural processes further influence the volume orientation of ice and can significantly impact the fabric statistics. The three that affect lattice orientation are rotation recrystallization (RRX), where new grain boundaries are formed through the progressive rotation and migration of subgrain boundaries (of which polygonization is a special case), and strain-induced boundary migration (SIBM; also called migration recrystallization) from old/existing grains (SIBM-O) and from nucleation of new grains (SIBM-N) (see Reference Faria, Weikusat and AzumaFaria and others, 2014b, appendix A). Of these three, only SIMB-N is known to affect the fabric strength significantly. RRX produces new grains, of differing size, with small lattice misorientations (<10°; Reference Alley, Gow and MeeseAlley and others, 1995), but the volume average of these new grains, and what is left of the old grain, will closely match the average before RRX, resulting in a small weakening of the fabric. SIBM-O, in a statistical sense, is erasing the orientation of a bit of ice and replacing it with an orientation drawn from the same parent distribution of grains. Given a large number of grains, this will not affect the overall fabric statistics as long as there is not a preference to recrystallize grains in a certain orientation and the total population of grains remains large. Due to the large amount of strain heterogeneity in deforming ice, there should not be an orientation preference for SIBM-O (Reference Faria, Weikusat and AzumaFaria and others, 2014b).
SIBM-N, in contrast, nucleates new grains with a random orientation (Reference Wilson, Peternell, Piazolo and LuzinWilson and others, 2014). The fabrics that arise when SIBM-N dominates the fabric evolution are typically aligned for easy glide in the basal planes (the softest orientation) (Reference Montagnat, Durand and DuvalMontagnat and others, 2009), indicating that the nucleated grains most likely to grow are the ones oriented for easy glide. The influence of SIBM-N on a fabric variation will then depend on the rates of SIBM-N in each layer, as well as the rates of grain rotation. As long as the rates of SIBM-N remain low, or there is a differing rate in the varying layers, SIBM-N will not immediately eliminate the fabric variation (as shown below).
Therefore, due to the way fabric is influenced by the microstructural processes, and the way it is measured, we expect fabric to be particularly amenable to preserving variations.
3. The Model
We use the topological model developed by Reference Kennedy, Pettit and Di PrinzioKennedy and others (2013), based on the analytic flow law developed by Reference ThorsteinssonThorsteinsson (2001, Reference Thorsteinsson2002). This polycrystal model solves for fabric through time, while incorporating nearest-neighbor interactions (NNIs) and the tripartite parameterizations of normal grain growth, polygonization and migration recrystallization (SIBM-N). This model does not predict ice flow; therefore, it does not account for possible strain enhancements, such as impurity-enhanced ice flow (Reference PatersonPaterson, 1991; Reference FariaFaria and others, 2009). Nor does it include the feedbacks between rheologically distinct layers that can lead to concentrated shearing on layers with crystals oriented to be soft in shear (Reference Budd and JackaBudd and Jacka, 1989; Reference DurandDurand and others, 2007; Reference Pettit, Thorsteinsson, Jacobson and WaddingtonPettit and others, 2007).
The model averages over a representative distribution of N individual ice crystals to calculate the bulk response of the ice to stress. The crystals are arranged on a regular cuboidal grid (Fig. 1), where each crystal has six nearest neighbors. The crystals however, are considered to evolve independently of each other and are embedded in an ice matrix. The matrix accommodates crystal-boundary migration and acts as seeds for migration recrystallization (Reference ThorsteinssonThorsteinsson, 2002). In the case of NNIs, the resolved shear stress of the crystal is modified by a factor depending on the average orientation of the surrounding crystals.
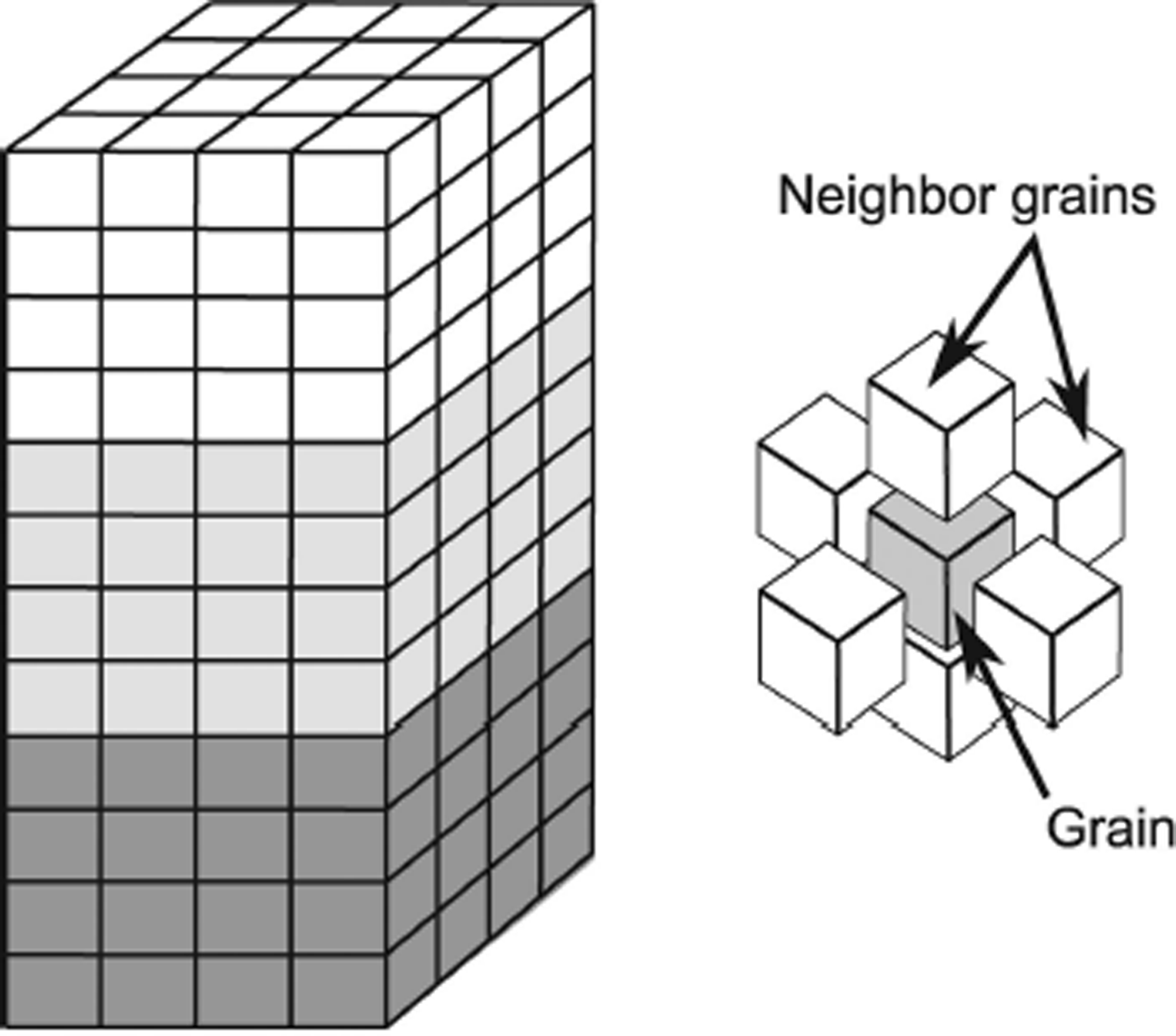
Fig. 1. The polycrystal structure. Left: An example of a polycrystalline cuboid with three distinct fabric layers, where each color represents a different fabric. Each small cube indicates one grain and each layer has 4 × 4 × 4 = 64 grains. The three-layered cuboid in our model has 20 × 20 × 20 = 8000 grains in each layer. Right: An illustration of the grain packing where each grain (gray) has six neighboring grains (white).
The distribution of N crystals can be divided into sub-distributions with distinct fabrics. The evolution of each sub-distribution can then be calculated and compared with the others or with the entire distribution through time.
Each crystal in the distribution has an associated orientation, ![]() , given by the co-latitude, θn
, and azimuth, ϕn
, as well as an associated spherical size of diameter Dn
and dislocation density ρn
. The model accepts an initial crystal distribution, stress and temperature, then evolves the distribution through uniform steps in time or strain. Figure 2 outlines the model process. First, the initial crystal distribution is created and passed to the model. The model then applies a stress to the distribution and calculates the individual crystal strain rates and velocity gradients using the flow law developed by Reference ThorsteinssonThorsteinsson (2001, Reference Thorsteinsson2002). Next, it checks the recrystallization conditions (outlined below), calculates the bulk crystal properties and then rotates the crystals. After each time- or strain-step, the model outputs the new distribution of crystals, the bulk strain, and the number and type of recrystallization events. This new distribution of crystals is then fed back into the model for the next time step, along with the new stress and temperature. Because stress is an input for this model, stress must be determined outside of the model.
, given by the co-latitude, θn
, and azimuth, ϕn
, as well as an associated spherical size of diameter Dn
and dislocation density ρn
. The model accepts an initial crystal distribution, stress and temperature, then evolves the distribution through uniform steps in time or strain. Figure 2 outlines the model process. First, the initial crystal distribution is created and passed to the model. The model then applies a stress to the distribution and calculates the individual crystal strain rates and velocity gradients using the flow law developed by Reference ThorsteinssonThorsteinsson (2001, Reference Thorsteinsson2002). Next, it checks the recrystallization conditions (outlined below), calculates the bulk crystal properties and then rotates the crystals. After each time- or strain-step, the model outputs the new distribution of crystals, the bulk strain, and the number and type of recrystallization events. This new distribution of crystals is then fed back into the model for the next time step, along with the new stress and temperature. Because stress is an input for this model, stress must be determined outside of the model.
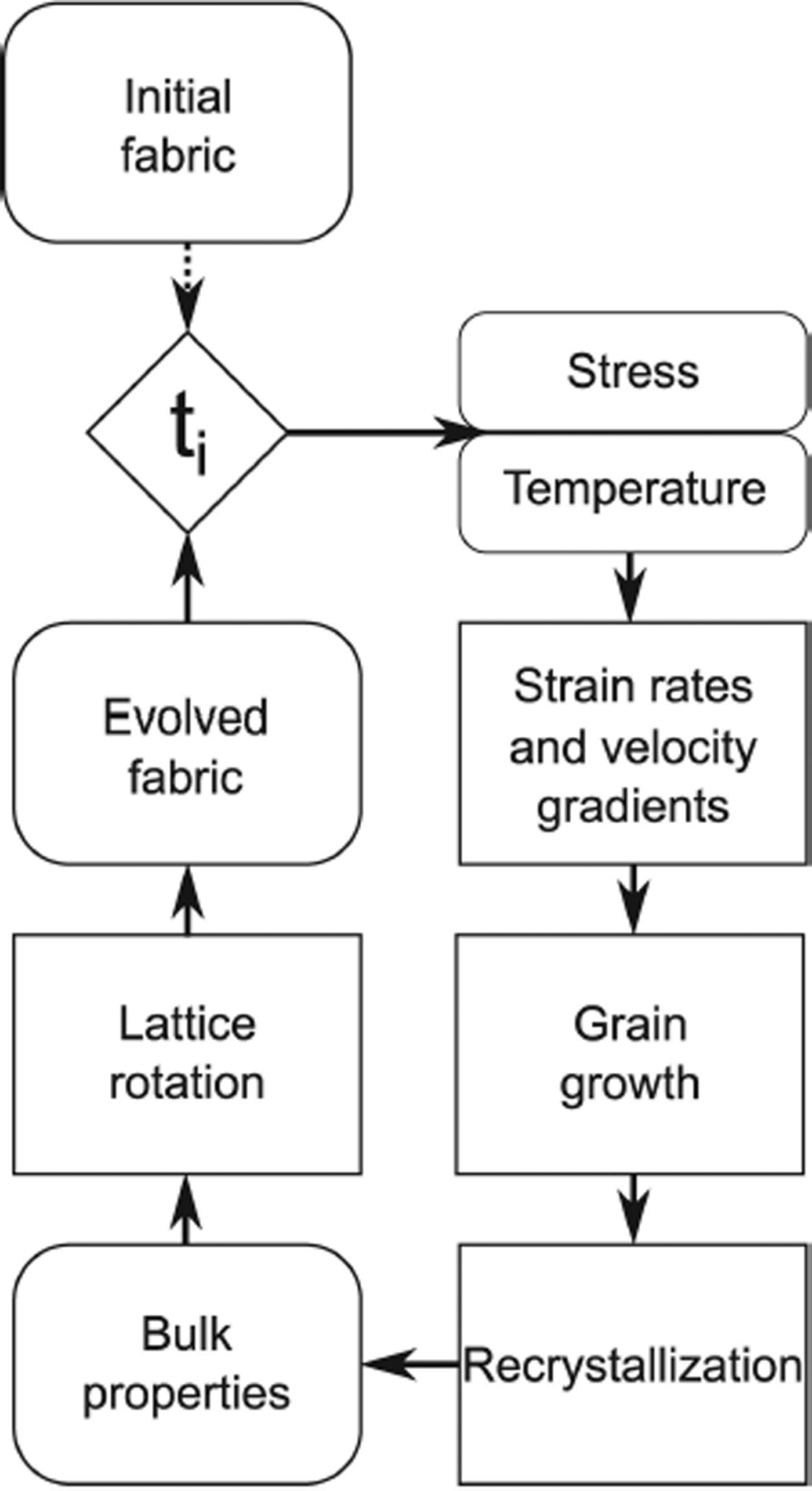
Fig. 2. Flow chart of the model. The model is initialized with fabric data, deviatoric stress and temperature. For each time step, strain rates and velocity gradients are calculated, dynamic recrystallization processes are applied to the fabric and then the grains are rotated to calculate new fabric data. The new fabric data together with new stresses and temperatures are fed back into the model to start the next time step.
3.1. Model physics
Grains rotate due to gradients in velocity, which result from internal stresses experienced by the ice. For polycrystalline ice, these stresses lie somewhere between two end-member assumptions: uniform stress and uniform strain rates. In the uniform-stress assumption, each grain experiences the same stress as the surrounding grains. Because ice crystals are highly anisotropic, an individual grain’s strain rate, therefore, depends on its lattice orientation. In the uniform-strain-rate assumption, each grain has the same strain rate as the surrounding grains. The stress the grain experiences, then, depends on the grain’s orientation. Although the true nature of ice is somewhere in between, the uniform-stress assumption is well adapted to describing polycrystalline ice, due to strong crystal anisotropy (Reference Castelnau, Duval, Lebensohn and CanovaCastelnau and others, 1996). Therefore, we apply a uniform stress to each grain in the distribution. Furthermore, we restrict the deformation of a grain to be along the slip systems in the basal plane, causing the grain to only respond to the components of stress that are parallel to the basal plane (termed the resolved shear stress, or RSS). The RSS, τ (s), on a slip system, (s), is
where
S
(s) is the Schmidt tensor, which describes the orientation of the grain’s slip system,
σ
′ is the deviatoric stress tensor for the stress applied to the fabric and ![]() summing over repeated indexes. The magnitude of the RSS,
summing over repeated indexes. The magnitude of the RSS, ![]() , can then be calculated as
, can then be calculated as
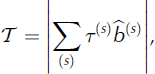
where ![]() is the direction of the Burgers vector for the slip system. Schmidt plots of
is the direction of the Burgers vector for the slip system. Schmidt plots of ![]() for a variety of stress states are shown in Figure 3.
for a variety of stress states are shown in Figure 3.
Using the analytic flow law (Reference ThorsteinssonThorsteinsson, 2001, Reference Thorsteinsson2002), the velocity gradient of a grain in response to a stress, L c , is
where β is an adjustable constant to control the isotropic ice softness, ![]() is the temperature-dependent flow parameter from Glen’s flow law (Reference Cuffey and PatersonCuffey and Paterson, 2010, p. 72),
is the temperature-dependent flow parameter from Glen’s flow law (Reference Cuffey and PatersonCuffey and Paterson, 2010, p. 72), ![]() is the local softness parameter due to NNIs, and n is the exponent in Glen’s flow law (Reference GlenGlen, 1955).
is the local softness parameter due to NNIs, and n is the exponent in Glen’s flow law (Reference GlenGlen, 1955).
The flow parameter ![]() follows an Arrhenius relation with a switch of activation energy at a transition temperature, T
⋆ = −10°C. The relationship for T in kelvin is
follows an Arrhenius relation with a switch of activation energy at a transition temperature, T
⋆ = −10°C. The relationship for T in kelvin is
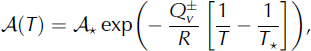
where ![]() is a constant, R is the universal gas constant and
is a constant, R is the universal gas constant and ![]() is the activation energy for volume self-diffusion (Reference Cuffey and PatersonCuffey and Paterson, 2010, p. 72).
is the activation energy for volume self-diffusion (Reference Cuffey and PatersonCuffey and Paterson, 2010, p. 72). ![]() for T ≥ T
⋆ and
for T ≥ T
⋆ and ![]() for T < T
⋆ (Table 1).
for T < T
⋆ (Table 1).
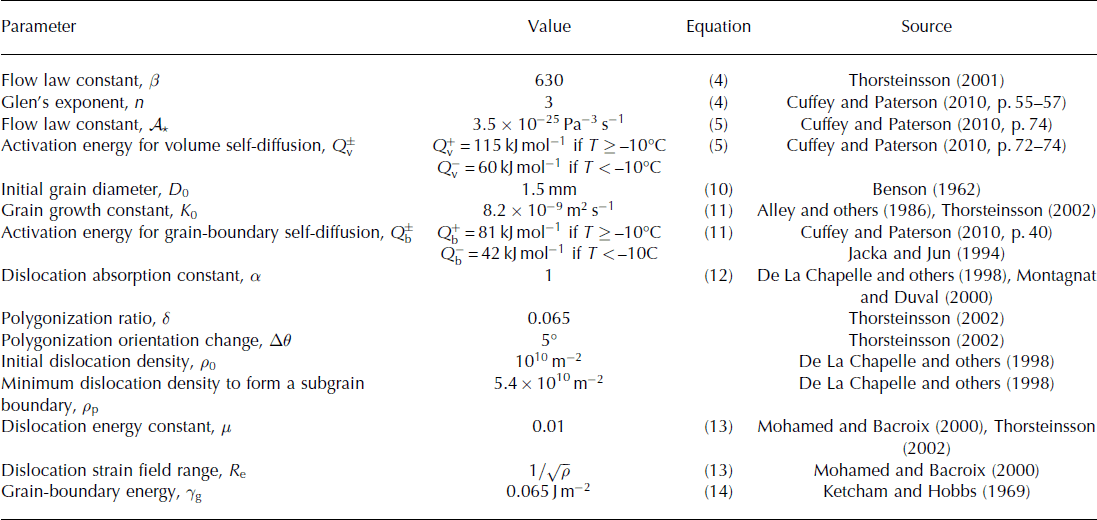
Table 1. Values of the parameters used in the model
The local softness parameter, ![]() , averages the magnitude of RSS the neighboring grains are experiencing,
, averages the magnitude of RSS the neighboring grains are experiencing, ![]() , relative to the magnitude of RSS the grain is experiencing,
, relative to the magnitude of RSS the grain is experiencing, ![]() :
:

where ζ is the relative contribution of the center grain, and is the relative contribution of each neighbor (Fig. 1). Because the RSS, ![]() , can be zero, there is a specified cap for the maximum value of
, can be zero, there is a specified cap for the maximum value of ![]() . Setting [ζ , ξ] to [1, 0] in Eqn (6) is equivalent to the uniform-stress assumption with no NNIs. Changing the values of [ζ , ξ] modifies the uniform-stress assumption (toward the uniform-strain assumption) by redistributing the stress through explicit NNIs. Mild NNIs occur when [ζ , ξ] is set to [6, 1], such that the center grain contribution to
. Setting [ζ , ξ] to [1, 0] in Eqn (6) is equivalent to the uniform-stress assumption with no NNIs. Changing the values of [ζ , ξ] modifies the uniform-stress assumption (toward the uniform-strain assumption) by redistributing the stress through explicit NNIs. Mild NNIs occur when [ζ , ξ] is set to [6, 1], such that the center grain contribution to ![]() is the same as the sum of the neighboring grains. Full NNIs occur when [ζ , ξ] is set to [1, 1], such that the center grain and individual neighbor grains all contribute equally to
is the same as the sum of the neighboring grains. Full NNIs occur when [ζ , ξ] is set to [1, 1], such that the center grain and individual neighbor grains all contribute equally to ![]() .
.
Finally, the strain rate of a single grain is
where ( L c)T refers to the matrix transpose of L c.
The bulk velocity gradient is calculated by averaging the single-crystal velocity gradients, and will be influenced more by larger crystals than smaller crystals. We calculate the volume of a crystal from its diameter, D, and use its volume fraction, f, as a statistical weight for the calculation of the bulk velocity gradient (Reference Gödert and HutterGödert and Hutter, 1998; Reference MontagnatMontagnat and others, 2014). Therefore, the modeled bulk velocity gradient is
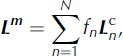
where N is the number of crystals in the representative distribution and
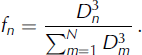
The modeled bulk strain rate is then
However, we caution readers that this modeled strain rate will not correspond to strain rates measured in situ, because we are solving for fabric evolution, not ice flow. The deformation of ice is not only a function of fabric (as modeled here) but of many co-dependent processes, which accommodate ice deformation (Reference Thorsteinsson, Waddington, Taylor, Alley and BlankenshipThorsteinsson and others, 1999). Further, using the uniform-stress assumption results in ice that is too stiff (Reference MontagnatMontagnat and others, 2014), meaning the fabric evolves too much for the modeled strain rates compared with measured strain rates. Using NNIs partially alleviates this problem by allowing hard grains to deform.
Nevertheless, the cumulative modeled bulk strain, provides a good measure of the overall fabric evolution (in the context of the model), and is useful when comparing different model runs, as we do below. In order to compare results from our model with measured fabrics, the flow law constant, β (Eqn (4)), and parameters controlling the local softness, [ζ, ξ] (Eqn (6)), need to be tuned to reproduce the observed fabric evolution in time. How much the strain rate is under-represented in the model can then be determined. The effects of changing these parameters in our model are discussed below.
3.2. Recrystallization processes
Once the velocity gradient and strain rates are calculated for each grain, the parameterizations of normal grain growth, polygonization and migration recrystallization (SIBM-N) are applied to the grain distribution before the grains are rotated into new orientations.
3.2.1. Normal grain growth
Under the tripartite paradigm, normal grain growth occurs when grain boundaries migrate, in order to reduce the overall grain-boundary energy. The grain growth is a function of boundary curvature, intrinsic properties (e.g. temperature, thickness, diffusivity of water molecules) and extrinsic material (e.g. impurities, bubbles). This grain growth can be described by a parabolic growth law (Reference Alley, Perepezko and BentleyAlley and others, 1986), where the grain diameter, D, increases with time:
where K is the grain-growth factor, t is time, t 0 is the initial time and D 0 is the grain diameter at time t 0. The grain-growth factor is a function of the intrinsic properties of the ice and the temperature:
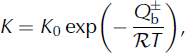
where K
0 is a constant that depends on the intrinsic properties of the grain boundaries, ![]() is the activation energy for grain-boundary self-diffusion,
is the activation energy for grain-boundary self-diffusion, ![]() is the gas constant and T is the temperature.
is the gas constant and T is the temperature. ![]() is
is ![]() (Reference Cuffey and PatersonCuffey and Paterson, 2010, p.40) and, similarly to the activation energy for volume self-diffusion,
(Reference Cuffey and PatersonCuffey and Paterson, 2010, p.40) and, similarly to the activation energy for volume self-diffusion, ![]() for T ≥ T
⋆ and
for T ≥ T
⋆ and ![]() for T < T
⋆ (Table 1). Extrinsic materials, such as dust particles, reduce the rate of boundary migration and can be described by a drag force on the boundary (Reference Alley, Perepezko and BentleyAlley and others, 1986). This drag effectively reduces the grain-growth factor, K. We list the values used for these constants in Table 1.
for T < T
⋆ (Table 1). Extrinsic materials, such as dust particles, reduce the rate of boundary migration and can be described by a drag force on the boundary (Reference Alley, Perepezko and BentleyAlley and others, 1986). This drag effectively reduces the grain-growth factor, K. We list the values used for these constants in Table 1.
Normal grain growth is then implemented by growing the diameter of the grain, D, according to Eqn (10). We reset the growth law after each recrystallization, such that t 0 and D 0 are the time and size immediately after the recrystallization.
3.2.2. Polygonization
Under the tripartite paradigm, a stable grain size is typically reached, even though grains continue growing through time and depth, because polygonization counteracts normal grain growth. Polygonization creates new grain boundaries within large ice grains, effectively dividing the grain in two. Large grains can become highly strained and experience differential stress, which is relieved by the organization of dislocations into subgrain boundaries (Reference AlleyAlley, 1992). Reference De La Chapelle, Castelnau, Lipenkov and DuvalDe La Chapelle and others (1998) determined that the minimum dislocation density needed to form a subgrain boundary is, ρ p = 5.4 × 1010 m−2.
Because polygonization depends on reaching a minimum dislocation density, the rate of polygonization can be indirectly described through the dislocation density’s rate of change. The dislocation density changes due to two dominant processes: it increases due to work hardening and decreases due to the absorption of dislocations by the grain boundary (Reference Miguel, Vespignani, Zapperi, Weiss and GrassoMiguel and others, 2001). Therefore, the change in a grain’s dislocation density can be described as
where the first term on the right describes work hardening: ![]() is the second invariant of the strain-rate tensor, b is the length of the Burgers vectors and D is the grain diameter (Reference Montagnat and DuvalMontagnat and Duval, 2000). The second term describes the absorption of dislocations by the grain boundaries, α is an adjustable constant and K is the grain-growth factor.
is the second invariant of the strain-rate tensor, b is the length of the Burgers vectors and D is the grain diameter (Reference Montagnat and DuvalMontagnat and Duval, 2000). The second term describes the absorption of dislocations by the grain boundaries, α is an adjustable constant and K is the grain-growth factor.
We implement polygonization such that once the minimum dislocation density is reached, a grain experiencing a differential stress may polygonize. Because our NNIs only modify the RSS and cannot directly apply a differential stress, we use a proxy for differential stress on a grain (Reference ThorsteinssonThorsteinsson, 2002). Grains that have a small amount of the applied stress resolved onto the basal plane (RSS) will likely be experiencing a differential stress from their neighboring grains which are deforming. Specifically, if the ratio of the magnitude of the RSS, ![]() , to the second invariant of the applied stress, ∥
σ
′∥, is less than a given value,
, to the second invariant of the applied stress, ∥
σ
′∥, is less than a given value, ![]() , and the dislocation density, ρ, in the grain is sufficient to form a subgrain wall (ρ > ρ
p), then the grain will polygonize. When a grain polygonizes, the orientation is changed by an angle, Δθ, in a direction that increases the RSS, the grain size is halved and the dislocation density is reduced by ρ
p. Values for these parameters are listed in Table 1. Polygonization tends to slow the development of fabric because grains that are oriented very close to the preferred orientation (small RSS) of the fabric will polygonize preferentially by the selection criteria. Because polygonization rotates the grains away from the preferred orientation, this process tends to weaken the fabric.
, and the dislocation density, ρ, in the grain is sufficient to form a subgrain wall (ρ > ρ
p), then the grain will polygonize. When a grain polygonizes, the orientation is changed by an angle, Δθ, in a direction that increases the RSS, the grain size is halved and the dislocation density is reduced by ρ
p. Values for these parameters are listed in Table 1. Polygonization tends to slow the development of fabric because grains that are oriented very close to the preferred orientation (small RSS) of the fabric will polygonize preferentially by the selection criteria. Because polygonization rotates the grains away from the preferred orientation, this process tends to weaken the fabric.
3.2.3. Migration recrystallization (SIBM-N)
According to the tripartite paradigm, through most of the depth of an ice sheet, the rate of fabric evolution is controlled by a balance between the grain growth, polygonization and grain rotation processes. However, migration recrystallization dominates fabric evolution at high temperatures (typically >−10°C; Reference Duval and CastelnauDuval and Castelnau, 1995). Migration recrystallization occurs when the stored strain energy (due to dislocations) in a grain is greater than the grain-boundary energy of a new strain-free grain. This new strain-free grain rapidly grows at the expense of the old grain (Reference Duval and CastelnauDuval and Castelnau, 1995). The stored energy due to dislocations, E d, can be estimated as
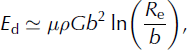
where μ is a constant, G is the shear modulus and R e is the mean average of the dislocation strain field range (Reference ThorsteinssonThorsteinsson, 2002). The energy associated with grain boundaries, E c, is
where γ g is the energy per unit area on the boundary (for high-angle boundaries). When E d > E c it is energetically favorable to nucleate a new grain, which quickly grows to a diameter that scales with the effective stress, due to a balance between nucleation of grains and grain-boundary migration (e.g. Reference ShimizuShimizu, 2008). The nucleated grain that grows most rapidly will be the one in the most energetically favorable position: about halfway between the compressional and tensional axes, which maximizes the resolved shear stress on the basal planes, causing them to deform easily (Reference AlleyAlley, 1992). For uniaxial compression or pure shear, for example, this is 45° from the axis of compression, while for simple shear, it is 45° from the principal stress axis (Fig. 3). The new grain is initially strain-free and has a much lower strain energy than the surrounding grains, allowing it to grow. As the new grain grows preferentially at an orientation favorable for the bulk deformation (highest RSS), the fabric can change significantly when there are large numbers of migration recrystallization events.
We implement migration recrystallization by immediately creating a new grain when the dislocation energy, E
d, exceeds the boundary energy, E
c (Eqns (13) and (14)). An old grain is replaced with a new ‘strain-free’ grain that has a dislocation density ρ
0 and a diameter that scales with the effective stress, ![]() (Reference ThorsteinssonThorsteinsson, 2002; Reference ShimizuShimizu, 2008). We assume the grain grows fast enough to reach a diameter of D within a single time step. The new grain is given the orientation with the highest RSS (or softest orientation; Fig. 3), taken from a random distribution of 50 orientations in the applied stress state (Reference ThorsteinssonThorsteinsson, 2002).
(Reference ThorsteinssonThorsteinsson, 2002; Reference ShimizuShimizu, 2008). We assume the grain grows fast enough to reach a diameter of D within a single time step. The new grain is given the orientation with the highest RSS (or softest orientation; Fig. 3), taken from a random distribution of 50 orientations in the applied stress state (Reference ThorsteinssonThorsteinsson, 2002).
3.2.4. Lattice rotation
If the surrounding ice is fixed, each grain rotates as it deforms, according to the standard continuum mechanics rotation rate tensor:
where ![]() is the rotation rate of a single grain and
L
c is the velocity gradient of a grain in response to stress from Eqn (4). If the surrounding ice is rotating within the frame of reference, however, the model calculates a relative grain rotation rate:
is the rotation rate of a single grain and
L
c is the velocity gradient of a grain in response to stress from Eqn (4). If the surrounding ice is rotating within the frame of reference, however, the model calculates a relative grain rotation rate:
where ![]() is the bulk rotation rate of the modeled ice in response to stress. The new orientation of the grain is then
is the bulk rotation rate of the modeled ice in response to stress. The new orientation of the grain is then
4. Experimental Set-Up
The model domain is a 24 000-grain cuboid that is 20 grains wide, 20 grains deep and 60 grains high (Fig. 1). The cuboid is split into three vertically layered cubes of 8000 grains each and the middle layer is initialized with a different fabric to the top and bottom layers. Each layer of the initial fabric is generated using a Watson distribution (Reference Kennedy, Pettit and Di PrinzioKennedy and others, 2013). The top and bottom layers have a concentration parameter for the Watson distribution of k
tb = −2.0. This results in a vertical single-maximum fabric, where the largest eigenvalue of the second-order orientation tensor is ![]() . The middle layer has a stronger fabric, with a concentration parameter of
. The middle layer has a stronger fabric, with a concentration parameter of ![]() . These concentration parameters are characteristic of ice fabrics found near the firn–ice transition in polar ice sheets, and correspond to fabrics at ∼100 m depth in Taylor Dome, East Antarctica (Reference Kennedy, Pettit and Di PrinzioKennedy and others, 2013), and at <500 m depth at Dome C, East Antarctica (Reference Wang, Kipfstuhl, Azuma, Thorsteinsson and MillerWang and others, 2003; Reference DurandDurand and others, 2009). We measure the fabric variation through time by calculating the difference in the fabric e
1 eigenvalues between the middle and top (or bottom) layers:
. These concentration parameters are characteristic of ice fabrics found near the firn–ice transition in polar ice sheets, and correspond to fabrics at ∼100 m depth in Taylor Dome, East Antarctica (Reference Kennedy, Pettit and Di PrinzioKennedy and others, 2013), and at <500 m depth at Dome C, East Antarctica (Reference Wang, Kipfstuhl, Azuma, Thorsteinsson and MillerWang and others, 2003; Reference DurandDurand and others, 2009). We measure the fabric variation through time by calculating the difference in the fabric e
1 eigenvalues between the middle and top (or bottom) layers: ![]() . e
1 will best represent single-maximum-type grain distributions typically found in ice sheets. Initially, Δe
1 = 0.029. A contoured Schmidt plot of the initial fabrics is shown in Figure 4.
. e
1 will best represent single-maximum-type grain distributions typically found in ice sheets. Initially, Δe
1 = 0.029. A contoured Schmidt plot of the initial fabrics is shown in Figure 4.

Fig. 4. Contoured Schmidt plot of the initial fabrics for both the constant-stress and Taylor Dome experiments. The fabrics are contoured at levels of 0,2Σ, …, 10Σ. Σ is the standard deviation of the density of grains from the expected density for isotropic ice (Reference KambKamb, 1959). The upper two are contour plots of the continuous Watson distribution (an infinite number of grains), with concentration parameters k = −2.0 (left) and k = −2.4 (right). Two random 8000-grain fabrics generated from the upper Watson distributions are depicted in the lower two plots. The fabric generated from the k = −2.0 and k = −2.4 distributions have eigenvalues of e 1 = 0.538 and e 1 = 0.567, respectively.
Over time, as the cuboid is stressed, Δe 1 will change and may become smaller than the uncertainty in eigenvalues, due to under-sampling the distribution with a finite number of grains. Reference DurandDurand and others (2006b) found the maximum under-sampling error to be δ = 0.004 for a distribution with 8000 grains. For this study, we consider the minimum separation resolvable above the error in the eigenvalue calculation to be twice the maximum error: 2δ ≈ 0.01. The fabric variation is then preserved, as long as Δe 1 > 0.01. In situ, the minimum separation required to measure a fabric anomaly will depend on the measurement technique, the number of grains sampled and the assumed in situ distribution of orientations.
To model how our fabrics respond to stress, we apply a constant temperature, T, and constant deviatoric stress, σ ′, at each time step. The basic stress states within an ice sheet are uniaxial compression, pure shear and simple shear. The deviatoric-stress tensor for uniaxial compression has the form

the deviatoric-stress tensor for pure shear has the form
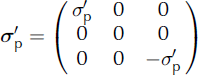
and the deviatoric-stress tensor for simple shear has the form
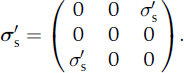
We use ![]() of 0.01 and 0.04 MPa to provide a lower and upper bound on the characteristic deviatoric stresses typically found in ice sheets (Reference Pettit and WaddingtonPettit and Waddington, 2003). The model calculates a strain rate at each time step,
of 0.01 and 0.04 MPa to provide a lower and upper bound on the characteristic deviatoric stresses typically found in ice sheets (Reference Pettit and WaddingtonPettit and Waddington, 2003). The model calculates a strain rate at each time step, ![]() , and then the fabric is evolved for the amount of time required to achieve a strain step of 0.001, ti
. The total bulk strain undergone by the modeled ice is then
, and then the fabric is evolved for the amount of time required to achieve a strain step of 0.001, ti
. The total bulk strain undergone by the modeled ice is then ![]() .
.
Ice in the vicinity of an ice divide will typically experience a regime of compressive stress before experiencing significant shear stress and, for simple ice-sheet geometries, simple-shear stresses are most important in the bottom half of the ice sheet (Reference Cuffey and PatersonCuffey and Paterson, 2010). Therefore we apply a constant compressive-stress regime (R1) to the modeled ice up to a total bulk strain of ∊ R1. We then apply a constant-shear-stress regime (R2) to the modeled ice up to a total bulk strain of ∊R2. The shear-stress regimes consist of simple shear alone, a combination of simple shear and pure shear, or a combination of simple shear and uniaxial compression (Table 2).
Table 2. Stress regimes, stress magnitude, NNI parameters and temperature values used in the constant-stress experiments. Two hundred and eighty-eight model runs were computed, where each run used a permutation of the listed values. ![]() indicates uniaxial compression,
indicates uniaxial compression, ![]() indicates pure shear and
indicates pure shear and ![]() indicates simple shear (Eqns (18–20))
indicates simple shear (Eqns (18–20))
Reference Kennedy, Pettit and Di PrinzioKennedy and others (2013) showed that the separation in eigenvalues between the fabric layers drops below 0.01 after 0.30 bulk strain in our model when undergoing uniaxial compression and pure shear. Simple shear, however, causes the fabric to rotate into a ‘soft’ orientation rather than a ‘hard’ orientation. Because the rate of grain rotation depends on the velocity gradient, the stronger fabric (soft in simple shear) will evolve more quickly than the weaker fabric (hard in simple shear). Therefore, the fabric separation between layers can increase in simple shear as the fabric evolves with each time step. This will cause fabrics to maintain their separation to a higher modeled bulk strain than 0.30. However, after 0.35 strain in our model runs dominated by high magnitudes of uniaxial compression or pure shear, the time step necessary for a 0.001 strain-step increases by over three orders of magnitude due to stress hardening. Further evolution becomes computationally impractical, because time steps that result in realistic amounts of recrystallization become too small. We therefore set ∊ R2 = 0.35 in our model, to capture the possible enhancement of the eigenvalue separation between fabric layers due to simple shear, but do not evolve the fabric further to avoid excessively large time steps. Reference Kennedy, Pettit and Di PrinzioKennedy and others (2013) found that for dome-like and ridge-like ice sheets, 0.30 modeled bulk strain corresponds to evolution through ∼200 ka while ∼0.20 bulk strain was ∼100 ka. We then set ∊ R1 = 0.20 so that ∊ R1 corresponds to about half of our fabric evolution time.
5. Results and Discussion
We evolve the layered fabric shown in Figure 4 through each of the 288 permutations of the stress style, stress magnitudes, NNI parameters and temperature values shown in Table 2. Figure 5 shows a contoured ternary plot of the eigenvalues for every time step of all 288 model runs. The fabrics all evolve towards the expected single-maximum-type fabrics found in ice sheets. The layered fabric initially has an eigenvalue separation of Δe 1 = 0.029 between the top/bottom layer and the middle layer. The total amount of strain where Δe 1 is greater than the under-sampling error (0.01) depends on the rates and magnitudes of several competing processes: grain rotation; NNIs; the stress regime; and the resulting amount of recrystallization.

Fig. 5. Contoured ternary plot of the eigenvalues of the fabrics for every time step of all 288 model runs. Because by definition e 1 > e 2 > e 3, only one-sixth of the equilateral triangle is used. The fabric density, ρ f, has been normalized by the maximum fabric density (ρ f/max(ρ f)). Example Schmidt plots show the fabrics with the eigenvalues directly adjacent to them.
We focus on the results that best illustrate the effects of simple shear, temperature and NNIs on the eigenvalue separation. Because each of these processes affects the rate and type of recrystallization events, recrystallization is discussed throughout.
5.1. Simple shear
Figure 6 shows the evolution of the fabric for the stress regimes (R1→R2) of: uniaxial compression only ![]() ; uniaxial compression to simple shear
; uniaxial compression to simple shear ![]() ; and uniaxial compression to uniaxial compression plus simple shear
; and uniaxial compression to uniaxial compression plus simple shear ![]() . The fabrics were evolved at −30 C with mild NNI ([ζ, ξ] = [6, 1]; Eqn (6)) and low stress magnitudes
. The fabrics were evolved at −30 C with mild NNI ([ζ, ξ] = [6, 1]; Eqn (6)) and low stress magnitudes ![]() .
.
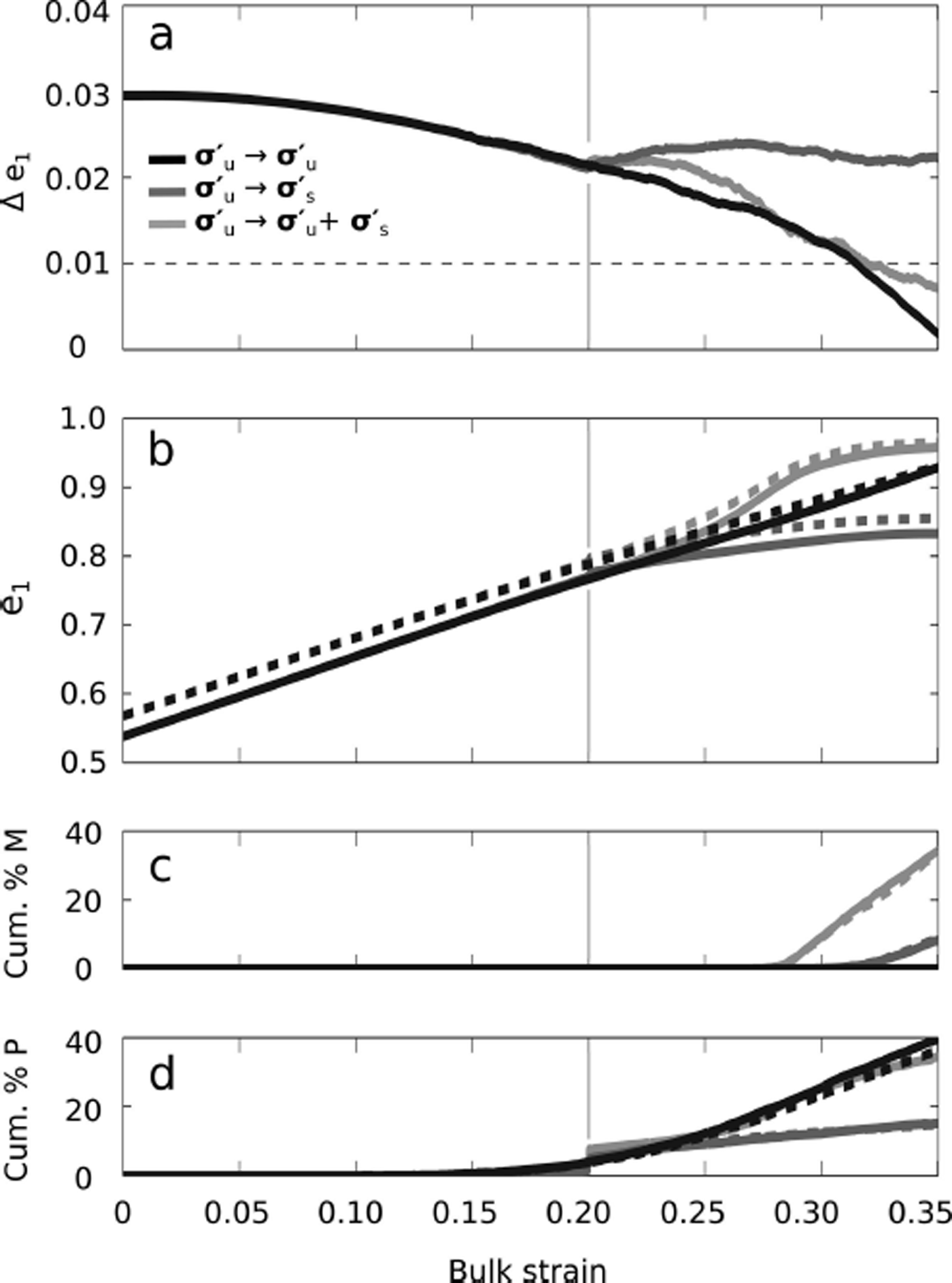
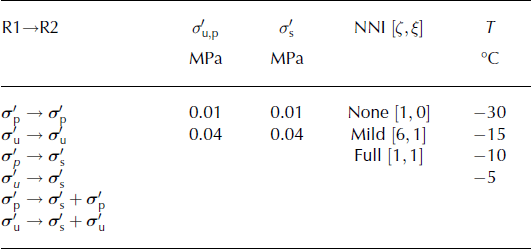
Fig. 6. The effects of simple shear on the evolution of the layered fabric (Fig. 4). The fabric was evolved at −30°C with mild NNI ([ζ, ξ] = [6, 1]; Eqn (6)) and low stress magnitudes ![]() for the stress regimes (R1→R2) of: uniaxial compression only (
for the stress regimes (R1→R2) of: uniaxial compression only (![]() , black curves); uniaxial compression to simple shear (
, black curves); uniaxial compression to simple shear (![]() , dark gray curves) and uniaxial compression to uniaxial compression plus simple shear (
, dark gray curves) and uniaxial compression to uniaxial compression plus simple shear (![]() , light gray curves). (a) The Δe
1 eigenvalue separation between the top/bottom and middle fabric layers. The horizontal dashed curve indicates the under-sampling error threshold, where Δe
1 may not be resolvable. (b–d) The fabric evolution (b), the cumulative percent of grains that have undergone migration recrystallization (c) and the cumulative percent of grains that have undergone a polygonization event (d). Solid curves indicate the top/bottom layer, while thick dashed curves indicate the middle layer. In all plots, light gray vertical lines mark the change from R1 to R2.
, light gray curves). (a) The Δe
1 eigenvalue separation between the top/bottom and middle fabric layers. The horizontal dashed curve indicates the under-sampling error threshold, where Δe
1 may not be resolvable. (b–d) The fabric evolution (b), the cumulative percent of grains that have undergone migration recrystallization (c) and the cumulative percent of grains that have undergone a polygonization event (d). Solid curves indicate the top/bottom layer, while thick dashed curves indicate the middle layer. In all plots, light gray vertical lines mark the change from R1 to R2.
In the ![]() model run, the eigenvalue separation, Δe
1, remains above the under-sampling error for the entire experiment. When compared with the
model run, the eigenvalue separation, Δe
1, remains above the under-sampling error for the entire experiment. When compared with the ![]() run, fabric evolution is slowed, polygonization events happen less frequently and there is some migration recrystallization (SIBM-N) happening at high modeled bulk strains (>0.30). The fabric evolution is slowed because at 0.20 modeled bulk strain, the fabrics are already mostly concentrated near vertical and the grains at the periphery of the distribution are now in the hardest orientation in simple shear (Fig. 3). These peripheral grains rotate towards the vertical slowly, causing e
1 to increase slowly. Likewise, the polygonization frequency is reduced because the grains in a hard orientation in simple shear (and therefore likely to be experiencing a bending moment;
run, fabric evolution is slowed, polygonization events happen less frequently and there is some migration recrystallization (SIBM-N) happening at high modeled bulk strains (>0.30). The fabric evolution is slowed because at 0.20 modeled bulk strain, the fabrics are already mostly concentrated near vertical and the grains at the periphery of the distribution are now in the hardest orientation in simple shear (Fig. 3). These peripheral grains rotate towards the vertical slowly, causing e
1 to increase slowly. Likewise, the polygonization frequency is reduced because the grains in a hard orientation in simple shear (and therefore likely to be experiencing a bending moment; ![]() , see Section 3.2.2) have not yet undergone enough modeled deformation to have a high dislocation density. The grains that have a high dislocation density are very close to vertical and located in a soft orientation (therefore unlikely to be experiencing a bending moment). Further, migration recrystallization events happen at the high modeled bulk strains for this run because the soft grains that already have high dislocation density increase their dislocation density further, to the point where migration recrystallization is possible even at such low temperatures. This agrees with observations by Reference KipfstuhlKipfstuhl and others (2009), which showed that recrystallization can be active at much lower temperatures than previously suggested. Because grains that undergo migration recrystallization are given a random orientation with a high RSS, they are likely to end up with an orientation either close to vertical or close to the direction of shearing (Fig. 3). The grains that end up pointing close to vertical will not strongly affect the fabric eigenvalues, as they stay within the vertically clustered distribution. The fabric in the
, see Section 3.2.2) have not yet undergone enough modeled deformation to have a high dislocation density. The grains that have a high dislocation density are very close to vertical and located in a soft orientation (therefore unlikely to be experiencing a bending moment). Further, migration recrystallization events happen at the high modeled bulk strains for this run because the soft grains that already have high dislocation density increase their dislocation density further, to the point where migration recrystallization is possible even at such low temperatures. This agrees with observations by Reference KipfstuhlKipfstuhl and others (2009), which showed that recrystallization can be active at much lower temperatures than previously suggested. Because grains that undergo migration recrystallization are given a random orientation with a high RSS, they are likely to end up with an orientation either close to vertical or close to the direction of shearing (Fig. 3). The grains that end up pointing close to vertical will not strongly affect the fabric eigenvalues, as they stay within the vertically clustered distribution. The fabric in the ![]() model run remains largely unaffected by the small number of migration recrystallization events.
model run remains largely unaffected by the small number of migration recrystallization events.
In the ![]() model run, Δe
1 remains above the under-sampling error to just slightly higher modeled bulk strains than in the
model run, Δe
1 remains above the under-sampling error to just slightly higher modeled bulk strains than in the ![]() run. Simple shear does not slow the fabric evolution in this case because the majority of grains will have a large RSS (Fig. 3), causing a rapid evolution of the fabric to the point where the fabric is too strongly orientated to maintain much separation. Both polygonization and migration recrystallization are active in this model run, due to the high RSS, which causes high modeled strain rates and a rapid build-up of dislocations. In this stress state, migration recrystallization will grow grains in almost any orientation. However, these grains will rapidly rotate to a vertical orientation and the rate of migration recrystallization events seen here does not change the fabric eigenvalues.
run. Simple shear does not slow the fabric evolution in this case because the majority of grains will have a large RSS (Fig. 3), causing a rapid evolution of the fabric to the point where the fabric is too strongly orientated to maintain much separation. Both polygonization and migration recrystallization are active in this model run, due to the high RSS, which causes high modeled strain rates and a rapid build-up of dislocations. In this stress state, migration recrystallization will grow grains in almost any orientation. However, these grains will rapidly rotate to a vertical orientation and the rate of migration recrystallization events seen here does not change the fabric eigenvalues.
Figure 7 shows the Δe 1 evolution for all model runs at −30 C with mild NNI (every permutation of stress and stress magnitude shown in Table 2). In all cases, simple shear stress causes the modeled bulk strain at which the eigenvalue separation stays above the under-sampling error (Δe 1 > 0.01) to either remain the same (once) or increase (15 times).
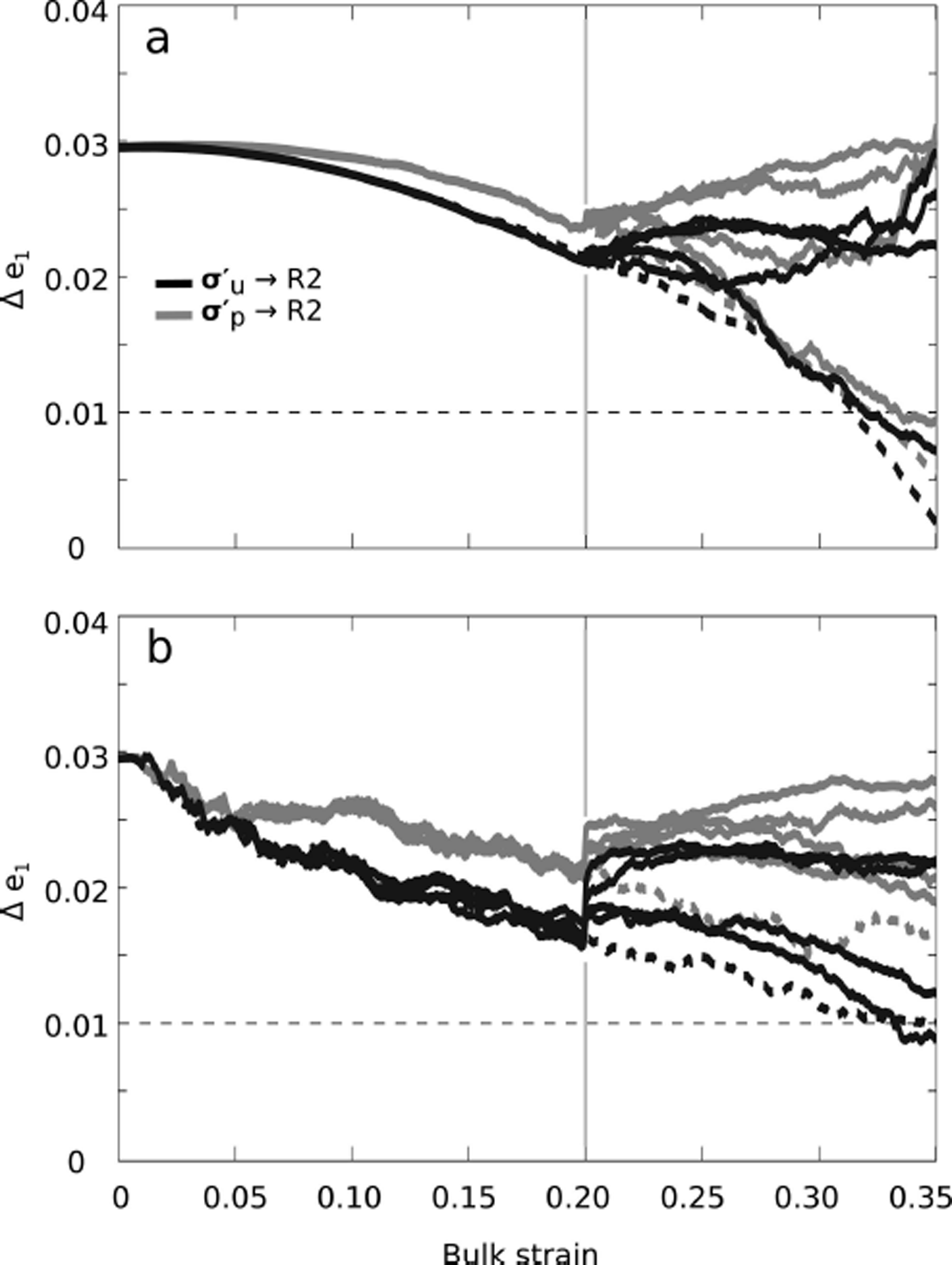
Fig. 7. The effects of simple shear on the evolution of the layered fabric (Fig. 4) eigenvalue separation between the top/bottom and middle fabric layers. The fabric was evolved at −30°C with mild NNI ([ζ, ξ] = [6, 1]; Eqn (6)) in every permutation of the stress regimes (R1→R2) and stress magnitudes ![]() shown in Table 2. Black curves indicate runs that started with uniaxial compression,
shown in Table 2. Black curves indicate runs that started with uniaxial compression, ![]() , while gray curves indicate runs that started with pure shear,
, while gray curves indicate runs that started with pure shear, ![]() . (a) Runs with a low stress magnitude initially
. (a) Runs with a low stress magnitude initially ![]() . (b) Runs with a high stress magnitude initially
. (b) Runs with a high stress magnitude initially ![]() . In both plots, the horizontal dashed line (b) indicates the under-sampling error threshold, where Δe
1 may not be resolvable, and light gray vertical lines in both plots mark the change from R1 to R2.
. In both plots, the horizontal dashed line (b) indicates the under-sampling error threshold, where Δe
1 may not be resolvable, and light gray vertical lines in both plots mark the change from R1 to R2.
5.2. Nearest-neighbor interaction
Figure 8 shows the repeated evolution of the same layered fabric with no NNI ([ζ, ξ] = [1, 0]; Eqn (6)), mild NNI ([ζ, ξ] = [6, 1]) and full NNI ([ζ, ξ] = [1, 1]) in the two stress regimes of uniaxial compression only (![]() ; Fig. 8a–d) and uniaxial compression to uniaxial compression plus simple shear (
; Fig. 8a–d) and uniaxial compression to uniaxial compression plus simple shear (![]() ; Fig. 8e–h). The fabric was evolved using T = −30°C and low stress magnitudes
; Fig. 8e–h). The fabric was evolved using T = −30°C and low stress magnitudes ![]() for both the stress regimes. Higher amounts of NNIs reduce the fabric separation at earlier modeled bulk strains. This happens because NNIs minimize the modeled strain-rate differences between neighboring grains, such that the grains tend to evolve towards vertical more slowly. This causes the grains to spend more time in a higher strain-rate orientation, which increases the dislocation density. A higher dislocation density allows the recrystallization processes to happen at an earlier modeled bulk strain. Polygonization then slows the fabric evolution by moving grains away from vertical. This affects the stronger fabric preferentially, as it has more hard grains that are prone to polygonization. Therefore, higher levels of NNIs decrease the modeled bulk strain at which Δe
1 remains >0.01.
for both the stress regimes. Higher amounts of NNIs reduce the fabric separation at earlier modeled bulk strains. This happens because NNIs minimize the modeled strain-rate differences between neighboring grains, such that the grains tend to evolve towards vertical more slowly. This causes the grains to spend more time in a higher strain-rate orientation, which increases the dislocation density. A higher dislocation density allows the recrystallization processes to happen at an earlier modeled bulk strain. Polygonization then slows the fabric evolution by moving grains away from vertical. This affects the stronger fabric preferentially, as it has more hard grains that are prone to polygonization. Therefore, higher levels of NNIs decrease the modeled bulk strain at which Δe
1 remains >0.01.
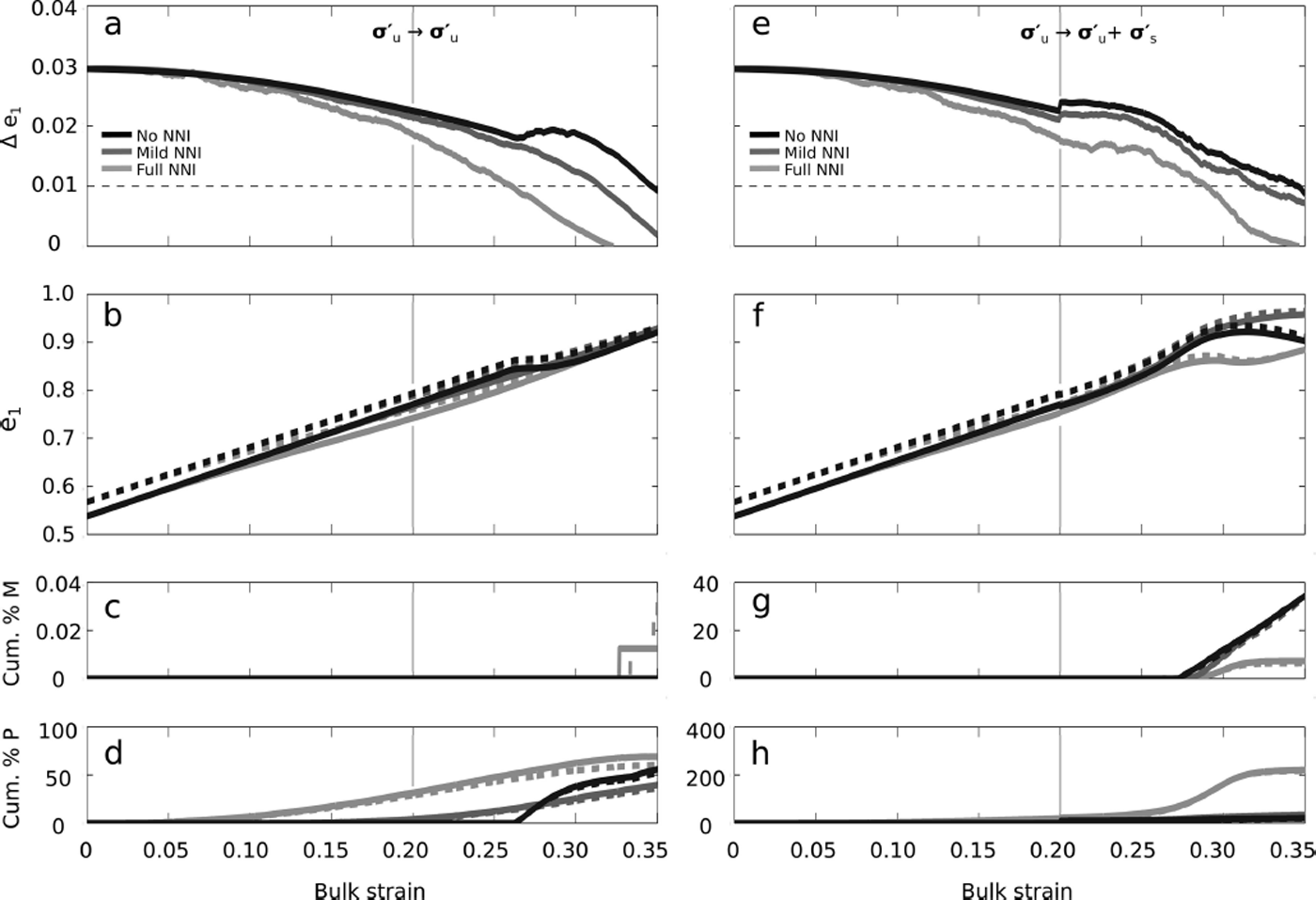
Fig. 8. The effects of NNI on the evolution of the layered fabric (Fig. 4). The fabric was evolved at T = −30°C with each of the NNIs shown in Table 2. (a–d) The evolution of uniaxial compression only ![]() with a low stress magnitude
with a low stress magnitude ![]() . (e–h) The evolution of uniaxial compression plus simple shear
. (e–h) The evolution of uniaxial compression plus simple shear ![]() with a low stress magnitude
with a low stress magnitude ![]() . Black curves indicate no NNI ([ζ, ξ] = [1, 0]; Eqn (6)), dark gray curves indicate mild NNI ([ζ, ξ] = [6, 1]) and light gray curves indicate full NNI ([ζ, ξ] = [1, 1]). (a) and (e) show the Δe
1 eigenvalue separation between the fabric’s top/bottom and middle layers, and horizontal dashed lines indicate the under-sampling error threshold, where Δe
1 may not be resolvable. (b–d) and (f–h) show the fabric evolution, the cumulative percent of grains that have undergone migration recrystallization and the cumulative percent of grains that have undergone a polygonization event, respectively. Solid curves indicate the fabric’s top/bottom layer, and dashed curves indicate the middle layer. In all plots, the light gray vertical lines mark the change from R1 to R2.
. Black curves indicate no NNI ([ζ, ξ] = [1, 0]; Eqn (6)), dark gray curves indicate mild NNI ([ζ, ξ] = [6, 1]) and light gray curves indicate full NNI ([ζ, ξ] = [1, 1]). (a) and (e) show the Δe
1 eigenvalue separation between the fabric’s top/bottom and middle layers, and horizontal dashed lines indicate the under-sampling error threshold, where Δe
1 may not be resolvable. (b–d) and (f–h) show the fabric evolution, the cumulative percent of grains that have undergone migration recrystallization and the cumulative percent of grains that have undergone a polygonization event, respectively. Solid curves indicate the fabric’s top/bottom layer, and dashed curves indicate the middle layer. In all plots, the light gray vertical lines mark the change from R1 to R2.
5.3. Temperature
Figure 9 shows the repeated evolution of the same layered fabric for the temperatures T = −30, −15, −10, −5°C in the two stress regimes of uniaxial compression only (![]() ; Fig. 9a–d) and uniaxial compression to uniaxial compression plus simple shear (
; Fig. 9a–d) and uniaxial compression to uniaxial compression plus simple shear (![]() ; Fig. 9e–h). The fabric was evolved using mild NNI ([ζ, ξ] = [6, 1]; Eqn (6)) and low stress magnitudes
; Fig. 9e–h). The fabric was evolved using mild NNI ([ζ, ξ] = [6, 1]; Eqn (6)) and low stress magnitudes ![]() for both the stress regimes. The results from these runs fall into two sets: T = −30, −15°C and T = −10, −5°C. The evolution of the fabric does not differ significantly within a set, but there is a large change in the fabric evolution between the sets, due to the step change in the activation energy, Q
b (Eqn (11), Table 1). At any given modeled bulk strain, the change in activation energy results in a decrease in the eigenvalue separation, Δe
1, a slowdown of the e
1 evolution and an increase in the polygonization events. Temperature, therefore, does not change the fabric evolution in the modeled bulk strain, except when crossing the activation energy threshold.
for both the stress regimes. The results from these runs fall into two sets: T = −30, −15°C and T = −10, −5°C. The evolution of the fabric does not differ significantly within a set, but there is a large change in the fabric evolution between the sets, due to the step change in the activation energy, Q
b (Eqn (11), Table 1). At any given modeled bulk strain, the change in activation energy results in a decrease in the eigenvalue separation, Δe
1, a slowdown of the e
1 evolution and an increase in the polygonization events. Temperature, therefore, does not change the fabric evolution in the modeled bulk strain, except when crossing the activation energy threshold.
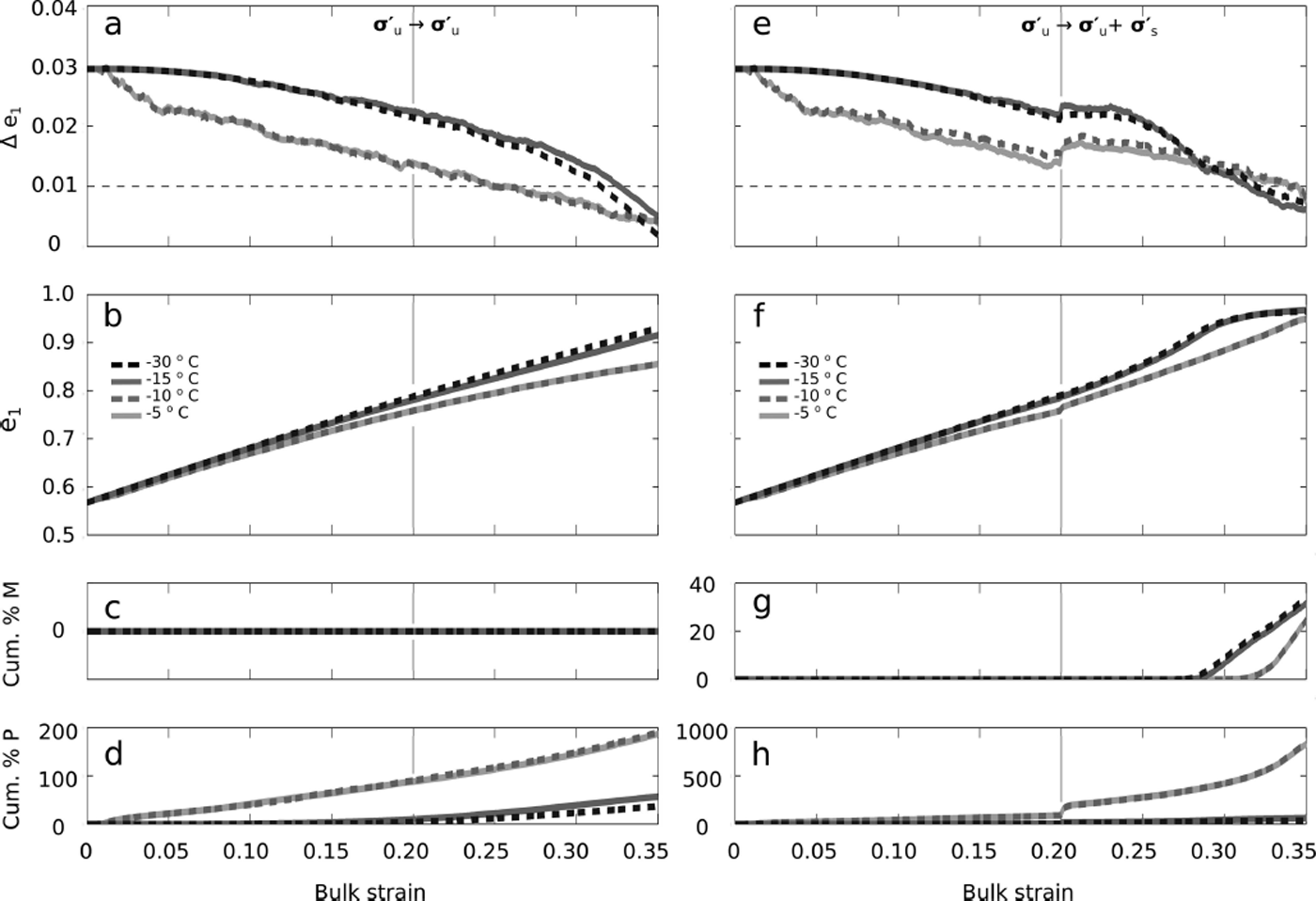
Fig. 9. The effects of temperature on the evolution of the layered fabric (Fig. 4). The fabric was evolved with mild NNI ([ζ, ξ] = [6, 1]; Eqn (6)) in each of the temperature regimes shown in Table 2 (T = −30, −15, −10 and −5°C). (a–d) The evolution of uniaxial compression only ![]() with a low stress magnitude
with a low stress magnitude ![]() . (e–h) The evolution of uniaxial compression plus simple shear
. (e–h) The evolution of uniaxial compression plus simple shear ![]() with a low stress magnitude
with a low stress magnitude ![]() . The black dashed curves indicate temperatures of T = −30°C, the solid dark gray curves indicate T = −15°C, the dashed dark gray curves indicate T = −10°C and the light gray curves indicate T = −5°C. (a) and (e) show the Δe
1 eigenvalue separation between the top/bottom and middle fabric layers, and the horizontal dashed line indicates the under-sampling error threshold where Δe
1 may not be resolvable. (b–d) and (f–h) show the fabric evolution, the cumulative percent of grains that have undergone migration recrystallization and the cumulative percent of grains that have undergone a polygonization event, respectively. The light gray vertical lines in all plots mark the change from R1 to R2.
. The black dashed curves indicate temperatures of T = −30°C, the solid dark gray curves indicate T = −15°C, the dashed dark gray curves indicate T = −10°C and the light gray curves indicate T = −5°C. (a) and (e) show the Δe
1 eigenvalue separation between the top/bottom and middle fabric layers, and the horizontal dashed line indicates the under-sampling error threshold where Δe
1 may not be resolvable. (b–d) and (f–h) show the fabric evolution, the cumulative percent of grains that have undergone migration recrystallization and the cumulative percent of grains that have undergone a polygonization event, respectively. The light gray vertical lines in all plots mark the change from R1 to R2.
Nevertheless, because ice at a higher temperature has a larger flow parameter (![]() , Eqn (4)), the ice will deform more quickly at higher temperatures. The actual time required for the modeled ice to reach any given bulk strain will then be shorter at higher temperatures. This also means that, for model runs that drop below an e
1 separation of 0.01 at the same modeled bulk strain, the actual time elapsed will be much shorter for runs at high temperatures (Fig. 10). Critically, migration recrystallization (SIBM-N) events are reduced for a given modeled bulk strain at the higher temperatures because of the very large number of polygonization events (which both depend on and reduce the dislocation density). Yet, because the time required to reach any given modeled bulk strain will be shorter, the earlier onset of migration recrystallization for higher temperatures still holds true.
, Eqn (4)), the ice will deform more quickly at higher temperatures. The actual time required for the modeled ice to reach any given bulk strain will then be shorter at higher temperatures. This also means that, for model runs that drop below an e
1 separation of 0.01 at the same modeled bulk strain, the actual time elapsed will be much shorter for runs at high temperatures (Fig. 10). Critically, migration recrystallization (SIBM-N) events are reduced for a given modeled bulk strain at the higher temperatures because of the very large number of polygonization events (which both depend on and reduce the dislocation density). Yet, because the time required to reach any given modeled bulk strain will be shorter, the earlier onset of migration recrystallization for higher temperatures still holds true.
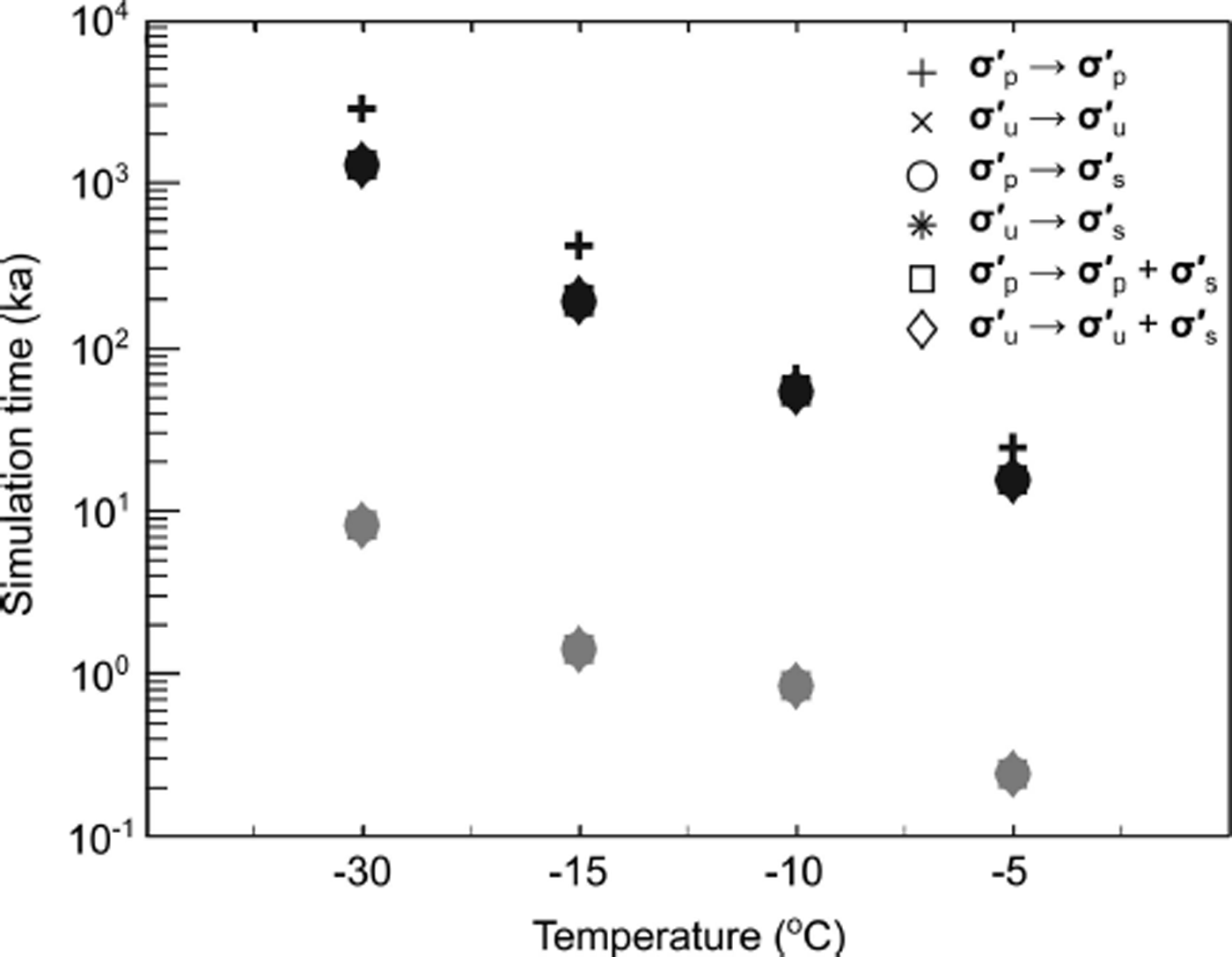
Fig. 10. The total simulation time to evolve the fabric to 0.35 bulk strain for our different model runs. Time is shown on a logarithmic scale. Black symbols indicate runs with low stress magnitudes ![]() and gray symbols indicate runs with high stress magnitudes
and gray symbols indicate runs with high stress magnitudes ![]() .
.
5.4. Further discussion
In all of our experiments, a variation in fabric is either preserved or enhanced under shear stresses. There is a ‘window of opportunity’ in which the separation of eigenvalues is sufficient to observe the variation before the fabric becomes too strongly oriented to maintain much separation. The length of time this window is open depends on the magnitude of the initial fabric variation, the initial strength of the weaker fabric, the magnitude of the applied stress, the strength of the NNIs and the resultant number of recrystallization events. If the initial fabric variation is sufficiently large, the weaker initial fabric controls the time the window is open – the window closes as the weaker fabric reaches the maximum fabric strength (the stronger fabric reaches the maximum fabric strength before the weaker fabric).
By finding the modeled strain (and therefore time) at which the e 1 separation is <0.01, we can determine how long the window stays open. Our model results suggest that the window will stay open at least through 0.3 modeled bulk strain in most of the modeled constant-stress regimes, and shear stress will keep the window open well past 0.35 modeled bulk strain. The total simulated time for any particular run is shown in Figure 10 and ranges from a few hundred years in the warmest, highest-stress cases to a few hundred thousand years in the coldest, lowest-stress cases (typical of an ice divide).
However, the parameter values in Table 1 may be different in situ, because we are not modeling a specific glacier. In order to test the sensitivity of our model to these parameters, we ran a variety of experiments varying parameters with an increase or decrease of 10%. We tested changes in the isotropic ice softness by varying (1) (Eqn (4)); the grain growth (which influences the change in dislocation density and the rates of polygonization and SIBM-N) by varying (2) the intrinsic grain growth factor, K 0, and (3) the thermal activation energy, Q (Eqns (11) and (12)); and the migration recrystallization (SIBM-N) threshold by varying (4) the dislocation energy constant, μ (Eqn (13)). These four parameters together allow us to vary all the processes captured in our model. For each parameter, we computed a set of model runs at T = −30°C, low uniaxial compression, low shear stress and mild NNIs. We computed another set of model runs at T = −5°C with the same stresses and NNIs. Each set consists of a control run, a run with a 10% increase in the parameter and a run with a 10% decrease in the parameter. In total, we computed runs for four parameters, each in two temperature regimes, with three values for the parameters for 24 more model runs.
Most of the model runs are not presented here as they show only negligible effects on the fabric evolution (the changes are smaller than the width of the plot lines). The only significant changes in results we see occur when varying the thermal activation energy, Q, at T = −30°C (Fig. 11a–d) and when varying the dislocation energy constant, μ, at T = −5°C (Fig. 11e–h). An increase in the thermal activation energy at T = −30°C caused more polygonization events, fewer migration recrystallization events and a slower fabric evolution (Fig. 11b–d). However, because these changes are small, the e 1 separation is negligibly affected (Fig. 11a). Decreasing the activation energy had negligible effects.
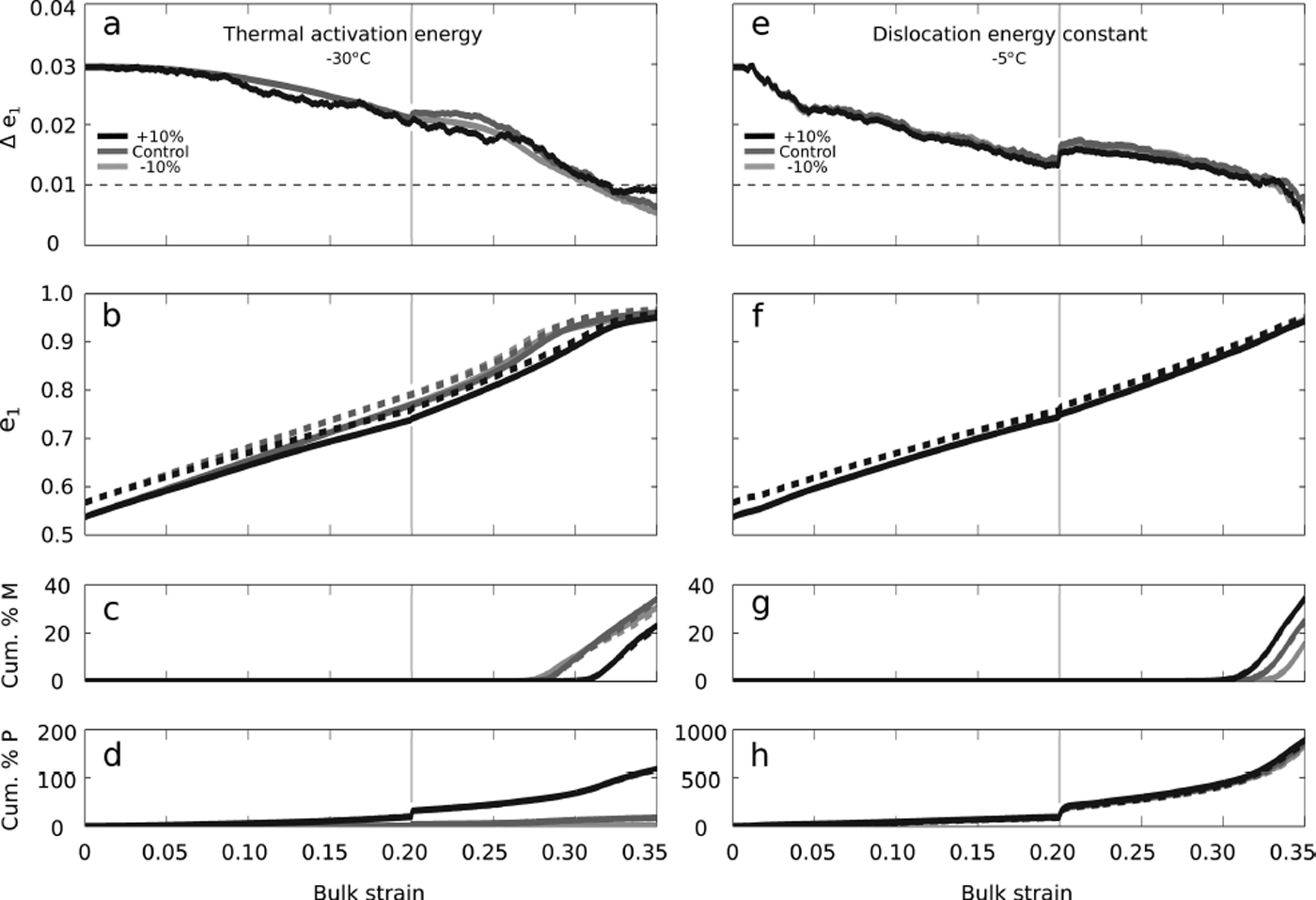
Fig. 11. Sensitivity to the model parameters (Table 1). (a–d) The result of varying the thermal activation energy, Q, at T = −30°C. (e–h) The result of varying the dislocation energy constant, μ, at T = −5°C. Dark gray curves indicate the control run, while black curves indicate a 10% increase in the parameter values and light gray curves indicate a 10% decrease in the parameter values. (a) and (e) show the Δe 1 eigenvalue separation between the fabric’s top/bottom and middle layers, and horizontal dashed lines indicate the under-sampling error threshold where Δe 1 may not be resolvable. (b–d) and (f–h) show the fabric evolution, the cumulative percent of grains that have undergone migration recrystallization and the cumulative percent of grains that have undergone a polygonization event respectively. Solid curves indicate the fabric’s top/bottom layer, and dashed curves indicate the middle layer. In all plots, the light gray vertical lines mark the change from R1 to R2.
Increasing the dislocation energy constant (Fig. 11g) causes a small increase in migration recrystallization events and, likewise, there was a small decrease in migration recrystallization events when the dislocation energy constant was decreased. Despite this change in migration recrystallization, the fabric evolution, polygonization and e 1 separation were negligibly affected (Fig. 11e, f and h). Therefore, we conclude that our model is insensitive to small changes in parameter values and the conclusions presented above are robust.
It should also be noted that the fabric eigenvalues are not a complete description of the ice, and layers with the same eigenvalues may have different distributions of dislocation densities. It is possible for a fabric that has evolved to its maximum e 1 eigenvalue and/or lost the distinction between its layers (Δe 1 < 0.01) to have its layers separate again due to different levels of recrystallization. We did not observe this re-separation in any of our model runs, but it may be seen with fabrics evolved to higher bulk strains than were modeled.
6. Conclusions
Our model predicts that for constant shear-stress regimes, modeled bulk strains >0.35 (for time, see Fig. 10) are necessary to rid glacial ice of its past ‘memory’ of fabrics and stress states. In our model, shear stress preserves a subtle variation in fabric longer than compressive-stress regimes and may act to enhance the fabric variation in certain stress regimes by rotating grains into softer orientations and reducing the number of polygonization events.
Our model further predicts that temperature does not affect the modeled bulk strain at which the fabric variation is sufficient to be observed, except when crossing a thermal activation energy threshold. The model shows that the much higher levels of recrystallization observed in warm, fast-flowing ice are balanced by the increased modeled strain rates and grain rotation, such that the fabric variation may be observable past 0.35 modeled bulk strain. For any combination of the modeled stresses or temperatures, migration recrystallization (SIBM-N) does not rid the modeled fabric of its memory. However, using higher amounts of NNIs within the model reduces the fabric variation for a given modeled bulk strain.
We therefore conclude that fabric variation below the firn–ice transition, can be preserved in polar ice sheets. Because the microstructural processes active in the firn layer are dependent on climate variables, it is possible that the fabric variations arise from climate variations. In order to quantify the effects of climatic changes on the microstructure evolution in the firn layer, more work is needed. A microstructure model that is able to simulate multiple fabrics with a statistically relevant number of grains, that captures the dynamics in the firn and ice region, and is coupled to a flow model, is needed.
Acknowledgements
We thank the Scientific Editor Sérgio H. Faria, Paul Duval and an anonymous reviewer for detailed comments that considerably improved the manuscript. We also thank Martin Truffer, Ed Bueler and Christina Carr for help throughout the preparation of this manuscript. The work presented here was supported by US National Science Foundation (NSF) grants OPP#0948247, OPP#0940650 and OPP#0636795.
















