Notation
1. Introduction
Underlying the paleoclimatic interpretation of ice cores is the assumption that a core samples the ice in the order in which it was deposited. Some post-depositional modification in the ice stratigraphy, such as thinning of annual layers, is anticipated and can be included in the interpretation of the climatic signal. Unanticipated thinning would introduce errors in some climatic signals, such as the accumulation rate, but actual alteration in the order of some of the stratigraphic layers in the core sample affects the entire climatic signal they carry.
1.1. Evidence from ice caps
The suggestion that the Greenland Icecore Project (GRIP) ice core showed evidence of major climatic shifts in part of the Eemian interglacial period (GRIP Members, 1993) proved to be particularly controversial when the nearby Greenland Ice Sheet Project 2 (GISP2) core lacked the corresponding oxygen-isotope oscillations (Reference Grootes, Stuiver, White, Johnsen and JouzelGrootes and others, 1993). It was suggested that one or both of the cores had been altered by folding or other forms of mixing. Further research found evidence for differential thinning, and possibly even folding, in the lower 10% of the ice by comparing the water isotope signal with the atmospheric dissolved gases signal (Reference Fuchs and LeuenbergerFuchs and Leuenberger, 1996). A detailed examination of visible stratigraphy showed dips of up to 20°, and even a few small overturned folds in the lower 25% of the cores (Reference Alley, Gow, Johnsen, Kipfstuhl, Meese and ThorsteinssonAlley and others, 1995). A small-scale structure, called “stripes”, was also identified in the GISP2 core (Reference Alley, Gow, Meese, Fitzpatrick, Waddington and BolzanAlley and others, 1997). Photographs of these stripes, and small folds associated with them, can be seen in Reference Alley, Gow, Meese, Fitzpatrick, Waddington and BolzanAlley and others (1997). The difficulty in identifying internal radar layers in deep ice may sometimes be an indication of stratigraphic disturbance at these depths (Reference Robin, de, Robin and deRobin, 1983).
Interaction of contrasting layers has been been proposed as a cause of such folding (Reference Dahl-Jensen, Thorsteinsson, Alley and ShojiDahl-Jensen and others, 1997). Layering in anisotropic ice directly under the divide, where it is subject to vertical compression, appears, in theory, to be potentially unstable (Reference Azuma and Goto-AzumaAzuma and Goto-Azuma, 1996; Reference CastelnauCastelnau and others, 1998; Reference Thorsteinsson and WaddingtonThorsteinsson and Waddington, 2002). Recumbent folding observed at the terminus of Barnes Ice Cap, Canadian Arctic, has been attributed to advancing or retreating margins (Reference HudlestonHudleston, 1977). Foliation developed under one flow pattern could be passively deformed and folded when subjected to a different flow.
The GRIP core was drilled close to the current summit divide of the Greenland ice sheet in the hope of observing a maximum possible thickness of undisturbed ice. The GISP2 core was placed ten ice thicknesses (30 km) to the west of the divide to give a complementary sample of nearby flank-flow ice. But if the divide moved around during the last glacial cycle (Reference Anandakrishnan, Alley and WaddingtonAnandakrishan and others, 1994; Reference Marshall and CuffeyMarshall and Cuffey, 2000) it may be best to consider both locations as near-divide sites. Other cores, such as Dye 3 (Greenland), Camp Century (Greenland) and Byrd (Antarctica) have been drilled on clearly flank positions.
Ice-penetrating radar can follow the internal stratigraphy over large horizontal extents, to complement the very small-scale details seen in ice cores. Examples can be found from Greenland (Reference Jacobel and HodgeJacobel and Hodge, 1995), East Antarctica (Reference Robin, de, Robin and deRobin, 1983) and Siple Dome, West Antarctica (Reference Nereson, Raymond, Waddington and JacobelNereson and others, 1998). Unfortunately, the ability of radar to image folds at scales smaller than tens to hundreds of meters may be limited. These intermediate-scale folds are also difficult to clearly identify in ice cores. Without azimuthal orientation information or reliable “up” indicators (Reference Alley, Gow, Johnsen, Kipfstuhl, Meese and ThorsteinssonAlley and others, 1995) it is difficult to say whether a dip in the stratigraphy in a core sample is the start of a fold, or the overturned limb of a well-developed fold.
1.2. A passive-shearing model of folding
To understand how stratigraphic layers in an ice sheet could be reordered, Reference Waddington, Bolzan and AlleyWaddington and others (2001) (also Reference Bolzan, Waddington, Alley and MeeseWaddington and others, 1995; Reference Jacobson and WaddingtonJacobson and Waddington, 1996; Reference JacobsonJacobson, 2001) have studied the kinematics of forming recumbent folds from gentle disturbances in otherwise steady-state stratigraphy. At scales of decimeters to decameters, these initial disturbances could have their roots in some transient dynamic process, most likely involving local rheological inhomogeneities. Reference Waddington, Bolzan and AlleyWaddington and others (2001) and Reference Thorsteinsson and WaddingtonThorsteinsson and Waddington (2002) evaluate in more detail some processes that could possibly generate such small-scale wrinkles. At the scale of hundreds of meters, the arches created in internal layers by the special flow pattern found under an ice divide (Reference RaymondRaymond, 1983) can be a source of initial layer disturbance if a stationary ice divide subsequently migrates rapidly. These arches have been observed in Antarctica at Fletcher Promontory (Reference Vaughan, Corr, Doake and WaddingtonVaughan and others, 1999), Siple Dome (Reference Nereson, Raymond, Waddington and JacobelNereson and others, 1998) and Roosevelt Island (Reference Conway, Hall, Denton, Gades and WaddingtonConway and others, 1999). In a separate paper (unpublished manuscript by Jacobson and Waddington) we investigate the potential for generating folds from these arches. However, we do not have a comprehensive theory of how and where injection of disturbances might occur at other places and at other spatial scales, and so we will limit this study to examining the consequences of injection at a variety of positions.
The deformation in an ice sheet in plane strain near its center can be represented as a combination of vertically compressive pure shear and bed-parallel simple shear. The pure shear thins and stretches the stratigraphic layers. It also flattens disturbances in these layers. The simple shear, on the other hand, “catches” these wrinkles and deforms them into order-disrupting recumbent folds. These two effects are illustrated in Figure 1, where the contrasting rotations of the A–B limb are highlighted. When we discuss the angle and rotation of a segment, it is the behavior of just such a portion of a disturbance that we have in mind.
Fig. 1. The deformation of a disturbed layer under (a) pure shear and (b) simple shear. Pure shear, with vertical compression, flattens the disturbance. Simple shear steepens (and overturns)the A–B limb while leaving the disturbance amplitude unchanged.
Reference Waddington, Bolzan and AlleyWaddington and others (2001) used this trade-off between stretching and shearing to determine where disturbances of any given slope would be flattening and where they would be overturning. They assessed the plausibility of several proposed disturbance sources, and applied their stability limit estimates to the Dye 3, GRIP, GISP2 and Siple Dome ice-core sites. Their simple approach was based entirely on the strain rate at a point (e.g. the point at which a disturbance might be created by localized inhomogeneous flow). As they noted, their assessment gave an optimistic view of stratigraphic integrity, because it neglected variations in strain rate experienced by disturbances as they moved (a) over undulating bedrock, and (b) into deeper regions with stronger bed-parallel shear strain rates. They were able to estimate the time required for disturbances to overturn, and the distance that disturbances would move during this time, but only for disturbances that were already rotating strongly at the point of injection. They suggested that finite-strain calculations, following disturbances as they moved along particle paths, would produce better assessments of the behavior of marginally unstable disturbances, and would greatly advance understanding of this passive-folding process. This paper analyzes those finite strains to understand features of folding that could not be addressed by Reference Waddington, Bolzan and AlleyWaddington and others (2001).
One measure of the mixture of pure and simple shear is the kinematic vorticity number,
(Reference Means, Hobbs, Lister and WilliamsMeans and others, 1980). This is defined so that W
k = 0 for pure shear, and W
k = 1 for simple shear.
is the rotation rate of the principal axes, and
is the difference in their strain rates,
. In Reference Hudleston, Le and HookeHudleston and Hooke (1980) this is called the index of simple shear, I
ss. Under pure shear, the principal axes do not rotate, while under simple shear, their rotation rate equals the strain rate.
The vorticity numberFootnote 1 for a simple ice-sheet flowband model is shown in Figure 2. Near the surface of the ice sheet, vertical compression dominates, so W k is close to 0. This is also true directly under the divide where the horizontal flow is negligible. On the flank, the proportion of simple shear increases with depth, and W k approaches unity.
Fig. 2. The kinematic vorticity number, Wk, and the critical wrinkle angle, θr, for a simple ice-sheet model. z/H describes the relative height in the ice sheet; x/L the distance from the ice-sheet center. The lefthand number on each contour, Wk, is a measure of the relative magnitudes of pure and simple shear. Pure shear dominates near the surface and under the divide (Wk close to 0) while simple shear dominates elsewhere (Wk close to 1). The righthand number, θr, is the segment angle that is not rotating at this point in the flow(cos–1 Wk).
In pure shear (as in Fig. 1a), vertical and horizontal segments do not rotate, while segments on either side of vertical rotate toward horizontal. Under simple shear, all segments, except those parallel to the plane of shear, rotate in the same direction (clockwise in Fig. 1b). In mixed pure and simple shear (0 < W k < 1), there is some angle, θ r ≈ cos–1 W k, between vertical and horizontal that is not rotating, and which separates the clockwise rotating segments from the anticlockwise ones (Reference BobyarchickBobyarchick, 1986). The contours in Figure 2 have been labeled with this angle. The critical wrinkle segment slope, m crit ≈ S –1, in Reference Waddington, Bolzan and AlleyWaddington and others (2001) is approximately the tangent of θ r, and their dimensionless shear number, S, is a variant on W k.
The wrinkle in Figure 1 with the A–B segment at about 41° would be flattening if it occurred above the 41° contour in Figure 2, but would be steepening (rotating clockwise) if it was below this contour.
θ r is not simply a divider between segments that rotate one way versus the other. As a segment moves along a particle path, W k increases and θ r decreases. The effect on the segment’s rotation can be seen by considering a segment with an angle equal to θ r at time t on the path. At this point it is not rotating. At t + dt, a short time later, it will have practically the same angle, but will be further along the path, where θ r is smaller. Since it is now steeper than θ r, its rotation is clockwise, away from θ r. Conversely, at an earlier time, t – dt, the segment angle would have been larger than the local θ r, which means that the segment was rotating anticlockwise, toward θ r. In effect, the θ r angle is a turnaround point. A segment can flatten until it reaches the local θ r, at which point it reverses rotation direction and starts to steepen.
1.3. Observation points
Since segments can change their direction of rotation, we need to look at the evolution of a disturbance over a finite interval along a path in order to gain a more detailed understanding of the folding process than that which the first analysis of θ r by Reference Waddington, Bolzan and AlleyWaddington and others (2001) provides. This requires choosing meaningful end-points for such an interval.
The obvious choice for the starting point is where the disturbance originated, assuming, of course, that there is a time when the transient dynamics generating the disturbance cease to be significant and we can focus on the kinematics. In this paper, we do not examine the complexities of this transition. In a separate paper (unpublished manuscript by Jacobson and Waddington) we investigate one such transition to kinematic overturning, which occurs in the special flow field found under an ice divide (Reference RaymondRaymond, 1983). Here we limit our study to following smaller-scale disturbances, injected at a variety of positions, after this transition has occurred.
We have found it equally productive to specify the interval end-point, as the place where we find an observed or hypothetical fold, and ask what sort of disturbance might have been its precursor. In particular, we look at a vertical set of observation points, such as might be sampled in an ice core.
To study this kinematic folding, we use a flowband model to calculate the ice velocity and its gradient at all points, and use these to calculate particle paths. Then we define core-relative isochrones and show their relevance to folding. Next we calculate the deformation gradient and show how it gives more general information on segment rotation. Finally, we ask how much information is needed to predict where observed folds might have originated. While the best evidence for folding has been found in the lower 20% of ice sheets, and while models predict the greatest likelihood of folding near the bed, nevertheless our models show that folds can be encountered virtually anywhere in an ice sheet, except close to the surface, or directly under a stable ice divide.
2. Flowband Model
After defining some terminology for disturbances and angles, we will describe a simple flowband model of an ice sheet. This model calculates the velocity at points in the flowband as a function of position and model geometry. Using this velocity field, we can calculate the velocity gradient, W k, and θ r at specific points. We can also calculate particle paths and finite strain along these paths.
2.1. Disturbance notation
A prototypical upward disturbance with key terms is depicted in Figure 3. Such a wrinkle might be the result of stratigraphic layers draping around a transient rheologically harder lump of ice (Reference Waddington, Bolzan and AlleyWaddington and others, 2001). Of particular interest is the leading limb (the A–B edge in Fig. 1), which is the portion of this disturbance which would overturn when sheared in the direction of flow. We will also refer to the trailing limb, the portion that will flatten under both pure and simple shear. If the disturbance were inverted (that is, a dip) the limb on the upstream side of the disturbance would be the limb at risk of overturning. The required adjustment in terminology is left to the reader.
Fig. 3. Prototypical disturbance, illustrating our notation, including leading limb, trailing limb and θ. Segment slope is measured relative to horizontal (pointing upstream). Not shown is the slight slope (relative to horizontal) of the undisturbed stratigraphy. One could imagine a disturbance such as this forming around a rheologically stiffer “lump” in the ice. Such a lump would also disturb the layers below it.
We will use θ for the angle of a segment, measuring it relative to the horizontal axis pointing in the upstream direction (to the left in our prototype). This choice of angle orientation means that the initial angle of a leading limb will be in the 0–90° range, and will increase to 90° and beyond when the leading limb overturns. A trailing limb will start in the 90–180° range and rotate toward 180°.
For the purposes of this paper, we ignore the distinction between horizontal and the slope of undisturbed stratigraphy. Near the center of an ice sheet, the slope of stratigraphy over a flat bed is negligible, on the order of 0.5° or less.
2.2. Velocity model
We use a simple flowband model, with enough detail to capture the change in the vorticity number along particle paths but without complicating details. This model assumes that surface slopes are small and that the bed is frozen. This is true for the central portion of many, though not all, ice sheets and ice caps. Allowing sliding on all or portions of the base would require a significantly more complicated flowband model; however, as long as some ice flow due to horizontal shear is present, folding as encapsulated in Figure 1 will be present.
Figure 4 illustrates our model. The coordinate system is aligned with the direction of flow. The horizontal coordinate in this direction is x, while z is the vertical coordinate. The corresponding velocity components are u and w (positive upward). Perpendicular to these is y, with its velocity component υ, being zero by definition.
Fig. 4. Flowband geometry and notation defined in text. Crosses on the particle path mark equal elapsed time intervals.
The geometric inputs to our velocity model are the surface profile S(x) and the bed profile B(x). The flowband ice equivalent thickness is h(x) = S – B.
The transverse geometry can be expressed in terms of a relative flowband width, and used to calculate the transverse spreading rate ∂yυ, as a function of u and x.
We also specify the flux Q(x), through the flowband cross-section at x. Dividing by the thickness gives a depth-averaged horizontal velocity,
.
Rounding out the inputs is an expression for the vertical profile (shape function) of the horizontal velocity,
. The source of this function is a dynamic model that includes momentum conservation and ice rheology. The horizontal velocity can then be written as
Since the integral of u over the thickness equals the flux, the integral of
over z must equal h. The vertical velocity can be derived from u(x, z) by incompressibility,
We simplify the calculations with a number of assumptions, which can be selectively relaxed to explore their effect on the results. Few are essential to this analysis, but they allow us to keep the description simple, while retaining the features of the flow that are key to folding. The resulting model was first proposed by Reference VialovVialov (1958) (see also Reference ReehReeh, 1988).
We assume that the base is flat, B(x) = 0, and that the ice is frozen to the bed, so that u(x, B) = w(x, B) = 0. The flowband width is uniform, so that all the gradient terms in the y direction vanish. This approximates the flow on an ice ridge or a highly elongated dome. The velocity gradient is then
We assume that the ice-sheet surface is in steady state. The flux Q(x) through a cross-section must equal the integrated accumulation upstream. If we also assume that the accumulation rate,
, is uniform in space, then the flux is
.
This uniform-accumulation assumption requires that we specify the length or span of the flowband L, in order to determine the model geometry. In effect, we specify the location of a calving front that can handle any flux. The conditions at such a terminus are not realistic, but they do not adversely affect the model a short distance inland. L could also be thought of as a virtual or effective length. If an ice sheet terminates in an ice stream (as Siple Dome does) or a narrow ablation zone, the terminus profile would be different, but this model would still be useful over a wide region around the divide.
To specify
and S, we assume that the ice is isothermal, and use the shallow-ice approximation (Reference HutterHutter, 1983; Reference PatersonPaterson, 1994, p. 262) with Glen’s flow law. This flow law assumes that the deviatoric stress σ′, and strain rate
, are related by
, where A is a temperature-dependent flow parameter. Since, in a typical ice sheet, the length is much larger than the thickness, the shearing component, ∂zu, is the largest term of the velocity gradient over much of the flowband, and the flow law can be written as
where S′ is the surface gradient. Integrating Equation (4) upward from the bed gives the horizontal velocity and its shape function.
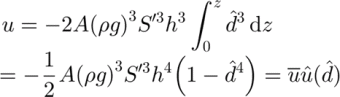
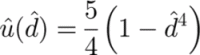
In this case,
is a function of only
.
The corresponding vertical velocity (using Equation (2)) is
A surface profile consistent with this
can be derived from the steady-state expression for the flux.
This can be rewritten as a differential equation in S′, which can be solved numerically. In the simple case of a flat bed and uniform accumulation, it can be solved analytically (Reference VialovVialov, 1958) giving
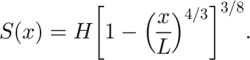
The maximum thickness, H = h(0), is related to the other parameters (L,
and A) by
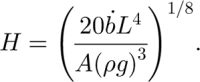
The horizontal coordinate x scales with L, while the vertical coordinate and ice-sheet thickness scale with H. With a typical H/L ratio of 1/50, the surface slope S′ (for x < 0.5L) is small. The time-scale is set by
. The velocities, u and w, scale with L/T and
respectively.
The velocity gradient, L (Equation (3)), scales as
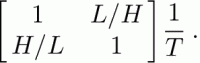
Since L is much larger than H, the ∂zu term clearly dominates. The ∂xw term is (H/L)2 times smaller, and can in many cases be assumed to be zero.
2.3. Segment rotation rate
With a velocity model we can calculate the velocity gradient, and from that the rotation rate
, of a segment with an angle of θ.
When W
k is small (mostly pure shear), the (∂xu – ∂zw) term dominates, resulting in rotation away from vertical for most angles. In most of the ice sheet ∂zu dominates, producing a positive
for most angles except a small set close to 0° (horizontal upstream). At some points over an uneven bed, it is possible for ∂zw to be sufficiently negative that
> 0 for all segment angles. At such points W
k > 1.
When ∂xw is negligible, the segment is not rotating (
= 0) if tan θ ≈ (∂xu – ∂zu. In this case, the vorticity number can be written as
confirming the relationship between W k and θ r shown in Figure 2.
In general there are two segment angles that do not rotate, one of which is the reference steady-state stratigraphy angle. They merge into one for simple shear. cos–1 W k is the sum of angles of these two non-rotating segments. For small ∂xw, the approximation in Expression (16) is valid because one of these is practically horizontal. Reference Waddington, Bolzan and AlleyWaddington and others (2001) refine this idea of a non-rotating segment by calculating the segment that is not rotating relative to the reference steady-state isochrone at a point. However, this requires knowing the slope and rotation rate of the isochrones, which must be calculated from particle paths.
2.4. Particle paths
We calculate particle paths by solving the pair of differential equations:
Path calculation can start at any point in the ice sheet, and run either forward or back in time. Each point along a path is defined by a triplet of values, [x, z, t]. For a steady-state geometry, only relative times are important. We solve these differential equations numerically with the ordinary differential equation (ODE) routines provided with MATLAB (Reference Shampine and ReicheltShampine and Reichelt, 1997).
In velocity and particle-path calculations, the horizontal and vertical coordinates can be rescaled independently, but the slope and finite deformation calculations (next section) retain a dependence on the H/L ratio. For most of our examples, we use an ice ridge with dimensions comparable to Siple Dome, which has a 1/50 ratio. We also examine a Greenland-like ridge which has a 1/100 ratio (Table 1).
Table. 1. Characteristic geometry parameters
3. Pre-Cores
A conventional isochrone is the set of glacial ice of the same age, where age is the time since the ice accumulated at the surface. We can equally well construct isochrones relative to another set of initial points such as the set of vertically aligned points at a possible core site (located at x = C). Such isochrones would show where the ice currently in the core was located at earlier times. A set of core-relative isochrones, which we call pre-cores, is shown in Figure 5 for a core at 0.2L.
Fig. 5. Core-relative isochrones (pre-cores) for an ice sheet with an H to L ratio of 1:50 and a core at 0.2L (10H). The heavier lines are at 1T intervals. Selected particle paths are drawn as dotted lines.
Figure 6 illustrates why pre-cores are relevant to the problem of turning open folds into recumbent folds. If a disturbance originates at point (p) with a leading-limb angle equal to the pre-core slope angle (24° in this example), this limb will be near-vertical when the disturbance reaches point (q) at x = 0.2L. This disturbance would appear as an obvious fold-in-progress in a core sample taken at this point (provided that it is small enough to fit in the core cross-section). Further downstream at point (r) it will appear as a nearly horizontal (θ = 176°) segment.
Fig. 6. The relation of pre-cores to the folding of a sample disturbance. A particle path (dotted line) is shown with three pre-cores (solid line). The pre-cores are at 0.4T before and after the core at 0.2L (10H). The small figures underneath show a representative disturbance at these three points, (p), (q) and (r). These three plots have the same scale, but a different aspect ratio from the larger plot. The particle path and pre-core through the center point is included on each subplot. The number in the upper right corner is the angle of the pre-core at that point.
A graphical way to use these pre-cores would be to overlay them with plots of representative disturbances. Any portion of a disturbance that is steeper than the corresponding pre-core will be overturned at the core location. Portions that are not as steep as the pre-core will not be overturned in this core, although overturning further downstream is still possible. Pre-cores can also be generated for more complicated flow models, as long as particle paths and stratigraphic isochrones can be calculated.
Figure 7a shows contours of the angles of the pre-cores in Figure 5, with the same particle paths shown. We denote this angle field as θ f(x, z; C. It is a function of the point in the ice sheet, and of the core location. Figure 7b shows the angles along three particle paths for segments that have an angle of 90° at x = C. The rotation through vertical is abrupt for deep paths, and much more gradual for paths near the surface. This contrast in rotation rates is largely a result of the larger vorticity number at depth, though the lower velocity near the bed makes the contrast stronger when plotted against distance (x) rather than against time.
Fig. 7. (a) Contours of the pre-core angles, θf, in degrees. (b) Pre-core angles along selected particle paths (marked with ⋄ at the surface). (p), (q) and (r) points in Figure 6 are also shown.
In Figure 7b, the angle at point (p) is close to the minimum along its particle path. This means that a segment with a slope angle of 24° is not rotating at this point in the flowband. In Figure 7a, the same property is seen in the fact that the angle contour is parallel to the particle path at this point. At this point, θ r ≈ 24°.
Consider a segment with an angle of 60° near the surface on the same particle path (the middle diamond). As it moves downstream, it is flattened (angle decreasing) until it reaches point (p). At this point it starts rotating in the other direction. It passes through vertical at (q) and continues rotating toward horizontal in the downstream direction. Disturbances can be flattened when W k is small (dominant pure shear), but farther along the path, W k grows to the point that the flattening changes to steepening and overturning.
The pre-core slope angles θ f(x, z; C) contoured in Figure 7a are the angles of segments that will reach vertical (θ = 90°) in the core at x = C. At any point in the ice sheet, we can also think of θ f as a threshold for disturbances that will be overturned in an ice core at C. Segments that are steeper than θ f will overturn prior to reaching the core location, C. Segments with a smaller θ < θ f will not overturn before they get to C and might never do so.
The f subscript in θ f alludes to the finite time interval over which this rotation to vertical occurs. This is in contrast to the critical wrinkle angle, θ r, derived by Reference Waddington, Bolzan and AlleyWaddington and others (2001), which focuses on the rate at which a segment is rotating at a point. θ f is a function of both the chosen core location, C, and the current location of the ice segment, while θ r is a function of only the velocity gradient at the current location. As noted above, in connection with Figure 7, along a particle path θ f decreases, reaches a minimum and then increases. At its minimum, θ f equals the local θ r. For points upstream, the θ f corresponding to this path (and core) is smaller than the local θ r. For points downstream from the minimum, the opposite is true.
The finite perpendicular material line (FPM) of Reference Grasemann and VannayGrasemann and Vannay (1999) is similar to our pre-cores. They show that currently inverted metamorphic zones in rock could have originated with tilted but otherwise normal (cold over hot) metamorphic isotherms. The FPM is the pre-deformation alignment of a set of rocks sampled in the currently deformed terrane.
4. Deformation-Gradient Tensor
Pre-cores and their slope angle, θ f, give an idea of how ice segments rotate as they move along particle paths toward the ice-core location. In particular they show which disturbances will be vertical in a core sample. We are also interested in layer disturbances that may not be exactly vertical in a core. A more general tool for relating segments, or small structures in general, at one point in the ice-flow field to their strained form at a core sample is the deformation-gradient (or finite-strain) tensor. In this section we explain how this tensor is calculated with our flow model, and use it to calculate θ f.
4.1. The strain from reference point to current point
The deformation-gradient tensor is a measure of the strain that occurs over a finite distance in a flow field. Let dX (with components dX and dZ) be a small segment at a reference point such as (p) in Figure 6. The corresponding deformed segment, dx at the current point (e.g.(q)), can be expressed as a linear function of dX.
where F 〈(p)(q)〉 is a tensor mapping dX onto dx. The bracketed subscripts denote the reference and current points. When it is clear which points we are referring to, we will just write F. The component Fxx = ∂x/∂X maps a reference horizontal segment (or the horizontal component of a segment), dX, onto the current horizontal component, dx. Fxz maps dZ onto dx (vertical to horizontal). In terms of the tensor components, Equation (18) is
The tensors for the deformations shown in Figure 1 are
We are particularly interested in the rotation of layer segments. If Θ is the angle of the segment at the reference point, then the current angle, θ, satisfies
(The negative signs result from defining angles relative to the –x coordinate.)
F can be calculated from closely spaced particle paths, much as finite strain is calculated in the field or laboratory; however, we can also find it using a set of differential equations
L (Equation (3)) is the spatial gradient of the velocity relative to the current-point coordinate frame, while
is the gradient of the velocity relative to the reference-point frame.
We can get a rough idea of where Equation (22) comes from by writing
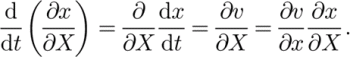
See Reference MalvernMalvern (1969, section 4.5) for details.
We solve Equation (22) for F when we calculate a particle path (Equation (17)), using I, the identity matrix, as its initial value. These form a differential-equation system of six variables (x, z and the four strain terms). L is calculated with an eight-point finite difference to maximize continuity. The error tolerances have to take into account the widely differing magnitudes of the variables. The result is a series of F tensors, one for each point along the particle path, relating dx at that point to dX at the path start. The components of such a series of tensors are shown in Figure 8b–d. The particle path is shown in Figure 8a. In Figure 8b and c the reference point is at the surface of the ice sheet. The diagonal components of the tensor, Fxx and Fzz , start at 1, while the two shear components, Fzx and Fxz , start at 0. Fzx remains too close to zero to plot with the other components (it is slightly negative, with some increase in magnitude near the terminus).
Fig. 8. F components of (dimensionless) finite strain along a particle path (a). In (b) and (c) the reference point (*) is at the surface; in (d) and (e) it is at x = 0.2L. (f) Finitestrain threshold, θf = tan–1(–Fzz/Fxz).
The determinant of F is the Jacobian (Reference MalvernMalvern, 1969, section (equation (4.5.25)) relating an infinitesimal deformed volume at the current point to the undeformed volume at the reference point. Since ice is incompressible, this determinant must be equal to unity at all points along the particle path.
While FzxFxz is small, Fzz ≈ 1/Fxx . When x/L < 1/3, Fxx is approximately linear in x. (See Appendix B for details.) This also means that Fzz ≈ x 0/x, so that the amplitude of a disturbance decreases inversely with the distance traveled away from the divide. A disturbance observed at 10H would be approximately half as high as it had been at 5H, regardless of the observation depth or slope.
4.2. Choosing the core as reference point
The reference point of F can be changed. Taking the inverse,
, interchanges the reference and current points, (p) and (q), in effect undoing the strain.
We use such an inverse to shift the reference point from the surface, (s), to the core, (q).
The components for such a shifted set of F tensors are shown in Figure 8d and e.
Since a segment aligned with the core at (q) (Fig. 6) is vertical (Θ = 90°), its angle at other points on the particle path can be calculated from a modified version of Equation (21),
This is the pre-core slope angle, θ f, contoured in Figure 7 and plotted in Figure 8f.
The minimum point of θ f along the path, where θ f = θ r, is a consequence of the variation of the velocity gradient, L, along the path. As L changes, θ r decreases, leading to the change in rotation direction for certain segments (section 1.2). On the other hand, the rapid change in θ f while it passes through 90° (at the core) does not depend on L changing. This rapid rotation through vertical occurs even when L is assumed to be constant (see Appendix C).
4.3. Patterns of segment deformation
The θ f plot in Figure 8 (and Fig. 7b) shows the angle evolution of an ice segment that is vertical at the core. The series of F tensors along a particle path can be used to track the history of any segment. Figure 9 shows the angle evolution that a set of ice-layer segments would undergo as they travel along a particle path. The history varies depending on the initial angle Θ of the segment. On the left, pure shear dominates, because the path is near the surface. All segments rotate toward horizontal (0° and 180°). Segments near vertical are under compression (the shaded region) while near-horizontal segments are under extension. As the proportion of simple shear increases, the range of angles under compression shifts to angles less than 90°. All segments with an angle less than that of the particle path itself, θ p, continue to rotate toward 0°.
Fig. 9. Rotation of segments of various initial slope angle Θ along a particle path (Fig. 8a). The line marked θf is the pre-core angle for a core at 0.2L. The heavy dashed line is the angle of the particle path, θp. Shading marks where segments are undergoing shortening. The dotted line marks the zerorotation angle, θr, which was used to formulate a folding criterion in earlier studies (Reference Waddington, Bolzan and AlleyWaddington and others, 2001).
5. Predicting the Origin Site of Observed Folds
We can start with an observed structure in a core, and attempt to predict where it originated and what its shape was there. The amount of information that we can deduce about the original disturbance depends on how much information we can glean from the deformed structure. To further constrain the point of origin, we may have to make some additional assumptions about the source disturbance. For example, if we assume that gentle wrinkles are more likely to occur than steeper ones, then the point where the θ f curve has a minimum may be the most likely point of origin of a disturbance.
5.1. Minimum disturbance-angle assumption
In cores such as GISP2, stratigraphic layers with tilts of 5–20° have been observed (Reference Alley, Gow, Johnsen, Kipfstuhl, Meese and ThorsteinssonAlley and others, 1995). With our deformation model, we can project these tilted layers upstream and downstream from the observed location at 9H from the divide (≈ 0.1L). Figure 10a shows the angle history of the leading limb of a recumbent fold at a depth of 0.8H = 2400 m in the core. At the core site, its angle is slightly past vertical (100°). This recumbent fold could have originated from a disturbance with leading-limb angle of about 10° at x ≈ 6H. This disturbance has been largely unchanged or flattening for most of its history, with most of its rotation occurring close to the core site. Figure 10b is similar but for a 20° segment at 0.88H = 2640 m depth. Because the azimuthal orientation of the core is unknown, we show the history for segments that tilt 20° in both the upstream and downstream directions. During their prior history, the minimum angles are practically the same for both segments (about 5°). The most likely origin point of this disturbance is a broad region around 5H. For similar segments at a depth of 0.92H, the minimum angle is closer to 3°.
Fig.10. Predicted histories of observed disturbances in a core at 9H (≈ GISP2). (a) History of a 100° slightly overturned core segment at a depth of 0.8H (10° minimum value). For comparison the history of a segment that is at 5° in the core at the same depth is also plotted. (b) Histories of segments that are oriented at 20° and 160° at 0.88H depth in the core (5° minimum values).
It is apparent from Figure 7 that the θ f minimum is further upstream the deeper we look in the core (in Figure 7a the minimum θ f occurs along a particle path where the θ f contour is tangent to the path). However, as is evident from the curves in Figure 7b, the deeper we look in the core, the less ability we have to resolve that disturbance injection point, because on the deeper paths θ f has much broader minima. Thus disturbances with similar small angles that fall anywhere in a broad region can all cause overturning folds at the core site downstream.
We emphasize the fact that, when layer segments overturn, they overturn very quickly. The characteristic time-scale
for strain in central Greenland is 10 000 years (Table 1). The steady-state age of ice at 0.8H depth at the location of the GISP2 core is 25 000 years. The time for a segment to evolve from its upstream minimum value to 90° (vertical) at the core is about 700 years. In Figure 10b, at a deeper level, the age is 40 000 years, and the time from minimum slope to overturning is about 1000 years. In contrast, the time taken to rotate from 20° through vertical to 160° is only about 200 years, i.e. rotation through angles differing significantly from horizontal happens very quickly.
These steady-state depth–age values do not take into account the much lower accumulation rate during glacial times, so they are younger than measured core ages. However, the overturn times fall well within the current interglacial period, so the deformation causing this folding is not affected by the earlier accumulation rates.
Figure 11 shows a similar case with a different flowband model. The bed approximates the radar profile from the Greenland summit (Reference Jacobel and HodgeJacobel and Hodge, 1995; Reference CastelnauCastelnau and others 1998). The velocity profile
has been adapted from a finite-element flowband model (Reference Bolzan, Waddington, Alley and MeeseBolzan and others, 1995; Reference Nereson, Raymond, Waddington and JacobelNereson and others, 1998). Most of the difference between Figures 10 and 11, once the bed slope is accounted for, can be attributed to the polythermal nature of the finite-element model.
Fig. 11. Predicted histories of observed disturbances in a core at 9H(≈ GISP2), as in Figure 10, but with bed and velocity profiles that better approximate the Greenland summit area. (a) History of a 100° slightly overturned core segment at a depth of 0.8H (15° minimum slope upstream).(b) Histories of segments that are oriented at 20° and 160° at 0.88H depth in the core (2–4° minimum slope upstream). Relative to the bed slope these minima are (a) 15° and (b) 5–6°. The bed-slope angle is plotted at the top and bottom (centered on 180° and 0°).
It should be noted that with bed undulations (Fig. 11), the θ f curve has multiple local minima, suggesting that a fold observed in a core could have originated as a shallow disturbance in any of several distinct localities. If the segment angles are measured relative to the local steady-state isochrone (Reference Waddington, Bolzan and AlleyWaddington and others, 2001) this oscillation in θ f is reduced, but not eliminated (Reference JacobsonJacobson, 2001). These minima of θ f are also points where the rotation rate is zero. Thus the presence of bed undulations increases the need to look at the finite strain along a particle path, and not just the local rotation rate (Reference Waddington, Bolzan and AlleyWaddington and others, 2001), when evaluating fold potential.
5.2. Symmetric disturbance assumption
We could also constrain the disturbance location if we knew its initial shape. If the disturbance is the result of layers draping over a transient “hard lump” (Fig. 3) it might be reasonable to assume that, before shearing, the disturbance was symmetrical as depicted at point (p) in Figure 6. If we observe the fold at point (q) (in a core), and measure the angles of the leading limb and trailing limb, we can constrain the location of point (p), by running the wrinkle backwards from the core until its shape becomes symmetrical. See Appendix D for details of such a calculation.
Reference Thorsteinsson and WaddingtonThorsteinsson and Waddington (2002) investigated the deformation pattern in an anisotropic layer in which the c axes clustered in a cone, and the cone orientation varied with position; non-symmetric wrinkles were created in pure shear, which approximates the stress pattern in the upper part of an ice sheet near a divide. However, if the fabric was everywhere vertical, and varied spatially only in its degree of clustering about the vertical (cone angle), then we could expect that symmetric wrinkles would be created in pure shear. If a search for asymmetric origin of an observed wrinkle finds no solution (as shown in Appendix D), this could be an indication of variable and non-vertical fabrics at the source region. In such a case we would have to use a flow model that takes the fabrics into account.
6. Discussion
While the probability of a core containing a fold increases downstream, and deeper into the ice sheet, this fold may be harder to recognize. The interval during which a fold is obviously overturning is short, because the overturning limb rotates rapidly. Once a segment has overturned, it continues to rotate toward the orientation of the undisturbed isochrones. Since ice lacks reliable “up” indicators (Reference Alley, Gow, Johnsen, Kipfstuhl, Meese and ThorsteinssonAlley and others, 1995), the fold limbs will merge back into the otherwise undisturbed stratigraphy, leaving a stratigraphic “error” that may be undetectable in an ice core.
Folds can also be difficult to identify in radar layering. First, as noted above, folds can overturn very quickly when the leading limb is noticeably non-horizontal; the leading limb spends very little time at a high angle to the normal stratigraphy. When a fold is sub-parallel to the undisturbed stratigraphy, it is unlikely to be identified as a fold by radar. Second, as suggested by Reference Waddington, Bolzan and AlleyWaddington and others (2001), folds may appear on an increasing hierarchy of spatial scales. The youngest disturbances seen in the GISP2 core occur on scales of centimeters. At scales of decimeters to meters, ice-core records can be noticeably compromised. Folds of such small scale cannot be detected by ice-penetrating radar; in ice, the wavelength of the energy pulse is many meters to decameters, and the separation between successive radar traces is typically many meters. At 2–3 km below the surface, a fold of this small scale will also be a very weak point-diffractor. At spatial scales of tens to hundreds of meters, folds could be imaged by typical ice-penetrating radar if the limbs have not merged back with the undisturbed stratigraphy. Folds on these large scales are probably relatively rare. Finally, it has been suggested (Reference Robin, de, Robin and deRobin, 1983) that radar may detect stratigraphic disturbances through the existence of an “echo-free zone” deep in the ice sheet, i.e. through the inability of radar to generate coherent reflections from layers that have been geometrically disturbed by folding or other heterogeneous flow. On the other hand, absence of detectable radar layers does not always indicate disturbed stratigraphy; it can also result from power and sensitivity limitations of radar echo-sounding equipment, i.e. the connection between the lack of echo and the disturbance is not conclusive.
Folding has been found in the lower 20% of ice in the central Greenland ice cores (Reference Alley, Gow, Johnsen, Kipfstuhl, Meese and ThorsteinssonAlley and others 1995); however, ice cores are very poor at revealing structures larger than a few decimeters. Ice-penetrating radar also hints at folding in the deep echo-free zone (Reference Robin, de, Robin and deRobin, 1983); however, as noted above, radar may be poor at detecting structures smaller than tens to hundreds of meters. Direct evidence for folding at intermediate scales is even weaker, due to our inability to make critical observations. Nevertheless, the limited data suggest that folds are more common at depth, and our models also predict this. However, it is important to note that our models also show that folds may be encountered virtually anywhere in an ice sheet, except close to the surface and under a stable ice divide.
Although our examples assume steady flow and a frozen flat bed, our approach is equally applicable to transient ice sheets on rough beds, and to ice sheets with wet beds and sliding basal ice. We did not include basal sliding here, primarily to keep our ice-flow model simple; however, wherever an ice sheet has a component of ice flow due to internal shear deformation, folds such as we have described are possible. Even where internal shear deformation is insignificant, such as in ice streams, in ice shelves and over large subglacial lakes, the ice can contain folds that were acquired in shearing flow upstream.
In addition, transitions between sliding and frozen sections of partially frozen beds introduce local strain variations in the flow, and have the potential of altering stratigraphy. If these boundaries are transient, then their migration is likely to position some layer sections in orientations where they can subsequently be overturned by passive steady flow.
7. Conclusions
The kinematics of large-scale ice-sheet flow can deform gentle open folds into order-disturbing recumbent folds. To extend the results of Reference Waddington, Bolzan and AlleyWaddington and others (2001) to account for spatially variable strain rates, we have used three concepts: θ r the no-rotation angle, θ f the finite-strain threshold angle, and pre-cores.
From the velocity gradient at a point, we calculate W k, the kinematic vorticity number which measures the relative mix of pure and simple shear, and θ r, the angle that is not rotating at that point. Segments steeper than θ r are rotating toward vertical and overturning, while gentler ones are being flattened. But because segments move along paths into regions of higher W k, segments that were not rotating will begin to overturn. So, while the θ r criterion of Reference Waddington, Bolzan and AlleyWaddington and others (2001) is an approximate indicator of stability against recumbent folding, it is still optimistic about downstream stratigraphic integrity. Our finite-strain analysis can quantify this.
By calculating the finite-strain deformation-gradient tensor, F, along a particle path, we see how a disturbance segment rotates over a finite time interval. Given our limited understanding of the dynamic processes that inject disturbances, the most useful form of the angle-rotation function specifies a vertical segment at a reference (observation) point, and calculates the corresponding angle at other points along the path. We have called this the finite-strain threshold angle, θ f. At any point, this is the angle of the segment that will be in the process of overturning when it reaches the reference point.
θ r is a minimum angle on the θ f curve, i.e. the gentlest segment that will overturn at the reference point. A segment can flatten for a period of time, then reach the local θ r and proceed to steepen and overturn. Since this minimum can be broad, it gives little indication of how soon the overturn will occur. For that, the full θ f calculation in this paper is needed.
Pre-cores, or core-relative isochrones, extend the concept of the θ f curve to multiple particle paths. The reference isochrone is defined along a hypothetical ice core, and upstream pre-cores give the location of the core ice at earlier times. They also give the slope of segments that will be vertical in the core. A θ f curve gives the pre-core slope angle along its path. Thus the pre-cores and the θ f contours are graphical ways of showing just how steep disturbances must be upstream in order to be overturned in the core.
Other processes, such as shear-band development or various three-dimensional flow effects, can also disrupt stratigraphy. In that sense, our calculations may still err on the optimistic side when assessing stratigraphic integrity. Our analysis identifies scale parameters for processes that could generate initial disturbances. A process that cannot generate an adequate disturbance can be ruled out as a core-disrupting process.
Acknowledgements
This research was supported by U.S. National Science Foundation grants OPP-9123660, OPP-9420648 and OPP-9726113. We are grateful to C. Raymond, R. Fletcher, B. Hallet and T. Thorsteinsson for valuable insights. N. F. Glasser (Scientific Editor) and M. J. Siegert provided helpful reviews of the manuscript.
Appendix A
Pre-Core Scale Dependence
Pre-cores are a simple tool for determining what disturbances could appear as overturned folds in an ice core. All that is needed is a flow model that can calculate particle paths and travel times along those paths. The paths are determined by the flowband geometry, which in our simple example is determined by its horizontal and vertical extent, L and H. The core location C determines the shape of the pre-cores. The time-scale T for the ice sheet affects the contour interval of the pre-cores (as it does stratigraphic isochrones), but does not change their shape. We can gain further insight into pre-cores and the folding potential by looking at how the pre-core angles vary with these scaling factors.
Figure 12 shows how the pre-core angles vary with the core location C, while keeping H/L constant. The solid set of lines with the core at 10H are a subset of the contours in Figure 7. The dashed set are for a core at 20H = 0.4L. The gray lines mark where these angle contours are parallel to the particle paths, that is, where θ f = θ r.
Fig. 12. Pre-core slope-angle contours (θf = 10°, 30° and 50°) for two core locations, 10H (solid lines) and 20H (dashed lines). The thick gray lines mark where θr = θf. Dotted lines are particle paths.
For the inner portion of this simple ice sheet (x ≤ 0.4L), the pre-core shapes are controlled primarily by the location of the core, specifically the C/H ratio. The surface slope is small
, and w(x, z) is dominated by the
term (Equation (9)). The distance to the terminus has limited direct impact on the velocity field, the particle paths and the isochrones. When the contours of θ
f are plotted against
and x (not shown), they show little variation as H/L is varied, provided C/H is held constant.
On the other hand, if we keep C/L constant, the slope of a pre-core scales linearly with the H/L ratio. If the length L of the modeled ice sheet is doubled while keeping H the same, the pre-core slopes are halved. Since the slope is the tangent of the angle, the angles for pre-cores in two different sets of model geometries are related by
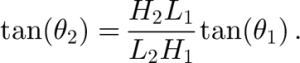
Figure 13 illustrates this H/L dependence of the slope angles for a vertical section through point (p) in Figure 7.
Fig. 13. The scaling of pre-core angles with variations in the H/L ratio. The heavy solid line shows the angles along a vertical transect through point (p) on Figure 6. In this case H/L = 1/50 and C/L = 0.2. The dashed lines show the equivalent angles for other H/L ratios (keeping C/L = 0.2). The curves are related by Equation (A1).
Appendix B
The Approximate Linearity of Fxx Along a Path
For our simple geometry, where
, the position x(t) along a flow path can be expressed as the exponential of an integral (using Equation (1)).
Since
decreases along the particle path, this expression is more linear in t than would be expected for a simple exponential.
The Fxx term of F, as a function of time along a path, can be approximated by a similar exponential. Starting with the differential equation for F (Equation (22)),
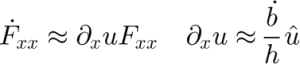
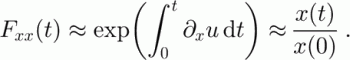
Here we assume that
and ∂xh are small, which is valid in the inner third of our ice-sheet model.
Appendix C
Homogeneous Strain-Rate Approximation
Over a short distance along a particle path, we can assume that L (Equation (3)) is approximately constant. It is then possible to derive an analytical expression for F as a function of time (Reference RambergRamberg, 1975, equations 33 and 38). In the neighborhood of the core, the equations are (t = 0 at the core; again using Equation (22))
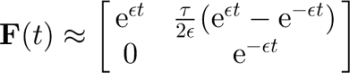
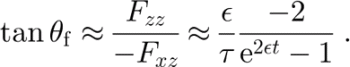
As seen in Figure 14, this approximation captures the rapid rotation of the pre-core slope near the core. Further away, the variation in the velocity gradient must be taken into account. A similar approximation is used in Reference Waddington, Bolzan and AlleyWaddington and others (2001) to estimate segment overturn times.
Fig. 14. Pre-core slope angles (solid lines) calculated from the “constant-strain-rate” approximation, using rates at the core location (10H). Pre-core slope contours (dotted lines) are included for comparison.
Appendix D
The Origin of a Symmetrical Disturbance
Consider a fold with a vertical leading edge at point (q). If its amplitude is Δz, and width is Δx, then its trailing-limb slope is Δz/Δx. We can approximate it by a right triangle with a set of points with relative positions (Fig. 15a)
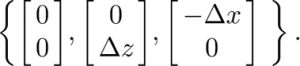
Fig. 15. (a) An overturning disturbance (*) and a possible symmetric predecessor (⋄). (b) The point at which FxzΔz equals – FxxΔx/2(⋄).
The relative positions at an earlier time would be (using Equation (19))
where the F reference point is (q). Here we assume that –Fzx Δx ≈ 0. When Fxz Δz = –Fxx Δx/2 as shown in Figure 15b, the earlier disturbance is a symmetrical triangle with height Fzz Δz. For smaller trailing Δz/Δx at the core, the symmetric injection time is earlier. For example, in Figure 6 (q), this slope is 0.04 and we would infer that the disturbance was injected at x/L ≈ 0.12. However, in Figure 15, where the fold is observed with Δz/Δx = 0.075, the symmetric injection point is closer to the core site (x/L = 0.16). It is possible, if Δz/Δx is too small, that no point satisfies this constraint. In this case, the observed fold could not have originated as a symmetric wrinkle.
