Introduction
Heat and mass transfer are important processes for interpreting ice cores (Reference McConnell, Bales, Stewart, Thompson, Albert and RamosMcConnell and others, 1998), understanding air–snow exchange processes (Reference AlbertAlbert, 1996; Reference Hutterli, McConnell, Chen, Bales, Davis and LenschowHutterli and others, 2004), ascertaining basic material characteristics of snow (Reference MellorMellor, 1977) and calculating the firn compaction relevant to altimetry-based ice-sheet mass-balance estimates (Reference Arthern and WinghamArthern and Wingham, 1998; Reference Li, Zwally and ComisoLi and others, 2007).
Conductive heat transfer through snow occurs through the ice lattice and less, but still significantly, through intervening air spaces (Reference Calonne, Flin, Morin, Lesaffre, du Roscoat and GeindreauCalonne and others, 2011). Together, these processes define the thermal conductivity (K), the parameter relating the macroscopic vertical temperature gradient and heat flux as described in Fourier’s law of heat conduction:
where Q is heat flux and T is temperature. In general, conductivity is treated as a scalar, with snow considered isotropic and heat transfer assumed vertical (Reference Calonne, Flin, Morin, Lesaffre, du Roscoat and GeindreauCalonne and others, 2011).
Conductivity has been the focus of many studies dating back to the 19th century (see Reference Sturm, Holmgren, König and MorrisSturm and others, 1997, for review), which generally follow one of four approaches. First, the Fourier method constrains the thermal diffusivity (κ = K/ρc, where ρ is density and c is heat capacity) by comparing the lag and/or amplitude decay of a periodic surface temperature forcing at different depths in the snowpack. Diffusivity can be constrained this way because it governs both the magnitude of amplitude attenuation, ![]() , and the velocity of signal propagation,
, and the velocity of signal propagation, ![]() , where ω is the angular frequency (Reference Cuffey and PatersonCuffey and Paterson, 2010). Given a diffusivity of 20 m2 a−1, for example, firn temperature at 6 m depth has an amplitude equal to only 9% of the annual seasonal cycle’s amplitude at the surface. Additionally, the peak summer temperature appears 139 days later. Once the diffusivity value is constrained through one or both relationships, multiplication by density and heat capacity yields conductivity.
, where ω is the angular frequency (Reference Cuffey and PatersonCuffey and Paterson, 2010). Given a diffusivity of 20 m2 a−1, for example, firn temperature at 6 m depth has an amplitude equal to only 9% of the annual seasonal cycle’s amplitude at the surface. Additionally, the peak summer temperature appears 139 days later. Once the diffusivity value is constrained through one or both relationships, multiplication by density and heat capacity yields conductivity.
Two methods involve direct measurement: a needle probe with a transient heat source (e.g. Reference Sturm, Holmgren, König and MorrisSturm and others, 1997; Reference Morin, Domine, Arnaud and PicardMorin and others, 2010) and a heated plate on which snow is permitted to reach thermal equilibrium (e.g. Reference Pitman and ZuckermanPitman and Zuckerman, 1967). The transient method gives conductivity by measuring the temperature rise at one end of the needle probe due to a given heating rate at the other end, with a greater temperature rise corresponding to a lower conductivity. The steady-state technique involves applying a heat source to a block of snow; once the temperature gradient in snow is constant in time, its relationship with the applied flux yields conductivity.
The majority of these studies present empirically-derived relationships between thermal conductivity and density of seasonal snow. It is widely accepted that conductivity depends on snow microstructure (e.g. Reference Arons and ColbeckArons and Colbeck, 1995), for which density is a proxy. Density–conductivity regressions exhibit significant scatter, however: conductivity can vary up to an order of magnitude for a given density (Reference Sturm, Holmgren, König and MorrisSturm and others, 1997). Reference Calonne, Flin, Morin, Lesaffre, du Roscoat and GeindreauCalonne and others (2011) carried out an analysis on samples representing the full range of seasonal snow types and suggested attributing scatter to differences in snow type and anisotropy. Reference Löwe, Riche and SchneebeliLöwe and others (2013) confirmed the anisotropy dependence by explicitly incorporating an anisotropy parameter into heat transport simulations. With the source of the scatter now generally known, Reference Calonne, Flin, Morin, Lesaffre, du Roscoat and GeindreauCalonne and others (2011) still conclude a strong correlation between conductivity and density.
Since the advent of microtomography within the past decade, it has become possible to develop a fourth method for investigating conductivity: numerical simulation of heat transport through the snow structure (Reference Kaempfer, Schneebeli and SokratovKaempfer and others, 2005). Microstructure-based simulations provide the only means through which the different heat transfer pathways (air and ice) can be resolved and the conductivity determined precisely and unambiguously (Reference Calonne, Flin, Morin, Lesaffre, du Roscoat and GeindreauCalonne and others, 2011). A particularly significant finding made possible through microtomography is the anisotropy of thermal conductivity (Reference Shertzer and AdamsShertzer and Adams, 2011; Reference Löwe, Riche and SchneebeliLöwe and others, 2013). Comparative studies have revealed significant, systematically lower conductivity measurements from the needle probe (Reference Riche and SchneebeliRiche and Schneebeli, 2010). Initially attributed to snow structure changes and associated poor needle–snow contact for short heating times (Reference Riche and SchneebeliRiche and Schneebeli, 2010), the source of the discrepancy remains an area for further study (Reference Calonne, Flin, Morin, Lesaffre, du Roscoat and GeindreauCalonne and others, 2011; Reference Riche and SchneebeliRiche and Schneebeli, 2013).
Here we use a Fourier-type analysis applied to 4 years of hourly temperature measurements at eight depths within the near-surface snow and firn column at Summit, Greenland, where firn is defined as snow older than 1 year. The phase shift method is useful for application to already-extant datasets and permits direct calculation of diffusivity, rendering density and heat capacity values unnecessary for solving the heat equation. Further, the thermistor spacing and duration of data collection make our analysis inclusive of both spatial and temporal heterogeneity, yielding potentially widely applicable findings.
Similar approaches deriving diffusivity or conductivity from temperature have been used for sites in Antarctica (Reference Brandt and WarrenBrandt and Warren, 1997; Reference Sergienko, MacAyeal and ThomSergienko and others, 2008), Switzerland (Reference Oldroyd, Higgins, Huwald, Selker and ParlangeOldroyd and others, 2012) and elsewhere. None of these studies provides a diffusivity magnitude or predictive relationship specifically for polar firn, which is different from the seasonal snow used to derive oft-cited empirical relationships (e.g. Reference YenYen, 1981; Reference Sturm, Holmgren, König and MorrisSturm and others, 1997; Reference Calonne, Flin, Morin, Lesaffre, du Roscoat and GeindreauCalonne and others, 2011). Moreover, conductivity of the top 1–2 m of firn at Summit Station, Greenland, has been modeled numerically from microstructural parameters (e.g. Reference Dadic, Schneebeli, Lehning, Hutterli and OhmuraDadic and others, 2008), but, to these authors’ knowledge, conductivity and diffusivity of firn to a greater depth have not previously been constrained.
Instrumental Temperature Profiles
Field location
An automatic weather station operating at Summit Station (72°35′ N, 34°30′ W) from May 2004 to July 2008 collected temperature data of the air and of eight points in the near-surface snow and firn. During this period, Summit received an annual net accumulation of 0.91 m a−1 snow (2.87 m total over study duration) and experienced a mean annual air temperature of −29.5°C. Summit is located in the dry snow zone and did not experience melt during this period.
Measurements
Nine thermistors registered temperature values of the air and of firn at 0.25, 0.50, 1.0, 1.5, 2.5, 4.5, 6.5 and 9.5 m from the original snow surface in a 10 m deep, 15 cm diameter borehole. These thermistors were buried progressively by snow accumulation and wind deposition (Fig. 1a), collectively measured roughly once per month as the distance between the snow surface and a fixed point on the borehole casing. Adjusted for measured accumulation, thermistor depths at the end of the 4 year data collection spanned 3.1–12.4 m.
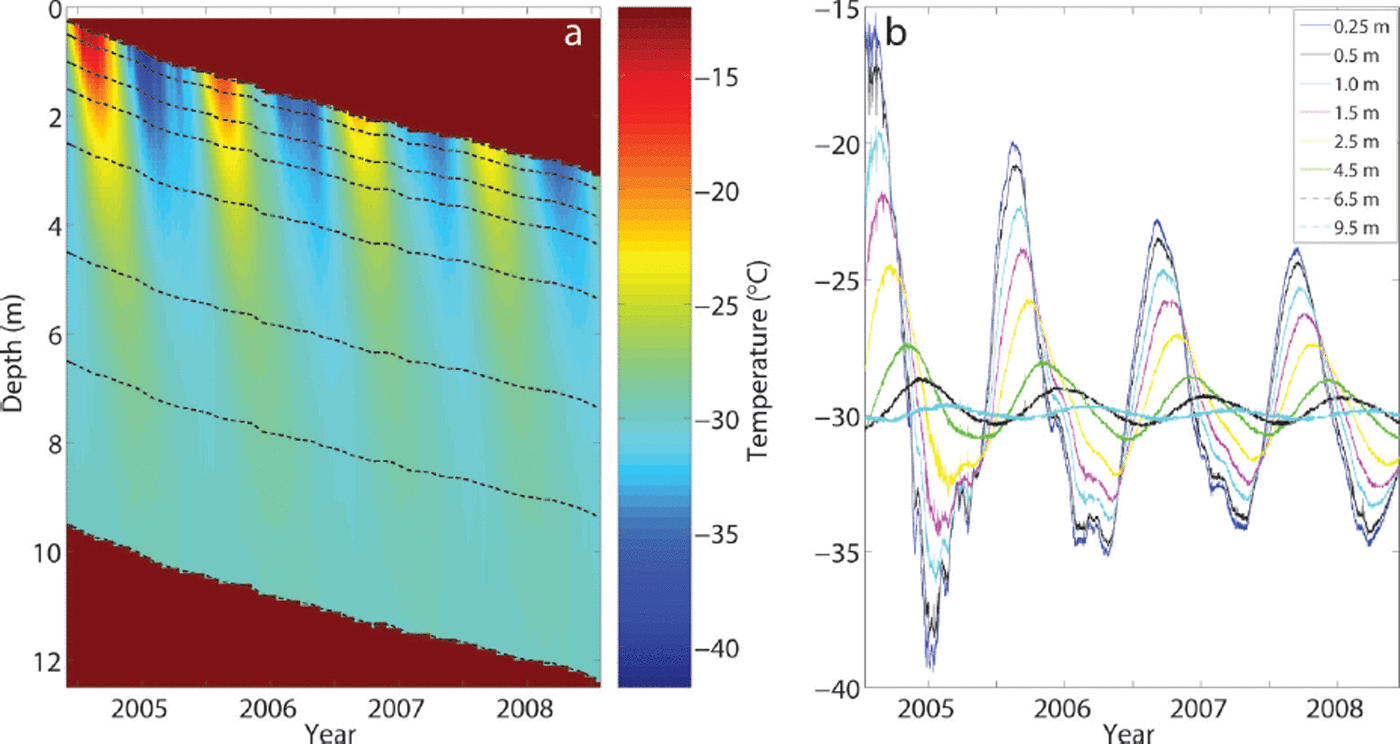
Fig. 1. Temperature data collected by a thermistor string installed at Summit Station 2004–08: shown as (a) linearly interpolated values and (b) recorded values for each thermistor progressively buried by accumulation. Dotted lines in (a) indicate the locations of the measured values between which interpolation was performed. The thermistors get deeper with time due to their burial under ∼3 m of snow, which is evident in the red, data-void regions and the downward translation of the temperature data. Both panels show characteristics of surface temperature propagation in an otherwise unbounded medium: the amplitude of the signal attenuates with depth, and the timing of the temperature extremes becomes increasingly delayed as the surface temperatures propagate through the snowpack. The thermistor closest to the surface (initial depth 0.25 m) has the greatest amplitude, whereas the deepest thermistor (initial depth 9.5 m) has the smallest. Temperature minima here are not as smooth as the maxima, due at least in part to high winds and pressure changes typical of polar night. Still, it is evident in both (a) and (b) that temperatures at depth lag behind the surface forcing. The 2004 seasonal maximum, for example, takes 130 days to propagate to 6.5 m. The length of this delay and the amount of amplitude damping are controlled by the thermal diffusivity.
Subsurface thermistors were wired to a Campbell AM16/ 32B multiplexer, and a Campbell CR10 Datalogger stored resistances later converted to the temperatures in Figure 1b. The resolution of data logging gave a precision of 0.006 K, and the thermistors were calibrated to an accuracy of ±0.05 K in a controlled temperature bath against a platinum resistance temperature detector. Vinyl disks (‘baffles’) positioned on either side of each thermistor and at the original snow surface greatly limited advection of air in the hole, although clear excursions from a harmonic signal in winter months do suggest some movement of air in the borehole during polar night.
Solving the Heat Equation
General overview
We simulate temperatures through a numerical solution to the heat equation. The specific energy of an ice body in an Eulerian reference frame is determined by heat flux from conduction, advection and internal heat production, respectively:
where ![]() is the velocity vector and f is the internal heat production, including ice deformation, firn compaction and meltwater refreezing (Reference HookeHooke, 2005; Reference Cuffey and PatersonCuffey and Paterson, 2010). Here we neglect internal heat production f based on its relative order of magnitude (Reference Li, Wang and ZwallyLi and others, 2002) and implicitly account for advection by using a Lagrangian rather than Eulerian reference frame.
is the velocity vector and f is the internal heat production, including ice deformation, firn compaction and meltwater refreezing (Reference HookeHooke, 2005; Reference Cuffey and PatersonCuffey and Paterson, 2010). Here we neglect internal heat production f based on its relative order of magnitude (Reference Li, Wang and ZwallyLi and others, 2002) and implicitly account for advection by using a Lagrangian rather than Eulerian reference frame.
Conductive heat transfer occurs through the ice lattice and less, but still significantly, through the intervening air pore spaces (Reference Calonne, Flin, Morin, Lesaffre, du Roscoat and GeindreauCalonne and others, 2011). Because conduction through the ice is two orders of magnitude larger than through the air, significant temperature gradients can be established in the pores. These thermal gradients induce sublimation and condensation within the pore space; such vapor diffusion is not specifically a conductive mechanism but is typically treated as the third component of an ‘effective’ conductivity value (Reference Adams and SatoAdams and Sato, 1993; Reference Sturm, Holmgren, König and MorrisSturm and others, 1997).
Simplifying assumptions
In general, firn temperatures are influenced by more than conduction alone: vapor advection (Reference Albert and McGilvaryAlbert and McGilvary, 1992), radiation (Reference ColbeckColbeck, 1989a) and convection (Reference Sturm and JohnsonSturm and Johnson, 1991; Reference Albert and HawleyAlbert and Hawley, 2002) may each play a role. We do not differentiate the impacts of each from conduction, instead encompassing their effects within the bulk diffusivity. We expect the impacts of vapor advection and radiation on the thermal regime to be small. Although air moving along pressure gradients generally carries vapor, Reference Albert and McGilvaryAlbert and McGilvary (1992) found that the contribution of vapor transport to a firn temperature profile is <2%. Indeed, calculation of latent heat flux using the effective vapor flux (following Reference Riche and SchneebeliRiche and Schneebeli, 2013) gives a maximum latent heat flux equal to only 3.5% of the total heat flux. Although latent heat flux should not be neglected in seasonal snow (Reference Oldroyd, Higgins, Huwald, Selker and ParlangeOldroyd and others, 2012), it can justifiably be left out in analyses of very cold, polar snow (Reference Brandt and WarrenBrandt and Warren, 1997). Solar radiative heating can significantly impact the temperature of very near-surface firn (Reference ColbeckColbeck, 1989a) but does not penetrate to the depths occupied by thermistors in this study (Reference Brandt and WarrenBrandt and Warren, 1993; Reference Dadic, Schneebeli, Lehning, Hutterli and OhmuraDadic and others, 2008). Furthermore, Summit has a particularly high reflectivity that lowers the contribution of shortwave radiation to the energy balance (Reference Cullen, Mölg, Conway and SteffenCullen and others, 2014).
Air movement in lower-density snow is induced by both temperature gradients (‘free convection’) and wind (‘wind pumping’) (Reference ColbeckColbeck, 1989b; Reference Sturm and JohnsonSturm and Johnson, 1991; Reference Albert and McGilvaryAlbert and McGilvary, 1992). It is thought to be responsible for the rapid and early fall cooling cycle across the Greenland ice sheet; near-surface firn temperature is consistently lower than would be expected from conduction alone by mid-August (Reference BensonBenson, 1962, p. 57). Convection also plays a role in the warm excursions and greater relative amplitudes characteristic of winter temperature series in air and snow in general (Reference Brandt and WarrenBrandt and Warren, 1997; Reference Albert and HawleyAlbert and Hawley, 2000; Reference Cullen, Mölg, Conway and SteffenCullen and others, 2014). Our data from the top 3 m are no exception to this trend, with deviation of data from a conduction-only model more than four times greater in winter and spring (December–May) than in summer and fall (June–November).
On Antarctic iceberg C16, Reference Sergienko, MacAyeal and ThomSergienko and others (2008) attributed errant diffusivities to wind speeds exceeding 40 m s−1 during which ventilation likely caused a firn temperature rise. Reference Brandt and WarrenBrandt and Warren (1997) explored several potential causes for the observed non-conductive heating of subsurface snow at South Pole: snow–air temperature difference; squared wind speed; and barometric pressure changes. Summarized in Figure 2, an exploration of these correlations for the 2004–08 Summit data reveals a large relative impact of wind, which accounts for 15% of the variance in the temperature changes not caused by conduction. The square of wind speed accounts for 24% of the variance, and the product of squared wind speed and strength of temperature inversion accounts for 16%. Indeed, high-speed wind events are known to be more common at Summit Station in September–March than in the summer months (Reference Albert and HawleyAlbert and Hawley, 2002). Winter temperature excursions are also due in part to cloud cover, which supplies more longwave radiation to the surface than a clear atmosphere would (Reference Brandt and WarrenBrandt and Warren, 1997), and to a positive sensible heat flux associated with a persistent temperature inversion (Reference Cullen, Mölg, Conway and SteffenCullen and others, 2014).
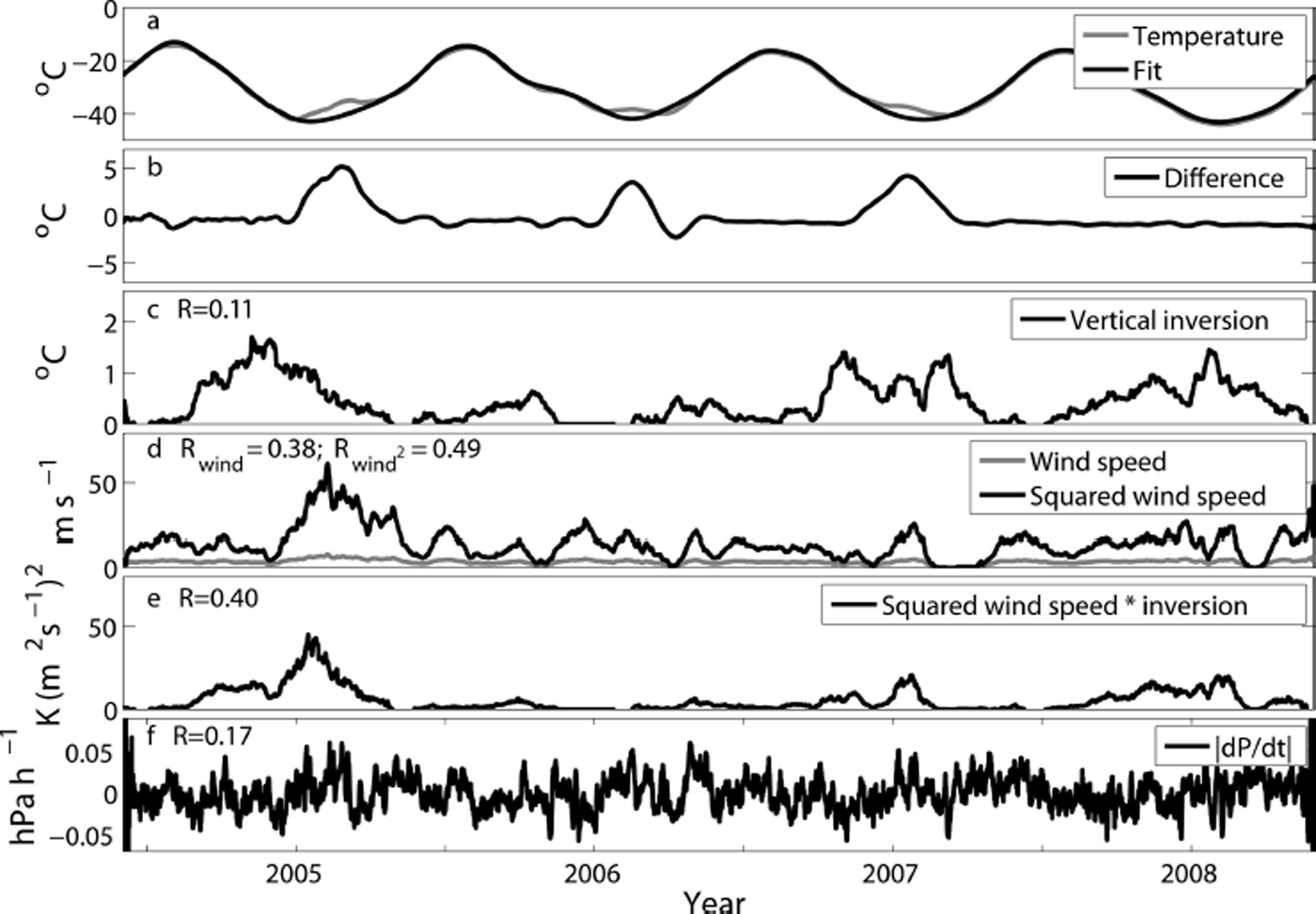
Fig. 2. Time series of (a) monthly-smoothed snow surface temperature data (grey) and the conduction-only model fit (black), with the difference shown in (b). Remaining plots show measurements of: (c) the difference between upper air temperature and lower air temperature, where a positive difference indicates a vertical temperature inversion; (d) wind speed; (e) the product of squared wind speed and vertical temperature inversion; and (f) the time derivative of barometric pressure. Air temperature and pressure data come from the Greenland Climate Network (Reference Steffen and BoxSteffen and Box, 2001); all measurements were recorded hourly. Wind accounts for more of the temperature excursions from the conductiononly model than temperature or pressure alone can.
Convection of air into the borehole certainly impacts winter temperatures and limits their utility in our analysis; these temperature excursions occur on timescales ranging from several hours to a week and are, thus, responses to forcings much shorter than seasonal ones. The disturbed winter temperature signal is an artifact of measurement collection in an air-filled borehole. Distinctly different (and smaller) convective effects impact near-surface firn, and the convection present in the firn itself is implicitly included in our analysis. It is worth noting, however, that relative to other areas, near-surface convection at Summit is comparatively reduced. Interstitial airflow is drastically limited below the first 1 m (Reference Albert and HawleyAlbert and Hawley, 2002), and 27 of the 28 seasonal maxima used in our study are for firn below the top 1 m. Furthermore, Summit has a surface wind pack which is the least permeable layer in the top 10 m of firn and limits subsurface airflow (Reference AlbertAlbert, 1996; Reference Albert and ShultzAlbert and Shultz, 2002).
Physical properties of snow, meteorological conditions at Summit Station, and a Lagrangian reference frame allow us to simplify the generalized heat transfer regime significantly. We then assume constant diffusivity over the 4 years, as well as horizontal homogeneity in the snowpack, and we simplify Eqns (1) and (2) to reflect conductive heat flux in the vertical direction only. The (∇K ·∇T)/ρc) term in Eqn (2), which represents the spatial variation of diffusivity due to temperature differences, has a relatively insignificant effect on ∂T/∂t and is neglected in common practice (Reference HookeHooke, 2005), leaving
Constraining diffusivity
We simulate firn temperatures through a numerical solution to Eqn (3), using a Crank–Nicolson approach with measured temperatures as initial and boundary conditions. Diffusion processes govern the amplitude attenuation and phase lag of temperatures with depth; thus, characteristics of and relationships between the measured and modeled temperatures can be used to constrain thermal diffusivity. For each integer value of diffusivity within a reasonable range (10 ≤ κ ≤ 60 m2 a−1), we calculate the time for peak summer temperatures at the top thermistor to register at each of the underlying ones. Close matching between simulated and measured temperature penetration times, averaged for all thermistors over the 4 years, indicates the most appropriate diffusivity value. The temperature excursions in winter months precluded identification of seasonal minima, so we used only the maximum (i.e. summer) temperatures in our analysis. Performance constraint J (years) quantifies the mismatch as the absolute root-mean-squared (rms) deviation between observed and modeled lags in the temperature maxima with depth:
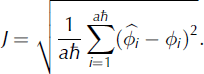
Here ħ is thermistor number, a is year, ![]() is lag (years) of the modeled temperature maxima behind those of the shallowest thermistor, and φ is lag of the measured temperatures (also in years). Use of phase lag for assessing goodness of fit between observed and simulated temperature series is more appropriate than directly comparing temperature magnitudes, which introduces a bias toward the deeper regions. For any given diffusivity, amplitude decreases with depth. Therefore, modeled temperatures will always appear to match observed temperatures more closely at the deep than at the shallow thermistors (Reference Brandt and WarrenBrandt and Warren, 1997). Motivation for using phase lag also stems from the fact that the temperatures measured in the air-filled borehole may differ slightly in magnitude, though not in phase, from those of the surrounding firn. Air is a relatively poor conductor, and the influence of the surface forcing on borehole air temperatures at depth is negligible compared to that of the surrounding firn (the surface temperature signal propagated through air damps to 10% of the surface amplitude by 1 m and to a constant temperature by 2 m).
is lag (years) of the modeled temperature maxima behind those of the shallowest thermistor, and φ is lag of the measured temperatures (also in years). Use of phase lag for assessing goodness of fit between observed and simulated temperature series is more appropriate than directly comparing temperature magnitudes, which introduces a bias toward the deeper regions. For any given diffusivity, amplitude decreases with depth. Therefore, modeled temperatures will always appear to match observed temperatures more closely at the deep than at the shallow thermistors (Reference Brandt and WarrenBrandt and Warren, 1997). Motivation for using phase lag also stems from the fact that the temperatures measured in the air-filled borehole may differ slightly in magnitude, though not in phase, from those of the surrounding firn. Air is a relatively poor conductor, and the influence of the surface forcing on borehole air temperatures at depth is negligible compared to that of the surrounding firn (the surface temperature signal propagated through air damps to 10% of the surface amplitude by 1 m and to a constant temperature by 2 m).
Assessing model–data match could also have been achieved through the amplitude attenuation; however, amplitude is more sensitive to non-conductive heat transfer (Reference Sergienko, MacAyeal and ThomSergienko and others, 2008), and damping in air is greater than in firn. We are confident that comparing annual temperature series’ properties throughout the measurement domain will yield a meaningful value since Reference Li, Wang and ZwallyLi and others (2002) have shown that firn down to at least 10 m depth is affected by seasonal and interannual temperature fluctuations. We extract single-maximum temperatures for each year by fitting the hourly data with Fourier series fits (Fig. 3). Through differences in timing of these temperature peaks, we identify the phase shift with depth. The Fourier fit is preferred over others such as higher-order polynomials or sum of sines because it gives the lowest average sum of squared errors for all 32 summer temperature series (eight thermistors over 4 years).

Fig. 3. Annual temperature maxima (triangles) identified by third-order Fourier series fits (dark curves) to data (light curves).
The series of temperatures recorded at the top thermistor provide the upper Dirichlet boundary condition for the numerical model. Since the top thermistor is buried progressively over the 4 years of data collection, its serving as a boundary condition permits use of a Lagrangian reference frame. This boundary condition therefore offers simple and implicit inclusion of thermal advection occurring with burial (the ![]() term in Eqn (2)). The lower boundary condition is the mean annual firn temperature at 30 m depth, below which firn temperature is insensitive to seasonal and interannual variations (Reference Li, Wang and ZwallyLi and others, 2002). A depth of 30 m is an appropriate choice also because it exceeds the e-folding depth of an annual surface forcing for the entire range of diffusivity values tested in our study (e-folding depth for κ = 60 m2 a−1 is 28 m). We use the frequency of data collection as the time step (dt = 1 hour) and a spatial resolution of dz = 25 cm, the distance between the two closest thermistors. A spline interpolation of the temperature profile at time 0 provides the initial condition.
term in Eqn (2)). The lower boundary condition is the mean annual firn temperature at 30 m depth, below which firn temperature is insensitive to seasonal and interannual variations (Reference Li, Wang and ZwallyLi and others, 2002). A depth of 30 m is an appropriate choice also because it exceeds the e-folding depth of an annual surface forcing for the entire range of diffusivity values tested in our study (e-folding depth for κ = 60 m2 a−1 is 28 m). We use the frequency of data collection as the time step (dt = 1 hour) and a spatial resolution of dz = 25 cm, the distance between the two closest thermistors. A spline interpolation of the temperature profile at time 0 provides the initial condition.
Results
A numerical solution to the heat equation matches phase shifts of peak summer temperatures most closely with a diffusivity value of 25 m2 a−1. However, the minimum in data–model deviation is shallow, and the diffusivity solution is non-unique, with a 95% confidence interval spanning 22–29 m2 a−1 (red horizontal line in Fig. 4a).

Fig. 4. Results of comparing measured temperature shifts with those modeled through an implicit finite-difference scheme. (a) J associated with different values of constant diffusivity. There are small variations in the deviation of each thermistor’s lag relative to data, the standard deviations of which provide the error bars for each. The horizontal red line indicates the statistically indistinguishable range of diffusivity values (at significance level = 0.05). (b–d) Temperature profiles simulated with the indicated diffusivity values; values in (b) and (d) give lag mismatches with errors exceeding the minimum J = 1.8 × 10−2 years (6 days) by 9.4 × 10−2 years (34 days). Note that amplitude and temperature lag time vary between the panels: a higher diffusivity allows deeper surface temperature penetration and a shorter lag time, whereas a lower-diffusivity system displays shallow over-damping of temperatures.
We note that other studies (e.g. Reference Oldroyd, Higgins, Huwald, Selker and ParlangeOldroyd and others, 2012) explore non-integer values of diffusivity and achieved lower values for rms error (RMSE). Given the range of statistically significant solutions, however, we deemed it unnecessary to constrain a particular diffusivity to such precision.
Figure 4 shows performance constraint J as a function of diffusivity, as well as temperature profiles for three points: a very low κ, the best-fit κ and a very high κ. The phase lags of seasonal maximum temperatures modeled with κ = 25 m2 a−1 differ from the measured phase shifts (Fig. 1) by an average of 6 days (1.6% the length of the 1 year forcing cycle). The solution reached with κ = 25 m2 a−1 exhibits appropriate patterns for amplitude attenuation and phase shift, and the generated temperatures differ from measured temperatures by <0.5°C at 6 m, the mean depth of the domain. The temperature distribution generated with a too-low diffusivity, on the other hand, displays a very long phase lag and minimal amplitude attenuation, while the too-high diffusivity gives temperatures that propagate faster and deeper than observed.
Discussion
Bulk value context
Our model gives an average, bulk value for diffusivity that does not show a statistically significant trend with depth (a t-test gives p = 0.78 for α = 0.05). We also carried out model runs with a density-dependent diffusivity, using density data from a 30 m core, ‘Katie’, drilled 35 m from the thermistor string on 7 June 2004 and profiled with a neutron probe on 8 June 2004 (Reference Hawley, Morris and McConnellHawley and others, 2008). These runs were inconclusive, with no better match to data than temperature series simulated with a single, bulk value. The fact that a clear trend with depth does not emerge in our solution is unsurprising: convection in the top few meters changes the temperature profile. Given the resolution of our data and the presence of convection, our temperature measurements lend themselves much better to a bulk solution, even though modeling with a bulk solution does understate the well-known layered nature of polar firn and its variations with depth. (Note our suggested application of a bulk value in the final subsection below.)
Still, comparing results to density–conductivity expressions determined by Reference YenYen (1981), Reference Sturm, Holmgren, König and MorrisSturm and others (1997) and Reference Calonne, Flin, Morin, Lesaffre, du Roscoat and GeindreauCalonne and others (2011) serves to place results in context and provide a first-order check on our findings (for comparison, we use density measurements from the Katie core concomitant with the thermistor data). Converting these published conductivity–density relationships to diffusivity–density relationships using a density-dependent heat capacity, we find that the mean Katie core density (425 kg m−3) corresponds to diffusivities of 23, 16 and 22 m2 a−1 for the three studies. Note that the needle probe technique of Reference Sturm, Holmgren, König and MorrisSturm and others (1997) gives systematically low conductivities and therefore provides only a lower bound. The values given by Reference YenYen (1981) and Reference Calonne, Flin, Morin, Lesaffre, du Roscoat and GeindreauCalonne and others (2011) do fall within the 95% confidence interval of our solution. An exact match with our numerical solution was not necessarily expected given that 10 of the 28 summer temperature maxima used for analysis come from the top 3 m of the firn column, which is disturbed by convection (Reference BensonBenson, 1962), and that the published studies describe seasonal snow rather than polar firn. Firn at Summit is a layered system of wind pack interspersed with large-grained and hoar layers (Reference Albert and ShultzAlbert and Shultz, 2002). As opposed to fresh snow, round grains and wind pack generally exhibit greater conductivities for a given density (Reference Calonne, Flin, Morin, Lesaffre, du Roscoat and GeindreauCalonne and others, 2011).
Uncertainty
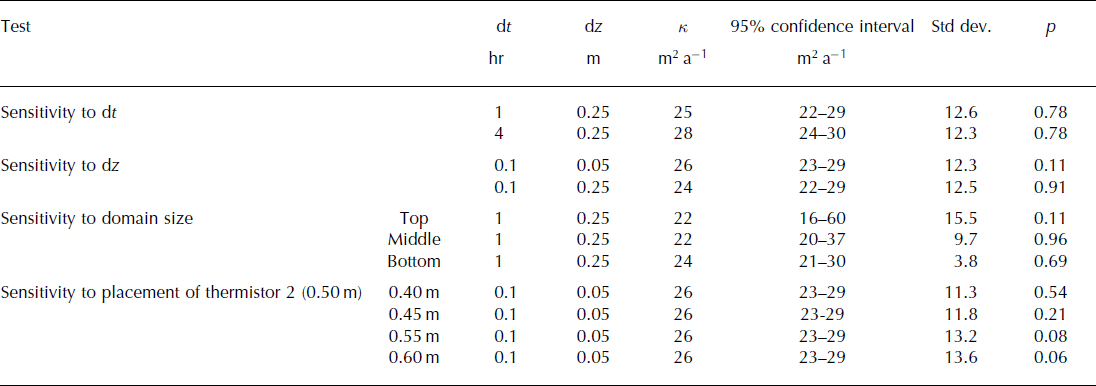
To understand the accuracy of our results and identify sources of error, from either modeling or measurements, we undertook the four sensitivity tests summarized in Table 1 and assessed the impacts of temporal resolution, spatial resolution, domain size and thermistor placement on the numerical solution. Perturbing the temporal and spatial resolutions independently does not give different values for optimal diffusivity. The solution achieved with dt = 1 hour and dz = 0.25 m is κ = 25 m2 a−1, with a 95% confidence interval spanning 22–29 m2 a−1. Model runs with a larger time step and smaller spatial discretization constrain similar ranges for diffusivity, all of which overlap.
Table 1. Summary of model perturbation experiments. All dt and dz ratios meet the accuracy condition for Crank–Nicolson. Sensitivity analyses show that the solution is not affected by temporal or spatial discretization, that neither the selected top boundary condition nor the domain size impacts the numerical solution and that scatter and spuriously high diffusivities can be reduced with the second thermistor placed closer to the first. Note that for all model runs, running a t-test for a possible depth trend in diffusivity always gives p > 0.05
Next, we ran the model for three layers of the domain (top, middle and bottom) to test whether the absence of a significant depth trend in diffusivity was a result of the 12 m domain being too large. The layer schemes used thermistors 1–4 (top scheme), 3–6 (middle scheme) and 5–8 (bottom scheme). These tests also served to assess sensitivity to the top boundary condition used in the numerical method. Although the model matches data better at greater depths where conduction is expected to be dominant (see ranges and standard deviations in Table 1), the optimal values of 22, 22 and 24 m2 a−1, respectively, fall within the 95% confidence interval output of the whole-domain run. Furthermore, t-tests (α = 0.05) on the slope of the diffusivity–depth regression lines failed to reject the null hypothesis of a constant diffusivity with depth for each layer scheme. While diffusivity’s dependence on snow microstructure and density is well established, the single bulk value constrained here nevertheless represents temperature trends reasonably well on the several-meter scale and is unaffected by domain size or which thermistor is used as a boundary condition. Figure 5 shows measured temperatures (Fig. 5a), temperatures modeled using κ = 25 m2 a−1 (Fig. 5b) and the difference between the two (Fig. 5c). The data–model difference is greatest in winter since the conduction-only model does not produce the high-frequency disturbances observed then in the near-surface (see above).

Fig. 5. (a, b) A comparison of (a) temperature data and (b) temperatures simulated by the numerical model with κ = 25 m2 a−1. (c) The difference in temperature, with general agreement but a clear difference in the near-surface where convection alters the temperature profile, particularly in winter.
The final round of sensitivity tests involved varying the position of the second thermistor (i.e. the shallowest thermistor which does not serve as a boundary condition). Diffusivity solutions for the second thermistor were larger than for others, suggesting that the recorded depth (0.50 m) may have been greater than the actual depth. Comparing temperatures generated with the second thermistor placed at 0.40, 0.45, 0.55 and 0.60 m reveals that spacing does influence the variability in the data: the standard deviation is 20% larger with the thermistor placed at 0.60 m compared to 0.40 m. Placement error does affect the variability of results but does not significantly affect the ultimate solution since all runs yield κ = 26 ± 3m2 a−1 without a distinguishable depth trend.
While errors in relative thermistor depths are more important than absolute depths given use of the topmost thermistor for a boundary condition, it is worth noting that the depth of each thermistor does change with the accumulation of snow. Because the thermistor string was installed in an air-filled borehole, we can reasonably expect the relative positions to stay constant; the entire system is translated relative to the surface. The translation is equivalent to the measured accumulation, which includes precipitation, wind deposition and compaction.
A further potential source of uncertainty stems from the fact that much of the seasonal temperature fluctuation occurs in the very near surface, a region where we have few data points. Reference Oldroyd, Higgins, Huwald, Selker and ParlangeOldroyd and others (2012) found that if temperature sensors are not placed close enough to each other (or to the surface) to represent the extent of curvature in the temperature profile (∂2 T/∂z 2), the diffusivity solution for a given ∂T/∂t will be larger than its physical value in compensation (see Eqn (3)). Given the scatter in the top 3 m, however, it is not clear that more near-surface data would give a different solution or more tightly constrained trend.
A Lagrangian reference frame is attractive because it allows for the implicit incorporation of thermal advection, due to burial from net accumulation. Reference Carslaw and JaegerCarslaw and Jaeger’s (1959) analytical solution to the heat equation does not incorporate advection and, thus, provides a useful comparison for assessing its importance relative to that of conduction. For a time-dependent harmonic surface forcing, T(0, t) = T s sin(ωt), where T s is amplitude, Reference Carslaw and JaegerCarslaw and Jaeger (1959) give the spatial and temporal temperature distribution in a semi-infinite solid:
Temperature distributions calculated with Eqn (5) show the closest match to data at 26 m2 a−1 with J = 1.7 × 10−2 years (6 days). That this falls within the 95% confidence interval of the numerical solution suggests minimal importance of advection in temperature profiles of near-surface polar snow and firn.
Application
Many of the conditions relevant to heat transfer in firn at Summit also characterize other areas of the Greenland ice sheet. Large-scale studies indicate relative homogeneity in climate across a significant portion of the dry snow zone (Reference Steffen and BoxSteffen and Box, 2001), with regional differences in weather. Spatial continuity of snow properties is supported by the fact that variability in snow hardness, grain size, and grain shape over several kilometers is on the same order as that within a single pit (Reference Dadic, Schneebeli, Lehning, Hutterli and OhmuraDadic and others, 2008). Additionally, the presence of wind slabs is widespread (Reference Sturm and BensonSturm and Benson, 2004), and wind slabs lessen ventilation and enhance insolation reflectance. Because the predominant meteorological and geophysical properties controlling heat transfer of firn are uniform on a large scale, our conduction-only model and solution may reasonably be applied to other areas of the dry snow zone, which constitutes 40% of the area of the Greenland ice sheet (Reference Cullen, Mölg, Conway and SteffenCullen and others, 2014).
Conclusions
Using a large range of physically plausible diffusivity values, we calculated firn temperatures at the depths of thermistors installed at Summit Station from 2004 to 2008. A numerical model with a constant diffusivity produced temperature series that matched measured series closely; the propagation times of generated annual maxima differed from measurements least when modeling with a diffusivity of 25 m2 a−1. This solution is slightly higher than predicted from empirical density relationships for seasonal snow, owing to the implicit inclusion of interstitial air movement in a bulk thermal diffusivity.
A constant diffusivity of 25 m2 a−1 gives the lowest RMSE but is statistically indistinguishable from 22–29 m2 a−1. Diffusivity is typically calculated using snow density; that density changes with depth are unknown for vast tracts of the Greenland ice sheet makes our physically based solution, though a bulk value, appealing. Furthermore, density-based diffusivity values are lower than those which more accurately simulate measured temperatures (and convection effects) using a simple conduction-only model. The bulk, measurement-based solution determined from temperatures at Summit can be applied in other parts of the dry snow zone when generating temperature profiles and considering temperature-dependent processes in the firn column.
Acknowledgements
We thank the Summit winter-over technicians for the accumulation data, and Ice Coring and Drilling Services for drilling. This work was supported under US National Science Foundation (NSF) grant OPP-0352584; A.L.G. was supported under NSF IGERT grant DGE-0801490 and NSF GRF grant DGE-1313911 during this project. Chris Polashenski’s feedback led to substantial improvement of the manuscript. Mary Albert and Rachel Jordan provided valuable feedback and discussion on the benefits and drawbacks of using a derived snow surface temperature for a model boundary condition. Finally, this study would not have been possible without the generous assistance and thoughtful guidance of Ed Waddington (principal investigator on NSF OPP-0352584).








