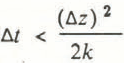1. Introduction
1.1 Englacial temperatures
The englacial temperatures of ice sheets and glaciers strongly determine their behaviour. An accurate knowledge of the thermal regime of these ice masses is therefore needed for understanding their dynamics and their response to climatic changes. Due to strong feed-back mechanisms, the modelling of both ice sheets and climate becomes strongly inter-dependent, especially when ice-age causes are investigated.
Most earlier studies focused on the temperatures in the large ice sheets of Antarctica and Greenland. Temperature measurements in deep bore holes have become available since the late 1950s (Reference BogoslovskiBogoslowski, 1958; Reference Hansen and LandauerHansen and Landauer, 1958; Reference GowGow, 1963; Reference Gow, Gow, Ueda and GarfieldGow and others, 1968; Reference Budd, Budd, Young and AustinBudd and others, 1976). Cold ice in high-altitude glaciers in the Alps was reported early on (Reference VallotVallot, 1913; Reference FisherFisher, 1955; Reference Haefeli and BrentaniHaefeli and Brentani, 1955). But relatively few studies con-centrated on the thermal regime of cold valley glaciers. However, many features of the thermal regime of ice sheets can also be found in valley glaciers, although there are great differences in time-scales and geometry. In the experimental and theoretical studies, mainly three different emphases can be recognized: (a) near-surface temperatures, (b) internal or deep temperatures, and (c) basal temperatures.
Since the climatic conditions generally determine the surface-boundary conditions, the near-surface temperatures have been extensively discussed for most climatic conditions in which glaciers exist. Usually, 10 m temperatures were related to various climatic or climate-related parameters; for dry-snow zones by Reference MellorMellor (1960), Reference Mock and WeeksMock and Weeks (1966), Reference KaneKane (1970), Reference LoeweLoewe (1970), Reference SatowSatow (1978), or for various other climatic and balance zones by Reference HookeHooke (1976), Reference MüllerMüller (1976), Reference ThomasThomas (1976), Reference Martin and PeelMartin and Peel (1978), Reference Hooke, Hooke, Gould and BrozowskiHooke and others ([1985]), and Reference OhmuraOhmura (in press).
An early approach to the discussion of measured vertical temperature profiles assumed steady-state conditions (Reference RobinRobin, 1955; Reference Radok, Radok, Jenssen and BuddRadok and others, 1970). However, non- stationarity was soon recognized as necessary for explaining the observed features (Reference Jenssen and RadokJenssen and Radok, 1961, Reference Jenssen and Radok1963; Reference WeertmanWeertman, 1968; Reference Budd, Budd, Jenssen and RadokBudd and others, 1971). The influence of ice flow on the thermal regime was investigated using two-dimensional flow and temperature models (Reference HookeHooke, 1976; Reference Hooke, Hooke, Raymond, Hotchkiss and GustafsonHooke and others, 1979, Reference Hooke, Hooke, Gould and Brozowski[1985]). The question of stability of ice sheets and glaciers under both stable and changing conditions became important in the discussion of ice-age causes and ice-age ice sheets (Reference WeertmanWeertman, 1961[b]; Reference RobinRobin 1970). Closely related to this is the intriguing problem of surging glaciers, considering “strain heating and creep instability” (Reference Clarke, Clarke, Nitsan and PatersonClarke and others, 1977) or temperate basal ice and bottom sliding (Reference ClarkeClarke, 1976). Basal temperatures were extensively discussed for the targe polar ice sheets (Reference LliboutryLliboutry, 1963; Reference Budd, Budd, Jenssen and RadokBudd and others, 1969; Reference HookeHooke, 1977). The question of temperate or non-temperate basal ice also became important in the discussion of glacial erosion and the formation of internal moraines (Reference WeertmanWeertman, 1961[a]). Geothermal heat sometimes shows anomalies which can be related to the basal temperatures of ice-age glaciers in today’s glacier-free areas (Reference Blatter and HaeberliBlatter and Haeberli, 1984; Reference Haeberli, Haeberli, Rellstab and HarrisonHaeberli and others, 1984).
Now, a wealth of information and theoretical studies is available for discussing measurements of englacial temperatures in large ice masses. The data set for White Glacier, Axel Heiberg Island, N.W.T., Canada, offers a good example for a cold Arctic valley glacier, where many features of the englacial temperatures can be partly explained by experience from other studies, and partly reveal new problems to be discussed further.
1.2 White Glacier
From 1959 to 1984, glaciological and climatological data were collected by members of the McGill Axel Heiberg Research Expedition of the late F. Müller. The main study focused on White Glacier, located at the end of Expedition Fjord on the west side of a mountain range on Axel Heiberg Island (Fig. 1).

Fig. 1. Topographic map of White Glacier with drilling sites and profile designation. The insert map shows the location on Axel Heiberg Island.
Among these various investigations, some relate directly to the problem of englacial temperatures (Reference MüllerMüller, 1963, Reference Müller1976; Reference BlatterBlatter, 1985), but most of them offer data which are necessary or very helpful for discussion of the temperature distribution in the ice. Large-scale maps (1 : 10 000) give a good picture of the surface topography (Reference MüllerMüller and others, 1963). There is now a 20 year long record of mass-balance measurements (Reference BraunBraun, unpublished; Reference WeissWeiss, unpublished), although the data are not homogeneous over the whole time span. Movement measurements were made along some transverse profiles. These measurements yield a good time resolution for some summers and reveal a substantial fluctuation in the surface velocities (Reference IkenIken, 1972, Reference Iken1974; Reference Müller and IkenMüller and Iken, 1973). Related to movement, a study of the structures and surface-ice deformation on White Glacier was carried out (Reference Hambrey and MüllerHambrey and Müller, 1978). Seismic soundings (Reference RedpathRedpath, 1965) and gravity investigations (Reference BeckerBecker, 1963) produced quite different glacier-thickness profiles. A radar-sounding experiment established a more accurate picture of the glacier-bed topography in the ablation area. In the accumulation zone, these soundings proved to be difficult to explain (Reference BlatterBlatter, 1987). More methodological work on determining short-term mass balance by terrestrial photogrammetry revealed a complicated pattern of surface lowering and rising in the lowest 2 km of the glacier tongue, thus documenting the non-stationarity of White Glacier (Reference ArnoldArnold, 1981).
These purely glaciological investigations were completed together with several climatological and micrometeorological studies. Several automatic weather stations recording air temperature, humidity, wind speed, wind direction, and radiation were run in different places and at different times on the glacier, over the tundra, and on the mountains (Reference OhmuraOhmura, 1981). Studies of the relations between meteorological parameters and short-term ablation were also carried out on the glacier (Reference AndrewsAndrews, 1964; Reference Havens, Havens, Müller and WilmotHavens and Muller, 1965; Reference BraithwaiteBraithwaite, 1972, Reference Braithwaiteunpublished).
Betweeen 1974 and 1981, a deep-drilling program was carried out and englacial temperatures were measured. The intention of this paper is to present these data and attempts a preliminary analysis. Numerical experiments for explaining some specific features more rigorously are in preparation.
2. Measurements and Results
2.1 Measurements and profile locations
Early measurements of englacial temperatures were obtained between 1960 and 1965 in several 10–30 m deep holes (Reference MüllerMüller, 1963, Reference Müller1976). Using an open-system hot-water drill (Reference Iken, Iken, Röthlisberger and HutterIken and others, [1977]) designed at the Versuchsanstalt für Wasserbau, Hydrologie und Glaziologie, ETH, Zürich, three men could drill to a depth of 380 m in a few hours. Between 1974 and 1981, a total of 32 holes was drilled on White Glacier and vertical temperature profiles in the ice were measured.
The temperature measurements were carried out using individually calibrated thermistors with electrical resistances of about 7000 ohm at a temperature of –20° C and of about 3000 ohm at 0° C. The calibration bath could be regulated within an accuracy of ±0.05° C. However, this accuracy could not be maintained in the in situ measurements. The accuracy of the temperature measurements in the glacier ice is estimated to be ±0.2° C, with some deviation in otherwise smooth profiles. With the large number of thermistors used, it is possible that some might have got mixed up.
The thermistors were inserted into Plexiglass tubes which were then filled with an epoxy resin to prevent breakage. The result was high resistance to damage; the calibration of the thermistors was hardly affected even when subjected to impact. The temperature readings were made using a resistance bridge. This method proved to be quite reliable under all air-temperature conditions encountered on the glacier.
The accuracy of the depth to which the thermistors were inserted into the holes is estimated to be better than ±2 m, though it is not known how vertical the holes were drilled. It is also difficult, or even impossible, to judge whether the drill reached the glacier bed because large rocks in the ice were likely to obstruct the drilling. At some sites in the lower ablation zone, the water level in the holes, which were usually filled with water, dropped abruptly at the termination of drilling. Since these holes terminated in a layer of temperate ice, we cannot be sure how near to the glacier bed the drill hole reached.
In May 1984, a depth-sounding program was carried out to settle this question (Reference BlatterBlatter, 1987). A total of 400 soundings along 15 profiles was carried out using monopulse radar equipment which was rebuilt on the basis of the model by the U.S. Geological Survey (Reference HodgeHodge, unpublished). The accuracy of the radar soundings is estimated to be 5–10% of the glacier thickness (Reference Haeberli and FischHaeberli and Fisch, 1984), except for the accumulation zone, where the soundings are difficult to explain.
The locations of the drilling sites and the profile definitions are shown in Figure 1. With the data, presented in Reference BlatterBlatter (1985), it is possible to draw two-dimensional temperature distributions for three longitudinal profiles. Profile 1 lies in the middle of the main ice stream in the accumulation basin and moves slightly to the orographic left side near the Moraine Profile, paralleling a flow line (Fig. 2). Two shorter profiles cover most of the tongue length. Profile 2 parallels the lowest part of profile 1 and ends at the Wind Profile (Fig. 2). Profile 3 starts at site 2/76 in the Anniversary Profile and reaches the glacier terminus (Fig.3).

Fig. 2. Ice temperatures in longitudinal profiles 1 and 2. The vertical lines indicate the measured profiles in the bore holes.

Fig. 3. Ice temperatures in longitudinal profile 3.
The locations of drilling sites and hence of the profiles were chosen to follow visible ice structures indicating the ice-flow direction. It is however not clear at all locations how accurately the defined profiles parallel flow lines. Even so, the important patterns of the englacial temperature distribution clearly show up in the profiles presented (Figs 2 and 3).
In the Wind Profile, 12 holes cover the entire transverse section of the glacier, but three more locations with two or three holes (Anniversary Profile, profiles C and D) across the glacier allow for two-dimensional temperature distributions. The four transverse profiles are presented (Figs 4 and 5) for documenting the discussion of the temperate-ice zone and the cold-ice core as it travels from the accumulation zone into part of the ablation zone.

Fig. 4. Ice temperatures in the Wind Profile looking down-glacier.

Fig. 5. Ice temperatures in the Anniversary Profile and in the transverse profiles C and D.
2.2 Basal temperatures
White Glacier is cold at the bed over most of its area. The basal temperatures are –10° to –15° C in the whole accumulation basin. Measurements of seasonal velocity fluctuations for the Wind Profile and Anniversary Profile indicate temperate basal ice at the glacier tongue (Reference IkenIken, 1972; Reference Müller and IkenMüller and Iken, 1973).
The amount of data available for the tongue area, from the Moraine Profile down-glacier, allows us to estimate the area where the glacier is sliding over its bed. However, the accuracy of the temperature measurements often does not enable one to judge whether the basal temperature is really at the pressure melting-point of the ice. If several thermistors near the bottom show temperatures close to 0° C, which indicates a near-zero temperature gradient, it can be assumed that the ice is temperate and there is some melt at the bed. This occurs over an extensive part of the tongue area where the geothermal heat, the heat generated by differential flow, and the sliding friction heat seem to be consumed by the melting process. As a result, there is a layer of temperate or near-temperate ice up to 40 m in thickness at the base of the glacier. The same feature was also observed in Laika Glacier, Coburg Island, N.W.T., Canada (Reference BlatterBlatter, 1985; paper in preparation by H. Blatter and G. Kappenberger).
This poses an intriguing problem for glacier modellers, since the treatment of an internal phase boundary may become necessary. The question remains whether this temperate layer is a matter of non-stationarity of the glacier geometry, or maybe of an earlier increase of the ice thickness. However, the surface of the glacier is lowering presently in the lowest part of the tongue (Reference ArnoldArnold, 1981).
Along the Anniversary Profile, the drilling depths match strikingly well the radar-sounding thicknesses (Fig. 5), in contrast to the earlier seismic and gravimetric soundings (Reference BeckerBecker, 1963; Reference RedpathRedpath, 1965). Along the Wind Profile, the radar seems to underestimate the glacier thickness by 5–10%, which is within the estimated accuracy of the soundings (Reference Haeberli and FischHaeberli and Fisch, 1984). But even within this accuracy, one can estimate the width of the zone of the temperate glacier bed on the Wind Profile (Fig. 4).
For the Moraine Profile, both temperature measurements and radar thickness exclude the possibility of temperate basal ice, although some velocity fluctuations were registered on this profile (Reference IkenIken, 1974). Considering the topography of the glacier bed and the ice-thickness distribution, one can conclude that the area of sliding begins shortly below the steeper part of the glacier near the Moraine Profile (Fig. 2).
Figure 6 is a map of the glacier tongue with the estimated area of bottom sliding, including the area with an assumed zero temperature gradient at the bottom of the ice.

Fig. 6. Estimated area where the glacier slides over its bed.
2.3 Near-surface temperatures
Measurements of 10 m temperatures carried out in the years 1961–65 at several locations on White Glacier were reported by Reference MüllerMüller (1963, Reference Müller1976). The 32 bore-hole temperature profiles measured between 1974 and 1981 were not primarily planned for 10 m temperature determination. Therefore, not all sites allowed a value to be obtained. Especially at sites in the lower ablation area, the thermistor depths changed over the years and hence 10 m temperatures had to be interpolated, adding another uncertainty. Some sites could be measured several times within 5 years.
The measured 10 m temperatures are plotted versus the altitude (Fig. 7), showing some trends for different altitudes and different balance zones, but also a wide scatter. This scatter can be traced mainly to two sources. First, sometimes several sites at the same altitude covered the whole transverse profile, Thus, some values represent the center-line situation in the glacier valley, but others more lateral situations on both sides of the glacier. This is only part of the contribution to the scatter of the values. Some 10 m temperatures measured at one specific site but for different years also showed different values. All values were measured in August; therefore, the influence of the annual temperature variations should not be reflected too much in the scatter.

Fig. 7. The 10 m temperatures and linearly extrapolated “surface temperatures” versus the attitude.
The 10 m temperatures at several sites show the same trend in the year-to-year variations (Fig. 8). For an explanation, the annual mean air temperatures at Eureka, Ellesmere Island, for the hydrological years (here taken from 1 September to 31 August) from 1973 to 1980 were calculated. Eureka is the nearest meteorological station and lies, similar to White Glacier, on the west side of a mountainous island in a fjord. The monthly mean air temperatures at Eureka and at the Axel Heiberg Expedition base camp correlate rather well (Reference BlatterBlatter, 1985) for the months April–August for which data exist. The annual means at Eureka differ by as much as 5° C (Fig. 8) between 1972–73 and 1976–77. Comparing the trends in 10 m temperatures with the trend in annual mean air temperatures suggests a strong influence of the longer-term climatic variations.

Fig. 8. Year-to-year trends of the 10 m temperatures and of the annual mean temperatures at Eureka meteorological station.
2.4 Internal temperatures
The temperature profiles observed on White Glacier show similar shapes to those described for ice sheets (Reference RobinRobin, 1955; Reference Clarke, Clarke, Nitsan and PatersonClarke and others, 1977; Reference HookeHooke, 1977). However, in the upper part of White Glacier, the temperature distribution shows a persistent minimum at a depth of 100–150 m below the glacier surface (Fig. 2). That this is an artefact of the drilling technique and the measurements can be excluded. The water running through the holes during drilling certainly heats the surrounding ice and especially the firn due to percolation. Most bore-hole temperatures were measured again 1–4 years after inserting the cables. In this way, it is confirmed that the bore-hole temperatures adjusted to reading accuracy within 3–4 weeks after drilling. Similar observations have also been reported by Reference Classen and ClarkeClassen and Clarke (1971).
The isothermal lines around the minimum should not be taken too literally, since the temperature distribution is very shallow and small errors in measurements would shift the lines substantially.
This cold ice seems to form a core along the center line of the main stream of the glacier and is carried along far into the ablation zone due to advection, but it seems to be absent at the glacier sides and in the tributaries. This can be seen partly in the transverse profiles C and D (Fig. 5), where bore-hole temperatures off the center line do not show the minimum. However, it will be difficult to explain this feature in detail since nothing is known about accumulation, ice movement, and ice thickness on these steep slopes to the side of the main stream. The internal temperature distribution shows a transition zone from typical accumulation-zone profiles to typical ablation-zone profiles between Moraine Profile and Anniversary Profile (Fig. 9). The small positive or even negative near-surface gradient increases with increasing ablation. The bottom gradient first increases due to increasing sliding-friction heat but decreases again lower down due to increasing melt at the glacier bed. This transition zone is strongly determined by horizontal advection of heat.

Fig. 9. The vertical ice-temperature profiles for various altitudes along the center line of White Glacier.
3. Discussion of the Temperature Minimum
3.1 Time-scales
Temperature minima, such as the one observed in White Glacier, can be caused essentially by two processes:
-
(1) Cold ice is advected into the minimum region from higher up in the glacier, and
-
(2) Changes of the surface-boundary conditions through climatic variations and therefore shifts of balance zones.
There is a large year-to-year variation in the equilibrium-line altitude (400–1400 m a.s.l.) and thus partly of the balance zones. Little is known about how these zones moved in the past decades or centuries. However, the temperature distribution shown in Figure 2 cannot be in a steady state. Assuming steady surface temperatures and geometry for the future, the minimum must disappear through diffusion.
Climatic changes, for example, of the annual mean air temperatures at screen level, show a spectrum with many roughly periodic variations. During the 100 years of temperature records at the Upernavik, Greenland, meteoro- logical station, these variations show large year-to-year fluctuations but also about 10 yearly and about 100 yearly periods. Taking the Little Ice Age and the medieval optimum into account, there could also be variations of 200–1000 year periods.
Diffusion processes filter short-period fluctuations. The 10 yearly variations are reduced to 10% of the surface amplitude at 25 m depth. Therefore, one can use smoothed surface-boundary conditions for modelling deep temperatures. For the temperature minimum considered, periodicities between 100 and 300 years seem to be relevant. The 100 year variations are reduced to 10% at 80 m and to 1% at 160 m depth.
A very rough estimate can be made by using the ratio P between characteristic time-scales for diffusion and advection of heat (personal communication from W.D. Harrison):

where k is the thermal diffusivity, L 1 and L 2 are characteristic distances, v is a characteristic velocity. T 1 and T 2 are respectively characteristic time constants for diffusion and advection of heat. In the case of L 1 = L 2, P is called the Peclet number. If P = 1, both advection and diffusion are of about the same importance. For P < 1, diffusion dominates over advection and for P > 1 vice versa. For the situation in White Glacier, the vertical velocity in the area considered is about v = 0.2 m/a and the depth of the minimum is 100–150 m. With the diffusivity of firn and ice between 30 and 38 m2/a, this yields P between 0.6 in the accumulation area and 1.7 near the equilibrium line. Diffusion and advection of heat are of similar importance.
Horizontal advection may have transported cold ice from the highest parts of the glacier during some earlier period. With the characteristic quantities v = 2.5 m/a for horizontal velocity and L 2 = 2000 m, the ratio of the time constants for diffusion in the vertical direction and for advection in the horizontal direction yields P = 0.35, indicating that diffusion substantially dominates over advection.
The situation appears different for the mean equilibrium-line altitude (around 1000 m a.s.l.). The characteristic quantities are v = 40 m/a for the horizontal surface velocity and L 2 = 4000 m. Thus, P = 2.5 indicates a dominant influence of advection.
3.2 Influence of climatic changes
A non-stationary surface-boundary condition is partly responsible for the observed temperature minimum in the accumulation area. To estimate the influence of climatic changes on englacial temperatures, a one-dimensional model that considers time-dependent boundary conditions was used. The one-dimensional approach seems justified because the top half of the ice in the area considered moves at a low velocity and as an almost non-deforming block. This calculation is only an estimate. The equation

was treated with the surface and bottom boundary conditions

where the thermal diffusivity was taken as k = 38 m2/a, the velocity w(z) was taken proportional to the distance to the glacier bed with a surface value of 0.5 m/a. The z-axis is assumed vertical to the glacier surface and t denotes the time. T s is the temperature of the ice at 10 m depth below the glacier surface and ∂Tb /∂z is the temperature gradient at the bottom of the ice.
Over the past 100 years, the meteorological records have shown a trend towards increasing air temperatures with some superposed shorter-term fluctuations. These temperature variations are larger at high latitudes. Comparisons between the stations at Upernavik, Gothab, Jakobshavn, and Dundas (Greenland), and Eureka and Isachsen (Canadian Arctic Archipelago), suggest the following boundary conditions for the White Glacier surface:
A constant temperature for the time before 1880 to account for the colder times during the Little Ice Age and a temperature variation following the trend of the measured air temperatures at a nearby meteorological station with a sufficiently long record.
For the model calculation presented, the following specific assumptions were made:
-
(1) A constant surface temperature of T s = –16.4° C for a long enough period to reach steady state at 1880. This T s was selected in such a way that the calculated steady-state temperature profile fits the bottom half of the measured profile 1/81 best.
-
(2) A variable surface temperature following the trend of the 10 yearly means of the screen temperatures at Upernavik station (Fig. 10) for the period 1880–1980.

Fig. 10. Top boundary conditions (10 m temperatures) as used in the calculation for estimating the influellce of the climatic variations on ice temperatures. The 10 m temperatures are taken constant as −16.4° C to arrive at the steady-state profile in 1880 and follow the air temperatures at Upernavik. Greenlalld, meteorological station for the period 1880 to 1980.
Equation (2) with boundary conditions (3) was solved numerically by using a one-dimensional grid with 50 grid points over a depth of 380 m. The integration was performed by two different numerical schemes:
-
(1) Finite differences with explicit forward integration in time. The time steps Δt were chosen to meet the stability criterion (Reference Jenssen and RadokJenssen and Radok, 1963)
(4)
for a grid interval Δz.
-
(2) The second-order differential Equation (2) was transformed into a set of first-order equations (one equation for each grid point), again by applying the finite differences as described above. A program package called SDRIVE, available at the program library of the ETH, Zürich, was used to integrate the equations (Reference BlatterBlatter, 1985). The time steps were chosen by the program according to the required accuracy.
Both calculation schemes produced virtually the same results. A run for 500 years model time was enough to reach steady state. Since convergence of iterations may play strange tricks, several even very exotic initial conditions were used. The programs always converged towards the same steady-state profiles. Figure 11 shows the measured (dots) and the calculated temperature profiles (solid lines) for site 1/81 on White Glacier, The line labelled s.s. shows the steady-state profile which was used to fit the lower half of the measured profile and from which the variable period at 1880 was started. The line labelled n.s. shows the calculated profile for 1980 with non-stationary boundary conditions according to Figure 10.

Fig. 11. Measured (dots) and calculated (solid lines) ice temperatures for drilling site 1/81 on White Glacier. The label s.s. indicates the steady-state profile for adjusting the initial 10 m temperature. The label n.s. indicates the calculated profile for 1980.
Model calculations (Reference Paterson and ClarkePaterson and Clarke, 1978) show that the temperature regime of an ice cap reacts very sensitively to variations in the amount of melt water refreezing in the firn. However, quantitative information for the heat input due to this process is not available for White Glacier. It cannot be excluded that the surface-boundary conditions did not follow exactly the trend of the air temperatures but a trend influenced by shifts in the balance zones.
It must be re-emphasized that the result given in Figure 11 is not a model calculation for the temperature profile 1/81. The result merely shows how the climatic trend towards higher temperatures over the past 100 years can explain a substantial fraction of the negative gradient in the top 100 m of the accumulation zone of White Glacier.
4. Discussion of Near-Surface Temperatures
4.1 10 m temperatures and “surface temperatures”
For modelling glacier dynamics, some surface-boundary conditions are necessary. For climate modelling, on the other hand, glaciers and especially large ice sheets are an important boundary with a strong feed-back. Therefore, the interaction between the climate system and ice masses plays a crucial role for both fields, glaciology and climatology.
At times in the period 1950–60, the 10 m temperatures became popular among glaciologists and climatologists dealing with the thermal regime of ice sheets and glaciers. Since annual variations in surface temperatures are mostly damped at this depth, 10 m temperatures may reflect some relation to annual mean climatic parameters. It was soon recognized that the different balance zones show different patterns in 10 m temperatures due to a different vertical heat flux in the ice.
The first extended use of 10 m temperatures on the large ice sheets of Antarctica and Greenland revealed a rather close relation to the annual mean air temperatures (Reference MellorMellor, 1960; Reference Mock and WeeksMock and Weeks, 1966; Reference KaneKane, 1970; Reference LoeweLoewe, 1970; Reference SatowSatow, 1978; Reference OhmuraOhmura, in press) in the very cold dry-snow zones. On the other hand, the relation seems more diffuse and complex for zones with percolation in firn and in ablation zones on smaller ice caps and glaciers (Reference HookeHooke, 1976; Reference MüllerMüller, 1976; Reference Martin and PeelMartin and Peel, 1978; Reference Hooke, Hooke, Gould and BrozowskiHooke and others, [1985]). The 10 m temperatures seem to scatter by several degrees, either for different sites in the same climatological situation or for one specific site in different years (Reference ThomasThomas, 1976). Both effects have been observed in the 10 m temperatures measured on White Glacier.
In dry-snow zones, where no melting processes occur, the actual glacier surface may be taken at the visible firn surface. In percolation zones and ablation zones, on the other hand, rather complex energy-balance processes take place in the top few meters of the glacier, in seasonal snow layers, and in the top of the ice. It seems reasonable to define the “glacier surface” at the level where climatological processes are negligible, such that below the “surface" only heat diffusion and advection are taking place. Then, annual snow layers, radiation absorption in the top layers, cryoconite holes, and weathered ice layers belong to the meteorological parameters. This suggests an operational “glacier surface” which may be standardized.
The 10 m temperatures are sometimes measured together with some temperatures at levels above and below. Taking the temperature profile at a depth not affected by surface variabilities, one can extrapolate the profile to the surface by using a simple model calculation or, if the data are not adequate, determine the temperature gradient at that depth and interpolate linearly to the surface (Reference Hooke, Hooke, Gould and BrozowskiHooke and others, [1985]), thus taking a possible heat flux into account.
The data for White Glacier were not gained particularly for this purpose. However, Figure 7 illustrates the standard 10 m temperatures and the linearly extrapolated “surface temperatures” as far as it was possible with the available data. This picture confirms what can be guessed. The larger ablation generally produces a vertical ice movement upwards and thus a large positive near-surface temperature gradient. This gradient then produces a greater difference between the 10 m temperature and the extrapolated “surface temperature”, by definition.
4.2 Extrapolated “mean surface temperatures”
For glacier–climate interaction studies, a mean temperature of the ice at the “glacier surface” as described above is more informative than a mere 10 m temperature. To determine such a surface temperature, either the measurement of at least two temperatures or of a temperature and a temperature gradient at adequate depths is required.
A simple model, taking heat diffusion and advection into account, can provide a mean for such an extrapolation. Since the model will treat an ice layer between 20 and 50 m depth, where the annual variations are no longer significant, a one-dimensional stationary model is suggested. The equation for the heat flux, with respect to the temperature profile is then

with constant heat diffusivity k. A constant vertical velocity w is justified if the glacier thickness is substantially larger than the layer under consideration. The solution of Equation (1) is

where ΔT is the temperature difference between two depths with the distance Δz and a is the temperature gradient at the lower depth. Then, the vertical velocity w is positive for upward movement, i.e. for ablation zones. For zero velocity w = 0, this solution converges to the linear extrapolation described in section 4.1.
However, this calculation assumes only annual surface- temperature variations and does not allow for longer-term climatic variations and influences of other heat fluxes, such as horizontal advection and diffusion.
Taking this extrapolation scheme for calculating “surface temperatures” by using a measured temperature and temperature gradient at a depth d, the still existing annual variations may cause an error in the extrapolated values. However, an estimation of this error using a model with sinusoidal surface variation in uniform, non-moving ice shows a rapid decrease in this error with increasing depth. Below 25 m depth, this error drops below 1% of the amplitude of the surface variation for the annual wave. However, to reach the same accuracy from measurements of the temperature gradient at 25 m depth, this gradient must be accurate within ±0.04 deg/m for w = 0 and ±0.01 deg/m for w = 5 m/a. It seems easier to extrapolate the temperature profile by using two temperatures about 10–20 m apart and determine a also by using Equation (6).
4.3 Extrapolation of measured profiles
Only measured temperature profiles in the lower ablation area can be used to test the extrapolation in Equation (6). There, horizontal advection of cold ice from the accumulation zone is no longer important. The mass-balance values measured on White Glacier could not provide a value for w. Therefore, three measured temperatures at three different levels were used to fit a profile accordingly to Equation (6). The thickness of the modelled layer was chosen to be less than one-third of the total glacier thickness at this site in order not to stress the approximations made. This usually required a glacier thickness of more than 150 m.
For most profiles, more than three temperatures between 10 and 70 m were available for fitting of the curves. However, the 10 m temperatures usually proved to be off a reasonable profile, possibly due to the still relatively large annual variations. Most measurements were made at the end of the summer and, therefore, the preceding winter’s temperature minimum had then arrived at the 10 m level.
Figure 12 depicts the results for three sites on the Wind Profile and two sites on the Anniversary Profile. The higher “surface temperature” in the Wind Profile (–15oC; Anniversary Profile: –17oC) may partly be explained by the thicker and longer-lasting seasonal snow cover. Wind Profile lies in a flat part of the glacier, Anniversary Profile lies in an area with a slightly convex surface and is more exposed to winds eroding the snow.

Fig. 12. Measured and calculated near-surface temperature profiles in the ablation zone. The extrapolated “surface temperatures” for the Wind Profile (6/75, 4/75, and 2/80) lie around −15° C and around −17° C for the Anniversary Profile (1/76 and 2/76).
If more than three values were available, tests by choosing different triples for fitting the curve could be performed. This proved to produce extrapolated “surface temperatures” as much as 2° C different for the same profile, indicating that higher accuracy for the measured temperatures is needed as a basis for any extrapolation scheme. Even then, it still has to be tested how much longer-term climatic changes influence the deeper parts of the near-surface temperature profiles.
Also, strong horizontal heat advection may make the extrapolation impossible. This seems to reduce the applicability of this extrapolation scheme to the tower part of the ablation zone. Higher up on the glacier, where the vertical movement points downwards, longer-term temperature variations are transported into the ice and make an application of Equation (6) impossible.
5. Summary and Conclusions
The thermal regime of a cold glacier is determined by the boundary conditions and the internal heat flux by diffusion and advection. The interpretation of vertical temperature profiles as measured in bore holes may be ambiguous. Horizontal advection, as well as variable surface-boundary conditions, may cause negative gradients in the upper part of profiles, especially in the accumulation zone.
The profiles in Figure 9 illustrate the various temperature regimes from the highest part in the upper percolation zone (Reference MüllerMüller, 1962) down to the glacier terminus. In the highest part, the temperature profile is similar to what can be expected in the center of ice sheets (Reference RobinRobin, 1955), although non-stationary surface conditions influence the near-surface profile. The cold ice is advected down-glacier. This is visible in the temperatures near the equilibrium line and in the higher ablation zone. The upward movement of the ice then gradually removes the cold ice until the typical ablation-zone profiles dominate. These profiles, with large positive temperature gradients near the surface, are observed closer to the glacier sides at higher altitudes than in the center of the ice stream where advection is larger.
In the case of high surface velocities, the differential and sliding friction heat is larger and increases the bottom gradient. However, this is again reduced by bottom melting and reaches isothermal conditions in the lowest part of the glacier tongue. One consequence is a layer of temperate or near-temperate ice up to 40 m thick. Near the glacier sides and along the terminus, the bottom ice is cold and frozen to the ground.
The thermal regime of the valley glacier described here shows some intriguing features, which may be the starting point for future studies:
-
(1) The near-surface temperatures do not show a clear relation to climate (elevation, lapse rate, balance zone). To study glacier–climate relations, an adequate “surface temperature has to be defined. This will also increase the effort needed in the field work to determine such surface temperatures.
-
(2) Climate-glacier relations for different balance zones will be important to explain non-steady-state features in the temperature distribution. Two-dimensional, non-stationary numerical models, using a reconstructed history of the surface-boundary conditions, may help to separate the influence of diffusion and advection, both horizontal and vertical, from the influence of variable climatic conditions. This will be especially important for the zone of transition between “accumulation-zone profiles" and ablation-zone profiles”. This zone usually coincides with the area of the highest ice velocities and advection may dominate over diffusion.
-
(3) The large positive near-surface gradients caused by the upward movement of ice in the ablation zone produces large temperature differences between surface and bottom even for small ice thicknesses. The almost isothermal temperate bottom ice poses an intriguing problem for modelling, since an internal phase boundary may have to be handled. Even the question whether this temperate layer can occur in a steady state will be difficult to answer. However, more accurate temperature measurements are necessary to prove the existence of a really temperate zone as described above.
Acknowledgements
All field activities were made possible by the logistic support of the Polar Continental Shelf Project, Ottawa, Canada, and financial support by the Eidgenössische Technische Hochschule, Zürich, Switzerland. H.-J. Frei undertook most of the drilling during the years 1976–81 and helped improve the drilling equipment substantially. The author wishes to thank Dr H. Röthlisberger and Dr A. Iken who helped in designing the drilling system. Dr A. Ohmura encouraged the continuation of the project and supported it with many stimulating discussions. Dr W. Haeberli read the manuscript carefully and helped to improve it extensively.