I. Introduction

The search for simple empirical formulae to describe the relation between sea-ice thickness h and surface freezing exposure Σθ ₀Δt. At in the form

where a and b are empirical constants, has created some unfortunate impressions. A number of expressions of the form (1.1) have been reviewed by Reference MellorMellor (1964). Since none of these considers the time required for the transmission of heat through the ice each of them must be considered as unique, having values of a and b relating to some specific time interval used in the empirical determination. Furthermore the right-hand side of equation (1.1) is a function of temperature and time only, and thus cannot reflect the influence of heat transported by water below the ice on the thickness of the cover. Unless applied to very similar conditions of locality, time, and temperature, these relationships can have only very limited usefulness as prognostic tools. In fact, since Stefan’s simple equation Reference Stefan(1891) may be expressed in the form

where 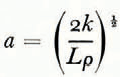and k, L and ρ are the thermal conductivity, latent heat and density of the ice respectively, it becomes clear from the author’s earlier work (Reference SchwerdtfegerSchwerdtfeger, 1964), as well as Stefan’s own paper, that neither equation (1.2) nor (1.1) can provide a valid solution in general. Stefan’s rigorous solution of the ice growth problem is restricted to the case of a uniform ice cover whose thickness increases linearly with time.

In the absence of a heat flux in the water below the ice, it is often more appropriate to use a simple analysis along the lines indicated by Reference SchwerdtfegerSchwerdtfeger (1964). In this paper the lag coefficient χ was introduced as a new concept, and defined by the equation

where t _θ represents the time elapsed between the occurrence of a temperature extreme at the surface of an ice cover and the corresponding stationary ice growth rate (Fig. 1), and h ² the mean-square thickness during this time. A useful property of χ is that it remains independent of water currents and heat fluxes influencing the ice from below.

Fig. 1. Time delay between related stationary values of we surface temperatures and growth rate

Temperature disturbances move through the ice with speeds that depend on their frequency as well as on the thickness and thermal properties of the ice. The lag coefftcient as specified above therefore is meaningful only for a series of disturbances of similar duration. Fortunately the air temperature variations controlling the behaviour of an ice cover appear to conform to this requirement, building up and decaying usually over periods of several days.

It followed from the analysis of the earlier paper (Reference SchwerdtfegerSchwerdtfeger, 1964) that for a uniform ice cover

where K is the thermal diffusivity. Although it is undesirable to introduce new physical quantities unnecessarily there does appear to be justification for defining χ which is a property of an entire ice cover, unlike K with its strong temperature and salinity dependence in a non-uniform cover.

2. Lag Coefficient and Thermal Diffusivity

The method of determining the lag coefficient was described in the earlier paper (Reference SchwerdtfegerSchwerdtfeger, 1964) using Hudson Bay sea ice at lat. 58° 40′ N., long. 94° 30′ W. as an example. The same procedure has been adopted in analysing new data for sea-ice growth during 1964 at Davis, Antarctica (lat. 68° 30′ S., long. 78° 00′ E.) and the results are shown in Figure 2. Those new data provide 12 values for χ covering a wide range of ice conditions and temperatures.

Fig. 2. Values of the lag coefficient for Hudson Bay and Antarctic sea ice shown with the theoretically expected reciprocal diffusivity

In order to compare these lag coefficients with the reciprocals of the corresponding thermal diffusivities, both χ and K ⁻¹ must be associated with representative temperature values. For the lag coefficient χ this temperature was chosen as the mean surface temperature θ ₀. for an interval of length 2t _e where t _e is the time lag between the occurrence of the surface temperature extreme (assumed to occur at t = t _e) and that of the extreme ice growth rate (at time 2t _e). Thus

and as shown by Figure 1 all surface temperatures which influence the inner ice temperatures during the time interval t _e following the surface temperature extreme are given weight.

The mean values of the thermal diffusivity were computed from the author’s (Reference SchwerdtfegerSchwerdtfeger, 1963) data for the mean temperatures of the ice cover where θ _F is the freezing point, −1.8°C. This procedure gives mean diffusivities which in general are larger than the true mean diffusivities of an ice cover of given surface temperatures but because of the unknown and varying temperatures within the ice no advantage is gained by a more complex analysis. In any case a similar bias applies to the determination of the lag coefftcient.

The results for χ are compared with the reciprocal diffusivity K ⁻¹ in Figure 2 which displays their remarkable parallelism. Figure 2 suggests that K_χ = 2.5 but in view of the approximations and restrictions discussed it is difftcult to attach a physical interpretation to this fact.

3. Conclusions

The principal interest of the results presented lies in the fact that the values of the lag coefficient obtained for Hudson Bay sea ice agree well with those obtained for Antarctic sea ice at Davis. It would be difficult to imagine two more contrasting sea-ice covers—one land-locked and protected by the small inlet of Button Bay, the other continually facing the disruptive influence of the Southern Ocean and clearly subject to thermal erosion by marked currents beneath the ice. We are therefore justified in concluding that the lag coefficient is indeed a general bulk property of sea-ice covers.

Certainly, in most open areas of water, including the site near Davis, Antarctica, the measured ice thickness will be less than that calculated along the lines of Schwerdtfeger (1964). In these cases, the difference between the computed and the actual thickness is a measure of the integrated heat flow in the water below. Reference WishartWishart (unpublished) has had some success in determining bottom melting near Mawson, Antarctica, by this method. Thus, although bottom melting has no effect on the lag coefficient, whose magnitude allows us to link ice growth and its cause, thermal erosion must be considered as a separate process.

No great significance can of course be attached to the statistical limits of accuracy attached to the values of the lag coefficient in Figure 2. The chief application of the lag coefficient is in analyses of longer term or seasonal ice growth by means of the author’s modified Stefan equation (Schwerdtfeger, 1964). From this earlier work it became clear that any attempt to correlate thermal events at the upper and lower faces of an ice cover contributed to a significant improvement in a basically simple method of analysis. The present paper gives reason to believe that for many purposes values of the lag coefficient can be tabulated as a function of temperature and have general validity.

It will have been noticed that the ice salinity has not been introduced as a parameter, this is because salinity is assumed to be a function of the rate of freezing, in turn, dependent on temperature. Nevertheless, there will be a distinct set of values for the lag coefficient for sea ice and freshwater ice.

4. Acknowledgements

The author is indebted to Mr. Norman Trott, Officer in Charge of the Australian National Antarctic Research Expedition at Davis in 1964, for the measurement of sea-ice thickness and surface temperatures throughout the season; these provided most of the data for this paper, comments on which by Dr. U. Radok have been appreciated.