1. Introduction and statement of problem

When a river, lake, or part of a sea freezes over, the formed ice cover is often in contact with a variety of structures, such as bridge piers, dams, hydroelectric power stations, and offshore drilling platforms. Subsequently, any attempt to change the position of the ice cover (by changing the water level, or by the movement of the water base beneath it or the air above it, or by the change in the air temperature) creates forces between the structures and the formed ice cover.

For a rational design of a structure which comes in contact with a floating ice cover, the engineer needs to know the forces the ice will exert on this structure; especially the value of the largest possible force.

An early description of problems of this type was given by Reference BarnesBarnes (1906, Reference Barnes1928) and by Reference KomarovskiyKomarovskiy (1932–33). The effort and progress made in this field during the following few decades was very modest, as evidenced by the results presented at the ASCE symposium on Ice pressure against dams in 1954.

During the past decade the problem of ice forces gained in importance, partly because of the discovery of oil in the northern regions and the resulting increased activity in this area. The intensified research effort that followed is evidenced by the recent increase of conferences on this subject, such as the conference on Ice pressures against structures (Reference Gold and WilliamsGold and Williams, 1968), the Ice seminar (1969), the international conferences on Port and ocean engineering under Arctic conditions (Trondheim, Norway, 1971; Reykjavik, Iceland, 1973; Fairbanks, Alaska, U.S.A., 1975), as well as the IAHR symposia on Ice and its action on hydraulic structures (Reykjavik, Iceland, 1970; Leningrad, U.S.S.R., 1972; Hanover, New Hampshire, U.S.A., 1975). In spite of all these efforts, to date there are no reliable methods for predicting the ice forces an ice cover may exert on a structure.

The analyses of these forces are usually grouped into several categories. For example, analyses of forces due to a rise or drop in the water level, analyses of forces because a structure constrains the movement of the ice cover in the horizontal plane, and analyses of forces due to impact of a moving ice flow and a structure. The present paper discusses problems in the second category. Examples of such problems are shown in Figure 1.

Fig. 1 Typical situations in which forces due to ice constraints are applied to a structure: (a) ice cover pressing against a rigid wall, (b) ice cover pressing against a rectangular pier.

Since ice is a visco-elastic material, the forces an ice cover exerts on a structure are time-dependent. The study of these forces, caused by constrained thermal expansions, was initiated by N. Royen in 1922. The analytical and test results by Royen, as well as the more recent results of a number of other investigators, were reviewed by Reference KorzhavinKorzhavin (1962, chapter 14), by Reference DrouinDrouin (1968), and by Reference MichelMichel (1970). Other attempts to solve this problem were presented by Reference PanfilovPanfilov (1965), Reference NevelNevel (1968) and Reference Jumppanen and KarlssonJumppanen ([1974]).

The conclusion of the survey by Drouin was that the determination of ice forces as a function of time is not yet solved satisfactorily. The relevant results of Reference PanfilovPanfilov (1965), Reference NevelNevel (1968), and Reference Jumppanen and KarlssonJumppanen ([1974]) are as yet not conclusive either. A major difficulty in solving this problem is the absence of appropriate constitutive equations for the ice cover. It should also be noted that even if expressions which determine the ice forces were available, the magnitude of these forces may sometimes be limited by a possible failure (crushing or buckling) of the ice cover, as discussed previously.

For the design of a structure which is in contact with an ice cover, it is often sufficient to know the largest force the ice cover may exert on the structure. This approach simplifies the necessary analyses.

To demonstrate the essential aspects of this ice-force problem, consider as an example, an ice cover constrained by two parallel "rigid" walls, as shown in Figure 2. Assume that (at a time t = 0) the temperature of the ice plate is instantaneously raised by a constant value, ΔT. Then, the corresponding axial compression force (per unit length of wall) is approximately

(1)

Fig. 2 Floating ice cover constrained by two parallel "rigid" walls.

Equation (1) is based on the assumption that, at the instant of the temperature rise (t = 0), the ice obeys Hooke's law, that Young's modulus E is an averaged value across the plate thickness, and that the coefficient of linear expansion α is also an average value which does not vary noticeably in the temperature range of interest.

Because of the visco-elastic response of the ice cover, the pressure p, for t > 0, will be smaller than the p ₀ value given in Equation (1), namely

(2)

A similar argument leads to the conclusion that Equation (2) is also valid for the case when the temperature rise is not instantaneous but proceeds gradually, as is the case in the field. Thus Equation (1) yields the largest possible axial compression force due to ΔT. This suggests that, for many engineering problems, it may be sufficient to determine the design forces acting on a structure by assuming that the ice cover responds elastically.

At this point it should be noted that the force estimate given by Equation (1), or the more accurate expression which takes into consideration the visco-elastic response of the ice cover, is valid as long as the ice cover does not fail. Thus, beyond a certain compression force, Equation (1), or its visco-elastic equivalent, yields too high values for the ice force, and it has to be bounded by a failure criterion. This criterion is obtained by noting that an ice force cannot be larger than the force capable of breaking up the ice cover. Thus the needed bound for in-plane compression forces is established by determining the intensity of the force at which the ice cover fails. Note, that this criterion is valid for the determination of the largest ice forces that may be caused by a temperature change or due to any other reason such as the movement of the water in the horizontal direction.

Many published analyses are based on this notion. In the majority of these publications it is assumed that this failure load is directly related to a "crushing strength" of the ice. Namely, that the mechanism of failure is due to crushing or splitting of the floating ice plate in the immediate vicinity of the structure. For a review of the relevant literature up to 1962 refer to Reference KorzhavinKorzhavin (1962). For a more recent utilization of this approach refer to Reference Shadrin and PanfilovShadrin and Panfilov (1962), Reference Afanas'yevAfanas'yev (1968), Reference MichelMichel (1970), Reference SchwarzSchwarz ([1971]), Reference Afanas'yevAfanas'yev (1972) and Reference AssurAssur ([1974]).

However, in laboratory and field tests it was observed by Reference RoseE. Rose (1947), Reference Kheysin and YeKheysin (1961), Reference Afanas'yev, Afanas'yev, Yu., Dolgopolov and ShvayshteynAfanas'yev and others (1971) and Reference Nevel, Nevel, Perham and HogueNevel and others (1972), that for relatively thin ice plates (compared to the width of contact of plate and structure) the ice cover failed by buckling in the vicinity of the contact area.

The published analyses of ice forces on isolated structures which are based on the buckling failure mechanism, are not conclusive, however. The purpose of the present paper is first to review these few attempts and then to develop an improved method of analysis for the determination of the largest force that a relatively thin ice cover may exert on an isolated structure. The proposed analysis is based on the buckling mechanism of the floating ice plate.

2. Review of relevant analyses and tests

An early attempt to determine analytically the buckling force for an ice plate was presented by Reference AlbengaAlbenga (1921). However, because Albenga neglected the effect of the liquid base, the obtained results do not apply to floating ice covers.

On the basis of observations in the field, Reference RoseRose (1947, p. 883) stated that "arching and buckling of an ice sheet does occur but that there is a limiting thickness of about 1 foot [0.3 m] beyond which buckling will rarely occur". He also claimed (p. 880) that "for ice sheets less than 1 foot [0.3 m] thick the critical buckling load is the limiting factor governing the ice pressure on a dam, whereas for very thick ice sheets (about 2 feet [0.6 m] or more) the crushing strength pressure" is the limiting factor. No analysis was given for the determination of the buckling load.

Reference Shadrin and PanfilovShadrin and Panfilov (1962) presented an analysis for the semi-infinite ice cover whose straight edge is pressing against a rigid wall, as shown in Figures 1(a) or 2. The authors assumed that the type of ice cover failure depends on the thickness of the ice cover; namely, buckling for thin covers and local crushing at the contact area for thick covers. This assumption is in agreement with the observations made by Reference RoseRose (1947), as described above.

Shadrin and Panfilov expressed the failure load (per unit length) as

(3)

where σ_cf is a "compression strength" and h is the thickness of the ice cover.

For relatively thin covers the buckling load was determined from the differential equation

(4)

and the boundary conditions

(5)

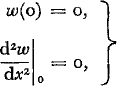
where w(x) is the vertical deflection at x and at any value − ∞ < y < ∞, D = Eh ³/[12(1 —v ²)] is the flexural rigidity of the cover, and γ is the specific weight of the liquid base. The solution of the above formulation yields

(6)

It should be noted that the above expression for p _b is also valid when the boundary at x = o is clamped (Reference HetényiHetényi, 1946, ch. 7), as may often be the case in the field.

Next, Equations (3) and (6) are compared by noting that according to tests, if the corresponding p _b < p _f ice cover fails by buckling and if p _f < p _b ice cover fails by crushing. Substituting Equations (3) and (6) in the first inequality, it follows that the ice cover will fail by buckling when

(7)

As an example, if v = 0.34, γ = 0.001 kg/cm³, E = 40 000 kg/cm², and σ _cf = 20 kg/cm² then according to %%Equation (7) the ice cover will buckle when h < 27 cm ≈ 10.5 inches. This result agrees reasonably well with the field observations reported by Reference RoseRose (1947).

According to the above analysis when Inequality (7) is satisfied, the largest force that the ice cover may exert on the long rigid structure is the buckling load ; otherwise the largest force is .

Next we review the calculation of the largest force an ice cover exerts on a ship hull, presented by Reference Kheysin and YeKheysin (1961); a problem closely related to the determination of ice forces on isolated structures. Kheysin reduced this problem to the determination of a uniform pressure p at which a floating elastic semi-infinite plate, shown in Figure 3, will fail. He based his analysis on observations in the field that ice cover failures often occur in two stages: the formation of cracks which emanate from the points 1 and 2, followed by the buckling of the inner part of the ice cover which is formed by these cracks.

Fig. 3 Ice pressing against a wall of limited length.

For his analysis Kheysin assumed that the cracks are initiated by the largest shear stress along the edge

(8)

Choosing for the "shear strength" of the (sea-)ice cover σ _sf = 30 Mg/m², and using the equation

(9)

as a crack criterion, he obtained from Equation (8) the pressure intensity which causes the formation of the cracks as

(10)

To simplify the buckling analysis, Kheysin assumed that the two cracks which emanate from the points (0, ±b/2) are parallel to the x-axis, and that the formed ice strip buckles when

(11)

Assuming v = 0.36, γ = 1 Mg/m³, and E = 40 000 Mg/m², the above equation reduces to

(12)

Comparing Equations (10) and (12), Kheysin found that for 0 < h < 2.2 m,^* which is the range of practical interest, the inequality

(13)

holds (although, according to Kheysin p _sf < p _b, where p _b is the buckling load of the un-cracked, semi-infinite plate). Based on observations that an ice cover cracks prior to its destruction, Reference Kheysin and YeKheysin (1961) concluded that the largest ice force is given by p _sf, namely Equation (10). According to the above analysis, after the plate cracks, buckling takes place immediately, since p _b bend < p _sf.

The above method is based on a number of questionable assumptions. Namely, that Equation (9) is a valid criterion, that the cracks are parallel and normal to the free edge, etc. It should also be noted that p _b given in Equation (11) is the critical buckling pressure when the edge is free to rotate and displace vertically, which is usually not the case when the ice cover is in contact with a fixed vertical structure or the hull of a ship. Other shortcomings of

Note that in the previous example (Shadrin and Panfilov, 1962) E = 400 000 Mg/m² was used. For this value of E the corresponding interval is 0 < h < 0.23 m.

Equation (11) are that the ice strip formed in the field is not of constant width and is constrained along the entire length of the formed edges by the surrounding ice cover. Also, according to Reference Nevel, Nevel, Perham and HogueNevel and others (1972), who conducted many closely related tests, the formation of radial cracks is not followed immediately by ice cover failure. Therefore, the results obtained by Kheysin, which are also reproduced in the book by Ya. N. Reference Popov, Yu, Popov, Fadeyev, Kheysin and YakovlevPopov and others (1967, p. 60–62) should be used with caution.

Reference Afanas'yev, Afanas'yev, Yu., Dolgopolov and ShvayshteynAfanas'yev and others (1971) published results of an extensive laboratory test program in which a number of thin floating ice plates (2.6 cm ⩽ h ⩽ 3.4 cm) were subjected to a horizontal force, by pressing a circular or a rectangular model pier against the free edge of the plate. According to these results, when b/h > 4 and the ice cover was not made more rigid by the proximity of the basin walls or the presence of simulated ridges, the ice plate failed by buckling. During these tests it was observed (p. 64) that at a certain intensity of the load, radial cracks formed in the plate. At a further increase of the load, the ice plate lifted along a nearly circular curve at a distance of about 14h from the pier. This was followed by a breakdown of the ice field.

Reference Afanas'yev, Afanas'yev, Yu., Dolgopolov and ShvayshteynAfanas'yev and others (1971) then presented an analysis for the semi-infinite ice plate pressing uniformly against a rigid wall, which is similar to the one given by Reference Shadrin and PanfilovShadrin and Panfilov (1962) and discussed previously. The obtained results are also similar, namely, that for fresh-water ice the ice cover buckles when h < 30 cm and for salt-water ice when h < 20 cm. Thus, for cases for which these inequalities are satisfied, the buckling load is the largest force the ice cover can exert against the wall.

Reference Nevel, Nevel, Perham and HogueNevel and others (1972) presented results of extensive ice force tests conducted at CRREL. The test set-up was similar to the one described by Reference Afanas'yev, Afanas'yev, Yu., Dolgopolov and ShvayshteynAfanas'yev and others (1971), except that the used basin (6.3 m × 6.3 m) and the thickness of the tested plates (6.5 cm ⩽ h ⩽ 22.4 cm) were larger in size. The description of the test results is also more complete. The test results with rectangular piers showed that for an average ice temperature of −4.3°C and h ≈ 12 cm, the ice plate failed in buckling for b/h > 2. For circular piers, instead of the b-value, the pier diameter D was used. From the presented test results it follows that for cold ice (−4.0°C) the ice plate buckled for D/h > 4.85 whereas for warmer ice (−2.7°C) buckling occurred for larger D/h ratios, namely D/h > 8.2. In some of these tests, it was observed that, as the load increased, cracks occurred as indicated in Figure 4. For rectangular piles (Fig. 4(a)) the cracks formed a funnel-shaped plate which buckled in the wider part.

Fig. 4 Form of cracking observed when an ice cover presses against a pier: (a) rectangular pier (left), (b) circular pier (right).

According to the above test results by Reference Afanas'yev, Afanas'yev, Yu., Dolgopolov and ShvayshteynAfanas'yev and others (1971) and Reference Nevel, Nevel, Perham and HogueNevel and others (1972), for rectangular piers a thin ice plate may fail in buckling for b/h > 2, and for circular piers for D/h > 5, ranges of practical interest. Thus, for a variety of isolated structures and relatively thin ice covers, the largest ice forces appear to be related to the buckling load of the ice cover and not to the local "crushing strength".

The results of the reviewed analyses for the determination of the largest force an ice cover may exert on a long vertical wall (for example a long dam), presented by Reference Shadrin and PanfilovShadrin and Panfilov (1962) and Reference Afanas'yev, Afanas'yev, Yu., Dolgopolov and ShvayshteynAfanas'yev and others (1971), are in agreement with observations in the field, regarding occurrence of buckling failures. Therefore, it is reasonable to expect that if the material parameters are chosen properly, the largest ice force for problems of this type can be estimated using these analyses, namely, Equations (4) and (7).

For the determination of the largest ice forces on isolated structures based on the buckling failure mode, only the analysis of Reference Kheysin and YeKheysin (1961) seems to be available. As shown above, this analysis is based on questionable assumptions. According to Kheysin, the failure load is the load at which the plate cracks, since buckling takes place immediately after the cracks form, which is not substantiated by the observations described by Reference Afanas'yev, Afanas'yev, Yu., Dolgopolov and ShvayshteynAfanas'yev and others (1971) and by Reference Nevel, Nevel, Perham and HogueNevel and others (1972).

The above findings suggest the need for an improved analysis for the determination of the largest forces an ice cover exerts on isolated structures, based on the buckling failure mechanism. Such an analysis is presented in the following section.

1. Determination of the largest ice force on an isolated structure

The buckling analysis of a floating wedge

Consider a floating truncated wedge, as shown in Figure 5. It is assumed that the buckling load P _b may be determined approximately from the eigenvalue problem consisting of the differential equation

(14)

the boundary conditions at the contact area

(15)

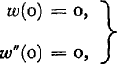
or

(16)

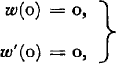
and regularity conditions at x = ∞. In the above formulation, w(x) is a vertical perturbation of the wedge axis at x. Furthermore

(17)

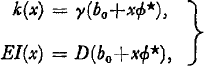
where

(18)

and γ is the specific weight of the liquid base. The term (1 − v ²) was inserted in the denominator of EI(x) to account for plate action, as done by Reference Papkovich and YekimovPapkovich (1962, p. 424–26) in connection with a related problem and discussed by Reference KerrKerr (1976).

Fig. 5 Geometry of a floating wedge with a force P tending to buckle it.

Substituting Equations (17) into Equation (14) we obtain

(19)

a fourth-order equation with variable coefficients. For ϕ ^★ = o (i.e. for ϕ = o) and with b ₀ = 1 the above equation reduces to the equation with constant coefficients used by Reference Kheysin and YeKheysin (1961).

Because of the nature of the variable coefficients, no exact closed-form solution is available. A numerical solution can be easily obtained using, for example, a finite-difference scheme, since the buckling mode is restricted to the vicinity of the contact region at x = o. However, the solution obtained will be valid only for the set of parameters assumed.

For the method to determine P _max proposed in the following, an analytical expression which shows the dependence of the buckling load P _b on the various geometrical and material parameters of the floating ice wedge and the width of the structure, is more suitable. Noting that the representation of the buckling of a cracked ice cover by the buckling of a floating wedge is, at best, an approximation, it appears sufficient to solve the wedge formulation approximately. In the following such an analytical solution is obtained first using the Stodola–Vianello method (Reference HildebrandHildebrand, 1962, p. 200).

For this purpose Equation (19) is rewritten as

(20)

where

(21)

Assuming for w ₁ the expression

(22)

and substituting it into Equation (20), we obtain a non-homogeneous ordinary differential equation with constant coefficients for w(x). Its solution, which satisfies the boundary conditions of a simply supported edge, Equations (15), is

(23)

where

(24)

The first eigenvalue is obtained by substituting Equations (24) into the condition (Reference HildebrandHildebrand, 1963, p. 216, equation 129)

(25)

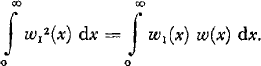
Performing the necessary integrations and noting that λ ² = P/(Db ₀), we obtain the approximate buckling load

(26)

If instead of the boundary conditions for a simply supported end the ones for a clamped end at x = 0 are used, the above procedure yields

(27)

Note, that in both cases the respective P _b expression consists of a sum of two terms:

each multiplied by a constant coefficient. Thus, for the P _b expressions obtained, the different boundary conditions at x = 0 affect only these coefficients.

To check if the above two terms are representative of the buckling solution for the compressed wedge, the wedge problem is next solved again using the energy method.

With the notation used above, the second variation of the total potential energy for the wedge problem shown in Figure 5, is

(28)

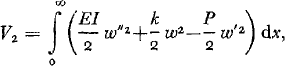
where EI and k are given in Reference AssurEquations (17). Assuming

(29)

as an approximate shape function, substituting it into V ₂, and performing the necessary integrations, we obtain

(30)

If β is chosen a priori as

(31)

the value which corresponds to the compressed semi-infinite plate, it follows that V ₂ = V ₂(A).

The condition δV ₂ = 0 then reduces to

(32)

The above equation yields

(33)

and thus

(34)

Noting that γ/(12D _k ′⁴) = 1/12 and , the expression for P _b reduces to

(35)

If β is not fixed a priori, then V ₂ = V ₂(A, β). The condition δV ₂ = 0 then reduces to

(36)

The first equation is identical to Equation (32) and yields Equation (34) with κ′ = β Namely,

(37)

The second equation in (36) yields, after eliminating P _b by using Equation (37),

(38)

This is the equation for the determination of β which appears in Equation (37).

Comparing Equation (35) with Equations (24) and (26) it follows that it is of the same functional form as these two equations except for the constant coefficients.

In order to compare the approximate expressions obtained for the buckling load P _b with each other, they were evaluated for E = 30 000 kg cm², v = 0.34, γ = 0.001 kg/cm-, b ₀ = 20 cm, and h = 10 cm. The results are shown in Figure 6.

Fig. 6 Critical buckling loads for a floating wedge. . The numbers by each curve indicate equation numbers in the paper.

Note that this equation may be obtained directly from the condition ∂P _b/∂β = o.

Proposed method to determine P_max

When an actual ice cover presses against a bridge pier or the leg of a drilling platform, the boundary conditions at the contact area between ice and structure will fluctuate, depending on a number of factors. Also, the value ϕ is usually not a measurable entity since according to test observations, at the onset of buckling, the ice cover exhibits many radial (and some non-radial) cracks.

It is therefore proposed to express the largest force an ice cover exerts on an isolated structure (when buckling dominates) by the expression

(39)

where according to Equations (18) and (21),

and n′ and m′ are parameters to be determined from field tests.

Since the effective values of E and v will depend upon the nature of the pre-cracked plate, the term E/[12(1−v ²)] = E ^★ should be determined from the same test data. Thus, the proposed expression for P _max is

(40)

where γ is the specific weight of the liquid base, h is the ice-cover thickness, and b ₀ is the width of pier. The parameters m, n, and E ^★ are to be determined from appropriate test results.

It is anticipated that m, n, and E ^★ will vary for different categories of problems and different ice temperatures (in particular in the vicinity of the melting temperature). This point, as well as the validity of Equation (40) to represent P _max (when the buckling failure mode predominates), can only be established by comparing it with the relevant results of laboratory and field tests.