In a recent paper in the Journal, Reference Thorsteinsson, Raymond, Gudmundsson, Bind-schadler, Vornberger and JoughinThorsteinsson and others (2003) presented an interesting method for obtaining information about basal conditions under ice streams from surface data by means of an inverse model. The discussion below applies as much to the forward theory on which their method is built, and which is presented in detail in Reference GudmundssonGudmundsson (2003), as to the inversion carried out by Thorsteinsson and others. Nevertheless, it is best addressed to the paper by Thorsteinsson and others as it extends the validity and applicability of their results.

Our aim is to address the apparent limitation of Gudmunds- son’s model to a particular sliding law of linear Weertman type. Although sliding laws of this type have a long pedigree in glaciology, more recent work has indicated that Coulomb- type friction laws may be more appropriate descriptions of ice-stream motion, and these have also found their way into the inversion of ice surface data (e.g. Reference Joughin, MacAyeal and TulaczykJoughin and others, 2004). Incidentally, the model which we propose also has the advantage that it is not formally based on a perturbation expansion which assumes small variations in stress and velocity about mean fields describing the laminar flow of a parallel-sided ice slab (as is the case for Gudmundsson’s theory); in fact, our method naturally allows for O(1) variations in the stress field compared with driving stress.

Let us first consider the question of a sliding law. Friction at the bed of an ice stream can arise either from ice-sediment interactions (e.g. Reference Tulaczyk, Mickelson and AttigTulaczyk, 1999) or from combined creep flow and regelation around bed obstacles (e.g. Reference NyeNye, 1969). In either case, there may be small-scale variations in drag at a local scale determined by clast size or the wavelength of bed obstacles. Provided this local length scale is small compared with the ice thickness, it is in principle possible to average locally over these variations and to obtain a sliding law which relates the shear stress experienced at a ‘smoothed bed’ by the bulk flow of the ice stream to other global variables such as sliding velocity, spatially averaged water pressure or normal stress. The relevant mathematical method, which separates the ice flow into a bulk flow occupying most of the thickness of the ice and a thin boundary layer near the bed, is outlined by Reference FowlerFowler (1981). We emphasize that this method is not contingent on the particular sliding physics considered by Fowler, but can in theory be applied to any small-scale ice-bed interactions. The result of this averaging procedure, and hence the resulting sliding law, naturally depends on the precise physics of the ice-bed interactions and, consequently, one generally does not know the precise functional form of the sliding law. Below, we will assume only a general functional relationship of the type τ_b = τ_b(x, u _b, o _nn) where τ_b is the shear stress experienced by the bulk flow of the ice stream at the smoothed bed and u _b is the bed-parallel sliding velocity of the bulk flow (both taken in the sense of Reference FowlerFowler, 1981), while o _nn is compressive normal stress at the bed and x denotes position along the bed. The rationale behind choosing this functional form is that hard-bed sliding theories (e.g. Reference NyeNye, 1969; Reference FowlerFowler, 1981) naturally lead to basal shear stress τ_b increasing with sliding velocity u _b, while studies of ice flow over deformable beds (Reference Tulaczyk, Mickelson and AttigTulaczyk, 1999) – or hard beds in the presence of subglacial cavities (Reference SchoofSchoof, 2004) – predict that basal shear stress should depend only weakly (if at all) on sliding velocity, while depending strongly on effective pressure, which we may take to be the difference between compressive normal stress o _nn and basal water pressure. An explicit dependence on position x is included in the sliding law to account for variations in bed roughness or basal water pressures over distances comparable with ice thickness, which cannot be averaged out by Reference FowlerFowler’s (1981) local smoothing. Indeed, the very aim of Reference Thorsteinsson, Raymond, Gudmundsson, Bind-schadler, Vornberger and JoughinThorsteinsson and others (2003) is to study spatial variations in basal properties, which we include through this explicit dependence on x.

Gudmundsson’s theory relies on a particular form of the sliding law considered above, namely

(1)

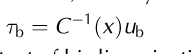
with C > 0. In the context of his linearization of the ice-flow problem, the use of this sliding law can be justified as a linearization of a more general sliding law τ_b = τ_b(x, u _b) in which basal drag is independent of normal stress (otherwise we would require an additional term in Equation (1) describing this dependence), and a strictly increasing function of sliding velocity; for a non-linear sliding law this linearization then requires small changes in sliding velocity. However, as pointed out above, such a sliding law may not be appropriate for ice streams, or even for hard-bedded glaciers when subglacial cavitation is widespread (Reference SchoofSchoof, 2004). An alternative approach to ice-stream flow with variations in basal properties over the kilometre scale, which avoids the need to linearize a sliding law inherent in Gudmundsson’s work, is the multiple-scales expansion technique developed in Reference SchoofSchoof (2002). Rather than arbitrarily introducing small perturbations to a mean flow field, this technique exploits some of the small parameters inherent in ice-stream flow, namely mean slip ratio and mean surface slope (just as the shallow-ice approximation exploits the small aspect ratio of ice sheets; see Reference Morland and JohnsonMorland and Johnson, 1980).

It is not our intention to reproduce a formal derivation of our model here, which closely follows Reference SchoofSchoof (2002). Instead, we motivate our model equations physically, although they could be derived using the same formalism as Reference SchoofSchoof (2002), but with a different choice of scales. Our model assumes that stress variations in the ice, induced by variations in basal stickiness represented by the x-dependence of τ_b(x, u _b, o _nn), and by flow over sufficiently shallow undulations in the bed, are comparable with the driving stress, and that sliding is rapid (it can be shown from these assumptions that the form drag caused by these bed undulations is a small correction in the ice stream’s force balance, which is where our theory departs from that of Reference SchoofSchoof (2002)). We restrict ourselves to ice of constant viscosity p, and to ice flow in two dimensions (x, z) with the z axis pointing vertically up and i denoting the unit vector in the x direction. We also consider only what happens on Reference SchoofSchoof’s (2002) ‘inner’ length scale associated with ice thickness, whilst ignoring the evolution of the ice stream as a whole (which is associated with a much longer time-scale than that relevant below). Denoting variations in velocity about the regional plug-flow velocity U i of the ice stream by u = (u,w) and pressure variations about a mean cryostatic pressure field by p, then u and p satisfy the Stokes equations. At leading order,

(2)

where the forcing term f =—pg D_x — ∂T _YY /∂Y, ρ is ice density, g gravity, D_X a regionally averaged surface slope as in Reference SchoofSchoof (2002), and ∂T_YY/∂Y is the contribution of lateral shearing on the outer length scale to force balance (e.g. Reference RaymondRaymond, 1996), with T_YY being lateral shear stress and γa transverse out coordinate. In order for stress variations to scale with driving stress, bed bumps must be shallow, as the vertical velocity variations introduced by flow over these bumps must scale with the shearing component of ice velocity, which is by assumption small compared with the plug-flow velocity U. As a result of this shallowness, we can linearize the geometry of the ice flow (but not the sliding law), and consider a domain 0 < z < D, where z = 0 denotes the mean (i.e. regionally averaged) bed elevation, and z = D the mean surface elevation, which is independent of the (inner) coordinate x (see Fig. 1). The effect of bed bumps of height h(x) on ice flow, and friction at the bed, can then be written as the boundary conditions

Fig. 1. Geometry of the ice flow problem.

(3)

The first of these conditions states that the friction experienced by the ice stream (when averaged over subkilometre-scale variations as described above) is given by the sliding law, in which the sliding velocity argument is simply taken as the plug velocity U, as velocity variations about this plug flow must remain small. Meanwhile, the normal stress argument is σ _nn = ρgD + p— 2p∂w/∂z evaluated at z = 0. The second boundary condition simply states that ice does not penetrate into the bed. At the upper surface z = D, we have no friction, while the excess cryostatic pressure caused by surface undulations (denoted by d(x);see Fig. 1) compensates for non-zero deviatoric normal stresses near the ice surface, so

(4)

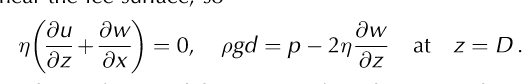
Lastly, surface undulations satisfy a kinematic boundary condition, at leading order of the form

(5)

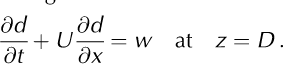
If we were to attempt a solution of the forward model, we would need to specify the exact form of the sliding law. However, the purpose of this note is to elucidate what happens in the inverse model. From the formulation above, it is evident that steady-state surface profiles d on the inner scale depend linearly on basal topography h (as is also the case in Gumdundsson's and Thorsteinsson and others' theories). Importantly, d also depends linearly on basal shear stress t b regardless of which particular functional form the sliding law takes, and this is where our theory differs from that used in Thorsteinsson and others (2004). We see that the introduction of the ‘slipperiness parameter’ C considered by Reference GudmundssonGudmundsson (2003) and Reference Thorsteinsson, Raymond, Gudmundsson, Bind-schadler, Vornberger and JoughinThorsteinsson and others (2003) is an unnecessary complication, and in any case, the linear dependence on perturbations in C is recovered only if we put T _b(x, u _b, σ_nn) = U/(C + AC(x)) and linearize on the basis that AC is small compared with C, so T _b(x) ~ U/C — (U/C²)AC(x). As pointed out before, this does require the use of a particular linear sliding law which may not hold in practice. The advantage of the approach advocated here is that no specific assumptions regarding basal sliding processes need to be made beyond the possibility of parameterizing them in the form of a sliding law T _b = T _b(x, U, g _nn), and that the inversion of surface data can be used to infer directly variations in basal shear stress. Consequently, it may make more sense to interpret Thorsteinsson and others' results for -DC as being a direct measure of variations in basal shear stress.

One further point remains to be made: once stress perturbations are similar to the driving stress, the use of a fully linear model is likely to fail in practice because of the non-linear rheology of ice. Thorsteinsson and others' use of a ‘stratified’ viscosity, which decreases with depth in the ice but is independent of strain rate, can mimic the effect of a non-linear rheology only if stress field variations in the ice are small compared with driving stress, and a non-linear forward model must be used for larger stress variations. In our framework above, this could be achieved by changing the Stokes Equations (2) to describe a non-linear stress- strain-rate relation, and by allowing v in the boundary conditions (3) and (4) to depend on strain rate in accordance with that non-linear rheology.