Introduction
Many models of ice-sheet and glacier evolution base their predictions on dynamical response to perturbations in the ice shelf or ice tongue, and the grounding line for marine outlet systems, as well as the surface mass balance driven by climatic forcing. Field-based studies have established that glacier and ice-sheet surface velocities can demonstrate a dynamic response to rising air temperature when surface- derived meltwater reaches the ice/bed interface, causing high subglacial water pressures, lubricating the glacier bed and promoting enhanced basal motion (Reference Iken and BindschadlerIken and Bind- schadler, 1986;Reference Zwally, Abdalati, Herring, Larson, Saba and SteffenZwally and others, 2002;Reference Bingham, Nienow and SharpBingham and others, 2003;Reference Shepherd, Hubbard, Nienow, McMillan and JoughinShepherd and others, 2009;Reference Bartholomew, Nienow, Mair, Hubbard, King and SoleBartholomew and others, 2010). There exists ongoing debate about the longterm significance of this effect on dynamic thinning and mass loss of glaciers and ice sheets, particularly in relation to the Greenland ice sheet (Reference Parizek and AlleyParizek and Alley, 2004;Reference Van de WalVan de Wal and others, 2008;Reference Sundal, Shepherd, Nienow, Hanna, Palmer and HuybrechtsSundal and others, 2011;Reference BartholomewBartholomew and others, 2012). Resolution of this issue requires more comprehensive temporal and spatial measurements of the association between melt and velocity, from which more empirically robust physical relationships can be derived for use in ice-sheet models that couple hydrology and dynamics. Both drainage of ponded meltwater (Reference DasDas and others, 2008) and the direct influx of meltwater in supraglacial streams into surface crevasses or moulins are likely sources for dynamic forcing in response to supraglacial meltwater inputs. Existing coupled models of glacial hydrology and dynamics prescribe rather than predict the location of connections between the supraglacial and subglacial systems (Reference Flowers and ClarkeFlowers and Clarke, 2002; Reference Pimentel, Flowers and SchoofPimentel and others, 2010). Representation of the dynamic response to surficially derived meltwater accessing the ice/bed interface is a mechanism which thus remains without physical basis in these models. To assess the long-term significance of this mechanism for ice-sheet mass evolution in a changing climate, it is necessary to model the temporal and spatial patterns of meltwater delivery to the ice/bed interface.
This study presents a spatially distributed model that predicts the spatial and temporal patterns of surface-derived meltwater delivery to the bed of a glacial catchment. The model structure is represented in Figure 1. Each stage of the modelling routine is explained in the context of the case- study site to which we apply it, the Croker Bay catchment area of Devon Ice Cap, Canada. Total summer surface ablation is modelled across the study catchment, in this case using a simple degree-day model, and daily distributed values of melt are subsequently used to weight meltwater flow accumulation across the ice surface. Areas of surface crevassing are identified where tensile resistive stresses, calculated from strain rates derived from interferometric synthetic aperture radar (InSAR) velocity data, exceed a threshold value of tensile strength (Fig. 1a). Following the principles of linear elastic fracture mechanics (LEFM), a model of water-driven fracture propagation for calculation of crevasse depths (Reference Van der VeenVan der Veen, 2007) is used to identify where and when surface-to-bed connections form (Fig. 1 and b). The transfer of surface-generated meltwater to the bed through full ice-thickness crevasses and drainage of supraglacial lakes through basal fractures are modelled (Fig. 1c).

Fig. 1. Model structure from data inputs to (a) surface processes, (b) fracture depth calculation and (c) outputs.
Study Area
Devon Island is one of the Queen Elizabeth Islands in Nunavut, High Arctic Canada. Devon Ice Cap at ~14 000km2 is one of the largest ice caps in the Arctic and has been the focus of extensive glacial research for nearly 50 years (Reference Boon, Burgess, Koerner and SharpBoon and others, 2010). This study investigates the southwest region of the ice cap, specifically the Croker Bay catchment (Fig. 2), which feeds North (NCB) and South Croker Bay (SCB) glaciers. This region was chosen due to the availability of data necessary for our model. The ice surface elevation in this catchment extends from the marine calving termini of NCB and SCB glaciers up to 1853 m, approaching the ice-cap summit at ~1930m. Distinct dynamic-flow regimes across the ice cap were identified from InSAR velocity data by Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others (2005). The first flow regime, regime 1, found in the upper reaches above outlet glaciers, was representative of flow through internal deformation where ice is likely frozen to the bed. Outlet glaciers, including NCB and SCB glaciers, were characterized by a transition from flow regime 2, indicative of a contribution to the surface velocity by basal motion, possibly promoted by constraining bedrock topography, to flow regime 3, characterized by a significantly increased contribution from basal motion, possibly enhanced by meltwater reaching the bed (Figs 2 and 3). This transition was particularly clear at NCB glacier where velocity increased from 60 m a-1 to 170 m a-1 along 1km of the flowline. The study noted that supraglacial meltwater streams terminating in crevasse fields on 1960s aerial photography were coincident with this area of flow regime transition (Fig. 3). The development of strong surface flow stripes has also been observed in this area. Both of these surface features provide evidence that the delivery of supraglacial meltwater to the glacier bed may have a direct effect on ice velocities in these catchments. A final flow regime, regime 4, was defined, largely in the terminal reaches of glaciers, characterized by low basal friction possibly indicative of deforming subglacial sediments.

Fig. 2. Devon Ice Cap ice surface elevation depicting the Croker catchment area and meteorological transect. Coordinates reference to Universal Transverse Mercator (UTM) zone 17° N. The insert shows the area of transition to an enhanced basal sliding flow regime, after Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others (2005).

Fig. 3. True downslope ice surface velocities, digitized supraglacial lakes and flow regimes for the Croker catchment (Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others, 2005). Flow regimes are 1. internal deformation; 2. contribution from basal motion; 3. enhanced basal motion; and 4. low basal friction. Aerial photo insert shows lake locations and streams disappearing into crevasses.
Methods
Melt modeling
To quantify total ice surface melt, a degree-day model is run using measured daily-averaged temperatures. A degree-day modelling approach was chosen for its simplicity and to accommodate the meteorological data available. Daily values of melt, M t, are determined by applying a degree- day factor (DDF) for all days when the mean temperature, Tt , is equal to or exceeds 0°C:
Total ablation, A, occurring over a period of N days is therefore given by the sum of daily melt values:
Melt is calculated cumulatively within the model for each day, allowing a DDF for snow (DDFs) to be applied initially, and a DDF for ice (DDFi) to be applied when cumulative melt exceeds the initial prescribed spring snowpack depth, plus any precipitation falling as snow. DDFs for snow and ice of 4 and 8mmw.e. d-1 °C respectively were applied for the standard model runs. These values are representative of typical DDFs for sites at high northerly latitudes as described by Reference HockHock (2003). No clear relationship was established between accumulation and elevation at this site to justify the application of a precipitation lapse rate (Reference BellBell and others, 2008), so the snowpack depth is set constant across the glacial catchment based on average snow depths in 2004 and 2006 respectively, measured along the meteorological transect (Fig. 2). The degree-day model is applied spatially across the Croker Bay catchment, with daily mean temperature adjusted for ice surface elevation using an air-temperature lapse rate of 0.0053°C m. This lapse rate was calculated from the means of air temperatures measured at 10 min intervals between days of year 136 and 235 in 2004 (Fig. 4), at 11 sites extending from near the ice-cap summit down to 478m elevation (Reference BellBell and others, 2008) along the transect shown in Figure 2.

Fig. 4. Air temperature lapse rate calculated along meteorological transect.
Meltwater routing and lake filling
The meltwater generated from degree-day modelling is subsequently used to weight flow accumulation across the catchment based on a single flow-direction algorithm (Reference Schwanghart and KuhnSchwanghart and Kuhn, 2010). We opted to distribute generated supraglacial meltwater across the ice surface by flow accumulation only, rather than by defining a threshold for supraglacial stream formation. This is due to the spatial resolution at which we run the model (500 m), the resolution of the ice surface DEM (Reference Dowdeswell, Benham, Gorman, Burgess and SharpDowdeswell and others, 2004) which was interpolated to 1 km gridcell sizes from a grid of transects flown 5-10 km apart, and also the error associated with defining stream formation thresholds manually (Reference Matsunaga, Nakaya and SugaiMatsu-naga and others, 2009). The uncertainty in matching observed stream networks with DEM-derived networks is particularly pronounced for glacial catchments due to the dynamic nature of the ice surface topography under varying climatic conditions, and the often transient positions of supraglacial streams, especially for ice surfaces characterized by shallow gradients. This model simplification results in some overestimation of available meltwater, which may be a driver of over-prediction of full ice-thickness crevassing in areas of low ice thickness. Underestimation of downstream melt transfer in areas characterized by true supraglacial streams may also occur;however, the spatial resolution of the model poses restrictions on where streams could be successfully modelled in areas where ice topography has a surface roughness finer than this resolution. Furthermore, transit time through the snowpack is not accounted for using the current approach, so melt generated in each cell will be routed across the ice surface and reach crevasse cells within one daily model time-step.
Numerous sites of supraglacial meltwater ponding are visible on remotely sensed imagery, and drainage of these meltwater lakes into the englacial system is seen within the results of ground-penetrating radar (Burgess, unpublished data). The flow-routing component was therefore modified to additionally account for filling of supraglacial lakes. Meltwater routed into a cell containing a lake, digitized from Landsat imagery (Fig. 3), will accumulate within that cell until the lake reaches its prescribed maximum volume, after which the lake will overtop and contribute to meltwater runoff downstream. Lake volume is determined based on a linear relationship with maximum observed lake surface area, calculated from satellite imagery-derived supraglacial melt lake dimensions for selected outburst events presented in Table 6 of Reference Box and SkiBox and Ski (2007).
Calculation of tensile stress from InSAR-derived velocity data
InSAR collected by the European Remote-sensing Satellites ERS-1 and -2 provided look-direction ice surface velocities for 98% of Devon Ice Cap, calculated from the pattern of interference created by the surface displacement between repeat-pass radar image acquisitions (Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others, 2005). Images used to derive velocities for the western region of the ice cap (Fig. 3) were obtained on 25 and 26 April 1996. These line-of-sight velocity values were used by Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others (2005) to determine true downslope velocities. The resultant data were resolved into ‘x’ (south to north) and ‘y’ (west to east) velocity components. Strain rates, ![]() were calculated as directional derivatives of the velocity data,
were calculated as directional derivatives of the velocity data, ![]() The constitutive relation for glacier ice, after Reference NyeNye (1957), is applied to convert each strain rate to a stress, σ
ij
.
The constitutive relation for glacier ice, after Reference NyeNye (1957), is applied to convert each strain rate to a stress, σ
ij
.
Here ![]() is the effective strain, and the flow law exponent, n, is 3. B is a viscosity parameter sensitive to ice temperature, such that B, and thus the ‘stiffness’ of the ice, will increase as temperature decreases. This parameter is related to the flow law as B = A
-1/n (Reference Vieli, Payne, Du and ShepherdVieli and others, 2006). For the Croker glaciers, an ice temperature of −13°C is assigned, based upon average winter sea-level temperatures at NCB and ice temperatures of −12.1 to −14.7°C recorded for White Glacier, Axel Heiberg Island (Reference VaughanVaughan, 1993). This gives a flow-law parameter value, A, of ~3.5 × 10-16s-1 kPa-3 (Reference PatersonPaterson, 1994) and a derived B value of 445 kPaa1/3.
is the effective strain, and the flow law exponent, n, is 3. B is a viscosity parameter sensitive to ice temperature, such that B, and thus the ‘stiffness’ of the ice, will increase as temperature decreases. This parameter is related to the flow law as B = A
-1/n (Reference Vieli, Payne, Du and ShepherdVieli and others, 2006). For the Croker glaciers, an ice temperature of −13°C is assigned, based upon average winter sea-level temperatures at NCB and ice temperatures of −12.1 to −14.7°C recorded for White Glacier, Axel Heiberg Island (Reference VaughanVaughan, 1993). This gives a flow-law parameter value, A, of ~3.5 × 10-16s-1 kPa-3 (Reference PatersonPaterson, 1994) and a derived B value of 445 kPaa1/3.
Surface tensile resistive stresses, Rij , are calculated using the von Mises criterion, σ v , for failure of ductile materials following Reference VaughanVaughan (1993):
Maximum and minimum, or ‘principal’, stresses, σ 1 and σ 3, are calculated from


where σ xx , σ yy and τ xy are the longitudinal, transverse and shear stresses respectively. The tensile stress may then be calculated from
The tensile stresses are subsequently used as input for fracture depth modelling, but also for determining the ratio of meltwater routed across the ice surface where runoff intersects a crevassed area. The value of tensile strength we apply, initially set at 300kPa, was determined by comparison of calculated surface tensile stresses with areas of surface crevassing visible on Landsat 7 panchromatic imagery of NCB and SCB glaciers from August 2000 (background image, Fig. 3). Where tensile stress exceeds the prescribed tensile strength, which is the maximum tensile stress that can be applied to a material before failure, the runoff ratio is set to zero, otherwise it equals 1. Thus upstream runoff is ‘captured’ by crevasses, and the flow accumulation of melt immediately downstream of a crevasse is reset to zero.
Crevasse depth modeling
To calculate penetration depths of individual water-filled crevasses, we apply the following model, based upon LEFM, after Reference Van der VeenVan der Veen (2007):
The three terms on the right describe stress intensity factors relating to the tensile stress, the lithostatic stress of the ice which would cause the crevasse to tend towards closure, and the effect of water-filling within the crevasse, respectively. Combined, these produce a net stress intensity factor, K l, describing the elastic stresses incident on the crevasse tip. We apply constant values of acceleration due to gravity, g, density of ice, ρi„ and density of fresh water, ρw . Surface tensile stress, Rxx , calculated as described above using the von Mises criterion, is used to calculate the first term in Eqn (9), and the water level in a crevasse, b, is determined from the meltwater accumulated in each cell having been routed across the ice surface each day. The propagation depth of a crevasse may be calculated by solving for depth, d, each day until K I is less than the prescribed ice fracture toughness, K lc. The fracture toughness of ice, or the critical stress at which a pre-existing flaw will propagate, was prescribed initially as 150kPam1/2. This was based on the average K IC of 145.7 kPa m1/2 calculated by Reference Fischer, Alley and EngelderFischer and others (1995) from modified ring testing of synthetic granular ice, and the zero-porosity K IC of 155kPam1/2 derived from crack-growth initiation experiments on Antarctic core ice by Reference RistRist and others (1999). The water level in the crevasse, b, is calculated using Q, the rate at which water fills a crevasse, and time, t, such that
Here we employ water-filling rates, Q, based on surface melt generated from measured temperature data to investigate crevasse penetration depths and meltwater delivery to the bed throughout two ablation seasons at a daily temporal resolution. The chosen seasons, 2004 and 2006, have distinct measured air-temperature records allowing model sensitivity to varying melt generation to be considered. In addition, we prescribe crevasse surface dimensions within the model, initially set at a depth-averaged width of 1 m and a length of 500 m for the standard model runs. The geometry of crevasses is a control on the level of the meltwater, b, in a crevasse, because accumulated daily surface meltwater is calculated as a depth of water equivalent generated across a 500 m × 500 m cell after the melt modelling and flow accumulation routines, but must be modified to converge into the prescribed surface area of a crevasse when applied to the fracture depth calculation. Figure 5 depicts a simple schematic of the model as described above.

Fig. 5. Water-filled crevasse penetration model. The supraglacial flow routing and accumulation method is depicted on the right, where numbers represent melt (mmw.e.) per unit area.
The modelling routine calculates crevasse penetration depths each day for cells within the Croker catchment where R xxequals or exceeds the prescribed tensile strength and thus surface crevassing can occur. We calculate crevasse depths for each daily time-step such that fracture propagation continues, and thus crevasse depth increases with time, in response to daily melt generation and inflow to the surface crevasse. The formation of moulins is predicted when calculated crevasse depths equal the ice thickness, which was measured across Devon Ice Cap by Reference Dowdeswell, Benham, Gorman, Burgess and SharpDowdeswell and others (2004) from airborne ice-penetrating radar. The ice thickness in itself is a control on moulin formation as more melt, or more time, is required to drive a crevasse through thicker ice. In addition, our model routine accounts for the drainage of supraglacial lakes through ice surface crevasses beneath lakes, which are assumed present beneath each lake included in the model. In contrast to modelling crevasse depths for lake-free cells, the model allows drainage of supraglacial lakes regardless of whether the tensile stress exceeds the prescribed ice tensile strength, due to the low tensile or even compressive surface stress regimes in which supraglacial lakes have been found to form (Reference Catania, Neumann and PriceCatania and others, 2008). In cells for which lakes have been identified from imagery, the accumulated melt content in each lake is used to calculate a depth of meltwater within a crevasse, b, as required by Eqn (9). This is achieved by converting the lake melt content in mmw.e. to crevasse water depth in mw.e., adjusted for crevasse width and length to produce the correct fill depth forgiven internal crevasse dimensions. When lake melt content reaches a level sufficient to drive a crevasse through the full ice thickness within one model time-step of 24 hours, solving Eqn (9) for K I ≥ K IC where d is set to equal the ice thickness, the lake will drain to the bed ‘instantaneously’ within that time-step. This allows for sub-daily rapid drainage of supraglacial lakes, as witnessed by Reference DasDas and others (2008). The meltwater delivered to the bed through both moulins and during lake drainage is quantified for each day in the model. The results that follow describe our investigation of moulin formation and lake drainage spatially and temporally for two melt seasons. We compare the percentage of surface-derived meltwater that is delivered to the subglacial system for the 2004 and 2006 ablation seasons, and evaluate the influence of crevasse width, ice fracture toughness, tensile strength and DDFs.
Results
Initial parameters: 2004 and 2006 ablation seasons
For the 2004 season run, we used a temperature series recorded at 478 m elevation for days of year 122−237 and prescribed a spring snowpack depth of 166mm w.e., which was an average of depths measured along the meteorological transect shown in Figure 2 (Reference BellBell and others, 2008). The temperature data series for 2006, recorded at 1414m elevation, spanned days of year 122−220 (Fig. 6), with an initial average spring snowpack of 155 mm w.e. By adjusting temperatures for sea level using the calculated lapse rate, we see that from mid-June onwards both the 2004 and 2006 data are typified by positive daily average temperatures (Fig. 6); the 2006 season, however, reaches a maximum temperature of 9.9°C compared to a 2004 maximum of 7.5°C. The 2006 season is significantly warmer during the period of positive degree-days spanning days of year 172−220 (late June to early August), as reflected by the respective mean temperatures for this period, of 3.8°C for 2004 and 5.8°C for 2006.

Fig. 6. Daily average air temperature at sea level for the Croker catchment.
The temporal formation of surface-to-bed connections predicted for the 2004 and 2006 model runs using initial standard run parameters is depicted in Figure 7. The data show that both moulin formation and drainage of lakes occurred at higher elevations and more quickly in 2006 in comparison to 2004 when less meltwater was generated to fill crevasses and lakes. The increased availability of meltwater also resulted in a higher frequency of drainage by lakes containing a larger melt volume during 2006.

Fig. 7. Temporal formation of surface-to-bed connections (initial parameters). Flow regime zones after Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others (2005).
Figure 8 shows the spatial coverage of surface-to-bed connections and illustrates that as well as forming at higher elevations, greater numbers of moulins (167 vs 137 in 2004; Table 1) and lake drainages are predicted for 2006, and they cover a much larger spatial extent than in 2004. The net result is that a slightly higher percentage of generated surface melt (97.8% vs 95.2%) reaches the glacier bed in 2006 vs 2004 (Table 2);however, the total volume of melt delivered to the bed increases significantly from 2.6 × 108 m3 in 2004 to 7.6 × 108 m3 in 2006.

Fig. 8. Spatial distribution of predicted surface-to-bed connection locations for (a) 2004 and (b) 2006. Photo inserts (Landsat) show examples of surface moulins and lake locations coincident with model predictions of surface-to-bed connections.
Table 1. Total number of surface-to-bed connections established during each model run

Table 2. Percentage of surface-generated meltwater delivered to the bed during each model run

Sensitivity testing
Degree-day factors
To investigate how sensitive the model is to an almost twofold increase in the DDF for ice, we applied DDFs of 14 mm w.e. d-1 °C for ice and 3.5 mm w.e. d-1 °C for snow to the 2004 and 2006 seasons, maintaining the initial values for the other input parameters. These DDFs were calculated by Reference Mair, Burgess and SharpMair and others (2005) as best-fit values for the southeast and southwest quadrants of Devon Ice Cap.
The results of altering the DDFs are shown in Figure 9. The data suggest that the lower DDF for snow applied by Reference Mair, Burgess and SharpMair and others (2005) results in a short temporal delay of 1-3 days to the formation of moulins. The total number of surface-to-bed connections decreases slightly by 1.2% in 2006 and by 2.2% in 2004. The larger decrease in 2004 is possibly due to the longer period for which the lower DDF for snow is applied during the colder season. There is also a very small decrease in transfer of meltwater to the bed in comparison to the initial parameter run for both years (Table 2). Applying the Reference Mair, Burgess and SharpMair and others (2005) DDF for ice resulted in a significant increase in the total melt generated during the melt season, of 37% for 2004 and 22% for 2006. Despite this, the delayed removal of the snowpack due to the lower DDF for snow caused a shift in the onset of the higher melt rate, the result of which is a limited impact on the number of surface-to-bed connections able to form. We conclude from these results that the model is not particularly sensitive to application of these DDFs, with only minimal impact on both moulin numbers and melt transfer to the bed, despite short delays in the initiation of surface-to-bed connections.

Fig. 9. Comparison of moulin formation for ice and snow DDFs of 8mmw.e. d–1 8C and 4mmw.e. d–1 °C (Reference HockHock, 2003), and 14mmw.e. d–1 °C and 3.5mmw.e. d–1 °C (Reference Mair, Burgess and SharpMair and others, 2005): (a) 2004, (b) 2006.
Ice fracture toughness
To investigate model sensitivity to the fracture toughness of ice, we ran the model for both years using a K IC value of 400kPam1/2. This is the upper limit applied to modelling surface crevasse penetration by Reference Van der VeenVan der Veen (1998) following the results of fracture toughness testing of Reference Fischer, Alley and EngelderFischer and others (1995) and Reference Rist, Sammonds, Murrell, Meredith, Oerter and DoakeRist and others (1996). Calculated crevasse depths were not significantly different for results of 150 and 400 kPa m1/2 KIC model runs. This was also noted by Reference Scott, Smith, Bingham and VaughanScott and others (2010) for crevasse-depth modelling applied to Pine Island Glacier, West Antarctica. Thus, applying a significantly higher fracture toughness value resulted in no change in either the number of moulins established, or the percentage of surface-generated melt transferred to the ice/bed interface (Tables 1 and 2).
Tensile strength
The value of tensile strength prescribed controls the spatial distribution of cells deemed to contain initial surface fractures, and thus those cells in which crevasse propagation can occur. Our initial estimation of tensile strength is 300 kPa. This value is just below the 320-400 kPa estimate for White Glacier, Axel Heiberg Island, Nunavut (Reference VaughanVaughan, 1993), which has a similar ice temperature (−12.1 to −14.7°C) to the −13°C assigned for the Croker catchment. From studies across a wide distribution of glaciers, Reference VaughanVaughan (1993) presents tensile strength values ranging from ~100 up to 400 kPa. We tested the sensitivity of our model within these upper and lower bounds by applying further tensile strength values of 100, 200 and 400 kPa.
From the spatial distribution of moulins predicted for 2004 by the model for these scenarios (Fig. 10), we see that the model is highly sensitive to tensile strength. Moulin locations predicted for a 100 kPa tensile strength far exceed the number of surface crevasses and lakes visible on remotely sensed imagery. Indeed, the total number of surface-to-bed connections predicted rises by 315.3% and 644.3% in 2004 and 2006 respectively (Table 1). The moulin numbers predicted from tensile strengths of 200 and 400 kPa differ less dramatically from the standard runs (Table 1), but the spatial extent of moulins predicted for the standard run, with a tensile strength of 300kPa, compares best with moulin distributions evident on remotely sensed imagery. While being an important control on the potential spatial distribution of fractures penetrating the full ice thickness, and indeed the overall spatial occurrence of surface crevassing (Table 1), this parameter does not significantly affect the timing of their formation at progressively higher elevations throughout the ablation season. It should be noted that tensile strength is also an important control on the transfer of surface-generated meltwater to the ice/bed interface (Table 2). There is a significant expansion of the area containing surface fractures in the 100 kPa run, which extends the area where surface meltwater can be captured by crevasses that do not penetrate to the bed, reducing the total melt reaching the bed, and thus increasing englacial storage in crevasses that have not propagated through the full ice thickness (Table 1).

Fig. 10. Spatial distribution of moulins in 2004 for tensile strength values of (a) 100, (b) 200, (c) 300 and (d) 400 kPa.
Crevasse width
The model was run for prescribed crevasse widths of 0.5, 1, 2 and 5 m, maintaining a 500 m length, to investigate model sensitivity to the meltwater head generated from different crevasse sizes. Locations of full thickness crevasses predicted for 2004 are shown in Figure 11 and illustrate a significant decrease in the spatial extent of moulins with increasing crevasse width.
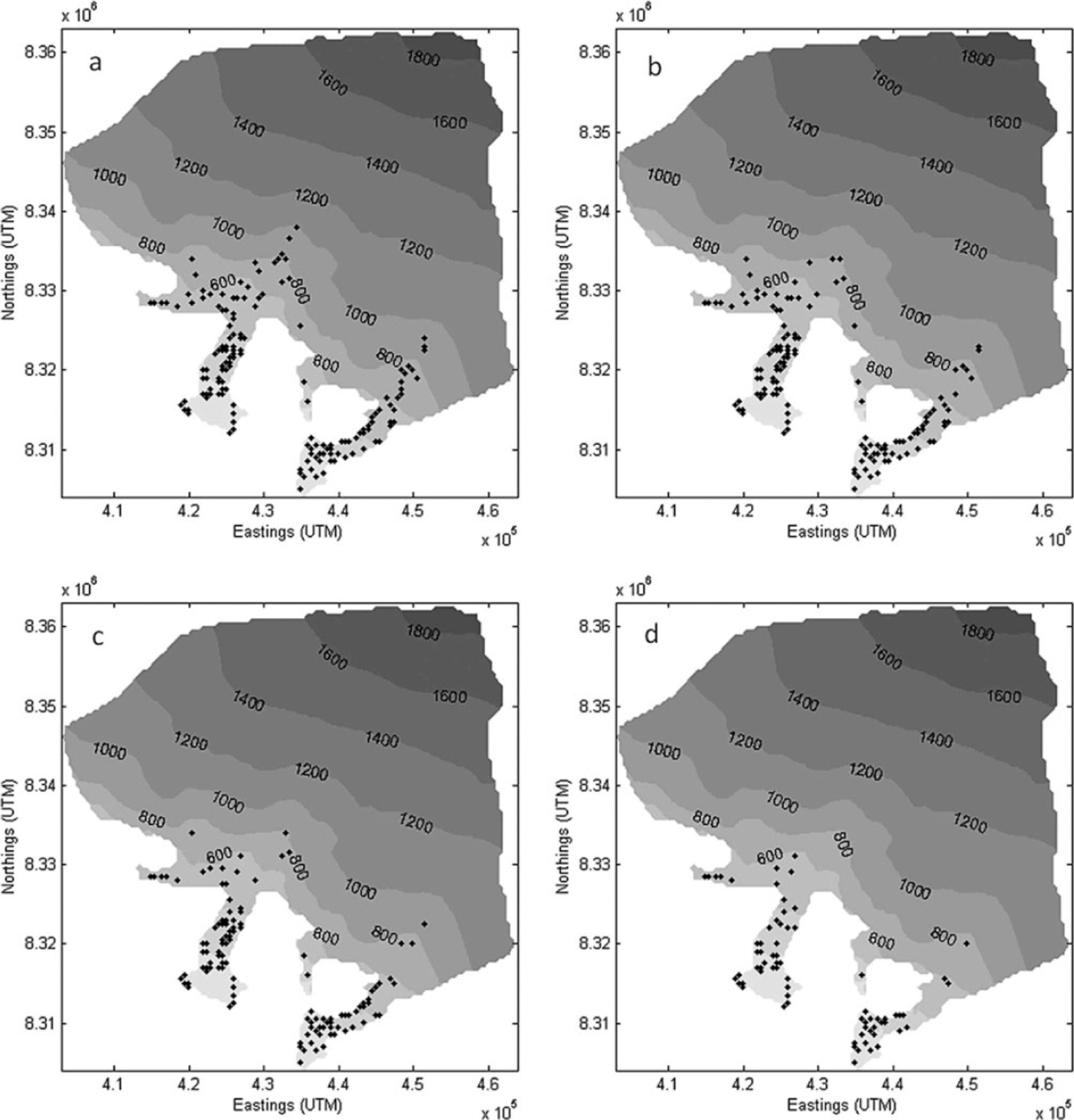
Fig. 11. Spatial distribution of moulins in 2004 for crevasse widths of (a) 0.5 m, (b) 1m, (c) 2m and (d) 5m.
With narrower crevasses requiring less water inflow to maintain a high water level than for wide crevasses, propagation of crevasses can occur more rapidly and can be more easily maintained to allow formation of fullthickness fractures, or moulins (Reference WeertmanWeertman, 1973;Reference SmithSmith, 1976). Thus, altering crevasse width does not result in a change in the number of surface crevasses, but does, however, affect the likelihood of those crevasses propagating through the full ice thickness to form moulins. This is demonstrated by the increasing number of crevasses not reaching the bed with increasing crevasse width (Table 1). By halving the initial width of 1 m to 0.5 m the model predicted an increase in moulin numbers of 10.2% and 3.6% for 2004 and 2006 respectively, while decreasing the number of surface crevasses that do not reach the bed (Table 1). Doubling of the crevasse width to 2 m led to a decrease in moulin numbers of 16.8% and 6.6%. Altering crevasse width also resulted in a shift in the temporal formation of moulins in both years (Fig. 12), where greater widths acted to delay the propagation of crevasses to the bed. In addition, a larger crevasse width resulted in a decrease in the proportion of surface-derived melt delivered to the bed (Table 2) and the converse.

Fig. 12. Comparison of temporal moulin formation for crevasse widths of 0.5, 1, 2 and 5m: (a) 2004, (b) 2006.
Lake drainages
The majority of predicted surface-to-bed connections are moulins created over time by meltwater inflow to a surface fracture, while a smaller proportion are moulins that form within 1 day, directly beneath supraglacial lakes, when lake meltwater content reaches a critical level to drive a preexisting surface fracture through the full ice thickness. Results of the tensile strength sensitivity tests (Table 1) suggest that decreasing the tensile strength, and thus increasing the number of surface fractures, acts to disrupt surface water inflow to lakes, reducing the potential for the formation of lakes with sufficient volume to force fracture to the bed. Altering the depth-averaged width of the crevasses also significantly affects the number, frequency and magnitude of lake drainages (Fig. 13);a product of the effect of crevasse width on the crevasse meltwater level, b, produced for a given lake melt volume. When applying larger crevasse widths, fewer lakes drain, but they drain later in the season and typically transfer a larger volume of meltwater to the bed during each drainage event. This is due to the larger quantity of meltwater accumulated in a lake necessary to enable a wider fracture to propagate through the full ice thickness.

Fig. 13. Temporal drainage of supraglacial lakes for fracture widths of 0.5, 1, 2 and 5m: (a) 2004, (b) 2006.
Discussion
The results of model testing described above indicate that the most important control on the spatial extent of moulins is the tensile strength (Fig. 10;Table 1). Due to its strong controlling influence on the spatial distribution of moulins, it is imperative that the tensile strength is parameterized reliably. This is an important consideration for moulin distribution under a warming climate, due to the temperature dependence of flow-law parameter A, which may rise in response to cryo-hydrologic warming (Reference Phillips, Rajaram and SteffenPhillips and others, 2010). Results also suggest that the delivery of surface-derived meltwater to the bed is highly sensitive to those input parameters which influence the rate at which water will fill a crevasse (Table 1). It is apparent from Table 1 that the crevasse surface geometry is an important control on the formation of crevasses through the full ice thickness when applying the Reference Van der VeenVan der Veen (2007) model for crevasse penetration. For both years, altering the crevasse width significantly affects the total number of surface crevasses that develop into surface-to-bed connections (Table 1). Altering the DDFs has a smaller effect on the numbers of moulins and drained lakes in each year. The percentage decrease in the number of surface-to-bed connections formed for the DDF sensitivity test is ~1% less for 2006 than for 2004, likely due to the greater average temperature in the 2006 ablation season which reduces the duration for which the lower DDF for snow is applied. Results of altering the ice fracture toughness suggest that the model is highly unresponsive to changes in this parameter. Crevasse depth calculated using the LEFM model applied here is most strongly controlled by the lithostatic and waterfilling stress terms, as discussed by Reference Van der VeenVan der Veen (2007). Thus the value of fracture toughness, although important for allowing initial fractures to develop, becomes negligible while propagation of crevasses due to meltwater influx is ongoing. Given the very small effect of fracture toughness on crevasse depth, the number of moulins predicted here is not altered by varying this input parameter.
Table 2 contains values of percentage transfer of surficially derived meltwater to the bed for each model run, along with the associated percentage change from the initial parameter run. As shown for the spatial distribution of moulins, the tensile strength is the strongest control on meltwater transfer to the ice/bed interface through its influence on the locations at which surface meltwater can be captured by crevasses. This highlights the importance of establishing a reliable value for this parameter, possibly based on the close integration of field-based observations and remotely sensed imagery. Crevasse width is also an important control on meltwater delivered to the bed. The size of crevasse surface openings controls the water level in crevasses, b, such that the higher the water level, the deeper a crevasse may penetrate, and the greater the number of initial surface crevasses that will have the potential to deliver meltwater to the bed. Crevasse width is unlikely to be spatially constant across a glacial catchment, so we suggest that for future applications crevasse width could be prescribed as a function of tensile stress. This may help to prevent, or allow for prediction of, full ice-thickness fractures, and thus meltwater delivery to the bed, in areas where crevasse dimensions may be under- or overestimated when applying a single depth-averaged crevasse geometry.
The changes in percentage transfer of surface-generated melt to the bed are small in comparison to changes in moulin numbers, suggesting that while the total melt delivery to the bed does not change much in response to varying input parameters, the spatial distribution and timing of melt delivery does. This is an important consideration for models of subglacial hydrology, as the spatial distribution and volumes of meltwater reaching the bed are likely a significant control on basal water pressure. It should be emphasized that while changes are small within each season, the actual modelled volumes of melt delivered to the bed during 2004 and 2006 differ significantly. Larger values of percentage transfer are predicted for the warmer 2006 season (Table 2), and an almost threefold increase in total meltwater routed from the surface to the bed is predicted in comparison to 2004. Furthermore, such enhanced drainage to the bed under scenarios of increased melt production may produce dynamic feedbacks resulting in larger tensile stresses via increased longitudinal stretching. This may result in more surface fracturing, and suggests that if tensile stresses were higher, less meltwater would be needed to propagate fractures through the full ice thickness. However, there would also be more crevasses present to disrupt the flow of water across the ice surface, which may in fact lead to a decrease in melt transfer to the bed.
As discussed previously, Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others (2005) identified a transition on both NCB and SCB glaciers from a flow regime of predominantly internal deformation (regime 1) to a regime where basal sliding, partially controlled by subglacial topography, begins to contribute to surface velocity (regime 2). Results of modelling suggest that transfer of supraglacial meltwater through moulins and during lake drainage occurs at elevations above this flow- regime boundary during the 2006 ablation season, although not in 2004 when less melt was generated (Figs 14 and 15). Moulins are predicted by the standard parameter run at about 600-1000 m elevation, where the main glacier tongue opens into the ice cap. These correspond closely with sites on both aerial photography and Landsat imagery where supraglacial streams disappear into crevasses (Fig. 8). This transition to regime 2 is coincident with the ice surface profile becoming concave-up, rather than the convex-up profile observed within flow regime 1 (Fig. 14). The transition from regime 2 to regime 3, a flow regime indicative of enhanced basal sliding (Figs 2 and 3), occurs at ~400m elevation. Modelling predicts that the density of moulins begins to increase significantly between 400 and 600m elevation, directly above the boundary between flow regimes 2 and 3 (Fig. 14), and remains high throughout the elevation extent of this flow regime. Meltwater delivered to the bed through moulins and lake drainages is significantly higher at these elevations, and indeed above, during 2006 (Fig. 15), which may suggest increased potential for melt- induced dynamic response. Consistencies between model outputs and identified flow regimes are encouraging and indicate that the model has some success in predicting the spatial distribution of possible full-thickness fractures. While field data of an appropriate temporal resolution against which to test model simulation of lake drainage events and moulin formation are not available, the model does produce results that are qualitatively realistic. This is particularly true for modelled spatial patterns of moulin formation within elevation bands, as supported by previous suggestions that meltwater reaching the bed may be a driver of increased ice surface velocities within flow regime 3.

Fig. 14. Density of moulins within elevation bands of 100 m. Glacier flow regime boundaries for NCB glacier (Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others, 2005) are illustrated.

Fig. 15. Total meltwater transfer through moulins and lake drainages within each 100m elevation band.
The spatial resolution of model input data is a limitation, particularly for meltwater routing across the ice surface. The mountain valley terrain surrounding the Croker Bay glaciers likely results in a significant proportion of meltwater running off the ice surface, and ending up between the glacier margin and valley walls. Additional melt may be produced by preferential heating of adjacent bedrock valley walls, and twinned with water running off the glacier margin this suggests that our estimates of the percentage of supraglacial melt reaching the ice/bed interface may be too high. Furthermore the model also does not account for attenuation of meltwater within the snowpack or firn layer, which may result in overestimation of the meltwater available for surface flow routing, and a decrease in the time lag between melt production and moulin formation and lake drainage events. The model prediction of moulin formation around day 130 in 2006 (Fig. 7) may be one example where early- melt-season snow cover may have resulted in an increased meltwater transit time, and thus may not have given rise to moulin formation that early in the season. Future studies could improve spatial patterns and magnitudes of supraglacial meltwater pathways by incorporating attenuation and refreezing of melt in near-surface snow and firn (Reference Van de WalVan den Broeke and others, 2008). The transit time of meltwater through the catchment could then be better represented, particularly in areas below the snowline, and would allow for improved temporal prediction of moulin formation over the ablation season. This highlights that while the model produces behaviour qualitatively comparable to what is seen in reality, particularly in spatial patterns of moulin formation, better constraints on physical processes and real-time observations of drainage events will help to improve the temporal component of the model.
Concluding Remarks
We have presented a new model designed for determining the spatial and temporal patterns of moulin formation, drainage of supraglacial lakes, and the delivery of surficially derived meltwater to the ice/bed interface of glaciers and ice sheets. The model has been applied to the Croker Bay catchment of Devon Ice Cap for the 2004 and 2006 ablation seasons and tested for sensitivity to input parameters. From model predictions, we conclude that accurate quantification of supraglacial meltwater is essential due to the controlling influence of crevasse water-filling levels on penetration depths. It is also clear that inaccuracies in prescribing crevasse geometry and the tensile strength of ice may lead to significant errors in modelling the location and timing of surface-to-bed connection formation during the ablation season. Response to increased meltwater generation, typified by results of modelling the warmer 2006 season, highlights the potential for enhanced surface-to-bed meltwater transfer under the scenario of a warmer climate. Thus, the delivery of surficially derived meltwater to the ice/bed interface should not be discounted as a mechanism for dynamic response to increased future ice surface melt.
Modelling surface-to-bed connections in the manner described here may have the potential to contribute towards integrating models of glacial hydrology and dynamics in a more physically based capacity, particularly for meltwater point inputs for models of subglacial hydrology (Reference Pimentel, Flowers and SchoofPimentel and others, 2010;Reference SchoofSchoof, 2010). The timing and quantity of meltwater reaching the ice/bed interface is an important controlling factor on water pressures at the bed and the configuration of the subglacial system (Reference Iken and BindschadlerIken and Bind- schadler, 1986). Given observed velocity responses to changes in subglacial hydrology, it is important that the spatial and temporal evolution of moulin formation and lake drainage events is accounted for in integrated modelling of glacier hydrology and dynamics.
Acknowledgements
We acknowledge the College of Physical Sciences, University of Aberdeen, for providing a graduate school studentship, and the Leverhulme Trust for awarding a Study Abroad Studentship, both to Caroline Clason. We thank Julian Dowdeswell for providing ice-thickness and surface-elevation data, and Martin Sharp for providing access to Devon Ice Cap data resources. We also thank Wolfgang Schwanghart for contributing his expertise, Gwenn Flowers and Mauro Werder for their invaluable input, and two anonymous reviewers whose comments improved the manuscript.



















