4.1. General description

In this paper, we use a modification of the power model, which we call the variable width/depth ratio (VWDR) model, to describe the overall morphology of glacial valley cross-sections. In this model we define G(y) by (Fig. 3):

where (y − y ₀) is the height above the valley bottom, taken to be at y = y ₀, w is the width of the valley at height y, and G(y) is the VWDR at elevation y. (When y is the altitude of the trimline, G(y) is equal to 1/FR, where FR is the form ratio defined by Reference GrafGraf (1970).)

Fig. 3. Definition of parameters in the VWDR.

In order to avoid the influence of postglacial cut or fill, the valley cross-section is smoothed before calculations are undertaken (Fig. 4). Specifically: (1) the altitude of the valley bottom is adjusted if the floor is incised by fluvial or other processes; and (2) valley-side morphology is interpolated where talus or till are present.

Fig. 4. Method of smoothing of valley cross-sections before calculating VWDR values: (1) interpolate across the valley bottom if the valley has been incised by fluvial or other processes in postglacial time; (2) interpolate beneath talus or moraines on valley sides.

The adjustments are rather simple in this area because deposits on the valley floor and sides are generally < 10–20 m thick. Even in the vicinity of Wangfeng station, which has the thickest deposits (40–60 m), in a dataset compiled from maps with 20 m contour intervals only one or two points need to be adjusted. Thus, we can easily adjust these points by interpolating, by eye, using neighboring points to define the curvature of the valley side. More commonly, the problem points were removed. This did not affect the calculations noticeably. Furthermore, postglacial rivers do not cut into the bedrock in most parts of these glacial valleys. Where rivers do cut into the bedrock, near Wangfeng station (Fig. 1), the depth of incision is only 2–3 m, which also is not enough to affect the calculations.

As with the power model, double-log plots of G(y) against (y − y ₀) typically result in straight lines (Fig. 5), which thus may be described by:

Fig. 5. Relationship between G and valley depth (d). Points A and B are discussed in text.

where d is the depth (y − y ₀), and m and n are constants. The 56 valley cross-sections shown in Figure 1 have been fit with this model, and values of m, n and the explained variance, R ², calculated by least-squares techniques (Table 1). While this model, unlike the power model, incorporates data from both sides of the valley and thus can be used to describe asymmetrical valley cross-sections, it does not describe a cross-section uniquely because the horizontal (or x) coordinates of the valley sides do not appear in the equations.

To provide a physical interpretation of m and n, replace G with w/d in Equation (4), thus:

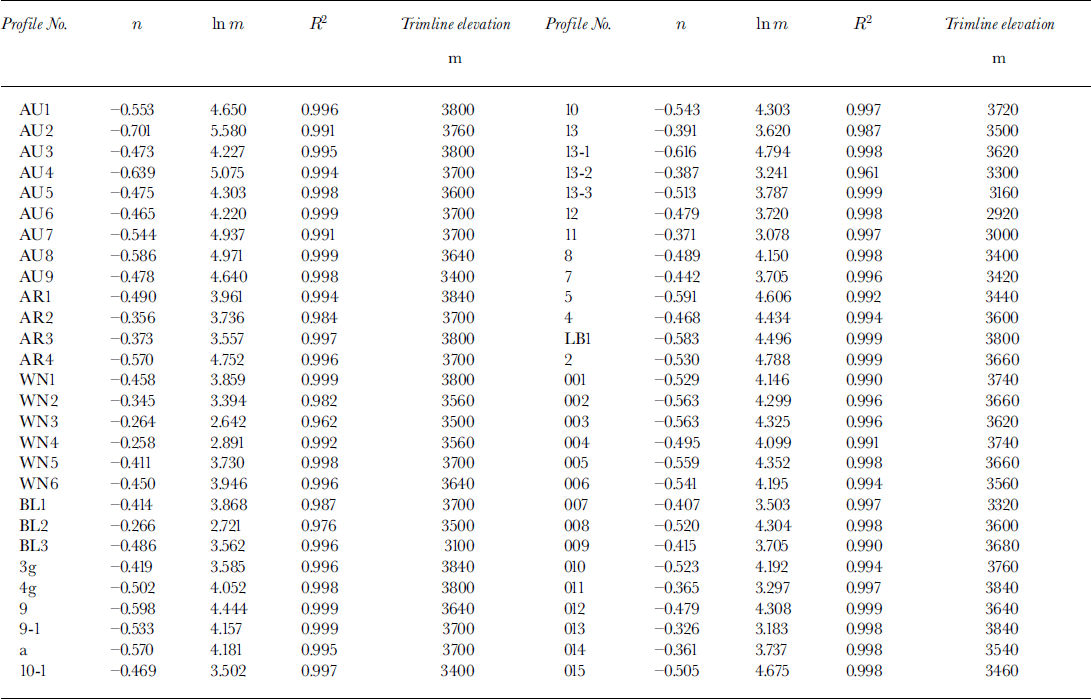
From this it is clear that m is the width of the valley when d = 1, so m is a measure of the width of the valley bottom. It is also clear that −1 < n <0. n = −1 describes a rectangular valley of constant width, m, with vertical sides. Values of n < −1 would describe a valley that narrows upward, which occasionally occurs but would be unrealistic in the present circumstances. n = 0 represents the limiting case of a V-shaped valley. Higher values of n correspond to valleys with convex upward sides. Thus, as n varies from −1 to 0 for a given value of m, valley-side slopes become progressively gentler and approach linear. Now consider the situation in which the valley cross-section is symmetrical so w = 2x. Then,

or

Comparison of this with Equation (1) will demonstrate that n = −0.5 corresponds to the parabolic case (b = 2).

4.2. Advantages and disadvantages of the VWDR model

The VWDR model can describe the integrated morphological characteristics of entire valley cross-sections, regard less of whether the valley is symmetrical or asymmetrical. Power functions cannot do this. Furthermore, because the w/d ratio is used, the data are less sensitive to lateral positioning than is the case with power models.

The VWDR model is directly linked to the form ratio, FR, because, by definition, G = 1/FR at the trimline altitude. The VWDR model can also be used to estimate the location of trimlines and the value of FR even where, owing to map errors or modification by postglacial processes, the trimline is not evident on maps or in the field. To do this, we plot ln G vs ln d and seek breaks in slope. For example, in Figure 5, the points to the left of A and B are for the inner valley, and A and B represent positions of the trimline. Where the valley walls rise above the trimline, the slope of the ln G vs ln d relation decreases (n becomes less negative), and the valley begins to widen out more rapidly with increasing elevation. This is inferred to represent valley sides formed by different processes or by an earlier glaciation. At the break in slope, G = 1/FR.

On the other hand, the VWDR model does not resolve all problems with traditional models. It, too, is sensitive to the determination of the valley-floor altitude in situations in which incision has occurred. Thus, although it can reduce problems associated with positioning in the x direction, the problems in the y direction still exist. Furthermore, although the VWDR model can describe the overall morphology of a valley cross-section, it loses the information on variability from the two sides, and cannot be used to generate a valley cross-section plot.

Although the VWDR model has some limitations, where valley-floor elevations are well known from previous fieldwork it can be used to compare different valley cross-sections and to study longitudinal variations in cross-section morphology along a glacial valley.

5.1. Classification of glacial valleys

To facilitate discussion, we classify glacial valleys into two basic types based on differences in map or plan form (Fig. 6):

Fig. 6. Classification of glacial valleys. A, B, simple valleys; C, compound valley. (1) upper simple-valley section; (2) confluent section; (3) lower simple section.

1. (1) Simple valleys: A simple valley is one that has a single glacially scoured channel over most of its length. It may have more than one cirque at its head, but otherwise has no major tributaries.

2. (2) Compound valleys: Compound valleys are valleys with one or more major tributaries. In general, the respective channels of a compound valley may be considered to be simple valleys. Compound valleys commonly can be subdivided into three sections: (i) an upper simple-valley section, (ii) a confluent section and (iii) a lower simple section.

5.2. Longitudinal variation in cross-section morphology along glacial valleys

Longitudinal variations in m, n and the trimline altitude along the valleys from which most of the cross-sections discussed herein were obtained are given in Figures 7 and 8. These parameters vary systematically downstream from the valley head in both simple and compound valleys.

Fig. 7. Longitudinal variation of trimline altitude, In m and n along some simple valleys: (a) Glacial valley No. 8; (b) Qongsaersayi valley; (c) Qindawangsayi valley; (d) Yawuertuaiken valley.

Fig. 8. Longitudinal variation of trimline altitude, In m and n along some compound valleys. The short vertical arrows in each panel show the locations of confluences, (a) Daxigou valley; (b) Glacier No. 8–Daxigou valley; (c) Akesudangha–Ayoutuai-ken valley; (d) Tawuertuaiken–Ayoutuaiken valley.

In simple valleys, m initially increases (the valley floor becomes wider) from the head of the valley, and then decreases to the valley end. Correspondingly, n decreases, or becomes more negative, initially (valley sides become steeper) and then increases. In compound valleys, the same pattern is observed except that m and n oscillate in confluent valley sections. As expected, the trimline altitude decreases with increasing distance down-valley, in both simple and compound valleys.

5.3. Discussion

Basal temperatures in alpine glaciers are likely to be at the pressure-melting point except, in some situations, for a region in the lower part of the ablation area where the glacier may be frozen to its bed (Reference Hooke, Gould and BrzozowskiHooke and others, 1983; Reference Xiangsong, Guocai, Songlin, Jiyang and YingZhang and others, 1985; Reference Baolin, Maohuan and ZichuCai and others, 1987). Such temperate or polythermal alpine glaciers are therefore highly erosive. Glacial valleys are one of the most important landforms produced by such glaciers. The morphological characteristics of these valleys reflect both glacial dynamics and boundary conditions such as bedrock lithology and structure (Reference Embleton and ThornesEmbleton and Thornes, 1979; Reference AugustinusAugustinus, 1992, Reference Augustinus1995; Reference HarborHarbor, 1995). As noted earlier, bedrock lithology and structure affect micro-landforms in the glacial valleys studied herein, but not their overall cross-sectional shape. Thus, we hypothesize that the observed longitudinal variations in these glacial valleys are largely a consequence of differences in glacial dynamics, and hence erosion potential. Specifically, the wider valley floors and steeper valley walls (U-shapes) indicated by higher values of m and lower values of n imply more glacial erosion.

The erosive potential of a temperate glacier is determined by the ice-volume flux and by the frequency and magnitude of fluctuations in basal water pressure (Reference Embleton and ThornesEmbleton and Thornes, 1979; Reference JingtaiWang, 1981b; Reference Iverson and MenziesIverson, 1995). Frequent large water-pressure fluctuations are likely to be particularly significant where convexities in the bed cause crevassing at the surface (Reference HookeHooke, 1991), but otherwise may occur anywhere along a glacial valley. Thus, they should not be expected to produce systematic down-valley changes in cross-sectional shape. The ice flux, however, reaches a maximum in the vicinity of the equilibrium line of glaciers in simple valleys. Thus, erosion is likely to be most vigorous there, resulting in broader valley bottoms and steeper valley sides.

Reference ZhenshuanZhang (1981) has studied variations in equilibrium-line altitude (ELA) at the head of Ürümqi River, a north-flowing river in the Bingdaban area, using several methods. He concluded that the ELA in this area was at 3630 ± 40 m during the Middle and Late Wangfeng Ice Ages, when the valleys under discussion were last modified by glacial erosion. Reference HeigangXiong (1991) pointed out that the ELA in the areas of southward flow is 100–150 m higher than in areas of northward flow in the Bingdaban area. The trimlines in Figure 7 are at or close to these elevations at cross-sections 9 (3640 m), 005 (3660 m), 13-1 (3620 m) and AU4 (3700 m) in Glacial valley No. 8 and in Qongsaersayi, Qindawangsayi and Yawuertuaiken valleys, respectively. This is consistent with the higher values of m and lower values of n at these cross-sections. We can also divide the cross-sections of simple valleys into three groups, namely those above, at and below the ELA, and average the values of m and n in each group (Tables 2 and 3). The average values of m are larger and of n are more negative for the middle group.

Most of the characteristics of glaciers in compound valleys are similar to those of glaciers in simple valleys, but in compound valleys there are important interactions at glacial confluences. This is because ice flux increases more at confluences than in other areas, so the potential for erosion is larger here.

In Figure 8, locations of confluences are indicated by short vertical arrows. It will be noted that m increases and n becomes more negative from the upper simple-valley section to the confluent section in each of these compound valleys, reflecting the expected increase in erosion at confluences. Although the confluences are, in some cases, near the ELA (e.g. 2 and 4 in Fig. 8a), the implied increases in erosion are inferred to result primarily from increases in ice flux from the tributary valleys. Supporting this interpretation is the observation that the valleys widen appreciably below confluences, whereas simple valleys do not widen as dramatically at the ELA. The values of m and n appear to oscillate within the confluent section, reflecting the impact of successive confluences, while undergoing an overall decline. From the confluent section to the lower simple section, as ice flux diminishes, m decreases and n becomes less negative. Again, if we sort the cross-sections of compound valleys into three groups, those in upper simple-valley sections, those near confluences in confluent sections, and those further from confluences in confluent sections, it will be seen that the average value of m is larger and of n is more negative near confluences (Tables 4 and 5).