The precise method of distance averaging is investigated carefully. Two methods are considered: a running arithmetic mean and a digital low-pass filter. By Fourier analysis the former method is converted to the form of a frequency operator for comparison with the latter. Because the magnitudes of 2G and T depend on the wavelength of the averaging scale, it is argued that for our case the digital low-pass filter is more appropriate. This method has the additional advantage that high-frequency noise in the data, predominantly a result of measurement errors, is more effectively removed.
Both operators are applied to the data to test the ability of 2G to correct τ g for averages of ¼, 1, 2, 4, and 10 km. The average depth of the glacier is 270 m, and T is neglected in all cases. Remnant high frequency in the data arithmetically averaged interferes with any attempt to judge the effectiveness of 2G as a correction. For no averaging length does the correction seem to be effective, although an averaging scale of 4 km appears to be the least poor. Comparison is easier with the frequency-filtered data. The agreement is best for the 4 km filter, where 2G accounts for a large fraction of the difference between τ b and τ g over most of the filtered region. However, for large-scale filters, most data are only partially filtered. For the 4 km filter, these edge effects eliminate 75% of the data field.
The conclusion is that in this analysis, 2G does not provide an effective means of improving the calculation of base shear stress on Variegated Glacier. This contrasts with the agreement found by Reference BuddBudd (1970) using Wilkes Ice Cap data. Possible explanations of this discrepancy include: errors in the field data or the shape factor may be too large to permit meaningful evaluation of a small correction term; T may be significant over some regions of this glacier; the relation used to evaluate 2G may be inappropriate for this valley glacier.
Discussion
W. F. Budd: Can you use your results to calculate an effective “viscosity” parameter for longitudinal stress ?
R. A. Bindschadler : Yes, I foresee no difficulty.


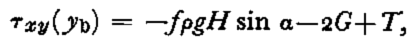
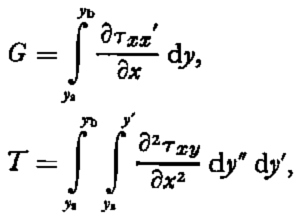
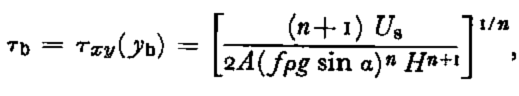
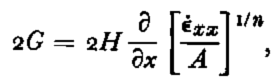
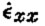 is the surface longitudinal strain-rate. The expression for 2
is the surface longitudinal strain-rate. The expression for 2