Introduction
Ice-penetrating radar is an established and powerful tool for observing the englacial and subglacial environments of ice masses (e.g. Reference Robin, Evans and BaileyRobin and others, 1969; Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others, 1985). Although electromagnetic waves at frequencies between a few MHz and several hundred MHz propagate well in cold ice, they reflect off surfaces where there is a contrast in the complex dielectric property of ice (i.e. dielectric permittivity or electrical conductivity). Such contrasts occur not only at the surface and base of the ice sheet, but also within the ice. These englacial dielectric boundaries are known as “internal layers”. The causes of internal layers have been investigated by a number of researchers since their discovery in the 1960s (see Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others, 1985, for a review of this early work). Two major causes were identified: (1) changes in dielectric permittivity due to density fluctuations (hereafter P D), and (2) changes in electrical conductivity due to changes in acidity (hereafter C A). In particular, internal reflections that occur deeper than about 1000 m were attributed wholly to C A by many researchers. After 1992, it emerged that the Ih (hexagonal) ice crystal has a dielectric anisotropy of about 1% of the permittivity (Reference Fujita, Shiraishi, Mae, Maeno and HondohFujita and others, 1992, Reference Fujita, Mae and Matsuoka1993; Reference Matsuoka, Fujita, Morishima and MaeMatsuoka and others, 1997; Reference Fujita, Matsuoka, Ishida, Matsuoka, Mae and HondohFujita and others, 2000) at frequency ranges used for radar sounding. This dielectric anisotropy is thought to be large enough that small changes in crystal-orientation fabrics cause contrasts in the dielectric permittivity sufficient to produce detectable internal reflections (Reference Fujita and MaeFujita and Mae, 1994). In order to investigate causes of internal reflections and their possible spatial variation, the Japanese Antarctic Research Expedition (JARE) recently carried out a dual-frequency (60 and 179 MHz) radar experiment across a transect from Dome Fuji to the ice margin in the vicinity of Syowa station (Fig. 1) (Reference FujitaFujita and others, 1999). The experiment found that permittivity- and conductivity-based reflections can be distinguished using two frequencies, because the amplitudes of these distinct internal reflections are related differently to frequency. They concluded that the change in permittivity due to crystal-orientation fabrics (hereafter P COF) is a major cause of internal reflections, and that the ice sheet comprises four main zones in which different reflection mechanisms dominate. They are P D , C A , P COF and the basal echo-free zone (EFZ) where no significant reflector exists. In particular, the P COF zone and the EFZ are important for ice dynamics because they are indicators of two distinct ice-flow regimes (Reference FujitaFujita and others, 1999). In contrast, P D and C A are important mainly to the understanding of the ice sheet’s depositional history.
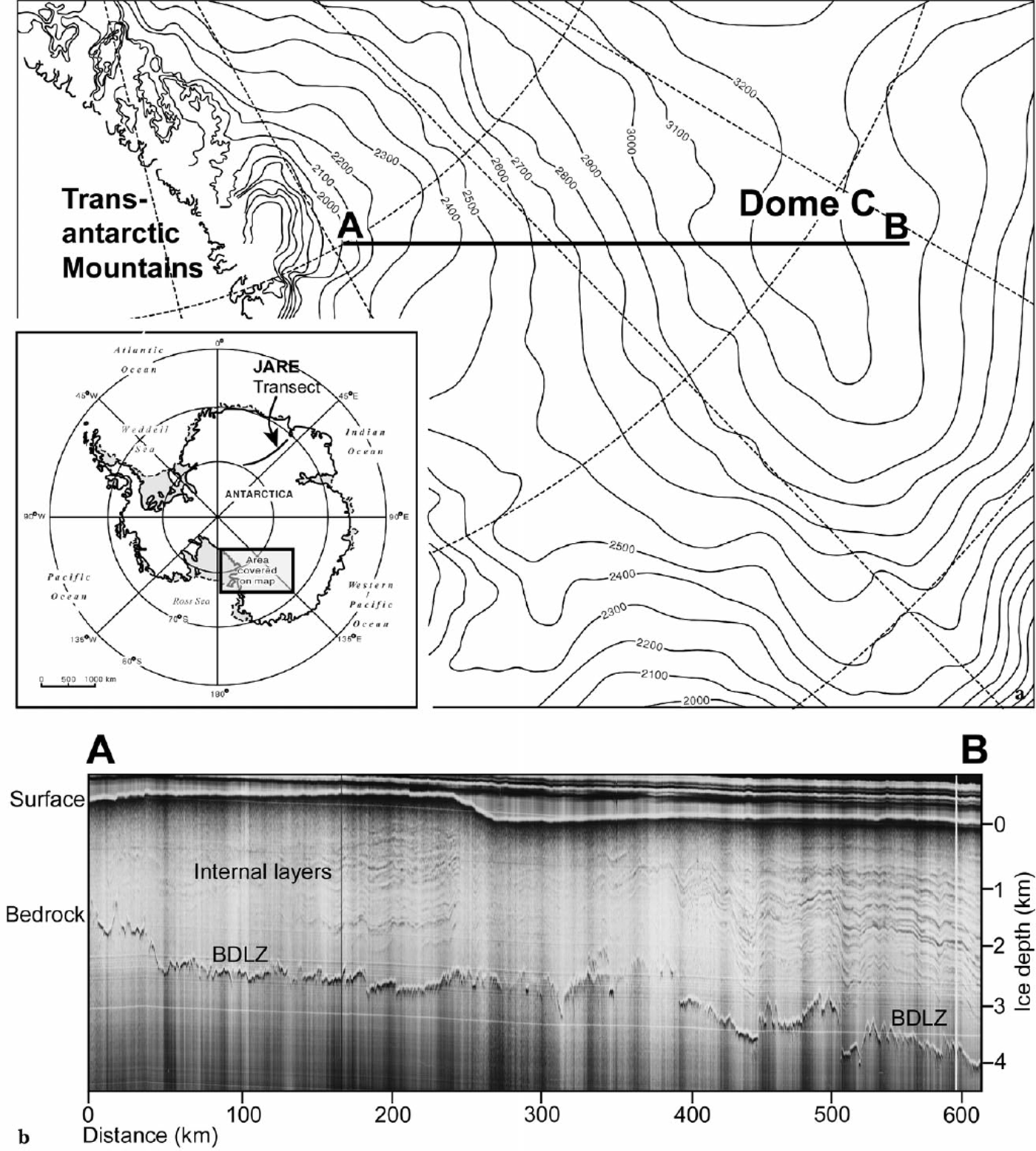
Fig. 1. (a) Map showing the location of a radar transect AB, between Dome C and the Transantarctic Mountains, and the JARE radar transect from Dome Fuji to Mizuho station. (b) Z-scope radar data along transect AB. Surface elevation contours are provided in metres above sea level. BDLZ refers to “below detection-limit zone”.
One of the most extensive Antarctic radar datasets was collected in the 1970s by a consortium of the Scott Polar Research Institute (SPRI), U.K., the U.S. National Science Foundation and the Technical University of Denmark (e.g. Reference Robin, Drewry and MeldrumRobin and others, 1977). The data archive from this international operation is held at SPRI (hereafter, these data are referred to as the SPRI data). The SPRI data were largely collected using two frequencies, 60 and 300 MHz (Reference Robin, Drewry and MeldrumRobin and others, 1977; Reference MillarMillar, 1981a, b). At first, it was expected that SPRI data at both frequencies could be analyzed in a similar way to Reference FujitaFujita and others’ (1999) analysis of the JARE data. However, it was soon realized that the 300 MHz data were insufficiently calibrated for that purpose (Reference MillarMillar, 1981a, Reference Millarb), and that a dual-frequency analysis of the SPRI data was not possible. However, through this preliminary, unsuccessful trial of the dual-frequency analysis, we found that there are several features that are similar to both the well-calibrated SPRI 60 MHz and the JARE 60 MHz radar data.
Using the SPRI 60 MHz data, Reference MillarMillar (1981a, Reference Millarb, Reference Millar1982) interpreted the causes of internal reflections and their variations in the ice sheet. His analyses focused on extracting information on acidity since no information was available for the crystal-orientation effects. In the light of recent knowledge, we have re-examined part of this 60 MHz dataset. In doing so, we are able to establish that some of the internal reflections in the SPRI data are from changes in crystal-orientation fabrics. This paper demonstrates how it may be possible for the 25 year-old SPRI data archive to reveal information on ice-reflection mechanisms through further analysis.
Similarities in SPRI and JARE Data
The SPRI 60 MHz data
General features
The SPRI and JARE 60 MHz radar datasets were both collected with a pulse width of 250 ns. We verified that the SPRI data were reliable by comparing them with calibrated records. Originally, the received power of the radar was calibrated in two ways. The first calibrated the level of the received power by connecting a series of attenuators between the transmitter and receiver, and recording the strength of the received signal. The second calibrated the reflectivity at known ice depths using reflections from the smooth, flat water/ice boundary over the Vostok subglacial lake (Reference MillarMillar, 1981a). For our analyses, we chose a transect (radar flight-line) approximately parallel to ice flow from Dome C to the Transantarctic Mountains (TAM) (AB in Fig. 1a). This transect lies between the TAM and 100 km beyond the summit of Dome C in central East Antarctica, in a similar way to the JARE transect across Dome Fuji to the ice margin close to Syowa station (Reference FujitaFujita and others, 1999). The SPRI data were recorded in two formats: first, as “A-scopes”, which comprise graphs of signal strength vs depth from single radio-wave pulses, and second, as “Z-scopes”, which represent a series of single radio-wave returns, collected in a time-dependent manner and intensity-modulated. The depth of a reflection is calculated from the two-way travel time and the radio-wave velocity in ice (168 μs −1). The radar power received from a boundary on or in an ice sheet, P R, is expressed by a radar equation (e.g. Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others, 1985). The form of the equation depends on the platform of the radar and the nature of the scatterers and reflectors. Assuming that the radar is on the ground, an example of the radar equation is:
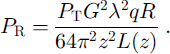
Here P T is the transmitted power, R is the power reflection coefficient, G is the antenna gain, λ is the wavelength of radio waves in a vacuum, q is the signal gain due to refraction at the air–ice interface, and L(z) = exp(2αz), where α is the attenuation coefficient due to energy absorption and z is the depth to the reflector. In the ice sheet, the only variable parameters are R, L and z. R is a complex function of internal reflection mechanisms (P D, P COF or C A). L is a function of the chemistry (mainly acidity) and temperature of the ice. Note that this equation assumes an idealized situation in which the reflecting boundaries are smooth planes from which no scattering occurs. This assumption has been widely used in most of the previous studies on ice-sheet internal reflections. In a non-idealized case (i.e. if the scattering component from an undulating surface or a slightly rough surface cannot be ignored), we must use a different form of the radar equation. In this situation, the equation must include a scattering cross-section factor, which can be established from one of two widely known models, namely, the surface scattering theory of Kirchhoff or the small-perturbation method. In each scattering model, the scattering cross-section is usually proportional to the power reflection coefficient, so P R is also proportional to the power reflection coefficient, as in the non-scattering case (Equation (1)). It should also be noted that a small loss occurs as a result of the surface transmission process at a dielectric boundary (Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others, 1985). In the case of ground-based measurements, this small loss is included in the antenna gain G because the antennae and the air/ice surface are effectively coupled.
Z-scope data, when plotted as two-way radio-wave travel time along a track, yield pseudo-cross-sections of the ice sheet (Fig. 1b). In much of the SPRI 60 MHz dataset, internal radar layering can be identified and traced across the ice sheet from analysis of both types of radar record (for details see Reference MillarMillar, 1981a; Reference Siegert, Hodgkins and DowdeswellSiegert and others, 1998). Z-scope radar data across the Dome C-TAM transect (Fig. 1b) indicate that ice-sheet layering and basal topography are observable along our chosen transect.
Transect from Dome C to the TAM
Figure 2 shows the variation of surface elevation, ice thickness, bed elevation and internal layering along the transect between Dome C and the TAM (AB in Fig. 1). The surface elevation increases steadily from 2000 m a.s.l. near the TAM to > 3200 m close to the summit of Dome C (Fig. 1a). Bedrock topography and ice thickness are more variable along the transect (Figs 1b and 2b). At the downstream end of the Dome C-TAM transect, subglacial hills are present and the ice is only 2000 m thick. Between 50 and 250 km, a subglacial valley (the Wilkes Subglacial Basin) of relatively constant level (500 m b.s.l.) is located. The ice thickness in this region increases from 2800 m to > 3000 m in conjunction with the change in the elevation of the ice-sheet surface. Subglacial highlands between 300 and 400 km are associated with ice thickness of around 2500 m, which then increases to 3800 m at the end of the transect as the bedrock surface drops to 700 m b.s.l. (Fig. 2a). The flight-line is aligned approximately perpendicular to ice surface contours, so we expect a significant proportion of ice flow to be along the line of the transect (Fig. 1). This means we can examine the role of subglacial topography in internal radar layering as ice flows over the subglacial hills and valleys identified in the transect.
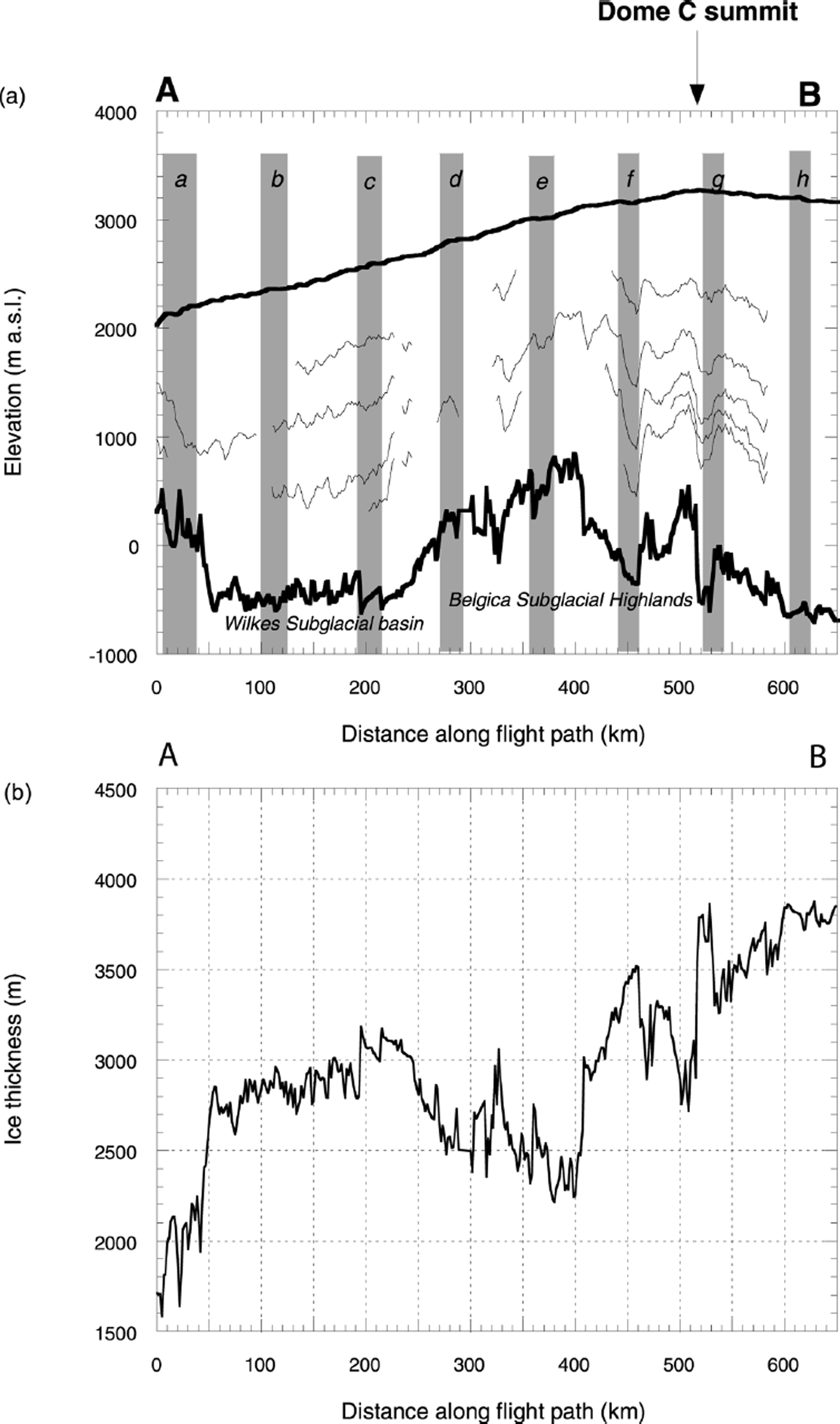
Fig. 2. (a) Ice-surface elevation and bedrock elevation along transect AB. Eight sites (a-h) mark the positions of A-scopes shown in Figure 3. (b) Ice thickness along transect AB.
A-scope data
60 MHz radar A-scopes were digitized from the original 1970s analogue records (in 35 mm negative films) by electronic scanning. In the SPRI database, A-scopes are available at 1.6 km intervals along the flight track. Eighty A-scopes were digitized and examined along the transect AB (Fig. 1) across eight regularly spaced zones (10 in each zone). Radar A-scopes were then examined at these eight sites (Fig. 2a). At each site, 10 A-scopes separated by a total of 16 km are available. Analysis of these data confirms that there is little variation in these closely spaced radar signals. Therefore a single representative A-scope can be extracted for further examination at each site. The A-scope data from each location can be linked to other locations through the internal layering observable in the Z-scope mode. A-scopes from each of the eight sites can therefore be compared directly (Fig. 3). From this comparison, the change in the power reflected off an internal layer along the transect can be established.
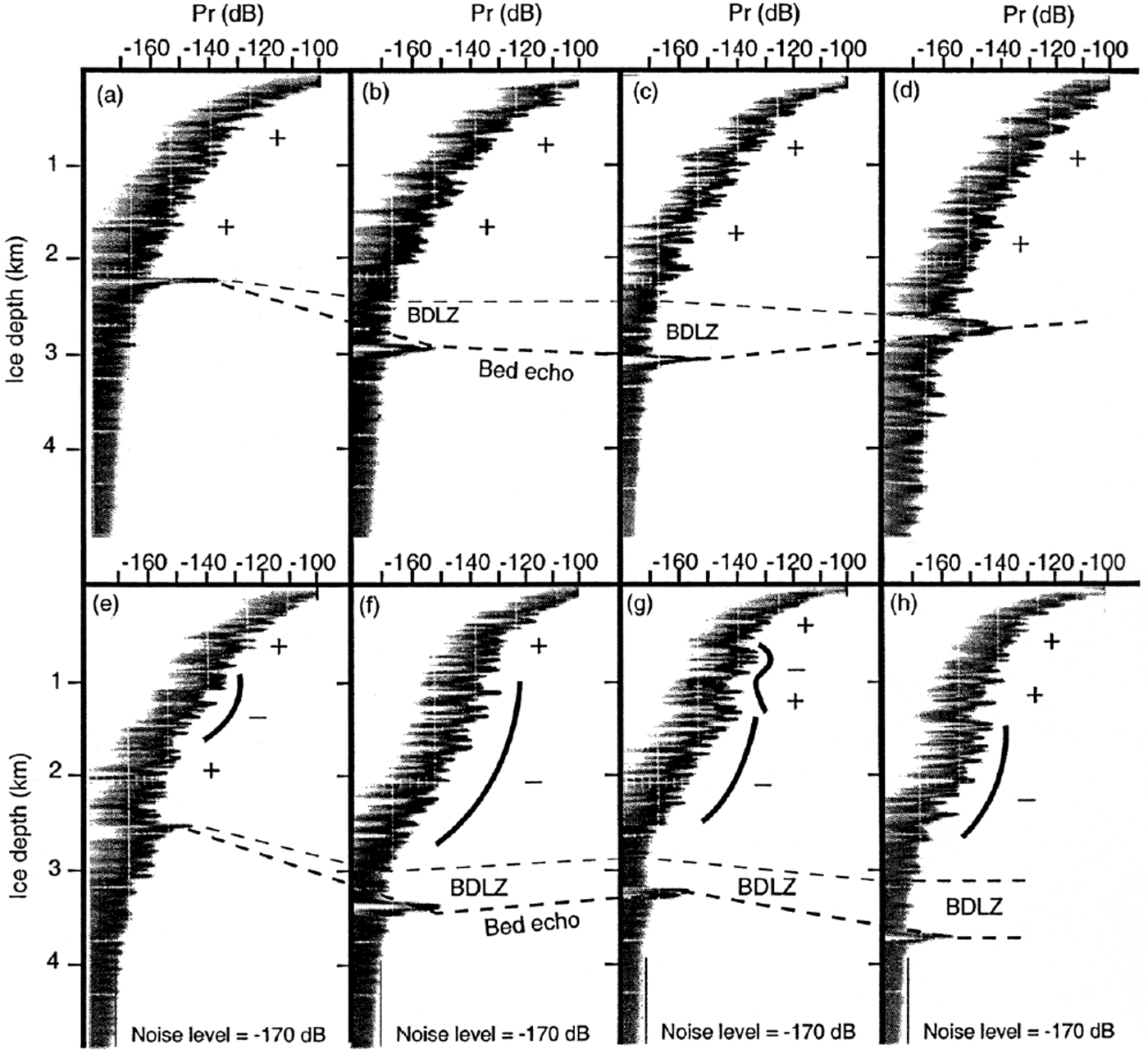
Fig. 3. Eight 60 MHz radar A-scopes at locations indicated in Figure 2a. Note that the abscissa is the received power compared with the transmitted power. Therefore unit is dB, which simply shows the relative magnitude. The ordinate is the ice-sheet depth calculated from the two-way travel time of the electromagnetic wave. The signs of the second derivative (∂ 2 P R/∂z 2) of the signal envelope with depth are indicated. The detection limit of the radar was about −170 dB. Below this level, signals are noise and not significant. Zones with noise only are indicated as “BDLZ”. The BDLZ is determined with the aid of the Z-scope information, where the position of internal layers and the morphology of bedrock can be viewed (Fig 1b)
Depth-related features observed in the SPRI data
We are able to determine a number of features in the SPRI A-scope records between Dome C and the TAM as follows (Fig. 3). P R decreases with increasing depth. This is due to both the geometrical spreading of the electromagnetic wave (i.e. the effect of increasing z) and energy loss due to absorption (i.e. the effect of L in the radar equation).
To extract the depth-related fluctuation of the A-scope returns, we observed qualitatively the second derivative (∂ 2 P R/∂z 2) of an envelope involving only the peaks of the A-scopes in a decibel power scale with linear ice depth. The second derivative simply shows where the A-scope shape (dominated by the maximum peaks) is convex (i.e. a negative second derivative, ∂ 2 P R/∂z 2< 0) or concave (i.e. a positive second derivative, ∂ 2 P R/∂z 2 >0). Our observation of the A-scope shape can be summarized in four points as follows. (1) At ice depths less than 700–900 m, ∂ 2 P R/∂z 2 >0 in all cases. This depth range is generally characterized by the dominant P D reflections (Reference FujitaFujita and others, 1999). (2) At depths below about 700–900 m, ∂ 2 P R/∂z 2 is sometimes positive and sometimes negative, depending on location and ice depth. Far inland, in particular around the dome summit, ∂ 2 P R/∂z 2 tends to be negative below ice depths of ∼1 km (Fig. 3f–h). (3) In contrast, closer to the ice margin, ∂ 2 P R/∂z 2 tends to be positive at all depths in the ice (Fig. 3a–c). (4) Near the ice-sheet base, there are regions where no internal reflections are observed (i.e. the reflected power is less than the detection limit (–170 dB compared to the transmitted power)). This depth range is referred to as the zone “below the detection limit” (BDLZ). Note that the BDLZ may be caused in two ways. The first is because of an absence of significant reflectors. In this case, the zone should be referred to as the basal “echo-free zone” (see Reference Robin, Drewry and MeldrumRobin and others, 1977; Reference Robin and MillarRobin and Millar, 1982; Reference FujitaFujita and others, 1999). In the second, P R is simply below the detection limit due to absorption loss, thus leaving significant reflectors unrecorded. A number of authors claim that at least some of the BDLZs in the SPRI data are actually EFZs (Reference Robin, Drewry and MeldrumRobin and others, 1977; Reference MillarMillar, 1981a; Reference Robin and MillarRobin and Millar, 1982).
The JARE 60 MHz data
General features
From analysis of the JARE dual-frequency radar data (Reference FujitaFujita and others, 1999), four zones were detected where different reflection mechanisms operate (P D, P COF, C A and EFZ). The distribution of these zones is related to the variation of physical conditions in the ice sheet.
To demonstrate the features common to both the SPRI and JARE 60 MHz data, we analyzed five A-scope examples from the JARE dataset, published previously in Reference FujitaFujita and others (1999) (Fig. 4). Like the SPRI data (Fig. 3), the JARE A-scopes are arranged from the ice-marginal area (Mizuho, left in Fig. 4) across the dome (Dome Fuji, second from right in Fig. 4) to a site beyond the dome (SSE150, right in Fig. 4). The geographical location of each site is schematically shown in Figure 5. The original raw data were characterized by many individual reflections in the ice and by interference effects from multiple reflectors in the radar pulse. To depict the general shape of the A-scope envelope, the mean values within a depth window of 200 m, at intervals of 10 m, were calculated for each record. For reference, the JARE data from the 179 MHz radar are also shown, smoothed in a similar manner to the JARE 60 MHz results (Fig. 4).

Fig. 4. JARE dual-frequency (60 and 179 MHz) radarA-scopes from the JARE transect from Mizuho station across Dome Fuji (Fig 1). Published curves (Reference FujitaFujita and others, 1999) have been smoothed over 200 m of ice thickness at several sites from the marginal region of the ice sheet (left side) and across the dome summit to a site beyond the dome. They are at Mizuho, MD364, MD550, Dome Fuji (deep drilling site) and SSE150. Geographical locations are shown diagrammatically in Figure 5 along with the interpreted reflection mechanisms. The raw data and experimental details are given by Reference FujitaFujita and others (1999). Note that the abscissa is the power expressed by a unit dBm, which is a unit for the expression of power level in decibels with reference to a power of 1 mW. Because the radars from JARE used 1 W (60 dBm) for the transmitted power, the minimum detection level of −110 dBm is comparable to the −170 dB of the SPRI data. 179 MHz records are given to show the reflection mechanisms determined by the dual-frequency technique. The difference between the 179 MHz and 60 MHz signals is shaded. When the 179 MHz signals are larger than the 60 MHz signal by about 10 dB, the dominant reflection mechanism is related to changes in permittivity (P D or P COF ) When the difference is close to zero, the dominant mechanism is caused by changes in conductivity (C A). The signs of the second derivative of the 60 MHz signal (envelope) along depth (∂ 2 P R/∂z 2) are also shown as in Figure 3. At the four sites from the ice margin to the dome (i.e. Mizuho, MD364, MD550 and Dome Fuji), signs of ∂ 2 P R/∂z 2 and reflection mechanisms correlate well. The zones where ∂ 2 P R/∂z 2 >0 tend to agree with the zone of P D or P COF. The zones where ∂ 2 P R/∂z 2< 0 tend to coincide with C A-based reflections.
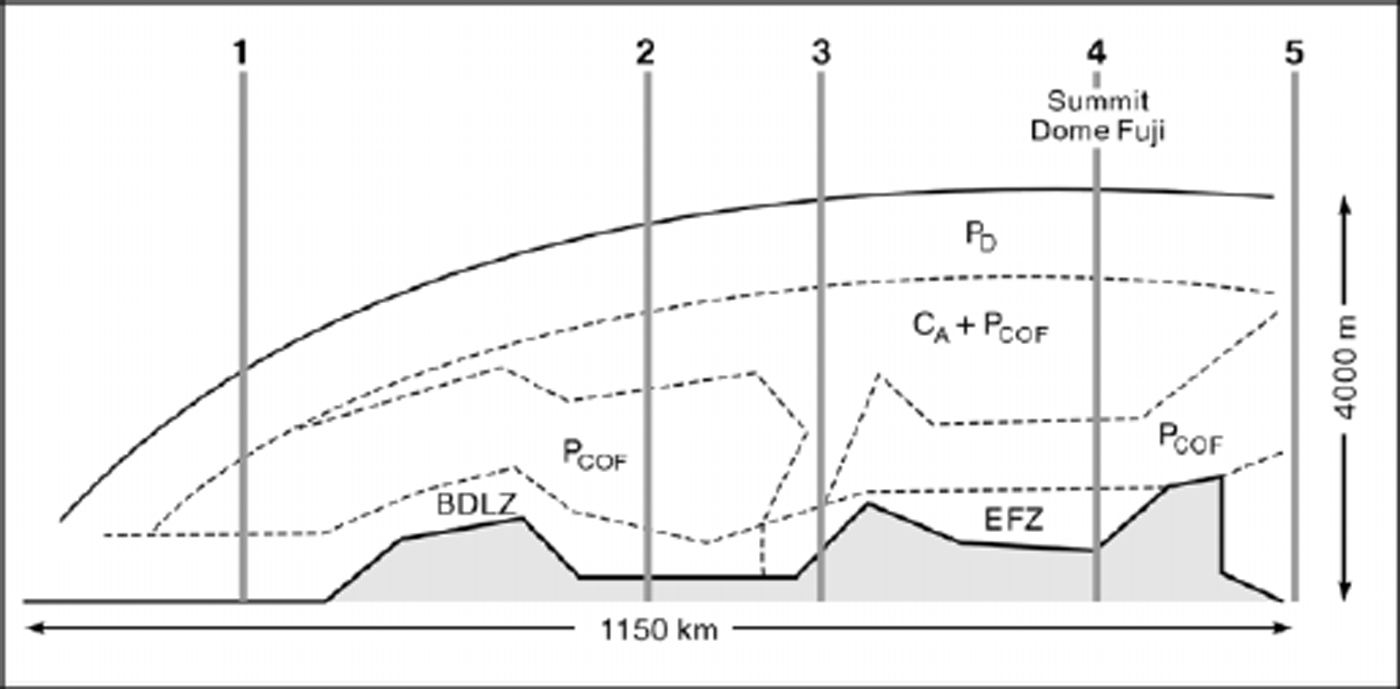
Fig 5. Location of each A-scope site in a schematic diagram of the JARE transect and the interpreted reflection mechanisms (adapted from Reference FujitaFujita and others, 1999).
Three depth-related features observed in the SPRI 60 MHz data can be readily identified in the JARE 60 MHz data. These features, discussed earlier, are: (1) ∂ 2 P R /∂z 2 >0 to ice depths of 700–900 m, in all places along the transect; (2) ∂ 2 P R /∂z 2 >0 or ∂ 2 P R/∂z 2<0 at ice depths of >900 m, depending on depth and the location in the transect; and (3) ∂ 2 P R /∂z 2> 0 at all depths close to the ice margin (Fig.4). The fourth depth-related feature is the EFZ zone, which is thought to be included within the SPRI BDLZ. The JARE 60 MHz radar could not identify the EFZ near the ice-sheet base because the transmitted power was only 1 kW (which is one-tenth of the 60 MHz radar used for the SPRI data (10 kW)). However, a clear EFZ was observed in the 179 MHz data (see raw data in Reference FujitaFujita and others, 1999). Therefore, both the SPRI and JARE data show signs of an EFZ in the lower regions of the ice sheet. The similarities between the 60 MHz A-scopes along these two remote transects suggest the existence of some similar physical mechanisms in the Antarctic ice sheet.
Correlation between A-scope shape and reflection mechanisms
One advantage of the dual-frequency JARE data is that the causes of internal reflections can be unambiguously determined at each depth range. When the difference between reflections from 179 and 60 MHz data is about 10 dB, the main cause of internal reflection must be changes in dielectric permittivity (P D or P COF) (Reference FujitaFujita and others, 1999). If the difference is close to zero, then the main cause of the layering is changes in electrical conductivity (C A). The reflection mechanisms determined across the JARE Dome Fuji transect are indicated in Figure 4. We notice from the JARE data that the sign of ∂ 2 P R/∂z 2 often correlates with the reflection mechanism. For example, when ∂ 2 P R/∂z 2 is negative, the reflection mechanism is most often C A. Further, when ∂ 2 P R/∂z 2 is positive, the reflection mechanism is most often P COF. However, at one location (site SSE150, Fig. 4) this correlation is absent. Provided that anomalous sites like SSE150 can be identified and excluded from further study, the shape of 60 MHz data can be used to identify the reflection mechanisms without the need for 179 MHz data. This analysis of the JARE data demonstrates that internal reflection mechanisms can be identified from inspection of the SPRI 60 MHz dataset.
Diagnostic features of anomalous A-scope records
Of the 10 A-scope examples provided in Reference FujitaFujita and others (1999), only A-scope shapes from sites around SSE150 show a relatively poor correlation with reflection mechanisms. It is important to understand how these anomalous records occur because, without such knowledge, it could be questioned whether we are able to distinguish those sites that are reliable for our analysis and those that are not. SSE150 is located in a very special situation, on the downstream side of a vertical > 1 km high subglacial step. As the ice flows down the step, upward shear strain occurs (see plate 2 (a) in Reference FujitaFujita and others (1999)). Because of this shearing, the C A zone, which usually appears at depths around 1000 m, is obscured. We can identify this kind of site by the occurrence of two features specific to SSE150. The first is the unusual bedrock topography mentioned above. The second is the strength of the reflections from internal layers. If we compare P R from several sites surrounding SSE150, it is roughly 10 dB smaller at SSE150. These two conditions are diagnostic of the A-scope record at SSE150. Although the mechanisms behind the noticeable reduction in reflected power in the high shear zone are not clear at present, Reference FujitaFujita and others (1999) noted that enhanced shearing at depths around 1000 m is likely to destroy the distribution of the acidic layering.
Discussion
Interpretation of reflection zones in SPRI data
Based on the similar features of the two radar datasets, and the correlation between the shapes of A-scope and the reflection mechanisms in the JARE data, the interpretation of ∂ 2 P R/∂z 2 measured in the SPRI A-scopes allows us to suggest how zones of permittivity and conductivity layering vary along the Dome C-TAM transect (Fig. 6). In all areas, we attribute layering in the top 700–900 m of ice mostly to ice-density variations. Below this, the nature of internal layering is related to geographical position. Along the entire transect, there is no situation where both of the diagnostic conditions of the anomalous case were met. This suggests that the convex and concave shape of the SPRI 60 MHz data can be attributed simply to the reflection mechanisms P D, C A and P COF.
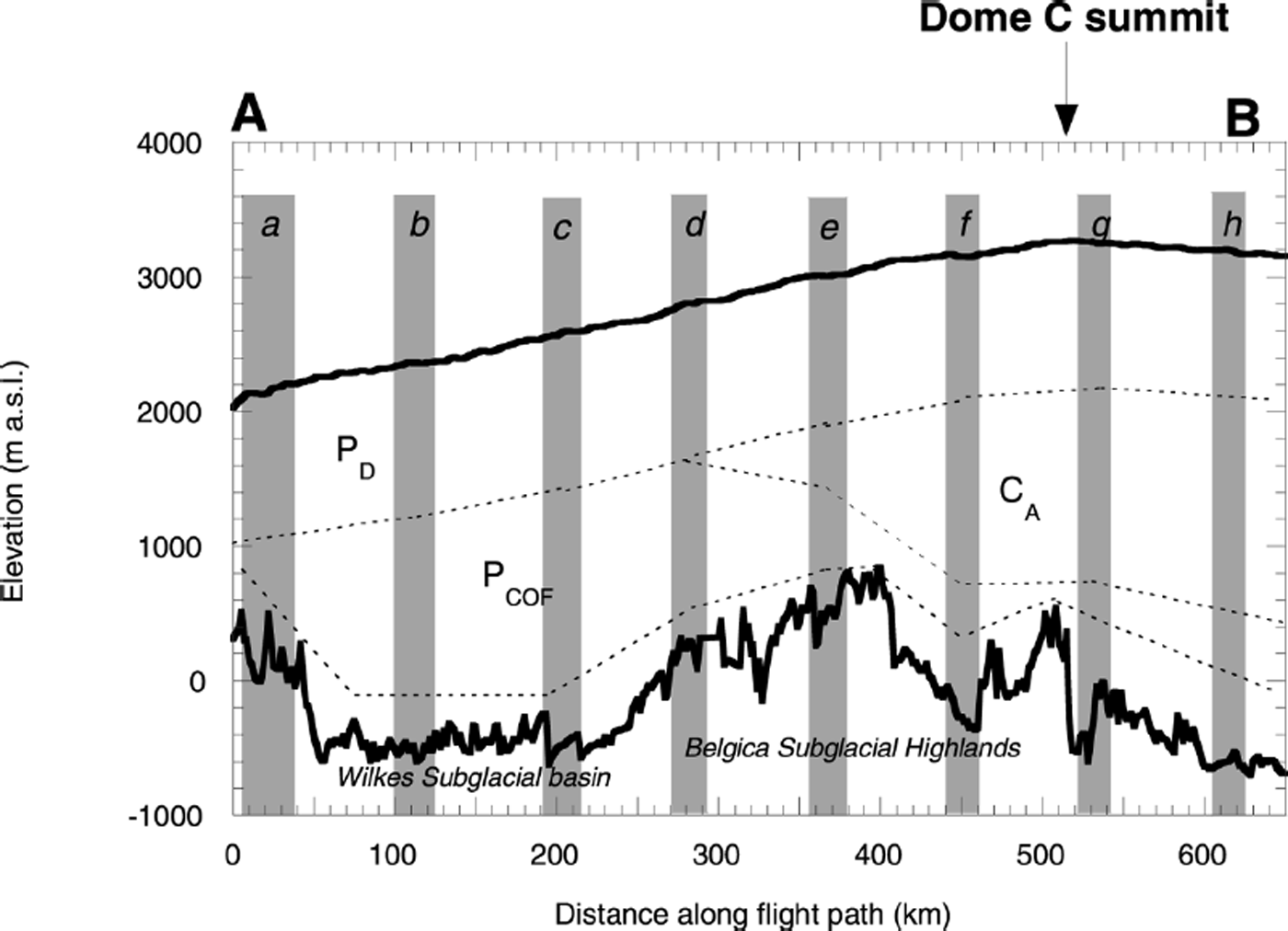
Fig. 6. Interpreted dominant reflection mechanisms along the SPRI radar transect (Fig 1) from Dome C to the TAM. In the JARE data, the zone dominated by C A reflections also contains some P COF reflections (Reference FujitaFujita and others, 1999).
Below the summit of Dome C (site g, Fig. 3a) conductivity-based reflections from acidic ice layers are located approximately between ice depths of 1000 and 2500 m. This zone thins away from the dome, and disappears entirely at site d and beyond (Fig. 3). The P COF zone exists to some extent at all locations (Fig. 3) and thickens as ice flows up the stoss side of the Belgica Subglacial Highlands (see Fig. 6). Downstream from site e the P COF zone increases further so that by site c it is > 1000 m thick.
The thickness of the BDLZ is observed from the Z-scope data to be related to bedrock morphology (Fig. 1). Where there are subglacial hollows the BDLZ is thickest (e.g. around 600 m at site h), whereas over the crest of subglacial hills the BDLZ is thinnest (e.g. <200 m at site e) (Fig. 3e).
The interpretation of the JARE transect (for details see Reference FujitaFujita and others, 1999) is adapted here to explain the flow of ice from Dome C to the TAM. At Dome C, we suggest that a lack of horizontal shear strain in the ice sheet results in the preservation of acidic layers of ice at depths of 1000–2000 m (C A). Below this, shear straining may occur across C A layers to produce crystal-orientation fabrics, although this idea cannot be verified from the A-scope data. Downstream from Dome C, the P COF zone generally thickens with distance from the ice divide. The most rapid increases in the thickness of this zone are related to the regions of greatest expected strain. For example, downstream from site f, the stoss face of the subglacial highlands may cause enhanced shearing and the formation of crystal-orientation fabrics (Figs 3 and 6). We estimate that by site e the thickness of the acidic-layer zone has decreased to around 500 m. Downstream from site e we expect that the dominance of crystal-orientation fabric layering is related to strong shearing in the ice column.
Further support for the correlation between concave A-scope shape, P COF and high shearing
The link between positive A-scope second derivatives and P COF reflections is supported by SPRI A-scopes near the Vostok ice core. Reference Siegert and KwokSiegert and Kwok (2000) found that a positive second derivative forms upstream of the ice-core site across a large subglacial hill. The internal layers at this location can be traced continuously across the ice sheet to the zone in which “deformed glacier ice” was reported in the Vostok ice core by Reference Lipenkov and BarkovLipenkov and Barkov (1998).
Limitations of the interpretation of A-scope shape
The correlation between the A-scope shape and the internal reflection mechanisms applies only in a general sense. In principle, the shape of an A-scope is controlled by the relative strength of the three reflection mechanisms, P D, C A and P COF. Therefore, a full understanding of an A-scope shape requires detailed knowledge of the ice-density fluctuations, variations in the ice-acidity level and changes in the crystal-orientation fabric. Such information, ideally at a centimetre-scale resolution, can come only from ice cores. Unfortunately, at the moment, the number of deep ice cores from the inland area of Antarctica is low (e.g. Dome F, Byrd and Vostok). Moreover, continuous high-resolution data at a fine resolution are rarely available even from these ice cores. Without such information, we cannot provide a fully quantitative explanation for the shape of 60 MHz A-scopes.
Conclusions
SPRI 60 MHz A-scope radar data along a flight-line transect between Dome C and the TAM were analyzed to determine the nature of internal layering. First, these data were compared with the JARE dual-frequency data (179 and 60 MHz) taken along a comparable transect from Dome Fuji to Mizuho station. Analysis of the JARE data showed that the sign of ∂ 2 P R/∂z 2 is a useful indicator of the internal reflection mechanisms. Although the sign of ∂ 2 P R/∂z 2 is not always correlated to the reflection mechanisms (the JARE data demonstrate that a mismatch occurs if high-shear zones are developed in the middle depth range of the ice sheet), we can identify such cases by observing (1) unusually high subglacial relief over which ice flows, and (2) relatively low strengths of reflections from internal layers. These diagnostic features measured at one location by the JARE dual-frequency data are absent in the SPRI 60 MHz data along the Dome C–TAM transect. This means that the SPRI data can be used to identify reflection mechanisms, which has two important consequences. First is that the occurrence of the P COF zone, due to the deformation of ice, along the transect can be evaluated. Second, and more importantly, SPRI 60 MHz radar data from other regions of Antarctica can be analyzed in future by the simple technique to establish the nature of ice-sheet radar layering at a continental scale.
A comparison of the Dome C–TAM transect with the Dome F–Mizuho transect suggests that there are similar distributions of the reflection mechanisms in the similar situations in the ice sheet. First, reflections from the P D mechanism dominate in the upper 700–900 m of the ice sheet due to contrasts in ice density. This reflection mechanism does not occur at ice depths > 700–900 m, because the density of ice becomes essentially constant. Second, the C A mechanism dominates in the depth range below 1000 m at the centre of the ice sheet. Third, the P COF mechanism dominates at ice depths of > 1000 m in the marginal area.
More specifically, internal reflection mechanisms along the transect are related to subglacial topography and distance from the ice divide. Beneath the summit of Dome C, the dominant cause of internal layering below 700–900 m is electrical conductivity boundaries (acidic ice layers). However, as ice flows toward the TAM, strain within the ice sheet produces crystal fabric layering sufficient to cause radar reflections. In the transect, 100 km from Dome C, ice flows over the stoss face of a subglacial hill. Here, strain is presumably high within the lower layers of ice, causing crystal-orientation fabrics to develop. Downstream of the subglacial hill, crystal-orientation fabrics develop in all of the ice below 1000 m. Thus, by 300 km from Dome C, the entire ice column at depths greater than 700–900 m is dominated by radar reflections from permittivity changes.
Acknowledgements
We thank the director of the SPRI, University of Cambridge, for access to radar data. We also thank two anonymous referees, one for providing thorough, highly detailed reviews of the manuscript, and the other for additional valuable comments. Funding for this work was provided by U.K. National Environment Research Council grant GR9/4782 to M.J.S. S.F. thanks O. Watanabe at the National Institute of Polar Research, Japan, for assistance with the travel funding to Bristol and Cambridge.








