2.1. Definition of benchmarks and of

Suppose that an elevation change ΔE ⁰ is observed over some measurement interval of N years. We wish to ask whether the magnitude of ΔE ⁰ is unusual. Is ΔE ⁰ typical for the past century? For the past millennium? Such questions are answered by comparing ΔE ⁰ to a PDF showing the relative likelihood of some given ΔE. This density function is the benchmark. Many different benchmarks can be defined. For example, the distribution of all N year elevation changes during the past 1000 years defines one benchmark, whereas the distribution of all N year elevation changes during the past 100 years defines another. If the accumulation-variability and densification-rate controls have not changed during this millennium, then these two benchmarks are identical, despite the difference in number of years. If the accumulation variability of the last 100 years differs from that of the last 1000, the benchmarks will be different. This analysis does not address the significance of such an underlying difference in 100 year climate vs 1000 year climate. For example, the 100 year climate may or may not be likely to arise by stochastic sampling from the 1000 year climate distribution. Either way, if the ΔE ⁰ is improbable according to the 100 year benchmark, it suggests that the dominant physical controls on Greenland annual climate are changing relative to their characteristic values of the past 100 years. It is beyond the scope of the present analysis to ascertain whether this change has broader significance (e.g. is related to changes of global climate forcings).

The following, more technical description is intended to eliminate possible ambiguity in the term “benchmark” and to define variables. Suppose that in a period of N years duration, the ice-sheet surface elevation changes by a net amount ΔE(N). Over a longer period of M years duration, the M − N + 1 values for ΔE for each N can be compiled to define a random variable whose distribution is characterized by statistics including a variance (the square root of which is the standard deviation ). A set of these distributions for various values of N based on a common M years ending at some time t ₀ constitute a “benchmark” to which future observations of ΔE(N) can be compared, and judged to be typical or anomalous. The Reference Van der Veen and BolzanVan der Veen and Bolzan (1999) statistics, after a correction is made for effective density, constitute a current-climate benchmark for elevation changes, a theoretical construct for which M is a small number of years and t ₀ is the present (a little more than two decades of record were used for their analysis). This is the useful benchmark from which to look for a contemporaneous climate change.

To compare the magnitude of any observed elevation change to historical changes, longer-term benchmarks can be defined (i.e. to ask whether an anomaly relative to the current-climate benchmark is also anomalous with respect to a longer period of time during which accumulation variability may have been greater or smaller). Here I calculate the “one-century benchmark”, for which M = 100 and t ₀ is the present, the “three-century benchmark”, for which M = 300 and t ₀ is the present, and the “millennial benchmark”, for which M = 1000 and t ₀ is the present.

It is important to recognize that is the standard deviation of the PDF that characterizes net elevation changes for a specified N and M. It is calculated from the second moment of the distribution and therefore is unbiased by sample size M − N. It is therefore independent of M if the accumulation variability is constant, unless there has been a change in firn density due to a change in mean accumulation rate or temperature.

2.2. Model physics

Ice-sheet surface elevation E rises or falls due to imbalances between net addition of mass by accumulation (ice-equivalent rate ) and the downward velocity of surface firn, which is due to a deformational velocity (w _s) and to basal vertical motion (rate ):

(1)

where ρ _i and ρ ₀ are ice and surface density, respectively, here taken to be 920 and 320 kg m⁻³. The basal motion results generally from bedrock uplift and from melting/refreezing. In central Greenland the latter process is absent because the basal temperature is ∼−10°C (Reference Cuffey, Clow, Alley, Stuiver, Waddington and SaltusCuffey and others, 1995). The w _s consists of a dynamic term due to the vertically integrated longitudinal stretching of ice in shear flow, and a term due to densification of firn and ice

(2)

where z is elevation above ice-sheet bed, H is ice-sheet thickness, is vertical strain rate due to volume-conserving deformation, ρ is bulk density and is rate of densification of a specified layer. w _d is a function only of ice-sheet geometry and rheology and therefore changes only on millennial scales (Reference OerlemansOerlemans, 1981; Reference WhillansWhillans, 1981). The annual snowfall rate, by contrast, has large stochastic changes (Reference OerlemansOerlemans, 1981), so ∂E/∂t is rarely close to zero; the ice-sheet surface will rise and sink in coherence with the fluctuations of . This response is modulated somewhat by changes in w _p which operate at intermediate time-scales (Reference Arthern and WinghamArthern and Wingham, 1998). Time-dependent densification implies that an elevation increase due to a mean increase is larger than for a steady density–depth profile (the firn column thickens), and that a temperature increase causes a surface lowering (thinning of the firn column).

Mechanisms for changes in the dynamic velocity w _d are reasonably well understood theoretically for an ice sheet immobile at its bed, but precise predictions of w _d for a given location on an ice sheet are uncertain. In central Greenland the most important ongoing elevation changes resulting from controls on w _d are thought to be:

1. (1) a decrease due to propagation of Holocene warmth (Reference WhillansWhillans, 1981);

2. (2) an increase due to late-Holocene rise in accumulation rate (Reference Cuffey and ClowCuffey and Clow, 1997);

3. (3) a possible increase due to advection of viscosity stratification (Reference ReehReeh, 1985).

In the present analysis, all of these changes are estimated using a quasi-one-dimensional flow model, described elsewhere (Reference Cuffey, Clow, Alley, Stuiver, Waddington and SaltusCuffey and others, 1995; Reference Cuffey and ClowCuffey and Clow, 1997). As with the zero-dimensional model of Reference OerlemansOerlemans (1981), this model responds to a change with an exponentially decaying rate, with a characteristic time of greater than a millennium, so the characteristics of the ice dynamics in this model are not otherwise important for analyses of short-term variability.

2.2.1. Densification

Variations in w_ρ are not understood in detail, and there is no standard physical model for predicting densification rate in the firn column; here using semi-empirical relations is a necessity. The most rapid response of the firn is in the uppermost section (ρ < 550), and understanding this region is most important for understanding time-dependent elevation on annual to decadal time-scales (Reference Arthern and WinghamArthern and Wingham, 1998). For the lower firn (ρ > 550) the relations of Reference Barnola, Pimienta, Raynaud and KorotkevichBarnola and others (1991) are used here (see Reference Schwander, Sowers, Barnola, Blunier, Fuchs and MalaizéSchwander and others, 1997).

For the upper firn I view the densification rate as resulting from two additive mechanisms

(3)

(4)

(5)

of which the dominant one is grain-boundary sliding (rate ) (Reference AlleyAlley, 1987), and the secondary one (rate ) results from vapor flux in the firn pore spaces.

The grain-boundary sliding rule (Equation (4)) is Alley’s (1987) model. I have followed Reference Arthern and WinghamArthern and Wingham’s (1998) suggestion and set the density at which grain-boundary sliding ceases (ρ ⁺) to a slightly higher value than the 550 kg m⁻³ used by Alley, and have arbitrarily chosen to use a 5% higher value. The prefactor k _G and activation constant Q _G are then treated as adjustable parameters here. Other terms in Equation (4) are: T is the absolute temperature, P is overburden pressure and P ₀ is air pressure.

As recognized by Alley, the sliding mechanism is inadequate in the topmost few meters, where densification occurs much more rapidly than predicted by Equation (4), and Equation (5) is supposed to contribute the extra densification. Based on the observation that it is needed only in the top few meters, it is assumed here that the missing mechanism is related to vapor flux in the snowpack, driven by the strong temperature and pressure gradients associated with penetration of the seasonal thermal cycle, with winds, and with the high vapor pressures associated with summer-time warmth. I am not confident of the physical mechanism important here but suggest that the continual rearrangement of the firn structure facilitates densification by creating voids that may be filled. Equation (5) is the simplest plausible description: a rapid depth decay (z _v = 2 m), a direct proportionality to the saturation water-vapor pressure P _vs as a function of temperature (Reference Iribarne and GodsonIribarne and Godson, 1973) and a tunable prefactor, k _v.

The densification model thus has three adjustable parameters: k _G, Q _G and k _v. Values for these are found by matching predictions of the density–depth profile to the observed density–depth profiles at GISP2 and at Dye 3. The resulting match is excellent (Fig. 1), with mks values k _G = 9.5 × 10⁸, Q _G = 6.5 × 10³ and k _v = 4 × 10⁻⁷. Though it is not a satisfactory physical model, I do consider this empirical description to be valid for small climate deviations around the present GISP2 value, of the sort that have occurred in central Greenland over the past several millennia.

Fig. 1. Comparison of model and measured density–depth structure. For GISP2, model results are the dashed line, and measurements (Reference Alley and KociAlley and Koci, 1990) shown as points (indicated by plus symbols) along the curve fit to the higher-resolution measurements. For Dye 3, model results are the solid line, and measurements are the diamonds (Reference Hammer, Clausen, Dansgaard, Gundestrup, Johnsen and ReehHammer and others, 1978). These model calculations use actual annual accumulation rate and temperature for GISP2, and a mean annual accumulation rate and a seasonal temperature cycle with a constant mean for Dye 3.

2.2.3. Effective density ρ_N

To interpret elevation-change statistics in terms of accumulation-rate variability, it is necessary to know the effective density corresponding to an N year observation interval. Specifically, if there is a standard deviation of climatic annual water-equivalent accumulation rate given by σ _c, then the effective density ρ_N is defined so that can be calculated from

(6)

In the limit of steady climate forcings and negligible elevation change, ρ_N is simply the depth-averaged density for the firn column between the surface and layers of age N. Such a depth-averaged value would probably offer a reasonable estimate of ρ_N in a variable climate, but in this study I calculate ρ_N directly from the time-dependent model to avoid any assumptions in this regard. Calculations show (see below) that ρ_N is indistinguishable from the depth-averaged value for N = 5 or 10, but rises to be 13% higher than the depth- averaged value for N = 50.

By writing as the sum , Equations (1) and (2) can be decomposed as

(7)

(8)

(9)

and the net elevation change over a time period t = N years written as

(10)

Over the time-scales considered here, the term can be neglected in central Greenland. Thus thickness changes are enhanced relative to their ice-equivalent values by an amount , which allows calculation of ρ_N for an N year observation interval as

(11)

2.3. Numerical implementation

I have added this time-dependent densification model to the quasi-one-dimensional heat-flow/ice-flow model of Reference Cuffey, Clow, Alley, Stuiver, Waddington and SaltusCuffey and others (1995) and Reference Cuffey and ClowCuffey and Clow (1997). As described in these studies, this model uses an Eulerian control volume mesh (Reference PatankarPatankar, 1980) with an adjustable grid to allow for elevation changes of the ice-sheet surface. Using this model in the present context is overkill in so far as the ice-dynamical part is unnecessarily complex, being designed foremost to look at problems coupling long-term firn-density changes to climate changes. It does, however, obviate questions as to how to treat lower boundary conditions, and fully accounts for propagation of thermal anomalies through the firn column. The resolution of the grid near the surface, where density gradients are large, is 2 cm. To avoid numerical instabilities, a small time-step of 0.2 years was used to counter the rapid densification rate near the surface.

2.4. Model response to simple forcings

Model behavior is most simply illustrated as the response to a step change in climate (Fig. 2). A step increase of from 0.24 m a⁻¹ to 0.28 m a⁻¹ results in thickening that is amplified by the time-dependent densification. A step increase in temperature from −31.5°C to −26.5°C results in thinning as the firn column warms. These responses are consistent with results of Reference Arthern and WinghamArthern and Wingham (1998).

Fig. 2. Modelled elevation response to step changes in climate, as described in the text (upper and lower curves). The middle dashed line shows the response to the accumulation-rate increase if the density–depth profile is held fixed.

3.1. Effective densities

The model calculations produce effective density values that vary significantly as a function of the N year observation interval (Fig. 3). This indicates that a single assumption such as ρ_N = 0.5ρ _i (Reference Van der VeenVan der Veen, 1993) may result in misinterpretation in some cases. The increase of ρ_N as a function of N is similar to the increase of depth-averaged density between the surface and layers of age N (Fig. 1). However, effective density rises more rapidly with N, and attains a 13% higher value by N = 50, implying that elevation variations are modestly smaller than expected from mean depth-averaged density. This results from the dependence of densification rate on overburden. High accumulation rate at the surface increases load on layers of given age at depth, causing the deep layers to densify more rapidly. This slightly reduces the elevation increase caused by the higher accumulation rate.

Fig. 3. Effective densities ρ_N as a function of observation interval N (solid line) Also shown is the depth-averaged density between the surface and the layer of age N (dashed line).

3.2. Current-climate benchmark

These ρ_N values can be used to construct a current-climate benchmark of N year net elevation changes, using the estimates for standard deviation of climatic water-equivalent annual accumulation rate (σ _c) for the recent past. The benchmark standard deviations of N year net elevation changes are then given by Equation (6). The corresponding statistics for annual average rate of elevation change are

(12)

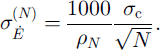
From the analyses of nine 24 year core records in the Summit region, Reference Van der Veen and BolzanVan der Veen and Bolzan (1999) estimate σ _c = 0.024 m a⁻¹, giving, for example, , , and . The corresponding average rates of elevation change are 0.03 and 0.02 m a⁻¹, respectively. The σ _c estimated from the GISP2 core for the most recent five decades available (1938–88) is larger, and is ∼ σ _c = 0.034 m a⁻¹. The corresponding benchmark statistics are , and (with corresponding average elevation change rates of 0.042 and 0.028 m a⁻¹). Both of these are viable estimates for a current-climate benchmark.

3.3. Multi-century benchmarks

The distributions of net elevation changes based on 100, 300 and 1000 years of climate forcing are all similar, and show greater variability than the current-climate benchmarks (Figs 4 and 5). This is directly a consequence of lower average accumulation variability during the most recent several decades compared to variability over the longer intervals (Fig. 6).

Fig. 4. (a) as a function of N (curve labelled “total”) and the corresponding variability holding density–depth structure constant (labelled “dynamic only”), (b) the standard deviation of annual average rate of elevation change, rather than net elevation change.

Fig. 5. These are benchmarks. Shown here are inferred PDFs for average rate of elevation change over 5 and 10 year observation intervals. Solid lines: density-adjusted current-climate benchmark using Reference Van der Veen and BolzanVan der Veen and BolzanS (1999) estimate for σ _c. Black diamonds: the multi-century benchmark.

Fig. 6. GISP2 core estimate of σ _c for periods from 1988 back to the number of years indicated. Also shown is the 1000 year average value. Here σ _c was calculated from annual accumulation variability (measured as σ _b) as , with σ _s = 0.027.

The σ_E for the 100, 300 and 1000 year benchmarks have relative magnitudes of 0.94, 1.0 and 1.04, respectively. These are close enough to be considered indistinguishable, so hereafter I will use the three-century benchmark as a representative multi-century benchmark. σ_E for this multi-century benchmark (Figs 4 and 5) is 1.23 times larger than the 50 year current-climate one, and 1.8 times larger than the current-climate one based on Van der Veen and Bolzan’s short-term but regional analysis.

This increase is not necessarily expected; more climate regimes are sampled as the basis for the benchmark is extended back through time, but these could be characterized by either smaller or greater variability. The late 20th century was a time of relatively small variability. It can be thought of as a biased sample of the long-term distribution. Note that higher variability appears to be a characteristic of the Little Ice Age climate, a thermal minimum which is seen clearly in the temperature-depth signal in central Greenland (Reference Alley and KociAlley and Koci, 1990; Reference Cuffey, Alley, Grootes, Bolzan and AnandakrishnanCuffey and others, 1994).

The increase of σ_E with N (Fig. 4) is similar to, but smaller than, the pattern expected for a Gaussian random forcing, the difference resulting from the increase of ρ_N . Not surprisingly, the empirical PDFs are individually very nearly normal distributions (e.g. Fig. 7).

Fig. 7. Black diamonds: PDF for 20 year average rate of elevation change, for the three-century benchmark. Dashed line: the normal distribution with equivalent mean and variance.

4.1. Sensitivities

Results are only weakly sensitive to reasonable changes in the model densification rates. Reducing the rate of the densification mechanisms in the upper firn (ρ < 550) by 20%, for example, reduces by only 2%. This low sensitivity reflects the slow pace of the densification; ρ ₅ is only ∼30 kg m⁻³ higher than surface density. With 20% slower densification, ρ ₅ is ∼24 kg m⁻³ higher than the surface density, implying a real change of 1 − (344/350) = 0.02. The difference becomes greater for longer observation intervals, of course, but these are also harder to interpret in practice because the mean ice-dynamical and isostatic elevation-change rate has more of an impact.

Even with our poor current understanding of the physics of the densification process, it is clear that the degree of covariation of temperature and accumulation-rate fluctuations is a potentially important control on . The foregoing analyses have assumed that the temperature history is given exactly by the δ ¹⁸O record. Although claims for a strong correlation of mean annual δ ¹⁸O and temperature are supported by studies spanning a few years (Reference ShumanShuman and others, 1997), and spanning centuries to millennia (Reference Cuffey, Alley, Grootes, Bolzan and AnandakrishnanCuffey and others, 1994, Reference Cuffey, Clow, Alley, Stuiver, Waddington and Saltus1995), a strong correlation has been neither demonstrated nor refuted for the 5–50 year intervals most relevant here. It is unlikely that the assumption of a perfect δ − T correlation has a large impact on the results, because the correlation of and T at these scales is weak in central Greenland (Reference Kapsner, Alley, Shuman, Anandakrishnan and GrootesKapsner and others, 1995). However, I have conducted an extreme sensitivity test for heuristic purposes, by repeating the analyses with the assumption that T and are perfectly correlated or anticorrelated so that

(13)

Given that from year to year typically varies by less than ∼0.12 m a⁻¹, and mean annual T is known to vary ∼3 K (Reference ShumanShuman and others, 1997), I choose γ = 3/0.12 = 25 K a m⁻¹ as an extreme. The result (Table 1) is that σ_E increases by < 10% if and T are negatively correlated, and σ_E decreases by < 20% if they are positively correlated.

Table 1. Fractional change in and for the sensitivity tests concerning correlation of and T, as described in the text

4.2. Generalization

The preceding results are for the Greenland Summit (where , T = −31.5°C), but may be used to approximate elevation-change statistics elsewhere on the ice sheet in the dry-snow zone, provided that the results for are normalized to the total ice accumulation over N years and that the location of interest has a ratio similar to that at GISP2.

To illustrate that changes in ρ_N do not damage this approximation severely, the model has been run with mean climatic conditions similar to those of Dye 3, by using T = T _GISP2 + 10 and . The resulting elevation variability normalized to the ice accumulation rate is roughly 15% less than that at GISP2 (Fig. 8).

Fig. 8. normalized to , the annual ice-equivalent accumulation rate. Diamonds: result from GISP2 forcing, as before. Squares: result for “Dye 3-like” mean climatic conditions, assuming σ _s = 0.027 m a⁻¹ ice equivalent. Plus symbols: for comparison, the same result assuming σ _s = 0.

Thus ρ_N changes are modest as long as the snow is dry. Note, however, that summer melt becomes increasingly important as mean climate warms from GISP2 conditions to Dye 3 conditions. Although the densification model accurately describes the rise of density with depth at Dye 3, the variability calculations do not allow for changes in near surface density associated with melt production. Near surface density changes resulting from changes in the magnitude of surface melt production would propagate to depth. Thus the variability benchmark results presented here should not be used in regions with regular summer melt.

The uncertainty associated with surface melt variability is potentially large in southern Greenland. The mean fraction of the Dye 3 core that is refrozen meltwater is only approximately 5% (Reference Herron, Herron and LangwayHerron and others, 1981). Yet as melt fraction increases from 0% to 10%, ρ ₅ increases from ∼350 to ∼400 kg m⁻³, corresponding to a 15% decrease in the elevation variability.

4.3. Mean value

The model estimate for the mean value of elevation change is an increase of ∼8 mm a⁻¹, or a net increase of 0.04 and 0.4 m over 5 and 50 years, respectively. This slow increase is the continuing response to increased accumulation rate late in the Holocene (Reference Cuffey and ClowCuffey and Clow, 1997), balanced somewhat by thinning due to propagation of the Holocene thermal perturbation (Reference WhillansWhillans, 1981). The effect of this slow increase is negligible relative to the accumulation variability over 5 or 10 year intervals, but becomes important by 50 years, for which it is a substantial fraction of one standard deviation.

The uncertainty in this mean value is difficult to quantify, as it depends on factors like temporal changes in the spatial gradient of accumulation rate, which are not known. It is important to recognize, therefore, that an observed elevation change that appears anomalous relative to either the current-climate benchmark or the multi-century benchmark may indicate either a climate change or a persistent ice-dynamic or isostatic response.