Introduction
The spatial distribution of mountain snow cover is of interest in cryospheric science for issues such as modelling mass balance of glaciers (e.g. Reference Huss, Farinotti, Bauder and FunkHuss and others, 2008; Reference Dadic, Mott, Lehning and BurlandoDadic and others, 2010a), determining the snow-cover duration for ecological investigations (e.g. Reference Tappeiner, Tappeiner, Aschenwald, Tasser and OstendorfTappeiner and others, 2001), identifying risks from natural hazards (e.g. Reference Schweizer, Kronholm, Jamieson and BirkelandSchweizer and others, 2008) and simulating the runoff regime of mountain catchments (e.g. Reference Lundquist and DettingerLundquist and Dettinger, 2005; Reference Achleitner and KirnbauerSchöber and others, 2010; Reference Bavay and LehningBavay and others, 2013). The spatial variability of snow depths is recognized as a challenging feature, especially regarding scaling issues and the simulation of the fundamental processes causing the heterogeneity of snow (e.g. Reference PomeroyPomeroy and others, 1998; Blöschl, 1999; Reference Deems, Fassnacht and ElderDeems and others, 2006, Reference Deems, Fassnacht and Elder2008; Reference TrujilloTrujillo, 2007; Grünewald and others, 2013). Since simulations of mountain hydrology require not only runoff measurements but also ground-truth data of the snow cover for validation (e.g. Reference Gutknecht and KirnbauerBlöschl and others, 1991; Reference Huss, Zemp, Joerg and SalzmannHuss and others, 2014), snow-cover distribution is measured using in situ measurements (e.g. Reference Elder, Dozier and MichaelsenElder and others, 1991; Reference Kaser, Fountain and JanssonKaser and others, 2003; Reference Lundberg, Granlund and GustafssonLundberg and others, 2010) and remote-sensing techniques (e.g. Reference NolinNolin, 2010; Reference Rittger, Painter and DozierRittger and others, 2013). Point information from weather stations or snow depth measurements is used to interpolate and extrapolate the mountain snow cover to the catchment scale for snow-hydrological studies (e.g. Reference Gutknecht and KirnbauerBlöschl and others, 1991; Reference Anderton, White and AlveraAnderton and others, 2004). However, the representativeness of individual measurements is uncertain (Reference Sevruk and SevrukSevruk, 1986; Reference LehningGrünewald and Lehning, 2011). The lidar remote-sensing technique (e.g. Reference BaltsaviasBaltsavias, 1999; Reference Wehr and LohrWehr and Lohr, 1999) is a useful tool to obtain spatially distributed snow depth data at high spatial resolution from repeated surveys (Reference Deems, Painter and FinneganDeems and others, 2013). Lidar was applied to derive snow depths in test areas (e.g. Reference Hopkinson, Hardy and FrankensteinHopkinson and others, 2001; Reference Deems, Fassnacht and ElderDeems and others, 2006, Reference Deems, Fassnacht and Elder2008), on individual mountain slopes (e.g. Reference Prokop, Schirmer, Rub, Lehning and StockerProkop and others, 2008; Reference Sailer, Fromm, Schaffhauser and AdamsSailer and others, 2008; Reference SchaffhauserSchaffhauser and others, 2008; Reference Schirmer, Mott and LehningGrünewald and others, 2010; Reference Schirmer and LehningSchirmer and others, 2011), for individual glaciers (e.g. Reference Fromm, Sailer and SchaffhauserJörg and others, 2006; Reference GeistGeist and Stötter, 2007; Reference Sold, Huss, Hoelzle, Andereggen, Joerg and ZempSold and others, 2013; Reference Helfricht, Kuhn, Keuschnig and HeiligHelfricht and others, 2014) and entire mountain catchments (e.g. Reference Dadic, Mott, Lehning and BurlandoDadic and others, 2010a; Reference Helfricht, Seiser, Fischer and KuhnHelfricht and others, 2012; Grünewald and others, 2013; Schöber and others, in press). However, multi-annual data of spatial snow depth distribution, i.e. the total volume of snow cover over entire catchments, are rare.
Interannual persistence of the spatial snow distribution is a prerequisite for applying simple parameterizations of snow redistribution in hydro-meteorological models simulating the snow cover of high mountain catchments (e.g. Reference Huss, Farinotti, Bauder and FunkHuss and others, 2008; Reference StrasserStrasser, 2008; Reference Dadic, Mott, Lehning and BurlandoDadic and others, 2010b; Reference Mott, Schirmer, Bavay and LehningMott and others, 2010; Schöber and others, in press). Until now, long-term observations of spatially distributed snow depths have been based on manually taken snow depth samples (Reference Sturm and WagnerSturm and Wagner, 2010; Reference Jepsen, Molotch, Williams, Rittger and SickmanJepsen and others, 2012; Reference Winstral and MarksWinstral and Marks, 2014). Reference Sturm and WagnerSturm and Wagner (2010) showed that climatological snow patterns derived from multi-annually measured snow depth distributions are suitable for simulating the snow depth distribution. In alpine mountain catchments, spatial snow distribution is attributed to preferential deposition of snow and the subsequent wind-induced snow transport processes acting on various scales (e.g. Reference Lehning, Ryser and RadeschallLehning and others, 2008; Reference Dadic, Mott, Lehning and BurlandoDadic and others, 2010a; Reference Mott, Schirmer, Bavay and LehningMott and others, 2010). Reference Mott, Schirmer and LehningMott and others (2011a) suggest that a model resolution of 5 m is not sufficient to capture all processes that drive snow-cover variability in areas of complex alpine topography.
Geostatistical analyses are the basis for the spatial design of measurements of snow depth and snow-cover models (Blöschl, 1999). Snow cover presents a multi-scaling behavior (e.g. Reference Shook and GrayShook and Gray, 1996; Reference Deems, Fassnacht and ElderDeems and others, 2008; Reference Schirmer and LehningSchirmer and Lehning, 2011) with a short-range fractal and a long-range fractal separated by a scale break. Typical scale breaks of snow depths were observed between meters and tens of meters, both for manually taken snow samples (e.g. Reference Shook and GrayShook and Gray, 1996) and snow depths derived from lidar data (Reference Deems, Fassnacht and ElderDeems and others, 2006, Reference Deems, Fassnacht and Elder2008; Reference TrujilloTrujillo, 2007; Reference Schirmer and LehningSchirmer and Lehning, 2011). The fractal (Hausdorff–Besicovich) dimension was found to be useful for analyzing the irregularity of objects and surfaces (Reference BurroughBurrough, 1993; Reference Gao and XiaGao and Xia, 1996). The fractal dimension allows the influence of short-range fluctuations (caused by, e.g., snow surface structures, sastrugi and cornices) to be differentiated from long-range fluctuations, related to topography, on snow-cover variability (e.g. Reference Schirmer and LehningSchirmer and Lehning, 2011). Detailed analyses of multi-annual consistency in scaling behavior based on high-resolution lidar data are limited to the comparison of two accumulation seasons. Reference Schirmer and LehningSchirmer and Lehning (2011) and Deems and others (2008) indicate an interannual consistency of fractal dimensions and scale breaks of snow depths at the end of the accumulation season. Reference Schirmer and LehningSchirmer and Lehning (2011) showed that the scale breaks increase while short-range fractal dimensions decrease, due to smoothing of the surface by snow accumulation associated with northwesterly storms towards the end of the accumulation season.
In this study, a unique multi-year dataset of snow depths is introduced, derived from airborne laser scanning (ALS) surveys of the seasonal snow cover in a partly glacierized mountain catchment of ~36 km2. The detailed snow depth data allow the combination of the advantages of high spatial resolution and multi-annual data. The study aims to investigate the temporal and spatial interannual persistence of seasonal snow depths, snow patterns and scaling behavior of the snow cover.
Annual mean snow depths and their spatial variability are determined, to compare the overall temporal persistence of snow accumulation in the investigated basin. Correlation coefficients between each of the annual snow depth distributions are calculated at spatial resolutions of 1–100 m. This allows us to differentiate between processes causing high interannual variability, even at coarser resolutions; and the increasing correlation with decreasing resolution as a result of a reduction of the spatial variability of snow depth (e.g. Blöschl, 1999; Reference Melvold and SkaugenMelvold and Skaugen, 2013). Areas with persistent snow cover are distinguished from areas with variable snow cover by analyzing the temporal variability in standardized snow depths. Maps of squared errors of standardized snow depths are shown to locate processes causing interannual differences in snow patterns. A k –means clustering is used to detect areas of similar spatial and temporal characteristics of the residuals of snow depths from the mean snow depth in their vicinity. Finally, the interannual variability in fractal dimensions and scale breaks of the snow depth distribution is derived from a semivariance analysis.
The results help emphasize the main characteristics of the snow depth distribution in this Alpine catchment and support simulations of the snow cover in this mountain region and comparable mountain basins.
Study Site and Data
The investigated area is located on the main Alpine ridge in the Ötztal Alps, Austria (46°48’ N, 10°46’ E). It covers a partly glacierized catchment of the upper Rofen valley (Fig. 1). The total area is 35.9 km2, of which 50% was glacierized in 2001 and 44% in 2011; i.e. a loss in glacier area of 12% in 10 years. The elevation within the study area ranges from 2234 to 3738 m a.s.l. The mean elevation over the investigated area is 3005 m a.s.l. Aspect is predominantly southeast at elevations below 2500 m a.s.l. (Fig. 1). Most slopes face southeast and northwest at elevations between 2500 and 3500 m a.s.l. Aspects from southwest to west are, in general, less frequent. Most of the area below 3000 m a.s.l. has a slope angle of 20–40°. Between 3000 and 3500 m a.s.l., glacier surfaces with a slope of <30° are most frequent. The glaciers Hintereisferner (HEF) and Kesselwandferner (KWF) are located in the investigated area. Both glaciers have been monitored for decades (Reference HoinkesHoinkes, 1970; Reference Kuhn, Dreiseitl, Hofinger, Markl, Span and KaserKuhn and others, 1999; Reference FischerFischer, 2010; Reference Fischer, Markl and KuhFischer and others, 2012). The upper parts of the glaciers Gepatschferner (GPF) and Langtauferer Ferner (LF) are partly included in the investigated area. Since 2001, annual ALS flights have been conducted in this mountain area, from which annual glacier volume changes (Reference Geist and JacksonGeist and others, 2005; Reference BollmannBollmann, 2010) and intra-annual surface elevation changes (Reference GeistGeist and Stötter, 2007) have been calculated. For this study, glacier outlines were derived separately for the date of ALS(t 1) according to Reference Abermann, Fischer, Lambrecht and GeistAbermann and others (2010). Available ALS data cover five accumulation seasons between 2001 and 2012.
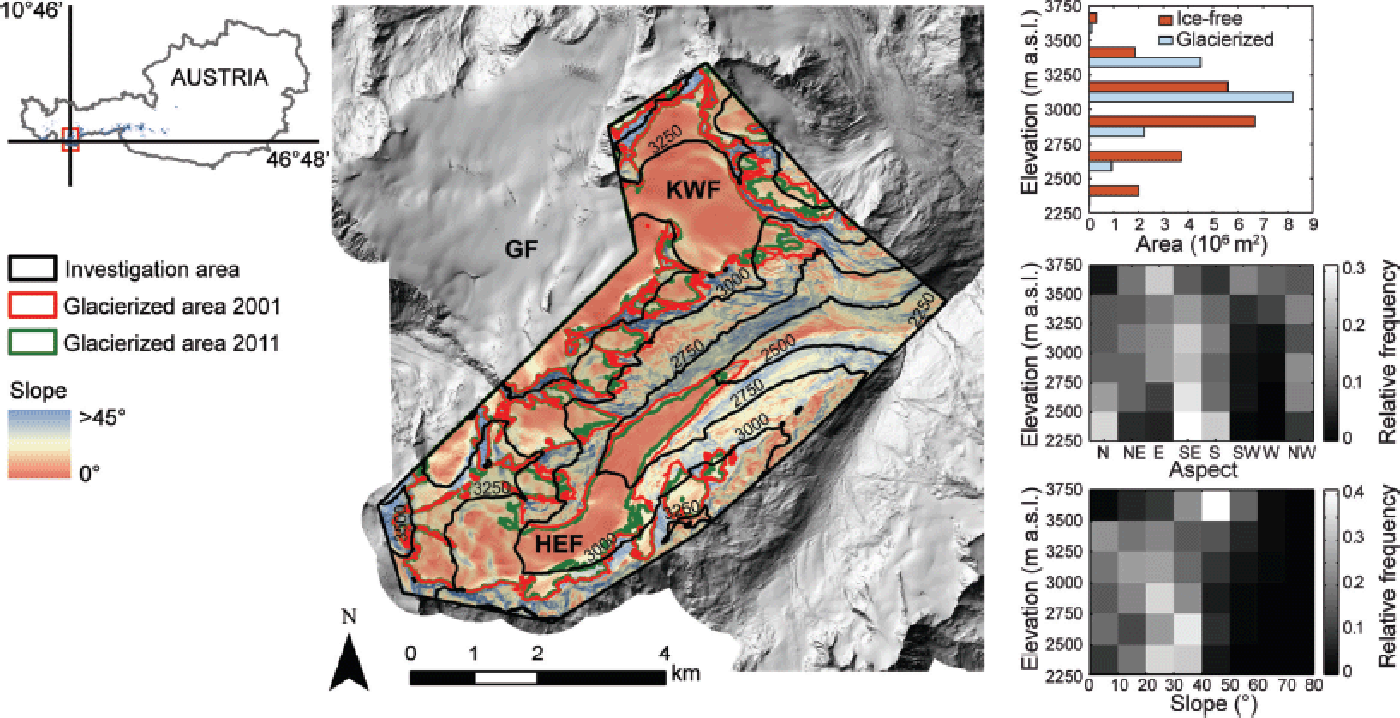
Fig. 1. Map of the investigated area, including the glaciers Hintereisferner (HEF), Kesselwandferner (KWF) and the uppermost part of Gepatschferner (GF). The color scale shows the slope of the surface. Glacier outlines for the years 2001 (red) and 2011 (green) and contour lines of elevation in 250 m steps (black) are presented. The area/elevation distribution (upper right) and the frequency distribution of aspect (middle right) and slope (lower right) of 250 m elevation zones are shown.
Table 1 shows the dates of the ALS surveys, along with the devices used, maximum scan angles, laser repetition rates, scan frequencies and assessments of the vertical accuracy since 2002. Vertical accuracy was derived by comparing ALS data with a flat and snow-free reference surface down the valley near the study area. Mean deviation between actual altitude of the reference surface and the z –value of the lidar points had a maximum of 0.076 m and a maximum standard deviation of 0.11 m (Table 1). Point densities increase over time due to the improvement in scanner devices. Mean flight speed was 65–70 m s–1 . Mean flight altitude was 1000–1200 m above ground.
Table 1. Overview of the ALS flight campaigns investigated in this study. The accuracy is obtained from deviations between ALS surface elevations and elevations of a known reference surface. Mean flight altitude was 1000–1200 m above ground

Point clouds were filtered to bare ground using last returns of the laser signal. All points within a gridcell were averaged to generate digital elevation models (DEMs) with a grid size of 1 m. Gridcells without lidar point measurements were filled using inverse distance weighting. Due to the high number of measured points and the location of the investigation area above the tree line, simple interpolation schemes deliver high-accuracy DEMs (Reference Deems, Painter and FinneganDeems and others, 2013). Reference Bollmann, Sailer, Briese and FritzmannBollmann and others (2011) estimated that DEMs produced in the Hintereisferner region had a relative vertical accuracy better than ±0.15 m for slopes less than 35°. The accuracy of the ALS measurements decreases considerably with increasing laser distance and decreasing illumination angle (Reference Bollmann, Sailer, Briese and FritzmannBollmann and others, 2011; Reference Joerg, Morsdorf and ZempJoerg and others, 2012). Early-stage application of ALS measurements in 2002 might be influenced by higher uncertainties due to the lower point densities compared with the subsequent years (Reference Bollmann, Sailer, Briese and FritzmannBollmann and others, 2011; Reference Fritzmann, Vetter, Sailer and BollmannFritzmann and others, 2011).
Two lidar surveys are required to extract seasonal snow depth from multi-temporal ALS data (e.g. Reference Hopkinson, Hardy and FrankensteinHopkinson and others, 2001; Reference Deems, Painter and FinneganDeems and others, 2013). Data have to be recorded prior to the accumulation season (‘snow-off’, here referred to as date t 1) and at the time of maximum snow depth (‘snow-on’, here referred to as date t 2; Table 1). In mountain catchments with a high elevation range it is difficult to cover the date of the minimum and maximum accumulation exactly. While snow accumulates at higher elevations, ice- and snowmelt can simultaneously occur at lower elevations.
The densification of fresh snow accumulated prior to ALS (t 1) causes underestimation of snow depths by lidar measurements. Snow ablation or ice ablation lowers the surface between ALS(t 1) and the final formation of the seasonal snow cover and thus can also lead to underestimation of the snow depths. The densification of the firn cover and ice flow causes underestimation of the snow depths by lidar in typical accumulation areas of the glaciers (e.g. Reference Sold, Huss, Hoelzle, Andereggen, Joerg and ZempSold and others, 2013; Reference Helfricht, Kuhn, Keuschnig and HeiligHelfricht and others, 2014). With respect to the glacierized study area, the dates of the ALS flights (Table 1) were chosen to be close to the typical dates of glacier mass-balance measurements using the fixed date system (e.g. Reference Kaser, Fountain and JanssonKaser and others, 2003).
Meteorological Conditions
Meteorological measurements located in the investigation area do not cover the whole period of this study. To give an overview of the weather conditions, temperature and precipitation measured at six weather stations next to the investigated basin are spatially interpolated using an inverse distance weighting algorithm for precipitation and a regression approach for temperature, implemented in the preprocessing module of the flood-forecasting system of the river Inn (Reference AchleitnerAchleitner and others, 2012). The data are valid for an elevation of 2400 m a.s.l., which coincides with the lowest elevations of the investigated basin (Fig. 1). Mean daily temperatures and cumulative precipitation of all five accumulation seasons are shown in Figure 2.
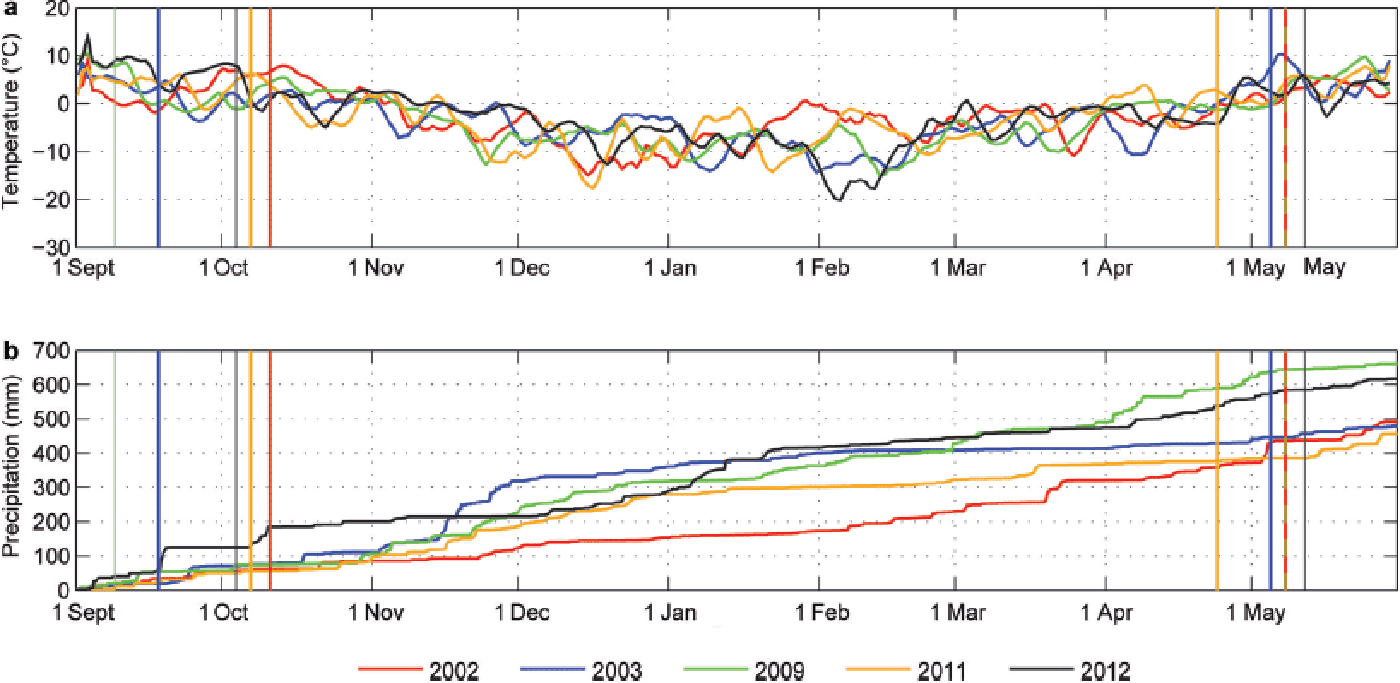
Fig. 2. Mean daily air temperatures valid for an elevation of 2400 m a.s.l. (a) and the cumulative precipitation (b) of the five accumulation seasons. Dates of the ALS surveys are shown as vertical lines. Note that t 2 of 2002 and 2009 coincide on 7 May.
In September 2001, a snow cover was accumulated in the study area and persisted until ALS(t 1) (e.g. Reference Bollmann, Sailer, Briese and FritzmannBollmann and others, 2011). The mean temperatures after ALS(t 1) provided melt conditions from the end of September to mid-October. Only 30% of the seasonal precipitation had accumulated by the end of January. Snow accumulated frequently in February and March 2002. A precipitation event caused a distinct increase in snow depth a few days prior to ALS(t 2) in 2002.
In 2002, ALS(t 1) was performed in mid-September. Temperatures decreased to 0°C shortly thereafter, indicating less melting of the ice or snow until the formation of the seasonal snow cover. While ~50% of the seasonal precipitation was accumulated in November, particularly the second half of this accumulation season continued with precipitation below average.
In 2008, mean daily temperatures were ~0°C after ALS (t 1). In October 2008, a period of positive temperatures caused potential melt at the glacier tongues (Schöber and others, in press). However, the highest cumulative precipitation during the five investigated accumulation seasons was measured in 2009, due to a steady occurrence of precipitation events in the second half of the accumulation season.
Snow accumulated prior to ALS(t 1) in 2010 (Reference Helfricht, Kuhn, Keuschnig and HeiligHelfricht and others, 2014; Schöber and others, in press). Until late January 2011, the cumulative precipitation was similar to 2009. Subsequently the accumulation season stayed dry. Positive temperatures enabled snowmelt on several days prior to ALS(t 2) in April 2011.
Prior to ALS(t 1) in 2011, a snow cover was accumulated in mid-September. However, this was distinctly reduced by melt until the date of ALS(t 1) (personal communication from Reference Fischer, Markl and KuhA. Fischer, 2012). A snowfall was recorded shortly after ALS (t 1), followed by almost dry conditions for 2 months. Higher accumulation rates were observed in December and January 2012.
Schöber and others (in press) discussed the influence of melt and sublimation during the 2009 and 2011 winter seasons based on model simulations of the energy balance of the snow cover. Whereas melt and sublimation accumulate to 0.17 m of the surface elevation change between ALS(t 1) in 2008 and ALS(t 2) in 2009, the same calculations resulted in a surface lowering by only 0.04 m between ALS(t 1) in 2010 and ALS(t 2) in 2011. Results for the accumulation periods 2002 and 2003 were found to be between these values.
Precipitation measured at three cumulative precipitation gauges located in the investigated catchment, namely Hintereisferner (HEF), Rofenberg (RB) and Proviantdepot (PD), allows comparison of the variability in precipitation of the five investigated seasons with a climatic series. Precipitation measured at the gauges is summarized for October–April in the period 1983–2012 (Table 2). The mean cumulative precipitation of the five investigated accumulation periods is slightly higher than mean cumulative precipitation over the 30 year period at all three gauges. The maximum winter precipitation measured in this catchment during the past 30 years (in 2009) is included in the five investigated seasons. Cumulative winter precipitation was lower than the climatic mean in the 2011 season, but within one standard deviation of the winter precipitation between 1983 and 2012. The temporal coefficient of variation, CV, of measured winter precipitation was 0.22 for the 30 year period (Table 2).
Table 2. Precipitation measured between 1 October and 30 April at the three cumulative precipitation gauges: Hintereisferner (HEF), Rofenberg (RB) and Proviantdepot (PD). Winter precipitation measured in the investigated seasons is shown for each accumulation season separately. Minimum, mean and maximum values and the temporal CV are presented for the 30 year period 1983–2012

Methods of Snow-Cover Analysis
Analysis of spatial and temporal distribution
Seasonal snow cover is analyzed based on DEMs with a grid size of 1 m. The surface elevation at ALS(t 1) is subtracted from the surface elevation at ALS(t 2) to calculate surface elevation change, Δz ALS:
Values of Δz
ALS are interpreted as snow depth, HS. HS values in the range −10 m ≤ HS ≤ 15 m are used for the analysis. Negative HS, which are an artifact of the measurement principle (Reference Hopkinson, Hardy and FrankensteinHopkinson and others, 2001), are not removed, to maintain the original distribution of the ALS-derived information. The temporal variability of the mean annual snow depth, ![]() , and its spatial variability in terms of the standard deviation, σ, and the corresponding CV are analyzed. A threshold HS of 0.15 m is used to distinguish between snow-free and snow-covered areas. According to the assumed relative vertical accuracy (Reference Bollmann, Sailer, Briese and FritzmannBollmann and others, 2011), this threshold accounts for the distribution of zero snow depths at ±0.15 m, i.e. HS < 0.15 m can result from zero snow depth and DEM error. Areas of HS < 0.15 m are also assumed to feature a scattered snow cover. The interannual persistence of HS and snow-covered area, SCA, with altitude is analyzed in 25 m elevation zones.
, and its spatial variability in terms of the standard deviation, σ, and the corresponding CV are analyzed. A threshold HS of 0.15 m is used to distinguish between snow-free and snow-covered areas. According to the assumed relative vertical accuracy (Reference Bollmann, Sailer, Briese and FritzmannBollmann and others, 2011), this threshold accounts for the distribution of zero snow depths at ±0.15 m, i.e. HS < 0.15 m can result from zero snow depth and DEM error. Areas of HS < 0.15 m are also assumed to feature a scattered snow cover. The interannual persistence of HS and snow-covered area, SCA, with altitude is analyzed in 25 m elevation zones.
Pearson correlation coefficients, r, of HS are calculated between each combination of the five HS distributions. HS are sampled to coarser grid sizes (10, 30, 50 and 100 m) using the area-weighted mean of the 1 m HS values. Variability is known to decrease with increase of spatial aggregation (e.g. Reference Gutknecht and KirnbauerBlöschl, 1999). The spatial scale of 10 m is chosen to reduce the noise of the original 1 m data without losing too much information about snow-cover variability. A spatial resolution of 30 m was used by Reference Sturm and WagnerSturm and Wagner (2010) and Reference Winstral and MarksWinstral and Marks (2014), who analyzed manually sampled snow depth data. A typical scale of 50 m is used for the simulation of high-mountain snow cover and mountain hydrology (e.g. Reference StrasserStrasser, 2008; Schöber and others, in press). Spatial scales of >100 m show a reduction in variability of high-resolution snow depth data (e.g. Grünewald and others, 2013) and cause a distinct loss in information on spatial snow depth patterns (e.g. Reference Melvold and SkaugenMelvold and Skaugen, 2013).
Spatially distributed standardized snow depths, HS s, are calculated according to Reference Sturm and WagnerSturm and Wagner (2010) for the interannual comparison of seasonal snow depths, using
where σHS is the annual areal standard deviation of HS in one winter. Squared errors of HS s (SEs) are calculated for all possible combinations of two available snow depth distributions (1 and 2) using
The resulting maps of SEs (ten in total) are used to identify regions of high interannual snow depth variability and areas of interannually persistent HS s. Areal means of the squared errors of standardized snow depths, MSEs, are used as a metric of overall similarity of the snow depth distributions.
Residual analysis
Spatial snow-cover variability is expressed by residuals of HS (rHS ) to their vicinity. We use a moving-window approach to calculate the residual of each HS to the mean HS of its squared vicinity of 5 × 5 raster cells:
where n is the number of cells of the window and i, j are the distances in the x – and y –directions from the center. While a homogeneous snow cover is characterized by almost zero rHS , a heterogeneous snow cover shows distinctly negative and positive values of rHS . The magnitude of rHS is controlled by spatial variations in the underlying topography and variability of the snow on its surface. Values of rHS are calculated at a raster resolution of 10 m within a 50 m square. Thus, the residual analysis covers the scale for which snow typically shows a high spatial autocorrelation (e.g. Reference Shook and GrayShook and Gray, 1996; Reference Deems, Fassnacht and ElderDeems and others, 2008; Reference Schirmer and LehningSchirmer and Lehning, 2011). We use a k –means clustering algorithm (Reference ForgyForgy, 1965; Reference MacQueen, Le Cam and NeymanMacQueen, 1967; Reference Hartigan and WongHartigan and Wong, 1979) integrated in SAGA (System for Automated Geoscientific Analyses) to automatically group observations with similar characteristics in magnitude and temporal variability of rHS . A set of ~36 000 spatially distributed observations of rHS is used. Each observation consists of a five-dimensional vector representing rHS values over the five years. This clustering method does not create spatially connected clusters (e.g. as image segmentation algorithms). Rather, the high number of observations distributed over the entire basin are grouped into classes. We clustered the observations to a pre-set of ten classes. Frequency distributions are calculated for the annual rHS of all observations grouped in each of the ten classes. The advantage of clustering the rHS is the spatially distributed information obtained on the temporal persistence of snow depth residuals to mean snow depth in their vicinity.
Geostatistical analysis
Geostatistical analyses are used in cryospheric sciences for scaling issues (e.g. Reference Shook and GrayShook and Gray, 1996; Blöschl, 1999), to investigate topographic and wind control on spatial snow depth distribution and to analyze regional and temporal variability of fractal dimensions and typical scale breaks of mountain snow cover (e.g. Reference Deems, Fassnacht and ElderDeems and others, 2006, Reference Deems, Fassnacht and Elder2008; Reference TrujilloTrujillo, 2007; Reference Lehning and SchirmerLehning and others, 2011; Reference Mott, Schirmer and LehningMott and others, 2011a; Reference Schirmer and LehningSchirmer and Lehning, 2011).
Experimental variograms are used to analyze the spatial autocorrelation of data pairs as a function of their separation distance h (Reference OleaOlea, 1999; Reference Sun, Xu, Gong and LiangSun and others, 2006). The semivariance, γ (hk ), of HS is given for the mean lag distance h of bin k as
where HS are snow depths at locations i and i + h, and nk is the number of data pairs in bin k. The spatial characteristics of HS can be explored by the properties of the variogram, i.e. nugget, sill and range (Reference OleaOlea, 1999). The nugget indicates small-scale variability that has not been captured by the measurement. The sill is the overall variability, γ (hk ), in the dataset, i.e. the higher the sill, the higher the spatial variability in the data. The distance between sampling points (range) where the increase in γ (hk ) with increasing h changes considerably is called the scale break distance, L. In the case of flattening of the increase in γ (hk ) on a log-log plot, L marks the separation of the sampling points at which there is no further autocorrelation between data pairs.
The fractal (Hausdorff–Besicovich) dimension D was found to be useful to analyze the irregularity of objects and surfaces (Reference BurroughBurrough, 1993; Reference Gao and XiaGao and Xia, 1996). Nearly planar surface features have D = 2, while a rugged surface has a limiting D = 3.
Fractal dimensions are estimated from the slope of a power law fitted to the log-spaced data
where α is the ordinal intercept and the power β is the slope of the linear fit in the log-transformed variogram. The fractal dimension D is calculated from β (Reference Gao and XiaGao and Xia, 1996):
The application and interpretation of geostatistics is strongly limited by the measurement scale and the sampling design. For example, if the spacing between the sampling points is large compared with the extent of the sampled area, the true variability in the data might not be captured. The high spatial resolution of the ALS data supports the applicability of the semivariance analysis. However, the results of L and D are highly influenced by the methods used. Sources of different estimates for scale breaks and fractal dimensions are discussed by Reference Xu, Moore and GallantXu and others (1993) and Reference Sun, Xu, Gong and LiangSun and others (2006).
For this study, semivariance is calculated for HS over the entire ice-free terrain with respect to the largest glacier extent in 2001 (17.75 km2), separately for HS on Hintereisferner (HEF; 6.99 km2) and on Kesselwandferner (KWF; 3.65 km2) and for HS on the remaining small glaciers (2.00 km2). With respect to the results of other studies analyzing geostatistical properties of Alpine HS (e.g. Reference Deems, Fassnacht and ElderDeems and others, 2008; Reference MottMott and others, 2011b; Reference Schirmer and LehningSchirmer and Lehning, 2011), scale breaks in the order of meters to tens of meters are expected. Considering this length characteristic we calculate omni-directional variograms with 2 m grid spacing. The lag distance h is subdivided into 20 log-spaced bins for each power of ten. The maximum h is set to 200 m for ice-free terrain. With respect to the more homogeneous snow cover on glaciers, semivariance is calculated with a maximum h = 1000 m for small glaciers and of h = 3000 m for the two large glaciers, HEF and KWF.
For ice-free terrain, a preliminary first break distance L p is calculated by automatically fitting an exponential function to h and using a threshold of 95% of γ (hk ) (Reference Webster and OliverWebster and Oliver, 2007). This automatically fitted L is only used to separate the data of the used bins into a short-range set and a long-range set. Power laws are fitted to the two datasets in the log-transformed variogram, solving least squares to calculate the short-range fractal dimension, D s, for h ≤ L p and the long-range fractal dimension, D l, for h > L p. The intersection of the two fitted lines presents the final L, which depends on the slope of the power laws and differs from L p.
In contrast to Reference Shook and GrayShook and Gray (1996), who used a fixed D l = 3 (completely random spatial distribution), we also calculated D l for the long-range section.
Results
Spatial and temporal snow distribution
Mean snow depth at the end of each accumulation season, , and its spatial and temporal variability are shown in Table 3. ranged from 1.31 m in 2011 to 2.58 m in 2009. This range corresponds to 68% of the temporal mean, , of 1.88 m. Whereas the temporal CV of and the long-term temporal CV of winter precipitation measured at cumulative gauges in the investigated catchment (Table 2) are similar, the observed range between minimum and maximum winter precipitation is higher than the range of ![]() in the five investigated years.
in the five investigated years.
Table 3. Mean snow depth, HS, the standard deviation of spatially distributed snow depth, σHS , the corresponding spatial CV and the snow-covered area, SCA, for each accumulation season calculated from 1 m gridded snow depth data. The interannual mean and interannual variability in terms of range, σ and temporal CV are also shown
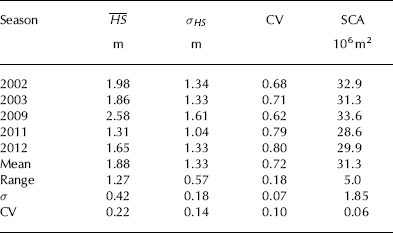
Snow-covered area, SCA, varied interannually by 16% of its mean value. The temporal mean snow-covered area fraction was 87% of the total area. The standard deviation of spatially distributed HS (σHS
) was lowest in the year of minimum ![]() , 2011. σHS
was similar in 2002, 2003 and 2012. In these years, the spatial CV varies due to interannual variations in
, 2011. σHS
was similar in 2002, 2003 and 2012. In these years, the spatial CV varies due to interannual variations in ![]() . Maximum σHS
occurred in 2009, whereas the spatial CV was lowest in this year of highest
. Maximum σHS
occurred in 2009, whereas the spatial CV was lowest in this year of highest ![]() . This shows the great influence of
. This shows the great influence of ![]() on the spatial CV of one year compared with the influence of σHS
. The mean spatial CV of
on the spatial CV of one year compared with the influence of σHS
. The mean spatial CV of ![]() was 0.72. The temporal CV shows that
was 0.72. The temporal CV shows that ![]() was interannually more variable than σHS
and the spatial CV.
was interannually more variable than σHS
and the spatial CV.
Pearson correlation coefficients (r; Table 4) of spatially distributed HS show a high correlation of HS between all accumulation seasons. At the high spatial resolution of 1 m, r is highest for the two seasons with a high fraction of snow-free area in 2011 and 2012 and second highest for the two seasons of the lowest ![]() in 2011 and the highest
in 2011 and the highest ![]() in 2009. The correlations are lower for combinations that include the HS distributions of 2002 and 2003. Thus, there is no clear dependence of correlation on
in 2009. The correlations are lower for combinations that include the HS distributions of 2002 and 2003. Thus, there is no clear dependence of correlation on ![]() . In general, correlations of HS distributions decrease with increasing time lag between the two seasons. At a spatial resolution of 100 m, correlations between the HS distribution of 2003 and later years are similar, but correlations including HS distributions of 2002 still show lower values. In general, an increase in correlation with decrease in raster resolution is obvious, due to a reduction in small-scale variability by spatial aggregation, as shown by, for example, Reference Melvold and SkaugenMelvold and Skaugen (2013).
. In general, correlations of HS distributions decrease with increasing time lag between the two seasons. At a spatial resolution of 100 m, correlations between the HS distribution of 2003 and later years are similar, but correlations including HS distributions of 2002 still show lower values. In general, an increase in correlation with decrease in raster resolution is obvious, due to a reduction in small-scale variability by spatial aggregation, as shown by, for example, Reference Melvold and SkaugenMelvold and Skaugen (2013).
Table 4. Correlation coefficients, r, of spatially distributed HS calculated in raster resolutions from 1 to 100 m for each possible combination of the individual accumulation seasons

A high Pearson correlation (r = 0: 94) was found between ![]() and SCA with lower
and SCA with lower ![]() , indicating less SCA. This is clear from Figure 3, where mean HS and SCA fraction of the investigated years are shown for 25 m elevation zones. In this figure, large triangles represent elevation zones with a large area and, thus, a high contribution to total snow-cover volume compared to elevation zones marked with small triangles. In these elevations of largest contribution to total catchment area, HS varied by a factor of two, whereas SCA fraction varied by only 11% (between 87% in 2011 and 98% in 2009).
, indicating less SCA. This is clear from Figure 3, where mean HS and SCA fraction of the investigated years are shown for 25 m elevation zones. In this figure, large triangles represent elevation zones with a large area and, thus, a high contribution to total snow-cover volume compared to elevation zones marked with small triangles. In these elevations of largest contribution to total catchment area, HS varied by a factor of two, whereas SCA fraction varied by only 11% (between 87% in 2011 and 98% in 2009).

Fig. 3. Mean snow depth, HS (solid lines), and SCA fraction (triangles) of 25 m elevation zones. The size of the triangles represents the area of the corresponding elevation zone scaled by the total investigation area, i.e. small triangles represent only small areas with less contribution to total snow-cover volume compared with the contribution from areas marked with large triangles.
In general, the annual elevation distribution of HS and SCA fraction seem to run parallel (Fig. 3). HS increased to an elevation of 3100 m a.s.l. and decreased above 3200 m a.s.l. Interannual differences of HS and SCA fraction can be found at the lowest elevations and at mountain ridges >3400 m a.s.l. Differences in mean HS of up to 0.5 m occurred for interannually similar SCA fractions <2800 m a.s.l. (i.e. 2002 and 2009).
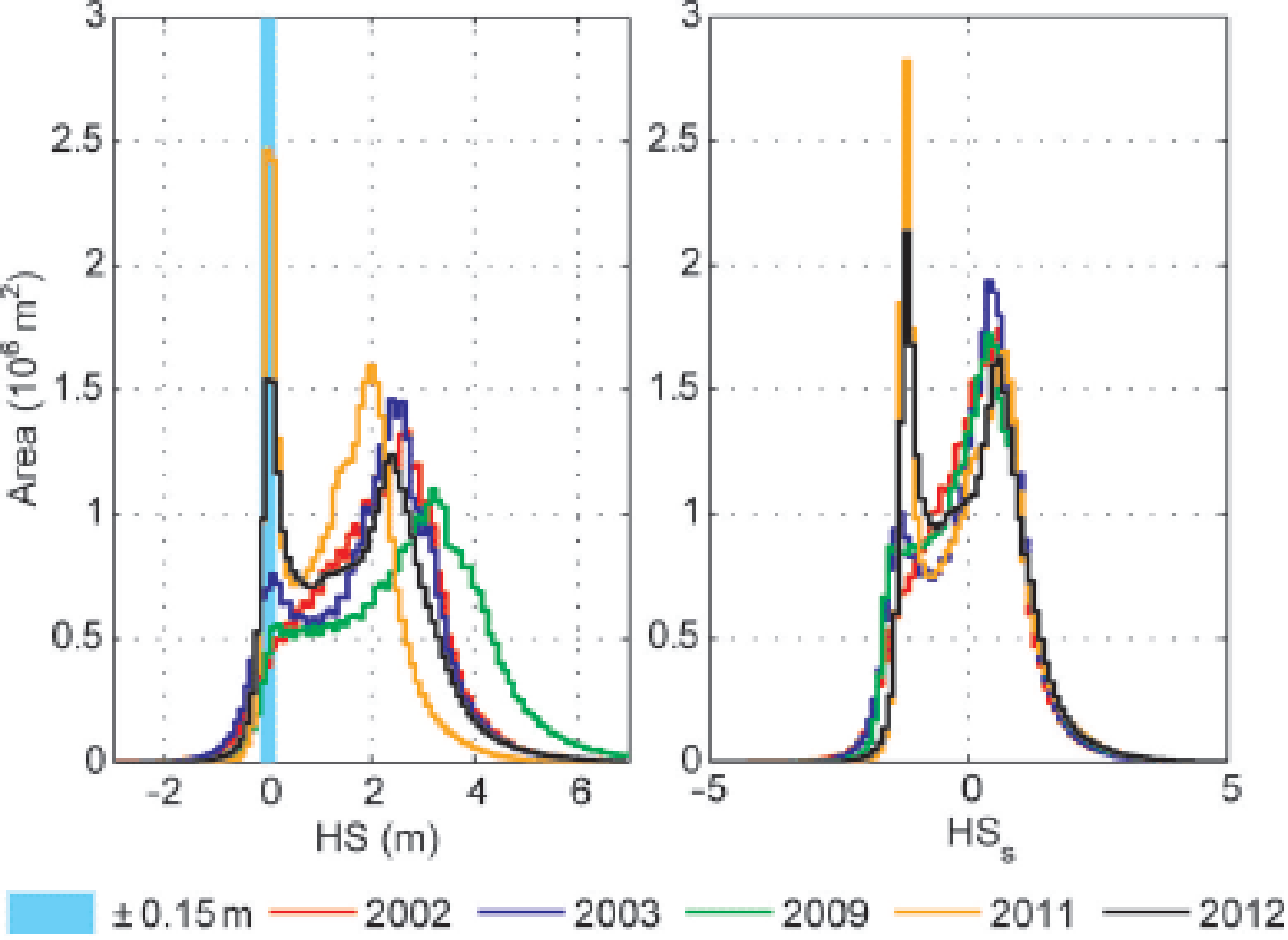
The remarkably high fraction of snow-free areas in 2011 and 2012 is clear at HS = 0 ± 0: 15 m in Figure 4. The year with lowest ![]() (2011) shows a peak of most frequent HS at 2 m. In contrast, the year with highest
(2011) shows a peak of most frequent HS at 2 m. In contrast, the year with highest ![]() (2009) has a peak of most frequent HS at 3.2 m. Frequency distributions of standardized snow depths, HS
s, were found to be inter-annually more consistent than frequency distributions of HS. Hence, HS
s was chosen to distinguish between areas of persistent snow cover and areas of high interannual snow depth variability.
(2009) has a peak of most frequent HS at 3.2 m. Frequency distributions of standardized snow depths, HS
s, were found to be inter-annually more consistent than frequency distributions of HS. Hence, HS
s was chosen to distinguish between areas of persistent snow cover and areas of high interannual snow depth variability.
The temporal mean of HS s (Fig. 5a) represents the standard snow pattern in the investigation area using the available ALS data. South-facing slopes at lower elevations showed almost no snow cover at the time of ALS(t 2). At higher elevations, low snow coverage can be found at sheer rock faces and along mountain crests. In general, HS s on the glacier surfaces was higher than HS s in ice-free areas. Increased HS s can be found at the base of steep slopes and along the glacier margins. These are the areas of high temporal standard deviation of HS s (σ HS s) with respect to the available ALS data.
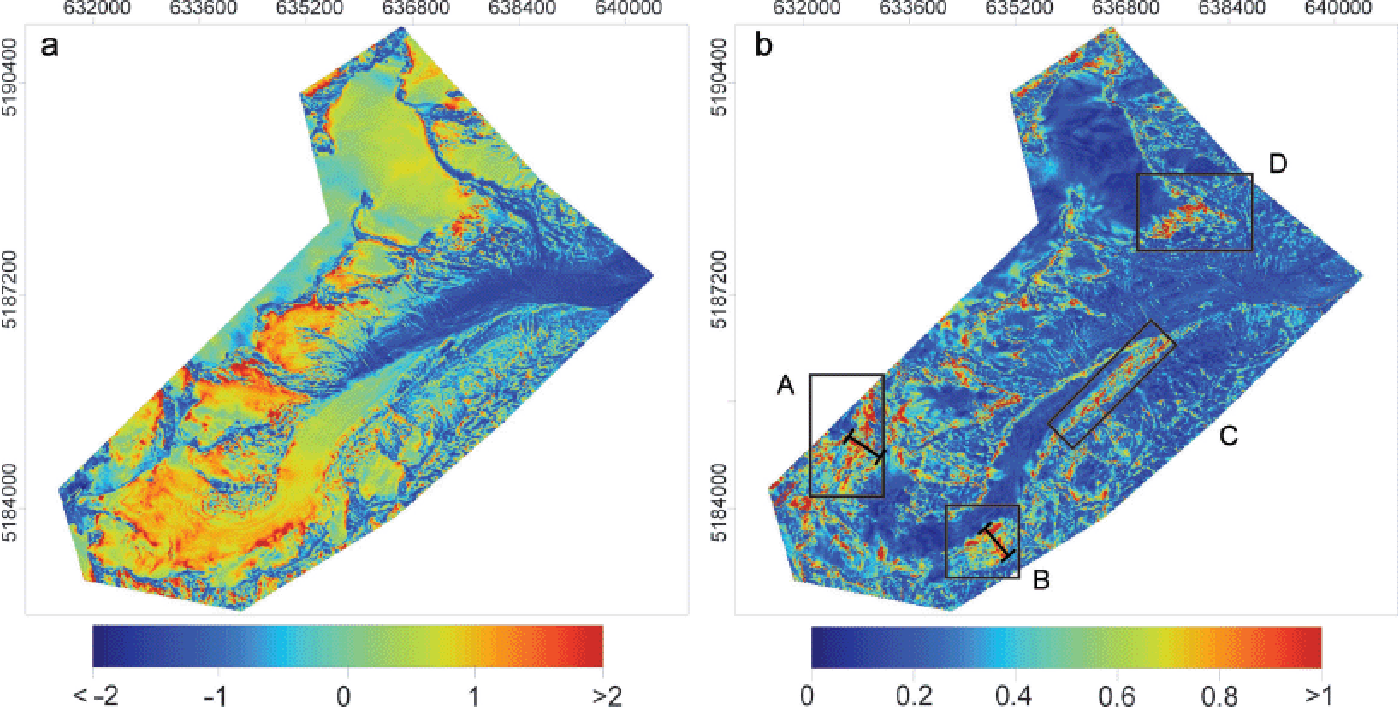
Fig. 5. Spatial distribution of (a) temporal mean standardized snow depth, HS s, and (b) its interannual standard deviation, σHS s, for all five accumulation seasons. A, B, C and D mark regions of high interannual variation of HS s.
Areas A and B in Figure 5b are examples of regions showing high σ HS s as a result of avalanche release and accumulation. Corresponding profiles of HS are shown in Figure 6. In both areas, HS for 2002 is low at steep slopes and high on glacier surfaces within ~100 m of the slope base. In profile A, high HS can be found directly at the slope base in the other years. Peaks of HS at a distances between 0 and 100 m in profile A and at 200 m in profile B are caused by crevasses at the ALS(t 1) reference surface. A substantial snow volume was kept on the slope in area B (Fig. 6b) and not released to the glacier surface prior to ALS(t 2) in 2009. Box C highlights a typical dead-ice area next to the tongue of Hintereisferner (investigated by, e.g., Reference Bollmann, Sailer, Briese and FritzmannBollmann and others, 2011; Reference Sailer, Bollmann, Hoinkes, Rieg and SprossSailer and others, 2012). In dead-ice zones, the high temporal variability of HS s results from spatially differing surface lowering within the 10 year period. The retreat of the glacier tongue of Kesselwandferner in the 10 year period caused a high interannual variability of HS s in box D (see also next subsection). In contrast to zones A–D, large parts of the investigation area have low σ HS s, which is indicated by the dominant blue color graduation in Figure 5b. An area fraction of 75% corresponds to a threshold σ HS s of 0.4 (Fig. 7). This large section is characterized by an inter-annually persistent HS s. Conversely, about a quarter of the total area shows a high interannual variability of HS s. These areas were found to be not necessarily located in steep terrain, and are more frequent at the base of steep slopes and along glacier margins (Figs 1 and 5).
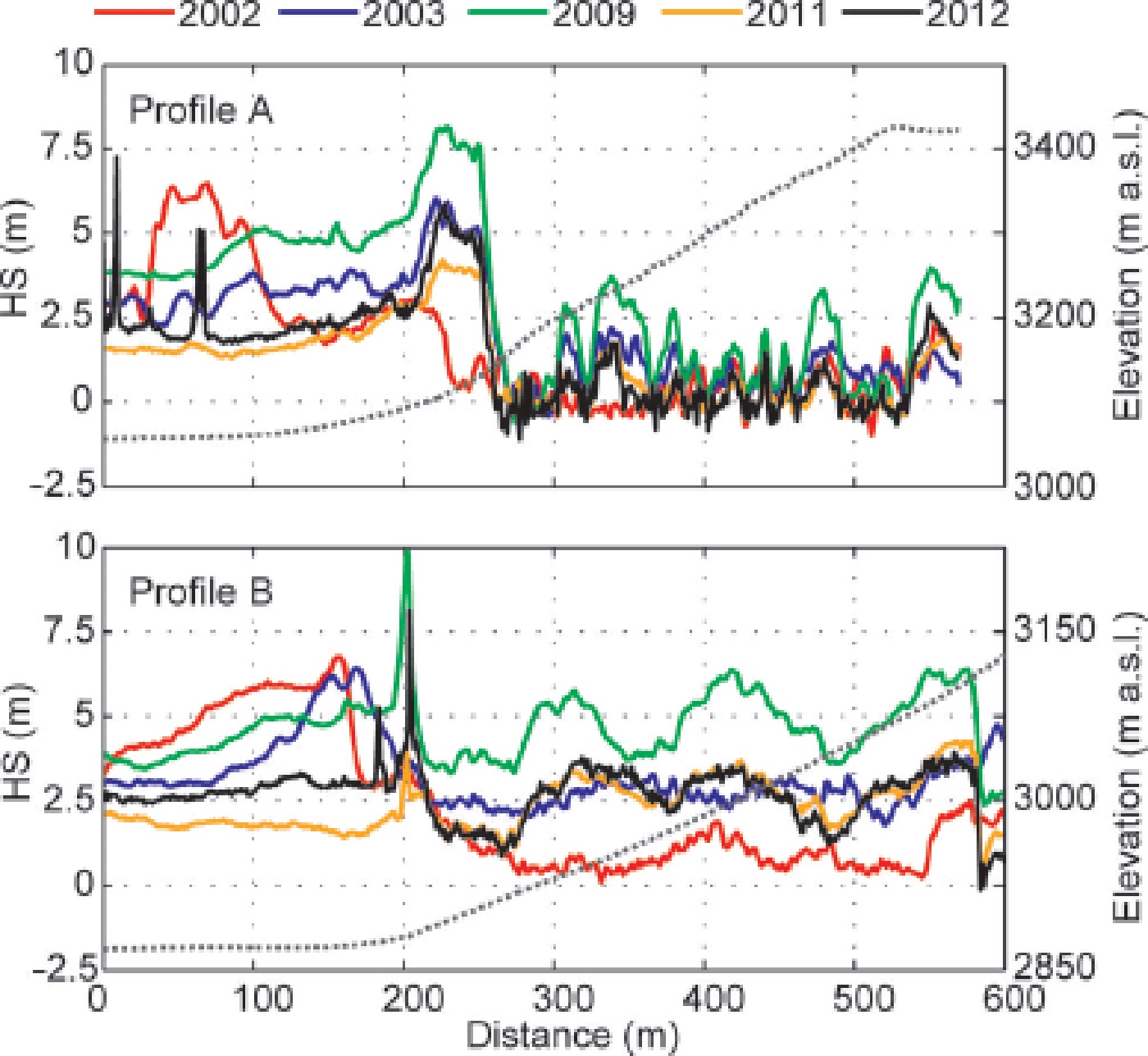
Fig. 6. Snow depth HS along profiles A and B (Fig. 5b) for the five accumulation seasons. The dotted lines show the corresponding mean elevation of the ALS(t 1) surface (right axis).

Fig. 7. Cumulative probability density function (PDF) of the temporal standard deviation of standardized snow depths, σHS s.
The multi-annual cross-combination of squared errors of HS s (SEs; Eqn (3)) helps in analysis of the temporal frequency of the processes causing high interannual variability of snow depths, and to explain the magnitude of spatial means of SEs (MSEs; Fig. 8). Most parts of the areas featuring SEs <0.5 (masked white in Fig. 8) correspond to areas of σ HS s < 0. 4 (Fig. 5b).

Fig. 8. Maps of squared errors of standardized snow depths, SEs (Eqn (3)), between all possible combinations of the five accumulation seasons. In the lower-left corner, mean squared errors, MSE, of the cross-combinations are shown for different spatial resolutions.
High SEs are clear within areas A and B (Fig. 8, upper row), where snow variability is a result of the release and accumulation of avalanches (Fig. 6). These interannual differences of HS s are especially pronounced in combinations that include 2002. High SEs between the years 2002, 2003 and the more recent surveys 2009, 2011 and 2012 are clear for areas C and D along the glacier margins. In these areas, high values of SEs are caused by continuous changes in topography, due to melt of dead ice, collapse of moraines and glacier retreat within at least 6 years between the surveys (e.g. Reference FischerFischer, 2011; Reference Sailer, Bollmann, Hoinkes, Rieg and SprossSailer and others, 2012). Thus, MSEs (Fig. 8) and correlation coefficients (r; Table 4) are highest for cross-combinations including 2002 and lower for shorter time lags between the years. Even in the 2 year period 2009–11 and the 3 year period 2009–12, high SEs can be found along the glacier margins (Fig. 5b, box C). SEs values along the glacier margins are small for the 1 year periods 2002/03 and 2011/12, which reduces MSEs for these cross-combinations.
Residual analysis
While high interannual variability was detected for areas along the glacier margins, it has not yet been shown what causes the interannual variability of SEs in these zones. The temporal clustering of the residuals of each HS value from its surrounding mean (rHS ; Eqn (4)) is applied to show more detail of the differences in the areas highlighted in the previous subsection. The clustering of rHS resulted in seven classes. Three of the ten initial classes are not discussed further because they originate from extreme values of individual seasons and cover only a small relative fraction (0.1%) of the total area. A map of the clusters with a zoom to the area of the tongue of KWF is shown in Figure 9.
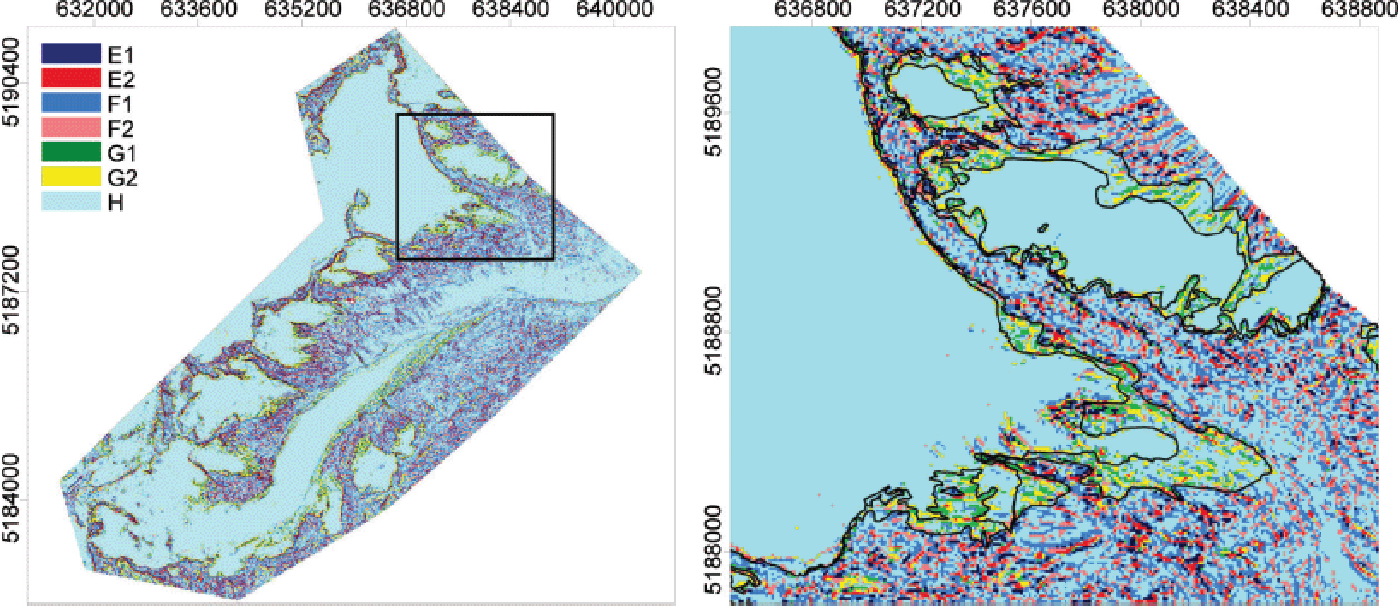
Fig. 9. Clusters derived by k –means clustering of snow depth residuals, rHS . The letters pair classes with similar temporal characteristics in magnitude of rHS . Index 1 indicates negative rHS and index 2 indicates positive rHS . The detailed view highlights areas of changes in snow accumulation as a result of glacier retreat (black glacier outlines) in the 10 year period 2001–11.
Figure 10 shows the frequency distribution of rHS within the classes E–H and for the total area. Sixty-three percent (22.5 km2) of the investigated area is characterized by a homogeneous snow cover, predominantly located on glaciers and in areas with no snow in any of the five years (class H). In these areas the mean rHS values are close to zero (maximum σ = 0.18 m) in all five accumulation seasons. The transition zone from homogeneous (rHS ≠ 0) to heterogeneous (rHS 0) snow distribution (class F1 and F2) covers 25% of the total area. Frequency distributions of rHS in F1and F2 were similar for the individual accumulation seasons (Fig. 10). More interannual variability of rHS is clear in classes E1 and E2 of distinct positive and negative rHS (Fig. 10). Maximum and minimum rHS were both found in 2009. This shows that the spatial variability of HS increases in years of high , i.e. HS increases in sinks and channels, whereas crests and bumps remain snow-free. In 2002, the frequency distribution of rHS shifted towards lower values in areas of positive rHS (Fig. 10). This resulted from a snow cover accumulated at the mountain crests prior to ALS(t 1). Classes G1 and G2 are characterized by a change in rHS within the five accumulation seasons. These two classes are located at the glacier margins (Fig. 9) and together cover 6% of the total area. They show homogeneous snow cover in 2002 and 2003, but distinct positive or negative rHS in 2009, 2011 and 2012 (Fig. 10). This change is a result of glacier retreat, which exposes the more heterogeneous surface of the former glacier bed compared with the homogeneous glacier surface. However, differences in these two classes are not visible in the frequency distribution of rHS for the total area, due to the large fraction of homogeneous snow cover (class H) within the investigation area.

Fig. 10. Histograms of annual rHS for the clusters derived by k –means clustering of snow depth residuals, rHS . Letters E–H are the classes shown in Figure 9. Note that the scales on the area axes vary between the classes.
Geostatistical analysis
Variograms were calculated for HS in ice-free terrain, for HS on Hintereisferner (HEF) and Kesselwandferner (KWF) and for HS on the remaining small glaciers (Fig. 11). The scale break, L, the corresponding sill, γ (hL ), the short-range fractal dimension, D s, and the long-range fractal dimension, D l, were calculated for ice-free terrain (Table 5).
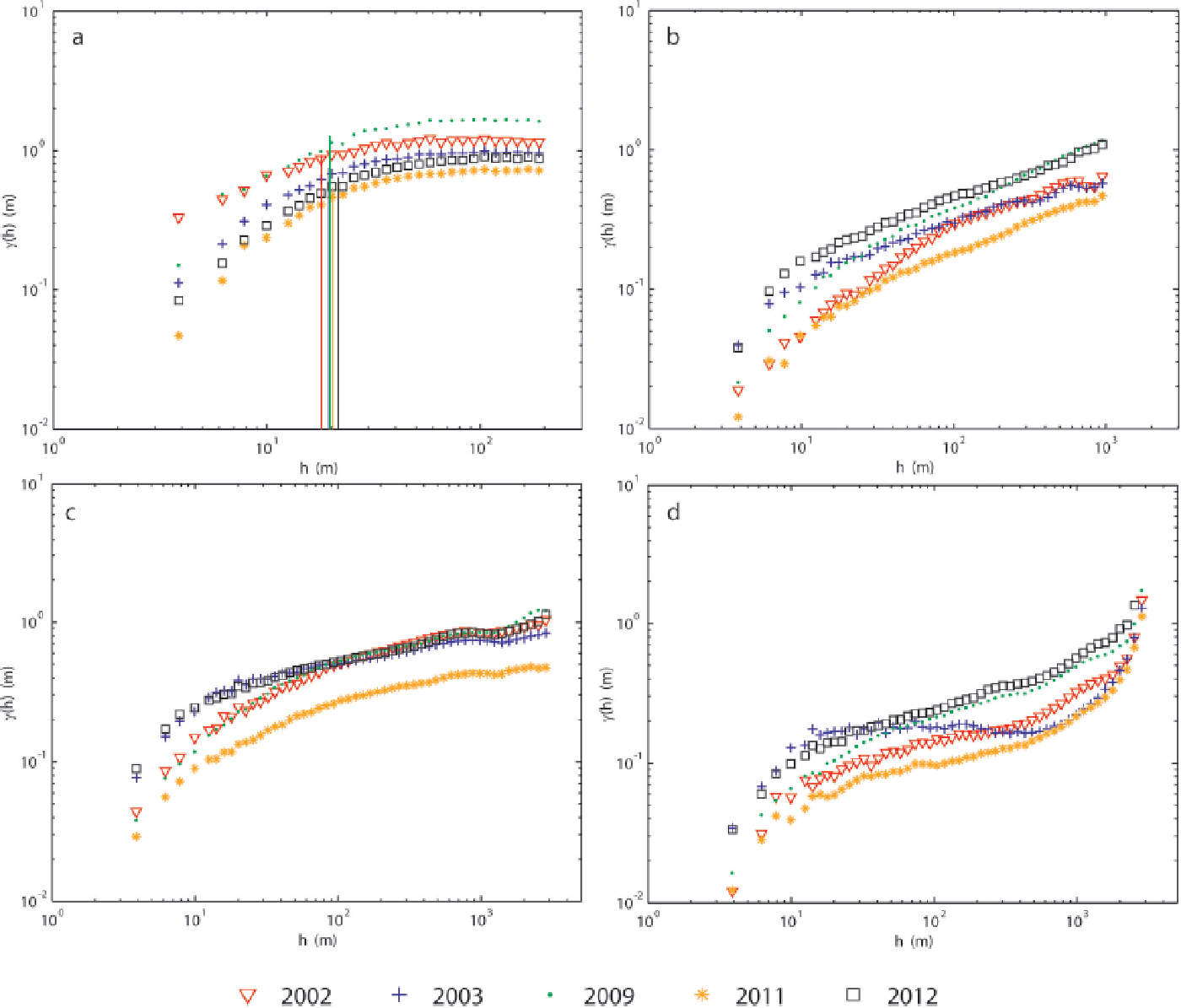
Fig. 11. Variograms for HS of the five accumulation seasons. (a) In ice-free terrain, (b) on small glaciers, (c) on Hintereisferner and (d) on Kesselwandferner. Vertical lines in (a) show the location of the calculated scale breaks, L.
Table 5. Annual scale break, L, the corresponding sill, γ (L), short-range fractal dimension, D s, and long-range fractal dimension, D l, calculated for HS in ice-free terrain
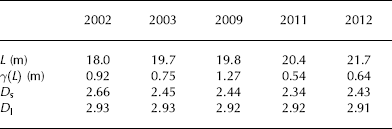
An interannually consistent L was found in ice-free terrain at ~20 m, whereas γ (hL
) ranged considerably between the two years of lowest and highest ![]() (Table 5). The short-range variability of HS is highest in 2002 (Fig. 11a). This results in a higher D
s than the interannually persistent D
s of the other four years (Table 5). In all five years, the increase of γ (h) with h flattens out to a consistent D
l of 2.9 for HS in ice-free terrain. γ (h) for h > L depends on the spatial mean snow depth,
(Table 5). The short-range variability of HS is highest in 2002 (Fig. 11a). This results in a higher D
s than the interannually persistent D
s of the other four years (Table 5). In all five years, the increase of γ (h) with h flattens out to a consistent D
l of 2.9 for HS in ice-free terrain. γ (h) for h > L depends on the spatial mean snow depth, ![]() , of the individual years with increasing γ (h) for increasing
, of the individual years with increasing γ (h) for increasing ![]() .
.
In contrast, no distinct flattening of γ (h) with increasing h could be found for h > 10 m on the glacier surface. The overall spatial variability of HS in ice-free terrain was found to be higher than γ (h) on glaciers. A break in scaling behavior of HS on glaciers is indicated at L = 10 m (Fig. 11b–d). However, γ (h) is of the magnitude of a few centimeters to one decimeter at h = 10 m and, thus, in the range of the assumed accuracy of Δz ALS. At h = 10 m, γ (h) is slightly higher on HEF than on small glaciers and on KWF.
At scales of h < 10 m, γ (h) is highest in 2003 and 2012 on all glaciers. Although γ (h) of HS is lowest in 2011, differences can be found between γ (h) in different accumulation seasons on the glaciers. In particular, HS in 2002 shows low variability at shorter scales, but γ (h) increases towards scales of ~100 m on small glaciers and on HEF. However, variability of HS in 2002 stays at comparatively low values on KWF. The variability of HS on KWF in 2003 does not increase over a large range of h.
Discussion
Spatial and temporal snow distribution
The interannual analysis of the snow cover in this partly glacierized catchment shows a higher range of (68% of its temporal mean) compared with the interannual range of SCA (16% of its temporal mean; Table 3). Nevertheless, annual SCA and ![]() of the total area have a high correlation (r = 0: 94). With respect to the total snow-cover volume, and hence
of the total area have a high correlation (r = 0: 94). With respect to the total snow-cover volume, and hence ![]() , elevations of the largest area present a roughly parallel shift in elevation distribution of HS and SCA (Fig. 3). But differences in SCA fraction are small at these elevations. This is a result of the large fraction of glacierized area that is totally snow-covered in all years. At lower elevations, snowmelt caused different HS and variable SCA, due to the seasonal course of weather conditions. However, variable HS at these elevations has less influence on
, elevations of the largest area present a roughly parallel shift in elevation distribution of HS and SCA (Fig. 3). But differences in SCA fraction are small at these elevations. This is a result of the large fraction of glacierized area that is totally snow-covered in all years. At lower elevations, snowmelt caused different HS and variable SCA, due to the seasonal course of weather conditions. However, variable HS at these elevations has less influence on ![]() , due to their small area fraction. The small variation of SCA compared with the variation of
, due to their small area fraction. The small variation of SCA compared with the variation of ![]() might be challenging for the determination of relationships between snow-covered area fraction and snow depths, such as those used to calculate subgrid variability of snow-cover products from satellite data (e.g. Reference Swenson and LawrenceSwenson and Lawrence, 2012) or to model spatial variability of snow depths (e.g. Reference Luce, Tarboton and CooleyLuce and others, 1999; Reference ListonListon, 2004; Reference ClarkClark and others, 2011). At the time of peak snow accumulation, very detailed surveys of SCA over the largest-area elevation zones would be necessary to obtain mean snow depth of the partly glacierized catchment from small changes in SCA.
might be challenging for the determination of relationships between snow-covered area fraction and snow depths, such as those used to calculate subgrid variability of snow-cover products from satellite data (e.g. Reference Swenson and LawrenceSwenson and Lawrence, 2012) or to model spatial variability of snow depths (e.g. Reference Luce, Tarboton and CooleyLuce and others, 1999; Reference ListonListon, 2004; Reference ClarkClark and others, 2011). At the time of peak snow accumulation, very detailed surveys of SCA over the largest-area elevation zones would be necessary to obtain mean snow depth of the partly glacierized catchment from small changes in SCA.
As a result of ice flow and densification of firn, HS can be underestimated in typical firn areas of the glaciers. This is more relevant for elevations >3250 m a.s.l. Reference Helfricht, Kuhn, Keuschnig and HeiligHelfricht and others (2014) compared ALS data and ground-penetrating radar measurements on the investigated glaciers and found a mean underestimation of HS of 0.4 m (σ = 0: 34 m) by ALS data in the firn areas of the glaciers. The decrease of mean HS in glacierized areas >3250 m a.s.l. (Fig. 3) can partly result from firn densification and ice dynamics. Areas of emergent ice flow were found to be small, having no considerable influence on the interpretation of HS. However, we assumed these dynamical processes to be constant in time, so no corrections were applied. Further, in many studies rough and steep surfaces were found to store less snow on average (Reference KirnbauerBlöschl and Kirnbauer, 1992; Reference LehningGrünewald and Lehning, 2011; Reference Helfricht, Seiser, Fischer and KuhnHelfricht and others, 2012; Grünewald and others, 2013; Schöber and others, in press).
An increase in annual σHS
with increasing was found. This was also noted by Reference Sturm and WagnerSturm and Wagner (2010), who analyzed derived from snow depth samples taken on a regular 30 m grid within a 1 km × 1 km Arctic test area. Reference Melvold and SkaugenMelvold and Skaugen (2013) also found a decreasing spatial CV with increasing HS with values between 0.86 (= 1.42 m) and 0.62 (![]() = 2.89 m). Reference Winstral and MarksWinstral and Marks (2014) discussed the variation of spatial CV when
= 2.89 m). Reference Winstral and MarksWinstral and Marks (2014) discussed the variation of spatial CV when ![]() changes at a faster rate than σ. In their study, the mean spatial CV over 11 years was 0.71, with a slightly higher value for snow surveys in spring (0.81). This finding is in agreement with the variability in mean spatial CV found in our study. Reference Winstral and MarksWinstral and Marks (2014) also found a high spatial CV, of 0.89, for 1 year ALS data. Reference Winstral and MarksWinstral and Marks (2014) related higher spatial CV of HS to higher wind speeds and higher melt rates. To some degree this might be true for the spatial CV of HS reported here, in 2011 and 2012, when potential melt conditions appeared prior to ALS(t 2).
changes at a faster rate than σ. In their study, the mean spatial CV over 11 years was 0.71, with a slightly higher value for snow surveys in spring (0.81). This finding is in agreement with the variability in mean spatial CV found in our study. Reference Winstral and MarksWinstral and Marks (2014) also found a high spatial CV, of 0.89, for 1 year ALS data. Reference Winstral and MarksWinstral and Marks (2014) related higher spatial CV of HS to higher wind speeds and higher melt rates. To some degree this might be true for the spatial CV of HS reported here, in 2011 and 2012, when potential melt conditions appeared prior to ALS(t 2).
Marchand and Killingtveit (2005) showed that the spatial CV is in the range 0.72–0.96 for open sites in Norway. Reference Jepsen, Molotch, Williams, Rittger and SickmanJepsen and others (2012) analyzed a total of 5300 snow depth measurements taken at the end of 12 accumulation seasons. They found the spatial CV of the snow cover ranged from 0.73 to 1.09 in a continental Alpine watershed. In their study, the temporal variability of the spatial CV was 0.15, which is higher than the temporal variability of CV of 0.1 found here. Reference Schirmer, Mott and LehningGrünewald and others (2010) derived a spatial CV of HS between 0.6 and 2.0 from terrestrial lidar data, with the lowest values at the beginning of the ablation season.
In general, the temporal mean spatial CV of ALS-derived HS in this study (0.72) is at the low end of values derived for open and high-elevation alpine areas in previous studies. Schöber and others (in press) present a map of spatially distributed CVs of HS in 2011, which includes the investigation area of the present study and shows low CV values on glaciers. Thus, with respect to the homogeneous snow cover on the glacier surface, annual and multi-annual mean spatial CVs of HS in partly glacierized catchments tend to be lower than the CVs in ice-free terrain.
Here we find the maximum correlation across two years is 0.84 (2011/2012) for the original spatial resolution of 1 m. This is lower than interannual correlations found for HS by Reference Deems, Fassnacht and ElderDeems and others (2008) (r = 0: 88–0.92), Reference Melvold and SkaugenMelvold and Skaugen (2013) (r = 0: 95) or Reference Schirmer and LehningSchirmer and others (2011) (up to r = 0: 97). This results from the large area and complex terrain investigated in our study. The wide range of snow depths (snow-free to HS > 5 m in avalanche accumulation areas), the high number of different topographic features (glaciers, rock walls, slopes, mountain crests, etc.) and the corresponding dynamical processes (glacier retreat, rockfall, collapse of moraines, etc.) reduce the interannual correlation compared with smaller, temporally more consistent test sites.
Since HS is scaled for statistical models to simulate snow-cover distribution (e.g. Reference Sturm and WagnerSturm and Wagner, 2010; Reference Lehning and SchirmerLehning and others, 2011; Grünewald and others, 2013), different measures of snow depth have been used. We found standardized snow depth, HS s, best suited to describe the interannual frequency distribution of HS of this area. Thus, we used HS s to distinguish between areas with interannually persistent snow cover and areas with high interannual variability. In the same way as Reference Sturm and WagnerSturm and Wagner (2010), we showed a climatological snow distribution pattern in terms of spatially distributed, temporal mean HS s of the investigated snow surveys. Although Reference Sturm and WagnerSturm and Wagner (2010) found that interannually persistent areas were visually striking, they did not present a measure to differentiate between interannually variable HS s and areas of persistent snow cover. We used the temporal standard deviation of HS s (HS s) (Fig. 5b) to demonstrate that 75% of the investigated area showed interannually consistent HS s for a threshold σHS s of 0.4.
In general, σHS s is low on glaciated areas and on gentle slopes (Fig. 5b). Especially in these areas, lidar measurements of HS have an appropriate accuracy and most of the snow-cover volume is accumulated there. Thus, ALS is suitable for recording characteristic snow depth distributions for the calibration and validation of hydro-meteorological models (e.g. Schöber and others, in press). High HS values were found consistently on glaciers characterized by flat, sheltered surfaces at high elevations. The preferential accumulation in these areas is also the reason why glaciers exist where they do. For instance, Reference Dadic, Mott, Lehning and BurlandoDadic and others (2010a) related the location of glaciers to differences in the wind field. Redistribution of snow to glacier surfaces has already been included in hydro-meteorological models adapted to the investigated catchment (Reference KuhnKuhn, 2003).
The reduction of MSEs with increasing aggregation of raster resolution (Fig. 8) is distinctly higher for MSEs values that include 2002 or 2003 compared with MSEs calculated between surveys since 2009. Small-scale features of high SEs are smoothed, especially in narrow areas along sheer rock walls and glacier margins. Two studies have calculated mean-squared errors of HS s (MSEs) for multi-annual data. Sturm and Wagner (2010) found HS s for snow surveys in March and April compared with one survey in March in the range 0.31–1.34. Lower MSEs values were found by Reference Winstral and MarksWinstral and Marks (2014). Based on the snow depth data over 11 years at a spatial resolution of 30 m, their calculated MSEs was in the range 0.06–0.6, with a mean MSEs of 0.31. This range is comparable with the mean MSEs found in our study (0.22–0.5) with a mean of 0.34 for a spatial resolution of 30 m (Fig. 8).
Areas of high interannual snow depth variability (i.e. high σHS s) are not restricted to mountain crests and steep slopes, where ALS data are affected by large errors. In general, 82% of all σHS s ≥ 0.4 were located at slopes of <40°. High σHS s values were found at gently inclined slope toes and on homogeneous glacier surfaces (Fig. 7). These are typical accumulation areas of gravitational snow transport by avalanches and snow sloughs.
Geomorphological processes continuously change the mountains’ surface topography (Reference Bollmann, Sailer, Briese and FritzmannBollmann and others, 2011; Reference Sailer, Bollmann, Hoinkes, Rieg and SprossSailer and others, 2012). Thus, the variation in the reference surface at ALS(t 1) affects snow depth variability. In addition, glacier retreat alters the surface relief from a more homogeneous surface to heterogeneous landforms featuring ridges and sinks, which lead to a heterogeneous snow depth distribution (Figs 9 and 10). This coincides with the findings of Reference Lehning and SchirmerLehning and others (2011) and Reference Schirmer and LehningSchirmer and others (2011), who demonstrated that topographic roughness controls snow-cover variability. The shift of the frequency distribution of rHS
towards more positive and negative values in the year of highest mean snow depth (2009) shows that differences of HS between preferential accumulation areas and areas with less or no snow increase with an increasing ![]() .
.
Scaling behavior of snow depths
We assessed the multi-scaling behavior of HS separated by a scale break distance, L, into a short-range fractal dimension, D s, and a long-range fractal dimension, D l. In ice-free terrain, L was found to be interannually consistent at ~20 m, comparable with the L = 17.3 and 20.4 m found by Schirmer and Lehning (2011) for a cross-loaded slope (i.e. variable wind direction) in complex mountain terrain. However, L found by Reference Deems, Fassnacht and ElderDeems and others (2008) for the HS distribution of two seasons in a forested, moderate-elevation terrain with low rolling topography (L = 15.5 and 15.9 m) and at an Alpine site above the tree line (L = 31.5 and 26.4 m) are slightly lower and slightly higher, respectively. Reference Mott, Schirmer and LehningMott and others (2011a) presented very similar values to those found in this study for peak HS calculated from terrestrial laser scanning measurements in a small Alpine area (L = 20: 4, D s = 2: 31), and Reference Schirmer and LehningSchirmer and Lehning (2011) showed a reduction in D s towards values between 2.3 and 2.5 at the end of the accumulation season. D l was found to be consistently close to 2.9 in all studies.
Here we found that L determined for HS in ice-free terrain marked the beginning of a curve-like reduction in the increase of γ (h), rather than a distinct bend in γ (h), unlike, for instance, those found by Reference Mott, Schirmer and LehningMott and others (2011a) and Reference Schirmer and LehningSchirmer and Lehning (2011). This is a result of the large area (~14 km2) and the high number of different surface types (rocks, boulders, talus, etc.) in a complex topography (sheer walls, gentle slopes, flat valley floors) with different exposure to meteorological conditions (radiation, wind). Since values of L depend strongly on the bin spacing, the grid resolution, the area considered for the variogram and the maximum range of h used for calculation, they give an order of magnitude (here a few tenths of a meter) rather than exact values.
We found γ (h) of HS at h = 2 m is highest in 2002 (0.23 m) and stays high for h lower than the scale break, L (Fig. 11a). Whereas γ (h) at h < 4 m might be influenced by the accuracy of the ALS data (Section 2), similarities between snow-cover distribution in 2002 and 2009 can also be found in SCA and HS at lower elevations (Fig. 3). In addition, the avalanche activity in 2002 (Fig. 7) increased the small-scale variability of HS. No distinct, interannually persistent scale break could be detected on glaciers. Nevertheless, the increase in γ (h) appeared to be higher at scales below 10-1m compared with the increase in γ (h) at larger h. Even though this variability is clear in some years, γ (h) below 10–1 m is close to the accuracy of Δz ALS, of ±0.15 m (Section 2). Thus, an interpretation of this scale break would be speculative. However, years without considerable snowfall prior to ALS(t 1) (2003, 2012) show higher γ (h) at short scales compared with years where snowfall occurred prior to the survey in autumn (see Section 3). This is a result of crevasses and surface structures, such as meltwater channels and moraines on the glacier surface which, if they are not covered by snow at ALS(t 1), increase small-scale variability.
Especially in 2011, γ (h) of HS was reduced over the whole range of h due to snow accumulation prior to ALS (t 1), the comparatively low precipitation over this season and the fact that melt had begun at the snow surface on the glaciers prior to ALS(t 2). The lower values of γ (h) on glaciers in comparison with γ (h) in ice-free terrain highlight the more homogeneous snow depth distribution on the ice surfaces.
Conclusions
In this paper we have reported a comprehensive analysis of the spatial distribution of the snow cover at the end of five accumulation seasons between 2002 and 2012 in a partly glacierized mountain catchment in Tyrol, Austria. The distribution of HS at the end of the accumulation season is of great relevance for cryospheric and hydrologic studies, such as snowmelt modelling or seasonal glacier mass balances. The analysis makes it clear that the snow-covered area, SCA, is interannually much more persistent than the mean annual snow depths, ![]() . Although a strong correlation was found between SCA and
. Although a strong correlation was found between SCA and ![]() , SCA varied only by 16% of its temporal mean, but
, SCA varied only by 16% of its temporal mean, but ![]() varied by a factor of two in the five years. The interannual variability of
varied by a factor of two in the five years. The interannual variability of ![]() in the five accumulation seasons (CV = 0.22) is of a similar magnitude to the climatic variability of winter precipitation in this region. Although five years of data do not make a climatic mean, the presented dataset – including one season of comparatively low HS and one season of extremely high HS – may provide a more reasonable base for statistical analysis and simulation of the snow depth distribution than data from single-year acquisitions. With respect to the statistical analysis, the frequency distribution of standardized snow depths was found to be more interannually consistent than the frequency distribution of absolute snow depths. Seventy-five percent of the investigated area was found to have an interannual standard deviation of standardized snow depth of <0.4 at a spatial scale of 10 m and, thus, can be interpreted as the standard snow pattern representing highly valuable information for snow-cover modelling in this area. The high interannual variability in snow depth in the remaining area is attributed to occasional avalanches, wind transport and changes in the surface topography. Especially areas associated with changes in glacierization were found to cause interannual snow depth variability. Ice melt in dead-ice bodies causes interannual variability in snow depth. A shift from homogeneous snow distribution towards a more heterogeneous snow cover was observed in areas that became ice-free, due to glacier retreat, within the investigated 10 year period. Compared with ice-free basins, this circumstance keeps the modelling of snow challenging with regard to the expected glacier retreat. So far, these changing zones cover only a low area fraction and still have a low impact with respect to (1) the total snow volume in the basin and (2) a coarse spatial resolution of the data, as typically used for modelling (e.g. 50–100 m). Nevertheless, areas of high interannual variability caused interannual differences in the correlation of snow depths which are even visible at a spatial resolution of 100 m. Geostatistical analysis is performed to show interannual persistence of the scaling behavior of the mountain snow cover. The differences between spatial autocorrelation of HS in ice-free terrain and spatial autocorrelation of HS on glaciers show the great influence of glaciers on the snow depth variability in mountain catchments. Spatial variability of snow depth was found to depend on mean snow depth in ice-free terrain, but is influenced by the existence of a snow layer at ALS(t 1) on glacier surfaces. In agreement with typical scale breaks shown by other authors for HS in alpine areas at the end of the accumulation season (e.g. Reference Deems, Fassnacht and ElderDeems and others, 2006; Reference Mott, Schirmer and LehningMott and others, 2011a; Reference Schirmer and LehningSchirmer and Lehning, 2011), interannually persistent scale breaks at 20 m were detected in ice-free terrain of the total investigated catchment. On smooth glacier surfaces, the short- and long-range fractal characteristics cannot be easily distinguished, indicating scale-invariant behavior of HS in such areas. However, disruptive surface structures (e.g. crevasses or meltwater channels) could turn the fractal parameters into length scales comparable with length scales in ice-free terrain. While our results in general confirm the fractal characteristics of HS indicated by other studies in ice-free terrain, these have so far only been shown for smaller areas. Fractal parameters calculated for irregular or small regular sub-areas may be a next step to obtain parameters for statistical snow models (e.g. Reference Lehning, Ryser and RadeschallLehning and others, 2011) or deterministic snow models working in a gridded model layout. The present study shows, for the first time, the persistence and variability of the snow pattern for five accumulation seasons in a comparatively large catchment with a complex topography of ice-free terrain and glaciers.
in the five accumulation seasons (CV = 0.22) is of a similar magnitude to the climatic variability of winter precipitation in this region. Although five years of data do not make a climatic mean, the presented dataset – including one season of comparatively low HS and one season of extremely high HS – may provide a more reasonable base for statistical analysis and simulation of the snow depth distribution than data from single-year acquisitions. With respect to the statistical analysis, the frequency distribution of standardized snow depths was found to be more interannually consistent than the frequency distribution of absolute snow depths. Seventy-five percent of the investigated area was found to have an interannual standard deviation of standardized snow depth of <0.4 at a spatial scale of 10 m and, thus, can be interpreted as the standard snow pattern representing highly valuable information for snow-cover modelling in this area. The high interannual variability in snow depth in the remaining area is attributed to occasional avalanches, wind transport and changes in the surface topography. Especially areas associated with changes in glacierization were found to cause interannual snow depth variability. Ice melt in dead-ice bodies causes interannual variability in snow depth. A shift from homogeneous snow distribution towards a more heterogeneous snow cover was observed in areas that became ice-free, due to glacier retreat, within the investigated 10 year period. Compared with ice-free basins, this circumstance keeps the modelling of snow challenging with regard to the expected glacier retreat. So far, these changing zones cover only a low area fraction and still have a low impact with respect to (1) the total snow volume in the basin and (2) a coarse spatial resolution of the data, as typically used for modelling (e.g. 50–100 m). Nevertheless, areas of high interannual variability caused interannual differences in the correlation of snow depths which are even visible at a spatial resolution of 100 m. Geostatistical analysis is performed to show interannual persistence of the scaling behavior of the mountain snow cover. The differences between spatial autocorrelation of HS in ice-free terrain and spatial autocorrelation of HS on glaciers show the great influence of glaciers on the snow depth variability in mountain catchments. Spatial variability of snow depth was found to depend on mean snow depth in ice-free terrain, but is influenced by the existence of a snow layer at ALS(t 1) on glacier surfaces. In agreement with typical scale breaks shown by other authors for HS in alpine areas at the end of the accumulation season (e.g. Reference Deems, Fassnacht and ElderDeems and others, 2006; Reference Mott, Schirmer and LehningMott and others, 2011a; Reference Schirmer and LehningSchirmer and Lehning, 2011), interannually persistent scale breaks at 20 m were detected in ice-free terrain of the total investigated catchment. On smooth glacier surfaces, the short- and long-range fractal characteristics cannot be easily distinguished, indicating scale-invariant behavior of HS in such areas. However, disruptive surface structures (e.g. crevasses or meltwater channels) could turn the fractal parameters into length scales comparable with length scales in ice-free terrain. While our results in general confirm the fractal characteristics of HS indicated by other studies in ice-free terrain, these have so far only been shown for smaller areas. Fractal parameters calculated for irregular or small regular sub-areas may be a next step to obtain parameters for statistical snow models (e.g. Reference Lehning, Ryser and RadeschallLehning and others, 2011) or deterministic snow models working in a gridded model layout. The present study shows, for the first time, the persistence and variability of the snow pattern for five accumulation seasons in a comparatively large catchment with a complex topography of ice-free terrain and glaciers.
Acknowledgements
This work was carried out within the framework of the alpS-Project ‘H03 MUSICALS A – Multiscale Snow/Ice Melt Discharge Simulations for Alpine Reservoirs’. We thank the Austrian Research Promotion Agency (FFG) and the TIWAG – Tiroler Wasserkraft AG, who support this project. The ALS data used were acquired within the EU-financed OMEGA-Project (Operational Monitoring System of European Glacial Areas, 5th Framework Programme: Environment and Sustainable Development, Development of generic Earth observation technologies, EVK-2-CT-2000–00069), the ALS-X-Project (Kombination und Bewertung von flugzeuggestützten Laserscannerdaten und TerraSAR-X Daten für glaziologische und schneehydrologische Fragestellungen, FFGASAP 815527) financed by FFG, the C4AUSTRIA-Project (Climate Change Consequences for the Cryosphere, K09AC0K00073) financed by the Österreichischen Klima und Energie Fond and the project H03 MUSICALS A financed by TIWAG – Tiroler Wasserkraft AG and FFG. We thank TopScan GmbH (Rheine, Germany) for performing and processing the ALS surveys at high quality for many years. Also we appreciate the efforts of Thomas Grünewald and an anonymous referee, whose constructive comments and critical remarks helped to improve the paper.