Introduction
Two processes can contribute to the total basal motion of a glacier that rests on a deformable bed: basal sliding and subglacial sediment deformation (Reference AlleyAlley, 1989). In order to advance our understanding of the physics that controls the partitioning between these two flow contributions at Trapridge Glacier, Yukon Territory, Canada, we are monitoring mechanical and hydrological processes at the glacier bed. Instruments which measure subglacial sediment deformation and indicate mechanical conditions at the base of the glacier have been described elsewhere (Reference BlakeBlake, 1992; Reference Blake, Clarke and GérinBlake and others, 1992; Reference Fischer and ClarkeFischer and Clarke, 1992, Reference Fischer and Clarke1993, Reference Fischer and Clarke1994); but the analysis of data from these sensors cannot be complete without some means of measuring basal sliding.
Early observations of basal sliding in tunnels excavated in glaciers (Reference HaefeliHaefeli, 1951; Reference McCallMcCall, 1952; Reference Kamb and LaChapelleKamb and LaChapelle, 1964, Reference Kamb and La Chapelle1968), in deep marginal crevasses (Reference CarolCarol, 1947) and in natural subglacial cavities (Reference Vivian and GVivian and Bocquet, 1973; Reference McKenzie, Peterson, Vivian and Bocquet.McKenzie and Peterson, 1975) have provided valuable information about the glacier-sliding process. These observations were confined to easily accessible parts of glaciers not flooded by subglacial streams and where the overlying ice is comparatively thin. Using borehole photography, sliding velocities were measured at the base of Blue Glacier, Washington, U.S.A., under roughly 120 m of ice (Reference Harrison and BHarrison and Kamb, 1970, Reference Harrison and B1973; Reference Engelhardt, Humphrey and KambEngelhardt and others, 1978; Reference Kamb, Engelhardt and HarrisonKamb and others, 1979).
Mechanical measurements of sliding over a deforming substrate are rare. Reference Boulton and HindmarshBoulton and Hindmarsh (1987) screwed an auger-like anchor into the sediment beneath the terminus of Breidamerkurjökull in Iceland. The anchor was inserted through a sealed hole in the floor of an englacial tunnel and connected by a string to a reel and chart recorder. As the glacier sole moved in relation to the underlying sediment, the string was pulled over the reel and its displacement recorded. Reference Engelhardt, Humphrey and KambEngelhardt and others (1990) used the same principle and anchored a tethered stake in till beneath Ice Stream B, immediately below the ice-bed interface. By observing the pull-in of the tether cable, they inferred a basal sliding rate high enough to account for the total motion of the ice stream.
In an effort to measure basal sliding under Trapridge Glacier, we have developed an instrument which is similar to the Boulton and Hindmarsh design in that an anchor is placed in the deformable bed and the amount of string paid out is measured. Our instrument can be installed in situ at the bottom of deep, narrow boreholes and has been termed a “drag spool”. The device consists of a multi-turn potentiometer connected to a spooled string. The drag spool is suspended within the borehole close to the glacier bed, and measures continuously the length of string paid out to an anchor in the bed. In this paper, we describe the physical characteristics and field operation of this device. We also present and discuss some results from our measurements beneath Trapridge Glacier.
Methods
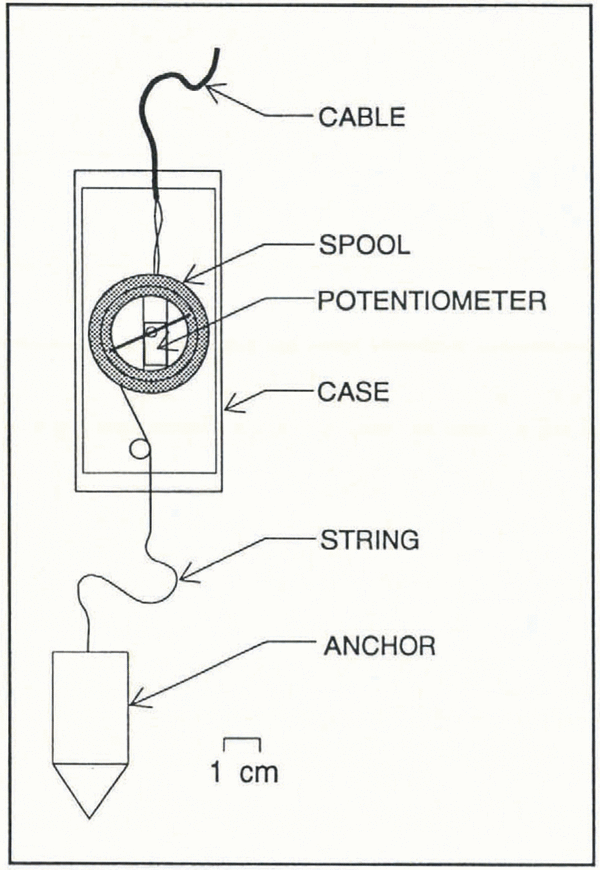
The basic components of a drag spool are an anchor, a multi-turn potentiometer, and a spooled string (Fig. 1). A thin nylon string is wound onto a 3.0 cm diameter spool. A 25-turn 5 kΩ potentiometer (Bourns, part No. 3296W-1-502) is connected to the spool so that turns of the spool can be measured electrically from the glacier surface. The spool-potentiometer assembly is enclosed in an acrylic casing. To prevent water that enters the case from shorting out the potentiometer leads, the interior of the spool is filled with an electrically insulating grease. The free end of the string is led through a small hole that penetrates the case and then attached to a conical anchor tip. A percussion hammer (Reference Blake, Clarke and GérinBlake and others, 1992), fitted with a 0.635 cm (0.25 in) diameter metal-dowel attachment, is used to insert the anchor into the soft glacier bed. The dowel fits into a 0.635 cm diameter socket drilled into the back of the anchor tip. The dowel passes through loose-fitting loops on the drag-spool casing. After the anchor is inserted, the hammer and dowel are withdrawn, leaving the anchor and the drag-spool case at the bottom of the borehole. Although the hammer and the wire rope supporting it are drawn past the drag-spool cable, we have not had any problem of ropes and cables becoming entangled. Additionally, the dead weight of the drag-spool cable appears to exceed the frictional force between wire and cable, since we have not observed any unwinding of the drag-spool string, which would indicate that the spool is being pulled, as the hammer is lifted. Once the hammer has been withdrawn, slack is removed from the drag-spool cable until a slight tension is sensed. Even though the force required to unwind the drag spool is only 1 N, it is possible to feel this tension point in the 70-80 m long cable that we use on Trapridge Glacier. Nevertheless, a few centimeters of string are usually pulled off the spool. As the cable freezes into the borehole, the position of the drag-spool case within the borehole becomes fixed. In response to glacier sliding, the anchor will distance itself from the glacier borehole and the spool will turn as the string is paid out. Approximately 2.5 m of thin nylon string are stored on the spool, which is enough to last for 3-5 weeks at the anticipated sliding rates.

Fig. 1. Schematic diagram of the drag spool. As the string attached to the anchor is paid out, the potentiometer screw is turned and the resistance change can be measured.
Results and Discussion
Figure 2 shows an example of data obtained from a drag spool during the 1992 field season on Trapridge Glacier. The data (Fig. 2a) indicate that the distance between anchor and drag-spool case increased by approximately 260 mm during the interval 21-27 July. This increase translates into an average rate of string-lengthening of roughly 43 mm d−1. The displacement record (solid line in Fig. 2a) shows distinct diurnal deviations from the general trend of increase (dashed line in Fig. 2a). Strong diurnal fluctuations in subglacial water pressure (Fig. 2b) were contemporaneously observed in a borehole located approximately 12 m up-flow from drag spool 92SM02 and appear to be correlated with the variations in the displacement record. We now present two alternative interpretations in an attempt to explain the available data.

Fig. 2. Data from drag spool 92SM02 and pressure sensor 92P06 (see text for details), (a) General increasing trend (dashed line) obtained by linear regression, superimposed on the relative displacement between anchor and drag-spool case (solid line). The arrow indicates the time when the spool started to turn, (b) Subglacial water pressure record. Flotation pressure corresponds to a water level of roughly 63 m (dashed line), (c) Rate of displacement between anchor and drag-spool case, obtained by numerical differentiation of the displacement record.
The stepwise increase in displacement seen in the drag-spool data (Fig. 2a) could indicate an increase in sliding velocity in response to a rise in subglacial water pressure. The idea of high sliding velocities resulting from smoothing of bed roughnesses by accumulation of pressurized water between ice and bed has been proposed by Reference WeertmanWeertman (1964) and further analyzed by Reference LliboutryLliboutry (1979). We computed the sliding velocity (rate of displacement; Fig. 2c) by applying a five-point first-derivative filter to the displacement record (Reference Abramowitz and StegunAbramowitz and Stegun, 1965, p. 914), followed by a Gaussian smoothing filter having a standard deviation of 100 min. Comparison of Figure 2b and c shows that peak displacement rates coincide with rises in water pressure. This result contrasts with observations by Reference Iken and BindschadlerIken and Bindschadler (1986), Reference KambKamb and others (1985) and Reference Kamb and EngelhardtKamb and Engelhardt (1987), where peak subglacial water pressure and peak surface velocity (and by implication basal sliding velocity) appear to coincide. The apparent 90° phase shift between water pressure and sliding rate is a puzzling feature of the data. Perhaps a localized stick-slip relaxation process is at work. As water pressure rises, a local strain build-up in the ice is released and the sliding rate increases momentarily; once the finite relaxation has occurred, further rises in water pressure do not produce additional enhancement of basal sliding. Unfortunately, the heavy smoothing required to clarify the displacement-rate record masks finer detail that might illuminate the motion mechanism; a small rapid motion would produce a (δ-function-like velocity record which when smoothed could resemble the data presented in Figure 2c.
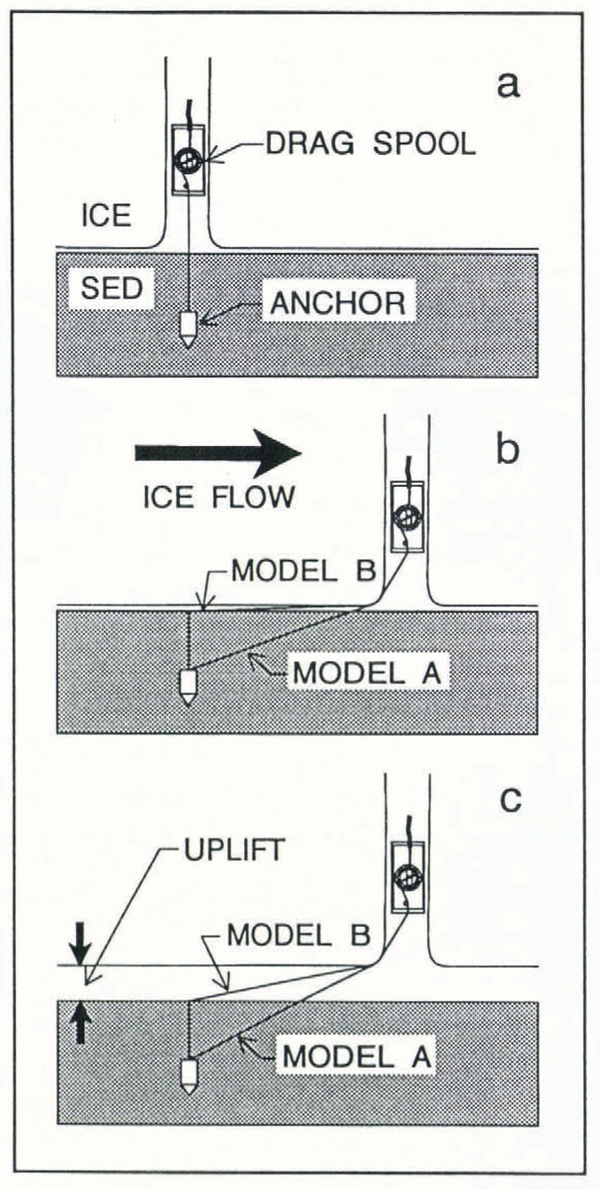
Alternatively, the stepwise increase in displacement could be interpreted in terms of the growth of water-filled cavities at the glacier bed as a function of subglacial water pressure. As cavities grow, the glacier is separated from its bed, which results in an increase in distance between the anchor and the drag-spool case. The concept of growing and shrinking cavities at the ice—bed interface has been introduced into glacier-sliding theories (Reference LliboutryLliboutry, 1968; Reference KambKamb, 1970; Reference IkenIken, 1981) to allow for the varying extents to which a glacier is separated from its bed. Field observations on Variegated Glacier in Alaska (Reference KambKamb and others, 1985; Reference Kamb and EngelhardtKamb and Engelhardt, 1987) and on two glaciers in the Swiss Alps — Unteraargletscher (Reference Iken, Röthlisberger, Flotron and HaeberliIken and others, 1983) and Findelengletscher (Reference Iken and BindschadlerIken and Bindschadler, 1986) — support the idea that glacier uplift is mainly due to basal cavitation driven by high basal-water pressures. We computed the corresponding vertical uplift for Trapridge Glacier from the general displacement trend (dashed line in Fig. 2a) and the actual displacement record. The dashed line was obtained by fitting a regression line to the data from the time the spool started to turn (see arrow in Fig. 2a) until the end of the record. To consider trigonometric effects, we used two different models of drag-spool operation, which represent end-members of a spectrum of possibilities (Fig. 3). In the first scenario the nylon string is free to move laterally through the soft sediment (Model A), while in the second the sediment is stiff enough to prevent the string from cutting through it (Model B). We expect that the position of the string is closer to Model B, since the tension required to unwind the spool is small (about IN); we do not believe that this tension is sufficient to allow the string to cut easily through the basal material. The exact depth of emplacement of the anchor in the basal sediment is uncertain. However, based on our experience with inserting other instruments using the same procedure (Reference Blake, Clarke and GérinBlake and others, 1992; Reference Fischer and ClarkeFischer and Clarke, 1994), we are able reasonably to constrain this uncertainty. For our calculations in this paper we assume an insertion depth of the anchor of 18 ± 3 cm.

Fig. 3. Scenarios of drag-spool operation. Model A allows for lateral movement of the string through soft sediment. The sediment in Model B is sufficiently stiff to keep the string in place, (a) Situation immediately after installation of the device at the glacier bed (SED, sediment), (b) Situation after some time has elapsed, (c) Same as (b) with vertical glacier uplift.
Model A requires a bed separation of 8 cm and Model B one of up to 20 cm to explain the available data. Daily surveying of marker poles on the glacier surface did not reveal vertical displacements of this magnitude. We therefore think that both models predict a vertical glacier uplift that is inconceivably high for Trapridge Glacier. While we cannot completely dismiss the possibility of fluctuating bed separation, we conclude that the diurnal character of the drag-spool data is mostly a result of variable sliding velocity. Unfortunately, we cannot settle this question using our current survey methodologies. We would require a survey accuracy of ±10 mm to resolve diurnal fluctuations in Trapridge Glacier flow.
During the 1992 field season, the surface velocity of Trapridge Glacier at our study site was about 80 mm d−1. Observations of lateral deformation of boreholes reveal that the velocity contribution from internal ice creep for this glacier does not exceed 10 mm d−1 (Reference BlakeBlake, 1992). Therefore, almost the entire surface motion of the glacier is attributable to sliding and deformation processes at the bed. Our estimate of ~ 40 mm d−1 for glacier sliding at this location leaves roughly 30-40 mm d−1 of motion to be accounted for by subglacial sediment deformation beneath the anchor.
Figure 4 shows drag-spool data from three consecutive field seasons. The results from our 1990 measurements indicate different basal sliding rates for different points across the glacier bed, ranging between ~ 40 mm d−1 (traces 90b and 90c) and ~ 80 mm d−1 (trace 90a). This finding is not paradoxical, since we expect mechanical coupling to vary with location because of spatial differences in the subglacial water system. With uniform surface motion observed over large parts of the glacier, our results imply a spatially varying partitioning between basal sliding and subglacial sediment deformation. In addition, changes in sliding rate that we observe from year to year (Fig. 4) probably reflect temporal variations of mechanical ice-bed coupling in response to changes in the subglacial hydrological system.

Fig. 4. Composite of drag-spool data from the 1990 (solid lines), 1991 (short dashed lines), and 1992 field seasons (long dashed lines), showing the variability of basal sliding observed at Trapridge Glacier. Measured sliding rates range between ~40 mm d−l (traces 90b, 90c, 91b, 92b) and ~80 mm d−l (trace 90a); (~60 mm d−l for traces 91a and 92a). Trace 92b shows the data from drag spool 92SM02, which is discussed in detail in the text (see also Fig. 2a).
Concluding Remarks
Our instrument enables continuous measurements of basal sliding over a soft substrate. In the case of a slow-flowing glacier such as Trapridge Glacier, sliding can be recorded for a period of up to several weeks. It should be noted, however, that the drag spool will place only an upper limit on glacier sliding because the anchor is placed within deformable sediment and some motion between the anchor and the ice may be caused by deformation of the intervening sediment. Alternatively, if the anchor is being pulled through the sediment by tension on the string, all the motion observed at the glacier surface could be due to basal sliding. We do not believe that this is the case, since the tension required to unwind the spool is small (~ 1 N). In other instrument-insertion experiments using similar-sized anchors, the force required to dislodge a freshly inserted anchor was at least 20 N, so it appears that the bed has a good grip on the anchor. One of the important features of the device is its small size, which permits in situ installation at the bottom of narrow boreholes (~ 5 cm diameter). Because the drag spool is simple in design and inexpensive to build, it is feasible to monitor basal sliding with an array of instruments at various locations across a glacier.
Acknowledgements
The authors wish to give special thanks to K. Dieter Schreiber and William Siep for their comments on the design and for their excellent machining skills. We thank the Natural Sciences and Engineering Research Council of Canada, the University of British Columbia and the Canadian Northern Studies Trust of the Association of Canadian Universities for Northern Studies for providing support for this research. The data presented in this paper were collected in Kluane National Park. We thank Parks Canada and the Government of the Yukon Territory for granting permission to conduct field studies in the park. We also acknowledge Neal Iverson and an anonymous reviewer for improving the manuscript.
The accuracy of references in the text and in this list is the responsibility of the authors, to whom queries should be addressed