Introduction

Radio-echo sounding in East Antarctica has revealed the existence of numerous subglacial lakes (Reference Oswald and RobinOswald and Robin, 1973; Reference Siegert, Dowdeswell, Gorman and McIntyreSiegert and others, 1996). The largest one is Vostok lake (14 000 km²) near Vostok station and drilling site. Vostok lake is associated with a prominent morphological surface feature within the Antarctic ice sheet. The ice-sheet surface above the lake is flat and featureless, consistent with the surface of an ice shelf. Ice flow over a large subglacial lake should be analogous to the flow of an ice shelf, where the lack of basal shear stress prevents deformation of internal layers (Reference Siegert, Kwok, Mayer and HubbardSiegert and others, 2000). Ice flows over the lake in a general west–east direction (Fig. 1). Once over the lake the ice flow in the south is diverted towards the southeast (Reference Kapitsa, Ridley, Robin, Siegert and ZotikovKapitsa and others, 1996), a feature that is confirmed from an analysis of internal radar reflection layers (Reference Bell, Studinger, Tikku, Clarke, Gutner and MeertensBell and others, 2002). Moreover, this along-lake flow component seems persistent since the Last Glacial Maximum (Reference Bell, Studinger, Tikku, Clarke, Gutner and MeertensBell and others, 2002). By contrast, velocity vectors derived from interferometry show a different direction, i.e. more eastward (Reference Kwok, Siegert and CarseyKwok and others, 2000). The northern part of the lake is largely unexplored, and velocity measurements are lacking (Fig. 1).

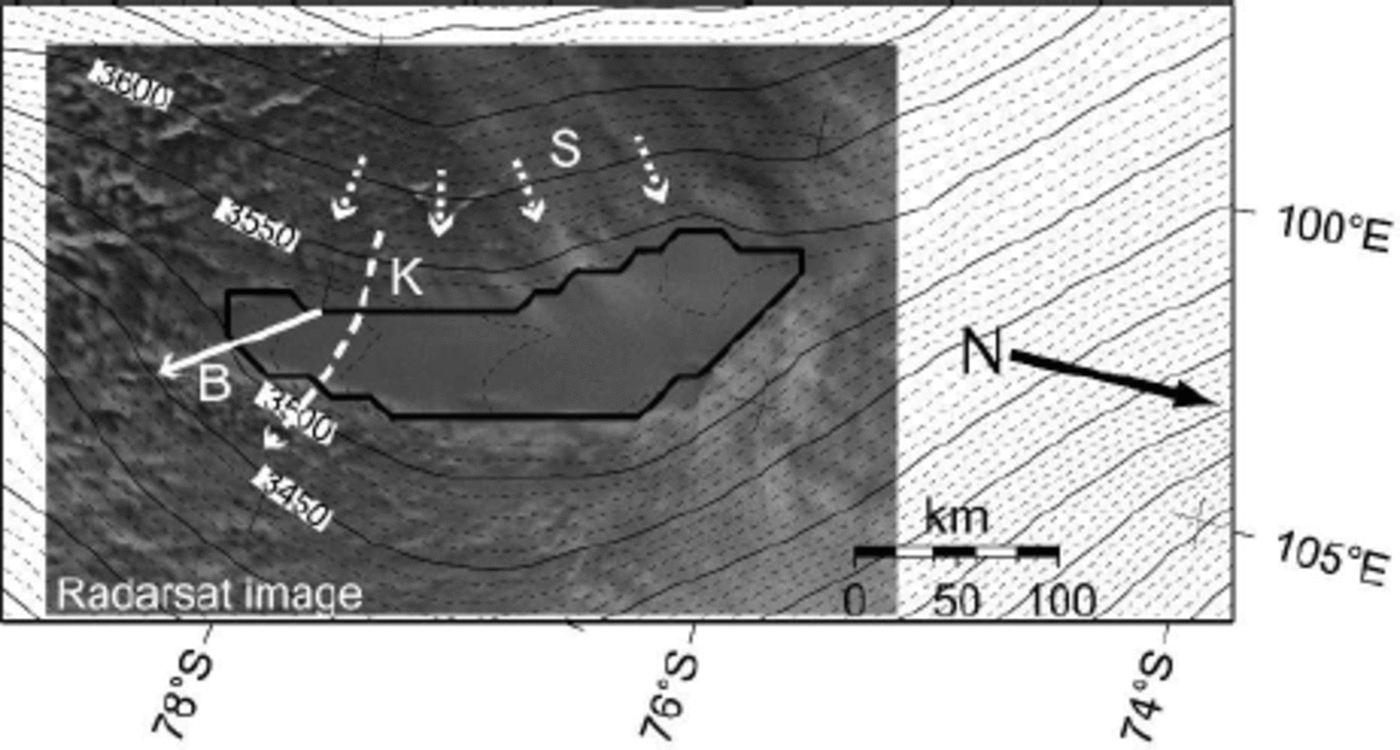
Fig. 1. Surface topography near Vostok lake, determined from satellite altimetry (Reference Liu, Jezek and LiLiu and others, 1999) superposed on a RADARSAT image. The general situation of the area is given in Figure 2. White vectors show different observed flow directions: B: ice flow across the southern part of the lake according to (Reference Bell, Studinger, Tikku, Clarke, Gutner and MeertensBell and others 2002); K: ice flow across the lake according to (Reference Kwok, Siegert and CarseyKwok and others 2000); S: grounded ice flow according to (Reference SiegertSiegert and others 2001).

Although the ice surface above the lake is relatively flat, an along-lake north–south slope is prominent, tilting 60m over a horizontal distance of > 250 km. Over the lake, the ice is thicker in the north (up to 4300 m) and thins to 3700 m in the south (Reference StudingerStudinger and others, 2003). Vostok lake has an ice/water interface sloping at 11 times the ice surface gradient (but in the opposite direction), which indicates that the overlying ice is in hydrostatic equilibrium (Reference SiegertSiegert and others, 2001). According to (Reference Souchez, Petit, Jouzel, de Angelis and TisonSouchez and others 2004), the inclined ice/lake interface should be considered as the result of a dynamic equilibrium: melting in the north of the lake and freezing in the south are conducive in the long run to a horizontal interface but, in the meantime, accreted ice is exported out of the lake by glacier movement, maintaining the inclination of the surface. This refreezing is due to well-developed water circulation in the lake (Reference Souchez, Petit, Tison, Jouzel and VerbekeSouchez and others, 2000; Wu¨estS and Carmack, 2000; Reference SiegertSiegert and others, 2001; Reference WilliamsWilliams, 2001; Reference Mayer, Grosfeld and SiegertMayer and others, 2003). Vostok lake is thus unique, encompassing a variety of ice-deformational features.

A comprehensive understanding of the ice flow across Vostok lake demands the use of a so-called higher-order icesheet model, i.e. a model that, besides deformation due to vertical shearing, also takes into account normal stress components. Mayer and (Reference Siegert and BamberSiegert 2000) investigated the ice flow along a longitudinal transect with a two-dimensional higher-order flowline model, but these experiments were carried out in a diagnostic fashion (ice-sheet geometry was kept fixed). In this paper, the ice flow across Vostok lake is investigated using a dynamical three-dimensional (3-D), thermomechanical, higher-order ice-sheet model, which shows, for the first time, the major ice-dynamical features of this area in a prognostic fashion. The purpose of the experiments is to determine the ice-flow field across the whole lake and to identify the processes responsible for the flat surface topography, the along-lake slope component, the ice flow turning across the lake and Vostok lake’s influence on the regional dynamics of the East Antarctic ice sheet.

Model Description

The model approach is based on continuum thermodynamic modelling, and encompasses balance laws of mass, momentum and energy, extended with a constitutive equation. A complete description of the model is given in (Reference PattynPattyn 2003). Treating ice as an incompressible fluid with constant density, the equations for conservation of mass, linear momentum and energy are written as

(1)

(2)

(3)

where ρ is the ice density, g gravitational acceleration, v the velocity vector, σ the stress tensor, θ the ice temperature, c _p and k_i the heat capacity and thermal conductivity of the ice, respectively, and Φ internal frictional heating due to deformation. The force-balance equations are derived from the conservation of momentum. A major approximation to the Stokes system was made by applying the hydrostatic approximation to the vertical force balance. Therefore, horizontal gradients in the vertical shear stresses σ’_xz and σ’_yz are ignored. Longitudinal normal stress and horizontal shear stress gradients are accounted for, so that the force balance is written as

(4)

(5)

where σ’ _ij is the deviatoric stress component and s is the surface of the ice mass. The constitutive equation governing the creep of polycrystalline ice and relating the deviatoric stresses to the strain rates is taken as a Glen-type flow law with exponent n = 3 (Reference PatersonPaterson, 1994):

(6)

where ε is the second invariant of the strain-rate tensor, defined by ε ² = Σ_ij ¹2 έ_ij έ_ij and η is the effective viscosity.έ₀ is a small number (10–³⁰) to make the viscosity finite. The flow-law rate factor is a function of temperature and obeys an Arrhenius relationship:

(7)

where a = 1:14 χ 10^-5 Pa–na–¹, Q = 60kJmol–¹ for Θ* < 263:15 K; a = 5:47 χ 10¹⁰ Pa^{– n} a–¹, Q = 139kJmol–¹ for Θ* > 263:15 K, and R is the universal gas constant (Θ* is the homologous temperature, i.e. corrected for pressure melting). The enhancement factor was taken as m = 5, a value used by (Reference HuybrechtsHuybrechts 1992) for Antarctic ice-sheet modelling. Heat transfer (Equation (3) is a result of vertical diffusion, horizontal and vertical advection, and internal friction due to deformational heating. Finally, the rate of change in ice thickness is obtained from mass conservation Equation (1), extended with a kinematic boundary condition, i.e. snow accumulation at the surface:

(8)

where H is the ice thickness and M_s the surface mass balance (accumulation rate). Basal melting and accretion were not considered because lake circulation was not taken into account. This is a reasonable assumption as the inclined ice/lake interface is a result of a dynamic equilibrium between melting and accretion due to the lake-water circulation (Reference Souchez, Petit, Jouzel, de Angelis and TisonSouchez and others, 2004).

Instead of modelling the whole Antarctic ice sheet, the model domain is limited to a regional catchment area comprising the ice flow between the ice divide and the coast. Boundary conditions to the model are zero ice thickness (H = 0) at the seaward edge of the ice sheet, and a zero surface slope perpendicular to the edge of the catchment area along the ice divide. At the upper surface a stress-free boundary condition is applied. At the base, where is the basal drag, the basal velocity (with components u _b and v _b) and β ² a friction coefficient coupled to the basal temperature field as:

(9)

where B ₀ = 10⁵ Pa am^–1 is taken as such that basal velocities are within the range of observed values for the interior Antarctic ice sheet, and θ_pmp is the pressure-melting temperature. Equation (9) allows for basal sliding at sub-freezing temperatures over a range of ϓ= 1 K^–1 (Reference Hindmarsh and Le MeurHindmarsh and Le Meur, 2001). Written in terms of velocities, the lower boundary condition becomes

(10)

(11)

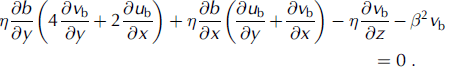
Basal sliding within the ice streams at the coast is probably underestimated in this manner, but the coastal area is considered to be a ‘far-field’ boundary condition for the ice flow of the interior (Vostok lake area). In this respect, grounding-line dynamics were not accounted for either. Sensitivity experiments with different ice thicknesses at the grounding line and different boundary conditions to the velocity at the grounding line did not affect the ice-dynamical behaviour near Vostok lake. Boundary conditions to the energy-balance equation follow from the mean annual air temperature at the surface. At the base the temperature gradient is a function of the geothermal heat flux taken as G = 0:045 W m^–1 (Reference PetitPetit, 2003).

Experimental Set-Up

The modelled domain consists of the East Antarctic catchment area between Dome Argus, Ridge B, the Transantarctic Mountains and the Southern Ocean (Fig. 2). Present ice geometry (ice thickness, bedrock elevation) is taken from the BEDMAP datasets (Reference Liu, Jezek and LiLiu and others, 1999; Reference Lythe, Vaughan and SiegertLythe and Vaughan, 2001). Surface accumulation is obtained from (Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others 1999). Data were resampled to a grid of 10 by 10 km, leading to 251 by 251 gridpoints in the horizontal, and 40 layers were considered in the vertical. The position and size of Vostok lake are derived from (Reference StudingerStudinger and others 2003) (Fig. 2). Instead of blending these newly observed and interpolated ice-thickness data into the BEDMAP dataset, a physically sound approach was preferred. Ice thickness across the lake is determined by considering the ice in hydrostatic equilibrium,

(12)

where h_ref = 3161 m a.s.l. is the reference elevation for buoyancy and p_w the water density. The resulting ice thickness is in very good agreement (within ±15m) with the observed thickness distribution of (Reference StudingerStudinger and others 2003).

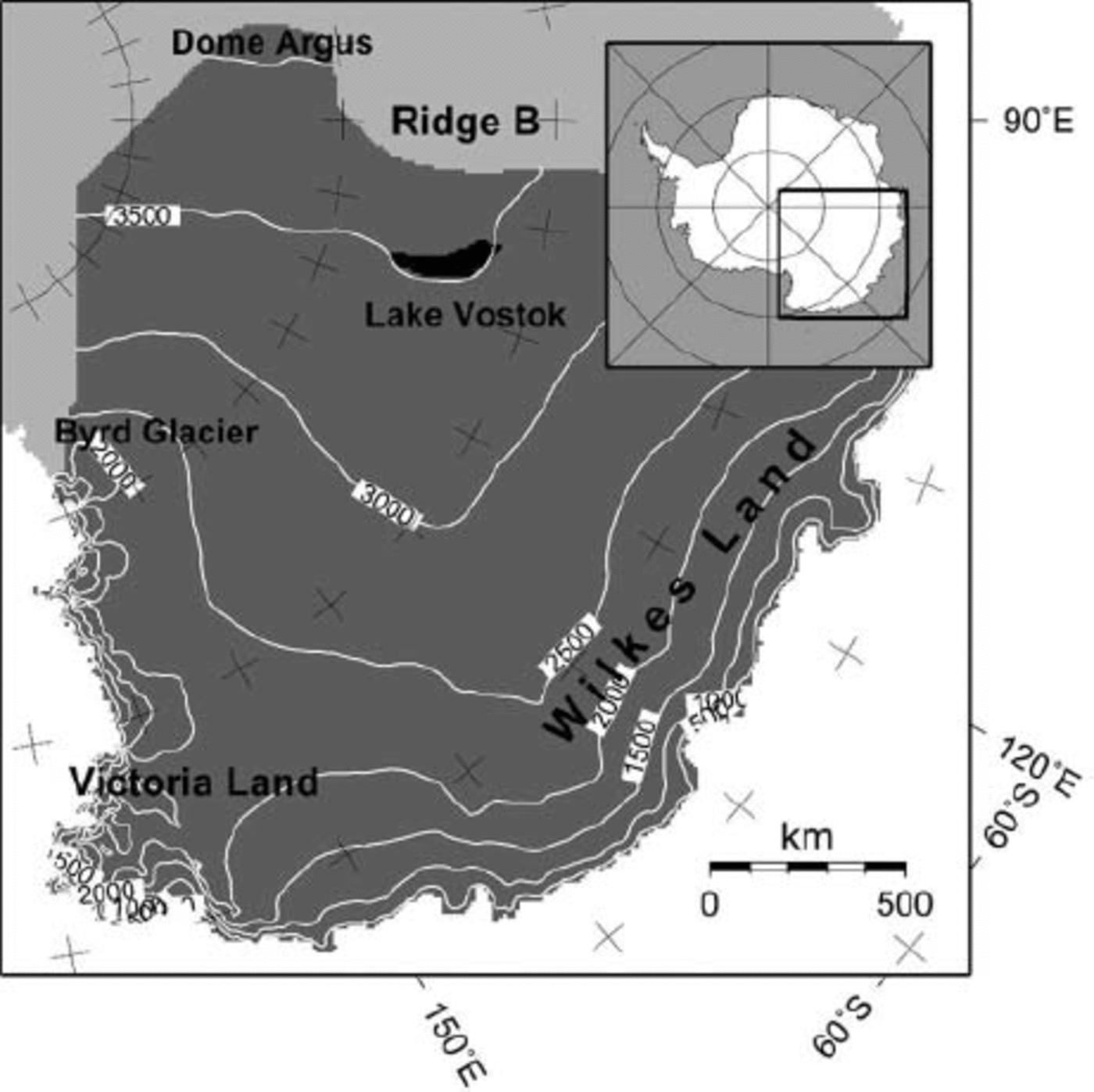
Fig. 2. Situation map of the modelled domain (dark grey). The position of Vostok lake is shown in black. For this black zone the condition ß² _lake = 0 is fulfilled.

Vostok lake is implemented in the model as a zone with a frictionless base, i.e. ß _l ² _a ke = 0. However, the boundary condition at the ice/water interface is not entirely stress-free, i.e.

(13)

where n _b is the outward-pointing unit normal vector to the bottom surface (Reference MayerMayer, 1996). The assumption is made that the pressure of the water at the bottom of the ice is equal to the hydrostatic pressure necessary to float the ice mass.

A first series of experiments are diagnostic, i.e. the velocity field is calculated based on the present observed ice-sheet geometry that was kept fixed. This involves a ‘no lake’ (DNL) and a ‘lake’ (DLE) experiment, where for the latter a stress-free basal surface was considered within the lake boundaries (ß ² _lake = 0). These experiments are also isothermal, i.e. the flow parameter A(θ*) was kept constant for the whole ice sheet (A(θ*) =2 χ 10^-17 Pa^-n a^-1). For large ice sheets, however, A(θ*) shows a clear temperature dependence and might vary over several orders of magnitude. Coupling the temperature to the ice-flow field in the diagnostic mode resulted in numerical instabilities since the ice-sheet geometry is not relaxed, and steep surface gradients lead to large horizontal and vertical temperature gradients, especially near the coast and the Transantarctic Mountains. Although such a coupling influences the magnitude variations of the velocity field, it has less impact on the direction of the ice flow, which is the main issue of the diagnostic experiments. Temperature coupling is included in the next series of experiments.

The prognostic experiments are defined as follows. Starting from the present observed ice geometry, the model ran forward in time in a diagnostic fashion, i.e. keeping the ice geometry fixed, until the temperature field attained a steady state (without coupling the temperature to ice dynamics). Subsequently, the temperature was coupled to the ice dynamics, and the surface topography was allowed to react (prognostic run). The model was thus run forward for another 10 000 years to reach a situation close to steady state. There is no explicit treatment of the lake/bed or the lake/ice interface, nor is there any treatment of water circulation. Our sensitivity analysis consists of three prognostic experiments, a ‘lake’ experiment (LE), where the lake is treated as a stress-free spot or ß ² _lake = 0, a ‘no lake’ experiment (NL) where ß ² _lake is determined from Equation (9), and a ‘lake’ experiment with buoyancy (LBE). For the LE experiment, the ice/water interface was kept fixed in time and only the ice/air surface changed with time according to Equation (8). In the LBE experiment, both ice/water and ice/air interfaces were altered to fulfil buoyancy. The prognostic experiments require 2–3 days of calculations on a personal computer with a 2.2 GHz Intel Pentium 4 processor (which is 50–200 times slower than a calculation according to the shallow-ice approximation).

Diagnostic Experiments (DNL and DLE)

Ice flow in a grounded ice sheet will generally follow the steepest surface gradient as, in the absence of a significant longitudinal stress contribution, the driving stress is balanced by the basal shear stress and hence is directly dependent on the surface slope and direction. This notion is confirmed by the DNL experiment (Fig. 3), accounting for a general west–east ice flow over the grounded ice sheet, perpendicular to the surface contours. The surface of the ice above Vostok lake, however, is very flat and slightly tilted in the north–south direction, which deviates the bulk ice flow to the southern sector of the lake area. The basal and surface velocities are lowest across the lake, as the area is nearly flat. This is not a realistic case, as it implies that the eastern margin of the lake receives no ice flux. The higher-order model solution (DNL) is very similar to the solution according to the shallow-ice approximation (SIA). In large ice sheets, the SIA is perfectly valid so long as surface and bedrock slopes are relatively low (typical interior ice flow) and basal friction is high. As shown by (Reference PattynPattyn 2003), the major difference between the SIA and a higher-order model solution occurs under the ice divide, in areas with pronounced bedrock variability and in zones of low basal friction. So long as Vostok lake is considered as a high-friction area, both model results will be complementary.

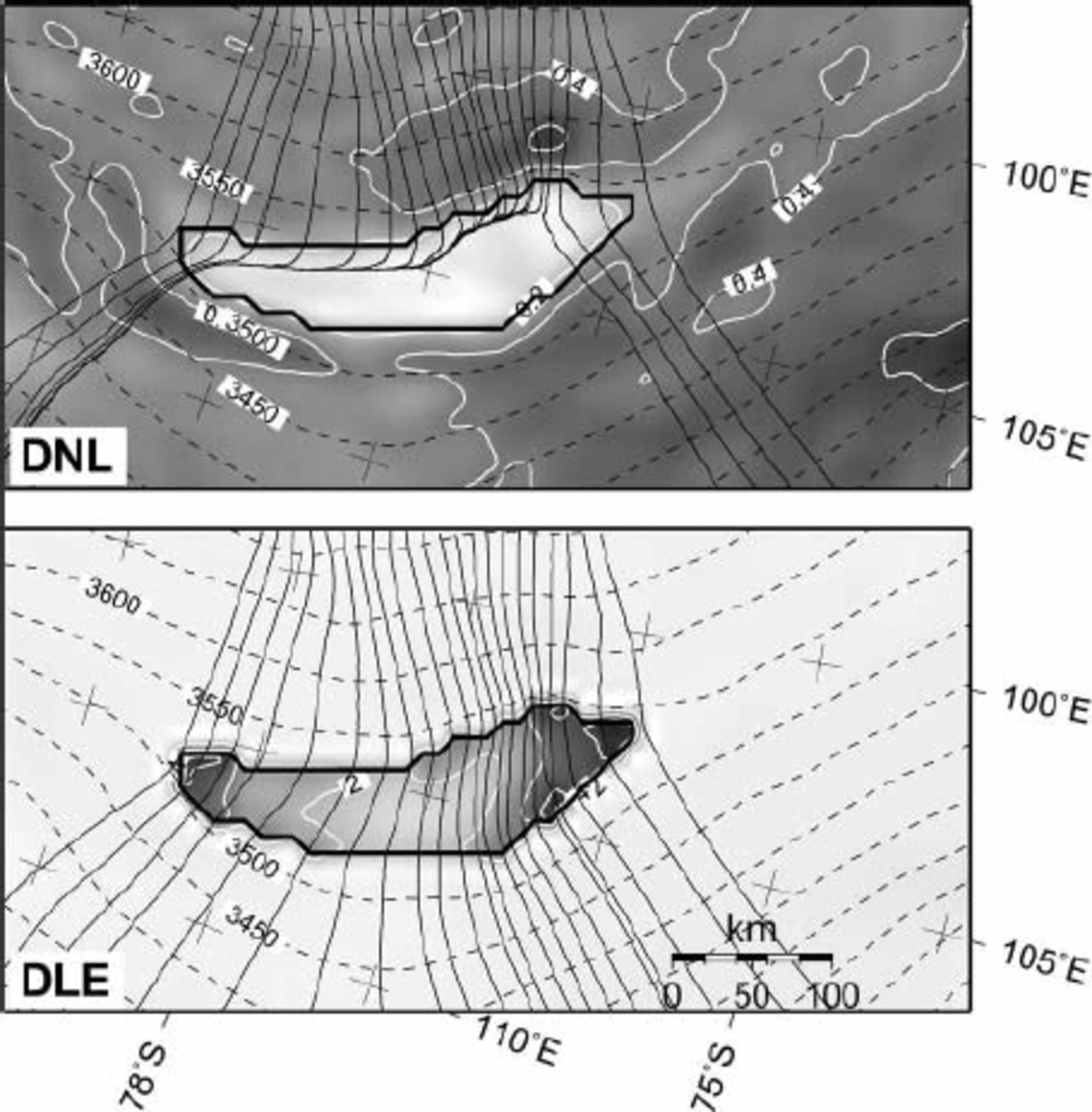
Fig. 3. Predicted basal velocity (m^–1, grey shaded and white contours), surface topography (m a.s.l., black dashed contours), and flowlines across Vostok lake for the DNL and DLE experiments. The position of Vostok lake is shown by the thick black outline. A different grey scale is used for each panel.

Treating the lake area as a stress-free basal spot within the ice sheet results in an ice-flow pattern that exhibits a general west–east flow component, also for the ice that crosses the lake. Experiment DLE puts a higher weight on the horizontal stress gradients as, due to the lack of basal friction, vertical shearing vanishes across the lake. While the ice flow is perpendicular to the surface contours for the grounded ice sheet, the ice flux at the lake margins controls the ice flow across the lake, which is in the direction of the highest ice flux and not necessarily in the direction of the steepest surface slope (e.g. an ice shelf). Contrary to experiment DNL, basal velocity is highest across the lake; due to the drag-free basal boundary condition, there is no shear-stress gradient near the ice base over the lake, so the basal velocity is a direct indication of the column velocity. The flow direction in the southern part of the lake is eastward, in agreement with the flow pattern of (Reference Kwok, Siegert and CarseyKwok and others 2000).

The major drawbacks of diagnostic model runs are that (i) the result is independent of the ice-sheet surface mass balance (accumulation), and hence a strong imbalance might exist, as the ice sheet is not in steady state; (ii) calculations apply to an isothermal ice sheet, which is not realistic for Antarctica, where a large temperature gradient exists between the cold surface of the ice sheet and the base close to or at pressure-melting point; and (iii) the result is still biased in favour of surface topography and slope, as satellite altimetry observations of the surface will exhibit far greater detail than measurements of the bedrock.

Prognostic Experiments (NL, LE and LBE)

The modelled ice-thickness distribution for the steady-state prognostic experiments is in overall agreement with the observed thickness distribution (OBS) for the whole drainage basin (Fig. 4). The modelled ice thicknesses are comparable to those obtained from other Antarctic model studies, such as (Reference HuybrechtsHuybrechts 1992), although ice shelves, grounding-line dynamics and fast-flow processes in the coastal area were ignored in our model. The difference between modelled (LE experiment) and observed ice thickness amount to an rms error of 196 m for the whole drainage basin and 77 m for the region near Vostok lake.

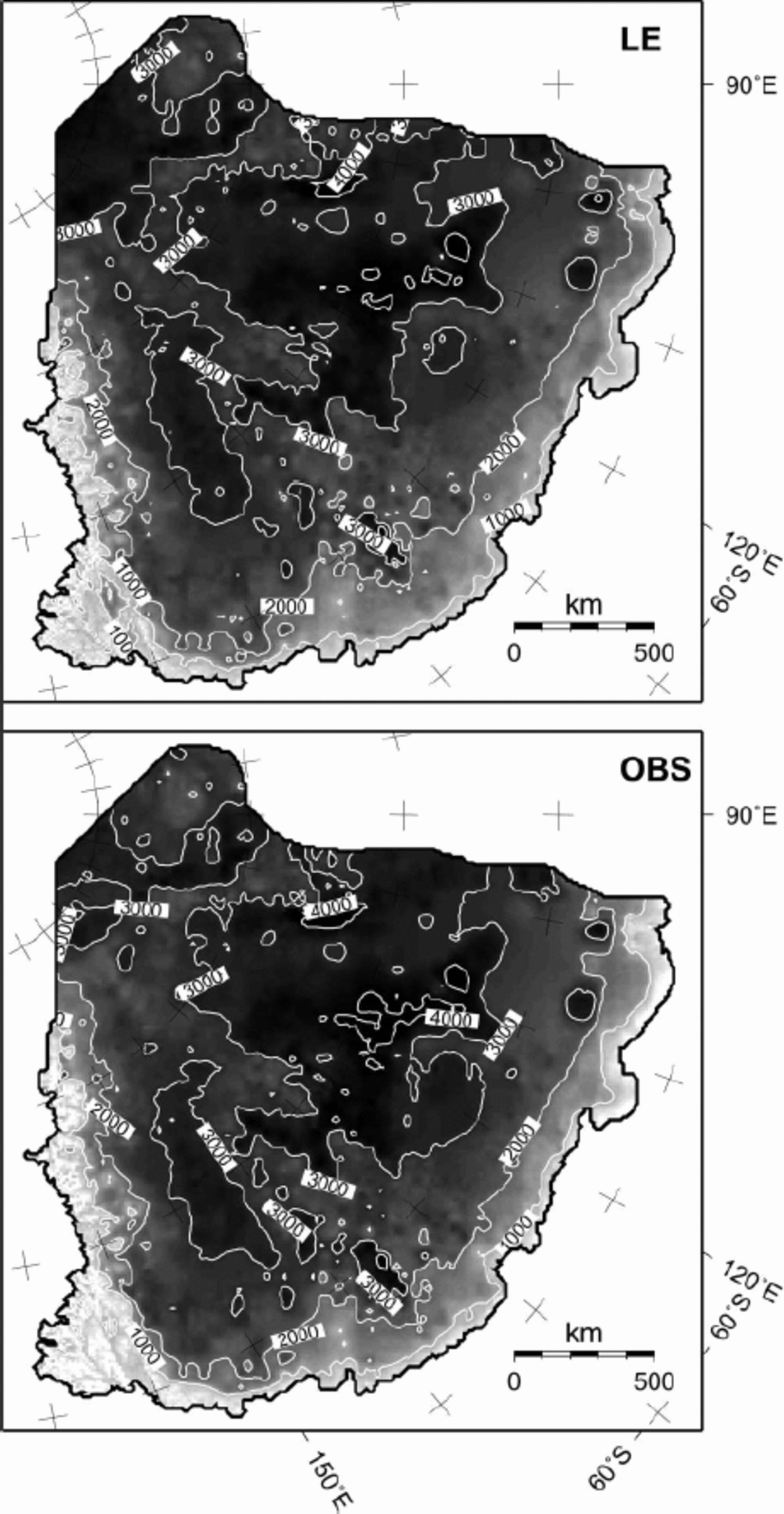
Fig. 4. Predicted ice thickness (m) according to the LE experiment, compared to the observed ice-thickness distribution within the whole drainage basin.

Figure 5. shows the surface elevation and surface slope according to the three prognostic experiments. Both the LE and LBE experiments exhibit a distinct surface flattening across Vostok lake, which is, as demonstrated by (Reference PattynPattyn 2003), associated with the stress-free base (ß ² _lake = 0). Such a feature is not observed in the NL experiment. The surface topography according to LBE gives a better fit to the observed situation across the lake. However, a mismatch between modelled and observed topography exists to the north of the lake (Fig. 5). This discrepancy is primarily dueto the lack of sufficient bedrock data in this area and further downstream towards the coast, as can be inferred from the BEDMAP coverage (Reference Lythe, Vaughan and SiegertLythe and Vaughan, 2001). Nevertheless, the modelled grounded surface topography is in overall agreement with the observed topography, at least for the area directly upstream of the lake, i.e. between the western margin of Vostok lake and Ridge B. Both ‘lake’ experiments (LE and LBE) also show a suspicious increase in surface slope east of the lake (downstream), which is not seen from satellite altimetry. This suspicious slope might be due to the fact that the observed ice sheet is not in steady state or that a lack of detailed bedrock data in this area prevents a proper determination of the ice-sheet surface through numerical modelling.

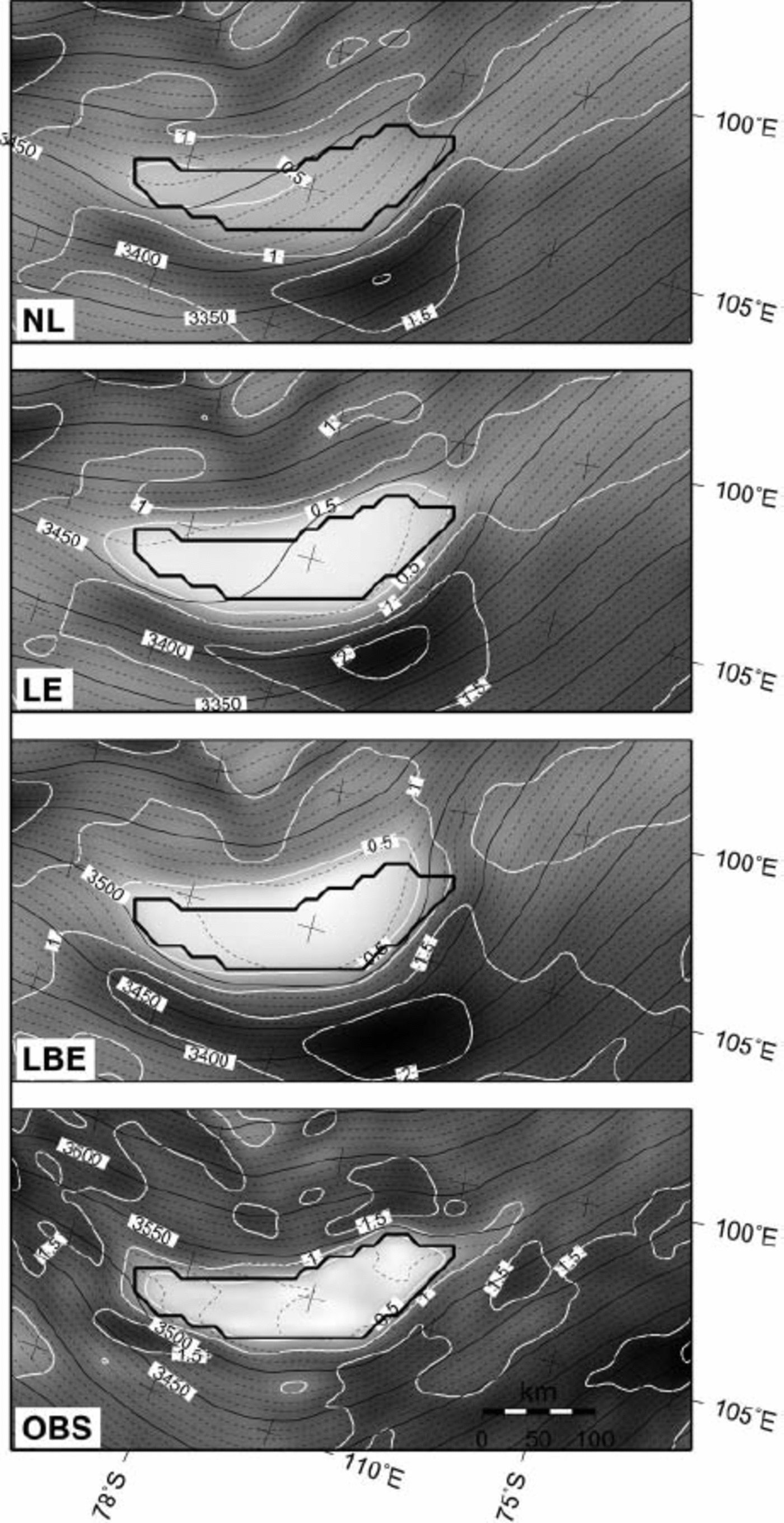
Fig. 5. Predicted surface slopes (grey shaded and white contours every 0.5 χ 10^-3 rad) and surface topography (ma.s.l., black contours) for the NL, LE and LBE experiments, as well as the altimetric observations (OBS). The position of Vostok lake is shown by the thick black outline.

The ice-flow direction across Vostok lake is highly dependent on the position of the local ice divide that, according to present observations, crosses the lake from west to east and divides the ice flow towards the Transantarctic Mountains from the ice flow towards Wilkes Land. As this series of experiments is dynamic, we have no control on the exact position of this ice divide, and its position will depend on the overall geometry of the drainage basin as well as local characteristics of the Vostok lake area. In a near-steady-state situation, this divide lies to the south of Vostok lake, giving rise to a northward along-lake slope component (Fig. 6, experiments NL and LE). Only when buoyancy is taken into account (LBE experiment) does the local divide lie across the lake, diverting the ice flow to the southeast in the southern sector of the lake, and to the northeast in the northern part. The flow pattern in the south is in accord with the findings of (Reference Bell, Studinger, Tikku, Clarke, Gutner and MeertensBell and others 2002). Also, the velocity magnitude and direction is in accord with the observations of (Reference Kapitsa, Ridley, Robin, Siegert and ZotikovKapitsa and others 1996). A prominent feature, however, is the turning of the ice flow across the lake, as shown in both LE and LBE experiments, while without the presence of a lake a steady west–east flow pattern is observed (panel NL in Fig. 6).

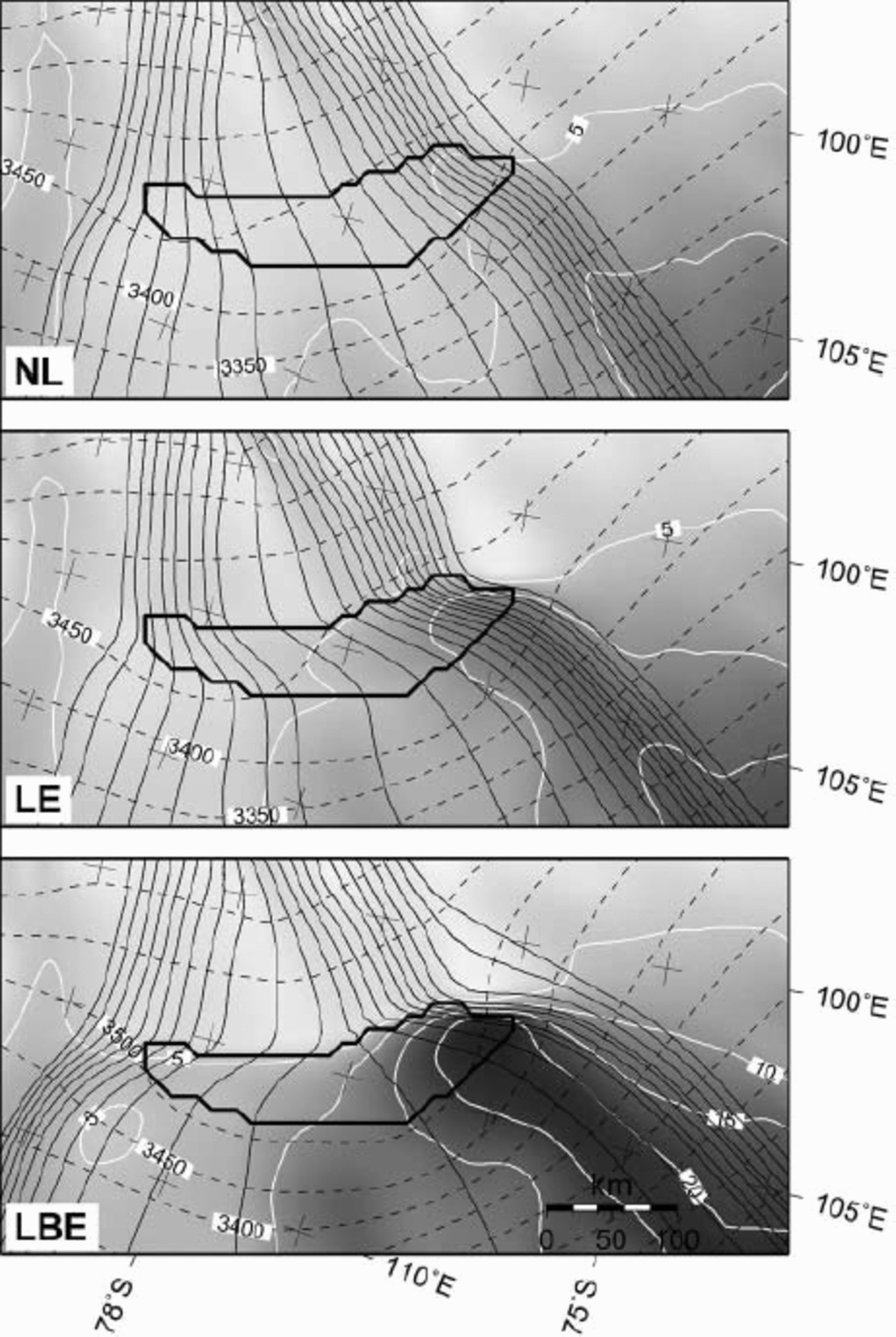
Fig. 6. Predicted surface velocity (grey shaded and white contours every 5 ma^–1), surface topography (m a.s.l., black, dashed contours), and flowlines across Vostok lake for the NL, LE and LBE experiments. The position of Vostok lake is shown by the thick black outline.

Figure 7 displays the modelled homologous basal temperature in the vicinity of Vostok lake. Both NL and LE experiments exhibit a similar pattern, i.e. most of the basal ice in the vicinity of Vostok lake is at the pressure-melting point, with the exception of the northwestern margin and the area downstream of the eastern margin of the lake. The ice directly above the lake is at the pressure-melting point. Note, however, that the calculations neglect the presence of subglacial water and only model the heat transfer from the bedrock to the ice through geothermal heating. Lake-water circulation and melting/accretion processes are also neglected. Therefore, Figure 7 only indicates that, given the present environmental conditions, subglacial melting is prevalent across the subglacial trench so that a subglacial lake can be maintained.

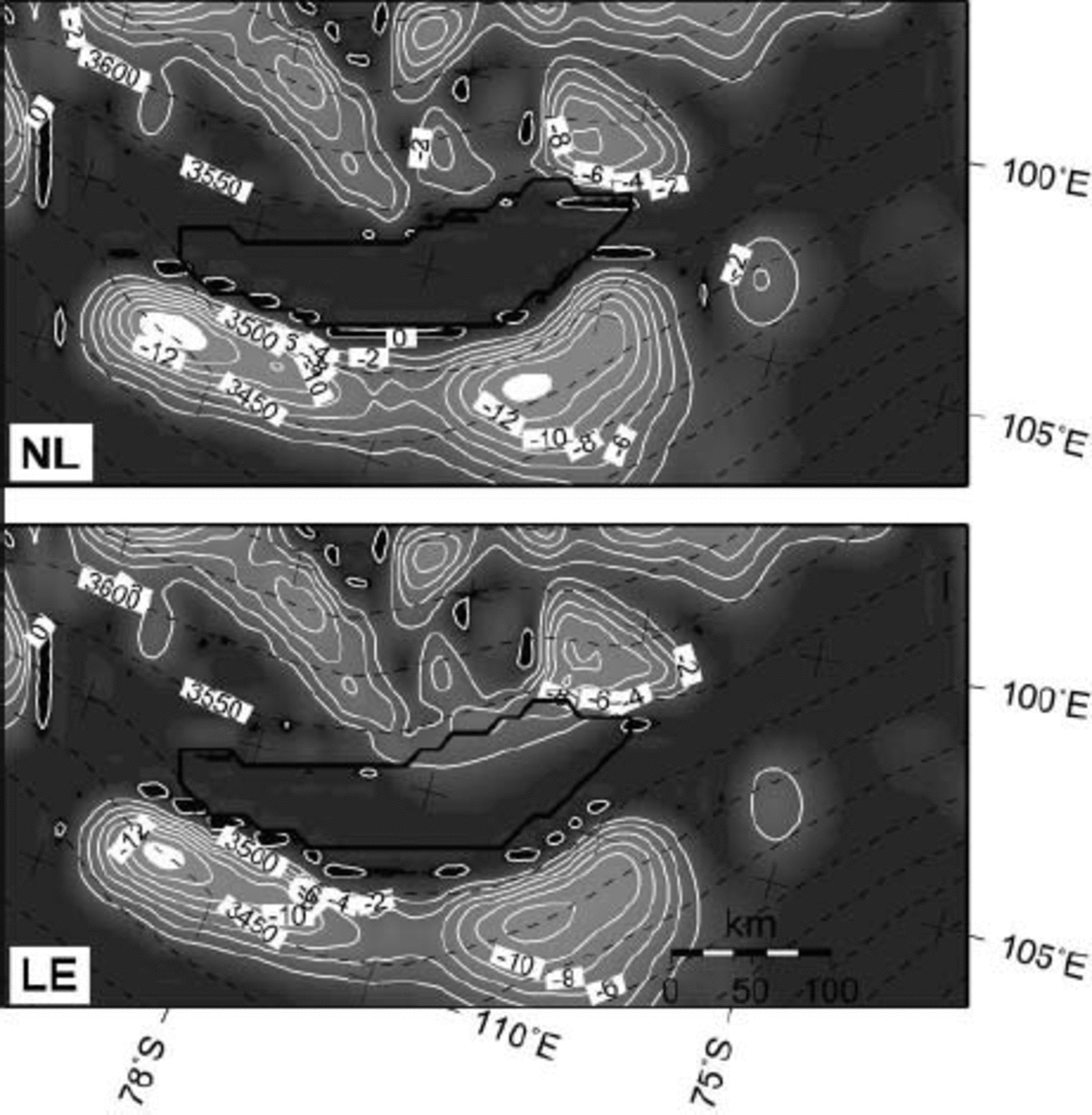
Fig. 7. Predicted homologous basal temperature (grey shaded and white contours every 28C) and surface topography (m a.s.l., black dashed contours) for the NL and LE experiments. The position of Vostok lake is given by the thick black line.

From the pattern of the modelled flowlines and ice velocity it is evident that a significant amount of ice is transported along the northern margin of the lake. The LE and LBE experiments show the highest velocity in the northern part, which is also the area where prominent basal melting at the ice/water interface occurs (Reference SiegertSiegert and others, 2001). The local speed-up over the lake is more pronounced in the LBE experiment, but is also visible in the LE experiment. In a region 40km downstream of the western grounding line, the ice speeds up. Further downstream, it slows down towards the eastern grounding line. The speedup is a direct consequence of the lack of basal drag when the ice crosses the grounding line and flows across the lake. The slow-down is due to the back-stress exerted by the grounded ice at the eastern margin of the lake. The ice speed-up is more pronounced in the north, as here (i) the ice flux across the western margin is larger than in the south; (ii) the ice is thicker; (iii) the along-flow surface slope across the margin is steeper than in the south; and (iv) the lake (hence the frictionless area) is wider. All these factors lead to a higher ice flux in the northern sector of the lake. According to the LBE experiment, the ice in the northern sector is somewhat thinner than it is in the LE experiment. At first sight, this should reduce the ice speed as the ice flux becomes smaller. However, the reverse is true and the reason probably lies in the fact that the northeastern lake margin is less steep in the LBE experiment, as the ice/water interface is situated higher within the subglacial trench (due to the flotation criterion). This would eventually reduce the amount of back-stress so that the ice can flow faster.

For both LE and LBE experiments, this higher ice flux in the north seems to start an enhanced flow feature in the direction of Totten Glacier, Wilkes Land. The onset of enhanced flow of ice in East Antarctica is believed to be associated in a number of cases with the presence of subglacial lakes (Reference Siegert, Kwok, Mayer and HubbardSiegert and Bamber, 2000). Storage of subglacial water has the potential to control the ice flow of the interior ice sheet, and several lakes lie at the onset of major enhanced ice-flow features such as those feeding into Byrd Glacier (Reference Siegert, Kwok, Mayer and HubbardSiegert and Bamber, 2000). However, their analysis is based on flux calculations, leading to balance velocities (Reference Budd and WarnerBudd and Warner, 1996). Since balance velocities are directly derived from surface slopes, they infer a flow mechanism that is based on gravitational downward motion. Ice flow over subglacial lakes is similar to the flow of ice shelves and is thus flux-driven, which is not accurately represented using the technique of (Reference Budd and WarnerBudd and Warner 1996). This is probably the reason why Vostok lake, lying relatively far inland, is not associated with any enhanced flow feature derived from balance velocities.

When buoyancy forces and hydrostatic equilibrium are taken into account, the along-lake surface slope is preserved, which is not the case for the LE experiment. Due to hydrostatic equilibrium, this tilted surface slope is also responsible for a tilted ice/water interface in the opposite direction. In the long run, however, when the LBE experiment is run forward for another 10 000 years, even the tilted surface disappears. The ice divide, however, remains more or less across the centre of the lake so that the southeastern flow pattern in the south is maintained. These findings corroborate the results of (Reference Bell, Studinger, Tikku, Clarke, Gutner and MeertensBell and others 2002) that the flow pattern did not change during the last 10 000 years. The levelling of the ice/water interface in the long run is due to a thinning of the ice across the lake in the northern sector – as the ice flux in the north is higher – and does not influence any other part of the ice sheet in the vicinity of Vostok lake. This means that the present tilted surface is either a transient feature or (more likely) controlled by the dynamic equilibrium between melting and accretion processes at the ice/water interface due to the lake circulation (Reference Souchez, Petit, Jouzel, de Angelis and TisonSouchez and others, 2004).

The lack of comprehensive velocity measurements in the northern part of the lake prevents a proper validation of the above model results. Ice velocities in the northern part are probably slightly overestimated by the LBE experiment, as anisotropic effects are not taken into account in the model description: crystal orientation in ice shelves is distinctly different than that in ice sheets, which has an impact on deformation rates (Reference PatersonPaterson, 1994).

Conclusions

For the first time, a dynamical 3-D, thermomechanical simulation of the ice flow across Vostok lake is presented. The model results show that by treating the ice/lake interface as a stress-free surface (similar to an ice shelf), major ice-dynamical features such as the surface flattening and turning of the ice flow across the lake are accurately reproduced, even though subglacial lake dynamics are not treated explicitly.

A relatively stable velocity pattern, with a local ice divide that crosses Vostok lake, is obtained when buoyancy effects are taken into account. This also assures an along-lake southward slope, maintaining the tilted ice/water interface. However, the tilted ice/water interface tends to level when the model is allowed to run on a longer time-scale, which indicates that the lake-water circulation plays a decisive role in balancing melting in the north and accretion in the south. Only when a model of lake-water circulation is coupled to the ice-sheet model might a more comprehensive insight into these processes be obtained.

According to the experiments, ice velocities are highest in the northern sector of the lake. Vostok lake can therefore be considered as the onset of an enhanced ice-flow feature, more precisely the onset of the Totten Glacier catchment.