1. Introduction
Many cold-based glaciers and ice sheets have prominent debris-rich basal-ice layers that crop out at the margins (Fig. 1). Basal ice is distinguished from ice formed from compression of snow at the glacier surface by spatially and compositionally diverse debris layers, distinct gas compositions, high solute concentrations and the presence of deformation structures (Reference Fitzsimons and KnightFitzsimons, 2006). Several studies have shown that debris-rich basal ice can deform more easily in horizontal shear than the overlying clean ice (Reference Echelmeyer and WangEchelmeyer and Wang, 1987; Reference Cuffey, Conway, Gades, Hallet, Raymond and WhitlowCuffey and others, 2000a; Reference Samyn, Fitzsimons and LorrainSamyn and others, 2005a). Field observations by Echel-meyer and Wang (1987) at Ürümqi Glacier No. 1, China, demonstrated that 60–80% of the glacier deformation was accommodated within the lowermost 1–2% of the glacier thickness at –5°C. The enhanced deformation occurred within the debris-rich basal ice, in discrete shear bands and planes, including sliding along the ice/sediment boundaries.

Fig. 1. Example of the layered structure of the debris-rich basal ice, as exposed on the south side of Taylor Glacier with person for scale.
At Taylor Glacier, McMurdo Dry Valleys, Antarctica, we observe surface velocities >5 m a–1 , nearly two orders of magnitude faster than expected for deformation of cold (–17°C), thin (~ < 100 m) ice with low surface slope (~0.1). Detailed studies of ice-crystal textures and gas content of the debris-rich basal ice show that significant shearing has occurred within this basal ice (Reference Samyn, Svensson, Fitzsimons and LorrainSamyn and others, 2005b). Furthermore, sliding velocities of 167 mm a–1 were measured at sliding interfaces along clasts within the basal-ice sequence (Reference Fitzsimons and KnightFitzsimons, 2006). Our surface-velocity observations and these past studies suggest that a significant majority of the total ice deformation is concentrated in the basal ice.
Examining basal and subglacial sediment deformation processes is difficult, due to the inaccessibility of the basal region, which hinders direct observations except at the glacier margins. In addition, it is likely that the behavior of the basal ice varies over time and space, making it difficult to capture with sparse borehole and tunnel measurements. Previous basal-process studies have either sought to understand the rheological behavior of the basal ice or, given some rheological properties, to determine its contribution to the overall glacier behavior (Reference Fitzsimons and KnightFitzsimons, 2006). Our inverse approach addresses both of these goals simultaneously and circumvents the logistical difficulties of gathering direct field observations from the basal ice and subglacial sediment.
The aim of this paper is to further understand how the debris-rich basal ice contributes to the overall deformation of Taylor Glacier (Figs 2 and 3) and to place bounds on the rheological properties of the basal ice. To do this, we formulate an inverse problem to infer the softness and thickness of the basal ice relative to the clean, overlying meteoric ice using a two-dimensional (2-D) shallow-ice approximation flowband model constrained by field measurements in the terminus region of Taylor Glacier. Our model results show that the observed surface velocities are largely due to deformation of the basal ice, which contributes well over 85% of the total deformation. Current models of cold-based ice flow often neglect rapid deformation in the basal ice. A cold-based glacier with easily deformable basal ice will have higher surface velocities and a thinner surface profile than a cold-based glacier without easily deformable basal ice. We show that it may be necessary to incorporate these effects into models in order to accurately represent the deformation in cold-based glaciers that are underlain by soft, easily deformable debris-rich basal ice. Given the characteristics of the basal ice that we infer for Taylor Glacier (at least 10 m thick and 40 times softer than clean glacier ice), we estimate that the total thickness of the glacier or ice-sheet ice must be at least 1000 m before the error in predicting surface velocities that is introduced by ignoring the basal ice falls below ~ 2%.

Fig. 2. NASA satellite image of Taylor Valley and Taylor Glacier. Field site is 105 km nearly due west of McMurdo Station.

Fig. 3. Hillshade representation of digital elevation model (DEM) (Reference Schenk, Csatho, Ahn, Yoon, Shin and HuhSchenk and others, 2004) for the Taylor Glacier terminus. Red arrows and corresponding numbers show velocities measured by repeat GPS measurements of surface stakes. Black curve shows location of flowband bounded by sites Nirvana and Grace, which were locations of shallow ice cores. DEM uncertainty estimated at <0.3 m. DEM elevations provided in ITRF-93.
2. Background
Glacier-ice flow is typically modeled using Glen’s flow law (Reference GlenGlen, 1958), which is an empirically derived function defining the strain rate as a nonlinear function of the deviatoric stress:
where ![]() is the strain-rate tensor, τij
is the deviatoric-stress tensor and τ is the square-root of the second invariant of the deviatoric stress tensor. The flow-law exponent, n, is generally assumed to be 3, based on field and laboratory data (Reference Cuffey and PatersonCuffey and Paterson, 2010). A
0 is an empirically derived softness parameter for clean, isotropic Holocene ice. The effects of temperature follow an Arrhenius relationship, where T is the temperature, Q is the thermal activation energy for creep (usually 60 kJ mol–1 ) and R is the universal gas constant (8.314 J K–1 mol–1 ). The enhancement factor, E, accounts for any significant strain-rate variations that cannot be described by Glen’s law alone. Reference Budd and JackaBudd and Jacka (1989) identified several ice properties, in addition to temperature, that can affect strain rate; these include crystal size and orientation, chemical and solid impurities, and water content.
is the strain-rate tensor, τij
is the deviatoric-stress tensor and τ is the square-root of the second invariant of the deviatoric stress tensor. The flow-law exponent, n, is generally assumed to be 3, based on field and laboratory data (Reference Cuffey and PatersonCuffey and Paterson, 2010). A
0 is an empirically derived softness parameter for clean, isotropic Holocene ice. The effects of temperature follow an Arrhenius relationship, where T is the temperature, Q is the thermal activation energy for creep (usually 60 kJ mol–1 ) and R is the universal gas constant (8.314 J K–1 mol–1 ). The enhancement factor, E, accounts for any significant strain-rate variations that cannot be described by Glen’s law alone. Reference Budd and JackaBudd and Jacka (1989) identified several ice properties, in addition to temperature, that can affect strain rate; these include crystal size and orientation, chemical and solid impurities, and water content.
Numerous field and experimental studies show that a preferred orientation of crystal c –axes, also called fabric, accounts for large variations in strain rates, due to the strong anisotropic behavior of a single ice crystal undergoing deformation (e.g. Reference Budd and JackaBudd and Jacka, 1989; Reference AlleyAlley, 1992). Ice fabric can explain as much as 75% of measured strain-rate deviations from Glen’s law at some ice-core sites (Reference Thorsteinsson, Waddington, Taylor, Alley and BlankenshipThorsteinsson and others, 1999). Uniaxial-compression laboratory experiments on polycrystalline ice indicate that ice with c-axes favorably oriented to the direction of maximum shear can strain at rates up to 40 times greater than isotropic ice (Reference MiyamotoMiyamoto and others, 1999). Enhancement values for anisotropic ice of 8–10 are, however, more widely accepted (e.g. Reference Budd and JackaBudd and Jacka, 1989), based on the theory of crystal deformation. Reference Cuffey, Conway, Gades, Hallet, Raymond and WhitlowCuffey and others (2000a,Reference Cuffey, Thorsteinsson and Waddingtonb) have further suggested that strain rate depends on crystal size. Their model indicates that both crystal size and soluble ion concentrations must be included to account for strain-rate variations (Reference Cuffey, Thorsteinsson and WaddingtonCuffey and others, 2000b).
Reference Thorsteinsson, Waddington, Taylor, Alley and BlankenshipThorsteinsson and others (1999) and Reference Cuffey, Thorsteinsson and WaddingtonCuffey and others (2000b) attribute residual variations (strain-rate variations not explained by the crystal size or fabric) primarily to chemical and solid impurities in the ice.
Chemical impurities concentrate in and increase the thickness of liquid-water films along ice-crystal boundaries (Reference Paren and WalkerParen and Walker, 1971) and likely enhance ice-flow mechanisms (e.g. grain-boundary sliding; Reference Holdsworth and BullHoldsworth and Bull, 1970; Reference Barnes, Tabor and WalkerBarnes and others, 1971; Reference Fisher and KoernerFisher and Koerner, 1986). Thin films that facilitate grain-boundary sliding have been observed in situ at –17°C (Reference Cuffey, Conway, Hallet, Gades and RaymondCuffey and others, 1999). Reference PatersonPaterson (1991) determined that chloride and sulfate ions increase ice softness, and postulated that these soluble impurities limit grain size by impeding crystal growth. Reference Cuffey, Conway, Gades, Hallet, Raymond and WhitlowCuffey and others (2000a) found that sulfate and calcium ions cause the greatest increase in ice softness.
The influence of solid impurities on the mechanical behavior of ice has not been well constrained because there are few studies, and results are often conflicting. Ice-deformation experiments on samples with 10% rock content by volume have shown both increases and decreases in ice viscosity (Reference LawsonLawson, 1996). However, analysis of strain rates and debris concentrations in the debris-rich basal ice at Meserve Glacier, Antarctica, suggested that the low viscosity of the debris-rich ice was not directly related to the solid impurities (Reference Cuffey, Conway, Gades, Hallet, Raymond and WhitlowCuffey and others, 2000a).
Reference Samyn, Svensson and FitzsimonsSamyn and others (2008) showed that the competence (resistence to deformation) of debris-rich ice compared to clean ice may depend on whether deformation is confined to centimeter-thick or millimeter-thick ice layers. Strain experiments on centimeter-scale samples from Taylor Glacier clean-ice and basal-ice sequences indicate that the debris-rich ice is up to twice as strong as the clean ice during compression at temperatures below –5°C (Reference LawsonLawson, 1996). Reference Samyn, Svensson and FitzsimonsSamyn and others (2008) point out that the compressive-stress tests do not correspond to the combined vertical pure and simple-shear stress regime at Taylor Glacier. Reference Fitzsimons, McManus, Sirota and LorrainFitzsimons and others (2001), however, show that direct shear experiments on layers with >70% debris content have twice the shear strength of basal ice with low debris content, which reinforces Lawson’s conclusion.
The analysis we present here assumes a bulk enhancement factor for the full thickness of the basal-ice sequence. We do not distinguish the causes for softness of the basal ice; rather we aim to show the relative importance of the basal-ice softness on a larger scale than has been reported before.
3. The Inverse Problem
3.1. The challenge of basal inference
All glacier motion depends heavily on processes at the base, but the base is difficult to observe directly, except in a few widely distributed boreholes. Over extended areas, parameters describing basal characteristics must be inferred using inverse theory. Solving an inverse problem for basal characteristics requires data and a forward algorithm that describes the mechanics of ice flow. For a glacier, we are typically limited to surface data (e.g. topography, velocities, temperatures and accumulation rates) borehole data (e.g. shear deformation, ice properties and temperature) and remotely sensed data (e.g. ice-penetrating radar profiles). The forward model must be a well-defined analytical or numerical algorithm, describing physical processes in which estimates of the desired basal parameters can be used in order to predict values of the observed surface data.
Reference Van der Veen and WhillansVan der Veen and Whillans (1989a,b) advanced the estimation of basal properties from surface measurements by developing a direct procedure to calculate basal shear stresses and velocities at depth, based on force balance, a constitutive law for ice and an assumption of depth-invariant strain rates. However, Reference Whillans and Van der VeenWhillans and Van der Veen (1993) found that their calculated basal drag could sometimes push the glacier downstream rather than resisting sliding motion. They rejected several possible explanations for this apparently unphysical result, including data errors, depth-variable strain rates and stiffness variability due to spatial variations in firn depth or crevasse distributions. They were unable to exclude stress-bridging effects or rheological variations related to the assumed form of the flow law (e.g. crystal anisotropy effects). Reference LliboutryLliboutry (1995) suggested that the effect could be real and caused by warm, soft, near-basal ice forced by pressure gradients to flow rapidly through the gaps between bedrock bumps and unbending cold and stiff overlying ice. Although the process of capped extrusion flow (Reference WaddingtonWaddington, 2010) has been observed (e.g. Reference CarolCarol, 1947; Reference Hooke, Holmlund and IversonHooke and others, 1987) and modeled (e.g. Reference GudmundssonGudmundsson, 1997a,b), Reference Whillans and Van der VeenWhillans and Van der Veen (1995) showed that the forces it could create would not significantly alter their inferred negative shear stresses.
Reference MacAyealMacAyeal (1997) subsequently showed that the negative basal stresses arose from a failure to include small but significant higher-order terms in the inferred velocity pattern, i.e. the assumption of uniform strain rate was unphysical for flow over bumps or sticky spots (e.g. Reference Balise and RaymondBalise and Raymond, 1985; Reference GudmundssonGudmundsson, 2003). With the realization that inference of basal properties from surface data could be an ill-posed problem, it became necessary to frame this as an inverse problem, in which the data are not fit exactly, in order to ensure physically reasonable solutions.
Reference MacAyealMacAyeal (1992, Reference MacAyeal1993) and Reference MacAyeal, Bindschadler and ScambosMacAyeal and others (1995) introduced control methods to infer a basal-friction parameter from surface-velocity data. Control methods have been used subsequently to infer basal shear stresses (e.g. Reference Joughin, Ayeal and TulaczykJoughin and others, 2004) and slipperiness and bed topography (e.g. Reference Vieli and PayneVieli and Payne, 2003; Reference Goldberg and SergienkoGoldberg and Sergienko, 2011). Using surface elevation and velocity data, Reference Thorsteinsson, Raymond, Gudmundsson, Bindschadler, Vornberger and JoughinThorsteinsson and others (2003) applied perturbation methods to separate bed topography from bed lubrication on MacAyeal Ice Stream, Antarctica. Reference Maxwell, Truffer, Avdonin and StueferMaxwell and others (2008) solved an inverse problem for basal stress and velocity by reformulating an iterative series of well-posed forward problems. Reference Raymond and GudmundssonRaymond and Gudmundsson (2009) and Reference Pralong and GudmundssonPralong and Gudmundsson (2011) used a Bayesian approach to infer bedrock topography and slipperiness under ice streams. Reference Petra, Zhu, Stadler, Hughes and GhattasPetra and others (2012) summarized previous work to infer basal properties from surface data using inverse approaches, and presented an efficient adjoint-based algorithm to infer basal properties and the Glen flow law exponent, n, with a three-dimensional full-Stokes flow model.
The goal of our inverse problem is also to infer basal properties from surface data; however, we address flow on a much smaller, colder and slower glacier. Furthermore, rather than investigating an interface, we seek properties of a layer of distinct basal ice that may exceed 10% or more of the total glacier thickness. We present a general inverse procedure for this type of problem before applying the method to Taylor Glacier (based on concepts described more fully by Reference Waddington, Neumann, Koutnik and MorseWaddington and others, 2007).
We infer basal-ice thickness, λ(x), enhancement factor for basal ice, E B(x), and enhancement factor for overlying clean ice, E C(x), along a flowband to the terminus of Taylor Glacier. These unknown properties comprise a model-parameter set, m = [E B(x), E C(x), λ(x)], along a flowband defined by horizontal position x.
The data for the inverse problem are discrete measurements, ![]() , of the surface horizontal velocity profile,
, of the surface horizontal velocity profile, ![]() , and discrete measurements,
, and discrete measurements, ![]() , of the ablation-rate profile,
, of the ablation-rate profile, ![]() , following the flowband. These observations can be combined into a single data vector,
, following the flowband. These observations can be combined into a single data vector, ![]() . The flowband width, W(x), and the depth to the top of the debrisrich basal ice, h(x), we accepted as given by velocity azimuths, syrface slopes and ground-penetrationg radar (GPR).
. The flowband width, W(x), and the depth to the top of the debrisrich basal ice, h(x), we accepted as given by velocity azimuths, syrface slopes and ground-penetrationg radar (GPR).
With three profiles of unknown parameters, m = [E
B(x), E
C(x), λ(x)], to be inferred from two (potentially sparse) datasets, ![]() , and
, and ![]() , the problem is under-determined. Therefore, we need to impose some regularization on the parameters in order to obtain a unique solution. The options we consider include smoothness constraints on some or all of the parameters and preconceptions or limits on the parameters based on other studies. Obtaining a unique solution is further challenged by loss of basal information as ice thickness increases (Reference Bahr, Pfeffer and MeierBahr and others, 1994).
, the problem is under-determined. Therefore, we need to impose some regularization on the parameters in order to obtain a unique solution. The options we consider include smoothness constraints on some or all of the parameters and preconceptions or limits on the parameters based on other studies. Obtaining a unique solution is further challenged by loss of basal information as ice thickness increases (Reference Bahr, Pfeffer and MeierBahr and others, 1994).
3.2. Forward model
The forward algorithm must produce modeled estimates, ![]() , of all the observed quantities that form the data vector, o
(d), when given a parameter vector, m.
, of all the observed quantities that form the data vector, o
(d), when given a parameter vector, m.
Because the top of the basal ice is relatively flat (Fig. 4), the ice thickness varies slowly and the ice temperature is close to isothermal, we base our forward algorithm on the isothermal shallow-ice approximation (SIA). The z-axis is vertical (z = 0 at the base of the debris-rich ice) and the x-axis is horizontal following the flowband (Fig. 5).

Fig. 4. Radar profile of transect along flowband from Nirvana to Grace. (a) The unmigrated radar data. The thin blue horizontal line shows the elevation of the surface of Benchmark TP01 on the shore of Lake Bonney for reference (73.44 m a.s.l. and 18.39 ITRF-93). (b) Our interpretation: red line shows the reflector, which we interpret as the bottom of the clean ice assuming this reflector obscures any reflection from the bottom of the basal ice.

Fig. 5. The geometry of the flowband model, showing surface elevation profile, S(x), clean-ice thickness, h(x), top of the basal ice, D(x), thickness of the basal ice, λ(x), bottom of the basal ice, B(x), and flowband width, W(x).
Modeled surface velocity,
The surface velocity, ![]() , can be calculated from the flowband geometry and m:
, can be calculated from the flowband geometry and m:
where H(x) = [h(x) + λ(x)] is the total glacier thickness, U(x, z) is the vertical profile of horizontal velocity for ‘standard’ Holocene ice with thickness H(x) and E = 1, and E B and E C are the enhancement factors for the basal ice and the overlying clean (meteoric) ice, respectively. Using the SIA, the velocity, U(x, z), of clean, Holocene ice at height z can be written as
where U s(x), the velocity at the surface, is given by
Modeled ablation rate, 
The ice flux, ![]() , can be calculated from the glacier geometry and the model-parameter vector, m,
, can be calculated from the glacier geometry and the model-parameter vector, m,
where W(x) is the flowband width and ū m(x) is the depth-averaged velocity given by

Note that when E B = E C, when λ(x) = 0 or when λ(x) = H(x), Eqn (6) reduces to the standard SIA result for depth-averaged velocity
where E γ is the appropriate enhancement factor.
The modeled dynamic flux, ![]() , (Eqn (5)), produces an estimate,
, (Eqn (5)), produces an estimate, ![]() , of the accumulation-rate profile required to achieve steady-state flow, through the steadystate mass-conservation equation,
, of the accumulation-rate profile required to achieve steady-state flow, through the steadystate mass-conservation equation,
The spatial derivative, ![]() , can be obtained from Eqn (5) using the product rule for differentiation.
, can be obtained from Eqn (5) using the product rule for differentiation.
3.3. Inverse algorithm
Our goal is to infer model parameters, m, comprising the basal-ice thickness, λ(x), the enhancement factor for basal ice, E B(x), and the enhancement factor for overlying clean ice, E C(x), along a flowband. Here, we outline a formulation of this inverse problem and one way to solve it. To formalize this adjustment procedure, we form a data norm, ||d||, composed of residuals resulting from comparing model predictions with observations, and a model norm, ||m||, which incorporates the smoothness conditions we use to regularize the solution.
3.3.1 Data norm
Because observations of velocity, ![]() , and mass balance,
, and mass balance, ![]() , are discrete, the N
(d) observations in the data vector o
(d) can be represented as
, are discrete, the N
(d) observations in the data vector o
(d) can be represented as ![]() , where index j indicates the jth discrete observation. An estimate of m will produce predicted model quantities, o
(m), that do not perfectly match the observed quantities in the data vector, o
(d). Their difference can be used to form residuals, which are the portions of the data unexplained by the model:
, where index j indicates the jth discrete observation. An estimate of m will produce predicted model quantities, o
(m), that do not perfectly match the observed quantities in the data vector, o
(d). Their difference can be used to form residuals, which are the portions of the data unexplained by the model:
where ![]() is the standard deviation of the jth observation,
is the standard deviation of the jth observation, ![]() .
.
The data norm, ||d||, is defined as the sum of all the squared data residuals:
Weights, wj , different from unity can also be applied to the residuals from various data types if desired.
3.3.2. Model norm
The three model-parameter profiles, m = [E B(x), E C(x), λ(x)], can, in practice, also be treated as discrete series of N(m) parameters, such that mi is the ith model parameter. The model norm, ||m||, measures the degree of regularization imposed on the solution (e.g. the amount of smoothness imposed on each profile). Smoothness can be represented through a finite-difference second-derivative relationship among all triplets of adjacent points. For example, when the model parameters are equally spaced and separated by Δx, the second derivative at the ith model parameter is approximated by

Just as a data residual represents deviation from a targeted data profile, a parameter curvature represents deviation from a targeted profile of zero curvature. And just as the data residuals in Eqn (9) are nondimensionalized with the data standard deviation, which is a measure of characteristic variability, so too the curvature ‘residuals’ can be nondimensionalized with characteristic values, m (c), of the parameter and the lengths, L (c), over which they can vary.
These curvatures, ci , are
and the collection of curvatures (and possibly other model constraints) can be written as a vector, c, and a model norm, ||m||, can be written as
Of course, other variations are possible. For example, E C could be treated as a uniform adjustable scalar, or simply set equal to unity.
The model parameters, m, are selected to minimize these data residuals, rj , and smoothness residuals, ci , in some sense. One way to achieve this is to minimize a scalar functional, J (|d||, ||m||), of the norms, which could, for example, take the form
In this example, the tolerance, T 2 ≈ N(d) (Reference ParkerParker, 1994, p. 124), is the expected root-mean-square residual mismatch to be expected if all the normalized residuals in Eqn (10) were random variables from a normal distribution with zero mean and unit variance, and the trade-off parameter, υ, expresses the balance between obtaining a smooth model and fitting the data exactly; it can be adjusted until ||d||2 – T 2 = 0 when J is minimized. This regularization procedure is often called ‘Tikhonov regularization’ (e.g. Reference Aster, Borchers and ThurberAster and others, 2013).
3.4. Solution procedure
Because the forward problem is nonlinear in the model-parameter set, m, an iterative linearized solution procedure can be used to solve the inverse problem, using a gradient method to find the most appropriate m. The simplest solution procedure is as follows. To find the k th estimate from the (k – 1)th estimate, we need to find the corrections, Δm (k):
Starting from an initial guess, m (0), for parameter set m, and an initial guess for υ, we find corrections, Δm, by solving a linearized set of algebraic equations
where matrix J c creates the second-derivative vector (d2 m/ dx 2) i in Eqn (11) from the parameter vector m; J r is a Jacobian matrix containing the partial derivatives Oj (m)/mi ; the matrices W c and W r are weights arising from the curvature and residual equations, respectively. W r, in particular, includes υ as part of the weighting (if all observations are weighted the same, then W r = υ1/2). This system can be solved, for example, using singular-value decomposition, but ultimately, the best solution method depends on the complexity and nonlinearity of the forward model.
This solution procedure will satisfy Eqn (14) given a value of υ; therefore, a solution also needs to iterate towards finding the best value of υ. If υ is too small, then the minimization of J overemphasizes the model norm, which includes our expectations for model smoothness or nearness to a specific value. If υ is too large, J results in overemphasis on fitting the data. We aim for a value of υ that minimizes J while allowing ||d||2 – T 2 to approach zero, which means that we are fitting the data to within our uncertainties. Reference Waddington, Neumann, Koutnik and MorseWaddington and others (2007) explain this solution procedure more fully, applied to a similar inverse problem.
3.5. Resolution
A straightforward way to judge the resolving ability of the inverse problem is to use the forward model to generate synthetic observations based on a prescribed model-parameter set that contains a spike (one value significantly different to the others). Then we can use the synthetic data and the inverse algorithm to see how well it reproduces the prescribed model parameters.
4. Application To Taylor Glacier
4.1. Field site characteristics
Taylor Glacier (–77.725° S, 162.26° E), located in the McMurdo Dry Valleys, is an outlet glacier of Taylor Dome, part of the East Antarctic ice sheet. Taylor Glacier extends 100 km from Taylor Dome to its terminus in Lake Bonney, a perennially frozen lake (Fig. 2). Figure 3 shows a detail of our field site with pertinent locations, Nirvana (inland, upstream site) and Grace (near cliff, downstream site), identified.
The glacier flows on frozen unconsolidated sediments and fills the western part of Taylor Valley (Reference Mager, Fitzsimons, Frew and SamynMager and others, 2007). A layer of prominent debris-rich basal ice (Fig. 1) overlain by clean ice is observed along the 20–30 m high ice cliffs that characterize the glacier margin, although the basal ice is often obscured by an ice apron produced from dry calving. Because the average annual air temperature is –17.8°C (for 2004/05, from a meteorological station near the glacier terminus; also Reference Nylen, Fountain and DoranNylen and others, 2004), the conservation of energy for thin ice with a typical value of geothermal flux suggests that the glacier is frozen to its bed. Approximately 6 km upstream there is an overdeepening, where the basal ice may reach the local pressure-melting point for marine-based sediments with high salt content (Reference RobinsonRobinson, 1984; Reference Hubbard, Lawson, Anderson, Hubbard and BlatterHubbard and others, 2004). Along the 65 km ablation zone, sublimation accounts for 40–80% of mass loss, with the remaining mass removed by melting during the short summer (Reference Lewis, Fountain and DanaLewis and others, 1998; Reference Hoffman, Fountain and ListonHoffman and others, 2008; Reference Bliss, Cuffey and KavanaughBliss and others, 2011). In the terminus region, summertime ephemeral streams flow down three large surface channels parallel to ice flow and into Lake Bonney, dominating the summer ablation process (Reference Johnston, Fountain and NylenJohnston and others, 2005).
4.2. The forward model
As explained above, we use a 2-D flowband model with the geometry shown in Figure 5 and velocities predicted by the SIA. The SIA states that when the ice thickness is much smaller than the horizontal ice extent and the wavelength of bedrock and glacier surface undulations is long relative to ice thickness, then the horizontal derivatives of stress, temperature and horizontal velocity are negligible compared with the vertical derivatives (Reference Cuffey and PatersonCuffey and Paterson, 2010). We feel this is a reasonable approximation along the flowband, because the ice is thin relative to the length scale of changes along the flowband, the boundary between the basal ice and the clean ice is smooth and we assume that the bed topography along the flowband is also relatively smooth.
To further show that the SIA is a reasonable approximation, we can estimate components of the deviatoric-stress tensor by estimating corresponding components of the strain-rate tensor, using characteristic thicknesses and velocities, with an assumption of uniform effective viscosity across the region. The vertical deviatoric shear stress can be approximated as τxz ∝ η∂u/∂z. Where the SIA is valid, this component of the deviatoric-stress tensor is at least one order of magnitude larger than all other components – preferably more than one order of magnitude. At the upstream end of our flowband, the horizontal velocity at the surface is ~ 5 m a–1 , this ice is ~ 125 m thick and ∂u/∂z ~ 0: 04. Towards the terminus, ∂u/∂z ~ 3/30 = 0: 1. The longitudinal deviatoric stress can be approximated τxz ∝ 2η∂u/ ∂x. The change in surface horizontal velocity along the flowband is 2 m a–1 over ~ 700 m distance, which gives an average strain rate of ∂u/∂x ~ 2/700 ~ 0: 003, an order of magnitude smaller than the vertical shear strain rate, ∂u/ ∂z. Similarly, the lateral extension along the flowband is also an order of magnitude smaller than the vertical shear stress, ∂v/ ∂y ~ 0: 0025, based on the rate at which the flowband widens. Our flowband SIA model incorporates this lateral extension component of stress through mass conservation, as described by Eqns (5) and (8). While one order of magnitude is perhaps the minimum acceptable criterion, the ability to use a numerically simpler model allows us to explore a wider range of model parameters.
The SIA is inadequate within one to two ice thicknesses from the ice cliff at the glacier margin; ice deformation in this immediate cliff region must be treated using a more sophisticated approach (e.g. one that solves for all components of the stress and strain tensors (full-Stokes model)).
Due to limited observations, we cannot solve the complete inverse problem as described in Section 3. In the calculations presented here, we approach the solution from two end-member assumptions that allow us to simplify the model-parameter set, m:
-
We assume that the softness of the basal ice and that of clean ice are spatially uniform, and we allow the thickness of the basal ice to vary along the flowband: m λ = [E B, E C, λ(x)].
-
We assume that the thickness of the basal ice is uniform, the softness of the clean ice is uniform and we allow the softness of the basal ice to vary along the flowband: m E B =[E B(x), E C, λ].
Because the true behavior of basal ice is more complex, as demonstrated by tunnel observations of fold and boudinage structures within basal ice (Reference Fitzsimons and KnightFitzsimons, 2006), these two assumption are considered end members of a continuum of possible behaviors.
4.3. Regularization
The straightforward calculation of the velocity profile along the flowband as described above is an underdetermined problem, because we do not have measurements of the thickness or softness of the basal ice. In order to determine the most likely solutions, we impose regularization on the model-parameter set to find a unique solution. The data norm includes the observed discrete measurements of accumulation rate, ![]() , the surface velocities,
, the surface velocities, ![]() , and their respective uncertainties which depend on the measurement method (discussed below).
, and their respective uncertainties which depend on the measurement method (discussed below).
Accepting that a complex material, such as basal ice, may change thickness or softness relatively suddenly due to shear band formation or folding processes, we choose to weakly constrain the smoothness of the basal-ice thickness profile or the basal-ice softness profile. We set the characteristic length and magnitude for changes in the basal thickness profile at L (C) = 10 m and m(C) = 5 (Eqn (12)). Because the only measurement of basal-ice thickness is that of Reference Samyn, Fitzsimons and LorrainSamyn and others (2005a), which does not provide a confirmed maximum thickness, we do not constrain the maximum thickness. We choose models that satisfy minimum thickness at the terminus (estimated as 4.5 m by Reference Samyn, Fitzsimons and LorrainSamyn and others, 2005a) for end member 1. Similarly for end member 2, we set the characteristic length and magnitude for changes in basal softness at L (C) =10 m and m(C) = 10.
Despite only weakly constraining the smoothness of the basal-ice characteristics, we assume that the surface-velocity and ablation-rate profiles should vary smoothly, because they are a function of the depth-integrated velocity. Therefore, in making the final choice among best-fitting model parameters from among all valid solutions using the data norm and model norm as defined above, we also constrain the smoothness of the predicted surface-velocity and the ablation-rate profiles as a curvature constraint within the model norm. The characteristic length and magnitude for changes in these are L(C) = 100 m and m(C) = 0: 5 for surface velocity, and L(C) = 100 m and m(C) = 0: 25 for ablation rate. We do this because the smoothness of the predicted velocity and ablation-rate profiles is not guaranteed without explicitly including this in the model norm, because the data norm does not distinguish between a positive and a negative residual for a particular location, x, therefore at xi we could have a positive residual (e.g. velocity predicted higher than observed), while at xi + 1 we could have a negative residual (e.g. velocity predicted lower than observed). By minimizing the square of these residuals, the solution cannot distinguish between a smooth velocity profile that is consistently above that observed and one that jumps above and below it. In a full-Stokes ice-flow model that includes longitudinal stresses, the smoothness of the surface velocity and ablation rate will arise from the physics of ice flow; but our mathematically simpler model does not efficiently impose this smoothness without our explicitly incorporating it into the inverse problem. By requiring the predicted velocity and accumulation to vary smoothly, we can distinguish between these otherwise equivalently valid solutions.
4.4. Solution method
The two end members of our analysis have model-parameter sets m λ = [E B, E C, λ(x)] for variable basal-ice thickness (end member 1) and m EB = [E B(x), E C, λ], for variable basal-ice softness (end member 2). To increase computational efficiency and because of our limited observations, we limit the x values to 11 discrete positions along the flowband and we limit the trade-off parameter to υ = 1, based on initial runs. Although solving for the best υ value would allow us to narrow the best solutions given the observations in the problem, we feel our limited observations at this stage lead to more general conclusions that are not sensitive to υ, as long as it is within an order of magnitude of unity.
To solve for m λ, we solved for λ(x) for given combinations of 2 ≤ E B ≤ 100 and 1 ≤ E C ≤ 10. For each combination of E B and E C, we started from five different initial λ(x) profiles to ensure the model converges towards a global minimum. Each of the five initial λ(x) profiles consists of 11 randomly chosen values ranging from 2.5 to 7.5 m. We solve this nonlinear constrained inverse problem using a computationally efficient interior point method (using MATLAB®’s fmincon function), which is based on the gradient method described in Section 3.4.
Similarly, to solve for m E B, we solved for E B(x) for given combinations of 0 ≤ λ ≤ 20 and 1 ≤ E C ≤ 10. We again begin with five different initial profiles, E B, consisting of 11 randomly chosen values ranging from 20 to 40.
5. Measurements
Our data were drawn from measurements made during two consecutive austral summers (2004/05 and 2005/06) and a subset of measurements that were repeated in the next austral summer (2006/07). Our measurements and observations focused on terminus dynamics and clean-ice properties of Taylor Glacier, which provide the core assumptions and constraints to guide our inverse problem. Our assumptions were also guided by studies on upstream dynamics by Reference Aciego, Cuffey, Kavanaugh, Morse and SeveringhausAciego and others (2007), Reference RobinsonRobinson (1984) and Reference Hubbard, Lawson, Anderson, Hubbard and BlatterHubbard and others (2004); on the basal ice of Taylor Glacier by Reference Samyn, Fitzsimons and LorrainSamyn and others (2005a); and on the basal ice of nearby Meserve Glacier by Reference Cuffey, Conway, Gades, Hallet, Raymond and WhitlowCuffey and others (2000a).
5.1. Properties of clean ice
In order to constrain the properties of the clean ice, which is more accessible than the basal ice, we used samples from two shallow cores: an ice core to 16 m depth at Nirvana and an ice core to 13 m depth at the Grace field site (Fig. 3). These cores were transported to the US National Ice Core Laboratory, where we measured electrical conductivity, cut thin sections to measure ice fabric using an automatic fabric analyzer (Reference WilenWilen, 2000) and cut samples for measuring ice chemistry.
The clean ice of Taylor Glacier originates from Taylor Dome. The ice is white and bubbly without any layers present in the visual stratigraphy or electrical conductivity measurements. Using an ice-flow model and the analysis of oxygen stable isotopes of ice samples collected along the length of Taylor Glacier, Reference Aciego, Cuffey, Kavanaugh, Morse and SeveringhausAciego and others (2007) concluded that ice from the Last Glacial Maximum is exposed on the lower 25 km of the ablation area, and ice in the terminus region may be older than 28 ka. Our measurements agree that this ice has typical properties of Ice Age ice (Reference PatersonPaterson, 1991), including high solute concentrations (mean values of 0.363 mg L–1 chloride, 0.292 mg L–1 sulfate and 0.206 mg L–1 nitrate). In comparison with values summarized by Reference PatersonPaterson (1991), we measured concentrations of chloride 3.9 times higher than Ice Age ice from the Vostok ice core (which is 22 times higher than Holocene ice at Vostok); concentrations of sulfate 1.6 times higher than Vostok Ice Age ice (which is 2.4 times higher than Holocene ice); and concentrations of nitrate 4 times higher than Vostok Ice Age ice (which is 14 times higher than Holocene ice). The accumulation area for Taylor Glacier (including Taylor Dome) has higher concentrations of marine-based solutes, such as chloride, than Vostok due to proximity to McMurdo Sound (Reference MayewskiMayewski and others, 1996). Several studies (e.g. Reference PatersonPaterson, 1991) suggest that these ions have the greatest effect on softening of the ice. We did not measure debris concentration directly, but assume that it is low, based on previous studies (0.05–0.1% by volume; Reference Samyn, Svensson, Fitzsimons and LorrainSamyn and others, 2005b).
All thin sections show generally small (<2 mm diameter) ice crystals and have a near-vertical, single-maximum fabric. Figure 6 shows two example thin sections from these samples. Fabric results from the Nirvana ice core suggest migration recrystallization is active, due to the presence of some larger crystals with c –axes at high angles from the vertical; this may be because of seasonally elevated temperatures, due to the proximity of this core to the meltwater channel. The age of the ice at the terminus and the long distance from the accumulation zone contribute to the development of the observed fabric. As other researchers have shown, these properties enhance strain in bed-parallel shear and inhibit strain in vertical compression in the clean ice relative to Holocene isotropic ice (e.g. Reference Budd and JackaBudd and Jacka, 1989; Reference MiyamotoMiyamoto and others, 1999; Reference Cuffey and PatersonCuffey and Paterson, 2010, ch. 3). Because our model assumes the flow is predominantly in bed-parallel shear, we do not incorporate a full description of anisotropic ice flow in the forward model. Instead, we assume an enhancement factor (Eqn (1)) within the range expected for isotropic to highly anisotropic ice (Reference Budd and JackaBudd and Jacka, 1989). In our analysis, we test clean-ice softness values between 1 and 10 (1 ≤ E C ≤ 10).

Fig. 6. Two examples of the crystal fabric from vertical thin sections of the ice core from Taylor Glacier. These sections are ~ 10 cm tall. For Schmidt plots, the vertical axis is up; some uncertainty in the true vertical exists because of the drilling process; borehole inclination was not measured but is likely <5°. (a) 7.9 m below the surface at the interior site Nirvana. (b) 13.6 m below the surface at the site Grace, near the cliff.
5.2. Properties of debris-rich basal ice
Because detailed information about the basal-ice sequence is known from other studies, we did not make any new measurements on the basal ice (Reference CuffeyCuffey and others, 2000c; Reference Samyn, Svensson, Fitzsimons and LorrainSamyn and others, 2005a; Reference Mager, Fitzsimons, Frew and SamynMager and others, 2007). The best published constraint on the basal-ice thickness comes from a vertical shaft dug by Reference Samyn, Fitzsimons and LorrainSamyn and others (2005a,b) at the end of a tunnel dug 25 m horizontally into the ice 1.4 km upstream of the terminus. The vertical shaft exposing the debris-rich basal-ice sequence was 4 m deep; however, they did not reach a distinct contact that defines a ‘bed’. The basal-ice sequence is likely a gradual change in the ice/sediment mixture, and a distinct contact between debris-rich ice and ice-rich subglacial sediment may not exist. We assume 4 m is the minimum thickness of the basal ice near the terminus.
The basal ice is composed of a sequence of visually distinct ice facies, with varying ice properties that have been described from tunnel observations at two Taylor Glacier sites (Reference Samyn, Fitzsimons and LorrainSamyn and others, 2005a; Reference Mager, Fitzsimons, Frew and SamynMager and others, 2007). The debris-rich basal ice contrasts sharply with the clean meteoric ice which stratigraphically overlies it. Bands of clean ice also intermix with the stratified debris-rich basal ice. From the base of the vertical shaft upwards, the basal-ice sequence is composed of a 0.7 m thick dispersed facies (silt particles in plurimillimetric ice layers), a 0.8 m thick clean facies, a >2 m thick stratified facies that can be distinguished as two sections, a massive facies (>50% of debris by volume) and a laminated facies, which consists of debris-laden layers (2–20 mm thick) that alternate with clean-ice layers of similar thicknesses. The dispersed facies was not excavated all the way to the bed, and may be up to 1–2 m thicker than described (Reference Samyn, Fitzsimons and LorrainSamyn and others, 2005a,b; Reference Mager, Fitzsimons, Frew and SamynMager and others, 2007). Because our measurements and model design cannot predict deformation within each of these layers, we infer only the bulk properties of the entire basal-ice sequence using our model. Furthermore, it is likely that the basal-ice thickness is spatially variable, due to variable longitudinal and transverse stress regimes along a flowband, and that the Taylor Glacier terminus rests on frozen unconsolidated sediments.
5.3. Geometry
We extracted surface elevation and slopes from a lidar 2 m DEM collected by NASA/US Geological Survey (USGS) (Fig. 3; Reference Schenk, Csatho, Ahn, Yoon, Shin and HuhSchenk and others, 2004). To determine the flowband surface elevation, and surface slope between sites Nirvana and Grace, we neglect the small-scale roughness of the surface by smoothing the DEM surface profile using a horizontal smoothing length approximately equal to one ice thickness (40–100 m). We calculate two parallel flowlines by the steepest-descent method (perpendicular to the contours) and use the lateral distance between these contours as the flowband width.
We collected GPR data using a 100 MHz MALÅ GeoScience RAMAC system, with trace locations defined by precision Trimble GPS units. The system stacked 64 traces approximately every 1 m using wheel triggering. Due to the rough surface topography, the radar transects were not collected in straight lines; however, when extracting ice-thickness data from these observations, we consolidated the small horizontal deviations into a smoothly curving profile along our flowband. The post-processing was limited to bandpass filtering (50–120 MHz) and gain applied to highlight the basal reflector (Fig. 4). We calculated the depth using a velocity of 0.168 m ns–1 ; we did not migrate the data. We estimate uncertainty in radar-measured depths at ± 1 m. The radar data show a single strong reflector, which we interpret as the uppermost debris-rich layer within the basal ice (Fig. 4). This is supported by observations of the basal ice at the ice cliff; if the reflector were extended horizontally ~ 20 m to the cliff outcrop at Grace, its depth would be within ± 2 m of the observed top of the basal ice. Although some of our radar data show stratified sediments below the strong reflector, it is not possible to determine directly the thickness of the deforming basal ice from these data. The geometry inputs (surface profile, surface slope, flowband width and clean-ice thickness) into the model are shown in Figure 7a–c.

Fig. 7. (a) Observations of the geometry along the flowband from DEM, GPS and GPR (surface is smoothed over a distance equal to the local average thickness of the ice. Upper line is the surface (smoothed from the DEM) and lower line is the boundary between clean ice and the debris-rich ice (not smoothed, from radar picks). Clean ice thickness is the difference between these two lines. (b–e) Observations of (b) the surface slope from DEM after smoothing; (c) the flowband width from following steepest-descent surface slope directions in DEM after smoothing; (d) the ablation rate from stakes and interpolation procedure and (e) the horizontal surface velocities from stakes and interpolation method. For horizontal velocity and ablation rate, the dashed curve indicates the uncertainty; the uncertainty at the end points is smaller than the thickness of the lines drawn (see Sections 5.5 and 5.6 for further discussion).
5.4. Temperature
The mean annual air temperature at Taylor Glacier is –17.8° C (Reference Nylen, Fountain and DoranNylen and others, 2004). Our thermistor measurements in a 13 m deep borehole drilled at Grace indicate an average ice temperature of –18.9°C at depths of 10–13 m. Tunnel thermistor measurements confirm the basal ice within 25 m of the terminus is at –17°C (Reference Samyn, Svensson, Fitzsimons and LorrainSamyn and others, 2005b; Reference Mager, Fitzsimons, Frew and SamynMager and others, 2007). Based on these measurements, we assume the average ice temperature along the flowband is –17°C.
5.5. Ice flow
We deployed stake arrays on the ice to measure ice deformation, velocity and ablation. At both Nirvana and Grace, arrays consisted of 13 stakes in a grid with 5 m spacing, from which we measured displacement over 1 or 2 years using repeat static GPS measurements (4 mm) from a base station <1 km away. This array was designed to provide strain information within the grid. The average displacement of all stakes within the arrays provided constraints for the flowband velocities. Similar arrays (unlabeled point clusters in Fig. 3) were deployed at two other sites, which help constrain our interpolation. In addition, we measured displacements of stakes spaced 100 m apart along a transect perpendicular to ice flow at Nirvana. The measurements from the transect stakes exhibit a near-parabolic shape (Fig. 3), where velocity is smallest at the margin and greatest at the glacier center; this pattern is typical for glacier deformation. A second-order polynomial was fitted to the transect velocity data. This velocity profile shape was scaled with the decreasing width of the glacier and adjusted to match magnitudes of measured stake arrays to interpolate the velocities between measured points and to estimate the velocity field across the entire terminus region below Nirvana. The interpolation between measured data points increases the uncertainty of those data beyond that stated above. The uncertainty is shown graphically in Figure 7.
5.6. Ablation
The ice-surface heights relative to the stakes were measured several times over 2 years. Annual ablation was calculated from these measurements and interpolated along the flowband between Nirvana and Grace by scaling the change in ablation rate between stakes to change in the surface slope. Again, we neglect small-scale surface undulations and assume that surface slope drives variation in ablation rate along the flowband; this surface slope maintains a nearly constant geographical aspect along the flowband. Ablation measurements (with uncertainty ± 0.5 cm a−1) at both ends of the flowband constrained our ablation-rate profile. The resulting ablation-rate profile is shown in Figure 7d. Similarly to the surface velocity, we assume that the uncertainty in the ablation rate parabolically increases with distance from the measured stakes (Fig. 7). Because this input to the model requires interpolation from the two end points and we measured ablation for only 2 years, we test the sensitivity of our results to the ablation magnitude, but not the slope or curvature of the ablation interpolation (this is outside the scope of this paper).
6. Results
We begin the analysis using a one-dimensional model at our two sites, Nirvana and Grace. We then explore the full flowline using the inverse approach outlined above.
6.1. One-dimensional model results
6.1.1. No deformable basal ice
If we assume that basal ice is not deforming or is not present beneath the flowband (or glacier terminus), then the clean meteoric ice must be much softer than is typically assumed for glacier ice in order to match the measured surface velocity at Nirvana (5.1 m a-1) or at Grace (3.0 m a–1 ). Figure 8a shows that for ice at –17°C, the observed ice temperature, the model requires clean-ice softness of at least E C = 21 at Nirvana to reach 90% of the observed velocity. That same softness, however, is not sufficient to allow the ice flow to also match the observed surface velocities at Grace (Fig. 8b).

Fig. 8. Predicted velocity profiles relative to the measured surface velocity for sites (a) Nirvana and (b) Grace. Colored curves show various temperature and clean-ice softness combinations, as labeled, and assume no basal-ice deformation; colors represent the same parameters in both plots. Black curves are results from selected best-fitting parameters from experiment 3, which includes basal-ice deformation. Profile A has clean-ice softness of 3.5, basal-ice softness of 53 and a basal-ice thickness of 9.5 m at Nirvana and 18.0 m at Grace. Profile B has clean-ice softness of 1, basal-ice softness of 72 and basal-ice thickness 7.6 m at Nirvana and 14.9 m at Grace.
If we allow for higher temperatures (because the ice nearest the bed may be warmer due to geothermal flux), a temperature of at least –8°C is necessary to match the surface velocity with a clean-ice softness, E C, within the range expected from theory (E C < 10, as described above). If we limit the clean-ice softness to E C < 5, which is in the recommended range for Ice Age ice (Reference Cuffey and PatersonCuffey and Paterson, 2010, p. 77), then the modeled surface velocity is too low for any reasonable temperature assumption (depending on the value of E C). Furthermore, temperature and clean-ice softness combinations that can match the surface velocity at Nirvana cannot also match the surface velocity at Grace (Fig. 8b). Although the softness of clean glacier ice can vary spatially, we do not expect it to vary substantially over the ~ 700 m between Nirvana and Grace. Also, the presence of the cliff within two ice thicknesses of Grace may affect its velocity by a modest amount compared with the SIA solution; however, the difference between the relative velocities at these two sites is nearly an order of magnitude – too large to be accounted for by longitudinal stresses near the cliff. This difference between the two sites suggests a significant variation in flow properties between Nirvana and Grace that cannot be explained by typical ice-flow assumptions; therefore, we suggest that basal ice must provide the faster deformation necessary to match the surface velocities and variability over this short flowline and the softening required to match the observed surface velocities.
6.1.2. Including deformable basal ice
The two black curves in Figure 8a and b show how the predicted surface horizontal velocities can match the observed surface horizontal velocities at Nirvana with reasonable assumptions for the clean-ice properties (1 < E C < 10) if we assume a nonzero thickness for basal ice that is significantly softer than the clean ice.
6.2. Flowband model results
As discussed above, we explore two end member model-parameter sets to describe the behavior of the basal ice: first, assuming constant softness for the basal ice while allowing thickness to vary spatially and, second, assuming constant thickness for the basal ice while allowing its softness to vary spatially. In reality, the best solution likely involves variations in both. In all models, the clean-ice thickness is fixed by the geometry derived from radar, and its softness is assumed spatially uniform, but allowed to vary within expected values (Section 5.1). Because the temperature at depth may be a few degrees above the measured temperatures, we ran selected experiments at –17°C, –15°C and –13°C, in order to determine the sensitivity of the results to the ice temperature. We also decreased the ablation rate by 10, 20 and up to 50% for selected experiments in order to determine the sensitivity of the results to ablation rate. Finally, we modified the shape of the ablation profile based on initial results for specific positions where our ablation-rate data are less constrained. Table 1 lists the experiments that resulted in successfully matching the data and associated model parameters.
Table 1. The primary experimetns. The basal thickness variation group is for models where we assumed the basal-ice softness was spatially uniform and we varied the basal-ice thickness, λ(x). The basal softness variation group is for the models where we assumed the basal-ice thickness was spatially uniform and we varied the basal-ice softness E B(x)

6.2.1. Spike resolving test
To test the resolving power of our inverse problem, we generated synthetic data using a λ(x) that is uniform, except for a spike at one x location (red in Fig. 9a). We used the forward model to calculate ![]() and
and ![]() (red curves in Fig. 9b and c). Using these synthetic observations, we followed the inverse procedure to recreate our given λ(x) profile (black curves). The size of the spike was chosen to be as large as possible, while not triggering model instability when the basal-ice thickness approaches the clean-ice thickness. Similar experiments were conducted with the spike in different positions along the flowline, and using different combinations of E
C and E
B, all achieving similar results. These tests confirm that given surface velocity and ablation rate, the variation in basal-ice thickness is resolvable.
(red curves in Fig. 9b and c). Using these synthetic observations, we followed the inverse procedure to recreate our given λ(x) profile (black curves). The size of the spike was chosen to be as large as possible, while not triggering model instability when the basal-ice thickness approaches the clean-ice thickness. Similar experiments were conducted with the spike in different positions along the flowline, and using different combinations of E
C and E
B, all achieving similar results. These tests confirm that given surface velocity and ablation rate, the variation in basal-ice thickness is resolvable.

Fig. 9. Example of spike test. The red curve in (a) is the given basal-ice thickness, the red curves in (b) and (c) are the synthetic ablation rate observations and the synthetic surface velocities, respectively. The black curves in each plot are the inferred basal thickness and predicted ablation and velocity using the inverse method.
6.2.2. Basal-ice thickness variation (end member 1)
The first six experiments we ran involved determining the basal-ice thickness variation assuming a constant basal softness, E B. Figure 10 shows the goodness of fit for each experiment. For each combination of clean-ice and basal-ice softness, we started from five randomly chosen initial basal-thickness profiles. The most robust solutions are those in which the five initial guesses resulted in similar final profiles – suggesting that the minimization process found a global minimum rather than local minima. The color of each point in these plots, however, is the smallest of the five cost functions, J. If a cluster of points form a global minimum, the five cost functions for each point will be similar and the smallest J will vary more smoothly from point to point in Figure 10. Where nearby points have strongly varying colors, it is more likely that the minimization process found several local minima. The best-fitting solutions are among those with a consistent global minimum: those within the bluer regions. The darker the blue, the better the solution fit is. The ranges we identify as the best-fitting solutions are specified in Table 1.

Fig. 10. Results from experiments 1–6, as defined in Table 1. Each color represents the log of the smallest cost function, J, from among the five initial starting profiles of basal thickness for each parameter set. Solutions most likely associated with a global minimum are the consistently blue areas. Solutions most likely associated with local minima are those surrounded by dissimilar colors. In each subplot heading, T defines the temperature for the experiment and B defines the relative ablation rate.
The clean-ice softness (the vertical axis in each plot) does not have a strong influence on the best-fitting solutions. The inverse problem, as we have defined it, can find equally good solutions over the whole range of clean-ice softness. This lack of sensitivity exists because most of the deformation happens in the deepest ice, which is the basal ice in this case; the clean ice contributes very little to the deformation (<10% in most cases). The softness of the clean ice, therefore, has a negligible effect on choosing a best-fitting solution.
The results in Figure 10 are spatially arranged such that the effect of increasing temperature is shown on the vertical axis and the effect of increasing ablation is shown on the horizontal axis. Because temperature acts to soften the ice, there is a trade off between increasing temperature and increasing the basal-ice softness, E B, to produce similar dynamics in the ice. This is seen most clearly in the dark red bands on the left of experiments 1–3. At lower temperatures (experiment 3) there is no solution possible without a basal-ice softness of at least E B = 22; however with higher temperatures (experiment 1) a minimum of E B = 14 is required to find a solution. The entire pattern of colors to the right of these dark-red bands is shifted to the left as temperatures increase.
Because we have very few ablation measurements and our interpolation scheme between those measurements is based on weak assumptions, we test the sensitivity to ablation magnitude and shape (the horizontal axis in Fig. 10). Experiments 2, 4 and 5 show the effect of decreasing the magnitude of the ablation by a uniform percentage along the entire profile: the blue region becomes larger and darker as ablation is decreased from 100% to 80%. Decreasing the ablation to 80% of the measured values increases the goodness of fit to the observations (decreases the value of the cost function). Decreasing the ablation any further results in solutions that do not fit the observations sufficiently to satisfy our criteria. An alternative to a percentage decrease in ablation is to modify the shape of the ablation-rate profile. In reviewing the best-fitting solutions, we found a consistent shape of the predicted ablation-rate profiles. Figure 11a–c show selected results from experiment 3. Figure 11a shows the basal thickness profiles for four values of E B (20, 30, 40 and 50) and E C = 3. Despite the measured ablation-rate profile gradually increasing along the flowband (red curve in Fig. 11b) all best-fitting solutions predict an ablation-rate profile that decreases first, then increases along the profile. Because of our lack of measurements in the central part of the flowband, our slope-based interpolation scheme may be a poor assumption. If we instead interpolate between our measurements with a curve that is more similar to the predicted curve, we can improve the overall best-fitting solutions. Figure 11d–f show solutions using the modified ablation-rate profile (red in Fig. 11e). When we adjust the curvature of the ablation-rate profile the solution is significantly better, suggesting this might be closer to the real ablation-rate profile.
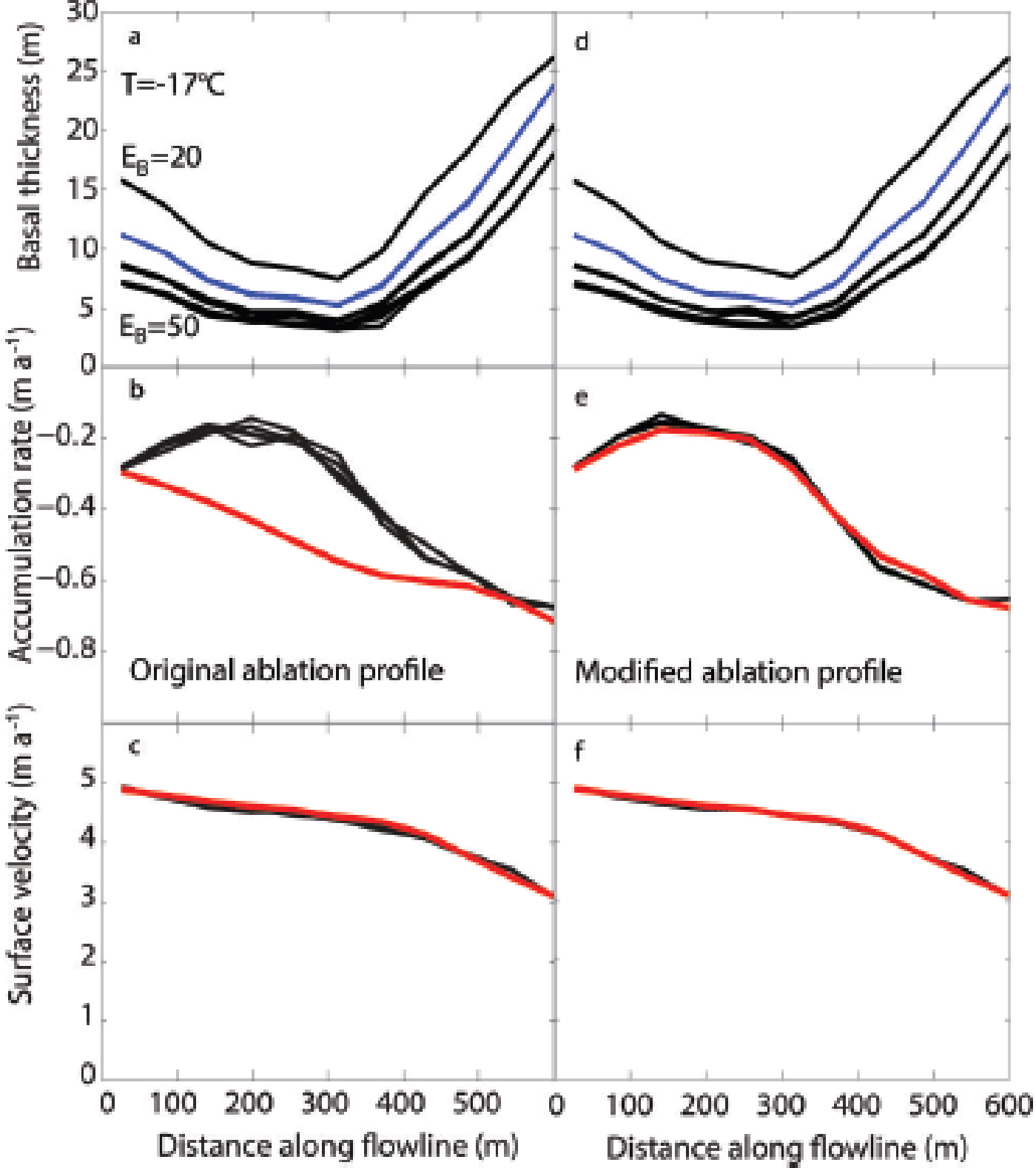
Fig. 11. Comparison of predicted ablation-rate profiles and velocity profiles for the original observed and interpolated ablation profile (experiment 3, E C = 3, E B = 20, 30, 40 and 50) and the modified ablation profile (experiment 6, E C = 3, E B = 20, 30, 40 and 50). Red curves are the observed datasets;, black and blue curves are predicted data, based on best-fitting solutions.
6.2.3. Basal-ice layer softness variation (end member 2)
For end member 2, we assume basal ice with uniform thickness but spatially variable softness. Experiments 7–12 target this question and test the sensitivity to temperature and accumulation rate, in a similar way to the first six experiments. Figure 12 shows the minimized cost function, J, for each combination of clean-ice softness and basal-ice thickness.

Fig. 12. Results from experiments 1–6, as defined in Table 1. Each color represents the log of the smallest of the cost functions, J, from the five initial starting profiles of basal softness for each parameter set. Solutions most likely associated with a global minimum are the consistently blue areas. Solutions most likely associated with local minima are those surrounded by dissimilar colors.
In parallel with the first set of experiments, increasing the temperature of the ice allows thinner basal ice to accommodate the deformation, because temperature acts to further soften the ice. If the ice is too warm, as in experiment 7, however, our assumption of a uniform basal-ice thickness narrows the range of best-fitting solutions by limiting the range of behavior. In general, it is more difficult to find a robust global minimum in these experiments. Figure 13a–c show example best-fitting solutions for experiment 9. Among these four solutions, the blue curve in Figure 13a provides the best fit (though the corresponding predicted surface-velocity and ablation-rate profiles do not match well). Furthermore, the scatter in the ablation-rate profile and the basal softness profile for λ = 6 show that some solutions find local rather than global minima.

Fig. 13. Comparison of predicted ablation-rate profiles and velocity profiles for the original observed and interpolated ablation profile (experiment 9, E C = 6, λ = 6, 10, 14 18 m) and the modified ablation profile (experiment 12, E C = 6, λ = 6, 10, 14, 18 m). Red curves are the observed datasets; black and blue curves are predicted data based on best-fitting solutions (blue curve is the best-fitting among these solutions, λ = 14).
Decreasing the ablation does not have as strong an effect in experiments 7–12 as in experiments 1–6. Figure 13d–f show solutions using a modified ablation curve to test the sensitivity to the ablation pattern. The modified ablation-rate profile improves the best-fitting solutions; however, predicted surface velocities still do not match the observations well.
7. Discussion
In order to fit the surface-velocity measurements and ablation rates, all of our models required actively deforming basal ice with a softness in the range 20–70 and a thickness 6–20 m. The general trends we observe in our results are:
-
The radar image shows a strong, horizontal, smooth reflector, that we interpret as the bottom of the clean meteoric ice. The flatness and smoothness of this reflector alone suggests that the clean ice is behaving as a stiff material, flowing nearly as ‘plug flow’, over a softer, more deformable material. The soft basal material deforms and accommodates the shape of the stiff clean ice.
-
This plug-like flow of the meteoric ice is confirmed by our measurements of deformation on the cliff face within the clean ice. Although difficult to measure, due to 2 m of calving and 1 m of ablation on the cliff face each year, we installed stakes horizontally in the cliff face to measure outward motion of the cliff face. The results (Reference SniffenSniffen, 2008) suggest that the clean ice is flowing more as plug flow; no internal deformation was measurable beyond the uncertainty of our measurements. These cliff-face measurements, however, are not ideal for direct comparison with our model, because they were made at the ice cliff, where the shallow-ice approximation does not hold.
-
None of the models can fit the observations without at least several meters of basal ice and with a softness an order of magnitude softer than the clean ice. As we have shown in Figure 8, without deformable basal ice, the softness of the clean ice must be much higher than has been documented in the literature even for highly anisotropic ice. Furthermore, with the given geometry, we cannot fit the surface velocity at both ends of the flowband (i.e. the Nirvana and Grace sites) with the same clean-ice softness parameter. While the properties of the clean ice may vary somewhat spatially, there is little in the literature to suggest that clean glacier ice along a flowline would vary enough to generate the observed surface velocities without the presence of basal ice. To fit the observations along our flowband without deformable basal ice, the clean-ice softness must more than double as the ice flows the 700 m between Nirvana and Grace.
-
We can fit the observations best with highly active basal ice with softness 20 ≤ E B ≤ 70 and thickness upwards of 20 m. As expected, for a given E C, there is a strong trade off between the basal-ice softness and thickness. We can fit the data with either thinner basal ice that is extremely soft (we explored up to E B = 200; results for experiments beyond 100, however, are not shown) or a thicker basal ice that is not as soft. Experiments 1–6 show a broader range of basal-ice characteristics that fit the data than experiments 7–12. Ultimately, however, basal ice that varies spatially in both thickness and softness is more likely to capture the real behavior.
-
Our conclusion that soft basal ice is necessary to explain flow patterns for Taylor Glacier is not sensitive to the ice temperature for a reasonable temperature range (we explored up to T = –13°C). A change in the temperature alters the exact trade-off relation between basal-ice thickness and softness, but it still requires a basal-ice softness an order of magnitude larger than the clean-ice softness.
-
Our conclusion that soft basal ice is necessary to explain flow patterns for Taylor Glacier is also not sensitive to small changes in the magnitude of ablation. A decrease in the magnitude of the ablation rate by 10% or 20% actually provides more parameter sets that can predict surface velocities and ablation rates that match our observations, but the spatial patterns for thickness and softness of the basal ice are similar among all well-fitting parameter sets. When we applied a more significant decrease in ablation magnitude (50%) to the profile, however, no reasonable combination of parameters could predict the observed surface velocity. This ablation rate is too small to maintain a steady-state surface profile.
-
The solutions consistently fit best with basal ice that is thinner or stiffer in the middle columns of our flowband. Although this may be real, it is also possibly a result of uncertainty in our interpolated ablation-rate profiles. If we have overestimated the ablation in the middle of the flowband, then we are underestimating the flux of ice within the flowband for those columns. This underestimation would require thinner or stiffer basal ice than columns with a more accurate flux measurement. This is most likely the reason that our solutions fit the observations better when we modify the shape of the ablation-rate profile by decreasing the ablation in the middle of the profile. This uncertainty in the ablation-rate profile will subtly change the numbers provided in Table 1, but not change our overall conclusions.
-
In all models, the basal ice must get significantly thicker and/or softer near the terminus. This thickening/softening of the basal ice is required to maintain the high surface velocities (>3 m a-1) despite the thinner clean ice. Near the terminus, the flowlines diverge as the ice spreads to fill the valley floor. Uncertainty in our flowband width will affect the details of the basal-ice thickening/softening closer to the terminus.
8. Conclusions
Observed surface velocities at Taylor Glacier are 30–50 times greater than that predicted by laminar flow for clean, homogenous, isotropic ice (enhancement factor equal to unity). This velocity anomaly can be explained by rapid deformation of thick, debris-rich basal ice. The other possible explanation for such high surface velocities is basal sliding. However, from the cliff margin to ~ 6 km up-glacier, all evidence suggests that Taylor Glacier is cold-based and frozen to its bed (Reference CalkinCalkin, 1974; Reference RobinsonRobinson, 1984; Reference Hubbard, Lawson, Anderson, Hubbard and BlatterHubbard and others, 2004), which supports the no-basal sliding assumption in the model. A small amount of basal sliding has been observed at Meserve Glacier (–17°C; Reference Cuffey, Conway, Gades, Hallet, Raymond and WhitlowCuffey and others, 2000a). The maximum sliding rate observed was 8 mm a-1. If we assume this rate of sliding at Taylor Glacier, then sliding accounts for <0.2% of the observed maximum annual surface velocity in our domain.
Along the north margin of Taylor Glacier, the basal ice can be clearly distinguished from the overlying clean ice; the transition between the two ice types is abrupt. However, it is difficult to measure the basal-ice thickness along the entire margin for three reasons: (1) ice aprons formed from ice blocks that have calved off the cliffs conceal the basal ice; (2) marginal summer meltwater streams also prevent visual observations; and (3) the lower boundary of the basal ice is difficult to distinguish from the nearly identical frozen sediment. Despite these challenges, the top of the basal ice appears to be a relatively consistent depth below the surface along marginal ice cliffs. Radar imagery confirms the flatness of the top boundary of the basal ice (Fig. 4). The flat boundary between the clean ice and the basal ice is evidence of a stiff upper material flowing over a soft basal material.
Several studies of glaciers that rest on unconsolidated valley-floor sediments in the McMurdo Dry Valleys have indicated that the lower boundary of the debris-rich basal ice (where it transitions to ice-rich sediment) is not clearly defined. Compared with glaciers that do not reach the valley floor, these glaciers have thicker basal ice, higher debris concentrations, ice-marginal moraines and frozen blocks of sediment within the basal ice due to accretion of the glacier substrate (Reference FitzsimonsFitzsimons, 1996, Reference Fitzsimons and Knight2006; Reference Humphreys and FitzsimonsHumphreys and Fitz-simons, 1996). Both Reference WallerWaller (2001) and Reference Fitzsimons and KnightFitzsimons (2006) advocate that the base of the glacier should be defined as a zone and not as a single zero-velocity boundary. Instead, the base of these glaciers is a continuum of physical properties and deformation processes that vary spatially and temporally. These variable basal conditions could explain why we find that a thick basal ice layer is required to meet the surface-velocity observations.
We have demonstrated that it may be crucial to incorporate rheologically distinct layers into ice-flow models for polar glaciers with debris-rich basal ice. Current ice-dynamics models seldom use a two-layer approach, particularly for cold-based polar glaciers. An alternative approach is to incorporate a spatially variable basal shear stress (e.g. Reference Habermann, Maxwell and TrufferHabermann and others, 2012), which can capture some of the effects of spatially variable basal ice. The basal-ice sequence observed in tunnels is composed of different ice facies that differ in their physical structure, solute concentration, ice fabric and debris concentration. Presumably, these variable physical and chemical properties alter the mechanical behavior for each facies. Observations of both small- and large-scale strain features inside two tunnels at Taylor Glacier indicate high strain rates occur in the laminated section (Reference Samyn, Fitzsimons and LorrainSamyn and others, 2005a). However, the particle-to-particle contact due to the high debris concentrations (>50% by volume) in the massive facies may prevent rapid deformation from occurring. The spatial variability of the basal-ice contribution suggests that folding of the basal ice may be an active process in debris-rich basal ice. Our study does not include these small-scale basal-ice structures, but allows for variation in basal-ice softness and thickness that captures the range of possible behaviors.
Thick, deformable basal ice flowing at speeds of up to 3 ma-1 at the terminus suggests a non-negligible flux of sediment at the terminus. For example, a 10 m thick layer of basal ice with an average of 5% by volume of sediment flowing at an average of 2 m a-1 is a flux of 1 m3 a –1 of sediment per meter of terminus. This sediment must then either become part of the moraine or wash down into Lake Bonney. The sediment flux could provide a means of confirming or constraining our results; it is difficult, however, to measure the bulk sediment content of the basal ice.
Combined with inverse theory, the shallow-ice approximation is a useful tool to explore ice-dynamics questions without resorting to full-stress models. It is a practical approach that provides a first-order approximation into how the debris-rich basal ice contributes to the deformation rates at Taylor Glacier. We can deduce properties of the basal ice from a set of relatively simple surface-based measurements. Here, our dataset was limited; with a more complete dataset our method can be used to deduce additional details of basal-ice properties. At a minimum, more complete surface-velocity and ablation-rate profiles would allow higher resolution analysis. Furthermore, data along multiple, longer flowbands would provide a better assessment of the terminus region as a whole. Finally, the finding of a weak bed along the flowband suggests that longitudinal stresses might be more important than we initially expected; a more detailed future analysis of Taylor Glacier should consider using a more advanced model.
Our results, supported by 3 years of observations, suggest that the debris-rich basal ice (1) controls the large-scale deformation field in the terminus region of Taylor Glacier and (2) is spatially variable along the flowband. The basal ice contributes an average of 90% to the flow rates observed at Taylor. At its thickest, the basal ice may be >15 m. The model demonstrates that the observed surface velocities can only be simulated if the basal ice is present beneath the entire length of the flowband and is softer than the clean ice. For example, a 10 m thick basal ice with a softness of 40 times that of clean, isotropic Holocene ice will contribute >2% to the surface velocity for ice thicknesses up to 1000 m. Because many polar glaciers and ice sheets have debris-rich basal ice visible at their margins, and because this weak ice can significantly increase the overall glacier flow rate, it is essential to incorporate rheologically distinct layers in models of polar glacier flow.
Acknowledgements
We thank Andrew Fountain, Josh Carmichael, Peter Sniffen, Matt Hoffman, Thomas Nylen, Hassan Basagic, Michelle Koutnik, Lou Albershardt, Matt Szundy and Erik Barnes for discussions and field assistance. We thank the University Navstar Consortium (UNAVCO) for GPS equipment and field support. We appreciate John Glen’s efforts as scientific editor and thorough reviews were greatly appreciated. This work was supported by grants OPP-0230338 and OPP-0233823 from the US National Science Foundation and an NSF GK-12 fellowship to Erin Whorton.
















