Introduction
The rapid flow of ice streams dominates the dynamic character of ice sheets (Reference BentleyBentley, 1987; Reference Alley and BindschadlerAlley and Bindschadler, 2001). Their demonstrated ability to stagnate (Reference BentleyRetzlaff and Bentley, 1993; Reference Smith, Lord and BentleySmith and others, 2002), gradually decelerate (Reference Bindschadler and VornbergerBindschadler and Vornberger, 1998; Reference Joughin, Tulaczyk, Bindschadler and PriceJoughin and others, 2002) and suddenly stop and start on the timescale of minutes (Reference Bindschadler, King, Alley, Anandakrishnan and PadmanBindschadler and others, 2003) implies an ability to significantly alter the mass balance of the surrounding ice sheet on many timescales.
An outstanding question concerning ice streams is by what process they form. Ice streams exhibit the unusual characteristic of increasing speed downstream as driving stress decreases. Various explanations exist for this behavior (Reference Whillans and van der VeenWhillans and Van der Veen, 1993; Reference Bindschadler, Bamber and Anandakrishnan.Bindschadler and others, 2001; Reference KambKamb, 2001). Many depend on a decreasing amount of basal friction downstream, although stream widening (where it occurs) also can result in faster flow (Reference RaymondRaymond, 1996). Ice streams are fed by tributaries within which the opposite condition applies, i.e. downstream acceleration of the ice is accompanied by an increase in driving stress. The transition between flow regimes is referred to as the ice-stream ‘onset’ (Reference Bindschadler, Bamber and Anandakrishnan.Bindschadler and others, 2001). The change in flow mode reflects a change in the nature of the basal sliding and is likely tied to a change in the character of basal lubrication. The presence and presumably the amount of water along with the pressure of this hydraulic system and the material properties and state of the subglacial till, as influenced by the water, determine the basal friction. From analysis of bed echo strength, Reference BlankenshipBlankenship and others (2001) have interpreted a change in the subglacial material from hard bedrock to soft sediments at many of the West Antarctic ice-stream onsets and attribute this change as the cause of the tributary to ice-stream flow transition. Here we consider the importance of water in explaining not only this transition from tributary to ice-stream flow, but also the more widespread gradual acceleration of flow speed along the tributary–ice-stream system.
The concept we explore includes three characteristics of ice dynamics which have not been linked previously: faster ice is more effective at transmitting basal topography to the surface topography; subglacial water pressures are much more sensitive to surface topography than to basal topography; and a more spatially variable water-pressure field will tend to include more regions of lower pressure where more subglacial water will be retained locally, reducing basal friction in these areas while increasing basal shear stress in areas of higher hydraulic potential. We work stepwise through each relationship before combining them in a ‘lubrication index’. This index increases downflow along the tributary–ice-stream system, indicating a tendency for increasing water storage and, presumably, lower basal friction. Finally we discuss the possible use of this lubrication index as a useful parameterization of the positive feedback between ice-flow speed and basal lubrication, for numerical models of ice-stream flow and evolution.
Transmission of Bed Topography to Surface
The surface topography of ice streams is rougher than either the adjacent ice ridges or the upstream catchment areas (Reference Bindschadler and VornbergerBindschadler and Vornberger, 1990). The underlying reason for this relationship rests in the rheologic characteristics of ice as a viscoelastic material. These determine the specific relationship between the surface topography of the ice and the topography of the bed over which the ice flows, its speed (both sliding and deformation components) and its thickness. Numerous treatments of this problem have been published. The first correct solution was by Reference JóhannessonJóhannesson (1992). Here we employ a later treatment because it provides explicit equations for the parameters we seek to examine (Reference GudmundssonGudmundsson, 2003). Although Gudmundsson’s theory also assumes a linear rheology of constant viscosity, it addresses high ratios of sliding to deformation speed for a range of perturbation to ice-thickness ratios. A more complete treatment comparing non-linear ice rheologies is reported by Reference Raymond and GudmundssonRaymond and Gudmundsson (2005).
In the case where basal sliding dominates over the effects of internal deformation, Reference GudmundssonGudmundsson (2003, equation 70) showed that for a linear rheology the surface expression of a regular, periodically undulated bed, defined by the ‘transmission efficiency’, T sb, is:
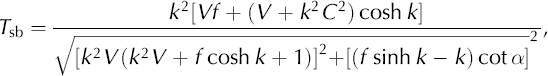
where f = cosh k + kC sinh k and k is the bed wavenumber (non-dimensionalized by ice thickness, H), V is the surface speed (non-dimensionalized by deformation speed at the surface), C is the sliding speed (also non-dimensionalized by deformation speed at the surface) and α is the mean surface slope. In physical terms, T sb is the ratio of the surface undulation amplitude to the bed undulation amplitude. The published theory considers both horizontal dimensions separately: here we confine ourselves to the along-flow direction only. The wavelength of the surface topography matches that of the bed, with the phase shift between the two given by:
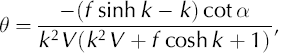
where a positive phase shift represents a downstream offset of the surface topography relative to the bed.
Transmission efficiency, T sb, and phase shift, θ, are shown in Figure 1 for a range of bed wavelengths (in units of ice thickness). The shortest bed wavelengths are strongly damped with minor surface expression and the phase shift is least for relatively faster sliding speeds. In contrast, the longest bed wavelengths are preserved at full amplitude and with a small phase shift. These consequences are intuitive and match observations. What is less intuitive is that there is a range of intermediate wavelengths where the effective transmission of the basal amplitude to the surface is relatively enhanced and that both the range of enhanced wavelengths shifts to longer wavelengths, and the enhancement amplitude increases as the sliding speed becomes a larger multiple of the deformation speed. Within this range of enhanced bed-to-surface transmission wavelengths, the phase shift is largest for the relatively slower sliding speeds and shorter wavelengths.

Fig. 1. Transmission efficiency, Tsb (a), and phase shift, θ, in degrees (b) of surface topography caused by ice flow over basal topography. Wavelength, λ, is plotted on log scale and in units of ice thickness. C refers to sliding speed (in units of surface deformation speed).
Figure 2 illustrates the general solution space of Equations (1) and (2) for a wider range of sliding speeds. The same characteristics outlined above are illustrated, but in a continuous fashion. The local maximum of T sb begins at a value of about 0.15 at a low sliding/deformation ratio of 2.5 and at a wavelength about three times the ice thickness, and increases to more than 0.5 at a sliding ratio of 50 and a wavelength of four times the ice thickness. The phase shift has a strong local minimum beginning at values of −82° at sliding ratios of 2.5 and bed wavelengths of 10 ice thicknesses, decreasing to values of −64° at sliding ratios of 50 and bed wavelengths of 45 ice thicknesses.

Fig. 2. Contours of transmission efficiency, Tsb (a), and phase shift in degrees (b) of surface topography caused by ice flow over basal topography. Wavelength, λ, is plotted on log scale (in units of ice thickness). C refers to sliding speed (in units of surface deformation speed).
A direct result of the variation of transmission efficiency and phase shift with sliding speed is that for a periodically repeating bed topography, the surface shape will change as the surface speed changes either spatially or temporally. The implications of this will be explored more fully later.
This theory is checked using data from the tributary feeding Bindschadler Ice Stream (formerly Ice Stream D), West Antarctica. Data of surface speed and topography, ice thickness and basal topography are described in Reference BlankenshipBlankenship and others (2001) and Price and others (2002). A 150km long profile defined by Price and others following the kinematic center line, i.e. the points of maximum speed for every cross-flow profile, is shown in Figure 3. The general slope, calculated from a least-squares fit, is 0.3° and the mean ice thickness is 2300 m. The dominant bed wavelength is estimated by eye as 20 km, or 8.7 times the ice thickness. The mean amplitude of this bed wavelength is approximately 125 m. The surface profile also shows a dominant topography at this wavelength with mean amplitude about 15 m. Therefore, the transmission efficiency for this case is 0.12. The surface speed along this profile increases from roughly 10 m a−1 to 100 m a−1 with a mean of about 50 m a−1. The deformation speed is not known, but if we use the value of 13 m a−1 at Byrd Station (Reference WhillansWhillans, 1979), only 25 km from the profile’s upstream end, then we estimate C = 3.85. Plotting the coordinate C = 3.85, A = 8.7 in Figure 2a, the result falls between the T contours of 0.1 and 0.15, close to the calculated value of T = 0.12, derived above.

Fig. 3. Profile of surface and bed topography along the kinematic center line of a major tributary feeding Bindschadler Ice Stream. Surface topography is shown both at same scale as bed and vertically amplified by a factor of five (right axis).
Subglacial Hydraulic Potential
We consider next the behavior of subglacial water. As first discussed by Reference ShreveShreve (1972), subglacial water will move along the negative gradient of a potential field, ϕ, that results from the gravitational potential and the pressure of overlying ice:
where ρ w and ρ i are the densities of water and ice respectively, g is the gravitational acceleration, z b and z s are the bed and surface elevations respectively and the potential is relative to sea level. Equation (3) assumes that the water pressure resisting closure of water cavities and/or conduits is equal to the ice overburden pressure. This is reasonable for our examination of the equilibrium state. Confining this discussion to the axis of ice motion, the water will move in accordance with the gradient of this potential field which, after rearrangement of terms in Equation (3), can be written as:
to emphasize the fact that the surface elevation gradient (i.e. surface slope) is more influential than the bed elevation gradient by the factor ρ i/(ρ w–ρ i), or roughly an order of magnitude. Figure 2 confirms that for all but the shortest wavelengths (less than twice the ice thickness) and slowest sliding speeds (less than twice the surface deformation speeds) the surface gradient term in Equation (4) is more important than the bed gradient term, but it is important to note that in these extreme cases Gudmundsson’s (2003) theory may not be valid at low values of C. The pressure gradient, along with the hydraulic cross-section of the subglacial water system, determines the flow rate of water moving downstream. Here we are concerned only with flow direction.
Water Storage
When the hydraulic potential gradient is zero, water will no longer be driven downstream. A negative potential gradient implies upstream water flow. Because the potential field is continuous, zones of negative downstream potential gradient bounded by lines of zero gradient define areas where subglacial water is expected to be stored.
Before calculating the hydraulic potential fields of specific cases, we separate the oscillating component of the bed slope, ![]() from the mean bed slope,
from the mean bed slope, ![]() and rewrite Equation (4) as:
and rewrite Equation (4) as:
Other terms cancel by assuming the mean slopes of surface and bed are equal, i.e. there is no ice pressure gradient.
Equation (5) allows us to calculate the hydraulic potential gradient for any surface and bed geometry. If the bed elevation is known, the hydraulic potential gradient can be integrated along the flowline to convert it to a profile of water pressure. This is sometimes represented as a profile of equivalent water column height called the ‘hydraulic grade line’.
Equations (1) and (2) allow us to calculate the surface topography for bed topography, sliding and deformation speed and mean values for bed slope and ice thickness. We examine the dependence of hydraulic potential on this latter list of variables for a periodic, single-wavelength bed. Figure 4 shows an example using typical ice-stream values: bed wavelength ten times the mean ice thickness of 1 km; an amplitude of 50 m and a mean slope of 1° are specified for ice flowing with a sliding ratio of C = 10. From Equations (1) and (2), the resulting transmission efficiency and phase shift are 0.62 and −48° respectively (see Fig. 1). This determines the geometry of the surface (see Fig. 4). The corresponding water potential gradient (Equation (5)) follows from this geometry. Figure 4 illustrates the typical case where the hydraulic grade line closely follows the shape of the surface.

Fig. 4. Example of calculated surface geometry (from Equations (1) and (2)), hydraulic grade line (height of equivalent water column to represent subglacial water pressure; see text) and hydraulic potential gradient (∇ϕ, from Equation (5)) for a sinusoidal bed with a wavelength ten times the mean 1 km ice thickness and an undulation amplitude of 50 m. Sliding ratio, C, is 10 and mean slope is 1°. Elevation values are plotted with respect to the mean slope.
Higher and lower values of the hydraulic potential gradient identify where water flow will be enhanced and retarded respectively. The resultant flow rate also depends on the hydraulic conductivity of the subglacial hydrologic system. We do not deal with this parameter, but leave it as a qualitative expectation that regions of large hydraulic potential gradient will have a shorter residence time of through-flowing water and therefore contain less water (i.e. be drier) than areas of smaller hydraulic potential gradient. Because the surface elevation and hydraulic grade lines are nearly parallel, the minima in the hydraulic potential gradient are nearly coincident with the minimum downstream surface slopes. In some cases, the minimum local surface slope may be negative, i.e. elevation decreases upstream, creating a ‘backslope’. The few observations inferred to represent large, short-term changes of subglacial water coincide with regions of strong surface backslopes (Reference Gray, Joughin, Tulaczyk, Spikes, Bindschadler and JezekGray and others, 2005). The phase shift between the surface and bed determines how far upstream these minima are displaced from the minima of basal elevation gradient (i.e. minimum bed slope).
Our two-dimensional analysis cannot identify where water would be stored because lateral (cross-flow) variations do occur and flow-parallel undulations are not constant cross-flow. Nevertheless, identifying the spatial variation in the hydraulic potential is instructive, with more negative and more positive values indicating wetter and drier basal regions respectively. To quantify the spatial heterogeneity, we define a ‘lubrication index’, L, as the ratio of the maximum magnitude of the topographic-variable term (square-bracketed term in Equation (5)) to the magnitude of the mean-slope term (first term in Equation (5)):
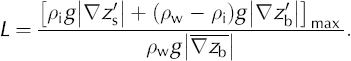
In the absence of lateral variations, L = 1 defines the condition where the subglacial hydraulic potential gradient equals zero and the water feels no force to move in any direction. For the case shown in Figure 4, the lubrication index, L, equals 1.19. For values of the lubrication index above unity, the range of negative hydraulic potential gradient values defines a zone over which water does not escape. In general, these are the areas of surface backslope (when the mean slope is removed) (see Fig. 4). Because the phase shift between bed and surface undulations is always <90°, water will also collect in the upstream lee of basal undulations.
The area of collected water per unit width, A, (or, more correctly, of negative hydraulic potential gradient) will increase with the value of L according to:
As L becomes larger, the areas where water can be expected to collect (hydraulic gradient less zero) become more extensive and presumably collect more water (due to the stronger gradients) as the ‘drier’ areas shrink in extent and contain less water. As L approaches infinity, the area of collected water approaches the limit λ/2.
Sensitivity Study
The lubrication index is linearly proportional to the amplitude of bed undulations. Its relationships to the bed geometry, the sliding speed and the mean slope are more complicated. We examine this multi-parameter space by calculating the lubrication index for multiple cases where bed geometry (single wavelengths of varying distances and undulation amplitudes), sliding speed and regional slope are varied. Additional relationships between L and the dependent variables of surface topography and hydraulic potential gradient follow from the above equations.
The influences of bed wavelength (λ) and sliding ratio (C) on L required a series of calculations to explore a reasonable parameter space (see Fig. 5). There are three major characteristics. The first is the relatively narrow range of bed wavelengths for which the lubrication index exhibits a sharp local maximum for all but the lowest sliding ratios. Second, at longer bed wavelengths, the tendency is for L to decrease as either the wavelength increases or the sliding velocity decreases. Third, for shorter wavelengths, L increases rapidly, independent of sliding speed.

Fig. 5. Contoured values of lubrication index (a measure of the spatial heterogeneity of the subglacial water distribution; see text) for combinations of bed wavelength, λ, (in units of ice thickness) and sliding ratio, C. Mean slope is fixed at 0.3°, and the bed undulation amplitude is 100 m. Unlabeled contours approaching bottom of figure increase in value as λ decreases.
Varying the bed wavelength while keeping the bed amplitude constant causes bed roughness, the ratio of the bed amplitude to the bed wavelength, to vary greatly. Figure 6 presents the same parameter space as Figure 5 but scales the bed amplitude so that bed roughness remains constant. The first two features mentioned above are consistent with Figure 5; however, for the shortest bed wavelengths, the lubrication index decreases with wavelength, rather than increases as was the case in Figure 5. For bed wavelengths less than the ice thickness, the lubrication index is very close to unity.

Fig. 6. Contoured values of lubrication index for combinations of bed wavelength, λ, (in units of ice thickness) and sliding ratio, C, as in Figure 5. Mean slope is fixed at 0.3°, but unlike Figure 5, the bed undulation amplitude is scaled to the bed wavelength such that the ratio of bed amplitude to bed wavelength is equal to 0.01.
The first characteristic, a sharp maximum L for a given sliding speed, is a result of the higher transmission efficiency of a selected set of bed wavelengths (see Fig. 1). Beds in this wavelength range will have surfaces with larger amplitudes (relative to other bed wavelengths), a stronger variation of the hydraulic potential and, thus, larger values of L. This higher efficiency diminishes at lower sliding ratios (recall Figs 1 and 2), so the local maximum feature in Figure 5 decreases at these lower sliding speeds. Figure 1 also illustrates that the wavelength of the local maximum of transmission efficiency increases with sliding speed. This appears in Figure 5 as the gradual increase in the wavelength of the local maximum L value as the sliding ratio increases. Figure 5 indicates that the wavelength for the maximum lubrication index increases very slowly at sliding ratios above 50.
The second feature of Figures 5 and 6, i.e. decreasing L for increasing bed wavelength or decreasing sliding speed, expresses the fact that for bed wavelengths longer than those in the high transmission efficiency range, the transmission efficiency decreases as either bed wavelength increases or sliding decreases (see Fig. 1). For much longer bed wavelengths, i.e. beyond 20 times the ice thickness, the transmission efficiency begins to increase again. If the bed amplitude stays constant, the bed slope decreases as wavelength increases. This effect more than compensates for a higher transmission efficiency, so L decreases. For constant bed roughness, values of L begin to increase for longer bed wavelengths, as shown in Figure 7. A cautionary note is warranted for these longer wavelengths because, at these longer scales, bed amplitudes become substantial fractions of the ice thickness, violating Gudmundsson’s (2003) perturbation assumptions.

Fig. 7. Contoured values of lubrication index for combinations of a bed wavelength, λ, beyond the range shown in Figure 6, and sliding ratio, C. Mean slope is fixed at 0.3°, and bed undulation amplitude is scaled to the bed wavelength such that the ratio of bed amplitude to bed wavelength remains constant at 0.01. Contour values increase to the bottom of the plot.
The third feature of Figure 5 is the rapid increase in L with decreasing bed wavelength. As the bed wavelength decreases to values of the ice thickness and below, the transmission efficiency falls below 0.1 (see Fig. 1), making the surface ever smoother and increasing the influence of the bed on the hydraulic potential gradient (see Equation (4)). This reduces the relevance and importance of the impact of sliding on surface topography and explains the independence of L on sliding speed illustrated in Figures 5 and 6. In Figure 5, the tendency for L to increase rapidly as wavelength decreases is a consequence of increasing bed slopes forced by the constant bed undulation amplitude. This tendency is reversed and strongly dampened for the constant bed roughness conditions illustrated in Figure 6.
At undulation wavelengths less than 10–20 times the ice thickness, local normal and shear stresses are not necessarily equilibrated and longitudinal stress gradients must be considered. In the case considered here, these are most conveniently presented as ‘bridging stresses’ that vary the bed-normal stress across the bed undulations, thus modifying the ice overburden term in Equation (3). Following Reference Van der VeenVan der Veen (1999), a periodic, undulated bed can be described by:

where x is the position along the bed, H = z
s–z
b is the ice thickness and B
0 and λH are the undulation amplitude and wavelength in non-scaled units. The oscillating component of the bed slope, ![]() is
is
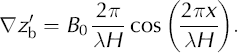
The normal stress on the bed, N, is
where ![]() is the mean bed slope. The maximum and minimum normal stresses occur at x = 0 and x = λH/2, respectively the upstream and downstream sides of the undulations. This function is not symmetric, due to the cosine factor in Equation (10). The variation is nearly independent of the mean bed slope, scales linearly with roughness and is constant for a given bed roughness. (Note that Van der Veen’s (1999, p. 73) treatment is incorrect and gives the invalid result that the maximum normal stress decreases with roughness.) Evaluation of Equation (10) confirms that the ice overburden term in Equation (3) varies less than 1% for λ > H, so bridging stresses do not significantly affect our results.
is the mean bed slope. The maximum and minimum normal stresses occur at x = 0 and x = λH/2, respectively the upstream and downstream sides of the undulations. This function is not symmetric, due to the cosine factor in Equation (10). The variation is nearly independent of the mean bed slope, scales linearly with roughness and is constant for a given bed roughness. (Note that Van der Veen’s (1999, p. 73) treatment is incorrect and gives the invalid result that the maximum normal stress decreases with roughness.) Evaluation of Equation (10) confirms that the ice overburden term in Equation (3) varies less than 1% for λ > H, so bridging stresses do not significantly affect our results.
Cavity formation on the lee sides of basal undulations must also be considered and will occur when the water pressure exceeds the normal stress (Reference IkenIken, 1981). On the spatial scale we are considering, the hydraulic potential gradients across the undulations are much larger than the gradients caused by bridging stresses. However, the importance of bridging stresses will increase for the smaller scale where roughness can be much larger. At that scale, the focus would shift to the details of how water is stored in the general region identified by our analysis.
Returning to the sensitivity study of the lubrication index, the dependence of L on variations in mean slope and sliding speed for a fixed bed wavelength is illustrated in Figure 8. Unlike bridging stresses, the mean slope is very important in the determination of the lubrication index, and its influence dominates for most cases. The dramatic increase of L as mean slope decreases is forced by the increasing relative magnitude of the bed slopes which have a maximum value of about 2°. At low sliding speeds and slopes above 0.5°, the slope has far less influence than the sliding speed and lubrication index increases with sliding speed. At low sliding speeds and low slopes, the lubrication index increases with increasing sliding and decreasing slope.

Fig. 8. Contoured values of lubrication index for combinations of sliding ratio, C, and mean slope, α, in degrees. Bed wavelength is fixed at two times the 1 km ice thickness, and the bed undulation amplitude is fixed at 0.01 times the ice thickness. Contour values increase to the extreme left of the plot.
The choice of bed wavelength is important. A value of two times the 1 km ice thickness was chosen because it samples the maximum feature of Figures 5 and 6 and focuses on the bed wavelengths for which lubrication increases most. A plot similar to Figure 8 results when the bed wavelength is three times the ice thickness. From Figures 5 and 6, for bed wavelengths less than the ice thickness, the lubrication index is independent of sliding speed, so contours of Figure 8 for that range of bed wavelengths would be vertical. For very long bed wavelengths, there would be some dependence on sliding speed, but it would be much less than in Figure 8.
The final parameter pair to examine is bed wavelength vs mean slope. Figure 9 shows an example of their combined influence on lubrication index for an intermediate choice of sliding (C = 10) and a constant roughness bed. The strong influence of the transmission efficiency for a narrow range of bed wavelengths is a dominant feature of this plot, and the value of the dominant wavelength decreases as slope decreases. The continued presence of a dominant wavelength supports our contention that it is a narrow range of wavelengths that dictates the nature of the subglacial hydrologic system and, thereby, the dynamics of sliding ice masses. The primary influence of slope is superimposed on this dependence and causes higher lubrication indices with decreasing slope.

Fig. 9. Contoured values of lubrication index for combinations of bed wavelength, λ, (in units of ice thickness) and mean slope, α (in degrees). The sliding ratio, C, is 10, and the bed undulation amplitude is scaled to the bed wavelength such that the ratio of bed amplitude to bed wavelength is equal to 0.01. Contour values increase to the extreme left of the plot.
These results can be used to analyze more complex cases, although we do not illustrate that here. For example, a known geometry could be decomposed into component wavelengths, each wavelength treated as a separate case with the same assignment of slope and velocity, and the results reconstructed through superposition. Additionally, the sliding velocity could be varied along the flow direction.
Implications for Ice-Stream Tributaries and Onsets
The sensitivity study presented above supplies a physically based concept of how the subglacial hydrologic system beneath an ice-stream tributary may evolve as the tributary speeds up and eventually becomes an ice stream. The locations of tributaries emerging from the surrounding ice sheet are correlated with the basal topography (Reference JoughinJoughin and others, 1999). Prior to the development of high sliding velocities, the surface topography of the incipient tributaries remains subdued, i.e. the transmission efficiency (Equation (1)) is low. As a result, the subglacial water flow should be controlled by the relatively much stronger basal topography. This basal topographic control and concentration of subglacial water may well be responsible for increasing lubrication and increasing sliding rates downstream along the tributaries. We have shown that this increase in sliding speed will produce an increase in transmission efficiency and cause a more undulated surface topography. This will, in turn, cause the subglacial hydraulic potential to be more heterogeneous (i.e. larger L). This heterogeneity implies that relatively wetter areas will tend to retain even more water, providing a better-lubricated bed to the overlying ice sheet, while relatively drier areas will retain even less water. Better-lubricated areas support a decreasing amount of basal shear stress, forcing an ever increasing portion of driving force to be supported at the relatively drier areas of the bed. These drier areas shrink as sliding speed increases for all but the shortest bed wavelengths (see Fig. 5), leading to an increase in the basal shear stress. Through a standard basal flow relationship where sliding speed is proportional to the basal stress to some power (see discussions in Reference PatersonPaterson, 1994; Reference Van der VeenVan der Veen, 1999), the sliding speed is expected to increase. The downstream progression of smaller, relatively dry areas experiencing more shear stress, and thus sliding faster, is consistent with the progression we expect, namely, that as sliding speed increases, the heterogeneity of the subglacial system will increase, leading to smaller areas of increasing basal stress that encourage further increases in sliding speed. This feedback loop may describe the tributary-to-ice-stream evolution.
Positive feedback concepts for ice-stream motion are not new. Budd and McInnes (1974) used a conceptually similar connection between increasing sliding speed and decreasing basal friction in a numerical model to produce surges that was later applied to the Antarctic ice sheet.
More recent treatments considered possible compensating effects. Reference RaymondRaymond (2000) considered the energy balance across an ice stream. He parameterized basal lubrication through the expression 1 –τ b/τ d (where τ b and τ d are basal and driving shear stresses, respectively). This factor ranged from 0 to 1 to represent the extreme conditions of a dry (τ b = τ d) and wet bed (τ b = 0), respectively. Reference RaymondRaymond (2000, fig. 2c) showed that the maximum rate of subglacial water production occurred when this factor equaled 0.75 (or τ b = 0.25τ d). Our Equation (6) provides another measure of lubrication. Equating these two lubrication measures by matching their limiting values (Equation (6) must be divided by 2/λ) results in the relationship:
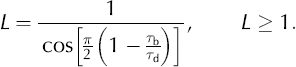
Using this relationship, the maximum water production occurs at L = 2.6. From Raymond’s work, if lubrication exceeds this amount, any increase in speed is more than offset by a reduction in basal shear stress, reducing the amount of water produced locally by frictional heat. This threshold of L = 2.6 is beyond the lesser threshold of L = 1 when water first begins to collect under the ice and not drain away.
Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others (2000b) discussed ice-stream stability from the point of view of coupled relationships between sliding velocity, till strength, basal melt rate and till water storage. Much of this theory rested on the concept of an undrained bed along which water does not flow, and a dynamic equilibrium is achieved to produce no basal melting; however, the basic stability conditions are not altered when some drainage is allowed. Our view is that subglacial water flow must occur because there are significant hydraulic potential gradients and water has been repeatedly observed at the bottom of ice streams.
Acceleration of the ice within tributaries is by no means assured and Reference JoughinJoughin and others (1999) discuss and show examples of ‘failed tributaries’. Other conditions may be required to ensure the continued evolution of a tributary to an ice stream; however, we suggest that the feedback of sliding speed and the pattern of the subglacial hydraulic potential is important.
At some point, the dynamics of a tributary (increased sliding speed with increased driving stress) changes to the dynamics of an ice stream (increased sliding speed with decreased driving stress). Water availability is very important for the maintenance of streaming flow (Reference Blankenship, Bentley, Rooney and AlleyBlankenship and others, 1987; Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000a; Reference KambKamb, 2001). It is reasonable to assume that it is also important for the initiation of streaming flow. Our mechanism describes how the capacity for water retention increases along a tributary. We suggest that the transition from tributary to ice-stream dynamics may be associated with a threshold in stored water or its distribution.
A further consideration, not incorporated here, is the expectation that heterogeneous lubrication at the bed will cause longitudinal oscillations of the surface velocity. These will create longitudinal stress gradients through the entire ice thickness and be another source of bridging stresses. Bridging stresses concentrated at the base were discussed in an earlier section and shown to be negligible at scales longer than the ice thickness. We cannot be sure the same is true of this other source of longitudinal stress gradients, but we leave this for future work.
We check some of our results by returning to the real case of Bindschadler Ice Stream considered earlier. Taking the value of surface velocity of 100 m a−1 as the typical value at the onset (see Reference Alley and BindschadlerBindschadler and others, 2001), the corresponding value of C at the onset of the ice stream is 7.7. For the dominant wavelength measurable in the field data (λ = 8.7) the amplitude scaled to the ice thickness is 0.05 and the regional slope is 0.16°. Our method produces a lubrication index of 1.2. This crude measure of the lubrication index applies for only one wavelength and is constrained by the sampling frequency of the field data. Shorter wavelengths with higher transmission efficiencies (in the range of λ = 2–3; see Fig. 2) might produce higher lubrication indices, but field data are lacking. Nevertheless, the result that L is greater than unity gives us some confidence that the lubrication index may be a useful guide to subglacial dynamics and the transition between tributaries and ice streams.
The difficulties in trying to apply to real data our idea that subglacial water’s influence on ice-stream initiation can be quantified through our lubrication index highlight the fact that if we are correct and the wavelengths on the scale of a few kilometers are critical, then the sampling strategy for field ice-penetrating radar measurements of ice thickness is very challenging. There have been recent attempts to try to invert surface measurements of surface topography and velocity to bed topography and conditions, but these are still very limited (Reference Thorsteinsson, Raymond, Gudmundsson, Bindschadler, Vornberger and JoughinThorsteinsson and others, 2003). The detailed topography being supplied by satellite laser altimetry, augmented by high-resolution imagery, is one means to produce improved detail in surface elevation fields. This could, in turn, provide new insights into the detailed nature of subglacial drainage and the dynamics of the ice motion influenced by that drainage.
Conclusions
The non-uniform filtering of basal topography to surface topography through rapidly sliding ice strongly affects the character of the subglacial hydrologic system. The larger transmission efficiency of a range of basal wavelengths was identified by Reference GudmundssonGudmundsson (2003). This range of wavelengths, the transmission efficiency and the corresponding phase shift between the surface and bed undulations depend on sliding speed, mean slope, basal wavelength and ice thickness.
Basal and surface topographies, in turn, determine the subglacial hydraulic potential, with the surface topography dominating this relationship. Wavelengths most efficiently transmitted from bed to surface are responsible for the greatest heterogeneity of the hydraulic potential. The physical interpretation of this heterogeneity is that the bed is better lubricated in areas where the subglacial hydraulic potential is lowest, while areas of highest hydraulic potential will support the majority of the driving force through basal shear stress. As speed increases, the heterogeneity of the hydraulic potential will increase, decreasing the size of the areas of high friction where driving force is concentrated. This will lead to increased basal shear stress, and thereby lead to increased sliding speeds. We surmise that this positive feedback will eventually lead to speeds where an ice stream is formed and at which the ice stream can sustain its own sliding motion through production of sufficient amounts of basal water. Although we do not examine any temporal dependence, we do define a water lubrication index and show that this is related to the lubrication factor used in a previous analysis of ice-stream energy balance (Reference RaymondRaymond, 2000).
The sensitivity study of this hydraulic potential variation is conducted in terms of the lubrication index. In a wide range of conditions, the lubrication index exceeds unity, which corresponds to water storage in the simplified twodimensional case. This usually occurs beneath the upstream sides of surface undulations. The dominant wavelengths in bed-to-surface transmission efficiency reach this water storage condition at the lowest sliding speeds and shallowest mean slopes.
Our single case study using field data supports our theory and indicates that the identified threshold when subglacial water is first stored is in rough agreement with the position where a tributary sliding by ‘traditional’ kinematics (basal shear stress positively correlated with speed) switches to ‘streaming’ kinematics (basal shear stress negatively correlated with speed).
Acknowledgements
This work was an outgrowth of two earlier studies. The first was the discovery of isolated topographic inflations and deflations led by L. Gray, and the second a summer-student study by C. Wobeter on the subglacial hydraulic potential of Antarctica. C. Raymond offered many helpful comments that substantially improved the research. Formal reviews that also improved the submitted manuscript were offered by G.H. Gudmundsson, S. Tulaczyk and J.S. Walder. The work was conducted while the authors were supported by NASA’s Cryosphere Program and the US National Science Foundation’s Office of Polar Programs.











