Introduction
Deep ice cores provide greenhouse gas records over almost a million years (EPICA Community Members, 2004). The air entrapped in polar ice, when the critical density of pore close-off (820–830 kg m−3) is reached at the transition of firn to ice at depths of 50–120 m, is significantly younger than the ice at the same depth. Because the depth of pore close-off depends on temperature, accumulation rate and impurities, the age difference varies with climate. Present firn models, which are used to date the air, simulate the densification process by semi-empirical approaches derived from profiles of the mean density. They assume homogeneous firn and ignore any stratification within the firn. It is an open question whether such simplifications could be responsible for the discrepancies between model predictions and the interpretation of measurements of air isotopic composition (δ15N or δ40Ar) as proxy for the diffusion column heights, particularly for conditions on the East Antarctic plateau during glacial periods (Reference LandaisLandais and others, 2006).
The most commonly used densification models are those of Reference Herron and LangwayHerron and Langway (1980) and Pimienta and Barnola (Reference Barnola, Pimienta, Raynaud and KorotkevichBarnola and others, 1991), hereafter referred to respectively as the HL model and PB model approaches. The HL approach suggests that a decrease in porosity of a certain layer is proportional to the increase in stress due to the weight of the overlying firn, but with different activation energies for the settling- and creep-dominated intervals. The PB approach is based on sintering theory (Reference Wilkinson and AshbyWilkinson and Ashby, 1975) and describes densification in the intermediate stage as creep satisfying a power law in stress with exponent 3. Both models are driven by surface density, temperature and accumulation rate at the specific polar site. The HL model is a steady-state model, whereas the PB model can be used for simulations with varying accumulation rate and temperature. More recently, Reference Arnaud, Barnola, Duval and HondohArnaud and others (2000) proposed a model that includes geometrical aspects. Reference Arthern, Vaughan, Rankin, Mulvaney and ThomasArthern and others (2010) explained densification by grain-size-dependent creep combined with grain growth. Reference Zwally and LiZwally and Li (2002) assumed temperature-dependent activation energy to explain seasonal variations of firn heights. All the different models have in common that the rate coefficients for certain densification processes are based on an Arrhenius law with process-dependent activation energies.
Existing firn models simulate depth profiles of mean density. They ignore the stratified structure of firn, which reflects deposition history, redistribution by wind, post-depositional metamorphism and potential effects of the chemical impurities. In particular, it is assumed that at low-accumulation sites the density stratification decreases with depth and is absent at the firn–ice transition (Reference LandaisLandais and others, 2006). In contrast, observed high-resolution density profiles reveal a strong stratification in the deep firn down to the transition to polar ice (Reference Gerland, Oerter, Kipfstuhl, Wilhelms, Miller and MinersGerland and others, 1999; Reference HoriHori and others, 1999; Reference Freitag, Wilhelms and KipfstuhlFreitag and others, 2004; Reference Hörhold, Kipfstuhl, Wilhelms, Freitag and FrenzelHörhold and others, 2011, Reference Hörhold, Laepple, Freitag, Bigler and Fischer Hand Kipfstuhl2012). Surprisingly, all investigated sites from Antarctica as well as Greenland exhibit the same stratification behaviour, independent of their climatic conditions: after a rapid decrease of the density variability over the uppermost 10–30 m depth, the density variability increases noticeably by ∼5–10 kg m−3 above the firn–ice transition and then slowly diminishes. The increase of the density variability is accompanied by an increasing correlation between density and the logarithm of calcium ion concentration (ln([Ca2+])) in the ice. Reference Hörhold, Laepple, Freitag, Bigler and Fischer Hand KipfstuhlHörhold and others (2012) attributed this correlation to an accelerating influence of impurity concentration on the densification rate of snow to ice. Further evidence of an impurity effect on densification is found by comparison of [Ca2+] with density frequency spectra. A dominant wavelengths band, also occurring in the spectrum of the [Ca2+] record, develops with depth from the random noise associated with deposition and post-deposition processes close to the surface. This suggests that the density variations at the firn–ice transition are almost completely caused by variations in the impurity load.
In this paper we describe the incorporation of the impurity effect into two existing firn models to simulate the density layering observed in modern firn. The modified models are calibrated using firn cores B29 and B32 from Greenland and Antarctica, respectively.
Firn Densification Model
The activation energy E for deformation, which arises in the Arrhenius factor, is usually kept constant. We now assume that impurities reduce the activation energy E for deformation processes. Thus, our concept introduces a dependency of E on the impurity concentration in a specific firn layer.
We formulate a continuous densification process of layers with varying impurity concentration, and calculate the densification of the stratified firn, instead of modelling mean density within a homogeneous firn column. We focus on the modification of the HL model in the main text and present the modifications for the PB approach in the Appendix. The modifications can also be applied to other firn models (e.g. Reference Arnaud, Barnola, Duval and HondohArnaud and others, 2000; Reference Goujon, Barnola and RitzGoujon and others, 2003; Reference Arthern, Vaughan, Rankin, Mulvaney and ThomasArthern and others, 2010). For consistency with the HL/PB models, we adopt the differential equations of HL and PB with their constants, but add a separate impurity term in the activation energy: Eqn (1a,b). The impurity term consists of two factors, f 1 and f 2. The factor f 1 corrects the activation energy for the mean impurity effect that is already implicitly included in the model constants of the classical approaches, because they are derived empirically by data-fitting on firn with impurity content. Factor f 1 multiplied by the classical activation energy describes the activation energy for impurity-free firn. It is assumed to be constant. Factor f 2 reflects the introduced dependence of the activation energy on impurities. The impurity dependence f 2([Ca2+]) is parameterized by the Ca2+ concentration [Ca2+] and is defined as a linear function of its natural logarithm, motivated by the observations of Reference Hörhold, Laepple, Freitag, Bigler and Fischer Hand KipfstuhlHörhold and others (2012). The sensitivity of E to changes in impurity concentration is represented in f 2 by a constant factor β. [Ca2+] is normalized with a critical Ca2+ concentration [Ca2+]crit, which is defined as the minimum concentration at which impurities affect densification. In our simulations [Ca2+]crit is set to the detection limit of 0.5 ng g−1 associated with the continuous flow analysis (CFA) method used for measuring impurities continuously with depth. In order to ensure positive values for the natural logarithm (meaning that [Ca2+] can only enhance and not reduce densification rates) the Ca2+ concentrations [Ca2+] are normalized with [Ca2+]crit. All [Ca2+] below [Ca2+]crit are set to the value of [Ca2+]crit. Then the activation energy E([Ca2+]) is given by

for [Ca2+] ≥ [Ca2+]crit and by

for [Ca2+] ≥ [Ca2+]crit, with E classical the activation energy used in the equations of HL (J mol−1).
The differential equations used for the modified HL approach are
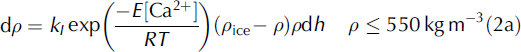

with terminology and the rate values taken from Reference Herron and LangwayHerron and Langway (1980). These equations are derived from Herron and Langway’s eqn (4a,b) by replacing dt with (ρA −1)dh. The density of pure ice ρ ice is derived from ρ ice = 917.13 kg m−3 − (T − 273.15 K) × 0.1307 kg m−3 K−1.The vertical depth interval is dh (m) and A is the accumulation rate (Mg m−2 a−1, i.e. mw.e. a−1). The rate constants are kI = 11 m2 kg−1 and kII = 575 m1.5 kg−1 a0.5, and R = 8.314 J K−1 mol−1 is the gas constant. The activation energy E given in Eqn (1) is a layer-specific property. E classical in Eqn (1) is taken from Reference Herron and LangwayHerron and Langway (1980) and is equal to 10 160 J mol−1 for ρ < 550 kg m−3 and 21 400 J mol−1 for 850 kg m−3 > ρ > 550 kg m−3. The HL approach assumes constant accumulation rate and temperature.
We introduce density variations into the model by modifying the initial density at the snow surface (z = 0 m) ![]() with a noise Δp(t) contribution, thus
with a noise Δp(t) contribution, thus
The stochastic component Δρ(t) is drawn as a Gaussian distribution with mean zero and standard deviation σρ surf. Simulating a density profile with varying surface densities in time results in a profile of varying density over depth. The resulting profile can be interpreted as a composite of density values from an array of profiles given by different surface densities that are constant over time. From Eqn (2a,b) the incremental densification dρ of a certain layer is linearly linked to the associated density and is not dependent on overburden pressure or the density history of other layers. This fact reflects the stationary character of the HL approach and tells us that the simulated density variations in the framework of the HL model tend to overestimate the influence of varying surface conditions.
Tuning of Impurity Sensitivity
Now we describe how to derive f
1 and the sensitivity factor β in f
2([Ca2+]) for the HL approach. Tables 1 and 2 provide information on the data used and the glaciological conditions at the drill sites. For simpler simulation, we choose total accumulated mass per area, i.e. a water-equivalent depth scale, as the independent parameter. Then, if the accumulation rate is constant, water-equivalent depth and time are linearly related. We choose a vertical resolution of 5 kg m−2, which corresponds to time-steps of 12–30 days. The simulations cover time periods of 400–1100 years to establish the whole firn column down to the firn–ice transition. Temperature and accumulation rate are kept constant over the whole simulation period. The model input data for the surface density (i.e. the mean density ![]() and its standard deviation σρ
surf used in Eqn (3)) are derived separately for each site from the measured density record of the uppermost 2 m. The input data of [Ca2+] are taken for each time-step from the depth-inverted data record measured by CFA on the specific firn-core site. The critical Ca2+ concentration [Ca2+]crit is set to the detection limit of the CFA system, noted as 0.5 ng g−1. Concentrations in the input data below the detection limit are set to this threshold value.
and its standard deviation σρ
surf used in Eqn (3)) are derived separately for each site from the measured density record of the uppermost 2 m. The input data of [Ca2+] are taken for each time-step from the depth-inverted data record measured by CFA on the specific firn-core site. The critical Ca2+ concentration [Ca2+]crit is set to the detection limit of the CFA system, noted as 0.5 ng g−1. Concentrations in the input data below the detection limit are set to this threshold value.
Table 1. Input data used in the simulations

Table 2. Applied methods of measured density and [Ca2+] records and their spatial resolution

In order to determine the best set of fitting parameters f 1 and β, we simulate the density profiles of both cores over a wide range of f 1 and β values. To compare the simulated and observed density profiles in terms of mean density evolution and density variability evolution, we calculate the rootmean-square error (RMSE) of the mean density (running mean over 2 m windows) and of the density variation (running standard deviation over 2 m windows) in the depth interval between 10 m and the end of the firn–ice transition (firn–ice transition is defined here as a 15 m band either side of the depth where the mean density reaches 825 kg m−3). The firn–ice transition for B29 occurs at 63 m depth, equivalent to 42 mw.e., and the firn–ice transition for B32 is at 87 m depth, equivalent to 55 m w.e. As a first step, a range of sensible parameters was determined. Then, within this range, we simulated for each core the density profiles for the parameter sequences space f 1 = [0.98, 0.985, … ,1.1] and β= [0, 0.0005, …, 0.0180], which results in 925 simulations for each core. In all simulations [Ca2+]crit was set to 0.5 ng g−1. The plot of how RMSE varies with f 1 and β, displayed in Figure 1, shows which combination of these parameters leads to the most realistic simulations.

Fig. 1. Contour plots of the RMSE (kg m−3) between modelled and measured mean density (a, c) and RMSE between modelled and measured density variations (b, d) over the firn columns between 10 and 70 m for B29 and between 10 and 94 m for B32. The best model realization is obtained for both core sites when f 1 = 1.025 and β = 0.010 (the point where the dotted lines cross in (b) and (d)).
We find that small-scale density variations are well represented in the model when β = 0.010 at both firn sites (Fig. 1b and d). β is almost independent of f 1. Changes of ±20% in β double the deviation between model and measurement. The mean density depends mainly on the choice of f 1, with a slight improvement given by a small change of β (Fig. 1a and c). Since the impurity effect acts positively on the densification rate by reducing the activation energy, with separate influence of β (if [Ca2+] > [Ca2+]crit then f 2 < 1), it is expected that f 1 is slightly larger than 1 to balance the net effect of [Ca2+] on densification. This is consistent with the best-fitting parameter set, which is f 1 =1.025 and β = 0.010, from simulating the small-scale density variations (cross-hairs in Fig. 1 b and d).
Figures 2 and 3 display the simulated profiles for B29 and B32 using the best-fitting parameter set f 1 =1.025 and β = 0.010. The modelled mean density and the small-scale density fluctuations are surprisingly well reproduced by the model, and even details of the density variability at the firn– ice transitions are reproduced. It is evident that the classical HL model overestimates the densification for B32. The tendency of the classical HL model to overestimate densification at cold sites has already been pointed out by Reference Hörhold, Kipfstuhl, Wilhelms, Freitag and FrenzelHörhold and others (2011). The modified HL model simulates the mean density profile for the cold site B32 much better than the classical approach. The density variability simulated by the modified HL model shows the typical behaviour of layer-specific densification: it decreases in the upper firn down to about 10–20 m depth, with a pronounced increase for deep firn, followed by a further decrease below the firn–ice transition. In the model, this behaviour is caused by the successive impact of the impurities on the density profile of deep firn. Layers with high impurity concentration densify faster than layers with low impurity concentration, leading to a density variability that is almost completely driven by [Ca2+] variations in deep firn. It is interesting to note that variations on the metre scale observed in the density variability profiles are also visible in the simulated density profiles (arrows in Figs 2a and 3a). This can be explained by anomalies of the seasonal [Ca2+] at the specific sites.

Fig. 2. Application of the firn model to the Greenland firn core B29. Measured (black curves) and modelled (red curves) evolution of the (a) density variability and (b) mean density over depth (w.e.) calculated in a running window of 2 m width. Vertical grey dotted lines indicate beginning and end of the pore close-off region. Simulations with the classical HL model are added as blue curves for comparison. (c) Measured and modelled density in the close-off region at the firn–ice transition. The modified HL model is run with f 1 =1.025 and β = 0.010.

Fig. 3. Application of the firn model to Antarctic firn core B32. Measured (black curves) and modelled (red curves) evolution of the (a) density variability and (b) mean density over depth (w.e.) calculated in a running window of 2 m width. Vertical grey dotted lines indicate beginning and end of the pore close-off region. Simulations with the classical HL model are added as blue curves for comparison. (c) Measured and modelled density in the close-off region at the firn–ice transition. The modified HL model is run with f 1 =1.025 and β = 0.010.
Discussion
The new densification models enable us to simulate the mean density together with the density layering in modern polar firn. It is interesting to note that the modified HL model is able to simulate the mean density at warm and cold sites, whereas the classical model fits only the data for relatively warm sites (Figs 2 and 3). The classical HL model overestimates densification for cold sites because it uses an activation energy that is calibrated mostly on warmer sites with high impurity load. The impossibility of the classical HL approach simulating the mean density profiles for sites over the whole temperature range (and impurity range) points to the significant impact of impurities on the mean values of density in recent firn. The vertical shift of the firn–ice transition is ∼10 m. Unlike the approaches of Reference Arthern, Vaughan, Rankin, Mulvaney and ThomasArthern and others (2010) and Reference Zwally and LiZwally and Li (2002), the simulated density profiles agree well with observations over the whole firn column for both sites. In particular, they reproduce the density variability at the firn–ice transition and exhibit the typical behaviour of the density variability with the rapid decrease in the upper firn followed by a slight increase of density variability down to the firn–ice transition (Reference Hörhold, Kipfstuhl, Wilhelms, Freitag and FrenzelHörhold and others, 2011).
The good agreement is strong support for the hypothesis that impurities control densification in deep firn. In the model, it is assumed that impurities act like a catalyst and reduce the activation energy for processes causing enhanced deformation. Owing to the seasonal variability in the impurity content, layers of varying softness develop in the firn column on the centimetre scale. This results in unexpected large density variations in deep firn and an increasing synchronization between density and impurity content with depth (Reference Hörhold, Laepple, Freitag, Bigler and Fischer Hand KipfstuhlHörhold and others, 2012).
The impurity effect in the models, parameterized by the Ca2+ concentration, is motivated by the observed link between density and the Ca2+ concentration in deep firn. B29 and B32, with relatively large differences in the mean impurity concentration (factor of 5 in mean [Ca2+]; Table 1), show surprisingly little difference in the density variability at the firn–ice transition, indicating a sensitivity of the densification to the impurity concentration over several orders of magnitude. Therefore, the impurity effect is introduced in the present model as a function of the natural logarithm of Ca2+ concentration. The model reproduces most density variations in deep firn by using the Ca2+ concentration as proxy for the impurity effect (Figs 2 and 3). The agreement, even in detail, is excellent, although the model is driven by only one species out of a large variety of impurities found in polar ice (e.g. Reference Sommer, Wagenbach, Mulvaney and FischerSommer and others, 2000). From the overall good agreement of seasonal density variations on the centimetre scale we can exclude a strong influence of impurity species, with phasing in their seasonal deposition different from Ca2+.
The new densification models are based on the classical approaches from HL and PB and adopt all rate constants that have been derived from fitting the observed mean density profiles. By introducing f 2 as the component that describes the influence of impurities on densification, it becomes necessary to add a second parameter f 1 for readjusting the mean density profiles to the measured data. The best adjustment was achieved for f 1 = 1.025, indicating uniform rate constants for pure firn at both sites (Fig. 1). However, this conclusion is based only on two firn cores. Following the approach of Reference Arthern, Vaughan, Rankin, Mulvaney and ThomasArthern and others (2010), which combined densification with grain growth, one could also imagine that f 1 could mimic different initial grain sizes at different sites. However, there is no literature demonstrating that grain size varies on the seasonal scale. This aspect needs to be resolved in future by high-resolution grain-size measurements.
A critical aspect in deriving the model parameters is the limited data basis of only two firn cores and the measurement accuracy of the available data that we use to run and calibrate the model. One of the main difficulties is the limited accuracy of the Ca2+ concentration measurement. In our approach we handle the problem by introducing a critical concentration [Ca2+]crit of 0.5 ng g−1 for the impurities catalysing densification. It is unclear whether this threshold is realistic, but due to the 0.5 ng g−1 detection limit of our dataset we are not able to investigate the influence of [Ca2+] on densification lower than [Ca2+]crit. Therefore, the parameterization presented in Eqn (1) is restricted to sites with firn layers of impurity content larger than [Ca2+]crit. Another difficulty is the smoothing of the [Ca2+] records. The smoothing, caused by the CFA measurement system, is due to dispersion in the analytical unit and by capillarity and cohesion effects in the porous firn at the melting head. It can be of the order of centimetres, close to the size of single firn layers. As a consequence, concentration peaks or minima or fast transitions are heavily smoothed out, which we did not consider explicitly in our analysis. The diffusion of impurities within the firn and ice matrix is negligible on the timescale of the densification process (Reference Rempel, Waddington, Wettlaufer and WorsterRempel and others, 2001). Direct evidence for almost zero diffusion comes from the [Ca2+] record itself. There is no significant change of the spectral energy in the seasonal band of the [Ca2+] profile with depth (Reference Hörhold, Laepple, Freitag, Bigler and Fischer Hand KipfstuhlHörhold and others, 2012).
Densities measured by gamma-ray absorption also have intrinsic sources of uncertainty. We therefore relied on density measurements derived by radioscopic imaging techniques for B32 (Reference Freitag, Kipfstuhl and LaeppleFreitag and others, 2013). Differences in depth assignments between the [Ca2+] and density records of the order of millimetres to centimetres are not critical because the comparisons between model and measured data are performed on calculations of density variations in 1–2 m intervals.
Conclusion
We have presented densification models for layered firn that account for the impurity effect on densification. The new models simulate the density profile and the layering in seasonal resolution down to the firn–ice transition. The impurity effect has been introduced into two widely used firn models (Herron–Langway and Pimienta–Barnola) as additional terms in the Arhenius-type activation energy, using the Ca2+ ion concentration as proxy for the impurity content. Impurities reduce the activation energy for deformation and soften the firn, resulting in faster compaction. For modelling densification of layered firn, the Ca2+ ion concentration with a seasonal resolution is required as an additional input parameter.
The modified HL and PB models have been applied to one site on Greenland (B29) and one on the Antarctic plateau (B32) using available high-resolution Ca2+ ion records to find the best parameterizations. Although the two sites differ substantially in mean impurity concentration, the same parameterization of the impurity effect was found to match each core. Modelled and measured densities at the firn–ice transition show excellent agreement even in seasonal resolution. The new models require the Ca2+ ion concentration records as input parameter, which are usually available for deep ice cores. Therefore, the new model approach offers an important tool for investigating the impurity effect on densification under glacial climate conditions where the impurity load is 10–100-fold increased. It will lead to a better understanding of the processes controlling pore close-off of air and air entrapment in layered firn and to more realistic estimates of the gas ice age difference in polar ice cores. It seems that nature provides a simple way to simulate stratigraphy of polar firn during past climates by knowing only the small-scale variations of Ca2+ ion concentration within the ice.
Acknowledgements
We thank Maria Hörhold and Anna Wegner for interesting discussions about layering and impurities. Thomas Laepple was supported by the Daimler and Benz Foundation. We are grateful for improvements suggested by F. Ng and L.W. Morland.
Appendix
The Pimienta–Barnola model (PB model) is now modified similar to the above HL model modification by using Eqn (1) to introduce the dependence of activation energy on impurities. The differential equations that describe densification are Eqn (2a) for ρ < 550 kg m−3 and
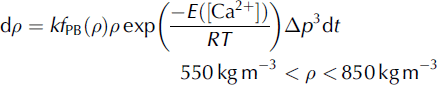
with the rate constant k = 2.54 × 104 MPa−3 s−1 and
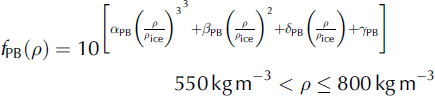
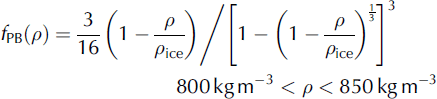
taken from Reference Barnola, Pimienta, Raynaud and KorotkevichBarnola and others (1991), with α PB = −29.166, β PB = 84.422, δ PB = −87.425 and γ PB = 30.673. The values for the activation energy E classical in Eqn (1) are 10 160 J mol−1 and 60 000 J mol−1 for densities below and above 550 kg m−3, respectively. Δp (Pa) is the effective pressure, i.e. overburden pressure minus the bubble pressure.
Sensitivity tests performed for B29 and B32 yield best agreements between measured and modelled density with β = 0.0105 and f 1 = 1.015 when [Ca2+]crit = 0.5 ng g−1 remains constant. There is a small trend for f 1 to decrease at sites with lower temperature (<1% over 20 K). The impurity-sensitive function f 2([Ca2+]) for the modified PB approach is almost the same as that for the HL approach. The general features of the profiles are similar, although the density variations derived from surface variations in the lower firn decrease much faster, with a stronger minimum at 20–30 m depth than observed in the field. In the deep firn the density variations increase continuously down to the firn–ice transition, as is also found in the observed density profiles.







