1. INTRODUCTION
Supraglacial deposits of rock particles strongly influence glacier energy and mass balance. Thin layers of a few millimetres tend to increase surface ablation but thicker layers are known to have an insulating effect (e.g. Mattson and others, Reference Mattson, Gardner and Young1993). This implies that the modification of glacier surface ablation by a supraglacial particle layer shows a characteristic variability according to layer thickness (Adhikary and others, Reference Adhikary, Nakawo, Seko and Shakya2000): Starting from uncovered conditions, the surface ablation increases with increasing thickness of the particle layer until the so-called effective thickness is reached. At this thickness, the ablation underneath the particle cover shows a maximum. Beyond it, the ablation decreases with increasing particle-layer thickness. The so-called critical thickness is reached where surface ablation is again equal to uncovered conditions. With further increasing particle-layer thickness, surface ablation is more and more reduced with an asymptotic behaviour towards zero.
This characteristic pattern of ablation changes with varying particle-layer thickness is governed by two counteracting processes. First, there is the reduction of albedo induced by the particle cover (Warren and Wiscombe, Reference Warren and Wiscombe1980) and the resulting increase of absorbed global radiation and available melt energy. Second, there is the thermal resistance of the particle layer and the resulting decrease of heat conduction towards the glacier surface (Nicholson and Benn, Reference Nicholson and Benn2006).
The reduction of albedo only occurs over the first few millimetres of layer thickness. Starting from uncovered conditions, albedo shows a continuous decrease with increasing particle deposition until a continuous coverage of the glacier surface by the deposited particles is reached. Thin deposits with thicknesses below the surface roughness of the glacier cannot exist in the form of such a continuous layer. Particle migration on the microscale leads to the formation of aggregates in hollows at the expense of particles on the ridges between the hollows (Conway and others, Reference Conway, Gades and Raymond1996). This process creates bare-ice outcrops on the microscale across the deposited particle layer (Fig. 1). As the roughness length of snow and glacier-ice surfaces usually lies in the range of up to a few millimetres (Brock and others, Reference Brock, Willis and Sharp2006), a completion of the albedo decrease can thus not be reached until the particle deposit exceeds this thickness. Beyond, the albedo does not show any further dependency on increased particle-layer thickness (Bozhinskiy and others, Reference Bozhinskiy, Krass and Popovnin1986).
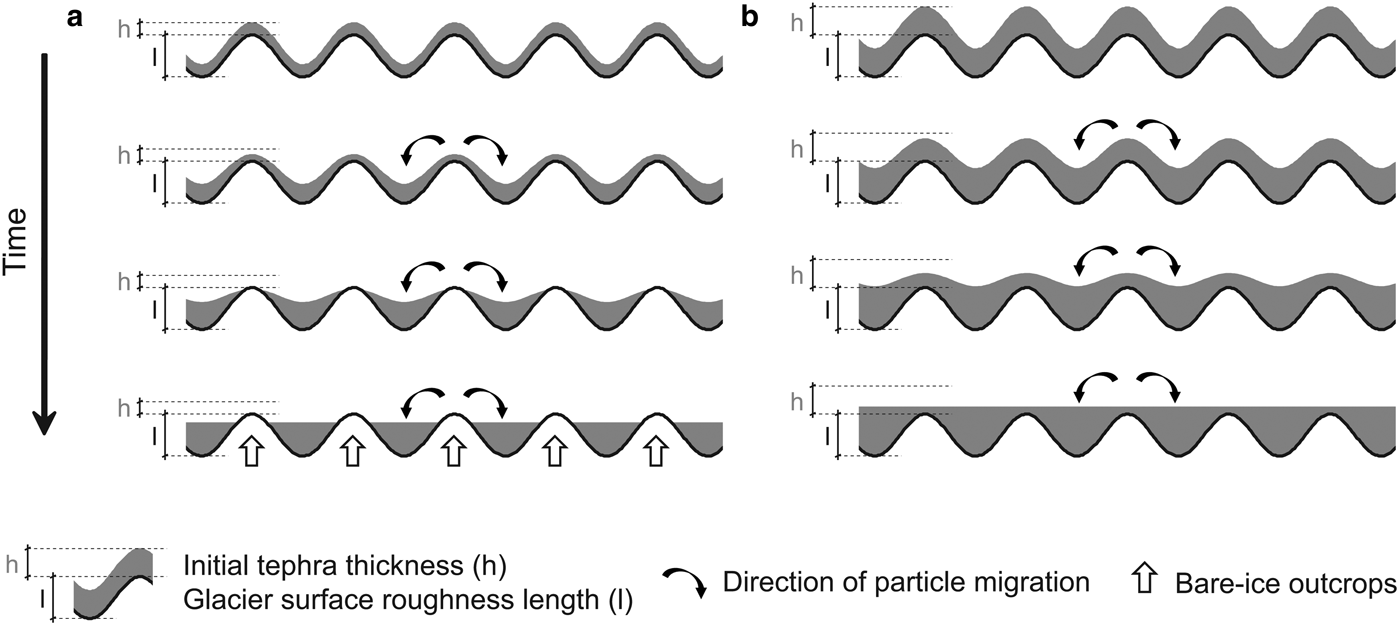
Fig. 1. Schematic overview of the relationship and interaction between tephra-deposition thickness, glacier surface roughness length and particle migration on the microscale for a thin tephra deposit (a) and for a thick tephra deposit (b). The formation of bare-ice outcrops throughout thin tephra deposits is indicated in the left panel.
Thermal resistance increases with particle-layer thickness. The rate of increase shows a turning point when the layer thickness exceeds the roughness length of the glacier surface. Layers with lower-millimetre scale thicknesses (thicknesses below ~4–5 mm) do not show continuous particle coverage. The integrated thermal resistance over a given surface is thus substantially lowered by bare-ice outcrops. Therefore, the increase of thermal resistance with thickness is nonlinear over this range and depends on the microscale relief of the glacier surface (Fig. 1). Not until a continuous coverage is reached does the thermal resistance start to increase at higher rates and proportionally to layer thickness.
For layers below the critical thickness, the increase in melt due to additionally absorbed energy resulting from decreased albedo overcompensates for the reduction in melt through limited heat conduction. Hence, the albedo effect outweighs the thermal-resistance effect until the critical thickness is reached and vice versa beyond it. Due to the strongly differing evolution of the magnitudes of both effects over the lower-millimetre scale the prevalence of the albedo effect over the thermal-resistance effect shows a discrete maximum, which leads to the formation of a positive peak in glacier melt under a particle cover with the so-called effective thickness.
The described characteristic pattern shows substantial differences depending on the type of material, i.e. erosion- or weathering-produced supraglacial debris or volcanic tephra deposits (Mattson and others, Reference Mattson, Gardner and Young1993; Kirkbride and Dugmore, Reference Kirkbride and Dugmore2003; Richardson and Brook, Reference Richardson and Brook2010). Both effective and critical thicknesses of volcanic tephra deposits are distinctly smaller when compared with those of moraine debris, because of their distinctly lower thermal conductivity (Clauser and Huenges, Reference Clauser, Huenges and Ahrens1995; Brock and others, Reference Brock, Rivera, Casassa, Bown and Acuña2007). Moreover, tephra deposits show smaller and more homogeneous grain sizes than moraine debris and a continuous coverage of the glacier surface already occurs under smaller thicknesses.
Studies related to supraglacial particle covers have either focused on the influence of extremely thin, sub-millimetre to millimetre scale atmospheric black carbon deposition (e.g. Ming and others, Reference Ming2009; Xu and others, Reference Xu2009; Yasunari and others, Reference Yasunari2010; Brandt and others, Reference Brandt, Warren and Clarke2011; Hadley and Kirchstetter, Reference Hadley and Kirchstetter2012; Jacobi and others, Reference Jacobi2015) or on the influence of thick, decimetre to metre scale moraine-debris coverage (e.g. Reznichenko and others, Reference Reznichenko, Davies, Shulmeister and McSaveney2010; Yang and others, Reference Yang, Yao, Xu and Zhou2010; Nicholson and Benn, Reference Nicholson and Benn2013). In general, the modification of glacier surface ablation by these types of supraglacial particle layers can be quantified by two different approaches. These are either statistics-based models that parameterize the impacts of particle covers on the basis of empirical data (Hagg and others, Reference Hagg, Mayer, Lambrecht and Helm2008; Lambrecht and others, Reference Lambrecht2011; Juen and others, Reference Juen, Mayer, Lambrecht, Han and Liu2014) or physics-based models that explicitly consider the heat conduction through the particle layer down to the glacier surface (Nicholson and Benn, Reference Nicholson and Benn2006; Brock and others, Reference Brock2010; Reid and Brock, Reference Reid and Brock2010; Reid and others, Reference Reid, Carenzo, Pellicciotti and Brock2012).
The statistics-based approaches use few meteorological data as input, but require extensive empirical calibration for each specific particle layer and target location (e.g. Mayer and others, Reference Mayer2010). Their main challenge is to establish functions that can be extrapolated beyond the specific particle covers and study sites used during calibration. Hence, most of these models only describe ablation under discrete particle thicknesses (e.g. Kayastha and others, Reference Kayastha, Takeuchi, Nakawo and Ageta2000) or use manually fitted splines for extrapolation over varying thickness (e.g. Lambrecht and others, Reference Lambrecht2011). Descriptions of the variability of model parameters with particle thickness that follow real mathematical functions are scarce though (e.g. Hagg and others, Reference Hagg, Mayer, Lambrecht and Helm2008). Moreover, existing statistical approaches only rely on air temperature forcing. Temperature index approaches that are extended by the incorporation of dedicated radiation terms have so far not been used for modelling of ablation under supraglacial particle deposits. The physics-based approaches, in contrast, demand a broad set of meteorological data and require data for albedo and thermal conductivity of the particle layer. Minimal physics-based models with only surface temperature instead of comprehensive meteorological data as input have also been presented (e.g. Han and others, Reference Han, Ding and Liu2006).
Volcanic tephra deposits differ significantly from deposits of atmospheric black carbon or moraine debris, as their thickness shows high spatial variability and ranges over several orders of magnitude (Brown and others, Reference Brown, Bonadonna and Durant2012). Areas close to the eruption site are covered by thick, metre scale layers, whereas areas farther away tend to be covered by thinner, millimetre to sub-millimetre scale layers. Supraglacial tephra layers thus span the ranges of thickness of both moraine debris and atmospheric black carbon in only one type of deposit. Moreover, their influence on albedo shows high spatiotemporal variability (Möller and others, Reference Möller2014). Estimations of the impact of volcanic ash fallout on glacier energy and mass balance are thus much more challenging than comparable calculations related to morain-debris deposits and few studies have explicitly addressed this topic so far (e.g. Driedger, Reference Driedger, Lipman and Mullineaux1981; Kirkbride and Dugmore, Reference Kirkbride and Dugmore2003; Brock and others, Reference Brock, Rivera, Casassa, Bown and Acuña2007; Richardson and Brook, Reference Richardson and Brook2010; Nield and others, Reference Nield2013).
All of these studies rely on natural tephra covers with the variability of thicknesses being determined by the deposition processes. Only a recent study by Dragosics and other (Reference Dragosics2016), which investigated the influences of ash from the 2010 Eyjafjallajökull eruption on ice ablation in a laboratory experiment, is based on preselected deposition thicknesses. The latter has the advantage that thicknesses can be chosen such that they facilitate a better model fitting. This means using a higher frequency of different thicknesses in the lower-millimetre scale, where substantial variability in tephra-induced ablation changes can be expected.
Here we present results of a field experiment (Fig. 2) in which we investigated the impact of tephra from Grímsvötn volcano, Iceland, on glacier ablation. The experiment was carried out on a natural, bare-ice glacier surface over a 2-week period. It comprised daily ablation measurements over a set of 13 tephra plots with specifically chosen thicknesses along with meteorological measurements at an automatic weather station (AWS). Based on this experiment we calibrate three different types of ablation models, i.e. a temperature-index model, a temperature/net shortwave radiation-index model and a partly energy-balance-based model. In order to be able to apply our models also for unstudied deposition thicknesses, all model parameters are described as mathematical functions of tephra-layer thickness. Moreover, we apply a cross-validation-based model calibration, which further helps to facilitate extrapolation.

Fig. 2. Overview map showing the site of tephra sampling at Grímsfjall and the site of the field experiment on Svínafellsjökull (a). The field experiment itself is shown as photography (b) and schematic plot (c). The plot numbers corresponds to those given in Table 1. Unnumbered plots are covered by a different tephra type and are not considered in this study.
We treat our choice of models as exemplary. The majority of the proposed formulations for modelling of ablation under particle deposits uses either temperature-index formulations or relies on some type of energy-balance calculation. Hence, these two types of models represent the current state of the art. Our third type of model, the temperature/net shortwave radiation-index model, has, however, never been used in this context before, even if it is known to yield substantially better results in calculating bare-ice ablation than simple temperature-index formulations (e.g. Hock, Reference Hock2003). We intend to test whether this known predominance also holds true for sub-tephra ablation modelling. In addition, we evaluate to which extent a partly physics-based approach is able to cope with the inhomogeneity of thickness in the lower-millimetre scale. Finally, we intend to answer the question: which type of approach best reproduces surface-ablation variability underneath millimetre to decimetre scale tephra deposits.
2. DATA AND METHODS
We investigated the influence of different thicknesses of supraglacial tephra coverage on glacier surface ablation in a field experiment (Fig. 2). This experiment was conducted on Svínafellsjökull, an outlet glacier of the southern Vatnajökull ice cap, Iceland, in May 2013. Tephra from Grímsvötn volcano was spread out over plots on the glacier surface. Ablation was measured on a daily basis. Meteorological data were recorded by an AWS setup next to the experimental site.
Based on the results of the field experiment two empirically based ablation models and one partly physics-based ablation model were developed and calibrated. Two of these models use daily albedo of the tephra as input data. The time-varying albedo was derived from measurements and on the basis of image analysis from terrestrial photography.
2.1. Field experiment
The field experiment (Fig. 2) was set up at an altitude of 140 m a.s.l. close to the lower margin of the tongue of Svínafellsjökull (63°59.55′N, 16°52.34′W), southern Iceland, on 17 May 2013. The exact experiment site was carefully chosen such that it features a flat, bare-ice surface characterized by a homogeneous surface microstructure and homogeneous natural dirt content. The tephra was from Grímsvötn volcano. It was collected about 1 week before the start of the experiment from an active geothermal site at Grímsfjall (1585 m a.s.l.), a region of rocky outcrops at the southern caldera rim of Grímsvötn volcano located in the western central part of Vatnajökull ice cap (64°23.64′N, 17°19.33′W). Its bulk density was determined to be 850 kg m−3. Grain sizes concentrate on the fractions below 5 mm, but few grains even reach the lower-centimetre scale.
A set of 12 plots of volcanic tephra with coverage thicknesses between 0.5 and 100 mm (Table 1) was prepared along with one uncovered plot for reference measurements. The plots were quadratic in shape with a footprint of 0.25 m2. The uniform dispersal of the tephra on the plots was carried out by hand and on the basis of weight by applying the measured bulk density as conversion factor (Table 1). On the lower-millimetre scale plots uniformity was ensured by visual inspection only, as no depth measurements were possible. On the upper millimetre and centimetre scale plots depth measurements were carried out to ensure uniform dispersal. Bare-ice outcrops were frequently present throughout the plot areas on plots with low tephra thickness (Fig. 2) because the grain-size distribution of the tephra material limited the possibility of a spatially homogeneous dispersal.
Table 1. Overview on thickness and mass of the tephra that was manually distributed over the plots
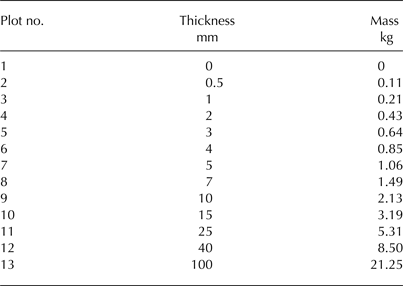
The conversion factor between both quantities is the measured bulk density of the Grímsvötn tephra (850 kg m−3). The plot numbers correspond to those given in Figure 1.
Next to the plots, an AWS was set up and configured for recordings at every 10 min (Fig. 3). Air temperature was measured at an accuracy of ± 0.9°C using a Campbell Scientific Ltd. CS215 air temperature and relative humidity probe mounted in a non-ventilated radiation shield. Incoming and reflected shortwave radiation was measured at an accuracy of ± 5% using a Kipp and Zonen CNR1 net radiometer that allows for separate measurement of shortwave and longwave downward and upward radiation fluxes. Total precipitation was measured with a manual rain gauge.

Fig. 3. Air temperature, global radiation and albedo measured at the AWS at the field experiment site. Measurement period is 16 May, 17:10 to 30 May, 8:00. Temporal resolution of the records is 10 min.
The experiment site was visited daily until 30 May, resulting in 13 ablation measurement intervals. Manual ablation measurements on the 13 plots were carried out at irregular times during the days of visit. This induces varying lengths of the measurement intervals (Table 2). Each plot was measured at 25 predefined points across a regular 5 × 5-point network in order to account for potential inhomogeneity within the tephra-cover thickness. This network omits the outer 9 cm of each plot in order to avoid the measurements to be influenced by potential marginal collapses of the tephra coverage. The inner part of each plot covered by the measurement network, we call the measurement region. To assure the spatial regularity of the measurements, light grey, low-conductivity plastic tubes were drilled into the ice at the four corners of each plot during initial deployment of the experiment site and an auxiliary frame was temporarily mounted on these tubes each time the measurements were performed. The daily ablation rate was calculated as the mean of all 25 individual readings.
Table 2. Overview of the length of the measurement intervals and the associated meteorological variables
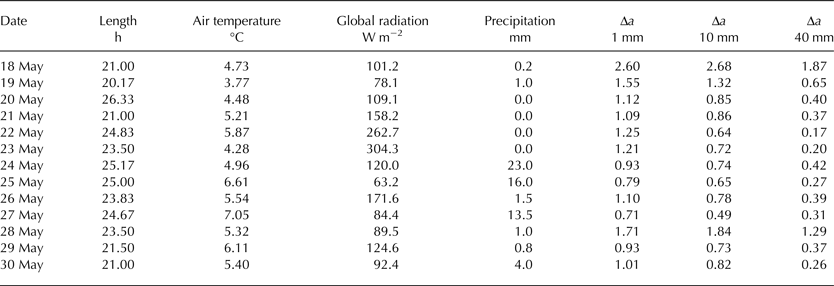
The values of air temperature and global radiation are given as means, those of precipitation as totals. Values of relative ablation changes (Δa; compared with bare-ice conditions) are shown for the effective thickness (1 mm), the critical thickness (10 mm) and an insulating thickness (40 mm). The dates given indicate the end of the respective measurement intervals.
Over the experiment period, we regularly observed homogeneous ablation at the 25 measurement points on each plot. This indicates that potential influences on ablation from outside the plots that might have disturbed the accuracy of our measurements had been small. Hence and despite the rather small plot sizes, our measurements can be seen as reliable. Nevertheless, since the experiment was based on an artificial setup, representativeness or any possibility of extrapolation cannot be deduced.
2.2. Albedo calculation
The albedo of the tephra plots was calculated from shortwave radiation measurements and with the help of 10-megapixel digital images. Nadir viewing shots of the plots from similar heights were taken during each visit of the field-experiment site. The images were stored as colour JPG files in the camera. Later, three steps of post-processing were carried out. First, each image was converted into an 8 bit greyscale TIF file. Second, the image was masked to the measurement region of the respective tephra plot. In cases where shadows of the plastic tubes at the corners of the plots were present, these were masked out, too. Third, Otsu thresholding (Otsu, Reference Otsu1979) was used for binarization of the masked greyscale TIF file, i.e. for discrimination between tephra-covered surface parts of the plot and surface parts showing bare glacier ice. This procedure makes use of the internal similarity of the greyscale values of both, tephra coverage and bare glacier ice.
Based on each binary image, the albedo of the plot can be calculated as the weighted mean of the bare-ice albedo and the tephra albedo. Weighting is done according to the numbers of bare-ice and tephra pixels. The time-varying bare-ice albedo was calculated from measurements of incoming and reflected shortwave radiation at the AWS (Fig. 3). The fixed albedo representing a continuous coverage by the Grímsvötn tephra was obtained from a net shortwave radiation measurement carried out for a completely tephra-covered plot. Two different values, one for dry tephra (0.19) and one for wet tephra (0.11) were determined. The former was applied in albedo calculations for rainless days, while the latter was applied for days with rainfall.
The method of albedo determination was applied for plots with thin tephra deposits (0.5–5 mm). For the thick tephra deposits (7–100 mm) the fixed albedo values of dry or wet tephra were used.
2.3. Model descriptions
The ablation under tephra coverage of varying thickness is modelled by three different formulations of varying complexity. Model 1, a pure temperature-index model, is the most basic one. Model 2 is a temperature/net shortwave radiation-index model and can be seen as an extended and advanced version of model 1. Model 3 extends beyond the purely parameterizing model formulations and is based on a partly physics-based approach that explicitly considers heat conduction through the tephra deposit.
All models predict ablation per day. As the intervals between two measurements in the field experiment are, however, of varying length (20–26 h), all model inputs and parameters are linearly scaled to represent a full 24 h day.
2.4. Temperature-index model
The pure temperature-index model (e.g. Ohmura, Reference Ohmura2001; Hock, Reference Hock2003) parameterizes the daily ablation (a) under the various tephra covers as a function of daily average air temperature (T) according to:
The empirical parameter in this formulation, the temperature factor (f T1), is described as a function of tephra thickness (h). To establish this function, f T1 was first calculated separately for each plot from the 12 daily ablation measurements and the mean air temperatures over the respective measurement intervals (cf. Table 2), using linear regression.
The relation between tephra thickness and the temperature factor is then described as an exponential decay function given by:
The empirical parameters of this function (a 1, b 1, a 2, b 2) were calibrated using least-squares fitting (Fig. 4). In the fitting procedure, only plots with given tephra cover are considered. The temperature factor of the uncovered bare-ice plot is calibrated independently. It corresponds to a degree-day factor for glacier-ice surfaces.
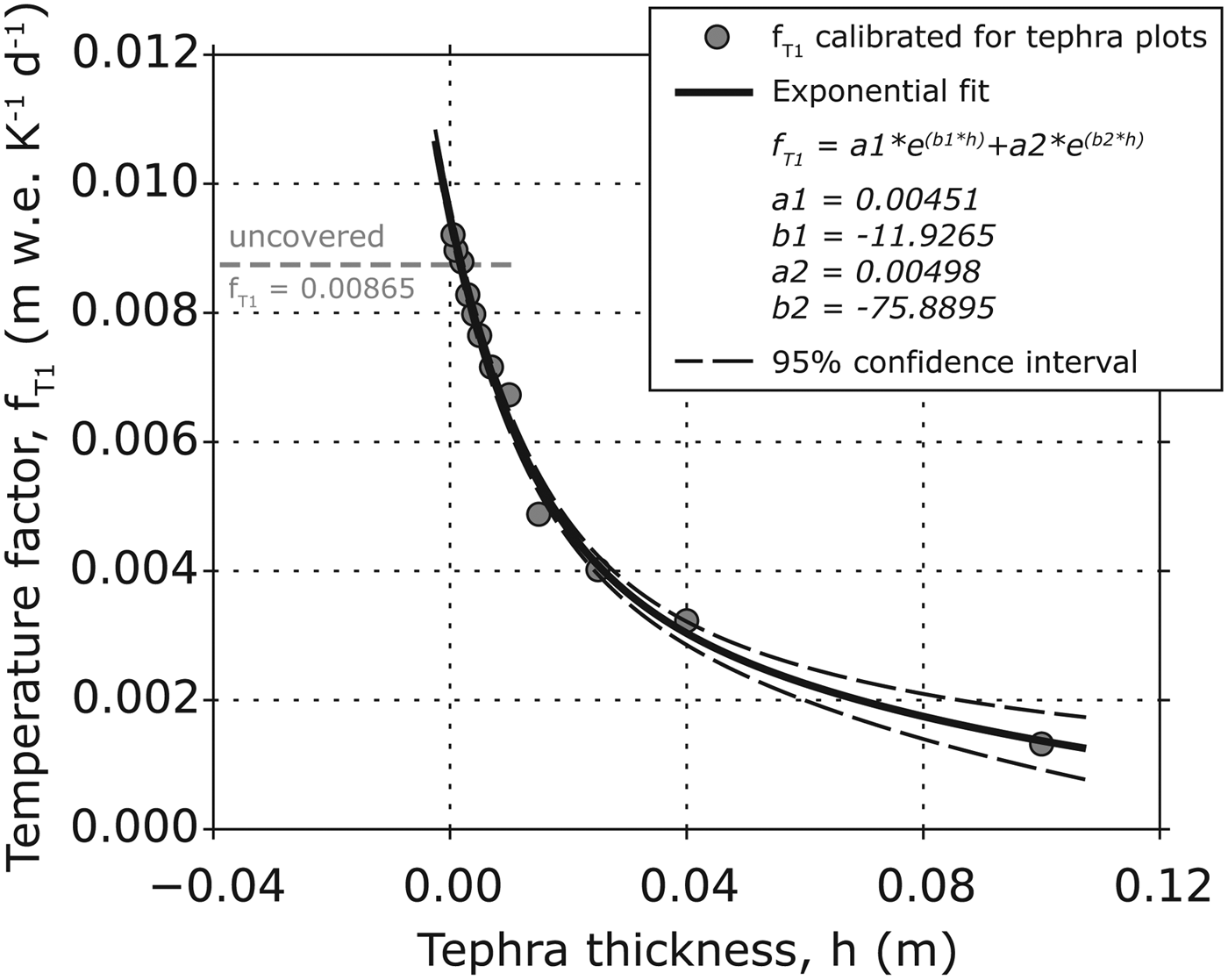
Fig. 4. Calibration results of the individual temperature factors f T1 of model 1 (grey circles) for the different tephra plots (indicated in form of varying tephra thickness) and the fitting of the related exponential decay function (Eqn (2)). The temperature factor for bare-ice conditions is additionally indicated by the dashed, grey line. Error bars indicating the spreads of the individual values of f T1 as they result from the different cross-validation runs are not shown because of their too limited extent.
2.5. Temperature/radiation-index model
The temperature/net shortwave radiation-index model parameterizes the ablation under the various tephra covers as a function of air temperature and net shortwave radiation. Thereby, the latter is expressed as a function of calculated albedo (α) and measured global radiation (R). This general type of ablation model was presented by Pellicciotti and others (Reference Pellicciotti2005) and has been successfully applied in other studies (e.g. Möller and others, Reference Möller, Finkelnburg, Braun, Scherer and Schneider2013). We here introduce an extended version of this model in order to account for supraglacial tephra coverage of variable thickness. Accordingly, ablation (a) is given as:
The empirical parameters in this formulation, the temperature factor (f T2) and the radiation factor (f R2), are both described as functions of tephra thickness. To establish these functions, the optimal combinations of f T2 and f R2 for the different plots were calibrated from the 12 daily ablation measurements and the mean air temperatures or mean net shortwave radiation fluxes over the respective measurement intervals (cf. Table 2). This was carried out by minimizing RMS errors between measured and modelled ablation.
As for the pure temperature-index model, the relations between tephra thickness and the empirically determined melt factors (f T2, f R2) are described by two different exponential decay functions that are given by:
The empirical parameters of these functions (a 3, b 3, a 4, b 4, a 5, b 5, a 6, b 6, c 1) were calibrated using least-squares fitting (Fig. 5). In the fitting procedures only plots with given tephra cover are considered. The temperature and the radiation factors of the uncovered bare-ice plot are calibrated independently.

Fig. 5. Calibration results of the individual temperature factors f T2 (a) and radiation factors f R2 (b) of model 2 (grey circles) for the different tephra plots (indicated in form of varying tephra thickness) and the fitting of the related exponential decay functions (Eqn (4)). The temperature and radiation factors for bare-ice conditions are additionally indicated by dashed, grey lines. The error bars extending the grey circles indicate the one-sigma spread of the individual values resulting from the cross-validation runs.
2.6. Partly physics-based model
In the partly physics-based model, the surface temperature of the tephra deposit (T s) is parameterized as an empirical function of air temperature and net shortwave radiation. Afterwards, the heat flux from the surface through the tephra deposit to the melting ice surface is calculated according to physical principles, following Nicholson and Benn (Reference Nicholson and Benn2006).
In the approach, the surface temperature is assumed to be given by:
This formulation uses the air temperature as a first approximation of the tephra surface temperature and corrects it by a radiation-based term that varies with tephra thickness. This variability is expressed by the empirical factor ω. It is calibrated as an exponential function of tephra thickness (Fig. 6) using least-squares fitting according to:
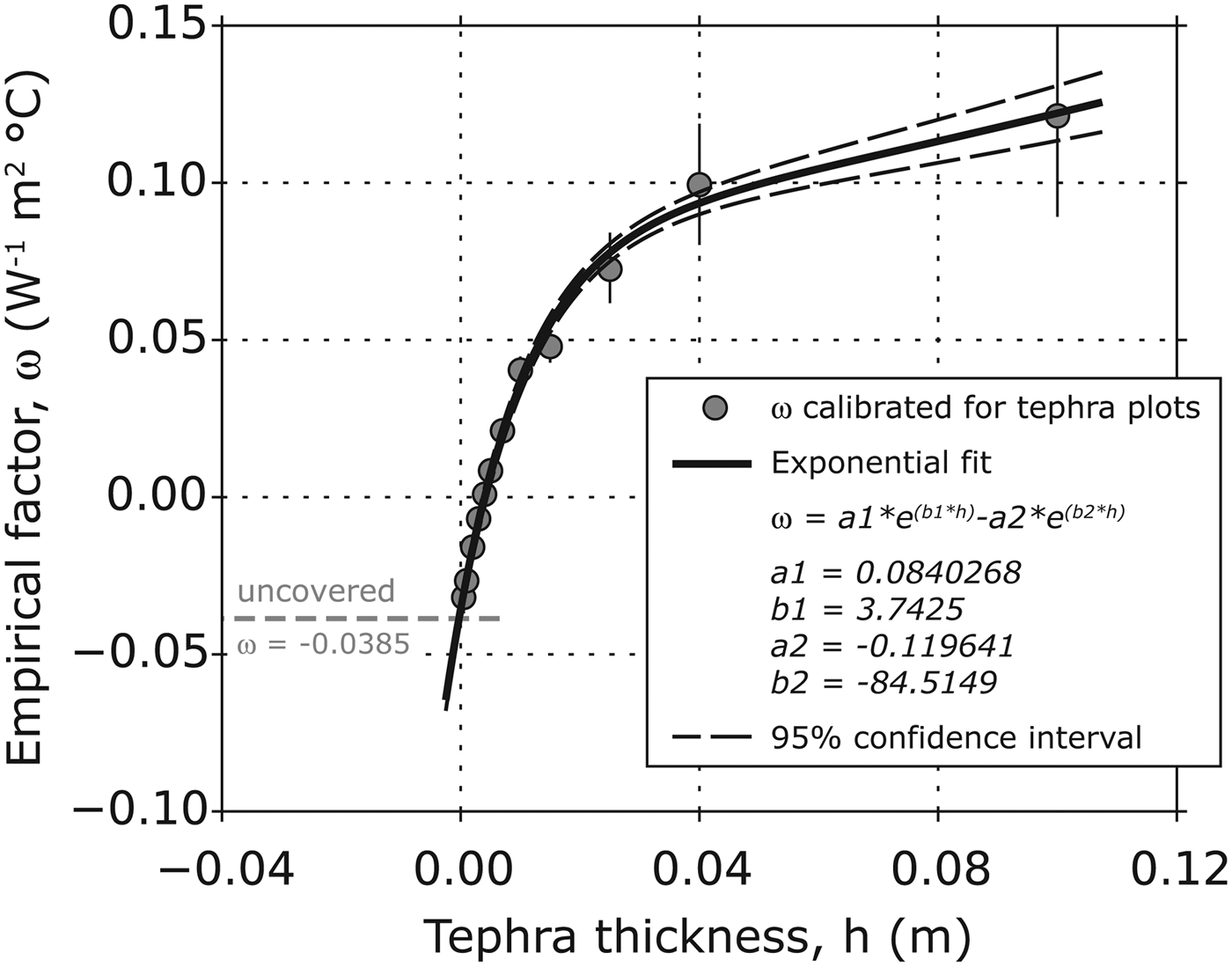
Fig. 6. Calibration results of the individual empirical factors ω of model 3 (grey circles) for the different tephra plots (indicated in form of varying tephra thickness) and the approximation of the related exponential fit (Eqn (6)). The empirical factor for bare-ice conditions is additionally indicated by the dashed, grey line. The error bars extending the grey circles indicate the one-sigma spread of the individual values resulting from the cross-validation runs.
By explicitly allowing ω(h) to become negative, it is possible to reduce the tephra-surface temperature with respect to air temperature if necessary. Based on the difference between the surface temperature and the temperature at the melting ice surface (T i = 0°C), the heat flux down to the ice surface is calculated according to:
The bulk thermal conductivity of the tephra (k = 0.104 W m−1 K−1) was determined from two different grain-size classes, i.e. 1–2 and 2–4 mm, using a TeKa TK04 thermal conductivity meter. Both measurements result in similar values of k.
Finally, ablation under the tephra deposit is calculated, considering the latent heat of fusion of ice (L f = 3.334 × 105 J kg−1) and the density of glacier ice (ρ i) according to:
Herein, we assume ρ i = 800 kg m−3 as a valid mean value for the density of glacier ice according to own measurements of near-surface conditions on Svínafellsjökull. The calibration of this approach, which is basically the calibration of ω(h), is done in an integrated manner for the entire model. First, the empirical factor ω is calculated separately for each plot from the 12 daily ablation measurements, the mean air temperatures and the mean net shortwave radiation fluxes over the respective measurement intervals (cf. Table 2) by minimizing the RMS errors between measured and modelled ablation. Afterwards, the relation between tephra thickness and the empirically determined factor ω is calibrated, using least-squares fitting. The empirical factor for the uncovered bare-ice plot is calibrated independently.
2.7. Calibration and cross-validation
In order to ensure transferability and to allow for an independent validation despite the temporally limited dataset, the model calibrations are done using k-fold cross-validation techniques (Kohavi, Reference Kohavi1995; Möller, Reference Möller2012). Therefore, the ablation dataset is divided into k = 13 daily subsets. Afterwards, the calibration procedures of all three models are repeated 13 times, iteratively leaving out one daily subset. Each calibration run is thus based on only 12 daily subsets but is validated against the 13th daily subset, which was left out.
As a result, we obtain 13 different values for f T1 (model 1), for f T2 and f R2 (model 2) and for ω (model 3) at each of the field-experiment plots. Further, we obtain 13 different calibrations of the exponential decay functions describing the variability of these model parameters with tephra thickness. Finally, the overall calibrations are derived by averaging the results of all 13 cross-validation runs. The associated standard deviations are taken as measures of uncertainty.
3. RESULTS AND DISCUSSION
3.1. Field experiment
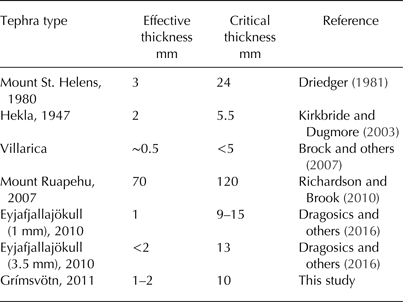
The observed changes of ablation due to influences of different thicknesses of tephra coverage (Fig. 7; Table 2) show substantial temporal variability but overall follow the pattern identified in previous studies (e.g. Mattson and others, Reference Mattson, Gardner and Young1993). The field experiment revealed an effective thickness of the Grímsvötn tephra of 1–2 mm, while the critical thickness was found to be ~10 mm. Beyond this value a continuous decrease of ablation rates with increasing tephra thickness was evident. This finding is in accordance with most of the few values so far reported for Icelandic and other tephras (Table 3). The effective thicknesses documented in the literature correspond well with each other and with our results. All values except for a volcano in New Zealand lie in the range 0.5–3.0 mm. Regarding the critical thickness the findings are much more diverse. Indeed our results fit well with findings for Icelandic tephras, indicating critical thicknesses in the range 5.5–15 mm. However, much higher values have been reported for other tephras, e.g. Mount St. Helens, USA, or Mount Ruapehu, New Zealand. The latter suggests that besides thickness and distinct thermal properties of the material coverage, other factors are also important for the change in ablation by tephra covers.
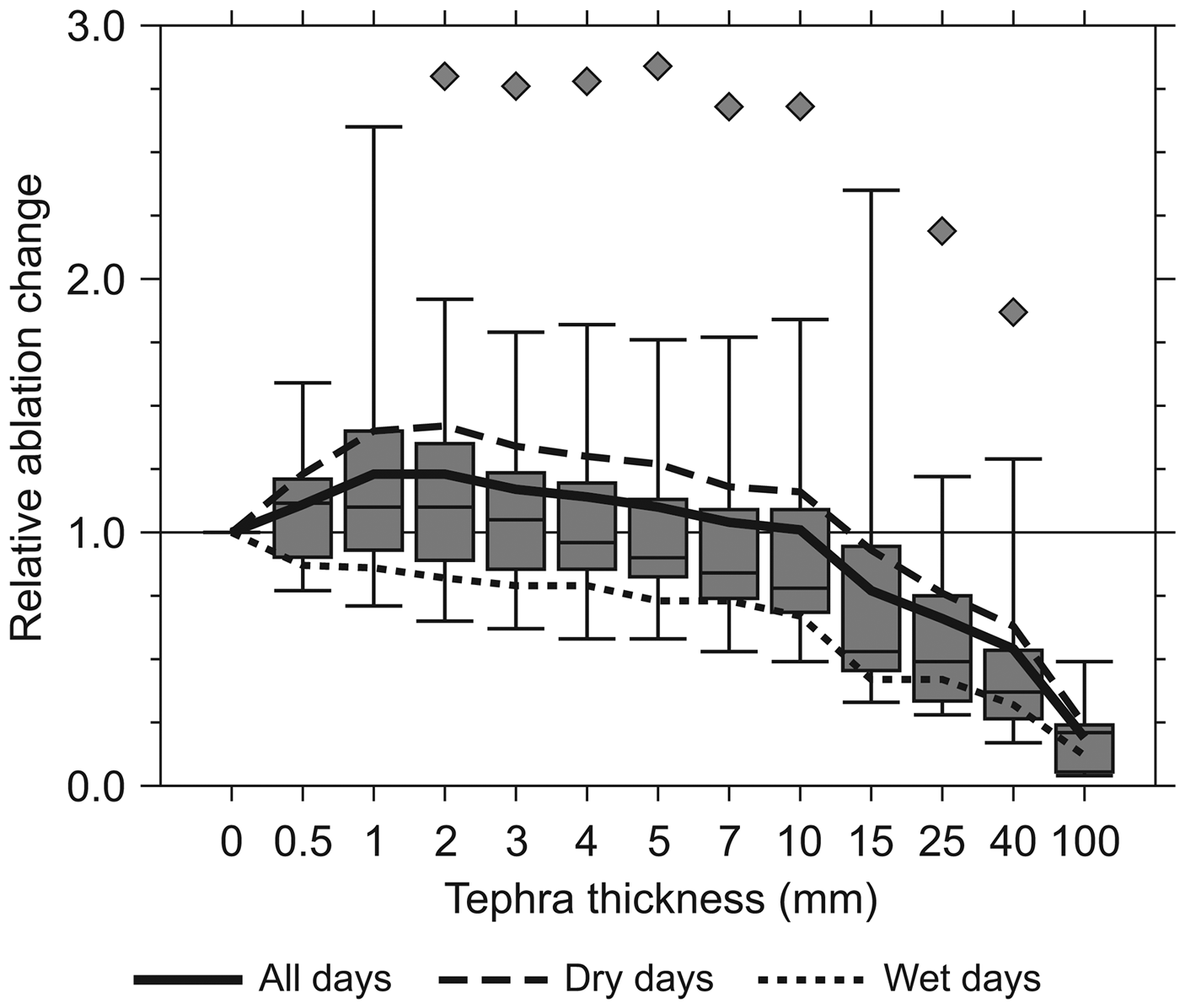
Fig. 7. Ablation at the different tephra plots relative to uncovered, bare-ice conditions. The box plots give an overview on all 13 measurement intervals. Outliers are indicated as diamond symbols. The means of relative ablation changes are shown as curves for all days as well as separated for dry and wet days.
Table 3. Effective and critical thicknesses of tephra coverage obtained in previous studies. For tephra type the source volcano is given along with the related eruption year if known. In case of Eyjafjalljökull the influences of two different grain-size classes are shown
In the lower-millimetre range especially, surface roughness can be an important factor. Due to its ability to control the distribution of bare-ice outcrops surface roughness influences the relation between albedo effect and thermal-resistance effect. An identical type and amount of material can therefore result in different influences on ablation when deposited on glacier surfaces with different surface roughness lengths. Another possible reason for the varying changes in ablation by tephra covers can result from differences in pore space of the material in combination with liquid water content. Our results indicate distinctly different ablation patterns depending on precipitation (Fig. 7). On the nine dry days with just 0.5 mm of rain on average (Table 2), the results match the expected pattern, showing a clear peak of ablation amplification at a tephra cover with effective thickness. However, on the four wet days with 14.1 mm of rain on average (Table 2), no amplification of ablation was evident at all. Neither an effective nor a critical thickness could be identified as the observed ablation rates decrease continuously over the entire range of tephra-cover thicknesses. Rhodes and others (Reference Rhodes, Armstrong and Warren1987) hypothesize that such a pattern is related to an energy partitioning that features turbulent heat fluxes as the exclusive source of melt energy. An amplified ablation across the effective thickness, in contrast, is related to a dominance of shortwave radiation fluxes.
3.2. Ablation models
For model 1, the calibration of individual temperature factors f T1 according to Eqn (1) yielded continuously decreasing values from 0.5 mm tephra thickness onwards. While the temperature factor for uncovered glacier ice was calculated to 8.65 ± 0.24 mm w.e. K−1 d−1, it increased by about 9.4% to a value of 9.21 ± 0.18 mm w.e. K−1 d−1 at 0.5 mm of tephra coverage. Beyond that the factors continuously decrease to reach 1.30 ± 0.10 mm w.e. K−1 d−1 at a 100 mm coverage. This decrease follows an almost perfect exponential decay function (Eqn (2); Fig. 4), showing an R 2 of 0.99. Together with the very small ranges of uncertainty obtained for the individual temperature factors, this suggests a robust calibration. Extrapolating the exponential decay function suggests that an almost complete insulation is present under tephra deposits exceeding ~0.5 m.
The exponential decay of the temperature factors has also been observed by Kayastha and others (Reference Kayastha, Takeuchi, Nakawo and Ageta2000) for ablation under debris cover on Kumbhu Glacier, Nepal. Hagg and others (Reference Hagg, Mayer, Lambrecht and Helm2008) used a power law for describing the decrease of temperature factors with increasing debris thickness on Inylchek Glacier, Tian Shan. The virtually asymptotic form of the decrease is thus a common feature.
The temperature factor for bare glacier ice (8.7 mm w.e. K−1 d−1), which corresponds to the classic degree-day factor, resembles other observations on Iceland. Jóhannesson and others (Reference Jóhannesson, Sigurdsson, Laumann and Kennett1995) reported a degree-day factor of 7.7 mm w.e. K−1 d−1 for Sátujökull, a northern outlet glacier of Hofsjökull ice cap. Jóhannesson (Reference Jóhannesson1997) proposes similar values for other outlets of Hofsjökull, i.e. Blöndujökull and Kvíslajökull (5.0 mm w.e. K−1 d−1) and Illviðrajökull (7.6 mm w.e. K−1 d−1). For glaciers belonging to Langjökull ice cap distinctly larger values of 11.1–13.5 mm w.e. K−1 d−1 (Guðmundsson and others, Reference Guðmundsson, Björnsson, Pálsson and Haraldsson2009) and 12.6–14.2 mm w.e. K−1 d−1 (Matthews and others, Reference Matthews2015) are reported.
For model 2, the calibration of individual temperature and radiation factors f T2 and f R2 according to Eqn (3) resulted in a less clear picture (Fig. 5). For thinner tephra deposits of 10 mm or less, the individual values of f T2 show a heterogeneous relation to tephra-cover thickness. For tephra thicknesses of 15 mm or greater a clear decrease of f T2 with increasing thickness of the tephra deposit is observable. Compared with the f T2 for bare glacier ice (7.48 ± 0.70 mm w.e. K−1 d−1), all individual values of f T2 for the different tephra plots were found to be lower by between 15% (6.36 ± 0.37 mm w.e. K−1 d−1 for 0.5 mm) and 89% (0.84 ± 0.25 mm w.e. K−1 d−1 for 100 mm). This indicates that the temperature-controlled energy fluxes that are parameterized by the temperature factor f T2 are predominantly influenced by the insulation effect induced by the tephra deposit. The calibrations of the individual temperature factors are robust, but on a lower level. For f T1 uncertainties lie in the range ~1–7%, while for f T2 uncertainties in the range ~4–30% are obtained.
The individual values of f R2, in contrast, show a very strong 135% increase from the bare-ice value (0.058 ± 0.027 mm w.e. W−1 m2 d−1) to that of the 0.5 mm tephra coverage (0.140 ± 0.013 mm w.e. W−1 m2 d−1) followed by a continuous decrease with increasing tephra thickness. Until a tephra-cover thickness of 7 mm the individual values of f R2 remain above the bare-ice equivalent. Their calibrations are generally robust, even if substantial uncertainty can be observed for thicker tephra plots (Fig. 5b).
The change of sign of f R2 at a thickness of ~25 mm (Fig. 5b) indicates that the radiation term of Eqn (3) adds to the temperature-dependent ablation for tephra covers <25 mm and reduces the temperature-dependent ablation in the case of tephra covers with thicknesses >25 mm. The change of sign of f R2 reflects the fact that the albedo effect outranges the insulation effect for thin tephra deposits. This in turn documents that the radiation-dependent energy fluxes are most important for ablation underneath a tephra deposit when the albedo effect predominates.
The decreases of both f T2 and f R2 show exponential decays with increasing tephra thickness (Fig. 5). The fitting of the corresponding exponential decay functions (Eqns (4a, b)) yielded highly reliable fits (R 2 = 0.89 for f T2, R 2 = 0.97 for f R2). f R2 starts to approach an asymptote at −0.02 mm w.e. W−1 m2 d−1 for deposition thicknesses of 40 mm and above.
For model 3, the calibration of the individual empirical factors ω according to Eqn (5) yielded continuously increasing values from 0.5 mm tephra thickness onwards. Starting from a value of −0.0320 ± 0.0025 W−1 m2°C at the 0.5 mm tephra deposit, ω changes sign at a tephra thickness of ~4 mm and afterwards shows a considerable, continuous increase leading to a value of 0.1212 ± 0.0160 W−1 m2°C at a coverage of 100 mm. Uncertainties are usually small (<10%), except for the thicker tephra covers (Fig. 6), and thus indicate a reliable model calibration. An empirical factor for uncovered glacier ice was also calibrated (−0.0385 ± 0.0027 W−1 m2°C) even if no heat flux through a supraglacial tephra deposit is present in this case. The observed increase of ω was approximated by an almost perfect exponential fit (Eqn (6); Fig. 6), showing an R 2 of 0.99.
In the calculation of the tephra-surface temperature (Eqn (5)) the sign of the empirical factor ω controls whether the radiation-dependent term is added to air temperature or subtracted from it. As ω stays negative up to a tephra thickness of 4 mm (Fig. 6), integrated tephra-surface temperature is lower than air temperature on plots with thin tephra coverage (<4 mm) and higher than air temperature on plots with thick tephra coverage (>4 mm). This indicates a noticeable cooling effect caused by the melting 0°C glacier-ice surface below thin tephra deposits (<4 mm). The cooling effect becomes weaker with increasing tephra thickness due to the insulation effect of the tephra layer. With further increasing layer thickness (>4 mm) the radiation-induced heating of the tephra surface starts to exceed the cooling effect, and tephra-surface temperature becomes increasingly decoupled from ice-surface temperature.
3.3. Model performance and comparison
The performance of all three ablation models is discussed in a comparative evaluation of the absolute and relative model accuracies calculated from a comparison between modelled and observed ablation at the different tephra plots. The absolute model accuracies (Fig. 8) are expressed as RMS errors that are calculated separately for each model and tephra plot. The relative model accuracies (Fig. 9) are determined by relating the calculated RMS errors to measured ablation and they thus account for the varying intensity of ablation under the different thicknesses of the tephra deposits.

Fig. 8. Absolute RMS errors between modelled and measured ablation for the different tephra plots of the field experiment.

Fig. 9. Relative RMS errors between modelled and measured ablation for the different tephra plots of the field experiment.
The absolute accuracies of all three models show an overall improvement with increasing tephra-cover thickness, associated with a decrease of the RMS errors. However, this is not surprising since the ablation amounts are decreasing with increasing tephra thickness. The relative model accuracies are best for medium range tephra thicknesses but become worse for the thicker deposits. For the latter, the measured ablation is so small that even the very small absolute RMS errors result in considerably larger relative deviations.
When comparing the three models it becomes obvious that the performance of the partly physics-based model 3 is, in general, much inferior to the purely statistical models 1 and 2 (Fig. 9). The median of the relative RMS errors belonging to model 3 amounts to 41.8%, while the corresponding medians of models 1 and 2 are much lower (23.9 and 16.3%). The accuracy of model 3 is very low for thin tephra covers but improves considerably with increasing tephra thickness. For thin tephra covers in the range 2–3 mm the calculation of ablation with model 3 results in low accuracies indicated by relative RMS errors in the range 38–64%. For an even lower tephra coverage of 0.5–1 mm, the relative RMS errors increase by one order of magnitude to 156–336%. For uncovered bare-ice conditions the model finally produces ablation amounts that are unrealistic. The relative RMS error increases by an additional two orders of magnitude compared with the 0.5–1 mm level. Not until tephra-cover thicknesses of 4 mm and above, does the performance of model 3 reach the same level of accuracy as that of models 1 and 2. Only for the thickest tephra deposit (100 mm) does model 3 yield the best results.
It is striking that the insufficiency of model 3 is limited to those tephra plots that show negative ω values and thus surface temperatures below air temperature. On these plots an efficient cooling of the surfaces of the lower-millimetre scale tephra covers by the underlying 0°C ice surface occurs because the thin tephra layers can be expected to be not thick enough to exceed the surface roughness of the glacier ice. Over these thin deposits the rates of increase of ω with tephra thickness are high and almost constant.
In the range 15–40 mm, the rates of increase of ω become smaller and smaller until they are almost constant (Fig. 6). This transition from large to small rates of increase of ω with tephra thickness happens parallel to the change of sign of the radiation factor f R2 of model 2, which occurs at ~25 mm (Fig. 5b). This coincidence shows the competing of albedo and insulation effects and the prevalence of the former against the latter on low-thickness tephra plots (< 25 mm). For higher thicknesses, this relation changes and the albedo effect soon becomes constant while the insulation effect increases linearly with layer thickness.
The evaluation of the performance of model 3 suggests that a calculation of heat flux through a discontinuous tephra deposit starting from one single, integrated surface temperature across the entire tephra plot is not feasible. Instead, complex three-dimensional (3-D) modelling of the interface between atmosphere and tephra/ice that resolves the micro topography of the glacier-surface roughness would be necessary. Hence, the application of 1-D, physics-based modelling approaches is limited to tephra deposits of higher thickness that clearly exceed the surface roughness of the glacier ice covered.
From the performance of models 1 and 2 across the lower-thickness tephra plots it becomes obvious that the accuracy of model 2 clearly exceeds that of model 1. The mean relative RMS error of model 2 over the tephra-thickness range 0.5–5 mm (14.4%) is less than two thirds of that of model 1 (23.0%). This substantial predominance of model 2 does not show up for thicker tephra layers. For tephra-cover thicknesses that can be expected to lie above the glacier surface roughness length the accuracy of model 1 closely resembles that of model 2. This suggests that for modelling of ablation under a thin tephra deposit, where the albedo effect outweighs the insulation effect, the explicit consideration of the influence of solar-radiation leads to substantially better model performances. A temperature/radiation-index model is hence the best choice for coping with the specific characteristics of thin tephra deposits that show a discontinuous appearance on the microscale, i.e. a coverage that is disturbed by the roughness of the glacier surface.
4. CONCLUSIONS
A field experiment was carried out on Svínafellsjökull, Iceland, in May 2013 that was designed to analyze the influence of supraglacial volcanic tephra deposits on glacier ablation. It was observed that surface ablation varies strongly with deposition thickness. Maximum increases of up to almost 25% compared with bare-ice conditions occur under 1.0–2.0 mm of tephra. Sub-tephra ablation equals bare-ice ablation at ~10 mm of tephra coverage. Above this thickness, a reduction of ablation is evident that consolidates with further thickening of the tephra deposit. Ablation is reduced by ~80% under a tephra layer of 100 mm thickness. Complete insulation is suggested for tephra thicknesses exceeding ~0.5 m. The general pattern of tephra thickness-dependent ablation varies with meteorological conditions, especially precipitation. Increased ablation under thin tephra layers is only found on dry days. On days with rainfall, ablation decreases continuously with increasing tephra-cover thickness.
Three different types of models were developed and calibrated to calculate ablation as a function of tephra thickness. Two of these models are based on empirical parameterizations while the third model is partly physics-based. The influences of tephra coverage on ablation are accounted for by varying the empirical parameters of all three models as functions of tephra thickness.
The performances of the three approaches differ markedly, both among themselves and across the varying tephra-cover thicknesses. The temperature/radiation-index model yielded by far the best results for ablation occurring under thin tephra deposits (<10 mm). The pure temperature-index model is less accurate over this range of tephra thickness. The partly physics-based model even yielded completely unrealistic results. Across thin tephra deposits particle migration on the microscale creates bare-ice outcrops and thus, discontinuities of the tephra layer that prohibit idealized 1-D physics-based calculations. The three models perform similarly over tephra thicknesses of 4–15 mm. For thicker tephra deposits in the order of centimetres to decimetres the results suggest that the partly physics-based modelling approach returns the most reliable results. All three models show their best performance over the intermediate range of tephra-cover thickness (~4–7 mm).
Our results suggest that especially non-elaborate, index-based models are able to reliably reproduce glacier ablation under very different thicknesses of tephra coverage that range over three orders of magnitude. However, room for further improvements is given by accounting for precipitation-induced changes in the variability of ablation according to tephra thickness and by further developing the partly physics-based modelling approach to a fully physical energy-balance model that is able to adequately handle thin, non-continuous tephra deposits.
5. ACKNOWLEDGEMENTS
The analysis and interpretation of the results of the field experiment were funded by grants no. SCHN680/6-1 and KU1476/5-1 of the German Research Foundation (DFG). We thank the Vatnajökull National Park office in Skaftafell for valuable assistance and great hospitality during the period of fieldwork on Svínafellsjökull. Two anonymous reviewers are acknowledged for valuable comments that helped to improve the manuscript.














