1. INTRODUCTION
Reliable knowledge of the mass and distribution of snow on the ground from the catchment to the global scale is essential to understand and predict cryospheric water resources, climate and natural hazards. High-resolution (~10 m) measurements of snow depth over large spatial extents (~10 km) are required to evaluate the performance of spatially distributed snow models (e.g. Marks and others, Reference Marks, Domingo, Susong, Link and Garen1999; Lehning and others, Reference Lehning2006; Liston and Elder, Reference Liston and Elder2006), as well as remote sensing observations from airborne (Liston and Sturm, Reference Liston and Sturm1998; Yueh and others, Reference Yueh, Cline and Elder2007) and satellite (Kelly, Reference Kelly2009; Rott and others, Reference Rott2010) platforms. In seasonal snowpacks, variability in bulk properties such as depth and snow water equivalent (SWE) typically occurs over length scales of 10–100 m (e.g. Shook and Gray, Reference Shook and Gray1996; Deems and others, Reference Deems, Fassnacht and Elder2006; Trujillo and others, Reference Trujillo, Ramirez and Elder2007). Snow stratigraphic variability is likely to exceed that of bulk snow properties and have a shorter correlation length (<10 m) (Sturm and Benson, Reference Sturm and Benson2004). Variability at small scales can have a large impact on microwave measurements, particularly where contrasts in dielectric properties are strong (Marshall and others, Reference Marshall, Koh and Forster2005; Durand and others, Reference Durand, Kim and Margulis2008, Reference Durand, Kim, Margulis and Molotch2011). Stratigraphic variability at the <10 m scale is infrequently documented (Benson and Sturm, Reference Benson and Sturm1993; Sturm and Benson, Reference Sturm and Benson2004; Domine and others, Reference Domine, Gallet, Bock and Morin2012; Rutter and others, Reference Rutter2014; King and others, Reference King2015) due to the time consuming nature of manual stratigraphic observations. These small-scale variations may introduce large uncertainties when one-dimensional (1-D) in-situ measurements are used for comparison with distributed snow modelling and remotely sensed measurements.
Broadband frequency-modulated continuous-wave (FMCW) radar measurements at near-nadir (~0 degrees) incidence angles allow the positions of the snow surface, snow/ground interface, and internal layer boundaries to be estimated from the propagation time of the radar returns, using an estimate of wave speed (Ellerbruch and Boyne, Reference Ellerbruch and Boyne1980; Gubler and Hiller, Reference Gubler and Hiller1984; Marshall and Koh, Reference Marshall and Koh2008). The difference in measured time between the recorded reflection from the snow surface and the snow/ground interface, which is the travel-time of the signal in the snowpack, can be used to estimate total snow depth. The accuracy of depth estimates in dry snow is of the order of 10% using a typical velocity, and the accuracy increases with availability of in-situ density estimates (Marshall and Koh, Reference Marshall and Koh2008). Similarly, the thickness of stratigraphic layers can be estimated from measurements of two-way travel time between continuous reflections, when referenced to layer locations in a calibration snowpit.
As the usage of ground-based active and passive microwave measurements of snow increases (Marshall and others, Reference Marshall, Koh and Sturm2008; Derksen and others, Reference Derksen2012), so too does the need to evaluate and understand snowpack layering and properties influencing radar amplitude and emission. Evaluation of microwave interactions with snowpack properties has commonly been only in one dimension, using vertical profiles of snow properties from either single or multiple snowpits within or adjacent to a sensor footprint. This employs the assumption that these properties are constant throughout the footprint (Durand and others, Reference Durand, Kim and Margulis2008; King and others, Reference King2013). However, the importance of spatially distributed measurements of snowpack properties for interpretation of microwave scattering within sensor footprints has recently been demonstrated using ground-based microwave radiometers (Rutter and others, Reference Rutter2014) and narrowband Ku band radar (King and others, Reference King2015). As the increased portability of broadband FMCW radar systems (Marshall and Koh, Reference Marshall and Koh2008; Marshall and others, Reference Marshall, Koh and Sturm2008) enhances the potential for measurement of snowpack properties over very long spatial scales, increased skill in interpreting the radar response to the snowpack is required. In particular, improved understanding of how the 2-D radar amplitude response is averaged across different spatial scales, is necessary to improve interpretation of snowpack properties over extended transects.
We collected high-resolution in-situ measurements of Arctic snowpack properties in parallel 10 m trenches, coincident with measurements of 12–18 GHz FMCW radar (see Fig. 11 in Marshall and Koh, Reference Marshall and Koh2008). We quantify spatial variability in snowpack stratigraphic layering at the sub-centimetre scale using Near-InfraRed (NIR) photography (Matzl and Schneebeli, Reference Matzl and Schneebeli2006; Tape and others, Reference Tape, Rutter, Marshall, Essery and Sturm2010), and traditional in-situ measurements of snowpack properties. Results are used to quantify the impact of spatial averaging of in-situ measurements of snowpack properties on the relationship between estimated reflectivity and radar surface scattering. Analyses focus on: (1) optimal horizontal ranges over which to spatially average in-situ measurements for comparison with nadir radar observations, and (2) horizontal averaging of radar observations using only single vertical profiles of snowpack properties (e.g. from traditional snowpits) to adequately evaluate radar amplitude. Implications of averaging snowpack properties are discussed with relevance to evaluation of airborne microwave remote sensing of snow and simulation of electromagnetic scattering in snowpacks.
2. METHODS
2.1. Field measurements
On 23 February 2008 measurements of snowpack physical and dielectric properties were made near Toolik Lake (68°38′N, 149°36′W), located on the North Slope of Alaska, USA. A 10 m transect was marked-out perpendicular to the edge of the north side of the lake and extended out from the shore onto lake ice. The site captured a range of snow conditions over a short horizontal extent.
FMCW radar (12–18 GHz) measurements were made ~1 m above the snow surface from antennas attached to an enclosed sled that housed radar hardware, using standard gain (20 dB) horn antennas with a 19° 3 dB beamwidth. The antennas have a maximum aperture dimension of 9 cm, giving a far-field distance at 12 and 18 GHz of 65 and 97 cm, respectively. An antenna height of ~1 m above the snow surface was chosen to place the snowpack in the far-field, to avoid complications associated with interpreting near-field measurements. The sled was very slowly winched (<2 cm s−1) along the transect, while recording radar measurements 40 times a second. Differential GPS (Trimble 5700) was used to geolocate the radar with an absolute horizontal accuracy of <5 cm. The standard gain horn antennas have a −3 dB beamwidth of 23.75° at 12 GHz and 16.0° at 18 GHz (i.e. the angle at which the power drops by 50%). A conservative estimate of the footprint size at the base of the snowpack, based on a 1 m antenna height and 80 cm snow depth, is 75 cm × 75 cm for 12 GHz, and 50 cm × 50 cm at 18 GHz. The actual footprint will be somewhat smaller due to refraction at the air/snow interface. The horizontal displacement necessary to get a nearly independent sample is therefore conservatively estimated to be 1 m.
After radar measurements were made, a 10 m trench, progressively cut back in 25 cm steps to create three parallel trench faces, was excavated to span the radar footprint (~50 cm × 50 cm at ground). The middle trench of the three excavated was located directly under the centre line of the radar profile. All trenches were cut with snow saws to be as near vertical as possible. Any artefacts resulting from the excavation process, for example teeth marks from the snow saws, were carefully removed using soft brushes and rounded wood blocks. Vertical profiles of layer boundary locations were manually measured at 20 cm intervals along each trench face. Relative hardness was the primary measurement, along with grain size and shape, used to manually distinguish layer boundaries. The horizontal positioning along the trench face of profiles of layer boundary measurements can be seen in Figure 1, in addition to the positions of all other in-situ measurements.
Fig. 1. Schematic diagram to illustrate the location of in-situ measurements in the middle trench face.
Prior to the hardness measurements, a series of NIR photographs (850 nm) was taken along the length of the middle trench at 35 cm intervals following the methods of Tape and others (Reference Tape, Rutter, Marshall, Essery and Sturm2010). This resulted in complete coverage of the trench with ~30% overlap between adjacent photographs. After the NIR photography, measurements of relative permittivity were made using a Toikka (Finnish) snow fork (Sihvola and Tiuri, Reference Sihvola and Tiuri1986) at 50 cm horizontal and 5 cm vertical spacing within each trench. The snow fork was inserted horizontally into the snowpack (integrating measurements over a volume of snow ~±2 cm above and below the fork), with adjacent measurements shifted slightly to alternating sides of a vertical profile to avoid any influence of disturbed snow (e.g. Marshall and others, Reference Marshall, Koh and Forster2005).
Destructive manual measurements of density, hardness, grain size and grain type were made after the completion of the NIR photography using standard techniques (e.g. Greene and others, Reference Greene2010). Density observations were made using a 100 cm3 box-type cutter (3 cm vertical height) at a horizontal spacing of 200 cm within individual layers. Where possible, two density samples were taken in each layer at each of the six vertical profiles along the trench. However, due to limitations of layer thicknesses and the occasional inability to get a reliable sample from each position along the trench, between 4 and 12 density samples were taken in each layer. Vertical profiles of hand hardness were used to identify layer boundaries every 20 cm along the trench, and detailed vertical profiles of grain size and grain type were made within each layer at three positions (0, 5 and 9.5 m) along the middle trench. Grain size was assessed by distributing a sample of snow grains from each layer across the field of view of a pocket microscope with a graduated reticule (0.1 mm graduations). The longest and shortest axis of a grain identified as being representative of the distribution of grains across the field of view were recorded for each layer, and detailed descriptions of the grain shapes and types were recorded. Hand hardness, grain shape and grain type were identified using standard international conventions (Fierz and others, Reference Fierz2009) with the addition of a slab-to-hoar classification, which has previously been reported in snow cover on Alaskan lakes (Sturm and Liston, Reference Sturm and Liston2003). A large rock on the edge of the lakeshore caused a rapid decrease in thickness of lower layers from 9 to 10 m. This was considered an untypical influence on snow stratigraphy relative to variability in the rest of the trench. So, while measurements throughout the whole trench length are presented in Figures 2–4, analyses were limited to measurements made between 0 and 9 m (Figs 5, 6; Tables 1–3).
Fig. 2. NIR image of example trench section (3.5–4.5 m), annotated with layer boundaries and snow types (Table 3). Scale of horizontal measuring tape is in decimetres and vertical ruler is in centimetres.
Fig. 3. Mean (red line) and range (grey area) of layer boundary positions from manual measurements at 20 cm horizontal resolution across all three trenches.
Fig. 4. Relative permittivity (Finnish snow fork) and layer boundaries (NIR photography).
Fig. 5. (a) Corrected radar amplitude and (b) statistically smoothed radar amplitude (median over a 5 cm vertical × 50 cm horizontal moving window) with layer boundaries (black lines) superimposed.
Fig. 6. Scatterplots of (a) paired reflectivities and radar amplitude across layer boundaries, and (b) mean reflectivities and smoothed radar amplitude across layer boundaries excluding surface and basal boundaries (error bars are one standard error of the mean).
Table 1. Range statistics (in cm) of boundary layer positions between 0 and 9 m of the three trenches within the radar profile
Table 2. Layer thickness statistics in the middle trench between 0 and 9 m using manual and NIR measurements
Table 3. Snow layer properties between 0 and 9 m
2.2. Data processing
Techniques used to record sub-centimetre variability in snowpack layer boundaries using NIR photography were documented in Tape and others (Reference Tape, Rutter, Marshall, Essery and Sturm2010). The vertical positions of layer boundaries in this study were georeferenced relative to a ruler visible in each picture (Fig. 2). The vertical reference point for georegistration (where the base of the vertical ruler rests on the ice surface) varied between adjacent images due to localised basal roughness. Consequently, when layer boundary positions identified in adjacent images were stitched, abrupt visual discontinuities occurred, which ranged between a maximum of 2.0 and 5.4 cm for individual layer boundaries. These discontinuities were smoothed by removing boundary positions on either side of the discontinuity and then gap-filling the missing values using a cubic spline interpolation. Over all layers, 11% of the layer boundary positions were removed (ranging between 4 and 24% for each layer boundary), before being gap-filled. This minimised the influence of errors resulting from the NIR measurement process and maximised the potential for accurate representation of the true layer boundary positions. As a result, eight layer boundaries at sub-centimetre vertical resolution were identified across the length of the trench. Some differences occurred in layer boundary identification of the same trench presented by Tape and others (Reference Tape, Rutter, Marshall, Essery and Sturm2010). Differences between 8 and 9 m along the trench in certain layer boundaries resulted from beneficial, a priori knowledge of manual field identification; knowledge that was intentionally made unavailable in Tape and others (Reference Tape, Rutter, Marshall, Essery and Sturm2010) to allow objective evaluation of the NIR stratigraphy method.
FMCW radar observations from 12 to 18 GHz were used to maximise resolution and cover the frequency (13.95 GHz) of a coincident airborne radar experiment (Rott and others, Reference Rott, Heidinger, Nagler, Cline and Yueh2009; Xu and others, Reference Xu, Tsang and Yueh2012). Vertical resolution for nadir radar observations is inversely proportional to bandwidth; while the ultra-broad bandwidth gave a vertical resolution of 2 cm (e.g. Marshall and Koh, Reference Marshall and Koh2008), uncertainties in radar wave speed caused the total absolute uncertainty in location of radar amplitude to be <5 cm (e.g. Marshall and others, Reference Marshall, Koh and Forster2005). The profile of radar measurements was made with 98% overlapping footprints, such that the measurement spacing was 1 cm while the footprint of the measurement was ~50 cm × 50 cm. The measured radar response was corrected for spherical geometrical spreading, using a depth scale based on the mean snowpack density. These corrected data were then smoothed along the 10 m trench with a moving window median filter of 5 cm (vertical) × 50 cm (horizontal), chosen based on the vertical uncertainty and ground projected footprint.
Reflectivity was estimated using vertical gradients in electrical properties, calculated between adjacent 5 cm measurements, in the 20 vertical profiles (50 cm horizontal spacing) of in-situ relative permittivity measurements:
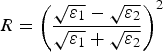$$R = \left( {\displaystyle{{\sqrt {\varepsilon _1} - \sqrt {\varepsilon _2}} \over {\sqrt {\varepsilon _1} + \sqrt {\varepsilon _2}}}} \right)^2 $$
where R is the reflectivity, and ε 1 and ε 2 are the real components of permittivity of two layers either side of a layer boundary (e.g. Ulaby and others, Reference Ulaby, Moore and Fung1981). To compare with reflectivity, radar amplitude was averaged over a window ±5.1 cm (vertical) and ±1 cm (horizontal) centred around layer boundaries. This ensured that the radar response overlapped with the positions of two adjacent relative permittivity measurements above and below layer boundaries, to be representative of the dielectric contrast across the layer boundary. Reflectivity and radar amplitude at locations other than layer boundaries were not analysed in this study.
3. RESULTS
Manual measurements showed eight major layer boundaries, including the snow surface and the snow-ice boundaries, in all three trenches across the radar footprint (Fig. 3). The mean vertical range in locations of individual layer boundaries across the three parallel trenches (Table 1), calculated from similar along-track positions in each trench, were always within 1 cm of the mean range of layer boundary positions along the length of the middle trench. Apart from the air to snow boundary, the difference between means across trenches and along the middle trench was 0.6 cm or less, and the difference between the standard deviations was 0.4 cm or less for all layer boundaries. The middle trench captured all major along-track changes in layer boundaries and as such was the sole trench used to compare with the radar measurements.
High-resolution identification of layer boundaries from NIR images captured 2-D variability in layering along the middle trench (the centre line of the radar profile). Compared with lower resolution manual measurements (20 cm horizontal, 1 cm vertical), the maximum range in layer boundary locations identified using NIR, across 40 cm moving windows of the middle trench, was higher for all boundaries (0.2–4.6 cm) other than the Slab-to-Hoar (SH) upper to SH lower boundary (Table 1). Consequently, while the higher resolution NIR measurements generally identify a greater range of layer boundary variability, the improvement over manual layer detection is sensitive to centimetre-scale variability in layer boundary height around the broader trend in slope.
Layer thickness, using high-resolution NIR measurements at 1 cm horizontal resolution, indicated that means and standard deviations were similar to manual measurements made at a lower horizontal resolution (Table 2). Layer thickness measurements using NIR showed that the proportional area of individual layers within the total trench area ranged between 8 and 24% (Table 2). Thicknesses of individual layers varied greatly along the trench with standard deviations from 1.4 to 9.4 cm. Also, of the seven major layers present (Fig. 2) two, Wind Slab (WS) upper and Depth Hoar (DH) upper, were discontinuous (Fig. 3). Layer thickness variability is shown in Table 2, where the range in the maximum percentage that an individual layer occupied within any single vertical profile varied between 49% (WS lower) and 13% (DH lower) along the trench.
Density measurements indicated that between-layer variability was much greater than the inter-layer variability (Table 3); mean density of each layer ±1 standard deviation did not overlap the mean density of adjacent layers. The range of grain size short axis was small (0.2–1.7 mm) across all layers, but the range in the long axis was much larger (0.8–5.3 mm). Consequently, long axis grain size helped highlight differences between layers, especially transitions between wind slab, depth hoar and slab-to-hoar. Increases or decreases in hardness from layer to layer were generally in-phase with density. However, hardness also allowed more subtle differences between layers to be identified, such as between the upper and lower wind slab layers, where the hardness strongly transitioned between 1-finger and knife despite density and grain size not changing greatly.
Layer boundaries were overlaid on regularly-spaced, 2-D grids of the real component of measured relative permittivity (Fig. 4) and radar amplitude (Fig. 5a). Major layer boundaries spatially delineate layers with relatively low permittivity (e.g. FS, DH upper and DH lower) and relatively high permittivity (e.g. WS lower, SH lower). Radar amplitude, though highly spatially variable, showed some consistent structure along the trench. The smoothed amplitude (median values of 5 cm vertical by 50 cm horizontal moving windows) better resembled the volume of the snowpack represented by the radar signal and the relative consistency of surface scattering at layer boundaries (Fig. 5b). Strong radar amplitude was evident continuously along the DH lower to Ice boundary, and discontinuously along the FS to WS upper and WS upper to WS lower boundaries. There was a large decrease in radar amplitude in the FS to WS boundaries between 7.5 and 8.5 m along the trench. Areas of moderate amplitude were evident around the DH upper to SH upper, and SH upper to SH lower layer boundaries, but were less consistent along the trench than areas of high-radar amplitude.
Although there was poor correlation between all individual pairs of radar amplitude and in-situ estimated reflectivity across layer boundaries (Fig. 6a: r = −0.03, p = 0.752), there was a very significant positive correlation (Fig. 6b: r = 0.94, p < 0.05) between the mean reflectivities and mean smoothed radar amplitude for each of the six internal boundaries, averaged along the trench. Of the three layer boundaries with the largest reflectivities, the high-radar amplitude attributed to the SH lower to DH lower boundary was partly influenced by very strong amplitude within the averaging window from the adjacent DH lower to Ice boundary. While surface scattering from layer boundaries increased with increased reflectivity as expected, the variability (expressed as error bars of one standard error of the mean in Fig. 6b) also increased with increased mean values. The effect of multi-path signals will not impact on this variability as reflectivity values at layer interfaces are <0.015 in all cases, with mean values <0.006 (see Fig. 6), meaning any multipath signal will be at least 2500 times smaller than a direct reflection from a layer boundary. In addition, the reduction in radar energy reaching the lower layer boundaries as a consequence of being reflected at upper boundaries is very small. As reflectivity values are less than 0.015, the total incoming radar energy at the lower boundaries is only a few percent lower than the total incoming radar energy at the upper boundaries.
When the horizontal averaging distance was adjusted from 0 to 9 m in increments of 0.5 m (Fig. 7), where correlation sample size (n) decreased from 107 to 4, correlations became statistically significant (p < 0.05) at horizontal averaging distances of 4 m (n = 52). Correlation coefficients continued to increase rapidly up to an averaging distance of 6 m (n = 30), after which the rate of increase in correlation reduced substantially. If the layer averages of radar amplitude and reflectivity are A 0 and R 0 with between-layer standard deviations σ A and σ R , the correlation between layer averages is
$$\rho = \displaystyle{{{\rm cov}(A_0, R_0 )} \over {\sigma _A \sigma _R}}. $$
Fig. 7. Correlation coefficients and statistical significance between radar amplitude and reflectivity when averaged over increasing horizontal extents. Solid line is given by Eqn (7) with parameters fitted to the data by nonlinear least squares, dashed line is p calculated for r from Eqn (7) and sample size (n) from data.
Suppose that the measurements of radar amplitude and reflectivity can be expressed as sums
$$A = A_0 + \varepsilon _A $$
and
$$R = R_0 + \varepsilon _R $$
where ε
A
and ε
R
represent spatial variability and measurement errors with standard deviations σ
εA
and σ
εR
, giving signal to noise ratios
$SNR_A = \sigma _A^2 /\sigma _{\varepsilon A}^2 $
and
$SNR_R = \sigma _R^2 /\sigma _{\varepsilon R}^2 $
. Assuming exponential spatial autocorrelations with correlation lengths L
A
and L
R
, the variances of measurements averaged over a distance L are
$$s_A^2 = \sigma _A^2 + \sigma _{\varepsilon A}^2 e^{ - L/L_A} = (1 + SNR_A^{ - 1} e^{ - L/L_A} )\sigma _A^2 $$
and
$$s_R^2 = \sigma _R^2 + \sigma _{\varepsilon R}^2 e^{ - L/L_R} = (1 + SNR_R^{ - 1} e^{ - L/L_R} )\sigma _R^2. $$
Reducing error by averaging measurements with autocorrelated noise requires repeated measurements spread over distances that are large compared with the correlation length. If there is no correlation between ε B and ε R , the correlation between horizontally-averaged measurements is
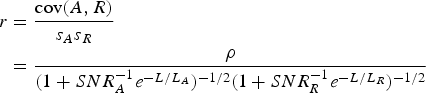$$\eqalign{r & = \displaystyle{{{\rm cov}(A,R)} \over {s_A s_R}} \cr & = \displaystyle{\rho \over {(1 + SNR_A^{ - 1} e^{ - L/L_A} )^{ - 1/2} (1 +SNR_R^{ - 1} e^{ - L/L_R} )^{ - 1/2}}}}$$
i.e. noise reduces the measured correlation towards 0 but horizontal averaging increases it towards ρ. The parameters in Eqn (7) were fitted to data in Figure 7 by nonlinear least squares, giving SNR of 4 × 10−5 and 7.5 × 10−3 and correlation lengths of 0.4 and 1.1 m; the correlation function is symmetric between reflectivity and radar amplitude so does not distinguish which is which. The low SNR are necessary to match the very low correlations for short averaging lengths. Equation (7) cannot reproduce the small and statistically insignificant negative correlation found for measurements averaged over distances of <~2 m, but the fitted curves otherwise follow the observations closely.
The impact of spatial averaging on correlation across a trench is important for accurate assessment of spatial variability in snowpack reflectivity. However, it is also of great practical interest to quantify the improved correlation resulting from identifying layer boundaries in two dimensions using NIR photography, rather than horizontally extrapolating layer boundaries from a single vertical profile in a snowpit. To investigate, the vertical positions of layer boundaries were extrapolated horizontally between 0 and 9 m from each of the individual 19 available vertical profiles across the trench and correlations between radar amplitude and in-situ reflectivity were calculated. Only one vertical profile (at 6.5 m along the trench) provided a significant correlation (r = 0.83, p < 0.05). When all 19 single vertical profiles were considered collectively, correlations between radar amplitude and reflectivity were low (r-values: mean = 0.16, standard deviation = 0.32).
4. DISCUSSION AND CONCLUSIONS
Variations in layer thickness were evident throughout the 9 m trench. Increased snow depth from left to right across the trench did not result in a proportional thickening of all internal layers. Instead, the upper wind slab layer and the lower slab-to-hoar layer increased in thickness at the expense of all other layers, most likely due to wind redistribution. Reduction in layer thickness often occurred where layers were structurally weak, for example in the upper depth hoar layer, which may have been scoured by wind. Observed layer expansion and contraction confirmed that even in the absence of melt, rough subnivean topography, or underlying vegetation, complex stratigraphic layering can develop in a similar manner to snow on tundra (e.g. Sturm and Benson, Reference Sturm and Benson2004; Domine and others, Reference Domine, Gallet, Bock and Morin2012). Such high horizontal variability in snowpack layer thickness and the vertical position of layer boundaries has important implications for: (1) spatial averaging of field measurements of physical snowpack properties used to interpret co-located variability in radar amplitude, and (2) one- and two-dimensional simulation of electromagnetic scattering in snow.
Mean values of near-nadir radar amplitude and in-situ reflectivity at layer boundaries, located at a centimetre-scale, were correlated (p < 0.05) when considered across a 9 m horizontal extent of an Arctic snowpack. Where high-resolution layer boundary measurements were available, there was an optimum range of horizontal averaging between 4 and 6 m to capture interactions among radar amplitude, stratigraphy and bulk layer properties. Averaging below 4 m, the correlation was statistically insignificant and above 6 m the rate of increase in the correlation markedly decreased. In addition, horizontal extrapolation across the trench of layer boundaries taken from single vertical profiles, which are representative of more commonly available snow pit measurements, very rarely demonstrated a significant correlation between radar amplitude and reflectivity. This suggests that conventional field measurement techniques involving vertical profiles of snowpack stratigraphy may not capture the spatial variability required for evaluation of near-nadir radar observations. Instead, it strengthens the argument (cf. Derksen and others, Reference Derksen2009) for the use of field techniques, such as NIR photography, to capture sub-centimetre scale variability in snowpack stratigraphy.
While ground-based FMCW radar offers the potential for orders of magnitude more measurements than snowpit or trench measurements, improved interpretation of radar amplitude will be necessary to enhance evaluation within sensor footprints for calibration and validation campaigns of future satellite sensors (e.g. Cline and others, Reference Cline, Kummerow, Jiang and Uratuka2003; Yueh and others, Reference Yueh2009; Rott and others, Reference Rott2010). In addition, although most radar measurements on airborne and satellite platforms are made at off-nadir incidence angles (30°–45°), internal layer boundaries, if they are not horizontal and are rough at the wavelength scale, add uncertainty to estimates of volume scattering, which increases in dominance relative to scattering at internal layer interfaces as incidence angles move away from nadir. Improved knowledge of changes in snowpack properties from nadir FMCW amplitude observations may, therefore, provide important information when interpreting off-nadir radar amplitude. The increase in variability with increasing mean radar amplitude and in-situ reflectivity, indicated by increasing error bars in Figure 6b, suggests a need to measure layer boundaries at the centimetre scale across a sufficiently characteristic range of variability that might be expected within sensor footprints. While the horizontal resolution of a remotely sensed measurement depends on the sensor antenna pattern and the altitude above the earth's surface, previous experiments have averaged airborne off-nadir Ku band radar measurements to 200 m grids (Yueh and others, Reference Yueh2009). These grids were evaluated using in-situ measurements consisting of five snowpit profiles of snowpack properties and hundreds of snow depths, at 10–20 m spacing in an ‘hourglass’ pattern, within 500 × 500 m areas of Colorado, USA. While this is relatively data-rich for in-situ evaluation of airborne measurements, it gives an indication of data paucity for considering the impact of local stratigraphic variability on radar amplitude.
The high horizontal variability of layer thickness in proportion to total depth also has important implications for computational electromagnetic models that describe scattering of microwave energy in snow (Tsang and others, Reference Tsang, Ding, Huang and Xu2013). In particular, it suggests that 1-D simulations for calibration or validation studies should use an ensemble approach to account for multiple stratigraphic possibilities, resulting in a distribution of simulated radar amplitude values to compare with measurements. Also, some electromagnetic models, which simulate scattering and absorption of microwave energy within layers as well as scattering at major dielectric boundaries can be used in a 2-D manner (e.g. Tsang and others, Reference Tsang2007), requiring realistic 2-D initialisation. Consequently, datasets containing measurements of radar response and snowpack properties at the spatial resolutions presented here are strongly suggested for future sensitivity experiments evaluating simulated narrowband, off-nadir radar amplitude.
This study has presented a detailed set of ground-based measurements to examine the impact of spatial averaging of in-situ snow stratigraphy and physical snowpack properties on variability in FMCW radar (12–18 GHz) amplitude. In doing so, an optimum range of horizontal averaging (4–6 m) was identified to capture centimetre-scale interactions between radar amplitude, snowpack stratigraphy and the bulk layer properties, which controlled reflectivity within an Arctic snowpack. Single vertical profiles of snowpack properties were highly unlikely to represent the local spatial variability in snowpack properties that influenced near-nadir radar amplitude. Future study will be required to assess how these implications for interpretation of amplitude from portable FMCW radar, would up-scale to airborne and satellite footprints, as well as entire hydrological catchments.
ACKNOWLEDGEMENTS
We thank M. Sturm, J. Holmgren, K. Elder, D. Cline and the winter crew at the University of Alaska Fairbanks Toolik Lake research facility for technical and logistical support. We thank the editor and two anonymous reviewers for their detailed and helpful comments on a previous version of the manuscript. Financial support through UK Natural Environment Research Council (NERC) Fellowship NE/E013902/1 (Rutter) and NASA THP/NEWS NNG06GE70G (Marshall) is gratefully acknowledged.
Open access
