Intoduction
The portion of Jakobshavn Isbræ that is floating in Jakobshavn Isfjord (698 N, 398 W), west-central Greenland, has completely disintegrated (Fig. 1). Reference Prescott, Kenneally and HughesPrescott and others (2003) determined ice elevations, velocities, melting rates, strains and rotations for the floating ice in 1985 (Fig. 2). They located grounding lines mainly on the basis of ice elevation measurements (Fig. 3), from which they calculated that combined top and bottom melting rates averaged 109ma–1 over the 30km2 of the floating main-trunk ice stream, i.e. a loss of 3.3 km3 a–1 by melting compared to 11.2 km3 a–1 by calving. Using a finite-element grid in which gridpoints were often sites where surface crevasses intersected, they calculated strains and rotations in the map plane that led them to conclude that blocks of ice in heavily crevassed regions moved partly independently of surrounding blocks. Was this merely a response of surface ice to regions of heavy surface crevassing, or a response of the whole ice thickness? That is the question we address here, in view of the recent rapid disintegration.

Fig. 1. Disintegration of the floating terminus of Jakobshavn Isbræ since 2002 revealed in an Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) image on 28 May 2003. Image provided by K. Steffen.

Fig. 2. Jakobshavn Isbræ in 1985. The major dynamic features are identified. Heavy lines denote accurate (solid) and approximate (dashed) grounding lines. The light dashed line separates the fast main-trunk ice stream from the slower ice stream from the north.

Fig. 3. Ice elevations on Jakobshavn Isbræ measured photogrammetrically and contoured at intervals of 10 m (Reference Prescott, Kenneally and HughesPrescott and others, 2003). The thick line was the grounding line assumed in this study. The dotted areas are zones of partial grounding deduced from this study. Density of dots represents firmness of grounding.
The floating ice averaged some 800m in thickness, surface crevasses were <50 m deep, and basal melting rates should exceed the penetration rate of bottom crevasses. Therefore the assumptions of continuum mechanics in the flow law of ice (Reference GlenGlen, 1958) should have held for >90% of the ice. The regions of former heaviest and deepest surface crevassing are shown in Figure 2 These were (1) toward the rear grounding line of the main-trunk ice stream where primary transverse crevasses open; (2) at the base of an icefall at the head of Jakobshavn Isfjord, where slow ice moving over the icefall encountered much faster ice to the north and south at the base of the icefall; (3) in a band of deep longitudinal crevasses called ‘the Zipper’ that opened due to transverse tension as the thick main-trunk ice stream pressed against thinner ice along the high north fjord wall and spilled over the lower south fjord wall; (4) along the sides of the main-trunk ice stream where shear crevasses were rotated into longitudinal orientations; (5) over and around ice rumples where ice was partly grounded just behind the south side of the calving ice front; and (6) near the calving ice front where transverse crevasses opened and released large tabular icebergs.
Domains used by Reference PrescottPrescott (1995) in modeling using the finite-element method were typically bounded by crevasses, so the finite-element grid in Figure 4 largely corresponded to the pattern of surface crevasses. Our analysis was applied chiefly to the floating part of the main-trunk ice stream, enclosed by the bold border in Figure 4, where all six kinds of crevasses noted above were observed and which had the simplest boundary conditions. The terminal region of Jakobshavn Isbrae seemed to have a relatively simple flow regime, but a more careful examination revealed substantial complications in flow, particularly as indicated by the surface deformation pattern analyzed by Reference Prescott, Kenneally and HughesPrescott and others (2003), and the fracture pattern of surface crevasses shown schematically in Figure 2 Transverse crevasses in the main-trunk ice stream were bounded by shear crevasses to the south, presumably along a lateral grounding line, and to the north along its boundary with a much slower ice stream. Ice spilled over the ill-defined grounding line to the south and formed an ice lobe in strongly compressive flow, as revealed by concentric folds that parallel the southern lobe margin. It is unclear whether the slower ice stream from the north entered the fjord primarily because of its own gravitational extending flow, or whether coupling to the much faster flow of the main-trunk ice stream largely induced its flow into the fjord along the lateral shear zone they shared in common. In addition, flow in the floating main-trunk ice stream proceeded with no longitudinal extension, except near the calving front, and with substantial transverse extension that opened the family of deep longitudinal crevasses called the Zipper. Ice rumples behind the southern part of the calving front may have accounted for the lack of longitudinal extension between the ice rumples and the grounding line south of the Zipper, but what caused this lack north of the Zipper?

Fig. 4. The finite-element mesh used for modeling Jakobshavn Isbræ. Elements within the bold border are for floating ice, with each finite-element domain subdivided into four smaller domains for this study.
These complications have influenced our modeling strategy. Not knowing the uncrevassed ice thickness, we began with a plane-stress solution. Then we applied a standard ice-shelf solution, initially assuming crevasses could be ignored. Finally, we considered ice jamming between the fjord walls to account for remaining inconsistencies. The floating part of Jakobshavn Isbræ can be modeled most readily using Cartesian coordinates, with x horizontal and positive downstream along the center line of the fjord, y horizontal and transverse to x in the map plane, and z vertical and positive upward.
A plane-stress solution
The floating part of Jakobshavn Isbræ is thin compared to its extent in the map plane, so plane-stress conditions may be a reasonable approximation, especially below the heavily crevassed surface layer. Plane-stress conditions are most closely approximated in thin elastic or ductile plates, with forces applied at their sides and for which body forces can be ignored (Reference Timoshenko and GoodierTimoshenko and Goodier, 1951, ch.2; Reference NadaiNadai, 1950, ch. 37). In deeper ice, σxx, σyy and σxy are interior stresses that presumably produce the measured surface strain rates έxx, εyy and εxy through the flow law of ice (Reference GlenGlen, 1958). Boundary conditions for the floating ice are ice velocities measured at grounding lines and water pressure specified at the calving front. No ‘internal’ boundaries are specified to model crevassing. Vertical thinning rate εzz is obtained by assuming εxx + έyy + εzz = 0 for incompressible ice.
Glen’s flow law is (Reference PatersonPaterson, 1981, p. 30; Reference Van der Veen and WhillansVan der Veen and Whillans, 1989)
An effective viscosity μ defined by 2μ = da/dé is therefore:
where ε is the effective strain rate, σ is the effective stress (2έ2 and 2σ 2 are the respective second invariants of the strain rate and deviator stress tensors), B is an ice-stiffness parameter, and n is an ice visco-plastic parameter. The field equation used is Cauchy’s first equation of motion, which is valid for any continuum, irrespective of the stress-strain relation (Reference ArisAris, 1962, p. 102).
Combining the field equation with the flow law and the definition of strain rates in terms of velocity gradients yields a differential equation in terms of velocities. These velocities are then solved using standard finite-element techniques.
This involves converting the differential equation into a matrix equation in which the vector of unknowns is obtained from the velocity components at each of the discretization nodes of the finite-element model (FEM). This is done by volume integration of FEM elements with appropriate weighting functions. A program in Fortran was written for the FEM used in the plane-stress analysis. The program used the penalty method. Biquadratic Lagrangian elements having nine nodes were used exclusively. The FEM program was validated by comparing its results with results from two standard analytical plane-stress solutions, one for constant stresses and one for radially varying stresses, taking n ¼ 1 in both cases (Reference PrescottPrescott, 1995).
Using control theory to convert ice stiffness into a tuning parameter
For our FEM formulation of Glen’s flow law, successful application of the FEM requires knowledge of ice-stiffness parameter B in Equation (2). In many instances, including this study, there is no information on ice temperature or other factors that contribute to ice stiffness. There are basically two approaches for numerically estimating or ‘tuning’ B: forward and inverse modeling. With the forward, or iterative, approach B is adjusted for each element based on the ratio between the observed and computed velocities. The system is re-solved and this process is repeated until updates to B are deemed insignificant. The inverse methods attempt to solve for the distribution of B along with the unknown velocities. In our inverse study, control (minimization) theory was used to estimate the variation of B. Although other inverse methods exist, control theory appears to be the best suited for this situation (Reference MacAyealMacAyeal, 1993).
The basic approach in applying control theory is to assume some form, usually a series, to represent the unknown function, and then determine the parameters controlling the function that minimize some measure of fit between the observed and computed variables. This technique has been widely used in oceanography and meteorology (e.g. Reference WunschWunsch, 1988; Reference ThackerThacker, 1989), and has been applied by Reference MacAyealMacAyeal (1992), for example, in a glaciological study of an Antarctic ice stream. For the application of control theory to this study, see Reference PrescottPrescott (1995). In control theory, μ is defined using β 2, the series approximation of B, so that Equation (2) becomes
The value of β is squared to insure a positive value of B, since ice stiffness cannot be negative. In this study, two series approximations for β 2 were used, Fourier and Walsh. These two were selected because of their ability to represent smooth (Fourier) and discontinuous (Walsh) functions. The standard form of the two-dimensional Fourier series (Reference TolstovTolstov, 1962, p. 177) was slightly modified to simplify programming (see Reference PrescottPrescott, 1995). The form for two-dimensional Walsh series was taken from Reference HarmouthHarmouth (1972, p. 38) and Beau-champ (1975, p. 21). In both cases, the series are expressed in terms of parameters a i whose values are calculated in order to determine values of the unknown ice-stiffness parameter B.
The fit between the respective observed and computed velocities uvi and u i is assessed using the least-squares measure over a finite-element domain Ω:
As with standard optimization procedures, the Lagrange multiplier is introduced to enforce conditionality (Reference PrescottPrescott, 1995)
Results of plane-stress modeling experiments
The first test kept B constant in all elements. Figure 5 shows the velocity magnitude percentage differences for the FEM using n = 3 and B = 180 kPa a1/3 (5.7 χ 104 Pa s1/3) obtained from Reference Iken, Echelmeyer, Harrison and FunkIken and others (1993). Near the grounding lines and the calving front, the agreement is better than 5%. Everywhere else, observed and calculated velocities differ by 10-20% (20-40 m for the 14 day period when ice motion was measured). This is up to one order of magnitude larger than the precision estimate of the observed displacements. Therefore, it seemed that some variation of B would be required to obtain a reasonable fit between the observed and computed displacements (using n = 1 has little effect).

Fig. 5. Comparison of measured velocities in the refined finite-element mesh with velocities calculated for plane stress, B = 180 kPa a1/3, and n = 3 in the Reference GlenGlen (1958) flow law of ice. Top: measured velocities contoured every 0.25kma–1. Bottom: per cent difference between measured and calculated velocities contoured every 5%.
Control theory converted B into a tuning parameter keeping calculated and measured ice velocities within 4% everywhere. These simulations produced a distribution and range of B values that depend strongly on the number of terms in the series expansion. Representative results are shown in Figure 6 Highest B values were concentrated near the calving front, with a lobe of high values extending from the ice rumples into the zone of nearly constant ice velocities for all Fourier expansions (from 12 to 168 terms). This lobe of artificially stiff ice in the zone of very low longitudinal strain rates may indicate a weaker extension of partial grounding that produced the ice rumples. Artificially high values of B in the Walsh expansions also emanated from the ice rumples and even more strongly coincided with the zone of nearly constant ice velocities and low longitudinal strain rates. However, we could not be sure these concentrations of high ‘tuned’ B values were reflecting variations in the deformation instead of the number of terms in the expansions. In the absence of partial grounding or defects in the model, something else must account for the nearly constant ice velocities that led to anomalously high B values in these tuning experiments.

Fig. 6. Results from calculating B using the control method and measured velocities for n = 3 and plane stress. Top: results from a Fourier series expansion in 52 terms contoured every 20kPa a1/3. Bottom: results from a Walsh series expansion in 12 terms contoured every 10kPa a1/3.
An Ice-Shelf Solution
The plane-stress solution eliminated ice thickness as a variable in order to sidestep not knowing the uncrevassed ice thickness that obeys the Reference GlenGlen (1958) flow law for ice. Next, we employed the Missoula model to obtain an ice-shelf solution that includes ice thickness but ignores the uncrevassed thickness. The reduced Morland equations can be solved to represent the flow of an ice shelf. A complete development of the equations is found in Reference Morland, Veen and OerlemansMorland (1987). These equations have become the standard for modeling ice-shelf flow. Application can be found in Reference Rommelaere and RitzRommelaere and Ritz (1996), Reference Hulbe and MacAyealHulbe and MacAyeal (1999), Reference Weis, Greve and HutterWeis and others (1999) and Reference HuybrechtsHuybrechts (2000). The equations, which characterize the velocity field, are

and
In this two-dimensional treatment the velocity is in the x-y plane and given by u and v components respectively, his the ice thickness, g is the acceleration due to gravity, zs is the surface elevation of the ice, and _ is the density of ice.
The effective viscosity η is found by assuming that the velocity field is uniform through the vertical coordinate.Effective viscosity here is defined by 2_ = o/e, so that:

where B is the vertically averaged temperature-dependent flow constant B in Equation (1).
Boundary conditions are either kinematic or dynamic. The kinematic boundary conditions are set from the velocity measurements around the grounded perimeter of the ice shelf. The dynamic boundary condition is determined from the following integral applied along the calving front:

where n is the outward-pointing normal vector along the front and p s is sea-water density. Model runs on Jakobshavn Isbræ have an additional level of complexity arising from the heavily crevassed surface of the region. Several approaches are taken in an effort to model this. Essentially, subdomains having different rheology are introduced. In these experiments the value of η is made a constant in specified subdomains, producing a linear rheology. We contend that this scheme can be used to represent the granular flow of broken ice that is flowing between larger cohesive blocks of ice.
The FEM was used for all model equations. The Missoula model for Equations (5-7) utilizes Lagrange, second-order elements. The steady-state solution to Equations (5) and (7) is found by an affine invariant form of the damped Newton-method iterative scheme (Reference DeuflhardDeuflhard, 1974), with Equation (7) updated after each iteration. Convergence is considered to be sufficient when (A · u — b) < 1 χ 10T6, where A is the matrix arising from the finite-element discretization scheme, b is the righthand side vector, and u is the solution vector.
Validation of the Missoula model for Equations (5-7) was carried out against the EISMINT (European Ice Sheet Modelling Initiative) suite of tests applied to the Ross Ice Shelf in Antarctica (Reference MacAyeal, Rommelaere, Huybrechts, Hulbe, Determann and RitzMacAyeal and others, 1996). Results using the Missoula model compare favorably with other ice-shelf models in the steady state. The Missoula model
compares favorably on all levels, showing exactly the same distribution and values of contour lines as those produced by the EISMINT experiments.
Results of ice-shelf modeling experiments
The floating portion of Jakobshavn Isbræ is investigated in three ways, which utilize Equations (5-7).
Uncrevassed ice shelf
In this experiment the floating portion of Jakobshavn Isbræ is treated as a continuous ice shelf with a single, uniform value of B = 180kPaa1/3, p =910 kg m–3 for ice density and p s = 1028 kg m–3 for sea-water density. The various features arising from crevassing in the region are not explicitly modeled. However, because the measured height field is used to compute the ice thickness (from buoyancy), there is some component of the fractured nature of the ice shelf. The kinematic boundary condition (ice velocity) is based on the data of Reference Prescott, Kenneally and HughesPrescott and others (2003) and is applied everywhere except the grid west side that corresponds to the calving front. Along this boundary, the dynamic boundary condition given by Equation (8) is applied. The finite-element domain was discretized with a triangular mesh consisting of 110498 degrees of freedom.
Figure 7 displays the base ten logarithm of the effective viscosity computed by interpolating the measured velocities onto the finite-element mesh, computing derivatives of the second-order Lagrange basis functions, and then using Equation (7) to compute the effective viscosity for B = 180kPaa1/3. Large (two orders of magnitude) changes in η occur across the domain, and the values of η are ‘clumpy’. The clumpyness is most clearly seen in the area of the main-trunk ice stream. There almost appears to be a wavelength of η. Measured surface elevation contours in Figure 3 are also clumpy. Figure 7 is a guide to all three modeling experiments.

Fig. 7. Calculated base 10 log of effective viscosities η for B = 180kPaa 1/3. Values are obtained from velocity data by using finite-element basis functions to compute ice-velocity derivatives for Equation (7). Contours show ice thickness at 25 m intervals.
Figure 8 shows that this experiment produces a set of smooth velocity contours. These are markedly different from the jagged contour lines that are seen in the measured velocities of Figure 5 In this and all subsequent figures, per cent difference is used to express the difference between the modeled data and the measured data, divided by the measured. While mismatch between measured and modeled velocities is generally <20%, concentrated areas of high mismatch are evident. This is most notable on the north and south boundaries, and along the west, where the calving front is. Another area of significant mismatch is along the east-west center line. Here, where potentially anomalous boundary effects are less likely to dominate, the fit should be good. Instead there were very large differences toward the calving front (cf. Fig. 5 and 8). Measured and calculated ice velocities in the main-trunk ice stream first decrease and then increase from the grounding line to the calving front, but the increase in measured velocities is long delayed. In addition, measured velocity vectors show divergent flow that opens longitudinal crevasses along the Zipper, but modeled velocity vectors are fundamentally parallel. This suggests some impediment to longitudinal flow that is not captured by the model.

Fig. 8. Results of the uncrevassed ice-shelf experiment. (a) Computed velocity field. Gray scale indicates magnitude of velocity; scaled arrows show direction. Contours are at 250 m a–1 intervals. (b) Percentage difference between computed and measured velocities for the floating portion of Jakobshavn Isbræ. Contours are at 5% intervals.
Ice shelf with Zipper
In this experiment, the Zipper is inserted into the geometry. We shall assume that crevassing in this region is so deep that Glen’s flow law no longer characterizes the rheology. A linear rheology is used and the viscosity is set to 3 χ 104 Pa a. The lower Newtonian value of viscosity used in the Zipper is based upon inspection of Figure 7 It allows enhanced flow anticipated in a fracture zone having granular flow of broken ice. The geometry of the Zipper as represented in this experiment is seen in Figure 9 The mesh used in this experiment consisted of 186 618 degrees of freedom.

Fig. 9. Results of the ice shelf with Zipper experiment. (a) Computed velocity field. Gray scale indicates magnitude of velocity; scaled arrows show direction. Contours are at 250m a–1 intervals. Feature modeled as the Zipper is shown with black line. (b) Percentage differences between computed and measured velocities for the floating portion of Jakobshavn Isbræ. Contours are at 5% intervals.
The model including the Zipper produces results that are more similar to the previous results than different. By introducing a low Newtonian viscosity along the Zipper, we hoped flow in the model would ‘pinch off flow in the smaller northern ice stream, as seen in Figure 2 In the model runs, some of this is evident, but the extent is not much more than that seen in the previous experiment. Figure 9 displays the modeled ice velocities and their misfit with measured ice velocities. Although models and measured velocities are generally similar, measured velocity isopleths often show irregularities. A low-viscosity Zipper generates a sharp gradient in modeled velocities across the Zipper that is not seen in measured velocities. This suggests the Zipper is a tensile feature, not a shear feature. As with the previous experiment, the most notable area of mismatch is the calving front where ice in the model is moving much too fast in the center and much too slow along the sides.
Fragmented ice shelf
In this experiment, possible granular regions in the floating portion of Jakobshavn Isbræ are modeled by assigning a linear rheology to regions in Figure 7 where the base ten logarithm of the effective viscosity is <5. These regions are identified in black in Figure 10 We argue that these are regions characterized by granular flow between larger blocks of ice. This idea is supported by inspection of Figure 7, which shows that regions of lower effective viscosity follow regions of thick ice flowing from the main-trunk ice stream. Hence, we impose the same linear rheology applied in the previous experiment to all regions having a measured log(η)<5.

Fig. 10. Results of the crevassed experiment. (a) Identification (in black) of the elements in the finite-element mesh that are assumed to be fragmented, and are therefore given a linear rheology in the fragmented ice-shelf experiment. (b) Results of the fragmented ice-shelf experiment. Gray scale indicates magnitude of velocity; scaled arrows show direction. Contours are at 250 m a–1 intervals.
The mesh used in this experiment consisted of 220 996 degrees of freedom.
The fragmented ice-shelf model produces ice velocities, shown in Figure 11, that are much faster than measured ice velocities in Figure 5 Velocity isopleths show a localized velocity high near the main-trunk grounding line, and the high velocity of the calving front extends much further back than it did in the previous two experiments. This is a direct result of assigning a low Newtonian viscosity to the black regions in Figure 10 It reduces constraints from side shear, and eliminates attempts of these constraints to bridge across the main-trunk ice stream. As Figure 10 implies, a degree of bridging takes place. In all three modeling experiments, substantial mismatch between the measured and modeled velocity fields is found. The most prominent mismatch is the low longitudinal strain rates in the measured data as compared to the modeled results. This indicates that the lower velocities that are applied as kinematic boundaries on the north and south border are insufficient to produce the correct amount of resistance to flow, and the result is the much higher velocities found in modeling of the calving front. The actual side resistance is high enough to partly bridge the main-trunk ice stream. How does this happen?
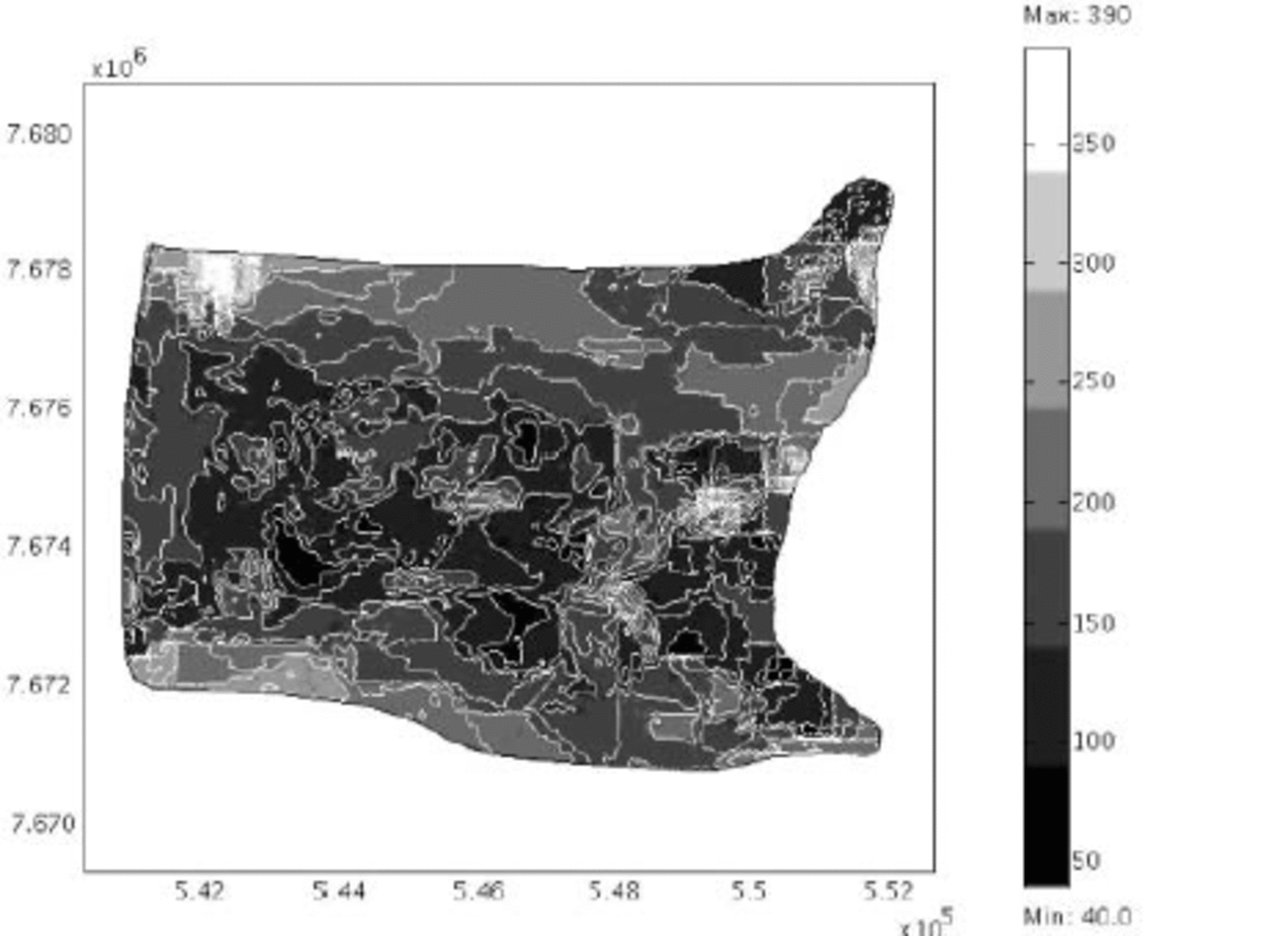
Fig. 11. Fig. 11. The effective stress field on the floating portion of Jakobshavn Isbræ, computed using measured velocities and their derivatives. Units of kPa. Contours are spaced at 25 kPa. Large fluctuations in the stress are seen propagating across the ice in the transverse direction, possibly indicating force chains, which resist longitudinal flow.
An Ice-Jamming Solution
The plane-stress and ice-shelf numerical experiments make clear that the exact nature of the flow in the floating portion of Jakobshavn Isbræ is difficult to reproduce using formulations based on control theory and continuum mechanics. In particular, the velocity field along the east–west center line is overestimated by the models. This suggests something more than lateral drag from the fjord walls is resisting the flow of the ice shelf. In order to explain the anomalously low longitudinal strain rates measured in Jakobshavn Isbræ we propose ice flow is being retarded by jamming. Heavy crevassing in Jakobshavn Isbræ may cause ice flow to resemble the flow of a granular material more than it does flow in a continuous body of ice. As a granular material, the highly fractured floating ice is susceptible to formation of chains of ice blocks that extend across the domain. These chains of blocks resist flow. This is called jamming.
Jamming of granular flow
Granular materials often flow in a manner that is consistent with a liquid state. For reasons that are being investigated, flow occasionally halts and the material then more closely resembles a solid. Such events are everyday occurrences, and are observed when granular materials pass through constrictions, ranging from holes in a salt-shaker to funnels in a grain elevator. The solid-like state is said to be jammed. To relieve the jam, the granular material must be jostled. A short introduction to jamming can be found in Reference Liu and NagelLiu and Nagel (1998). Jamming behavior has attracted the attention of scientists who work with granular materials or who study the mathematics of non-linear dynamics. Reference Cates, Whittmer, Bouchaud and ClaupinCates and others (1998) believe that the jammed state is fundamentally different from other states of matter in that it exhibits significant strength in one direction, along the principal stress axis, and can easily be broken by application of relatively small stresses in other directions. Such matter, which is strong in one direction and weak in others, is referred to as ‘fragile’.
Experimentation on fragile behavior is carried out by maintaining a constant strain rate in the granular material and monitoring the stress required. Fluctuations from the baseline stress correspond to some change in the flow behavior of the material, causing a transition from un-jammed to jammed states. The fluctuations that occur have been observed in various geometries and experimental setups (Reference Veje, Howell and BehringerVeje and others, 1999; Losert and others, 2000; Reference AlbertAlbert and others, 2001; Reference Komatsu, Inagaki, Nakagawa and NasunoKomatsu and others, 2001; Lootens and others, 2003). Several results are found for all geometries. One is that the relation between applied stress and strain rates can fluctuate suddenly by as much as a factor of ten (Lootens and others, 2003). Such fluctuations clearly represent transitions from the liquid-like to the solid-like (jammed) state. These transitions are abrupt and dramatic. Reference AlbertAlbert and others (2001) demonstrate that the frequency of jamming events can be periodic, random or stepped, depending upon the strain rate, and that the frequency of events follows a power-law distribution.
Such power-law behavior demonstrates that jamming exhibits self-organized criticality (Reference Bak, Tang and WiesenfeldBak and others, 1988). Self-organized systems are systems that exhibit a power-law scaling of events. Energy dissipated in jamming events has been shown to produce self-organized behavior (Lootens and others, 2003). Such phenomena are familiar from the study of earthquakes using the logarithmic Richter intensity scale. A relation between fault gouge, jamming and earthquakes is now being investigated (Reference MaroneMarone, 1998; Reference ScholzScholz, 1998). Such power-law behavior allows for an overall characterization of the system, because the power-law exponents are succinct and identify broad categories of self-organized systems. A focus of current research in jamming is characterization of a phase space for jammed matter (Reference Liu and NagelLiu and Nagel, 1998; Lootens and others, 2003). The phase diagram for such states would plot applied stress vs the concentration of particles. The jammed state is in some ways a function of the density of particles. A detailed exploration of the sensitivity of jamming to densities has led to the concept of a critical density. Jamming is frequent above the critical density and rare below it. Among the many theoretical investigations of jamming, Reference Cates, Whittmer, Bouchaud and ClaupinCates and others (1998) explained jamming as the formation of a network of force chains. This theory is well suited to the behavior of Jakobshavn Isbræ, where we theorize that individual ice blocks align across the fjord in some linear manner and produce a jam. A critical density of particles implies a critical fragmentation by crevassing in floating Jakobshavn ice.
Jamming in Jakobshavn Isbræ
Can jamming explain the behavior of floating ice in Jakobshavn Isbræ Clumping of ice elevation in Figure 3 and effective ice viscosity in Figure 7 imply more fracturing of ice in clumpy regions, perhaps due to partial grounding. From this we conjecture that jamming is possible due to the highly fractured nature of ice in these regions that allows force chains to bridge shattered ice, and thereby inhibit ice flow. If jamming in granular materials is any guide, there should be clear concentrations of the stress field across the fractured ice domains. These concentrations would correspond to the force chains arising from linear formations of ice blocks that span fractured regions in the transverse direction. Again, the effective stress is computed using the flow law of ice along with computed and measured ice velocities arising from the data in Reference Prescott, Kenneally and HughesPrescott and others (2003).
Figure 12 shows the effective stress field computed from the measured ice velocities. The well-known stress concentrations arising from lateral drag are apparent on the north and south walls. In places, effective stress concentrations bridge main-trunk ice in the transverse direction. These bridges may correspond to force chains that are retarding the flow of ice. Figure 13 shows the effective stress field computed from the modeled ice velocities. It is clear that no such force chains are produced by the model. Concentrations of stress appear on the north and south boundaries, but do not bridge across the domain. Hence, the commonly used ice-shelf model that utilizes the reduced Morland equations does not produce the critical force chains that help explain the measured velocity fields. From these results we conclude that jamming is indeed a distinct possibility for floating ice in Jakobshavn Isbræ.

Fig. 12. The effective stress field on the floating portion of Jakobshavn Isbræ computed from results of the uncrevassed ice-shelf experiment. Units are kPa. Contours are spaced at 25 kPa. There are no high-stress regions that propagate transversely across this ice, indicating that continuum mechanics fails to capture all the dynamics of this system.
Discussion
After the end of the Little Ice Age in Greenland, Jakobshavn Isbræ began a century-long retreat of nearly 30 km from 1850 to 1964 that could have included catastrophic retreat episodes, judging from 14 known positions of the calving front (Reference Carbonnell and BauerCarbonnell and Bauer, 1968; Reference HughesHughes, 1998, Fig. 1.5). The calving front was relatively stable from 1964 to 2002, when it rapidly retreated some 5 km until today it nearly coincides with the grounding line of floating ice (cf. Fig. 1 and 2). The cause for the rapid retreat, which occurred in only 1 year, was investigated using two modeling approaches.
In the plane-stress approach, a fit between measured and modeled ice velocities was attained mostly within <20%, using a constant ice-stiffness parameter (see Fig. 5). To reduce mismatch from under 20% to under 5% expected from measurement uncertainties, ice stiffness was converted into a ‘tuning’ parameter using control theory. Anomalously high ‘tuned’ ice stiffnesses, using both (continuous) Fourier and (discontinuous) Walsh series, occupied a zone of ice that bridged the main-trunk ice stream near the calving front, with ‘stiffening’ seeming to propagate from ice rumples behind the south side of the calving front (see Fig. 6).
In the ice-shelf approach, a constant ice-stiffness parameter was also used to isolate regions of mismatch between measured and modeled ice velocities. ‘Clumpiness’ in the distribution of calculated effective viscosities identified sites of maximum mismatch (see Fig. 7). A mismatch gradient occurred across the Zipper, and modeled velocities were too fast near the calving front (see Fig. 8). A low Newtonian viscosity was assigned to the Zipper, and the modeling experiment was repeated. This tended to concentrate mismatch in the lateral shear zones and near the calving front (see Fig. 9). Next, low Newtonian viscosities were assigned to all the clumpy effective viscosities in Figure 10 This resulted in the closest approach to ‘ideal’ flow in an ice shelf confined between parallel fjord walls (see Fig. 11). None of the ice-shelf modeling experiments produced the long region of nearly constant ice velocity in the main-trunk ice steam between the rear grounding line and the calving front, nor the divergent flow in this region that opened large transverse crevasses along the Zipper.
Conclusions
Both the plane-stress and ice-shelf experiments point to some mechanism that retards longitudinal extension of ice, with hints of partial grounding as the retarding feature. If the mismatch between modeled and measured ice velocities is caused by a degree of fragmentation of floating ice, which partial grounding would produce, then ‘force chains’ of fractured ice might form and ‘bridge’ the main-trunk ice stream, thereby impeding longitudinal extension and fostering transverse extension that opens longitudinal crevasses along the Zipper. High calculated effective stresses bridge main-trunk ice (see Fig. 11). The uncrevassed ice-shelf model does not produce stress bridges (see Fig. 12). ‘Jamming’ by force chains is commonly observed in flow of granular materials. If high basal melting rates calculated by Reference Prescott, Kenneally and HughesPrescott and others (2003) are a recent phenomenon, basal melting would eventually eliminate sites of partial grounding and thereby break any force chains that bridge main-trunk Jakobshavn flow. We recommend that jamming of highly crevassed floating ice moving between confining side-walls, and breaking of the force chains that jamming produces, should become a new direction for glaciological research on the catastrophic disintegration of ice shelves.
Acknowledgements
This work was funded by NASA and the US National Science Foundation, Office of Polar Programs. We thank J. Fastook for suggesting that rapid disintegration of the floating part of Jakobshavn Isbræ was caused when an ice jam became broken. We are most grateful to referees D. MacAyeal and R. Hindmarsh for suggestions that greatly improved the manuscript, and Scientific Editor R. Greve for guidance in bringing it to a publishable state. We also thank B. Hughes for preparing numerous versions of the manuscript over several years.














