1. Introduction
A water contact margin plays an important part in the local regime of a glacier or ice cap. At Generator Lake, the margin of Barnes Ice Cap has recently retreated about five times further than the retreat of the adjacent land-based margin, as determined from the glacial geology of the area. This part of the margin of the ice cap (Fig. 1) has been under close observation since 1969. Reference has also been made to earlier photographic records (1948 RCAF aerial photographs), some ground observations in 1950 (Reference BairdBaird, 1952; Reference WardWard, 1952), aerial photography in 1958 and 1961 as well as additional ground observations from 1966 (Reference BarnettBarnett, 1967; personal communication from D. M. Barnett).

Fig. 1. Map of part of Barnes Ice Cap and Generator Lake. Based on Generator Lake map sheet 27 C/12. 1: 50 000 (Canada. Department of Energy, Mines and Resources).
The purpose of the present paper is to describe the morphology of the ice margin at the proglacial Generator Lake, to discuss briefly calving in general, and in particular to draw attention to a significant calving event which was observed on 17 July 1970.
2. Lake Observations
Because water-level fluctuations in the lake have a critical influence on the stability of the ice front, particularly the ramps (see Section 3), water-level curves for 1970 and 1971 are given in Figure 2. Curves are also available for 1968 and 1969 (unpublished, Reference Barnett, Barnett, Forbes and WhytockBarnett and others, 1970). These are similar in form to the 1971 curve. The shape of the curves is explained on the following basis. During the winter months (October to May) the water level of the ice-covered lake remains essentially constant (assuming the outlet remains blocked during the winter and ignoring the effects of accumulating snow cover on the lake ice). This condition has been verified for a period of about one month in May 1970 and 1971.

Fig. 2. Water-level curves for Generator Lake as determined from continuous recordings on a Foxboro (pressure type) waler-level gauge and by precise levelling.
Beginning in the second half of June, depending on the year, the influx of melt-water run-off from the ice cap exceeds the outflow via Clyde River (Fig. 1) which is just starting to unjam. At this time the level of the lake rises rapidly until about mid-July when the outflow exceeds the inflow of melt water, and the lake level begins either to drop or to fluctuate depending on the ice conditions at the lake outlet and on the amount of run-off from the ice cap. Run-off is strongly dependent on the local meteorological conditions (Reference Andrews and SmithsonAnonymous, 1967). The maximum rise of water level about the spring low level in 1970 was about 30% greater than the average value for 1968, 1969, and 1971 which were all within about 10% of each other.
3. Observations At the Ice Front 1969–71
The present ice front (Fig. 3) is characterized by cliffs and ramps in the approximate ratio of 1: 1. A cliff is associated with an immediately grounded ice margin and a ramp is defined as a tapered projecting tongue of ice detached from the bottom of the lake but not necessarily floating in equilibrium. Cliffs occur in water shallower than about 30 m, whereas ramps predominate in water deeper than about 30 m. Typically, water depth exceeds 50 m just off the ramps.

Fig. 3. Aerial photograph of the ice cap margin at Generator Lake, 17 August 1971 (Photo: R. LeB. Hooke).
Observations of crumbling and sagging of parts of the cliff which rise 20–24 m above water level (1969–71) indicate that the cliff must be under-cut below the water line. Because of the danger of working in the immediate proximity of the cliffs, glaciological work was concentrated on the three main ramps.
Movement and ablation poles were set in place over the marginal area. From repeated surveys (1969–71) ice flow rates have been obtained (Fig. 4). Local strain-rates at some points (R3, R4, CI.1) have been determined from strain diamonds and at other points regional values were obtained from the velocity distribution.

Fig. 4. Map of ice front showing pole locations, horizontal ice flow rates, some strain-rates and major ice structure. The inset shows cross-sections through the three ramps.
Seismic soundings through the ice (1971) and sonic soundings in the lake water, using an ELAC (Castor type) echograph, combined with observations (1970) of the calving of the largest ramp have led to the reconstruction of the cross-section through the ice margin at T1 (Fig. 5). Figure 4 shows the position of the ramp on which T1 was located and the plan geometry of the fracture line.

Fig. 5. Detailed cross-section of the T1 ice ramp, before and after the calving event. The pre-calving thrust diagram, bending moment and stresses for the upper and lower surfaces are also shown.
3.1. Observations of calving
In general two types of ramp calving are possible, and these have been observed.
-
(a) Reeh-type calving (Reference ReehReeh, 1968), where, due to the imbalance of water pressure and ice stress, the margin of a floating section tends to curl forward and downward. Maximum effective stresses tend to build up at a distance behind the ice front approximately equal to the ice thickness there. As a result when calving occurs it tends to produce prismatic blocks of ice. Often, ice structure may significantly modify the geometry of the calving.
About 28–30 m of ramp ice must have broken away in front of R1 between 31 August 1969 and lake freeze-up of the same year because there was no evidence of the berg in the immediate vicinity of the margin in May, 1970 and open water was necessary to allow drift of the berg. Since the ice thickness there is estimated (on the basis of the hydrostatic condition and some water depth soundings) to be 25 to 35 m, it is concluded that the calving was probably of the Reeh type.Footnote *
-
(b) Calvings induced by changes in water level more rapid than the ramp can adjust to.
Water level may rise (Fig. 2) at rates exceeding 16 cm d−1 during the latter part of June and early July. By direct observation and by precise levelling it may be shown that the ramps, essentially in hydrostatic equilibrium in winter, are unable to adjust to the water-level rise by upward deflection and consequently some ramps may be completely flooded, submersing 1–2 m high vertical ice fronts at the ends of the ramps. As a result an upward buoyancy force acts along the length of the ramp (Fig. 5) tending to bend it upwards.
On 17 July 1970 at about 16.00 h a series of cracking noises were heard on the T1 ramp and at about 16.55 h a large fissure, about 400 m long appeared (Fig. 4) followed by a slow rigid rotation of the several detached blocks. The largest block of roughly triangular shape, measured about 100 m from the fracture line to the apex. At the end of its motion, the lakeward edge of this block (the apex) had risen from about 0.6 m above water level in the marginal lead to 6.5 to 7 m above water level (Fig. 5). The edge of the block adjacent to the ice cap had fallen from a few centimeters to 1.5 m, thus producing a normal fault. Despite heavily crushed ice in the fault zone, it was possible to detect a slight curvature of the fracture plane with depth. The fracture plane was essentially perpendicular to the plane of the surface.
The time of the calving was correlated directly with the water-level curve (Fig. 2) which was at that time approaching the maximum value, i.e. 2.08 m above the May low level. Since there were no other abnormal phenomena, e.g. meteorological or hydrological, at that time it may reasonably be assumed that the calving was entirely caused by up-bending of the ramp due to its submergence below the equilibrium level.
The progressive movement of the detached block was recorded until August 1971 (Fig. 6).

Fig. 6. Plot of the positions of the detached ramp from 17 July 1970 to 2 August 1971. Figure 3 shows the position of the berg after the break-up of lake ice.
4. Analysis of the Bending Problem
In Figure 5, a model is presented of a tapered ice slab of vertical thickness H(x) where x is the distance measured horizontally from the origin, which lies on the water line vertically above the hinge (line of floatation).
If ∆h(x′) is the vertical distance between the actual water level and its equilibrium level in relation to the ice slab, at a distance x′ from the hinge, the upward buoyancy force acting per unit width on an element of the ice length dx′ is
where ρ w is the water density, and g is the acceleration of gravity.
The equilibrium water level with respect to the slab is determined from the hydrostatic condition
where h(x) is the freeboard of the ice at distance x, and ρ i is the mean ice density (≈ 0.905 Mg m−3).
The distributed load given by Equation (1) induces a bending moment

at a distance x. x′ is the distance of the element dx′ from the origin and L is the full length of the ramp. For the pre-calving geometry, M(x) has been evaluated by semi-graphic numerical integration and is shown in Figure 5. In addition to the moment produced by the vertical forces, there is a moment, initially constant along the length of the slab, produced by the imbalance of horizontal stresses acting at the ice front. An analysis for the present case shows that this moment is in the opposite sense to the moment given by Equation (3) and is 3.8 MN m (0.38 × 106 kg cm) which is small compared to the moment produced by the vertical forces, particularly near the hinge (Fig. 5). Consequently the moment produced by horizontal forces will be neglected.
4.1. Bending stresses
The bending stresses through the slab may be determined if the stress–strain (or strainrate) relationship is known as well as the position of the neutral axis. Assuming the neutral axis to be defined by the point of contraflexure in the fracture curve (Fig. 5), the position of the neutral axis in bending lay, most probably, on the compression side of mid-depth of the slab. If the depth of the neutral axis below the top surface is denoted as ![]() , and if the variability and accuracy of measurement of the reconstructed post-fracture cross-sections is considered, then the factor ξ could have values
, and if the variability and accuracy of measurement of the reconstructed post-fracture cross-sections is considered, then the factor ξ could have values
For a given value of ξ it is possible to compute the corresponding ratio N e of the elastic compression modulus E c to the elastic tension modulus E t (Appendix A). A similar computation may be done for the plastic case.
It is possible that, before any fracture, the bending stresses developed according to a centrally located neutral axis and that, subsequent to the formation of a basal crack, the effective neutral axis moved upward so that the geometry of the later part of the crack was influenced by the actual crack history. In this connection the observations of Section 3.1 should be considered. Bearing in mind these possibilities, the range of bending stresses was calculated.
4.1.1. Elastic bending stresses
Following usual beam theory, (Reference TimoshenkoTimoshenko, 1958) the deviator stresses are obtained (Appendix B). The compressive stress

and the tensile stress
In the computations of the actual principal stresses, the hydrostatic stress (Section 4.4) may be taken into account. Because δ is small in the present case, the term (1 − δz 2)/(1 + δz 2) can be neglected in Equation (4).
The maximum stresses for a given vertical section are obtained by putting ![]() in (4) and
in (4) and ![]() H in Equation (5). These stresses (Appendix B) are plotted in Figure 5 as functions of x for ξ = 0.7 and ξ = 1.0. The corresponding surface compressive stresses are 0.21 MN m−2 and 0.15 MN m−2, respectively. The basal tensile stresses are 0.11 MN m−2 and 0.15 MN m−2 respectively at the hinge. The stress distribution through the slab is shown in Figure 7. These stress values may be considered as limits, the actual value lying somewhere between the upper and lower value of a pair.
H in Equation (5). These stresses (Appendix B) are plotted in Figure 5 as functions of x for ξ = 0.7 and ξ = 1.0. The corresponding surface compressive stresses are 0.21 MN m−2 and 0.15 MN m−2, respectively. The basal tensile stresses are 0.11 MN m−2 and 0.15 MN m−2 respectively at the hinge. The stress distribution through the slab is shown in Figure 7. These stress values may be considered as limits, the actual value lying somewhere between the upper and lower value of a pair.

Fig. 7. Bending stress distribution through the ramp at the hinge-line section, according to elastic and plastic theory, for two possible neutral-axis positions.
4.1.2. Plastic bending stresses
The bending stresses are now evaluated according to a plastic theory. It is assumed that a flow law (Reference NyeNye, 1953)
holds, where σ
ij
′ is a stress deviator component, ![]() is the strain-rate component; and λ = A
n
τ
n−1, where A is a physical constant, here called the plastic modulus, which depends on the ice properties, τ is the effective shear stress given by 2τ
2 = σ
ij
′/σ
ij
′ and n is a constant (n ≈ 3 for the magnitude of stresses encountered in the present problem).
is the strain-rate component; and λ = A
n
τ
n−1, where A is a physical constant, here called the plastic modulus, which depends on the ice properties, τ is the effective shear stress given by 2τ
2 = σ
ij
′/σ
ij
′ and n is a constant (n ≈ 3 for the magnitude of stresses encountered in the present problem).
Following the methods described in Appendix A it is shown that the plastic modulus ratio N p for the present problem is sufficiently given by
For

Ā c is the average value of A for compression (above the neutral axis) and Ā t is the average value of A for tension (below the neutral axis).
Using the methods presented in Appendix B, the plastic bending stresses are
in compression, and
in tension.
Equations (7) and (8) are used to compute the maximum stresses for a given vertical section and these are plotted against x in Figure 5. At the hinge section, the maximum compressive stress reaches 0.17 MN m−2 for ξ = 0.7 or 0.12 MN m−2 for ξ = 1.0. The maximum tensile stress (deviator) reaches 0.09 MN m−2 for ξ = 0.7 or 0.12 MN m−2 for ξ = 1.0. The complete stress distributions for this section are shown in Figure 7.
4.2. Induced normal stresses
A stress component will be induced in the vertical direction due to the horizontal compression or stretching caused by the bending.
For the elastic case, the simplifications involved in the derivation of the beam equation eliminate the need for consideration of the vertically induced stress. For the plastic case, considering the plane strain problem, the vertically induced stress deviator is equal to the horizontal stress component given by Equations (7) and (8) provided the signs are reversed.
4.3. Shear stresses
Because M(x) and hence σ xx are changing along the length of the ice ramp, shear stresses are generated within the ice. The derivation of the shear-stress distribution, assuming elastic bending, is presented in Appendix C. For the section at the hinge the shear-stress distribution is plotted in Figure 8.

Fig. 8. Shear-stress distributions through the ramp at the hinge-line section according to elastic and plastic theory, for two possible neutral-axes positions. The shear-stress distribution for a grounded section is also shown.
For the plastic case, Equations (C2) and (C4) (Appendix C) become

for 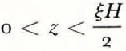 , and
, and

for  , where
, where 
For the section at the hinge, the plastic shear stress distribution is plotted in Figure 8. The maximum value of σ zx is determined from either Equation (9) or (10) when z = 0, and is
The shear stress in the grounded ice is approximately given by
if the longitudinal stress is neglected. In Equation (11), z is measured vertically downward from the surface, of slope α s. Figure 8 gives the shear stress distribution with depth according to Equation (11).
4.4. Hydrostatic stress
Within the grounded or floating ice the hydrostatic ice is approximately given by
4.5. Flow stresses
For the grounded part of the ice, the surface values of strain-rate (<1 × 10−5 a−1) indicate stresses of order 0.01 MN m−2 using the creep curves of Ramseier (in press). It is probably a fair assumption that the shear stress, as given by Equation (11) predominates in the ice below about mid-depth. However, in the zone surrounding the point of floatation of the ramp (Fig. 9) the longitudinal strain-rate and hence the longitudinal deviator stress is likely to reach high values (probably exceeding the bending stresses) because the ice, as it loses contact with the bottom, is forced to accelerate from the basal sliding rate to a flow rate approximately equal to the surface flow rate (27.6 m a−1 at T1).

Fig. 9. Cross-section of the T1 ramp showing the principal deviator stresses, before fracture.
Thus the values of bending and shear stress are superimposed on the flow stresses preexisting in the ice. In the absence of a reliable method of determining these latter stresses, the present analysis deals in detail only with those stresses associated with the bending problem. Of particular interest is a knowledge of the directions of the principal deviator stresses at points throughout the slab.
In the lower part of the ramp near the grounding line, the flow stresses could significantly change the actual values of the principal stresses, but the directions of the principal stresses will not be materially altered as the shear stress decays towards the bottom and is small compared to the normal stresses.
4.6. Principal stresses
Under the limitations just outlined, the magnitude and direction of the principal deviator stresses at several points in the ice have been determined using Mohr’s circle construction to combine bending and shear stresses in the ramp. Both elastic and plastic cases for ξ = 0.7 and 1.0 are considered. For the grounded ice near the surface (point G), an estimated longitudinal stress had been combined with the shear stress. The results are shown in Figure 9. For the ramp there is apparently no significant difference in the principal stress orientations if either the elastic or plastic stresses of bending and shear, together with their estimated errors are considered. Consequently, fan diagrams are shown (Fig. 9) which combine all the possibilities considered here. A progressive rotation of the principal (deviator) stress axes, from the top surface to the bottom, is immediately seen. If the postulation is made that a fracture (originating in this case from the bottom) travels upward following the direction of the maximum compressive stress (or perpendicular to the direction of least compressive stress—or tension) then a theoretical fracture curve resembling the observed one is seen as a result. In the case of beams (Reference LavrovLavrov, 1969) subjected to down-bending, the fracture plane clearly becomes perpendicular to the direction of maximum compression indicating a final stage of failure due to crushing.
5. Conclusion
To some extent the analysis has been successful in predicting a fracture geometry that has been observed in the field and in laboratory beam tests. However, in the field case marked anisotropy of the ice occurs. Furthermore, the effect of the advancing crack on the prefracture stress field is not formally accounted for, thus marked deviations from a theoretical fracture geometry can occur.
Such fracture shapes may be quite general and may apply also to the case of down-bending of ramps or to the Reeh mechanism of calving. In the latter case, this would explain why calved blocks often rotate backwards after detachment (Reference ReehReeh, 1969).
Insufficient knowledge of the physical condition of the basal ice and the flow stresses existing there, preclude a meaningful determination of the magnitude of the failure stress. Nevertheless it is possible to state that the additional bending stress (tension) of order 0. 1 MN m−2 was apparently sufficient to initiate a basal fracture which propagated up through about 54 m of ice.
The present results may be used to elucidate the mechanism of formation of sub-lacustrine moraines or cross-valley moraines (Reference Andrews and SmithsonAndrews and Smithson, 1966). This will be the subject of a further paper.
Appendix A
Calculation of the Ratio of the Average Elastic Compression Modulus to the Average Elastic Tension Modulus (Ē c/Ē t = N e) For an Elastic, Tapered Slab With A Displaced Natural Axis
Figure 10 shows a vertical section through an ice slab, deformed in bending. The upper and lower surfaces lie at distances ξH/2 and – (2 – ξ)H/2 from the neutral axis (z = 0). The x direction is measured along the neutral axis. A fibre of original length
lying at distance z above the neutral axis is compressed by an amount
where δx is the undeformed length of the element at the neutral axis, β is the fraction of the thinning of the slab contributed by the lower surface (0 < β > 1), R is the radius of curvature of the neutral axis and ϕ is the angle ![]() .
.

Fig. 10. Vertical section of a bent, tapered ice slab with displaced neutral axis.
Below the neutral axis a fibre of original length
is stretched by an amount
Making the approximations (R±z) ≈ R and ![]() for az
2 ⪡ 1, where a is an arbitrary factor, it can be shown that the strain at distance z above the neutral axis is
for az
2 ⪡ 1, where a is an arbitrary factor, it can be shown that the strain at distance z above the neutral axis is

and at z below the neutral axis it is
where c = dH/dx is a constant for a particular model.
The compressive stress in the x direction at distance z above the neutral axis is calculated from (A1)
where Ē c is the average value of the elastic modulus in the compression zone, and v is Poisson’s ratio. The longitudinal tensile stress at distance z below the neutral axis is calculated from (A2)
where Ē t is the average value of the elastic modulus in the tension zone. Assuming that the area under the compression curve is balanced by the area under the tension curve (a condition of equilibrium)

where
Solving (A5) it can be shown to a good approximation that
The point of contraflexure in the fracture curve (Fig. 5) lies approximately within an 8 m wide zone above the mid-depth level in the ice at the hinge.
This gives values of 1 ⩾ ξ ⩾ 0.7 and 1 ⩽ N e ⩽ 3.45.
In support of these results, it has been shown (Reference LavrovLavrov, 1969; Reference LafleurLafleur, unpublished) in model ice beam-bending experiments that in general the fracture curve is asymmetrical, with the point of contraflexure markedly displaced towards the compression side of the beam. As one possibility, this may be explained by a difference in value between E c and E t, although in the case of the model beams no reason is given (Reference LavrovLavrov, 1969).
In the Barnes Ice Cap ramp the mean (annual) temperature of the ice above the neutral axis is about − 6.7°C whereas below the neutral axis the mean temperature is close to −0.5°C. In addition, the lower ice probably possesses a stronger crystal fabric than the upper ice and contains more impurities. In fact, the lower few metres are expected to carry about 8% ±3% by volume of moraine (Holclsworth and McLaren, 1971). Therefore, good reasons exist for believing that the values of E e and E t may be different. In particular E e ⩾ E t. By a similar argument, the plastic modulus ratio, N p, (see section 4.1.2) is expected to be ⩾1.
Appendix B
Calculation of the Bending Stresses in A Tapered, Elastic Slab Where the Neutral Axis is Not Necessarily Central
Considering only the particular case of up-bending, Equations (A3) and (A4.) of Appendix A are used to obtain

from which
for
and
for
For the case ξ = 0.7, N e = 3.45, Equation (B2) gives for the top surface a maximum compressive stress
and for the base, Equation (B3) gives a maximum tensile stress
where H = H(x).
For the case where ξ = 1.0 (neutral axis centrally located)
Appendix C
Calculation of the Shear Stresses for the Elastic Case
The shear stress, σ
zx
, for the region ![]() is given by
is given by

where
where dx is the width of a vertical slice of the slab, and use has been made of Equation (B2) (Appendix B). To a good approximation Equation (C1) reduces to
where ![]() and
and ![]() is the taper coefficient.
is the taper coefficient.
In a similar manner, using Equation (B3) (Appendix B) the shear stress for the region – (2 –ξ)H/2 < z < o, may be determined from

which reduces to

For the vertical section through F (Fig. 5) at the hinge, the value of V, the total vertical shear force over the section, has been evaluated numerically by integrating Equation (1) to give
The maximum value of σ zx is determined either from (C2) or (C4.) when z = 0 and it is σ zx (max) ≈ 0.05 MN m−2.












