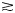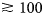1. Introduction
Ground penetrating radar (GPR) uses the electromagnetic field to infer sub-surface physical properties (Davis and Annan, Reference Davis and Annan1989). GPR has been widely used in glaciology to characterize englacial structures (e.g. internal ice layers, shear zones), the glacier thermal regime, the basal topography and ice thickness, or the glacier hydrology (see Plewes and Hubbard, Reference Plewes and Hubbard2001; Woodward and Burke, Reference Woodward and Burke2007; Navarro and Eisen, Reference Navarro and Eisen2009; Schroeder and others, Reference Schroeder2020, for reviews). The detection of a target object in ice through GPR relies on measurable reflections of the propagated electromagnetic field at the object's boundaries. These reflections are essentially due to a change of relative electrical permittivity. Alternatively, diffractions can occur when the target is small compared to the frequency-dependent wavelength. In the context of detecting sub- and englacial channels, such diffracted signals are mostly unwanted and are considered as noise.
GPR is particularly suitable for cold ice studies because liquid water is minimal in such cases and most of the reflected energy is conserved and the signal absorption is limited. In contrast, the use of GPR for temperate ice is more challenging. On one hand, the permittivity contrast between ice and water is large, resulting in clear reflections from englacial water bodies. On the other hand, the presence of individual water inclusions might enhance the energy loss of the GPR signal through diffractions. Bamber (Reference Bamber1988) demonstrated that at 60 MHz, the scattering power from englacial water bodies with a radius greater than 25 mm is larger than the scattering power from a perfectly plane boundary. This results in a strong attenuation of the reflected signals.
The last decades have seen a growing interest in GPR studies on temperate glaciers, and notable improvements on data acquisition and processing methods have been achieved (e.g. Schroeder and others, Reference Schroeder2020). In polythermal glaciers, strong diffractions from englacial liquid water and the associated noise signal has been used to identify the cold-temperate transition surface (e.g. Björnsson and others, Reference Björnsson1996), while in temperate glaciers it has been used to estimate the liquid water content (LWC) (e.g. Murray and others, Reference Murray, Stuart, Fry, Gamble and Crabtree2000). In many cases, however, the GPR signal in temperate ice is too blurry to interpret englacial characteristics or even bedrock positions. Some of the airborne-GPR profiles discussed in Grab and others (Reference Grab2021), for instance, do not reveal any bedrock reflections although the same instrumental setting gave good results for other profiles with similar bedrock geometries. Similar is true for ground-based GPR measurements acquired in 2019 on the two temperate Swiss glaciers Triftgletscher and Glacier du Trient (discussed later) which only reveal bedrock reflections at very few locations, even for glacier areas where the bedrock is expected to show a shallow slope (imaging of the bedrock might be precluded for geometrical reasons in sections with steeply dipping bedrock).
Smith and Evans (Reference Smith and Evans1972) suggested that it is the presence of liquid water – rather than the ice fabrics, the impurity content, or the temperature – which is mainly responsible for the back-scattered GPR signal in temperate ice. In response to Smith and Evans (Reference Smith and Evans1972), Watts and England (Reference Watts and England1976) recommended to use GPR frequencies below 10 MHz to limit the scattering power from englacial water bodies, for bedrock detection. However, there has been no systematic investigation on the subject so far. Although it is clear that the amount and distribution of englacial water impacts the interpretation of the GPR signal, water content variations and distribution have rarely been addressed quantitatively, rendering the interpretation of the GPR signal's ‘blurriness’ speculative.
Numerical modeling to emulate the GPR signal in synthetic glacial environments provides an avenue to tackle the problem, but so far, only few studies leveraged this possibility. For instance, Barrett and others (Reference Barrett, Murray, Clark and Matsuoka2008) characterized distribution and size of water inclusions from a surge-type glacier by comparing their field-based GPR results to forward modeling results. They were able to explain the observed GPR data by implementing decimeter-scale water inclusion confined in dipping planar features. Catania and others (Reference Catania, Neumann and Price2008) suggested the presence of moulins in the Greenland ice sheet from GPR measurements. They reproduced the synthetic moulin signature by numerical modeling and found a good correlation with the field-based data, thus validating their initial suggestion.
In this study, we use numerical modeling to validate the statement of Smith and Evans (Reference Smith and Evans1972) - that liquid water is mainly responsible for the back-scattered GPR signal in temperate ice - and to quantify the impact that the englacial water content has on the GPR signals. In particular, we perform a set of synthetic forward-simulations of the GPR signal, and explore the impact of changing snow thickness, ice permittivity distribution, LWC values and size of the water inclusions. Permittivity distribution, LWC and water inclusions size values are taken from field observations on temperate glaciers. Our aim is to indicate which values of water content and which size of water inclusions significantly diminish GPR reflection returns which are useful for interpretations of the GPR signal.
2. Method
2.1 Background theory
Diffraction patterns in GPR sections often appear as random, yet one would expect them to have a deterministic origin. We have three hypotheses for the origin of these patterns, namely (1) the presence of a wet snowpack at the glacier surface, (2) heterogeneous ice properties, such as variations in the ice permittivity, and (3) small-scale water inclusions which may act as distributed scatterers. We neglect the others type of inclusions such as rocks or air voids (see Section Discussion). Here, we test which of the three hypotheses is the most likely one, and do so by isolating the different cases. In the following, we refer to these three cases as ‘glacier models’.
2.2 Glacier models
A glacier model is defined by its geometry and materials properties. In order to assess the effects on the GPR data, we build our glacier models upon a reference model in two dimensions, and sequentially add new features to it. More specifically, we start with a reference model consisting of homogeneous, water-free ice, and then add, in turn, (i) a snowpack with a given LWC, (ii) heterogeneous ice properties with stochastic fluctuations, and (iii) small-scale water inclusions distributed amid the ice. All simulations share constant geometry parameters such as ice thickness and glacier width (Table 1) while the di-electrical properties of the ice are given in Table 2.
Table 1. Model parameters for the forward simulations of the GPR signal
The subglacial channel radius is considered to be a typical value (Fountain and Walder, Reference Fountain and Walder1998; Cuffey and Paterson, Reference Cuffey and Paterson2010). The maximal scatterer radius r max refers to the size of the randomly distributed water inclusions.
Table 2. Di-electrical properties of the space-domain for the gprMax simulations
Di-electric properties of granite and glacial melt water are taken from Plewes and Hubbard (Reference Plewes and Hubbard2001). Di-electric properties of ice vary stochastically with values according to Jezek and others (Reference Jezek, Clough, Bentley and Shabtaie1978), Johari and Charette (Reference Johari and Charette1975) and Plewes and Hubbard (Reference Plewes and Hubbard2001). Di-electric properties of wet snow are calculated from Tiuri and others (Reference Tiuri, Sihvola, Nyfors and Hallikaiken1984) and Granlund and others (Reference Granlund, Lundberg and Gustafsson2010) with a snow density of ρ snow = 500 kg m−3 and LWC = 3 %. Permeability μ and magnetic loss Ω are kept constant at μ = 1 and Ω = 0 Ohm m−1 for all materials.
2.2.1 Reference model: homogeneous, water-free glacier ice
The geometry and materials of the reference model are given in Figure 1a. The geometry includes a flat bedrock at 100 m depth and a subglacial channel with a radius of 2 m. We include the subglacial channel as a possible target for a GPR campaign. As such, the bedrock and the subglacial channel represent the two targets for which we will check how the imaging quality is affected by the model additions presented below.
Figure 1. 2D geometry of the investigated glacier models and relative permittivity ($\epsilon _r$
) for (a) the reference model, (b) the additional wet snowpack, here 10 m thick, (c) the additional stochastic variation of ice permittivity (note the different color scale), and (d) the additional water inclusions (here LWC = 0.2 % and r max = 0.1 m). The position of the bedrock (labeled ‘b’) and the subglacial channel (labeled ‘c’) are indicated by arrows for each model.
2.2.2 Model addition 1: wet snowpack at the glacier surface
Glacier ice is often overlain by snow or firn, and this layer might contain some liquid water. Such conditions are particularly prominent in spring, when GPR campaigns are often performed (e.g. Bauder and others, Reference Bauder2018). We assess the impact of such a layer by adding it to the surface of our reference model (Fig. 1b). The layer thickness is either 1 m or 10 m, which we consider being the range of a typical snowpack in Alpine settings. We calculate the layer's permittivity $\epsilon _s$
by using the parametrization suggested by Tiuri and others (Reference Tiuri, Sihvola, Nyfors and Hallikaiken1984):
where 0.1 and 0.8 are two empirically determined coefficients, LWC is the liquid water content, $\epsilon _w = 80$
is the relative permittivity of the water (Table 2), and $\epsilon _d$
is the relative permittivity of dry snow. The latter is calculated from the density ratio between snow and water, that is ρ snow/ρ w (dimensionless):
The wet snow conductivity σ (μS m−1) is calculated following Granlund and others (Reference Granlund, Lundberg and Gustafsson2010):
With the above equations, a typical spring snowpack over glaciers with ρ snow/ρ w = 0.5 and LWC = 3 % (Griessinger and others, Reference Griessinger, Mohr and Jonas2018), results in $\epsilon _s = 2.3$
and σ = 10−4 S m−1. These values are in good agreement with field observations (see e.g. Fig. 5 in Evans (Reference Evans1965)). Note that the value for $\epsilon _s$
is close to the permittivity of ice (see Table 2), and that we consider a bulk permittivity for the snowpack, i.e. we do not explicitly account for the snowpack's water inclusions. Our argument for doing so is that these water inclusions are expected to be very small when compared to the wavelength of the GPR signal in snow: at 25 MHz, the latter is in the order of 1 m, while the diameter of the water inclusions in snow are expected to be <1 mm (e.g. Coleou and others, Reference Coleou, Lesaffre, Brzoska, Ludwig and Boller2001). Moreover, we also ignore stochastic variations in permittivity that could occur because of a heterogeneous distribution of water content. We deem this omission to be acceptable after testing the effect that such a stochastic permittivity distribution would have in a 10 m thick snow pack (not shown) and after ascertaining that the effect is not large enough as to mask the strong diffraction patterns that we typically see in the field data and that we try to explain.
2.2.3 Model addition 2: heterogeneous ice permittivity
Measurements of the relative permittivity of ice $\epsilon _r$
(dimensionless) range between 2.89 and 3.26, with a mean value of ~3.2 (Robin and others, Reference Robin, Evans and Bailey1969; Johari and Charette, Reference Johari and Charette1975; Jezek and others, Reference Jezek, Clough, Bentley and Shabtaie1978; Plewes and Hubbard, Reference Plewes and Hubbard2001; Reynolds, Reference Reynolds2011; Bohleber and others, Reference Bohleber, Wagner and Eisen2012). Variations in $\epsilon _r$
occur due to the permittivity's dependence on ice density, temperature, and crystal orientation fabrics. The influence of ice density is discussed in Kovacs and others (Reference Kovacs, Gow and Morey1995), who proposed a slightly modified relationship proposed by Robin and others (Reference Robin, Evans and Bailey1969) for capturing such effects.
Ice density in alpine glaciers is most often considered to be homogeneous, and we thus expect $\epsilon _r$
to vary only slightly. Bohleber and others (Reference Bohleber, Wagner and Eisen2012), for example, reported variations in the order of a few percent (see their Fig. 4). Crystal orientation fabrics can also influence $\epsilon _r$
, with variations in the order of 1 % (Johari and Charette, Reference Johari and Charette1975; Fujita and others, Reference Fujita, Mae and Matsuoka1993).
Here, we account for the natural variations in ice permittivity by imposing stochastic variations on $\epsilon _r$
in the range of 2.89 to 3.26 (Fig. 1c). The stochastic distribution is parameterized with a von Karman type correlation function (Goff and Holliger, Reference Goff and Holliger2012) described by a Hurst number 0.5 (that is an exponential distribution) and a correlation length of 10 m (both in the horizontal and the vertical dimension). The Hurst number (also known as the ‘fractal dimension’) characterizes the amount of heterogeneity in a natural medium (Goff and Holliger, Reference Goff and Holliger2012), and we will explore the sensitivity of this value in the Results section.
2.2.4 Model addition 3: scattering water inclusions
Water inclusions are modeled as randomly distributed, spherical scatterers. We constrain LWC and the size of the scatterers based on literature values. Barrett and others (Reference Barrett, Murray, Clark and Matsuoka2008) explain strong scattering in a surging glacier by the presence of water inclusions of multi-decimeter scale. Likewise, Hodge (Reference Hodge1976) observed englacial voids in boreholes, reporting that typical vertical extents were of several decimeters (see their Fig. 3).
LWC in temperate ice has been estimated from GPR by analyzing the electromagnetic wave velocity (Macheret and others, Reference Macheret, Moskalevsky and Vasilenko1993; Moore and others, Reference Moore1999; Murray and others, Reference Murray, Stuart, Fry, Gamble and Crabtree2000) or from the back-scattered power in individual GPR sections (Bamber, Reference Bamber1988; Hamran and others, Reference Hamran, Aarholt, Hagen and Mo1996; Macheret and Glazovsky, Reference Macheret and Glazovsky2000). Reported LWC values ranges from 0.5 % to 1.5 % in Murray and others (Reference Murray, Stuart, Fry, Gamble and Crabtree2000), from 0.3 % to 1.7 % in Raymond and Harrison (Reference Raymond and Harrison1975); Vallon and others (Reference Vallon, Petit and Fabre1976), and from 0 % to 9 % in Pettersson and others (Reference Pettersson, Jansson and Blatter2004).
More recently, LWC has been estimated from surface nuclear magnetic resonance (SNMR). SNMR is a geophysical technique that allows the direct detection and quantification of liquid water in the subsurface. It takes advantage of the magnetic moment and spin of the hydrogen nuclei of water. Traditionally applied in hydrological applications, the technique has shown promising results in glacier applications too (e.g. Hertrich and others, Reference Hertrich, Braun, Gunther, Green and Yaramanci2007; Legchenko and others, Reference Legchenko2011; Garambois and others, Reference Garambois, Legchenko, Vincent and Thibert2016). In summer 2008, SNMR was for example performed at the tongue of Rhonegletscher, a temperate glacier in Switzerland, yielding an average LWC estimates of 0.8 % ± 0.4 % for the sampled vertical profile (Hertrich and Walbrecker, Reference Hertrich and Walbrecker2008).
To test the effect of different configurations of distributed scatterers on the GPR signals, we perform simulations in which we (i) vary the LWC between 0.1 % and 1.5 %, with increments of 0.1 % (i.e. fifteen different values for LWC) and (ii) randomly vary the radius of the water inclusions between 0 and a maximal radius of either r max = 0.1 m, r max = 0.5 m, or r max = 1.0 m. This results in a total of 15 × 3 = 45 simulations (Fig. 1d provides one example). The position of the scatterers is randomly generated but remains the same for each combination of LWC and r max. This is to allow for comparisons between simulations. The di-electric properties of the water inclusions are the ones of glacial melt water (see Table 2).
2.3 Numerical modeling and processing of GPR data
2.3.1 Modeling algorithm
For modeling the GPR signal numerically, we use the open source software gprMax (Warren and others, Reference Warren, Giannopoulos and Giannakis2016). gprMax implements Yee's algorithm to solve Maxwell's equations in 2D or 3D using the finite-difference method in the time-domain (FDTD, Kunz and Luebbers, Reference Kunz and Luebbers1993). Here, we use the 2D configuration, for which gprMax uses the so-called transverse magnetic mode. This is achieved by setting the length of one of the horizontal dimensions to the spatial discretization, thus reducing that dimension to a single grid point. We use this 2D modeling approach (as opposed to 3D) because GPR field-data are most often migrated in 2D profiles and to reduce computational cost.
The source signal in gprMax is set to a Hertzian dipole with a dominant frequency of 25 MHz (a typical frequency for investigations on Alpine glaciers; e.g. Church and others, Reference Church, Grab, Schmelzbach, Bauder and Maurer2020; Grab and others, Reference Grab2021) and with a Ricker type source-time function. To mimic field measurements, we place the transmitter and receiver antennas at 0.5 m above the glacier surface and perpendicular to the investigated profile. The spacing between the transmitter and the receiver is kept constant at 4 m (corresponding to one wavelength in air at 25 MHz). The spatial increment of the antennas position along the profile (i.e. the trace spacing) is of 0.5 m. The length of the GPR profile for each simulations is 95 m and corresponds to 190 traces. gprMax antennas characteristics are summarized in Table 3.
Table 3. Time and space parameters for the gprMax simulations
In order to run the gprMax simulations, we discretize the glacier models defined in the previous Section in space and time. To avoid numerical dispersion, the space discretization length Δl should be ≤λ min/10 (Warren and others, Reference Warren, Giannopoulos and Giannakis2016), where λ min is the smallest wavelength of the propagating electromagnetic field. For a given frequency, λ min is associated to the material with the smallest electromagnetic propagation velocity v min. We calculate λ min as follows:
where $\epsilon _r$
is the relative permittivity and f the central frequency (f max = 3 × f as we consider as null the amplitude beyond three times the central frequency for a Ricker waveform). In our case, λ min is found for water, which is the material with the largest relative permittivity (see Table 2) and thus the smallest velocity (v water = 0.33 × 108 m s−1).
For f = 25 MHz and water, λ min is 0.44 m, and we thus chose Δl = 0.05 m. This allows to speed up the simulations compared to Δl = 0.05 m by a factor of 5 (more information on computational time follows below). This means that the wavelength in the water is sampled by nine cells. The fact that we sample by nine cells instead of ten means that the highest frequency (and thus the shortest wave length) propagates with a velocity on the grid that is 0.93 % smaller than the desired velocity (Schneider, Reference Schneider2010) – a difference which we consider as being negligible. The time is discretized according to Δl and following the Courant-Freidrichs-Lewy stability condition (Warren and others, Reference Warren, Giannopoulos and Giannakis2016). The receiver recording time is set to 1.5 × 10−6 s, which corresponds to a penetration depth of the signal in ice of ~125 m (two-way travel time). A so-called perfectly matched layer width of ten cells (i.e. 0.5 m) is set on the model boundaries to absorb the signal and simulate an unbounded space (Berenger, Reference Berenger1996). Time and space model parameters for gprMax are summarized in Table 3.
Solving Maxwell's equations using the FDTD approach for high-resolution data is computationally expensive. To accelerate the simulations, we run gprMax on graphics processing units (GPUs). The FDTD discretization allows for a natural and efficient parallelization of the solver and allows leveraging the parallel processing capabilities of latest GPUs. We run the simulations using eight Nvidia A100 (SXM4, 40GB) GPUs. gprMax also allows for multi-GPU configurations, where independent trace computations are distributed among GPUs using message passing interface for distributed parallelization in a master-slave configuration. GPU computing permitted to speed up the simulations by a factor of 15 compared to multi-threaded central processing unit configurations. This results in a typical runtime for a single simulation of ~ 5 min. All data necessary to reproduce our gprMax simulations, including the MATLAB input files generator, are available in the Section Code and Data Availability.
2.3.2 GPR data processing
The gprMax output contains time series of the electromagnetic field strength for all grid cells and for all traces. As for field data, further processing is required to generate GPR sections that can actually be interpreted. For this, we employ our in-house Matlab-based toolbox GPRglaz (Grab and others, Reference Grab2018) and follow the processing workflow typically used for field-based investigations (e.g. Church and others, Reference Church, Grab, Schmelzbach, Bauder and Maurer2020; Grab and others, Reference Grab2021).
More specifically the workflow comprises (1) time zero correction based on the arrival of the direct wave, (2) bandpass filtering (10 MHz to 65 MHz) to cut undesirable low and high frequencies generated by numerical dispersion, and (3) image focusing and time-to-depth conversion that migrates the data with a constant radar wave velocity (0.167 m ns−1 for ice; Glen and Paren, Reference Glen and Paren1975). Migration is performed with a Kirchhoff time migration scheme (Margrave and Lamoureux, Reference Margrave and Lamoureux2019). For access to the generated GPRglaz results, see the Section Code and Data Availability.
3. Results
3.1 Impact of a wet snowpack (model addition 1) and a heterogeneous ice permittivity (model addition 2)
Figures 2a, 2b and 2c present the GPR-signals from our gprMax simulations for the reference model (i.e. homogeneous ice), the additional wet snow pack at glacier surface, and for the additional stochastic distribution of ice permittivity, respectively (see also Fig. 1). Early times carry the signature of the direct wave traveling from the transmitter to the receiver antenna. The bedrock reflection is clearly visible, and the channel structure manifests itself in form of an X-shaped pattern. This is an artifact from the Kirchhoff migration, which is due to its diffraction-limited characteristic (Özdemir and others, Reference Özdemir, Demirci, Yiğit and Yilmaz2014).
Figure 2. Results of the gprMax simulations for the (a) reference model, (b) additional wet snowpack, here 10 m thick, (c) additional stochastic variation of ice permittivity, and (d) and (e) additional water inclusions (here LWC = 0.1 % and r max = 0.1 m). The associated geometry and materials are shown in Figure 1. The positions of the bedrock (label ‘b’) and the subglacial channel (label ‘c’ are indicated by arrows for each model. All Results are presented for a frequency of 25 MHz. Results (a),(b),(c) and (d) are presented after Kirchhoff migration, and (e) is presented before Kirchhoff migration (time in y-axis).
The snowpack at the glacier's surface has no visible influence on the signal, even when it has a thickness of 10 m (see Fig. 2b). This is in agreement with Smith and Evans (Reference Smith and Evans1972), who stated that GPR signal attenuation of wet snow is relatively small as long as the liquid water is salt-free – a condition certainly met in Alpine environments.
A heterogeneous ice permittivity results in small perturbations of the signal (Fig. 2c). However, the strength of the signals is significantly weaker than the one reflected from the bedrock and the subglacial channel. The statement holds true also when varying the parameters that govern the stochastic distribution of the permittivity (these are the Horst number ν and the correlation length λ): Fig. 3 shows the results for simulations with ν = 0.1 and ν = 2, as well as λ = 1 m and λ = 20 m – a range of values that we assume cover any plausible variations in real-world conditions. Both the resulting field strengths and noise patterns are very similar to Fig. 2c, indicating that the choice of model parameters and, more importantly, of variations in permittivity as such, only have a marginal influence on the retrieved GPR signal.
Figure 3. Sensitivity test for the Horst number ν and the correlation length λ used for simulating a stochastic distribution of ice permittivity. The range of explored values (i.e. ν = [0.1, 2.0] and λ = [1, 20] m) are considered to be plausible upper- and lower-bounds. Data are presented after Kirchhoff migration. The bedrock (label ‘b’) and the subglacial channel (label ‘c’) are indicated.
We thus conclude that natural variations in ice permittivity are insufficient to explain the noise that characterizes many GPR data acquired in the field for temperate glaciers.
3.2 Impact of water inclusions (model addition 3)
The impact of water inclusions on the GPR signal is shown in Fig. 2d, and results in a signal that is qualitatively similar to field data (see the Discussion Section for more details). For the chosen parameters (i.e. LWC = 0.1%, r max = 0.1 m), the bedrock and the subglacial channel remain visible, although much less clearly than for the reference model. Fig. 2e presents the unmigrated GPR signal for LWC = 0.1 % and r max = 0.1 m too. The unmigrated signal shows more clearly the detrimental effect of the water inclusions on the bedrock and the subglacial channel detectability, which is partially improved by the Kirchhoff migration.
To further investigate the effects of water inclusions, the simulations are repeated with different LWCs and different sizes of the water inclusions. Figure 4 presents a selection of simulation for three values of each LWC and maximum scatterer radius. In all cases, the GPR signal is strongly attenuated with increasing depth because of the energy lost through scattering. For LWC = 0.1% and r max = 0.1 m, the bedrock and the subglacial channel are clearly visible. For higher LWC (e.g. 0.5% and 1 %), the bedrock and the subglacial channel are no longer visible, regardless of the radius of the water inclusions. This indicates that bulk LWC values in the range of 0.1 % – 0.5 %, associated to water inclusions with radii in the order of several decimeters, already constitute a limit beyond which a bedrock at 100 m depth becomes impossible to detect with a frequency of 25 MHz. When the scatterer size increases for a constant LWC (i.e. when the number of scatterers decreases), more sections of water-free ice appear between the surface and the bedrock. In these sections, the bedrock is more visible, as seen when comparing the results with r max = 1 m and r max = 0.5 m in Fig. 4. Also note that the bedrock depth tends to be slightly overestimated with increasing LWC. This is because our Kirchhoff migration ignores the presence of water, i.e. it applies the same velocity of propagation for the electromagnetic field for all materials.
Figure 4. Results from gprMax simulations for nine combinations of LWC and maximal radius of the water inclusions. The number of individual scatterers n is indicated on the bottom right of each panel. The bedrock (label ‘b’) and the subglacial channel (label ‘c’) are indicated by arrows. Results refer to 25 MHz and are presented after Kirchhoff migration.
While the results presented so far refer to GPR data collected with 25 MHz antennas, we note that using different frequencies would qualitatively lead to the same results as long as the size of the scatterers are scaled with the dominant wavelength. For example, using 50 MHz and scatterers with a radius of 0.5 m would give the same results as for 25 MHz and a radius of 1.0 m. At most, a difference is expected to emerge in the achievable penetration depth and the size of the identifiable features – with higher frequencies having stronger attenuation but better spatial resolution than lower frequencies (see, e.g. Watts and England, Reference Watts and England1976, for the spectral response of scatters according to their sizes and the frequency). When the wavelength of the electromagnetic signal in water is significantly smaller than the scatterer radius, one would also expect the appearance of multiple internal reflections. For 25 MHz and 50 MHz, this is the case for scatterers with r max > 1 m and r max > 0.5 m, respectively. We provide in the Section Code and data availability the additional simulations using 50 MHz for r max = 0.1 m, r max = 0.5 m, and r max = 1.0 m.
4. Discussion
4.1 Similarities of synthetic and field-data
Limited bedrock detectability has often been reported (e.g. Langhammer and others, Reference Langhammer, Rabenstein, Bauder and Maurer2017; Grab and others, Reference Grab2021; Rutishauser and others, Reference Rutishauser, Maurer and Bauder2016; Bradford and others, Reference Bradford, Nichols, Mikesell and Harper2009). Figure 5a and 5b present two GPR sections acquired in August 2021 on Glacier du Trient (Switzerland), and in July 2021 on Triftglestcher (Switzerland's Mattertal), respectively. Both glaciers are temperate, and the surveys were carried out with 25 MHz antennas. The GPR data were processed with GPRglaz using the same steps as described for the gprMax simulations.
Figure 5. Comparison between real-world GPR data and data simulated through numerical modeling. Field data are shown for (a) Glacier du Trient and (b) Triftgletscher (Mattertal), two temperate glaciers in Switzerland. The data simulated with gprMax (c) are obtained with LWC = 0.1 % and r max = 0.1 m, resulting in n = 1047 individual scatterers. The bedrock is indicated by black arrows. All three example refer to 25 MHz antennas and are presented after Kirchhoff migration.
For both the mentioned GPR sections, signal scattering is particularly pronounced at depths between 20 m and 60 m. The strong bedrock is clearly visible at depths between 70 m and 100 m for Glacier du Trient and between 110 m and 130 m for Triftgletscher, but the signal is not continuous across the profiles. Figure 5c presents one of the synthetic GPR sections, generated with gprMax with LWC = 0.1 % and r max = 0.1 m (same configuration as in Fig. 4 and same geometry as in Fig. 1d). The spatial pattern of the scatterers and the strength of the reflected energy are very similar to the real-world data shown in Fig. 5a and 5b. This similarity is only achieved when water inclusions are included in our numerical simulations, meaning that the variations in ice permittivity and the presence of a snowpack are not sufficient to reproduce the signal characteristics observed in actual field data.
4.2 Scatterer distribution within the glacier body
A simplification of our analyses is that the scatterers are distributed homogeneously in the entire glacier body. In reality, this might be different. It is known, for example, that the water level within a glacier can fluctuate in space and time as a response to pressure changes in the subglacial drainage system (e.g. Iken and others, Reference Iken, Fabri and Funk1996; Werder and others, Reference Werder, Schuler and Funk2010; Rada and Schoof, Reference Rada and Schoof2018; Gräff and Walter, Reference Gräff and Walter2021). In such cases, one would expect the scattering water inclusions to be preferentially located below an englacial water table.
Such a distribution is suggested, for example, by a second GPR section collected at Triftgletscher (Fig. 6). At horizontal distances between 0 and 450 m, the uppermost 30 m of the ice show an almost scatter-free, transparent zone (note that the some parts of this zone are partially obscured by remnants of the direct wave) while below that level, pronounced scattering is visible. Interestingly, the amount of scattering varies horizontally: between about 300 and 450 m horizontal distance, for example, the scattering decreased significantly, and as a consequence, the bedrock is clearly recognizable up to a depth of ~ 170 m. This is in contrast to the GPR section between 0 and 300 m horizontal distance, where strong scattering obscures the bedrock.
Figure 6. GPR field data after Kirchhoff migration on Triftglestcher (July 2021). The depth of the interpreted water table is marked by the horizontal dotted line above the scatterers.
We speculate that high amounts of scattering occur for ice sections with high LWC, e.g. in areas where englacial fracturing is more pronounced due to extensional strain (Bradford and others, Reference Bradford, Nichols, Mikesell and Harper2009) and where the resulting englacial voids are filled with water. To support this conjecture, we perform another set of numerical simulations in which we subdivide the ice column in two layers: an upper layer with no scatterers (i.e. LWC = 0 %) and a lower layer, containing all the scatterers. Results for LWC = 0.2% and r max = 0.1 m are presented in Fig. 7. A LWC of 0.2% is chosen because the bedrock reflections already start to be obscured in this case (see Fig. 4) and because our interest is in exploring the limits of detectability of both the bedrock and the subglacial channel.
Figure 7. gprMax results for scatterers distributed (a) along the entire ice column (labeled ‘single layer’) and (b) only in the lower half of the ice column (labeled ‘two layers’). LWC = 0.2 % for all simulations. The number of scatterers n is indicated at the bottom right of each panel. The bedrock and the subglacial channel are indicated by the arrows with labels ‘b’ and ‘c’, respectively.
For this two-layer configuration, the reflections stemming from both the bedrock and the subglacial channel are qualitatively similar to the one-layer case. We suggest that the reflected signal attenuation is more sensitive to LWC and scatterer-size than to the distribution of the layering. This supports the interpretation that the noisy patches often observed in field data correspond to regions with dense scatterers, the latter being in turn an expression for locally high LWC values.
The change between regions of weak and strong scattering has been often interpreted as a transition between cold and temperate ice (e.g. Blatter and Hutter, Reference Blatter and Hutter1991; Björnsson and others, Reference Björnsson1996; Moore and others, Reference Moore1999; Gusmeroli and others, Reference Gusmeroli, Jansson, Pettersson and Murray2012). This is consistent with the interpretation provided above, as cold ice is expected to have only very low LWC and thus only very few and small water inclusions that could produce scattering. However, we note that scatter-free ice section found for Triftgletscher (Fig. 6) is temperate, not cold (this information is derived from an in-situ temperature measurement (not shown) that we conducted in the middle of the shown profile at 15 m depth during August to September 2021). We therefore suggest that temperate ice with very low LWC can have a similar GPR-signature to cold ice. In turn, this indicates that the precise characterization of the thermal regime of a glacier from GPR data alone could be more challenging than assumed so far. This interpretation is in line with findings presented by Campbell and others (Reference Campbell2012) and, more recently, by Gerbi and others (Reference Gerbi2021).
4.3 Interpretation of the LWC variations with depth
The observations made in Fig. 6 (low scattering near the surface and much more pronounced scattering at depth) have been made on a number of other temperate glaciers too (see, e.g. Rutishauser and others, Reference Rutishauser, Maurer and Bauder2016, and references therein). Rutishauser and others (Reference Rutishauser, Maurer and Bauder2016) denoted these features as ‘internal reflection bands’ (see their Fig. 13).
Our hypothesis is that such differences in scattering are caused by small-scale water inclusions and by LWC variations with depth. This hypothesis is not only supported by the striking similarity between our modeling results and field data (see previous Section) but also by independent field observations. Indeed, the already mentioned SNMR measurements performed on Rhonegletscher in 2008 (Hertrich and Walbrecker, Reference Hertrich and Walbrecker2008), indicate such LWC variations, with $LWC\sim 0.3\%$
at 30 m below the surface and LWC > 1% below ~60 m.
A qualitatively similar LWC-profile was found by Bradford and others (Reference Bradford, Nichols, Mikesell and Harper2009) for a temperate Alaskan glacier. By analyzing GPR velocity profiles, they distinguished two distinct ice layers: a ~20–30 m thick layer with LWC between $\sim 0\%$
and 0.5% near the surface, underlain by a layer with LWC of $\sim 1\%$
to 2.5 % (see their Fig. 6).
Also, Murray and others (Reference Murray, Stuart, Fry, Gamble and Crabtree2000) found a layered LWC structure for a temperate Icelandic glacier. Their Fig. 8 shows LWC ~0.2% at the surface and a sharp increase to ~3.5% at 28 m depth. Conversely to our Rhone data, however, Murray and others (Reference Murray, Stuart, Fry, Gamble and Crabtree2000) found that the LWC decreases again with increasing depth, until reaching ~0.1 % at the bedrock.
While the field methodologies mentioned above do not allow identifying sharp transitions in LWC, we suggest that these marked LWC changes can be interpreted as indicative for the presence of a ‘water table,’ i.e. a feature similar to what is found for aquifers. In this scenario, ice fractures and other voids that are present below a certain depth would be water filled, while similar features above that level would be filled with air. This interpretation is broadly consistent with observations performed during drilling campaigns on temperate glaciers: boreholes drilled in temperate glaciers generally fill with water up to a certain level, that level being in hydrostatic equilibrium with the subglacial drainage system (e.g. Iken and others, Reference Iken, Fabri and Funk1996; Pohle and others, Reference Pohle, Werder, Gräff and Farinotti2022). With this interpretation, the finding by Murray and others (Reference Murray, Stuart, Fry, Gamble and Crabtree2000) (i.e. the fact that LWC decreases again close to the bedrock) could be explained by the fact that the ice overburden pressure increases with depth, thus tending to re-close any voids that might emerge.
4.4 Plausibility of the size of the water inclusions
In our simulations, we chose to limit the maximal radius of the water inclusions to r max = 1 m. For one, this choice allowed for obtaining a GPR signal that is qualitatively similar to real-world GPR data. For another, these dimensions are broadly compatible with indications found in the literature.
Holmlund (Reference Holmlund1988), for example, visually observed former water-filled pockets visible at the surface of a polythermal glacier in Sweden after the surface melted out. Fig. 8 and 9 of that publication suggest that these water-filled pockets can be several meters large.
Bradford and others (Reference Bradford, Nichols, Mikesell and Harper2009), as another example, performed GPR velocity analysis in a temperate Alaskan glacier to infer its LWC. They concluded that most of the englacial water is likely to be contained within voids having dimensions in the order of a few centimeters up to several meters, rather than at the ice grain boundaries.
Further literature examples are difficult to find, and we thus affirm that the question about the size and number of water-filled voids in temperate glaciers merits further attention.
4.5 Influence of scatterer distribution and ice permittivity
So far, the spatial distribution of the scatterers was kept unaltered. This allowed direct comparison of the different simulations. Here, we address the sensitivity of our results to the scatterer distribution by running four gprMax simulations with LWC = 0.2 % and r max = 0.1 m but by changing the scatterer locations. All models have a comparable number of scatterers, although the number is not exactly the same since the radii of the scatterers are randomly varied too. We call the four generated distributions ‘s1’ to ‘s4’ (Fig. 8).
Figure 8. Sensitivity test for four different distribution of scatterers (s1 to s4). All panels have LWC = 0.2 % while the radius of the scatterers is either (a) r max = 0.1 m or (b) r max = 1.0 m. The number of scatterers n is approximately the same for all cases (indicated at the bottom right of each panel) while the location of the scatterers is randomly varied. The bedrock and the subglacial channel are indicated by the arrows with labels ‘b’ and ‘c’, respectively.
Fig. 8a suggests that for a large number of scatterers, the spatial distribution has little impact on the signal. This is because the scattering is strong everywhere. When the LWC is small and/or scatterers are large (i.e. when scatterers are sparse), we observe a higher sensitivity of the distribution on the signal noise (Fig. 8b). Strong and uniform noise in the GPR signal is thus most likely due to a large number of relatively small scatterers.
4.6 Limitations of the method and neglected factors
Strictly speaking, the detection and imaging of isolated englacial features would require a 3D approach including a dense grid of GPR profiles. This is because side reflections from off-plane scatterers also affect the GPR signal – a situation that is neglected when applying a 2D migration (e.g. Barrett and others, Reference Barrett, Murray, Clark and Matsuoka2008). Although we ignored such effects in our study, the fact that our results look very similar to field data (Fig. 5) indicates that the first-order effect of water inclusions was sufficiently captured. Our main conclusion is, thus, that small-scale water inclusions are the main reason for the typical scattering observed in GPR data for temperate glaciers.
Related to the above, it is conceivable that other, non-considered englacial features may contribute to the scattering too. Such features could include internal ice structures such as deep crevasses, air voids or moraine material (e.g. rocks) buried within the ice. While such rock inclusions could be of similar size to the water inclusions we considered (diameters ranging from a few millimeters to a few meters), we note that the permittivity of rock ($\epsilon \sim 3$
–6) is much closer to the one of ice ($\epsilon \sim 3.2$
) than it is to the one of water ($\epsilon \sim 80$
; see Tab. 2). This means that the back-scattered energy from a signal originating from rocks is expected to be much weaker than the one from water inclusions. Moreover, the typical pattern of moraines and crevasses at the surface of a glacier, i.e. the fact that such features follow a rather clear spatial distribution, suggests that moraine materials and englacial crevasses are likely less ubiquitous than water inclusions. Although air also has a permittivity that is more similar to ice than water (for air, $\epsilon \sim 1$
), its radar velocity is much faster. This causes air voids to produce strong hyperbolas (Nobes, Reference Nobes2017). However, air voids are assumed to be mostly water-filled in temperate ice, or close by ice overburden pressure. Combined, these three arguments let us argue that although englacial crevasses, air voids and rock inclusions might influence the GPR signal, they are very unlikely to be the main source of scattering.
5. Conclusions
In this study, we used numerical modeling of GPR signals to characterize the influence that a wet snowpack, a heterogeneous ice permittivity, and distributed water inclusions have on GPR data acquired on temperate glaciers at 25 MHz. We showed that the presence of wet snow and heterogeneous ice permittivity are insufficient to explain the strong signal scattering often observed in the field, and instead suggest that englacial water inclusions are the main cause for such scattering.
In terms of practical implications, our results confirm that GPR surveys aiming at estimating subglacial characteristics of temperate glaciers are best conducted in winter, when englacial water contents are generally low and the related scattering is suppressed. In such water-free conditions, temperate ice can have a GPR signature that is similar to the one of cold ice. This implies that distinguishing between cold and temperate ice through GPR surveys – as sometimes is done in the literature – bares some pitfalls: while the presence of substantial scattering in the GPR signal can be interpreted as indicative for the presence of water and thus temperate ice, the absence of such scattering is indeed indicative for low water contents but these might occur for both temperate and cold ice. Stated differently: an area free of scatterers is a necessary but not a sufficient condition for interpreting a given ice portion as being cold.
Our numerical simulations also indicate that a bulk LWC of 0.2 %, associated to decimeter-scale water inclusions, is already sufficient to mask bedrock reflections through signal attenuation. The value is in the range of field-based LWC observations, thus explaining why real-world GPR data on temperate ice often fail to detect the bedrock. Our numerical experiments also showed that the GPR signal is sensitive to heterogeneous distributions of water inclusions. In particular, glacier sections with locally low LWC can be far less affected by scattering than sections with high LWC. This gives rise to individual sections that are ‘transparent’ to the GPR signal, i.e. sections with strong signal reflections from the targeted objects. Finally, we showed that the distribution of small scatterers has less of an impact on target detectability that the distribution of large scatterers. Overall, our results contribute to a better understanding and interpretability of GPR signals over temperate ice.
Data
The GPR measurements acquired at Triftgletscher and Glacier du Trient are available through ETH Zurich's Research Collection, https://doi.org/10.3929/ethz-b-000590672. The ice temperature measurements acquired at Triftgletscher are available through ETH Zurich's Research Collection, https://doi.org/10.3929/ethz-b-000609144. The results of the gprMax simulations and the MATLAB scripts to generate the gprMax input are available through ETH Zurich's Research Collection, https://doi.org/10.3929/ethz-b-000609177. gprMax is an open access software available at https://www.gprmax.com/.
Acknowledgements
This project was financially supported by the Swiss National Science Foundation (grant nr. 200021_212061). The authors thank the following persons for their support during the fieldwork at Triftgletscher and Glacier du Trient in 2021: Raphael Moser, Guillem Carcanade, Mathieu Cretet, Clement Valla, Lea Geibel, Manuela Köpfli, Lena Strauman, Josquin Pfaff and Inés Dussaillant.
Open access
