Modelled water-pressure effect on sliding (Iken, 1981)

Motivated by observations of short-term velocity variations in glacier flow speed (Reference IkenIken, 1978) and the relationship between measured vertical and horizontal velocities (Reference Iken, Rothlisberger, Flotron and HaeberliIken and others, 1983), Reference IkenIken (1981) constructed an idealized model to investigate the relationship between subglacial water pressure and glacier sliding. Although water pressure had been linked to basal motion through several proposed mechanisms (e.g. Reference LliboutryLliboutry, 1968;Reference JonesJones, 1979), the observations motivated the idealization of the glacier bed as an impermeable undulating surface. Building on the theoretical work of Reference LliboutryLliboutry (1968, Reference Lliboutry1979) and Reference KambKamb (1970), Reference IkenIken (1981) aimed specifically to examine the effect of water pressure on sliding during the transient stages of cavity development.

Assuming a perfectly lubricated glacier bed, a linear ice rheology and instantaneous water supply or drainage, Reference IkenIken (1981) employed a finite-element code for stress-strain analysis developed originally at Eidgenossische Technische Hochschule (ETH) for tunnel construction. Both sinusoidal and quasi-sinusoidal bed shapes were considered (undulations of 20 m wavelength and 1.5 m amplitude), with an ice thickness (310 m) and bed slope (4°) chosen to resemble those of Unteraargletscher, Switzerland. While the finite- element code was reasonably amenable to this problem, several manual interventions were required including: (1) an iteration to ensure consistency between a given water pressure and the affected bed area;(2) careful positioning of the nodes at the downstream end of the cavity roof to insure bed-parallel ice motion at the point of contact; and (3) a trial-and-error approach to defining correct steady-state cavity configurations for a given water pressure. Iken was among the first to employ finite-element methods to solve glacier flow problems (e.g. Reference IkenIken, 1977), in part because of the extraordinary patience required; iterations were performed manually with punch cards until convergence was reached.

The results of this modelling effort clearly illustrated sliding enhancement in response to an applied water pressure between the ‘separation pressure’ p _s (e.g. Reference LliboutryLliboutry, 1968;Reference NyeNye, 1969;Reference KambKamb, 1970), defining the onset of ice- bed separation, and the ‘limiting’ or ‘critical’ water pressure p ₁ = ρgdsin (β – α)/sin β derived by Iken (Fig. 1), beyond which unstable sliding was predicted to occur. At the onset of cavity formation, simulated ice flow near the bed became more plug-like; flow speeds exceeded those modelled when the cavities reached steady state, where ice-bed separation was at its maximum (cf. figs 4b, 5b and 6a in Reference IkenIken, 1981). A small decrease in water pressure precipitated a dramatic change in the modelled flow field, including transient reverse sliding above the stoss face of the downstream obstacle. This intriguing latter prediction remains neither confirmed nor refuted by observations, though some forms of reverse glacier motion have been documented (e.g. Reference Harrison, Raymond and MacKeithHarrison and others, 1986).

Fig. 1. Diagram illustrating the derivation of the limiting water pressure of stability. An ice slab of thickness d is resting on a stepped bed with a mean slope α (Reference IkenIken, 1981).

Reference IkenIken (1981) drew several important conclusions related to the effect of bed geometry, cavity extent and water pressure on sliding velocity: (1) bed configurations with lower separation pressures (e.g. obstacles with steep lee faces) produce a stronger sliding velocity response to water pressure;(2) sliding sensitivity to water-pressure increases with the area over which the water pressure acts and also depends on the orientation of the area; (3) if this area remains constant, sliding speed increases linearly with water pressure for a Newtonian ice rheology; and (4) sliding is most sensitive to water pressure at the inception of cavity formation, rather than when cavities reach their maximum steady-state sizes. Thus, sliding speed is predicted to be highest during the early stages of cavity growth.

Reference IkenIken (1981) concluded that ‘sliding velocity is neither simply a function of the subglacial water pressure nor of the size of cavities but depends on both variables’, and speculated that observations of early season glacier acceleration may be the manifestation of unstable sliding at water pressures below overburden. She suggested that the limited duration of these events may be related to limited water supply and imperfect hydraulic connectivity across the glacier bed. Future observations, including those of Reference Iken and BindschadlerIken and Bindschadler (1986), would reveal stable sliding at pressures greater than the critical pressure, pointing to a role for basal friction as suggested by Reference IkenIken (1981) and later modelled by Reference Schweizer and IkenSchweizer and Iken (1992) and to global force- balance controls on the sliding process (e.g. Reference Cuffey and PatersonCuffey and Paterson, 2010).

Seasonal uplift and basal water storage (Iken and others, 1983)

Up to 0.6 m of surface elevation increase was observed at the beginning of the melt season on Unteraargletscher by Reference Iken, Rothlisberger, Flotron and HaeberliIken and others (1983) using a combination of optical survey data and photographs from an automatic camera. The authors speculated that a similar ‘uplift’ may have been observed on Unteraargletscher as early as 1842/43 by Louis Agassiz (Reference AgassizAgassiz, 1847). In 1975, theodolite measurements of poles arranged in four transverse profiles were undertaken at intervals from 2 hours to 3 days. At the pole where the highest-resolution measurements were made, errors were controlled such that vertical positions were known to 2 mm. The data showed stable downward stake movement over winter giving way to a prolonged period of summer uplift, which was punctuated by several uplift events associated with periods of enhanced melt. Reference Iken, Rothlisberger, Flotron and HaeberliIken and others (1983) clearly documented the coincidence of maxima in horizontal velocities and maxima in vertical velocities, rather than vertical displacements (Fig. 2; Fig. 3 in Reference Iken, Rothlisberger, Flotron and HaeberliIken and others, 1983). That horizontal velocity maxima occurred during uplift appeared to confirm the principal finding of Reference IkenIken (1981).

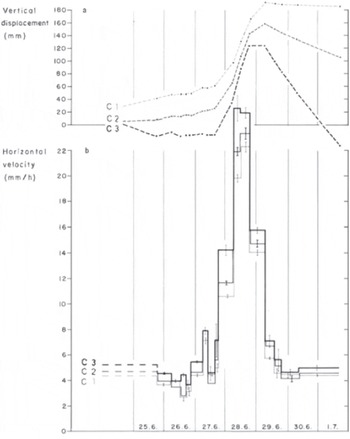
Fig. 2. Detailed theodolite measurements of glacier movement indicating an ‘uplift’. (a) Vertical displacement of three poles, C1 to C3; C1 is near the glacier margin, C3 on the medial moraine. (b) Horizontal velocity of the same poles (Reference Iken, Rothlisberger, Flotron and HaeberliIken and others, 1983). Data from Unteraargletscher, 1975.

Fig. 3. Velocity of pole C3 as a function of the subglacial water pressure (shown as depth of water level below surface). The water pressure, equal to the ice-overburden pressure a₀ at the centre line, corresponds to a depth of water level of 18m below the surface. Different symbols refer to different periods (Reference Iken and BindschadlerIken and Bindschadler, 1986). Data from Findelengletscher, 1980-82.

Reference Iken, Rothlisberger, Flotron and HaeberliIken and others (1983) interpreted these observations as the result of cavity growth at the glacier bed in response to pressurized water, pointing to the dominant influence of water pressure on glacier sliding speed. They came to this conclusion by systematically ruling out the following as leading explanations for the observed uplift: temporal variations in longitudinal strain rate, increases in glacier volume due to crevasse formation, expansion of intragranular veins and dilatation of subglacial sediments. This rigorous approach to attribution was characteristic of Iken’s work throughout her career. In seeking to explain how a minimum of 0.3 m of water could be stored in cavities at the bed without precipitating unstable sliding, Reference Iken, Rothlisberger, Flotron and HaeberliIken and others (1983) calculated that sinusoidal undulations of 0.56 m in amplitude covering most of the glacier bed could accommodate the water;however, they speculated that the cavities were probably more compact than this and perhaps asymmetric in shape, with more steeply inclined stoss faces. The data in Figure 2 have become the classical empirical demonstration of ‘hard-bedded’ sliding.

Observed water-pressure effect on sliding (Iken and Bindschadler, 1986)

Reference Iken and BindschadlerIken and Bindschadler (1986) put the theoretical underpinnings of basal sliding (e.g. Reference LliboutryLliboutry, 1968, Reference Lliboutry1979; Reference KambKamb, 1970;Reference IkenIken, 1981;Reference FowlerFowler, 1986) to the test with simultaneous measurements of borehole water level and surface velocity at Findelengletscher. This temperate valley glacier, located in the Pennine Alps of Switzerland, was chosen because of its observed sensitivity to changes in water input (e.g. Reference IkenIken, 1978). Ice-surface velocities were obtained from sub-daily optical surveys of velocity stakes arranged in four rows transverse to ice flow. These measurements were not automated, hence their temporal resolution was proportional to surveyor effort. Twenty-five boreholes were drilled to the bed over a laterally confined ~1 km section of the glacier, using hot-water drilling capability that Iken was instrumental in developing (Reference IkenIken and others, 1977). Borehole water levels were monitored with membrane gauges and Goerz ‘Miniscript’ recorders. These recorders employed pens and rolls of paper and had the advantage, according to Iken, of allowing one to easily verify their operation and inspect the data. Checking the Miniscript was usually the first task of the morning and in at least one case, when exceptionally high water levels were recorded, prompted a round of survey measurements before breakfast.

Hydraulic connections with the englacial/subglacial drainage system were observed in 11 of the 25 boreholes, and water levels in the connected holes were found to be roughly parallel to the ice surface across the borehole array. Diurnal cycling of water levels commenced in early June, with daily peaks generally being synchronous across the array and lagging the local peak in surface melt by 68 hours. Multi-day variations in horizontal velocity at the stake locations were strongly correlated to borehole water levels. Reference Iken and BindschadlerIken and Bindschadler (1986) emphasized this correlation between flow speed and basal water pressure, but commented little on the precise phasing between the two during transient events. The data they presented showed velocity maxima generally occurring during rising water pressures, though this relationship was not a tidy one.

When Reference Iken and BindschadlerIken and Bindschadler (1986) plotted one of these velocity records from the central study area against water level averaged over four of the connected boreholes (Fig. 3; Fig. 6 in Reference Iken and BindschadlerIken and Bindschadler, 1986), a relationship emerged that encapsulates the central result of this study. This relationship becomes asymptotic where basal water pressure approaches the ice overburden pressure, and appears to hold over a wide range of water levels and for data collected over different time periods and in two different years.

Reference Iken and BindschadlerIken and Bindschadler (1986) interpreted these data, along with the results of dye-tracing tests and electrical conductivity measurements, as evidence for drainage through a system of interconnected cavities (e.g. Reference LliboutryLliboutry, 1968, 1979) where cavity growth is a function of subglacial water pressure (e.g. Reference IkenIken, 1981). To arrive at this interpretation, they ruled out decoupling of the glacier sole from the bed by flotation, based on the measured water pressures being too low, and pervasive sediment deformation, which would not explain the persistence of the functional relationship at low water pressures. The stability of the relationship in time required that the basal shear stress and the fraction of the bed subject to water-pressure variations remained roughly constant. The rapid borehole response to several waves of high basal water pressure was interpreted as reflecting the enlargement of cavities and, in cases of water pressure meeting or exceeding overburden, rapid bed separation. The low propagation speeds of these pressure waves (~50-180m h^-1) also pointed to a system capable of water storage along a tortuous flow path. The behaviour described above contrasted with that documented by Reference Iken, Fabri and FunkIken and others (1996) for the central region of Gornergletscher, Valais, Switzerland, where the presence of a subglacial sediment layer was inferred from the damped and delayed response of the drainage system to hydraulic perturbations.

The data in Figure 3 were compared with theoretical predictions, namely the sliding speed over a perfectly lubricated sinusoidal bed for a constant basal shear stress. Empirical estimates of the separation pressure p _s corresponded to water levels of 140-180 m below the surface and were obtained from Figure 3 by extrapolating the relationship to a horizontal tangent at low water levels. Values of bed roughness a/λ ~ 0.02 were obtained for the empirical separation pressures according to p _s = σ₀ – λτ/πa, where σ₀ is the ice overburden pressure, λ and a are the wavelength and amplitude of sinusoidal bed undulations, respectively, and τ ≈ 1 bar is the basal shear stress. These roughness values were deemed consistent with the visible bedrock undulations of the proglacial area, but when used to calculate the limiting or critical pressure for a sinusoidal bed, p _c = σ₀ – λτ/2πa, predicted unstable sliding at pressures that were far too low. The data in fact suggested a critical pressure very near the ice overburden pressure. Reference Iken and BindschadlerIken and Bindschadler (1986) isolated the assumption of perfect basal lubrication as the leading shortcoming in their theoretical calculations and suggested that friction due to basal debris may play a significant role in reducing the basal shear stress that contributes to sliding. They concluded with one of the rarely mentioned but inevitable truths regarding the interpretation of field data: ‘In order to reach conclusions, it was often necessary to generalize the results of measurements made at a very limited number of points and, furthermore, to decide sometimes what was typical or irregular.’

In a germane follow-up study, Reference Iken and TrufferIken and Truffer (1997) made similar measurements to those of Reference Iken and BindschadlerIken and Bind-schadler (1986) on Findelengletscher during its advance in the early 1980s and its subsequent retreat. They found a different relationship between borehole water level and glacier flow speed than that plotted in Figure 3. Data from 1985, at the end of the advance, and from 1994, during the retreat, were distinct from one another and plotted below the data from 1980-82. By 1994, the variation in glacier velocity with water level was less than that of 1980-82 by about an order of magnitude. Reference Iken and TrufferIken and Truffer (1997) attributed this change in the relation between water level and sliding speed to a change in the nature of the subglacial drainage system over time, in which the connectivity between cavities had decreased. In effect, unconnected areas of the glacier bed buffered the velocity response to basal water pressure: high sliding rates were inhibited by limited water access to cavities, while the lowest sliding rates were precluded by isolated water pockets failing to drain.

Alpine glacier hydromechanics

Nowhere has the trio of works by Iken and colleagues been more influential than in the study of alpine glacier hydromechanics. These studies span a range of subjects from ‘spring events’ (e.g. Reference Anderson, Fernald, Anderson and HumphreyAnderson and others, 1999; Reference Kavanaugh and ClarkeKavanaugh and Clarke, 2001;Reference Mair, Nienow, Willis and SharpMair and others, 2001) to jokulhlaups (e.g. Reference BjornssonBjornsson, 1998;Reference RussellRussell and others, 2006; Reference Sugiyama, Bauder, Weiss and FunkSugiyama and others, 2007) to glacier erosion (e.g. Reference HookeHooke, 1991;Reference IversonIverson, 1991;Reference HarborHarbor, 1992;Reference Jamieson, Hulton and HagdornJamieson and others, 2008; Reference MacGregor, Anderson and WaddingtonMacGregor and others, 2009). Short-term to seasonal variations in velocity as observed by Iken and colleagues have been documented around the world on both temperate (e.g. Reference Naruse, Fukami and AniyaNaruse and others, 1992;Reference Raymond, Benedict, Harrison, Echelmeyer and SturmRaymond and others, 1995; Reference NienowNienow and others, 2005;Reference Purdie, Brook and FullerPurdie and others, 2008) and polythermal glaciers (e.g. Reference Hooke, Wold and HagenHooke and others, 1985;Reference JanssonJansson, 1995;Reference Copland, Sharp and NienowCopland and others, 2003;Reference Rippin, Willis, Arnold, Hodsonand and BrinkhausRippin and others, 2005; Reference Bingham, Nienow, Sharp and CoplandBingham and others, 2006). A review of this work through the early 1990s is given by Reference WillisWillis (1995).

Glacier surges furnish a dramatic example of flow variations, and accordingly references to the work of Iken and colleagues can be found in the numerous papers related to the 1982-83 surge of Variegated Glacier (e.g. Reference KambKamb and others, 1985;Reference Kamb and EngelhardtKamb and Engelhardt, 1987;Reference Raymond and HarrisonRaymond and Harrison, 1988). Reference IkenIken’s (1981) conceptualization of the sliding process is akin to Reference Kamb and EngelhardtKamb’s (1987) linked cavity model used to explain the surge mechanism for Variegated Glacier. Many features of the antecedent mini-surges of 1978-81 were likened to observations from Findelengletscher and Unteraargletscher: transient uplift and subsidence of the glacier surface, propagating waves of high basal water pressure and velocity and the correspondence of peak uplift rates with peak velocities (Reference KambKamb and others, 1985;Reference Kamb and EngelhardtKamb and Engelhardt, 1987). A notable exception was the maximum in observed velocities and pressures, the latter exceeding the limiting pressure calculated by Reference IkenIken (1981) at which sliding was predicted to become unstable. One explanation given for this was limited hydraulic connectivity during mini-surges, such that high-pressure water was confined to patches of the bed (Reference KambKamb and others, 1985).

Hydromechanical events reminiscent of the observations on Unteraargletscher and Findelengletscher have been documented on both temperate and polythermal glaciers from Haut Glacier d’Arolla in Switzerland (e.g. Reference Mair, Willis, Fischer, Hubbard, Nienow and HubbardMair and others, 2003) to John Evans Glacier in the Canadian High Arctic (e.g. Reference Bingham, Nienow, Sharp and CoplandBingham and others, 2006). In some cases these events appear to be driven by basal water pressure as interpreted by Reference Iken and BindschadlerIken and Bindschadler (1986) (e.g. Reference Copland, Sharp and NienowCopland and others, 2003), while in others the water pressure responds to a predominantly mechanical forcing (e.g. Reference Kavanaugh and ClarkeKavanaugh and Clarke, 2001). Basal hydromechanical events can temporarily alter the force balance of the glacier (e.g. Reference Howat, Tulaczyk, Waddington and BjornssonHowat and others, 2008), highlighting the limitations of the standard sliding law where the driving stress is assumed to be balanced locally by basal drag. In several cases Reference IkenIken’s (1981) modelling results have been used specifically to explain the occurrence of peak horizontal velocities during rising water pressures (e.g. Reference NienowNienow and others, 2005). For example, Reference Blake, Fischer and ClarkeBlake and others (1994) documented diurnal peaks in sliding velocity, measured at the bed of Trapridge Glacier during rising water pressures measured in a nearby borehole. Reference Fischer and ClarkeFischer and Clarke (1997) proposed a stick-slip relaxation process to explain this, whereby elastic strain in the ice is released when rising basal water pressure causes episodic decoupling of the ice from the underlying till.

Velocity perturbations driven by basal hydrology are not confined to land-terminating glaciers (e.g. Reference MeierMeier and others, 1994). For example, Reference O’Neel, Echelmeyer and MotykaO’Neel and others (2001) found flow speed near the terminus of LeConte Glacier, Alaska, to respond to surface melt and precipitation, in addition to ocean tides. Both Columbia Glacier in Alaska (Reference Kamb, Engelhardt, Fahnestock, Humphrey, Meier and StoneKamb and others, 1994) and Hansbreen in Spitsbergen (Reference Vieli, Jania, Blatter and FunkVieli and others, 2004) exhibited velocity variations in response to surface water input as documented for many land-terminating glaciers;however, velocity correlated better with water storage than pressure in both cases.

Many glaciers such as Unteraargletscher in Switzerland (Reference Sugiyama and GudmundssonSugiyama and Gudmundsson, 2004), Storglaciaren in Sweden (e.g. Reference JanssonJansson, 1995) and Kennicott Glacier in Alaska (Reference Bartholomaus, Anderson and AndersonBartholomaus and others, 2008) exhibit behaviour similar to that documented by Reference Iken, Rothlisberger, Flotron and HaeberliIken and others (1983) and Reference Iken and BindschadlerIken and Bindschadler (1986). Some studies, however, do not find a straightforward relationship between sliding speed and basal effective pressure and yet are not inconsistent with the observations of Iken and colleagues in other respects. For example, at Bench Glacier, Reference Harper, Humphrey, Pfeffer and LazarHarper and others (2007) observed accelerated motion associated either with enhanced ice-bed separation or elevated hydraulic connectivity at the glacier bed, but unaccompanied by low effective pressures.

Reference MacGregor, Riihimaki and AndersonMacGregor and others (2005) noted that the onset of the spring acceleration event at Bench Glacier coincided with a maximum in global englacial storage and that the propagation of the event was accompanied by a pattern of uplift and subsidence not unlike that observed by Reference Iken, Rothlisberger, Flotron and HaeberliIken and others (1983). Reference AndersonAnderson and others (2004) used the ‘tilted staircase’ model of Reference IkenIken (1981) to interpret a similar GPS dataset from Bench Glacier, where the relationship between calculated bed separation and sliding speed was explained in terms of cavity growth and collapse prior to the development of a channelized drainage system (see also Reference Kessler and AndersonKessler and Anderson, 2004). Using a sliding law of the general form proposed by Reference Iken and TrufferIken and Truffer (1997), Reference AndersonAnderson and others (2004) inferred water pressures from their data that were naturally averaged over the relevant spatial scale. There is clearly a relationship between water and sliding at Bench Glacier, but one that does not lend itself easily to a functional description in terms of measured borehole water pressure.

It would be raising a false dichotomy to suggest that the work of Iken and colleagues supports a relationship between sliding and water pressure to the exclusion of storage volume. The results above only serve to reinforce the significance of the connectedness of the drainage system (e.g. Reference Iken and TrufferIken and Truffer, 1997;Reference Hanson, Hooke and GraceHanson and others, 1998), the scales of heterogeneity over which glacier processes naturally average (e.g. Reference Kamb, Engelhardt, Fahnestock, Humphrey, Meier and StoneKamb and others, 1994) and the relative influences of local vs non-local forcing (e.g. Reference Rippin, Willis, Arnold, Hodsonand and BrinkhausRippin and others, 2005).

Ice-sheet hydromechanics

The extension of the early work of Iken and colleagues to the larger scale of the ice sheets is hardly surprising, given that they exported ideas about subglacial hydromechanics from the Swiss Alps to Greenland. Their work on Jakobshavn Isbr* (Reference Iken, Echelmeyer, Harrison and FunkIken and others, 1993;Reference Funk, Echelmeyer and IkenFunk and others, 1994; Reference Luthi, Funk, Iken, Gogineni and TrufferLuthi and others, 2002) remains the only work to have documented glacier-bed conditions through direct borehole observations, which included evidence of an active subglacial drainage system. Iken and colleagues combined measurements and modelling (Reference Iken, Echelmeyer, Harrison and FunkIken and others, 1993;Reference Funk, Echelmeyer and IkenFunk and others, 1994; Reference Luthi, Funk, Iken, Gogineni and TrufferLuthi and others, 2002) to infer a thick layer of rapidly deforming temperate ice at the base of Jakobshavn Isbr*. Their findings helped explain the fast flow of the ice stream and its lack of seasonal variation (Reference Echelmeyer and HarrisonEchelmeyer and Harrison, 1990).

Since the early 2000s, there have been a number of studies documenting a distinct coupling between hydrology and dynamics particularly on land-terminating glaciers in Greenland. GPS data have revealed diurnal, weekly and seasonal variations in surface velocity along the western margin of the ice sheet that have been interpreted as responses to variable meltwater input to the bed (e.g. Reference Bartholomew, Nienow, Mair, Hubbard, King and SoleBartholomew and others, 2010). Relatively coherent weekly variability in surface velocity was found by Reference Van de WalVan de Wal and others (2008) over a 60 km stretch of the Kangerlussuaq (‘K’) transect, where the ice is 1000-1500 m thick. They related acceleration on this timescale to the rate of surface meltwater production, rather than the absolute volume of meltwater. This observation indirectly supports Reference IkenIken’s (1981) conceptual model of sliding with cavitation.

Reference Shepherd, Hubbard, Nienow, McMillan and JoughinShepherd and others (2009) documented diurnal variations in horizontal flow speed and ice-surface elevation over several days in 2007 on the land-terminating Russell Glacier in western Greenland. They associated these variations with diurnal meltwater input, while they attributed longer-term flow variations to lake drainage events. On the basis of these observations, Reference Shepherd, Hubbard, Nienow, McMillan and JoughinShepherd and others (2009) proposed that alpine glaciers may be a reasonable analogue for Greenland in a warming climate. This suggestion seems to be confirmed by Reference Bartholomew, Nienow, Mair, Hubbard, King and SoleBartholomew and others (2010) for another transect inland from the Russell Glacier terminus, where the data look much like those in Figure 2, velocity magnitudes excepted. Although some of the outlet glaciers along Greenland’s western margin exhibit strong sliding responses to meltwater input reminiscent of alpine glaciers, they also appear to behave like alpine glaciers in adjusting their drainage systems to water flux (e.g. see Reference WillisWillis, 1995, for a review). This would explain their responsiveness to meltwater variability, rather than total volume in some cases (e.g. Reference Van de WalVan de Wal and others, 2008;Reference SchoofSchoof, 2010).

In Antarctica, discovery of saturated deformable sediments beneath fast-flowing ice streams in the early 1980s (e.g. Reference Blankenship, Bentley, Rooney and AlleyBlankenship and others, 1986) led researchers to consider the influence of water pressure on basal flow processes in an environment isolated from surface meltwater. Although the hard-bedded cavity-dominated drainage systems envisaged by Iken and colleagues would seem a far cry from the deforming beds of the Siple Coast ice streams, much of this work began by considering the fundamentals of sliding theory and observations from alpine glaciers (e.g. Reference BentleyBentley, 1987; Reference AlleyAlley, 1989, Reference Alley1993;Reference Engelhardt, Humphrey, Kamb and FahnestockEngelhardt and others, 1990;Reference Harrison, Echelmeyer and EngelhardtHarrison and others, 1993;Reference Engelhardt and KambEngelhardt and Kamb, 1997). Reference IkenIken’s (1981) theoretical bound on basal shear stress surfaced in a recent study of Pine Island and Thwaites Glaciers in the mass-shedding Amundsen Sea sector of West Antarctica. Reference JoughinJoughin and others (2009) noted a consistency between this bound and properties of the plastic-bed model they used which produced the best agreement between the modelled and measured extents of acceleration and thinning above the grounding line.

Other recent Antarctic work harks back to the observations of Reference Iken, Rothlisberger, Flotron and HaeberliIken and others (1983) by attributing short-term vertical deflections of the ice surface to the movement of subglacial water. Reference Gray, Joughin, Tulaczyk, Spikes, Bindschadler and JezekGray and others (2005) first observed this in Antarctica (cf. Reference Fatland and LingleFatland and Lingle, 2002) on Kamb and Bindschadler Ice Streams using interferometric synthetic aperture radar (InSAR) data. The short-term nature of the deflections and the spatial coincidence of uplift/subsidence with subglacial hydraulic potential minima led to the interpretation of these data as reflecting transient water storage and release. Similar phenomena have since been interpreted from ice-surface deflections on other ice streams and in other regions of Antarctica, painting a highly dynamic picture of sub-ice-sheet drainage (e.g. Reference Fricker and ScambosFricker and Scambos, 2009).

The sliding law

Adaptations to the classical form of the sliding law have been made, for example, to account for tangential forces (friction) at the bed (e.g. Reference MorlandMorland, 1976b;Reference Schweizer and IkenSchweizer and Iken, 1992) and to allow for unstable sliding above a critical pressure less than the overburden (Reference Iken and TrufferIken and Truffer, 1997; Reference Truffer and IkenTruffer and Iken, 1998). Much effort has also been devoted to understanding basal motion in the presence of unconsolidated sediments (e.g. Reference AlleyAlley, 1989;Reference IversonIverson, 1999).

An important recent development in sliding theory revisited Reference IkenIken’s (1981) derivation of the ‘limiting’ or ‘critical’ pressure, which implies that basal shear stress cannot exceed a maximum value for a given effective pressure and bed geometry. Interpreted physically, cavity water pressure limits the stress that can be concentrated on the stoss faces of bed obstacles as sliding with cavitation occurs. This is significant because it invalidates the traditional form of u = Cτ ^p /N ^q as a general sliding rule. In Reference IkenIken’s (1981) original notation, p ₁ = p ₀ – τ/tan β (equation 2), where p ₁ is the limiting pressure, p ₀ the overburden pressure, τ the basal shear stress and β the maximum slope of the stoss faces of bedrock obstacles with respect to the mean bed slope (Fig. 1). Rewriting gives τ ≤ N tan β. Reference SchoofSchoof (2005) showed that this relationship, which he termed ‘Iken’s bound’, could be extended to more realistic bed geometries and incorporated into a new sliding law (see also Reference FowlerFowler, 1987). Reference Gagliardini, Cohen, Rdback and ZwingerGagliardini and others (2007) extended Reference SchoofSchoof’s (2005) work to nonlinear ice rheology and locally infinite bed slopes (i.e. bed obstacles that are perpendicular to mean bed slope) and proposed a friction law of the form ≤/N = D _χ ^1/n /(1 + αχ^m)^1/n , where χ = u/(D ⁿ N ⁿ A _s), u is sliding speed, n is Glen’s exponent and D, A _s, m and α = α(m) depend only on bed geometry if properly chosen. Although such laws are more complicated to implement than the traditional sliding relation, they are now being incorporated into numerical ice-flow models (e.g. Reference Bueler and BrownBueler and Brown, 2009;Reference Pimentel, Flowers and SchoofPimentel and others, 2010).